Insight into the reaction mechanism and chemoselectivity in the cycloaddition of ynamides and isoxazoles with H₂O

Abstract

The mechanism and chemoselectivity in the cycloaddition of ynamides and isoxazoles have been explored by the density functional theory (DFT) in model systems composed of a Brønsted acid (HNTf₂), gold(I) [IPrAuNTf₂] or platinum(II) (PtCl₂/CO) catalyst, either with or without the presence of H₂O. The DFT calculations reveal that all these catalysts entail similar nucleophilic attack of isoxazole on the catalyst-ligated ynamide forming a vinyl intermediate, which can isomerize to an α-imino intermediate upon cleavage of the isoxazole N–O bond. The completely distinct reaction pathways are observed after the formation of the α-imino intermediate. For the Brønsted acid catalyst, [5 + 2 + 1] cycloaddition with H₂O is the favorable way to generate O-bridged tetrahydro-1,4-oxazepines. If the Brønsted acid is replaced by a gold(I) catalyst, a [3 + 2] cycloaddition product is produced, either in the absence or in the presence of H₂O. Regarding the Pt(II) catalyst, 1,3-oxazepines are formed through [5 + 2] annulation. Furthermore, the [5 + 2] annulation product in this Pt(II)-catalyzed system can also be predicted upon addition of H₂O. The unique properties of the three selected catalysts were explored in detail through distortion/interaction analysis. The obtained theoretical data account for an observed disparate product formation when using three catalytic systems and provide a theoretical foundation to choose the optimal catalyst for the title reaction. These results can be of particular significance for synthetic chemists toward the design of catalytic systems and cycloaddition transformations involving ynamides, isoxazoles and related derivatives.

---

1. Introduction

Ynamides have become very important and versatile alkyne-containing building blocks in a variety of prominent synthetic transformations in natural product synthesis.¹ Given the predictable regioselectivity of ynamide transformations, their synthetic utility has attracted great attention in organic chemistry.² The unique nature of ynamides facilitates the activation of carbon–carbon triple bonds, giving them both electrophilic and nucleophilic properties due to the electron-donating ability of the nitrogen center.³ The cyclization reactions of ynamides are useful in the quick synthesis of cyclic and polycyclic structural motifs, including processes such as radical cyclization, ring-closing metathesis, and metal-mediated cyclization.^1a Hence, ynamides have flourished as robust synthons for nitrogen-containing heterocycles and nitrogen-substituted rings.

In the past decades, the metal-catalyzed reactions of ynamides with different unsaturated N- or O-containing compounds such as reactive isoxazoles⁴ have been explored, especially using gold containing catalytic systems. For instance, Liu's group has discovered that ynamides can annulate with alkenes, nitriles, azidoalkenes, and isoxazoles in the presence of a gold(I) catalyst to furnish different heterocycles.⁵ Hashmi's group has reported a series of interesting Au(I)- or Au(III)-catalyzed annulation reactions of ynamides to generate heterocyclic scaffolds in high efficiency.⁶ Ye's group has also been active in the field,⁷ including a summary on a recent progress in the gold-catalyzed synthesis of N-containing tricyclic compounds from ynamides.⁸ In particular, they have developed remarkable Au-catalyzed formal [3 + 2] cycloaddition between ynamides and isoxazoles, leading to polysubstituted 2-aminopyrroles. Besides, they have performed a simple computation to explore the annulation mechanism,^7a followed by replacement of the Au(I) catalyst by a Pt(II)-containing system.^7c However, the reactivity of the same substrates has been dramatically different from that observed under the Au catalysis, which generated formal [5 + 2] annulation and 1,3-oxazepine derivatives (Scheme 1(b-2)).^7c Simple DFT calculations indicate that [5 + 2] annulation is favorable under the Pt(II)-catalyzed conditions, while [3 + 2] cyclization occurs in the presence of an Au(I) catalyst. It should be noted that both processes have been carried out under anhydrous conditions. Recently, the compelling formal [5 + 2 + 1] cycloaddition of ynamides and isoxazoles with water catalysed by a Brønsted acid has been developed by Wan's group (Scheme 1(c-1)).⁹ According to this inspiring study,⁹ ynamides and isoxazoles would give access to O-bridged tetrahydro-1,4-oxazepines through another cyclization after the [5 + 2] annulation catalyzed by the Brønsted acid. Furthermore, the O-bridged product could never be afforded if a gold(I) catalyst was used, despite attempts to add water; only [3 + 2] cycloaddition derivatives have been generated (Scheme 1(c-2)). Based on these very captivating experimental data, Wan and Ye have also proposed a mechanism with several pathways (Scheme 2).

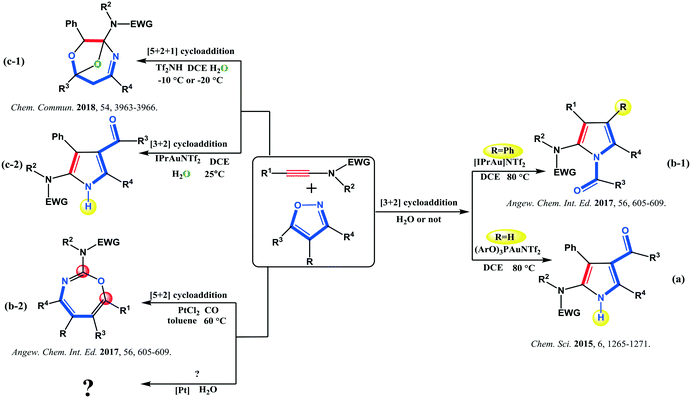Scheme 1 Different selective cycloaddition pathways between ynamides and isoxazoles catalysed by the three distinct catalytic systems according to studies by the groups of Wan⁹ and Ye.⁷

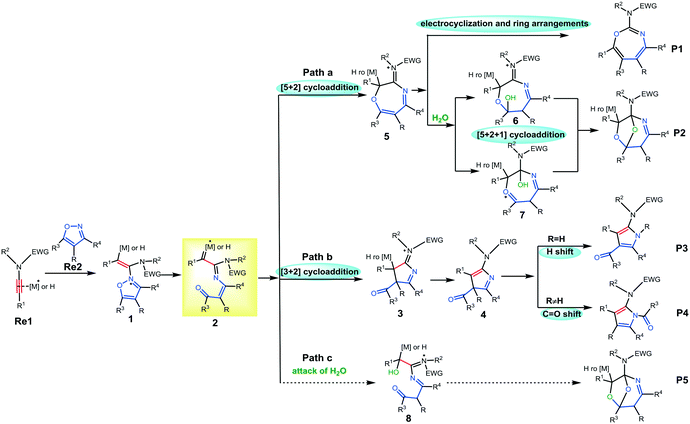Scheme 2 Proposed mechanism for selective cycloaddition between ynamides and isoxazoles (paths a, b, and c).

Initially, the Brønsted acid or the metal would react with ynamide, most likely involving a nucleophilic attack by the N atom of isoxazole to induce the formation of intermediate 1. After that, the cleavage of the isoxazole N–O bond leads to α-imino intermediate 2 due to the catalyst effect (Scheme 2). After the formation of 2, there are at least three feasible pathways to generate final products from ynamides and isoxazoles in the presence of water and using different catalytic systems. For path a, the intramolecular [5 + 2] cycloaddition of 2 furnishes seven-membered heterocycle 5. Subsequently, the electrocyclization and ring rearrangement of 5 would generate final product P1. Alternatively, the addition of H₂O to seven-membered heterocycle 5 and subsequent acid-catalyzed ketalization or acid-catalyzed O,O-acetal formation afford O-bridged tetrahydron-1,4-oxazepine P2. Apart from the [5 + 2] cycloaddition, the [3 + 2] cycloaddition between the acyl substituted carbon and α-C atom would also take place to generate pyridine derivative P3 or P4 (path b). For path c, the addition of water followed by the rupture of the N–O bond prior to the [5 + 2] cycloaddition would also produce the [5 + 2 + 1] cycloaddition product, O-bridged tetrahydron-1,4-oxazepine. In Ye's work, plausible mechanisms to rationalize the formation of pyrrole (Au-catalyzed) or oxazepane (Pt-catalyzed) derivatives have been reported, using experimental data and theoretical calculations.^7a,c However, some key issues in the catalytic activity and selectivity for the three pathways with the three catalysts still remain open with a number of interesting questions that can be made. For example: (1) the mechanism of this reaction catalyzed by the Brønsted acid has not been evaluated. How does the Brønsted acid affect the reaction? (2) The detailed mechanism to support the O-bridged 1,4-oxazepine derivative in the presence of water has not been found. What can be the effect of the three different catalysts? (3) Which is the favorable pathway for each catalyst when water is added? (4) What is the role of water in the reaction process and how this role can be rationalized?

With an aim to address all these questions and obtain an additional insight into this type of intriguing organic transformations, we have performed exhaustive DFT calculations. The principal objective of this study was to investigate and rationalize the experimentally observed and unique selectivity in the presence of different catalysts, either in the absence or in the presence of water. We thus believe that this study will allow a deep understanding of the reaction mechanisms, answer the above-mentioned questions, and supply valuable information toward catalyst design in this type of important cycloaddition reaction between ynamides and isoxazoles.

2. Computational details

All the calculations were performed with the Gaussian 09 program package.¹⁰ Geometry optimization for all species was carried out on the basis of density functional theory (DFT)¹¹ using the M06-2X¹² hybrid functional; this approach was commonly applied in recent mechanistic studies on Brønsted acid and metal-catalyzed organic transformations.¹³ The 6-31G(d,p) basis set was employed for main-group atoms and the Lanl2dz¹⁴ basis set with an additional f-polarization function (exponents of 1.05 and 0.993)¹⁵ in dichloroethane was used for Au and Pt, respectively (BSI). Harmonic vibrational frequency calculations at the M06-2X/6-31G (d,p)/Lanl2dz(f) level were performed and the nature of all stationary points was confirmed by the number of imaginary frequencies as the minima (number of imaginary frequency, NIMAG = 0) or transition states (NIMAG = 1). Intrinsic reaction coordinate (IRC)¹⁶ analysis was conducted to inspect the relationship of transition states with their forward and reverse minima. The modification of the relative energies to the vibrational zero-point energies (ZPE, not scaled) was performed. The effect of solvent was taken into consideration using the M06-2X/6-311++G (d,p) basis set. For Au and Pt, small core Los Alamos (LANL2TZ(f)) pseudopotentials and basis sets (including Dunning–Huzinaga full TZ and Los Alamos ECPS plus TZ) were adopted with an additional f-polarization function (BSII);¹⁷ an integral equation formalism polarizable continuum model (IEF-PCM) with dichloroethane (ε = 10.4) was used for single-point calculations. Non-electrostatic relations and radii were obtained using a general solvation model (SMD).¹⁸ Unless stated otherwise, the relative free energies discussed in this study were calculated in solution (ΔG_sol) at the M06-2X/SMD/6-311++G (d,p)//M06-2X/6-31G (d,p) (Lanl2dz) level; these were obtained by adding the solvation corrections to the computed gas-phase relative free energies (ΔG₂₉₈). The 3D molecular structures were drawn with the CYL-view.¹⁹

3. Results and discussion

3.1. Brønsted acid-catalyzed reaction (series A)

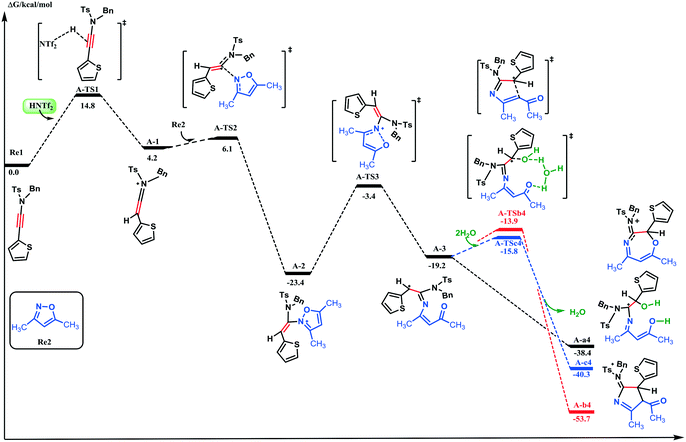
In our calculations, N-benzyl-4-methyl-N-(thiophen-2-ylethynyl)benzenesulfonamide Re1 and 3,5-dimethylisoxazole Re2 were selected as the model substrates based on the report by Wan and co-workers.⁹ The energy profiles for the HNTf₂-catalyzed reactions are shown in Fig. 1 and 2, while the main structures are represented in Fig. 3. For the first step of series A, ynamide Re1 is protonated by HNTf₂ on the C≡C bond to generate slightly unstable keteniminium intermediate A-1 requiring only an energy of 14.8 kcal mol⁻¹. Subsequently, the N site of Re2 would quickly attack A-1 on the α-carbon atom (requiring an energy of 1.9 kcal mol⁻¹) and yield stable adduct A-2; the energy barrier is −23.4 kcal mol⁻¹ relative to the substrate. Once A-2 is generated, it would undergo further ring fragmentation through the cleavage of the N–O bond (shown as A-TS3) to yield carbocation A-3; the activation energy for this step is 20.0 kcal mol⁻¹.

Fig. 1 Free energy profile for the competing pathways to generate [5 + 2] & [3 + 2] cycloaddition intermediates for series A (HNTf₂-catalyzed). The values are given in kcal mol⁻¹.

Fig. 2 Free energy profiles for the competing pathways to oxygen-bridged tetrahydro-1,4-oxazepines in series A (HNTf₂-catalyzed). The values are given in kcal mol⁻¹.

Fig. 3 Optimized structures of selected intermediates and transition states in series A. For clarity, all benzyl (∼Bn) and tosyl (∼Ts) functionalities are displayed by the green and rose balls, respectively. The bond distances are given in angstrom (Å).

After that, three alternative paths are possible to explain the experimentally observed results. For path a, the attack between the O atom and the C¹ site of carbocation A-3 would furnish seven-membered heterocycle A-a4. It should be noted that there is no transition state between A-3 and A-a4 based on our PES (potential energy surface) scan calculations (Fig. S1, ESI†). There is also another option wherein the α-carbon of the carbonyl group would attack carbocation A-3 to form five-membered aminopyrrole A-b4 with an activation energy of 5.3 kcal mol⁻¹ (path b). Alternatively, the reaction between water and A-3 would give intermediate A-c4 through A-TSc4 (path c). This step requires an activation energy of 3.4 kcal mol⁻¹, whereas the free energy for A-c4 formation is −21.1 kcal mol⁻¹ with respect to A-3. Comparison of the three pathways suggests that path a is energetically more favorable than paths b and c. On the basis of the experimental observations and the ¹⁸O-labeling experiment of Wan and co-workers, the HNTf₂-catalyzed formal [5 + 2 + 1] cycloaddition of ynamides and isoxazoles with water provides an atom-efficient access to O-bridged tetrahydro-1,4-oxazepines, wherein the bridging oxygen atom originates from water thus supporting path a. Our calculation results are fully consistent with the experimental data. A more favorable character of path a over b can be attributed to the following reasons. First, the C¹–O bond distance (2.183 Å) is smaller than that of C¹–C⁴ (3.266 Å); hence, it is more difficult for the C⁴ site to attack the C¹ atom than the O atom (Fig. 3). Secondly, compared with A-3, the C⁴–C³–C¹–C² dihedral angle of intermediate A-a4 is −46.5°, which is only rotating 58.3°. The C⁴–C³–C¹–C² dihedral angle of intermediate A-c4 is −10.2°, which indicates that the formation of A-c4 demands more energy to rotate than in the case of A-a4. From the above, path a is the favorable way to generate the seven-membered heterocycle under the catalysis by HNTf₂.

Subsequently, the following discussion will be based on A-a4, while the less plausible processes in paths b and c are described in the ESI† (Fig. S2 and S3). At the beginning, the NTf₂⁻ counteranion coming from the catalyst (HNTf₂) can assist in the proton migration from thienyl substituted carbon to regenerate the catalyst through A-TSa5-C; this transformation requires an activation energy of 22.3 kcal mol⁻¹. Then, an intramolecular ring rearrangement through three transition states A-TSa6-C, A-TSa7-C, and A-TSa8-C would consume elusive activation energy that reaches 22.9 kcal mol⁻¹. From the above discussion, the formation of a plausible A-P1 product is apparently difficult to occur under the experimental conditions, requiring an activation energy of 26.3 kcal mol⁻¹ (the barrier between A-TSa7-C and A-a4). As for the experimental product A-P2, there are two alternative paths wherein H₂O adds to the iminium ion (C²) or the acyl group (C⁵). The addition of H₂O to the acyl group (C⁵) is shown as the black potential energy surface in Fig. 2. Analysis of this figure indicates that the OH group of water attacks the C⁵ site through transition state A-TSa5-B, consuming an energy of 10.1 kcal mol⁻¹ to support the neutral intermediate A-a5-B and a hydrated proton. Then, the hydrated proton would add to the β-carbon (C⁵) consuming an energy of 13.0 kcal mol⁻¹, yielding seven-membered heterocycle carbocation A-a6-B. The intramolecular cyclization between the hydroxyl oxygen and carbocation would absorb an energy of 8.3 kcal mol⁻¹ to form the bridge ring, while the hydroxyl proton migrates from the hydroxyl group to H₂O at the same time. In contrast, the activation energy for the addition of H₂O to the iminium ion (C²) at the beginning of the transformation is higher than that of the water hydroxyl attack to the C⁵ site. H₂O would attack the C⁵ site preferably than the C² one, which can be explained by the following reasons. First, the NBO charge of C⁵ is 0.573 a.u., which is more positive than that of C² (0.531 a.u.). The NBO charge of the C² site in A-TSa5-A is slightly negative than the charge of the C⁵ atom in A-TSa5-B. Also, the charge of the O¹ site in A-TSa5-B is more negative than that in A-TSa5-A. In addition, we can also find that the C²–O¹ and C⁴–O¹ bond distances in A-TSa5-A and A-TSa5-B are 1.864 and 1.932 Å, respectively. These data indicate that the attack of H₂O to the C² site has more steric hindrance than to the C⁴ atom, which is also supported by our calculation results.

3.2. Gold(I)-catalyzed reaction (series B)

Next, a popular gold(I) complex [IPrAuNTf₂] was selected as a model catalyst (series B) to explore the chemoselectivity in the annulation of isoxazoles and ynamides. Fig. 4 and 5 schematically show the energy profiles for series B, while the selected optimized geometries for key intermediates and transition structures are shown in Fig. 6. The first step for series B would involve the formation of iminovinyl gold intermediate B-1. The nucleophilic attack of isoxazole Re2 to the iminovinyl functionality at the β-carbon results in vinyl gold intermediate B-2; it has a moderate energy barrier (12.0 kcal mol⁻¹) that is slightly higher than that in series A. Similar to series A, gold carbene intermediate B-3 would isomerize from the vinyl gold B-2 precursor upon cleaving the isoxalic N–O bond; this step requires an activation energy of 17.7 kcal mol⁻¹. Subsequently, the selectivity of the [5 + 2] and [3 + 2] annulation was explored.

Fig. 4 Free energy profiles for the competing pathways to generate [5 + 2] & [3 + 2] cycloaddition intermediates in series B ([IPrAuNTf₂]-catalyzed). The values are given in kcal mol⁻¹.

Fig. 5 Free energy profiles for the competing pathways of the 1,3-H-shift or 1,3-acyl-shift in series B ([IPrAuNTf₂]-catalyzed). The values are given in kcal mol⁻¹.

Fig. 6 Optimized structures of selected intermediates and transition states in series B. For clarity, all benzyl (∼Bn) and tosyl (∼Ts) functionalities are displayed by the green and rose balls, respectively. The bond distances are given in angstrom (Å).

DFT calculations show that the intramolecular [3 + 2] cyclization readily occurs to afford pyrrole intermediate B-b4 (B-TSb4), which overcomes a lower energy barrier (4.8 kcal mol⁻¹) than the one in the [5 + 2] cyclization (B-TSa4). These calculation results are not only consistent with the experimental reports of Wan and co-workers,⁹ but also with the experimental and computational data of Ye et al.⁷ Contrary to series A, the C¹–O bond in B-TSa4 (2.114 Å) is shorter than the C¹–C⁴ bond in B-TSb4, while the C⁴–C³–C²–C¹ dihedral angle of the former is larger than that of the latter; this means that the [5 + 2] cycloaddition is an unfavorable pathway. The antipodal calculation result of the selectivity between the gold(I)- and Brønsted acid-catalyzed processes provides a strong theoretical support for the experimental data. Namely, the [3 + 2] cycloaddition product is formed under the conditions of gold(I) catalysis, while the [5 + 2] cycloaddition product is generated in the Brønsted acid-catalyzed reaction. Compared with Ye's work, a possibility of water addition was also calculated in our study. However, a high barrier of this process makes it hardly possible.

Thus, the sequential processes based on B-a4 to generate the [5 + 2] and [5 + 2 + 1] cycloaddition products are described in the ESI† (Fig. S4 and S5). Next, the formation of the final B-P3 and B-P4 products through the 1,3-H-shift and 1,3-acyl-shift was studied. In the absence of water, the acyl would migrate from the C⁴ to C³ site through B-TSb5-B to yield 1,2-acyl-shift intermediate B-b6-B (this requires 20.7 kcal mol⁻¹ energy). Then, 2,3-acyl migration would require to overcome an activation energy barrier of 24.4 kcal mol⁻¹ to finalize the total reaction and form B-P3. There is also another possible pathway wherein the 1,3-H-shift occurs through two steps to furnish B-P4, the activation energies of which are 6.6 and 8.0 kcal mol⁻¹ higher than the two-step 1,3-acyl-shift. Comparison of the above two pathways suggests that the favorable product would be B-P3 rather than B-P4, which is inconsistent with the experimental result. Considering the presence of water in the system, we employed two H₂O molecules to assist the H-shift in one step. To our satisfaction, the activation free energy of the 1,3-H-shift decreases from 32.5 to 11.5 kcal mol⁻¹ through B-TSa5-A. The calculation results show that the presence of trace amounts of water has a very important acceleration effect on proton migration. Hence, an experimentally observed chemoselectivity can be rationalized for the formation of a kinetic product. Taking the panoramic view of all the three pathways into account, path a-A is the most favourable way to obtain the final product B-P4. Hence, the calculation results well rationalize the experimental data and the proposed mechanism.

3.3. Platinum(II)-catalyzed reaction (series C)

In this part, the third catalytic system, PtCl₂/CO (series C), was chosen to study the chemoselectivity of the Pt(II) catalyst in the cycloaddition of ynamides and isoxazoles. The free energy profiles for series C are shown in Fig. 7, while Fig. 8 shows the key structures. Carbene intermediate C-3 undergoes intramolecular [5 + 2] cyclization through C-TSa4 almost with no energy barrier (0.3 kcal mol⁻¹) to produce relatively stable intermediate C-a4 (Fig. 7). However, the activation free energy of the [3 + 2] cyclization through C-TSb4 is 5.5 kcal mol⁻¹. The specific chemoselectivity can also be explained by the change of the dihedral angle. It is obvious that the C⁴–C³–C²–C¹ dihedral angle in C-TSa4 (52.7°) is closer to that in intermediate C-3 (62.6°) rather than in C-TSb4 (37.9°) (Fig. 8). These dihedral angles reveal that C-TSa4 exhibits a more reactant-like character, thus having a lower activation barrier according to the Hammond postulate.²⁰ Then, another molecule of Re1 will combine with the catalyst, forming a more stable intermediate A-a5-C; this transformation is exothermic with a free energy of −19.6 kcal mol⁻¹ with respect to C-3. Next, the ring rearrangement experiences ring closure, cycloisomerization, and ring opening through A-TSa6-C, A-TSa7-C, and A-TSa8-C with activation energies of 7.1, 19.7, and 4.1 kcal mol⁻¹, respectively.

Fig. 7 Free energy profiles for the competing pathways in series C (PtCl₂/CO-catalyzed). The values are given in kcal mol⁻¹.

Fig. 8 Optimized structures of selected intermediates and transition states for series C. For clarity, all benzyl (∼Bn) and tosyl (~Ts) functionalities are displayed by the green and rose balls, respectively. The bond distances are given in angstrom (Å).

One of the differences between ours and Ye's work is that we predicted the [5 + 2 + 1] bridge cycloaddition product by DFT calculations. Like in series A, the addition of water OH group to the C⁵ site of the seven-membered heterocycle is more favorable than to the C² atom, with an activation free energy of 13.7 kcal mol⁻¹. Then, the hydrated proton attacks the C⁴ site to yield C-a6-B. The activation energy of this process is the rate-determining barrier (18.5 kcal mol⁻¹). Finally, the nucleophilic attack of the hydroxyl group to the C² site furnishes O-bridged tetrahydro-1,4-oxazepine product C-P2. However, the analysis of the total potential energy surface manifests that ynamides react with isoxazoles only to obtain the [5 + 2] cycloaddition products rather than the [5 + 2 + 1] bridge cycloaddition products. The calculation results thus predict that the [5 + 2] cycloaddition can occur whether water is added or not.

3.4. Origin of the chemoselectivity of the three catalytic systems

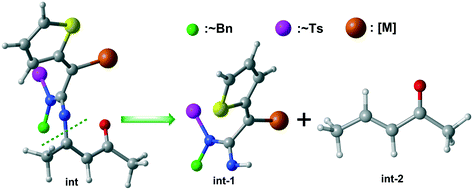
To rationalize the unique chemoselectivity of the three diverse catalytic systems that were computationally studied in the present work, distortion/interaction analysis was employed.²¹ The preliminary intermediate int was separated into two segments, int-1 and int-2, and the eliminated portion was replaced by a proton (Table 1). The calculation results for the [5 + 2] cycloaddition show that the ΔE_int values for B-TSa4 and C-TSa4 are equal (−29.9 kcal mol⁻¹). This suggests that ΔE_int has insignificant contribution to chemoselectivity. However, the ΔE_dist values for B-TSa4 and C-TSa4 are 37.3 and 35.3 kcal mol⁻¹, respectively. These results indicate that a larger catalyst structure would lead to higher contribution of the deformation effect and superior activation energy.

Table 1 Distortion/interaction analysis for the [5 + 2] & [3 + 2] cycloaddition between ynamides and isoxazoles catalyzed by Au(I) and Pt-containing systems^a

Transition state	ΔE^‡^b	ΔEdist-1^c	ΔEdist-2^d	ΔEdist^e	ΔEint^f
a The values are given in kcal mol^−1. b ΔE^‡, the activation energy. c ΔEdist-1, the distortion energy of TS-1. d ΔEdist-2, the distortion energy of TS-2, e ΔEdist = ΔEdist-1 + ΔEdist-2, the total distortion energy. f ΔEint = ΔE^‡ − ΔEdist, the interaction energy.
B-TSa4	7.5	25.0	12.4	37.3	−29.9
C-TSa4	5.4	24.3	11.0	35.3	−29.9
A-TSb4	2.3	14.6	15.1	29.7	−26.7
B-TSb4	5.9	15.3	20.4	35.7	−29.9
C-TSb4	11.0	19.8	23.2	42.9	−31.9

---

In series A, a proton acts as a catalytically active species representing the smallest catalyst structure. There is no doubt that the minimum activation energy should be observed in series A. In fact, our calculations also show that this step of series A is a barrier-free process. For the [3 + 2] cycloaddition, the ΔE_int values for A-TSb4, B-TSb4, and C-TSb4 are −26.7, −29.9, and −31.9 kcal mol⁻¹, respectively, while the corresponding ΔE_dist values are 25.7, 35.7, and 42.9 kcal mol⁻¹. The obtained results clearly indicate that for series B, the distortion of the [3 + 2] ring formation is significantly smaller than that of [5 + 2], while in series C, the opposite trend is observed. Hence, the difference in distortion energy determines the chemoselectivity. This is also consistent with the results obtained by analyzing the distortion effect of dihedral angles.

4. Conclusions

In summary, the reaction mechanism and chemoselectivity in the cycloaddition of ynamides and isoxazoles catalysed by the Brønsted acid, Au(I) and Pt-based systems, either with or without H₂O, were investigated in detail by DFT calculations. Different chemoselectivities in the presence of the three distinct catalytic systems were explored and mechanistically rationalized. The obtained calculation results can draw several conclusions as indicated below.

1) The calculations demonstrate that the ynamide protonated by the Brønsted acid is attacked by isoxazole and then undergoes intramolecular N–O bond breakage and subsequent H₂O-assisted [5 + 2 + 1] cycloaddition to generate O-bridged tetrahydro-1,4-oxazepine. [5 + 2] cycloaddition would happen if the reaction environment is anhydrous.

2) The [3 + 2] cycloaddition of ynamides and isoxazoles is the favorable path when the substrates react in the presence of the gold(I) catalyst, whether water is present or not.

3) Although the Pt(II)-catalyzed reaction in the presence of water has not been explored experimentally, the DFT calculations illustrate that the [5 + 2] cycloaddition product would be the only outcome either with or without water in the system.

4) Comparison of the three different catalytic systems was performed. A strongly Lewis acidic Au(I)-based catalyst facilitates the [3 + 2] cycloaddition. The Pt-based catalyst that features a more Brønsted acid-like character would trigger the [5 + 2] cycloaddition reaction, which is similar to the Brønsted acid-catalyzed system (HNTf₂). The addition of water to yield the bridged ring compounds is only catalyzed by the Brønsted acid. The chemoselectivity of the three different catalysts was well rationalized by the analysis of dihedral angles and distortion/interaction analysis.

In summary, this study provided us with a deep understanding of the cycloaddition reaction between ynamides and isoxazoles and offered precious information toward the future design of efficient and chemoselective catalytic systems in this type of important organic transformation. The work also highlighted the significance of water as a selectivity-guiding component of such transformation. We believe that the obtained results would be of particular importance for synthetic chemists when selecting an appropriate catalytic system in various cycloaddition reactions involving ynamides, isoxazoles or related derivatives.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been supported by the National Natural Science Foundation of China (No. 21672090 and 21301080). AMK acknowledges the FCT (UID/QUI/00100/2019) and the RUDN University (the publication has been prepared with the support of the RUDN University Program 5-100).

Notes and references

1. For important recent reviews on ynamides, see: (a) X.-N. Wang, H.-S. Yeom, L.-C. Fang, S. He, Z.-X. Ma, B. L. Kedrowski and R. P. Hsung, Acc. Chem. Res., 2013, 47, 560–578; (b) K. A. DeKorver, H. Li, A. G. Lohse, R. Hayashi, Z. Lu, Y. Zhang and R. P. Hsung, Chem. Rev., 2010, 110, 5064–5106; (c) S. Nayak, B. Prabagar and A. K. Sahoo, Org. Biomol. Chem., 2016, 14, 803–807; (d) B. Zhou, T.-D. Tan, X.-Q. Zhu, M. Shang and L.-W. Ye, ACS Catal., 2019, 9, 6393–6406; (e) G. Evano, C. Theunissen and M. Lecomte, Aldrichimica Acta, 2015, 48, 59–70; (f) X.-N. Wang, H.-S. Yeom, L.-C. Fang, S. He, Z.-X. Ma, B. L. Kedrowski and R. P. Hsung, Acc. Chem. Res., 2014, 47, 560–578.
2. (a) X. L. Han, X. G. Liu, E. Lin, Y. Chen, Z. Chen, H. Wang and Q. Li, Chem. Commun., 2018, 54, 11562–11565; (b) R. L. Sahani and R. S. Liu, Angew. Chem., Int. Ed., 2017, 56, 12736–12740; (c) W. Xu, G. Wang, N. Sun and Y. Liu, Org. Lett., 2017, 19, 3307–3310; (d) W. Xu, J. Zhao, X. Li and Y. Liu, J. Org. Chem., 2018, 83, 15470–15485; (e) Y. Zhao, Y. Hu, C. Wang, X. Li and B. Wan, J. Org. Chem., 2017, 82, 3935–3942.
3. (a) M. Lecomte and G. Evano, Angew. Chem., Int. Ed., 2016, 55, 4547–4551; (b) G. Evano, A. Coste and K. Jouvin, Angew. Chem., Int. Ed., 2010, 49, 2840–2859.
4. (a) E. Aguilar and J. Santamaría, Org. Chem. Front., 2019, 6, 1513–1540; (b) L. Li, T. D. Tan, Y. Q. Zhang, X. Liu and L. W. Ye, Org. Biomol. Chem., 2017, 15, 8483–8492; (c) F. Hu and M. Szostak, Adv. Synth. Catal., 2015, 357, 2583–2614.
5. (a) S. K. Pawar, R. L. Sahani and R. S. Liu, Chem. – Eur. J., 2015, 21, 10843–10850; (b) S. K. Pawar, D. Vasu and R.-S. Liu, Adv. Synth. Catal., 2014, 356, 2411–2416; (c) S. S. Giri, L.-H. Lin, P. D. Jadhav and R.-S. Liu, Adv. Synth. Catal., 2017, 359, 590–596; (d) S. S. Giri, L.-H. Lin and R.-S. Liu, Adv. Synth. Catal., 2017, 359, 3311–3318; (e) S. S. Giri and R. S. Liu, Chem. Sci., 2018, 9, 2991–2995; (f) P. D. Jadhav, X. Lu and R.-S. Liu, ACS Catal., 2018, 8, 9697–9701; (g) Y. C. Hsu, S. A. Hsieh and R. S. Liu, Chem. – Eur. J., 2019, 25, 5288–5297; (h) R. B. Dateer, B. S. Shaibu and R. S. Liu, Angew. Chem., Int. Ed., 2012, 51, 113–117; (i) S. N. Karad and R. S. Liu, Angew. Chem., Int. Ed., 2014, 53, 9072–9076; (j) Y. L. Chen, P. Sharma and R. S. Liu, Chem. Commun., 2016, 52, 3187–3190.
6. (a) Z. Zeng, H. Jin, J. Xie, B. Tian, M. Rudolph, F. Rominger and A. S. K. Hashmi, Org. Lett., 2017, 19, 1020–1023; (b) Y. Tokimizu, M. Wieteck, M. Rudolph, S. Oishi, N. Fujii, A. S. K. Hashmi and H. Ohno, Org. Lett., 2015, 17, 604–607; (c) X. Tian, L. Song, C. Han, C. Zhang, Y. Wu, M. Rudolph, F. Rominger and A. S. K. Hashmi, Org. Lett., 2019, 21, 2937–2940; (d) X. Zhao, X. Song, H. Jin, Z. Zeng, Q. Wang, M. Rudolph, F. Rominger and A. S. K. Hashmi, Adv. Synth. Catal., 2018, 360, 2720–2726; (e) Z. Zeng, H. Jin, X. Song, Q. Wang, M. Rudolph, F. Rominger and A. S. K. Hashmi, Chem. Commun., 2017, 53, 4304–4307; (f) X. Tian, L. Song, M. Rudolph, Q. Wang, X. Song, F. Rominger and A. S. K. Hashmi, Org. Lett., 2019, 21, 1598–1601; (g) X. Tian, L. Song, M. Rudolph, F. Rominger and A. S. K. Hashmi, Org. Lett., 2019, 21, 4327–4330.
7. (a) A. H. Zhou, Q. He, C. Shu, Y. F. Yu, S. Liu, T. Zhao, W. Zhang, X. Lu and L. W. Ye, Chem. Sci., 2015, 6, 1265–1271; (b) C. Shu, Y. H. Wang, B. Zhou, X. L. Li, Y. F. Ping, X. Lu and L. W. Ye, J. Am. Chem. Soc., 2015, 137, 9567–9570; (c) W. B. Shen, X. Y. Xiao, Q. Sun, B. Zhou, X. Q. Zhu, J. Z. Yan, X. Lu and L. W. Ye, Angew. Chem., Int. Ed., 2017, 56, 605–609.
8. F. Pan, C. Shu and L. W. Ye, Org. Biomol. Chem., 2016, 14, 9456–9465.
9. Y. Zhao, C. Wang, Y. Hu and B. Wan, Chem. Commun., 2018, 54, 3963–3966.
10. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford CT, 2013.
11. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377; (b) C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (c) B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
12. (a) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167; (b) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241; (c) Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 324–333; (d) Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382; (e) Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130.
13. (a) L. Zhou, Y. Zhang, R. Fang and L. Yang, ACS Omega, 2018, 3, 9339–9347; (b) R. Fang, L. Zhou, P.-C. Tu, A. M. Kirillov and L. Yang, Organometallics, 2018, 37, 1927–1936; (c) Y. Li, A. M. Kirillov, R. Fang and L. Yang, Organometallics, 2017, 36, 1164–1172; (d) R. Fang, L. Zhou, P.-C. Tu and L. Yang, Catal. Sci. Technol., 2018, 8, 2441–2448; (e) Y. Li, P.-C. Tu, L. Zhou, A. M. Kirillov, R. Fang and L. Yang, Organometallics, 2018, 37, 261–270; (f) R. Fang, X. Wei and L. Yang, Org. Biomol. Chem., 2014, 12, 8433–8441.
14. (a) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
15. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114.
16. (a) K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368; (c) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
17. L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031.
18. (a) Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095–1099; (b) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396; (c) D. Jacquemin, E. A. Perpète, I. Ciofini, C. Adamo, R. Valero, Y. Zhao and D. Truhlar, J. Chem. Theory Comput., 2010, 6, 2071–2085; (d) R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
19. C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, Sherbrooke, Quebec, Canada, 2009, www.cylview.org.
20. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.
21. (a) K. Morokuma, J. Chem. Phys., 1971, 55, 1236; (b) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1; (c) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646.

---

Footnote

† Electronic supplementary information (ESI) available: Additional calculated energy profiles and optimized Cartesian coordinates with the self-consistent field (SCF) energies and the imaginary frequencies of transition states, as described in the text (PDF). See DOI: 10.1039/c9cy01964b

---