Cu carbonyls enhance the performance of Ru-based SILP water–gas shift catalysts: a combined in situ DRIFTS and DFT study

Abstract

Ru-based supported ionic liquid phase (SILP) catalysts efficiently promote the water–gas shift reaction (WGSR). The addition of CuCl further improves the performance. This is attributed to the formation of labile Cu carbonyl species, which act as CO shuttles in the ionic liquid (IL) phase. We apply in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) to monitor the formation of these Cu carbonyls in an imidazolium-based SILP system. To aid the identification of the relevant Cu carbonyls, we perform density functional theory (DFT) calculations. In the present study, we investigate [Ru(CO)₃Cl₂]₂/CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ and CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ with various CuCl : IL ratios. The relevant Cu carbonyls are identified as neutral CuCl monomers and dimers, as well as monoanionic monomers and dimers. Moreover, we demonstrate that the ratio of the individual Cu carbonyl species depends on the CuCl : IL ratio.

---

1. Introduction

The water–gas shift reaction (WGSR) is used in a large number of technical applications. Prominent examples are ammonia synthesis and the production of high purity H₂, where the purpose is to reduce the amount of CO and to increase the amount of H₂ produced.^1–3 The WGSR is the mildly exothermic (≃41 kJ mol⁻¹), reversible conversion of H₂O and CO into CO₂ and H₂.^3,4 The most prominent catalysts applied at intermediate temperatures (∼300–450 °C) are based on supported Fe oxides. Catalysts based on supported Cu oxides are usually employed in the WGSR at lower temperatures (∼200–250 °C).^3–5 Moreover, the application of supported metals such as Au,⁶ Pt,⁷ or Ru⁵ was also reported in the literature. Due to the exothermic nature of the WGSR, it is desirable to shift the reaction conditions to even lower temperatures to obtain a product gas with maximum H₂ and minimal CO contents.

A decade ago, Ru-based supported ionic liquid phase (SILP) systems were shown to catalyze the WGSR at ultra-low temperatures (<200 °C) and under ambient conditions.⁸ Werner et al. demonstrated improved catalytic activity of a RuCl₃ precursor dissolved in the ionic liquid (IL) 1-butyl-2,3-dimethylimidazolium trifluoromethane sulfonate ([C₄C₁C₁Im][OTf]) supported on silica as compared to that of a commercial Cu-based catalyst.⁸ However, this improvement was observed only after an induction period (∼80 h). The induction period was attributed to the formation of active Ru chloro carbonyl species during the first stages of the reaction.⁹ Indeed, the system immediately reached full catalytic activity by using [Ru(CO)₃Cl₂]₂ as an active complex in the SILP. Thus, Werner et al. concluded that the active species is based on a Ru chloro carbonyl.¹⁰

In a follow-up study, Ru carbonyls formed from a [Ru(CO)₃Cl₂]₂ precursor in a 1-butyl-2,3-dimethylimidazolium chloride ([C₄C₁C₁Im]Cl)-based SILP catalyst were investigated by in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS). Bauer et al. assigned different Ru carbonyls by comparison with spectra calculated from density functional theory (DFT). Additionally, they demonstrated that an equilibrium of different carbonyl–chloro–ruthenium species is present in the IL.¹¹ Under realistic reaction conditions, the equilibrium was found to be dominated by a monomeric [Ru(CO)₃Cl₃]⁻ species. A reaction mechanism was suggested based on this species for this very efficient WGSR catalyst.¹²

Recently, we showed that the performance of the [Ru(CO)₃Cl₂]₂ SILP system can be further improved with metal chloride additives.¹³ The screening of different additives showed that the highest enhancement of the catalytic activity was achieved with CuCl. This was attributed to the higher availability of CO in the IL phase caused by the transfer of CO to the active Ru-species via a Cu-carbonyl acting as a ‘CO shuttle’. The presence of different [Cu_xCl_y]^z species in ILs,^14–19 as well as their capability to bind CO, was reported previously.^15,18 Indeed, we were able to prove the formation of several Cu carbonyls from chlorocuprates by the use of in situ DRIFTS and DFT calculations in our recent work.¹³

We expect that the formation of a certain Cu carbonyl species from [Cu_xCl_y]^z will depend on the amount of Cl⁻ in the SILP system. In the present work, we focus on the effect of varying the CuCl : IL ratio and the corresponding changes in activity. In particular, we aim to understand the role and the nature of Cu carbonyl complexes in different SILP environments. To this end, we initially compare the catalytic activity of [Ru(CO)₃Cl₂]₂/CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ samples (CuCl : IL = 0.2, 0.5, 1.2 and a CuCl-free benchmark) during the WGSR. In the in situ DRIFTS experiments, the corresponding Ru-free samples were investigated under a CO atmosphere, as the presence of carbonyl–chloro–ruthenium complexes leads to broad vibrational features. These may cover the peaks originating from the Cu carbonyls. Furthermore, a specific data treatment procedure was applied to subtract the CO gas phase signals from the IR spectra and reveal the carbonyl peaks of the CO-containing complexes. The carbonyl bands were assigned with the help of IR spectra obtained from DFT. The combination of our experimental and theoretical investigations allows us to identify neutral Cu carbonyl monomers and dimers, as well as monoanionic Cu carbonyl monomers and dimers in [C₄C₁C₁Im]Cl and to connect the presence of these complexes with the changes in catalytic performance.

2. Sample preparation and experimental methods

2.1 Preparation of the SILP systems under investigation

The SILP systems were prepared in a standard Schlenk flask under an argon atmosphere at ambient pressure and room temperature. In the first step, [C₄C₁C₁Im]Cl (Merck KGaA, LOT: 99/818) was dissolved in dichloromethane (DCM; Sigma-Aldrich, LOT: SZBG073AV) and stirred for 10–15 min. For Ru-based SILP catalysts, the Ru precursor complex [Ru(CO)₂Cl₃]₂ (Alfa Aesar, LOT: X06C034) was added to the mixture dissolved in DCM and stirred until full dissolution (approx. 10–15 min). For all Ru-free samples, this step was skipped.

In the case of CuCl addition, CuCl (Merck KGaA: CuCl, LOT: A999739833, ≥97.0%) was added with an additional 10 mL of DCM and the resulting mixture was stirred for 60–90 min. In the next step, alumina (γ-Al₂O₃, Sasol Germany GmbH, LOT: B39598) was added as a support material to the mixture and the suspension was stirred shortly for 2–5 min to avoid mechanical stress of the support material. In the last step, the solvent was removed using a rotary evaporator (step 1: 3 h, 40 °C, 900 mbar; step 2: 1 h, 40 °C, <3 mbar). Finally, a free-flowing SILP catalyst was obtained. The Ru-loading of the Ru-based SILP catalysts was w_Ru = 0.02 g_Ru g_support⁻¹. The pore filling grade of the support was α = 0.34, which describes the IL volume related to the total pore volume of the support material (V_IL V_support⁻¹).

The catalytic tests were performed with the Ru-based SILP systems. Here, the molar amount of CuCl to IL (in mol_CuCl L_IL⁻¹) was varied between 0.5 and 8 M equaling to a molar ratio χ (in mol_CuCl mol_IL⁻¹) in the range of 0.04–1.4. In the following, we refer to the molar ratio as χ = n(CuCl)/n(IL). For the IR measurements, Ru-free samples were used with a molar amount of CuCl to IL between 2 and 6 M, equaling to a molar ratio χ in the range of 0.3–1. In addition, pristine CuCl/Al₂O₃ was used as a reference.

2.2 CO pulse chemisorption

To investigate the CO uptake, a pulse chemisorption setup (AutoChem 2920 device from Micromeritics®) was used. Approximately 0.3–0.4 g of the Ru-based SILP catalysts (with and without CuCl) was placed in a U-bend quartz glass tube. With the help of a bed of glass wool, a possible discharge of the catalyst was prevented. Placing the catalyst bed in the isothermal zone of an oven guaranteed a uniform temperature field. Prior to the chemisorption measurements, the sample was heated to 130 °C with a heating rate of 5 °C min⁻¹ under a helium flow of 20 mL_N min⁻¹. Once the measurement conditions were reached, the sample was dried for 80 min before the pulse experiment was started with a sample loop volume of 0.5 mL_N of CO. Following every single pulse, a lag time of 6 minutes was maintained. The obtained thermal conductivity detector (TCD) signal of the eluting CO (as area and peak height) can directly be related to the amount of CO adsorbed by the sample under standard conditions (cm_N,CO³ g_sample⁻¹). The measurement is considered complete when two sequential peaks have the same area and height.

2.3 Catalyst testing

The evaluation of the SILP catalysts was performed in a fixed-bed reactor setup (1.4571 stainless steel) with an inner diameter of 10 mm and a total volume of 26 mL. The reactor together with its peripheral structures is depicted elsewhere.¹³ CO (Linde, >99.97%) and N₂ (Linde, >99.999%) were dosed via mass flow controllers (MFCs) from Bronkhorst. H₂O was dosed with a liquid flow controller and mixed with N₂ utilizing a controlled evaporator mixer (CEM) unit from Bronkhorst. The gas mixture consisting of N₂, CO and H₂O can either be directed through a bypass-line (for reference measurement purposes) or through the fixed-bed reactor. The catalyst samples were placed on a 0.5 μm frit to avoid particles from entering the downstream section. After the reactor or the bypass-line, respectively, the gas mixture passes a condenser unit (T = 1.5 °C) to remove excess moisture from the stream. Finally, the gas composition was analyzed by an Emerson X-Stream gas analyzer based on IR technology, which allows for in situ analysis of the gas mixture. A detailed explanation of the evaluation of the raw data can be found elsewhere.¹³

Due to the fact that the amount of IL is fixed with the pore filling grade, the amount of CuCl is related to that of the IL and given as molarity value M. For a better understanding, the conversion between molarities and the molar ratio CuCl : IL χ is given in Table 1. Additionally, the molar ratio CuCl : Ru ξ is calculated as well. To account for the catalytic activity of the different samples, the turnover frequency (TOF) for the WGSR was calculated for each sample. We use the data from a temperature dependent experiment at a constant feed flow and composition. Each temperature was held for 5 h before returning to the reference temperature of 120 °C afterwards.²⁰ This allows us to observe possible deactivation phenomena. Normally, the TOF would be calculated as TOF = ṅ_product/n_catalyst. However, the molar flow of the product cannot be determined with high accuracy. This is due to the condensation of water before the dry gas flow passes the online IR analyzer. Thus, we calculated the TOF based on the CO flow as TOF = ṅ_substrate × X/n_catalyst, where X is the conversion. For the molar amount of catalyst, we used the total amount of ruthenium immobilized on the catalyst. Copper is not considered as it was not catalytically active in the SILP, as shown recently.¹³ The data points (one data point per 30 s) were averaged over a stable operation regime of 30 minutes to obtain the TOF at the respective temperature.

Table 1 Conversion between molarities M of CuCl and molar ratios CuCl : IL (χ) and CuCl : Ru (ξ)

Molarity M	CuCl : IL (χ)	CuCl : Ru (ξ)
molCuCl LIL^−1	molCuCl molIL^−1	molCuCl molRu^−1
0 (benchmark)	0.00	0.00
1	0.17	0.77
3	0.52	2.31
5	0.87	3.86
7	1.22	5.40

---

2.4 DRIFTS setup and experimental procedures

All DRIFTS measurements were performed using a Bruker Vertex 80v Fourier transform infrared (FTIR) spectrometer. This spectrometer is equipped with a KBr beam splitter and a liquid-N₂ cooled HgCdTe-detector. The DRIFTS measurements were conducted in a home-built reactor system, which was described previously.^11,21 The system is equipped with a high temperature reactor chamber and Praying Mantis diffuse reflectance accessory (both from Harrick). The reactor system is placed in the sample compartment of the spectrometer and supplies all the electrical and gas dosing feedthroughs. Thus, the sample compartment and the optical path are evacuated during the IR measurements. This results in an outstanding stability, also throughout long-term experiments.

The DRIFTS reactor is equipped with two CaF₂ windows and a type K thermocouple, which is in direct contact with the powder sample. All DRIFT spectra were recorded with an acquisition time of 1 min and a spectral resolution of 2 cm⁻¹. A gas dosing system is connected to the DRIFTS reactor and allows dosage of five different gases. In the present study, Ar (Linde, >99.999%) and CO (Linde, >99.997%) were dosed. Ar was used without further purification. CO was fed through a carbonyl trap (Gaskleen® II Purifier from Pall Corporation) to supply a gas feed, which is free of metal carbonyls. Mass flow controllers (MFCs, Bronkhorst) control the gas dosing at flow rates up to 20 mL_N min⁻¹. The pressure in the gas lines can be adjusted by three pressure controllers (PCs, Bronkhorst) between 1 mbar and 20 bar. Finally, all devices run in a remote-controlled fashion, which enables us to perform long-term experiments with high reproducibility.

An identical experimental procedure was applied to all samples. Prior to the measurements, the samples were purged with Ar (2 mL_N min⁻¹, 1 bar) overnight at 30 °C to remove water residues. Under these conditions, a background spectrum (acquisition time: 2 min) was recorded. Subsequently, the reactor was evacuated (∼1 mbar, 1 min) and the procedure was started. The complete procedure is illustrated in Fig. 1.

Fig. 1 Schematic illustration of the experimental procedure: two consecutive heating/cooling cycles including CO dosing, evacuation and Ar purging at every temperature step.

Two identical and consecutive heating/cooling cycles were performed from 30 °C to 120 °C and back to 30 °C in steps of 30 °C. Only one heating/cooling cycle was performed for the samples with molar ratios χ = 0.3 and 0.7. At each temperature step, the sample was exposed to CO (1 bar, 9 min), evacuated (∼1 mbar, 1 min) and purged with Ar (1 bar, 10 min). The Ar atmosphere was maintained while heating/cooling (3 °C min⁻¹) to the next temperature step.

2.5 Post-data treatment

All IR spectra presented below were treated identically. Heating of a sample causes changes in the reflectivity. Thus, all spectra were normalized to compensate for this effect.²² Subsequently, the spectra were baseline (BL) corrected. In a previous work, we observed that the Cu carbonyls formed are highly labile and decompose rapidly upon evacuation.¹³ To account for this, we use a specific data treatment procedure to subtract the CO gas phase signals from the spectra. This procedure has already been described and successfully applied in previous publications.^21,23 The procedure is illustrated in Fig. 2 and the details are given in the following. In summary, this procedure enables us to study Cu carbonyls in the presence of a CO gas phase and under steady state conditions. Please note that the top left panel in Fig. 2 includes spectra recorded during evacuation and purging where carbonyl bands are even visible without the data treatment procedure.

Fig. 2 Steps during post-data treatment to remove the CO gas phase signals.

In the first step of the procedure, the as-recorded spectra and a suitable reference spectrum are Fourier transformed. The reference system should be similar to the system investigated and CO must not adsorb. Thus, we chose Al₂O₃ as a reference system. After Fourier transformation (FT), a low-pass filter (LPF) is applied. The filter removes the high frequency components, i.e. the fine structure of the CO gas phase features.^21,23 This results in spectra, which resemble the contour of the gas phase signals. In the following step, these spectra are normalized and the reference is subtracted. Finally, BL correction yields the resulting spectra, where the carbonyl peaks are clearly visible. The same procedure was applied to all IR spectra shown in this work and is outlined schematically in Fig. 2.

2.6 DFT calculations

The DFT calculations were carried out using the ORCA²⁴ software package. The RI-BP86^25–27 functional was used in combination with D3 dispersion corrections²⁸ and the def2-TZVPPD^29,30 basis set, which incorporates diffuse functions required for calculations on anionic species. This approach has been successfully applied to similar systems.¹² The resolution of identity approximation was used to speed up the calculations of the Coulomb part in combination with the def2/J auxiliary basis set.³¹ Optimizations were done without any constraints using the CPCM³² model with a dielectric constant of 12 to represent the IL.^33,34 Vibrational frequencies were determined using numerical derivatives of the energy as implemented in ORCA. The bond order was extracted using the Mayer^35,36 model.

3. Results and discussion

3.1 Catalytic tests and CO chemisorption studies

To compare the catalytic activity of the different SILP materials, the WGSR TOF was calculated for each system. A temperature variation experiment at constant feed flows and compositions is the basis for this evaluation. Fig. 3 shows selected results from different catalyst samples with various CuCl loadings. In this plot, the benchmark system without CuCl is indicated with a dashed line for better comparability.

Fig. 3 Selection of catalytic results for the variation of the CuCl content in the IL film of the catalyst samples. T = 120–140 °C, p = 1 bar, precursor = [Ru(CO)₃(Cl)₂]₂, loading (Ru) = 0.02 g g_Support⁻¹, IL = [C₄C₁C₁Im]Cl, α = 0.34, M_CuCl = 2–8 mol L_IL⁻¹, m_cat = 2.0 g, p_H2O : p_CO = 2 : 1, V̇_tot = 174 mL_N min⁻¹, TOS = 45 h.

There is a strong correlation between the CuCl loading of the IL film and the catalytic activity with pronounced activation effects for a wide range of CuCl loadings (Fig. 3). While the 1 M catalyst sample (with molar CuCl : IL ratio χ = 0.17) shows improvements in activity of +9% at 120 °C and +10% at 140 °C, the 3 M SILP catalyst (χ = 0.52) leads to improvements of +27% at 120 °C and +18% at 140 °C. Further addition of CuCl, however, results in the loss of the beneficial effect, as visible for the 7 M (χ = 1.22) sample. Here, we observed losses of activity of −64% at 120 °C and −42% at 140 °C.

The observed trend can be attributed to a change of the Lewis acid–base behavior of the different chlorocuprate species, which are formed upon CuCl addition to the IL. Depending on the molar CuCl : IL ratio χ, different complexes evolve, which are in dynamic equilibrium with each other.¹⁵ SILP catalysts with comparatively low CuCl loading contain primarily Lewis-basic species, such as [CuCl₂]⁻ or [CuCl₃]²⁻. On the other hand, higher CuCl concentrations lead to the formation of Lewis-acidic species, e.g. [Cu₂Cl₃]⁻ or [Cu₃Cl₄]⁻.^14–17,37 Such equilibria, generating either chloride-rich (Lewis-basic) or chloride-poor (Lewis-acidic) environments, have been reported previously for a selection of other halometallate IL systems.^37–39 The catalytic tests showcased in Fig. 3 and our previous results indicate that a Lewis basic environment is beneficial to the performance of the WGSR SILP catalysts.¹³

In order to compare the CO uptakes of the SILP catalysts with various CuCl loadings, CO pulse chemisorption experiments were performed. The results depicted in Fig. 4 reveal a maximum CO uptake at χ = 0.7 (4 M), which matches the maximum of the activity improvement reported in our previous work.¹³ The benchmark system showed an initial CO sorption of 0.92 mL_N g⁻¹, whereas the value of the maximum uptake can be nearly tripled to 2.71 mL_N g⁻¹ for χ = 0.7 (4 M). This affirms our assumption that the predominance of the Lewis-basic chlorocuprate species leads to increased availability of CO in the IL phase. This is most likely due to the formation of Cu carbonyl species, which efficiently shuttle CO to the active Ru species in the SILP.

Fig. 4 Mass specific volumetric CO uptakes of the dry SILP catalysts (including the Ru precursor) at 1 bar and 130 °C as a function of the CuCl concentration in the IL [C₄C₁C₁Im]Cl obtained by means of pulse chemisorption experiment with an AutoChem® analyzer.

3.2 CO adsorption studied by DRIFTS

We apply DRIFTS to identify Cu carbonyls present in the CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ SILP systems with χ = 0.3, 0.5, 0.7, 1.0 and a pristine CuCl/Al₂O₃ sample. In the IR measurements, we investigate exclusively the Ru-free SILP systems because the presence of Ru carbonyls results in strong CO adsorption peaks, which interfere with the assignment of the Cu carbonyl bands.

Peak assignment and temperature-dependent behavior. In Fig. 5a–e, spectra recorded in 1 bar CO (after subtraction of the CO gas phase) are shown for the first heating/cooling cycle. First, we focus on the temperature-dependent evolution in each set of spectra, which is very similar for all IL-containing samples (Fig. 5a–d). In the first spectrum recorded at 30 °C, two peaks located at wavenumbers >2100 cm⁻¹ were found, namely at 2132–2131 cm⁻¹ and 2121–2120 cm⁻¹. These peaks are highlighted in green. Additionally, several smaller peaks are present at wavenumbers <2100 cm⁻¹ (2092–2090 cm⁻¹, 2080–2073 cm⁻¹, 2073–2064 cm⁻¹ and 2044–2042 cm⁻¹), which are highlighted in blue. Upon heating to 120 °C, the peak intensity of the features at lower wavenumbers (<2100 cm⁻¹, blue) decreases. While cooling to 30 °C, the spectra of all IL-containing samples show the formation of two pronounced peaks at 2073–2064 cm⁻¹ and 2044–2042 cm⁻¹. The ratio of these two contributions depends on the molar ratio χ. This effect is explained in detail below.

Fig. 5 Results of the first heating/cooling cycle: a–e: offset DRIFT spectra; f: integrated peak areas during cooling from 120 to 30 °C, supported with guide to the eye curves.

In Fig. 5e, the spectra obtained from the pristine CuCl/Al₂O₃ sample are displayed. They show a different behavior during the experiment. At 30 °C, the same peaks as compared to those of the other samples are visible (2132, 2121, 2080, 2072 and 2044 cm⁻¹) and decrease slightly upon heating. However, no increase of the peak areas at <2100 cm⁻¹ is observed upon cooling back to room temperature. Instead, the peak areas remain the same. The most pronounced peaks obtained from the CuCl/Al₂O₃ sample are the features located at >2100 cm⁻¹ (highlighted in green). The peak intensities for all samples are affected by the temperature but the peaks are, nevertheless, clearly visible at all temperatures.

We assign the peaks on the basis of literature and DFT calculations. The variety of peaks in the IR spectra indicates that different [Cu_xCl_y]^z carbonyls are present in the liquid phase of the WGSR catalyst, which is in good agreement with the literature.^14–18 Huang et al. investigated CuCl dissolved in [C₄C₁Im]Cl by fast atom bombardment mass spectrometry (FAB-MS). They identified several monoanionic [Cu_xCl_y]⁻ species, such as [CuCl₂]⁻, [Cu₂Cl₃]⁻ and [Cu₃Cl₄]⁻.¹⁶ David et al. investigated supported IL membranes (SILMs), which are based on CuCl dissolved in [C₆C₁Im]Cl and are suitable for the recovery of CO from a gas stream.¹⁵ They gave an overview about several [Cu_xCl_y]^z− species, the stoichiometry of which depends on the molar ratio χ between CuCl and IL.^14–17,19 They concluded that [CuCl₃]²⁻ is the predominant species at χ = 0–1 and, moreover, that this species is responsible for the binding of CO.

The DFT calculations build on our previous work,¹³ but this time we also estimate the influence of the IL on the CO stretching frequency by using a continuum solvation model (CPCM).⁴⁰ With this, a high level of accuracy is achieved for the calculated peak positions (Δν(exp. − cal.) < ±20 cm⁻¹). For a detailed assignment of the bands, we refer to Table 2 where a summary of all calculated and experimental peak positions is given. For the assignment, we use the spectra at 30 °C after cooling because here the peaks are the largest and individual contributions are visible the best.

Table 2 Assignment of the IR peaks based on DFT calculations; for the calculated peak positions, the most intense peaks are labeled in bold and Δν is given for the largest difference

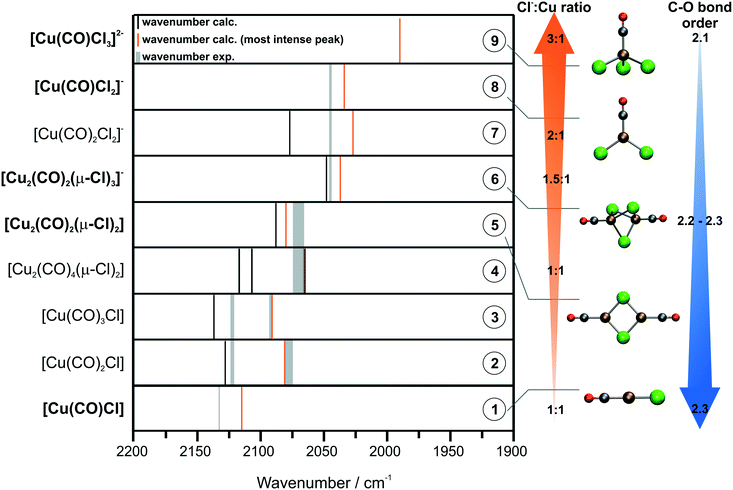
Species		ν(CO) (DFT)/cm^−1	ν(CO) (exp.)/cm^−1	Δν (exp. − calc.)/cm^−1
1	[Cu(CO)Cl]	2115	2132–2131	∼17
2	[Cu(CO)2Cl]	2128, 2081	2121–2120, 2092–2090, 2080–2073	∼8, ∼11, ≃8
3	[Cu(CO)3Cl]	2137, 2091	2121–2120, 2092–2090, 2080–2073	≃17, ∼1, ≃18
4	[Cu2(CO)4(μ-Cl)2]	2117, 2107, 2066, 2065	2073–2064	∼7
5	[Cu2(CO)2(μ-Cl)2]	2088, 2080	2073–2064	≃16
6	[Cu2(CO)2(μ-Cl)3]^−	2048, 2037	2044–2042	∼7
7	[Cu(CO)2Cl2]^−	2077, 2027	2044–2042	∼17
8	[Cu(CO)Cl2]^−	2034	2044–2042	∼10
9	[Cu(CO)Cl3]^2−	1990	—	—

---

According to the work of Haakansson and Jagner, we attribute the band at 2132–2131 cm⁻¹ to CO bound to a neutral CuCl monomer (species 1).⁴¹ Based on DFT calculations, the peaks at 2121–2120 cm⁻¹, 2092–2090 cm⁻¹ and 2080–2073 cm⁻¹ are assigned to neutral monomers with two or three CO molecules bound, respectively (species 2 and 3). The peaks at 2073–2064 cm⁻¹ are attributed to CO bound to neutral dimers with bridging chloride ligands (species 4 and 5). Finally, we assign the contributions at 2044–2042 cm⁻¹ to monoanionic monomers and dimers, which bind CO (species 6–8). Huang et al. already identified the corresponding chlorocuprates (species 6–8; without CO) by FAB-MS.¹⁶ Based on the assumptions of David et al., we also derived the peak position for [Cu(CO)Cl₃]²⁻.¹⁵ However, the calculated peak position of 1990 cm⁻¹ (species 9) agrees only poorly with the experimental data. Thus, we exclude the possibility that this carbonyl is present in our systems. The color code introduced in Fig. 5 illustrates the carbonyl speciation in each sample. According to our assignment and Table 2, features at >2100 cm⁻¹ (highlighted in green) correspond to neutral CuCl monomers with up to three CO ligands (species 1–3). In contrast, neutral CuCl dimers and monoanionic monomers and dimers (species 4–8) correspond to the peaks labeled in blue.

For the sake of clarity, the peak assignments are depicted schematically in Fig. 6. The Cu carbonyls are listed by the Cl⁻ : Cu ratio in the complex. The peak positions derived by DFT are indicated by black and orange lines, where orange indicates the most intense peak. The assigned, experimentally observed peak positions are shown as grey lines. Concerning the peak positions of the different CuCl species, a clear trend is visible in Fig. 6. Both experimental and calculated peak positions undergo a shift to lower wavenumbers with increasing Cl⁻ : Cu ratio in the Cu complex. This is rationalized by electronic effects arising from the interplay of the Cl⁻ and CO ligands: Cl⁻ is considered as a weak ligand exhibiting a π-donor effect. In contrast, CO is considered as a strong ligand and exhibits a π-accepting effect.⁴² An increasing Cl⁻ : Cu ratio indicates a higher partial charge on the Cu center and, hence, a higher tendency for backbonding from Cu to the available CO ligands.

Fig. 6 Comparison of the experimental and calculated peak positions for all of the relevant Cu species. Optimized structures of selected Cu carbonyls are shown and listed according to their Cl⁻ : Cu ratio and their calculated C–O Mayer bond order.

According to the Blyholder model, more π-backbonding to CO results in weakening of the C–O bond. This is due to the donation of electron density to the antibonding 2π* orbital of the CO molecule.⁴³ The actual amount of backbonding strongly depends on the electronic environment of the Cu(I) center. This can even lead to the so-called nonclassical Cu carbonyl species, which show ν(CO) values higher than those in free CO.^44,45 A useful indicator to discern chemical bonding in inorganic and organometallic systems based on quantum mechanical calculations is the Mayer bond order (MBO).^35,46,47 In order to obtain an insight into the CO bond strength of the species 1–9 and to underline our general assumptions based on the Blyholder model, we computed the MBO at the same level of theory for the optimized structures of the model species listed in Fig. 6. A more detailed summary of the MBOs and associated bond distances can be found in the ESI.† Indeed, the MBOs of the CO bonds roughly follow the trend of decreasing bond orders for increasing Cl⁻ : Cu ratios in the Cu complexes. While the lowest MBO of 2.1 is predicted for the singly and doubly negatively charged species (7 and 9), the highest MBO across the series is computed to be 2.3 for the neutral monomers (1–3). Furthermore, we observe a smooth transition between those extremes moving along the series of dimeric species (4–6). However, the computed bond orders are in a very narrow range and should only be considered as purely qualitative indicators. Nevertheless, they indicate weakening of the CO bond presumably due to increasing π-backbonding. This effect can be observed in a shift of the C–O stretching frequency to lower wavenumbers,⁴³ which is in line with our experimental and theoretical findings.

Effects induced by the IL and the molar ratio χ. Next, we focus on the differences induced by the IL and different CuCl : IL molar ratios χ. In the spectra shown in Fig. 5a–d, we clearly observe that the peaks at <2100 cm⁻¹ (highlighted in blue) grow for the IL-containing samples upon cooling to 30 °C, which is not the case for the pristine CuCl/Al₂O₃ sample (Fig. 5e). In Fig. 5f, the integration of the peak areas at wavenumbers <2100 cm⁻¹ is shown for all samples during cooling from 120 to 30 °C. This demonstrates again that the peak areas for all IL-containing samples increase upon cooling, whereas the peak area remains constant during CO dosing on CuCl/Al₂O₃. Thus, the formation of these Cu species is clearly related to the presence of [C₄C₁C₁Im]Cl. In the IL phase, CuCl molecules bind Cl⁻ ions and/or form dimers. This promotes the formation of the Cu carbonyls (species 4–8) assigned above, which are in equilibrium with each other. A similar dynamic equilibrium was already reported for a CuCl-free [Ru(CO)₃Cl₂]₂/[C₄C₁C₁Im]Cl/Al₂O₃ WGS catalyst.¹¹

Moreover, the peak growth upon cooling is rationalized by the exothermic nature of the CO complexation.¹⁵ However, the ratio of the two major contributions that increase in intensity upon cooling is different throughout the IL-containing samples. This becomes apparent by comparison of the bottom spectra recorded at 30 °C in Fig. 5a–e. This set of spectra shows that the ratio of the peaks at 2073–2064 cm⁻¹ and 2044–2042 cm⁻¹ varies systematically with the CuCl to [C₄C₁C₁Im]Cl molar ratio χ. For χ = 0.3, the peaks at 2073–2064 cm⁻¹ and 2044–2042 cm⁻¹ have approximately the same peak height. With increasing molar ratio χ, the peak at 2073–2064 cm⁻¹ becomes the most prominent one.

According to our DFT calculations, the band at 2044–2042 cm⁻¹ is assigned to the monoanionic monomers and dimers (species 6–8). Among the set of samples, this band is most pronounced for χ = 0.3, where the highest excess of Cl⁻-containing IL is present with respect to CuCl. This means that the formation of anions, which requires binding of Cl⁻, is more likely in environments where more Cl⁻ is available per CuCl. Vice versa, an increase of the molar ratio χ leads to an enhanced contribution of neutral dimers (2073–2064 cm⁻¹; species 4 and 5). This is due to a decrease of the Cl⁻ content per available Cu metal center, which promotes the formation of neutral dimers as compared to anionic Cu species. The observation that the nature of the Cu carbonyls depends on the relative amount of Cl⁻ in the SILP confirms our idea of an equilibrium existing between the anionic and neutral Cu carbonyl species.

Additionally, the IR features of the Cu carbonyls observed are apparent at all temperatures investigated. This is important because the highest temperatures are similar to those under real reaction conditions during the WGSR. Thus, we assume that the Cu carbonyls are present under the experimental conditions of the WGSR and are responsible for the improved catalytic activity. In our previous work, we demonstrated that the highest TOFs are obtained at a molar ratio of χ = 0.7.¹³ A comparison of the IR spectra reveals that the most intense peak at <2100 cm^{- 1} at a molar ratio χ = 0.7 is assigned to the neutral CuCl dimers (species 4 and 5) independent of the temperature. This observation suggests that the presence of neutral CuCl carbonyl dimers (species 4 and 5) is beneficial for the performance of [Ru(CO)₃Cl₂]₂/CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ as a WGS catalyst.

Stepić et al.¹² investigated the mechanism of the WGSR over Ru-based SILP catalysts in a computational and experimental study. They suggested a five-step mechanism of the WGSR, which starts with the activation of the Ru catalyst by addition of H₂O. Upon evolution of HCl, a metallocarboxylic acid is formed. Thereafter, a metal hydride is formed upon release of CO₂. The metal hydride recombines with HCl to form a dihydride complex. Finally, the H₂ dissociates and the catalyst is regenerated by the addition of CO.¹² Thus, the availability of CO in the IL phase is crucial for the regeneration of the catalyst. The CO shuttles increase the availability of CO, which is decisive for the completion of the catalytic cycle of the WGSR.

Reversibility of the Cu carbonyl formation. In our previous work, the catalysts proved to be stable and active in a long-term experiment with a time-on-stream of 45 h at different temperatures.¹³ Thus, we assume that the formation of the CuCl carbonyls should be reversible upon consecutive heating/cooling cycles. In order to probe the reversibility of the formation of Cu carbonyls, we performed two subsequent heating/cooling cycles. In Fig. 7a, the spectra are shown during the first and second cycles for the sample with a molar ratio of χ = 0.5. In Fig. S1 in the ESI,† the spectra of two consecutive cycles are shown for the CuCl/Al₂O₃ reference and for the sample with χ = 1. In Fig. 7b, the integrated peak area at <2100 cm⁻¹ is displayed for the samples with molar ratios χ = 0.5 and 1 and for the pristine CuCl/Al₂O₃ reference. The assignments in the IR spectra are summarized previously in Table 2. Please note that the peak positions and intensities after cooling to 30 °C are nearly identical for the first and second cycles.

Fig. 7 1^st and 2^nd heating/cooling cycles: a, representative IR spectra of the sample with molar ratio χ = 0.5; b, integrated peak areas for selected samples, supported with guide to the eye curves.

Referring to the integrated peak areas at <2100 cm⁻¹, striking differences are observed between the pure CuCl and the IL-containing samples. As one can see in Fig. 7b, the integrated peak area of the CuCl/Al₂O₃ reference remains constant throughout the experiment. In contrast, both IL-containing samples show the same behavior. The peak area stays constant upon heating to 120 °C in the first cycle. This is followed by an increase of the peak area during cooling to 30 °C. In the subsequent heating ramp of the second cycle, the peaks vanish nearly completely but reappear during cooling back to 30 °C.

We interpret these results as follows. For the CuCl/Al₂O₃ sample, no peak growth at <2100 cm⁻¹ upon cooling to 30 °C is apparent. This is due to the absence of the IL and, hence, the absence of a reaction medium and a Cl⁻ reservoir. For the IL-containing samples, the first heating ramp to 120 °C is associated with an induction period, which is known from the literature.^9,48–50 Thus, we attribute the induction period to reordering/mixing of the IL/CuCl phase including the formation of different [Cu_xCl_y]^z species. In Fig. 7b, this induction period is highlighted in red. Upon cooling to 30 °C, the Cu carbonyl peaks become more pronounced due to the exothermic nature of the CO complexation reaction.¹⁵ During the second cycle, no further induction period is observed. Instead, the behavior resembles the first cycle after the induction period. Namely, we observe a decrease of the peak area at <2100 cm⁻¹ upon heating and an increase of the peak area upon cooling to 30 °C. Thus, we conclude that the reordering/mixing of the IL/CuCl phase including the formation of CuCl species is completed after the first heating period.

Finally, we observe, in the presence of the chloride IL, only small Cu carbonyl peaks at temperatures close to the working conditions of the WGSR. In addition, these Cu carbonyls were demonstrated to be highly labile and they decompose rapidly upon evacuation or purging with Ar.¹³ This is further supported by the DFT-calculated Cu–C bond orders (Table S1†), which are all well below 1.0. These values contrast with the M–CO bond order for the carbonyl–chloro–ruthenium catalyst (1.20, as well as other well-known Ru carbonyl species with M–CO bond orders >1.25).⁵¹ The lability of the Cu carbonyls is crucial for them to work as efficient CO shuttles. Due to the fast kinetics of the Cu carbonyl decomposition, only a low concentration of these shuttles is necessary to have a strong influence on the performance of our [Ru(CO)₃Cl₂]₂/CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ WGSR catalyst.

4. Conclusion

In this work, we investigated the formation and equilibrium between different Cu carbonyls in CuCl/[C₄C₁C₁Im]Cl/Al₂O₃ by in situ DRIFTS. In the WGSR, these Cu species are assumed to take the role of CO shuttles in the Ru-based SILP system and were demonstrated to improve the performance of this specific SILP system. We identified the relevant Cu species based on their IR spectra with the help of DFT calculations. Our main results are the following:

(1) CuCl additives improve the performance of Ru-based SILP systems. The Cu carbonyls act as CO shuttles, resulting in an increase of catalytic activity in the WGSR.

(2) We identify several relevant Cu carbonyls, namely neutral monomers ([Cu(CO)_1–3Cl]) and dimers ([Cu₂(CO)_2,4(μ-Cl)₂]), as well as monoanionic monomers ([Cu(CO)_1,2Cl₂]⁻) and dimers ([Cu₂(CO)₂(μ-Cl)₃]⁻).

(3) Chloride ligands enhance π-backbonding from the Cu center to the carbonyl ligand, as revealed by the calculated C–O Mayer bond orders. The bond order decreases with increasing Cl⁻ : Cu ratio and, consequently, the corresponding CO bands shift to lower wavenumbers.

(4) The formation of specific Cu carbonyl species depends on the molar ratio between CuCl and the IL. The formation of anions is promoted by higher ratios of IL to CuCl due to an excess of Cl⁻. In contrast, neutral Cu dimers are dominant at lower IL to CuCl ratios.

(5) After an induction period, the peaks of different Cu carbonyl species increase in the presence of [C₄C₁C₁Im]Cl. The induction period is attributed to reordering/mixing of the CuCl : IL phase.

(6) The formation of the Cu carbonyls is fully reversible. Their concentration in the supported IL increases upon cooling because of the exothermic nature of the CO complexation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge funding from the European Commission within the Horizon 2020-SPIRE project ROMEO (grant agreement number 680395) as well as funding from the Deutsche Forschungsgemeinschaft (DFG) and the NIC project 11311 at the Jülich supercomputing facilities. Additional support by the DFG is acknowledged from the Excellence Cluster “Engineering of Advanced Materials” (project EXC 315) (Bridge Funding) and by the Free State of Bavaria through its funding for the Energie Campus Nürnberg (http://www.encn.de).

References

1. Y. Li, Q. Fu and M. Flytzani-Stephanopoulos, Appl. Catal., B, 2000, 27, 179–191.
2. D. Mendes, A. Mendes, L. Madeira, A. Iulianelli, J. Sousa and A. Basile, Asia-Pac. J. Chem. Eng., 2010, 5, 111–137.
3. D. S. Newsome, Catal. Rev.: Sci. Eng., 1980, 21, 275–318.
4. C. Rhodes, G. Hutchings and A. Ward, Catal. Today, 1995, 23, 43–58.
5. D. C. Grenoble, M. M. Estadt and D. F. Ollis, J. Catal., 1981, 67, 90–102.
6. D. Andreeva, V. Idakiev, T. Tabakova, A. Andreev and R. Giovanoli, Appl. Catal., A, 1996, 134, 275–283.
7. G. Jacobs, L. Williams, U. Graham, G. A. Thomas, D. E. Sparks and B. H. Davis, Appl. Catal., A, 2003, 252, 107–118.
8. S. Werner, N. Szesni, R. W. Fischer, M. Haumann and P. Wasserscheid, Phys. Chem. Chem. Phys., 2009, 11, 10817–10819.
9. S. Werner, N. Szesni, A. Bittermann, M. J. Schneider, P. Härter, M. Haumann and P. Wasserscheid, Appl. Catal., A, 2010, 377, 70–75.
10. S. Werner, N. Szesni, M. Kaiser, R. W. Fischer, M. Haumann and P. Wasserscheid, ChemCatChem, 2010, 2, 1399–1402.
11. T. Bauer, R. Stepic, P. Wolf, F. Kollhoff, W. Karawacka, C. R. Wick, M. Haumann, P. Wasserscheid, D. M. Smith, A.-S. Smith and J. Libuda, Catal. Sci. Technol., 2018, 8, 344–357.
12. R. Stepić, C. R. Wick, V. Strobel, D. Berger, V. A. Nataša, M. Haumann, P. Wasserscheid, A. S. Smith and D. M. Smith, Angew. Chem., 2019, 131, 751–755.
13. P. Wolf, M. Aubermann, M. Wolf, T. Bauer, D. Blaumeiser, R. Stepic, C. R. Wick, D. M. Smith, A.-S. Smith, P. Wasserscheid, J. Libuda and M. Haumann, Green Chem., 2019, 21, 5008–5018.
14. S. A. Bolkan and J. T. Yoke, J. Chem. Eng. Data, 1986, 31, 194–197.
15. O. C. David, G. Zarca, D. Gorri, A. Urtiaga and I. Ortiz, Sep. Purif. Technol., 2012, 97, 65–72.
16. C. Huang, B. Chen, J. Zhang, Z. Liu and Y. Li, Energy Fuels, 2004, 18, 1862–1864.
17. R. Lü, H. Tangbo and Z. Cao, J. Nat. Gas Chem., 2007, 16, 70–77.
18. G. Zarca, I. Ortiz and A. Urtiaga, J. Membr. Sci., 2013, 438, 38–45.
19. J. Zhang, C.-P. Huang, B.-H. Chen, Y.-X. Li and C.-Z. Qiao, J. Fuel Chem. Technol., 2005, 33, 431.
20. P. Wolf, M. Logemann, M. Schörner, L. Keller, M. Haumann and M. Wessling, RSC Adv., 2019, 9, 27732–27742.
21. T. Bauer, S. Maisel, D. Blaumeiser, J. Vecchietti, N. Taccardi, P. Wasserscheid, A. Bonivardi, A. Görling and J. Libuda, ACS Catal., 2019, 9, 2842–2853.
22. T. Xu, M. Schwarz, K. Werner, S. Mohr, M. Amende and J. Libuda, Phys. Chem. Chem. Phys., 2016, 18, 10419–10427.
23. A. Kaftan, A. Schönweiz, I. Nikiforidis, W. Hieringer, K. M. Dyballa, R. Franke, A. Görling, J. Libuda, P. Wasserscheid, M. Laurin and M. Haumann, J. Catal., 2015, 321, 32–38.
24. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
25. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
26. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
27. O. Vahtras, J. Almlöf and M. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518.
28. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
29. A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017.
30. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
31. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
32. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
33. M. Sobota, S. Schernich, H. Schulz, W. Hieringer, N. Paape, P. Wasserscheid, A. Görling, M. Laurin and J. Libuda, Phys. Chem. Chem. Phys., 2012, 14, 10603–10612.
34. H. Weingärtner, P. Sasisanker, C. Daguenet, P. J. Dyson, I. Krossing, J. M. Slattery and T. Schubert, J. Phys. Chem. B, 2007, 111, 4775–4780.
35. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
36. I. Mayer, Int. J. Quantum Chem., 1984, 26, 151–154.
37. L. C. Brown, J. M. Hogg and M. Swadźba-Kwaśny, Ionic Liquids II, Springer, 2017, pp. 185–224.
38. J. Estager, P. Nockemann, K. R. Seddon, M. Swadźba-Kwaśny and S. Tyrrell, Inorg. Chem., 2011, 50, 5258–5271.
39. C. L. Hussey, Pure Appl. Chem., 1988, 60, 1763–1772.
40. M. Cossi, M. Persico and J. Tomasi, J. Mol. Liq., 1994, 60, 87–105.
41. M. Haakansson and S. Jagner, Inorg. Chem., 1990, 29, 5241–5244.
42. A. F. Holleman, E. Wiberg and N. Wiberg, Lehrbuch der anorganischen Chemie, de Gruyter, Berlin, 102 edn, 2007.
43. K. W. Kolasinski, Surface science: foundations of catalysis and nanoscience, John Wiley & Sons, 2012.
44. R. D. Pike, Organometallics, 2012, 31, 7647–7660.
45. S. H. Strauss, J. Chem. Soc., Dalton Trans., 2000, 1–6,  10.1039/A908459B.
46. A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, J. Chem. Soc., Dalton Trans., 2001, 2095–2108,  10.1039/B102094N.
47. I. Mayer, J. Comput. Chem., 2007, 28, 204–221.
48. S. A. Forsyth, H. Q. N. Gunaratne, C. Hardacre, A. McKeown, D. W. Rooney and K. R. Seddon, J. Mol. Catal. A: Chem., 2005, 231, 61–66.
49. N. A. Hamill, C. Hardacre and S. J. McMath, Green Chem., 2002, 4, 139–142.
50. I. Kim, K. Anas, S. Lee, C.-S. Ha and D.-W. Park, Catal. Today, 2008, 131, 541–547.
51. N. Fritsch, C. R. Wick, T. Waidmann, S. Pflock, P. O. Dral, J. Tucher, C. Steiner, T. E. Shubina, S. Maier, T. Clark and N. Burzlaff, Eur. J. Inorg. Chem., 2018, 2018, 54–61.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cy01852b

‡ These authors share first authorship.

---