t ₁-Noise eliminated dipolar heteronuclear multiple-quantum coherence solid-state NMR spectroscopy

Abstract

Heteronuclear correlation (HETCOR) spectroscopy is one of the key tools in the arsenal of the solid-state NMR spectroscopist to probe chemical and spatial proximities between two different nuclei and enhance spectral resolution. Dipolar heteronuclear multiple-quantum coherence (D-HMQC) is a powerful technique that can be potentially utilized to obtain ¹H detected 2D HETCOR solid-state NMR spectra of any NMR active nucleus. A long-standing problem in ¹H detected D-HMQC solid-state NMR experiments is the presence of t₁-noise which reduces sensitivity and impedes spectral interpretation. In this contribution, we describe novel pulse sequences, termed t₁-noise eliminated (TONE) D-HMQC, that minimize t₁-noise and can provide higher sensitivity and resolution than conventional D-HMQC. Monte-Carlo and numerical simulations confirm that t₁-noise in conventional D-HMQC primarily occurs because random MAS frequency fluctuations cause variations in the NMR signal amplitude from scan to scan, leading to imperfect cancellation of uncorrelated signals by phase cycling. The TONE D-HMQC sequence uses ¹H π-pulses to refocus the evolution of ¹H CSA across each SR4²₁ recoupling block, improving the stability of the pulse sequence to random MAS frequency fluctuations. The ¹H refocusing pulses also restore the orthogonality of in-phase and anti-phase magnetization for all crystallite orientations at the end of each recoupling block, enabling the use of 90° flip-back or LG spin-lock trim pulses to reduce the intensity of uncorrelated signals. We demonstrate the application of these methods to acquire ¹H detected 2D ¹H{³⁵Cl} and ¹H{¹³C} HETCOR spectra of histidine·HCl·H₂O with reduced t₁-noise. To show generality, we also apply these methods to obtain 2D ¹H{¹⁷O} spectra of 20%-¹⁷O fmoc-alanine and for the first time at natural abundance, 2D ¹H{²⁵Mg} HETCOR spectra of magnesium hydroxide. The TONE D-HMQC sequences are also used to probe ¹H–²⁵Mg and ¹H–²⁷Al proximities in Mg–Al layered double hydroxides and confirm the even mixing of Mg and Al in these materials.

---

Introduction

Solid-state nuclear magnetic resonance (SSNMR) spectroscopy is a versatile tool for the structural characterization of inorganic and organic materials and biomolecules.^1–4 Sensitivity and resolution enhancement techniques such as fast magic angle spinning (MAS),^5–7 proton detection^8–13 and dynamic nuclear polarization (DNP)^14–16 have enabled the routine implementation of advanced multidimensional SSNMR experiments. Probing heteronuclear proximities using multidimensional heteronuclear correlation (HETCOR) experiments or dipolar coupling (D) measurements between nuclei is arguably one of the key strengths of SSNMR. HETCOR SSNMR experiments typically use cross polarization (CP)¹⁷ to transfer polarization between pairs of nuclei that are dipolar coupled. Unfortunately, barring a few favorable examples, CPMAS is non-trivial and rarely efficient for quadrupolar nuclei^18,19 and about 75% of the NMR-active isotopes in the periodic table are quadrupolar.¹⁸

Heteronuclear multiple-quantum coherence (HMQC) is a fundamental pulse sequence that is widely used in solution NMR spectroscopy.²⁰ HMQC is a valuable experiment for SSNMR spectroscopy because in principle it can be applied to indirectly observe any NMR active nucleus that is coupled to a “spy” nucleus, usually ¹H, ¹³C or ³¹P. Many HMQC SSNMR experiments using heteronuclear scalar (J-) or dipolar (D-) interactions for coherence transfer have been described.^21–28 Delevoye and co-workers recently demonstrated that ²⁷Al{¹H} D-HMQC is more robust and efficient in comparison to CP for the surface characterization of γ-alumina related catalysts.²⁹ We recently used D-HMQC to indirectly observe half-integer quadrupolar nuclei and spin-1/2 nuclei with large chemical shift anisotropy (CSA).^30,31 More recently, we have implemented frequency-selective HMQC schemes that offer enhanced sensitivity by reducing recycle delays.³² Fast MAS, proton-detected D-HMQC experiments are most commonly performed with the SR4²₁ recoupling pulse sequence³³ as it offers a heteronuclear dipolar coupling scaling factor of ca. 0.25, effective ¹H homonuclear decoupling, tolerance to rf inhomogeneity and is not dipolar truncated. However, t₁-noise³⁴ often plagues ¹H-detected 2D D-HMQC SSNMR spectra partly due to the high sensitivity of the recoupling sequence to rotor synchronization.^27,28,30,31 Recently, random signal fluctuations observed in ¹H{¹⁴N} RESPDOR experiments have also been attributed to MAS instability.³⁵ Generally, the strategies such as spin-lock trim pulses,³⁶ BIRD filters^37,38 or pulsed field gradients³⁹ often used to suppress t₁-noise in HMQC solution NMR experiments are either incompatible with existing pulse sequences, or simply cannot be implemented with current SSNMR probes. A number of t₁ sampling and processing techniques have been proposed to reduce t₁-noise in solution NMR experiments.^40–44 However, some of these rely on the fact that t₁-noise in solution NMR experiments often arises from slow signal intensity modulations; as such these methods are ineffective in solids where the t₁-noise is largely time-independent. Perras and Pruski pointed out that since t₁-noise scales linearly with the signal amplitude, relaxation delays in D-HMQC SSNMR experiments should be set to values far shorter than the 1.3 × T₁ value that is optimal in one-dimensional spectroscopy.⁴⁵ Robertson et al. demonstrated the use of selective saturation pulses to reduce t₁-noise in fast MAS ¹H SSNMR experiments.⁴⁶

One way to reduce t₁-noise is to change the recoupling sequence. For example, γ-encoded recoupling sequences such as rotary resonance recoupling (R³) and symmetry based R-sequences are robust with respect to MAS fluctuations.⁴⁷ However, the γ-encoded sequences are sensitive to rf inhomogeneity and suffer from dipolar truncation. As such, they typically offer lower efficiency than SR4²₁ and adiabatic zero-quantum recoupling methods.^48,49 Alternatively, in the TRAPDOR-HMQC (T-HMQC) experiment presented by Carravetta and co-workers,⁵⁰ long duration, high power pulses are used for both heteronuclear dipolar recoupling and excitation of the indirectly detected nucleus. T-HMQC has recently been shown to provide more sensitivity than D-HMQC with SR4²₁ applied on the ¹H channel for ¹H{¹⁴N} experiments.⁵¹ Part of the sensitivity gains with T-HMQC arise from a lessened t₁-noise, likely because the signal intensity is insensitive to MAS frequency variations.⁵¹ However, T-HMQC requires large B₁ fields for long recoupling durations. T-HMQC also results in simultaneous recoupling of the central (CT) and satellite transitions (ST) for half-integer quadrupolar nuclei.⁵² Further, only the irradiated peak will be excited, preventing detection of anisotropic sideband manifolds with T-HMQC.⁵¹

In this contribution, we present a family of novel pulse sequences called t₁-noise eliminated D-HMQC (TONE D-HMQC). As shown below, MAS instability is the leading cause of t₁-noise for fast MAS ¹H{X} D-HMQC experiments that use SR4²₁ recoupling. TONE D-HMQC sequences minimize t₁-noise by refocusing ¹H CSA after each recoupling block to reduce the variation of the NMR signal intensity with MAS frequency fluctuations and by reducing (saturating) signals from uncorrelated magnetization. The TONE D-HMQC sequences are shown to provide enhanced sensitivity for proton detected D-HMQC experiments with a wide range of spin-1/2 and half-integer quadrupolar nuclei such as ¹³C, ¹⁷O, ²⁵Mg, ²⁷Al and ³⁵Cl.

Results and discussion

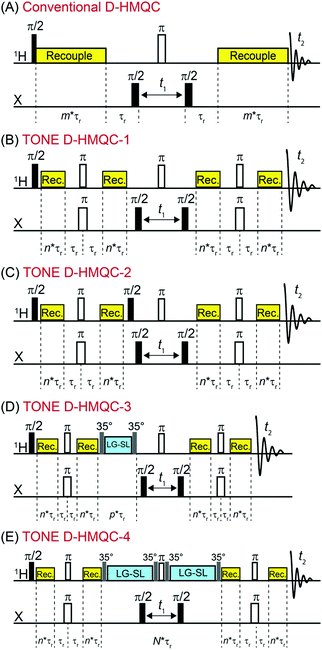
Henceforth, we will refer to the directly detected ¹H spins with I angular momentum operators while the indirectly-detected X spins will be denoted using S operators.⁵³Fig. 1A shows the conventional D-HMQC pulse sequence where the ¹H magnetization is excited using a π/2_y pulse to generate in-phase x transverse magnetization (I_x). Application of SR4²₁ dipolar recoupling causes evolution of heteronuclear dipolar couplings leading to creation of some anti-phase 2I_yS_z magnetization. However, ¹H CSA will also simultaneously evolve and will convert 2I_yS_z to a combination of 2I_yS_z and 2I_xS_z while I_x will evolve to a combination of I_x and I_y. The extent of this mixing depends upon the orientation of the CS tensor and will vary for the different crystallite orientations in a powder. The π/2 pulse on the X channel converts the anti-phase coherence, 2I_yS_z and 2I_xS_z, into heteronuclear multiple-quantum coherence, 2I_yS_y and 2I_xS_y, respectively. The evolution period following the X channel π/2 pulse will encode chemical shifts and quadrupolar interactions of the S spin. The multiple quantum coherence is then reconverted back to a single quantum anti-phase coherence by the second π/2 pulse on the X channel. The second recoupling block then converts the anti-phase magnetization into an observable in-phase coherence. The central π pulse on the ¹H channel serves to refocus isotropic ¹H chemical shifts and importantly, the ¹H CSA which is also reintroduced by heteronuclear dipolar recoupling sequences.⁵⁴ However, the ¹H CSA is only effectively refocused if the dipolar recoupling sequence and central pulse are properly rotor-synchronized.

Fig. 1 ¹H{X} D-HMQC pulse sequences. (A) Conventional D-HMQC, (B) TONE D-HMQC-1, (C) TONE D-HMQC-2, (D) TONE D-HMQC-3, (E) TONE D-HMQC-4. Recoupling (Rec.) and Lee-Goldberg spin-lock (LG-SL) are abbreviated. τ_r denotes rotor period and π/2, π, 35° indicate tip angles of pulses. m, n and p are integers denoting duration of the recoupling and LG-SL pulses. m and n are multiples of 2 and m usually equals 2n, except for samples featuring very strong ¹H–X dipolar coupling constants. In TONE D-HMQC-4, N is a constant that determines the total duration of the LG-SL and π pulses such that N*τ_r > maximum t₁ time.

The desired HMQC signal arises from the fraction of ¹H magnetization that is converted to anti-phase coherence, multiple quantum coherence, back to anti-phase and then ultimately reconverted to in-phase magnetization for detection. The intensity of the desired HMQC signal is denoted as correlated signal intensity (S_corr). The remaining ¹H magnetization that stays as in-phase/single spin operators throughout the HMQC sequence is responsible for the uncorrelated magnetization/NMR signal, denoted S_uncorr. Experimentally, the desired HMQC signal is retained, and signals from uncorrelated magnetization are eliminated, by synchronous 180° phase alternation of the receiver and one of the X-channel π/2 pulses on subsequent scans. As shown below, random fluctuations of the MAS frequency can cause S_uncorr to vary from scan to scan, leading to the imperfect cancellation of the uncorrelated signal by phase cycling and substantial t₁-noise when the ratio S_corr/S_uncorr is small. S_corr/S_uncorr will be small in cases where the X spin natural abundance is low and when the ¹H and X spins are weakly coupled. Here, weakly coupled means that the inverse of the scalar coupling or scaled dipolar coupling that evolves in the HMQC pulse sequence is larger than the ¹H refocused transverse relaxation time T₂′.

Fig. 1B–E show redesigned D-HMQC sequences that reduce t₁-noise by improving the robustness of the pulse sequence to MAS frequency variations and by reducing the magnitude of uncorrelated ¹H magnetization with flip-back or saturation pulses. TONE D-HMQC-1 features simultaneous, rotor-synchronized π pulses on the ¹H and X channel that break each recoupling block into two symmetric parts (Fig. 1B). The simultaneous ¹H and X π pulses sandwiched within each dipolar recoupling block permit evolution of the heteronuclear dipolar coupling while refocusing the ¹H CSA across each recoupling block. Refocusing the ¹H CSA restores the orthogonality of the correlated, anti-phase (2I_yS_z) and uncorrelated, in-phase ¹H magnetization (I_x) for all crystallite orientations. As discussed below, refocusing the ¹H CSA across each recoupling block also improves the robustness of the pulse sequence towards MAS frequency fluctuations. Analogous ideas but in different contexts have been reported previously; for instance, π pulses have been used to refocus the residual effects of dipolar coupling in continuous wave decoupling sequences⁵⁵ and the CSA contributions in T_1ρ measurements,⁵⁶ whereas the perfect echo sequences in solution NMR use π/2 pulses to refocus anti-phase components.⁵⁷ Brinkmann et al. have proposed the use of dual channel symmetry-based recoupling sequences to selectively recouple heteronuclear dipolar interactions while suppressing CSA terms.⁵⁸

TONE D-HMQC-2 is similar to TONE D-HMQC-1, except a π/2_±y pulse is appended at the end of the first refocused dipolar recoupling block (Fig. 1C). The π/2_±y pulse acts as a flip-back pulse for uncorrelated, in-phase I_x magnetization, transforming it to longitudinal magnetization (∓I_z). This flip-back pulse will reduce the magnitude of S_uncorr, helping to suppress the t₁-noise by increasing the ratio S_corr/S_uncorr,. The TONE D-HMQC-3 sequence replaces the flip-back pulse with a long duration (∼1 ms) Lee-Goldburg (LG) trim pulse.³⁶ The LG trim pulse spin-locks the correlated ¹H magnetization, while the uncorrelated magnetization rotates around the tilted effective B₁ field of the LG spin-lock pulse, resulting in dephasing due to rf inhomogeneity (Fig. 1D).³⁶ The LG condition suppresses ¹H spin-diffusion of the spin-locked, correlated magnetization. Suppression of ¹H spin diffusion is critical to ensure the anti-phase magnetization can be reconverted to in-phase magnetization in the second part of the sequence. We have previously identified low- and high-rf field LG conditions compatible with fast MAS frequencies.⁵⁹

Finally, in TONE D-HMQC-4 the LG spin-lock/trim pulse is applied symmetrically about the central ¹H π pulse for the entire duration of the indirect evolution period (t₁) (Fig. 1E). The LG pulses dephase the uncorrelated magnetization while spin-locking the correlated magnetization throughout the duration of the t₁ period. We have previously applied constant-time D-HMQC to enable arbitrary spectral widths,³⁰ however, the constant echo duration in the central part of the sequence causes reduced sensitivity because of ¹H transverse relaxation.³¹ The TONE D-HMQC-4 sequence offers the improved spectral resolution associated with a constant-time experiment and allows arbitrary indirect spectral widths, but reduces relaxation losses since the relaxation is determined by the ¹H spin-diffusion rate under the LG pulse, rather than ¹H T₂′ as occurs in the other HMQC sequences. Note that TONE D-HMQC-4 can also be performed in an incremented fashion by eliminating uncorrelated signals with LG spin-lock or flip-back pulses added prior to the t₁-period (discussed below; Fig. S7, ESI†). Various ¹H homonuclear decoupling schemes have previously been implemented into D-HMQC and D-HSQC (dipolar heteronuclear single quantum coherence) pulse sequences to improve resolution.^60,61

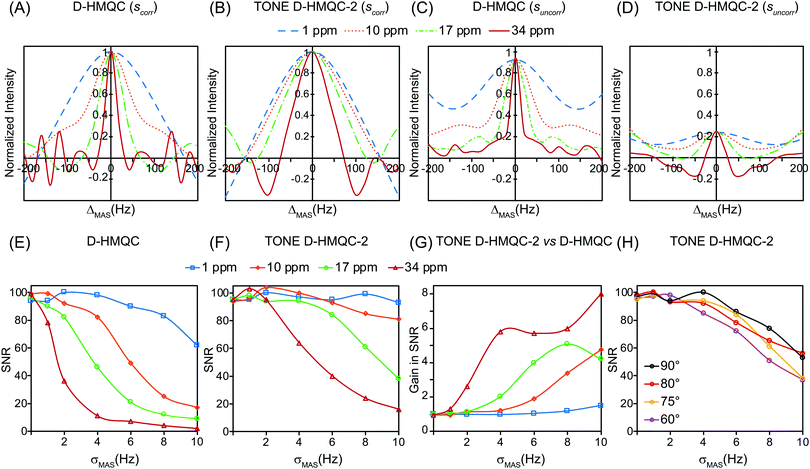
Numerical SIMPSON^62–64 and Monte Carlo simulations were used to demonstrate how random MAS frequency fluctuations cause t₁-noise and understand how the TONE family of pulse sequences can reduce t₁-noise (Fig. 2, see the ESI† for additional details and the input files). First, SIMPSON simulations of a ¹H–¹³C spin system were used to determine the MAS frequency dependence of 1D D-HMQC and TONE D-HMQC-2 signal intensities at a magnetic field of 9.4 T. Profiles showing the signal intensity as a function of the deviation from the set MAS frequency (Δ_MAS) were calculated for both the correlated magnetization (HMQC signal, Fig. 2A and B) and uncorrelated magnetization (background signals, Fig. 2C and D). For simplicity we compare standard D-HMQC and TONE D-HMQC-2 in this section as the analysis will be similar for comparison of D-HMQC and any of the TONE sequences. The SIMPSON simulations were performed with ¹H reduced anisotropy (δ_aniso) values of 1, 10, 17 and 34 ppm to illustrate the contribution of improper refocusing of the ¹H CSA to t₁-noise. For reference, a plane-wave DFT GIPAW calculation predicts that the ammonium ¹H NMR signal at 17.2 ppm in histidine has a reduced anisotropy of 17 ppm. Doubling the static Zeeman field from 9.4 T to 18.8 T would double the size of the CSA in units of Hz, hence, calculations were also performed with a ¹H δ_aniso of 34 ppm to mimic the effects of higher static magnetic fields. The simulations were performed with a model ¹H–¹³C spin system and a heteronuclear dipolar coupling of 2 kHz. The total recoupling time was separately optimized in SIMPSON and set to a total duration of 72 rotor cycles (1.44 ms) in all simulations. In these simulations the recoupling pulse widths, timings and echo durations were calculated and fixed based upon an MAS frequency of 50 kHz, then the signal intensities were calculated in SIMPSON for different input MAS frequencies.

Fig. 2 SIMPSON numerical simulations and Monte Carlo simulations to predict the extent of t₁-noise in D-HMQC spectra. (A–D) SIMPSON simulations of correlated and uncorrelated signal intensity as a function of the deviation from the target MAS frequency (Δ_MAS) for D-HMQC and TONE D-HMQC-2. Profiles are shown for ¹H CSA values of 1 ppm, 10 ppm, 17 ppm and 34 ppm; the indicated CSA values correspond to reduced anisotropy (δ_aniso) in the Haeberlen convention. (E and F) Monte Carlo simulations of the signal-to-noise ratio (SNR) of the indirect dimension of a HMQC spectrum calculated for different uncertainties in the MAS frequency (σ_MAS). (G) The relative gain in SNR provided by TONE D-HMQC-2 as compared to D-HMQC as a function of σ_MAS for four different ¹H δ_aniso values. In (B, D, F and G) the tip angle of the flip-back pulse was 75°. (H) The predicted effect of the flip-back pulse tip angle on the SNR of TONE D-HMQC-2. The ¹H CSA was fixed at 17 ppm. See text for details on all calculations and simulations.

Fig. 2A–D show the variation of the correlated and uncorrelated D-HMQC and TONE D-HMQC-2 signal intensities for Δ_MAS = ± 200 Hz. A flip-back pulse with a tip angle of 75° was used in the TONE D-HMQC-2 simulations to account for rf inhomogeneity (Fig. 2B and D). With δ_aniso = 1 ppm (blue dashed curves) the dependence of the correlated and uncorrelated D-HMQC and TONE D-HMQC-2 signals on Δ_MAS is relatively flat in the range of Δ_MAS = ±50 Hz, which is the range of most interest as experimental MAS fluctuations will likely be less than 50 Hz. However, the D-HMQC and TONE D-HMQC-2 signal intensity-MAS frequency profiles considerably sharpen as δ_aniso increases. Notably, the profiles for both correlated and uncorrelated TONE D-HMQC-2 signals are broader than the corresponding profiles for D-HMQC (when comparing profiles with the same δ_aniso), illustrating the improved tolerance of TONE D-HMQC-2 to MAS frequency variations. Additionally, for each value of δ_aniso, the profiles for the uncorrelated signal are slightly sharper than the corresponding profile for the correlated signal. This observation suggests that experimental random fluctuations of MAS frequency could cause substantial t₁-noise because uncorrelated signals will be imperfectly cancelled by phase cycling. Therefore, in the absence of extremely stable MAS frequencies (variations of 1–2 Hz), reducing the magnitude of the uncorrelated signal is critical to reducing t₁-noise.

A Monte-Carlo style code built in MATLAB was used to simulate the variation of t₁-noise in 2D HMQC experiments with the different pulse sequences (Fig. 2E–H). The code performs the following steps: First, a Gaussian probability function is used to randomize the MAS frequency for each scan. Then, the scaling factors for the correlated and uncorrelated signals are calculated using the randomly generated MAS frequency and the intensity-MAS frequency profiles obtained from SIMPSON (Fig. 2A–D). The scaling factors are then used to calculate the correlated and uncorrelated time domain signal intensities for each scan followed by the calculation of the final time domain intensity for each t₁-point by summing across 16 scans. This procedure was repeated for 500 t₁-points with Δt₁ = 10 μs and the resulting noised-FID was subject to Fourier transformation and signal-to-noise ratio (SNR) measurements. A more detailed description of the MATLAB code with examples is provided with the ESI.†

Fig. 2E shows a plot of the calculated SNR of the indirect dimension as a function of σ_MAS for standard D-HMQC with different δ_aniso values. There are two clear and expected trends: the SNR worsens as σ_MAS increases and as δ_aniso increases. An increase in σ_MAS corresponds to less stable MAS, and as illustrated in Fig. 2A and C, the amplitude of correlated and uncorrelated signals show greater variation with MAS frequency as δ_aniso increases. On the other hand, in all cases TONE D-HMQC-2 is more robust to changes in σ_MAS (Fig. 2F). For instance, with δ_aniso of 17 ppm and σ_MAS of 4 Hz, the SNR with D-HMQC is calculated to be 46 whereas the SNR with TONE D-HMQC-2 is calculated to be 94, which corresponds to a factor 2 gain in SNR. Furthermore, taking into consideration the reference SNR was 95, the calculations suggest that TONE D-HMQC-2 has effectively eliminated the t₁-noise arising from MAS instability. The predicted gain in SNR with TONE D-HMQC-2 is plotted in Fig. 2G. There is no appreciable gain in SNR with TONE when δ_aniso is 1 ppm or when σ_MAS is close to zero. However, the SNR with the TONE sequence is predicted to increase by a factor 2–8 when δ_aniso is 17 or 34 ppm and when σ_MAS > 4 Hz. Finally, Fig. 2H shows the effects of varying the tip angle of the flip-back pulse in TONE D-HMQC-2 for a fixed δ_aniso of 17 ppm. Tip angles of less than 90° were considered to illustrate the effects of rf inhomogeneity. As the pulse tip-angle is reduced from 90° to 60° the SNR reduces slightly due to an imperfect flip-back of the uncorrelated magnetization. In summary, the simulations demonstrate that TONE D-HMQC reduces t₁-noise by improving the robustness of the sequences to MAS fluctuations and suppressing undesired uncorrelated ¹H NMR signals. The similarity of the predicted and experimentally observed sensitivity gains for ¹H{³⁵Cl} D-HMQC experiments validates the model of D-HMQC t₁-noise arising from the random variation of signal intensities because of MAS frequency fluctuations (vide infra).

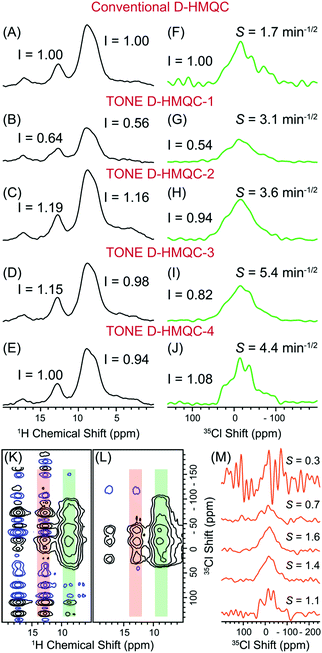
The TONE D-HMQC pulse sequences were experimentally tested for ¹H detection of a variety of NMR active nuclei including ³⁵Cl, ²⁵Mg, ¹³C and ¹⁷O. Fig. 3 shows experimental data acquired with the different D-HMQC pulse sequences on histidine hydrochloride monohydrate, denoted as histidine, at 9.4 T and 50 kHz MAS frequency. For these experiments σ_MAS was estimated to be 2 Hz based upon analysis of the MAS frequency log output by the spectrometer (Fig. S1, ESI†), but the true experimental σ_MAS values are likely larger considering that spectrometer outputs time-averaged MAS frequencies.⁶⁵ 1D ¹H{³⁵Cl} D-HMQC spectra (from the first t₁-increment of the 2D experiment) obtained with the different pulse sequences are shown in Fig. 3A–E. The relative intensity of the ¹H signals at 9.0 ppm and 12.7 ppm are indicated. The ³⁵Cl spectra shown in Fig. 3F–J were extracted from the most intense column (the ammonium signal at δ_iso = 9.0 ppm) of the corresponding 2D D-HMQC spectra (Fig. S2, ESI†). TONE D-HMQC-1 has ¹H signal intensities that are reduced by ca. 35–45% as compared to D-HMQC (Fig. 3B). 1D ¹H NMR spectra acquired with recoupled echo pulse sequences show minimal losses due to the incorporation of CSA refocusing π pulses on the ¹H channel (Fig. S3, ESI†). Therefore, the significant reduction in ¹H intensity observed with TONE D-HMQC-1 must be due to the efficiency of the CT-selective π inversion pulses (Fig. 3B). Indeed, a reduction in intensity due to imperfect CT-selective inversion pulses is also predicted by SIMPSON simulations (Fig. S4, ESI†). However, despite the reduction in the direct dimension signal intensity, the sensitivity (S = SNR/√time) of the ³⁵Cl trace increases from 1.7 to 3.1 min^−1/2, corresponding to a gain of 1.8 (3.1/1.7 min^−1/2), due to reduction of t₁-noise (Fig. 3G). This gain demonstrates the efficacy of refocusing the ¹H CSA across each recoupling block.

Fig. 3 ¹H{³⁵Cl} D-HMQC spectra of histidine hydrochloride monohydrate. (A–E) 1D ¹H{³⁵Cl} D-HMQC spectra (the first t₁-point from 2D experiments), and ³⁵Cl traces extracted from 2D ¹H{³⁵Cl} D-HMQC spectra at (F–J) ¹H δ_iso = 9.0 ppm, acquired using (top to bottom) conventional D-HMQC and TONE D-HMQC-1–4 pulse sequences. 2D ¹H{³⁵Cl} (K) conventional D-HMQC and (L) TONE D-HMQC-4 spectra. (M) ³⁵Cl traces extracted from 2D ¹H{³⁵Cl} spectra at ¹H δ_iso = 12.7 ppm for the five pulse sequences in order (top to bottom). Sensitivity (S), defined as the SNR per square root of unit time, is provided for all ³⁵Cl traces in units of min^−1/2. The 2D spectra were processed with the same contour floor level to aid the visual comparison of signal and noise.

Surprisingly the ¹H signal intensity given with TONE D-HMQC-2 was higher by ca. 16–19% in comparison to the conventional D-HMQC sequence (Fig. 3C). This result is unexpected because additional pulses typically reduce the efficiency of SSNMR experiments. With the addition of the π/2 flip-back pulse, the symmetry of the TONE D-HMQC-2 pulse sequence is reminiscent of the perfect echo pulse sequences,⁵⁷ which are known to refocus homonuclear ¹H couplings. 2-Spin ¹H–¹H SIMPSON numerical simulations and experiments with dipolar recoupled perfect echo pulse sequences show increased ¹H signal intensity, suggesting that the introduction of purge pulses (π/2 or LG spin-lock) may refocus ¹H homonuclear dipolar couplings (Fig. S3, ESI†). In summary, the intensity lost in TONE D-HMQC-1 due to the inefficiency of the inversion π pulses on the ³⁵Cl channel is compensated by the intensity gained from the partial refocusing of the ¹H homonuclear dipolar couplings by the purge pulse, resulting in an overall net gain in signal with TONE D-HMQC-2. The TONE D-HMQC-2 ³⁵Cl trace shows a similar intensity (I = 0.94) in comparison to the conventional D-HMQC spectrum, but the ³⁵Cl sensitivity is 2.1 times better with TONE D-HQMC-2. On comparing TONE D-HMQC-2 with TONE D-HMQC-1, we note that the intensity of the ³⁵Cl trace improves by a factor 1.74 (0.94/0.54), while there is only a modest gain in ³⁵Cl sensitivity by a factor 1.2 (3.6 min^−1/2/3.1 min^−1/2) (Fig. 3H). As t₁-noise is multiplicative, meaning it is proportional to the signal intensity, the t₁-noise is likely also higher in the case of TONE D-HMQC-2 and this leads to a smaller gain in sensitivity with respect to TONE D-HMQC-1.⁴⁵ A slight improvement in sensitivity could possibly be obtained with TONE D-HMQC-2 by removing pre-saturation pulses and adjusting the phase of the flip-back pulse to always return uncorrelated magnetization to +I_z. Preserving the uncorrelated magnetization could result in reduced optimal recycle delays as is observed with flip-back CP⁶⁶ or FS-HMQC sequences.³²Fig. 3D and I show the ¹H and ³⁵Cl traces, respectively, acquired using TONE D-HMQC-3 with a LG spin-lock trim pulse duration of 497.85 μs (25 rotor cycles). The 1D ¹H intensity is comparable to D-HMQC (0.98 and 1.15 for the ¹H signals at 9.0 and 12.7 ppm). The ³⁵Cl sensitivity improves to 5.4 min^−1/2, corresponding to an overall gain in sensitivity by a factor 3.2 (5.4 min^−1/2/1.7 min^−1/2) with respect to conventional D-HMQC. The duration of LG spin-lock trim pulse in TONE D-HMQC-3 should be experimentally optimized to find the best compromise between minimizing HMQC signal losses and eliminating t₁-noise (Fig. S5, ESI†).

Finally, we observe that TONE D-HMQC-4 with total LG spin-lock pulse duration of 1315.7 μs (33 rotor cycles) shows a reduction in ¹H signal by only ca. 6% as compared to D-HMQC (Fig. 3E). On comparing 1D ¹H{³⁵Cl} TONE D-HMQC-3 and TONE D-HMQC-4 spectra acquired with a two rotor cycle LG spin-lock duration, we observed that the TONE D-HMQC-4 ¹H signal is higher by ca. 20%, likely due to partial refocusing of ¹H homonuclear dipolar couplings (Fig. S6, ESI†). However, the rate of decay of the ¹H signal under the LG spin-lock is slightly faster with TONE D-HMQC-4 than TONE D-HMQC-3 (Fig. S5, ESI†) causing the HMQC intensities to become similar, despite the longer LG spin-lock duration used in TONE D-HMQC-4 (Fig. 3D and E). The signal loss in TONE D-HMQC-4 occurs due to residual ¹H–¹H spin-diffusion during the central LG pulses, likely between ¹H sites with the same chemical shift within the lattice.⁵⁹ When a correlated ¹H spin undergoes spin exchange (diffusion) with an uncorrelated ¹H spin, the ¹H HMQC signal is not refocused or recoupled properly, resulting in an increased rate of signal loss. Fig. 3J shows that the ³⁵Cl trace obtained with TONE D-HMQC-4 has a sensitivity of 4.4 min^−1/2. The overall gain in sensitivity with TONE D-HMQC-4 is 2.6 compared to conventional D-HMQC (Fig. 3E and J). The efficacy of t₁-noise elimination is evident from the comparison of 2D D-HMQC and 2D TONE D-HMQC-4 spectra shown in Fig. 3K and L. Additionally, the resolution of the ³⁵Cl trace offered by TONE D-HMQC-4 is dramatically higher than any other method because it is a constant-time sequence.³⁰ The LG pulses used in TONE D-HMQC-4 increase sensitivity as compared to a constant time D-HMQC experiment because the correlated ¹H magnetization will decay more slowly under the LG spin-lock than it does under transverse free-evolution (Fig. S5, ESI†).

Fig. S7 (ESI†) shows an additional pulse sequence, denoted as TONE D-HMQC-5, which combines TONE D-HMQC-3 and -4 to enable t₁-noise elimination and incremented t₁ periods. The resolution decreases slightly with the TONE D-HMQC-5 as compared to TONE D-HMQC-4 because relaxation during the variable LG spin-lock used in TONE D-HMQC-5 results in slight additional broadening of the indirect dimension signals (Fig. S5, ESI†). When the decay of the ¹H magnetization is slower under the LG spin-lock than for ¹H transverse relaxation, both TONE D-HMQC-4 and TONE D-HMQC-5 sequences are expected to perform similarly, whereas when the LG spin-lock decay rate is comparable to the transverse decay rate, TONE D-HMQC-5 will provide more signal, but with lower resolution.

³⁵Cl traces extracted from the 2D NMR spectra at a ¹H shift of 12.7 ppm demonstrates the feasibility of using the TONE D-HMQC sequences to observe correlations between weakly dipolar coupled spin pairs (Fig. 3M). A plane-wave density-functional theory (DFT) optimized structure of histidine shows that the shortest H–Cl distance (2.26 Å or dipolar coupling (b/2π) of 1021 Hz) corresponds to the ammonium ¹H signal at 9 ppm, in agreement with the observation that this ¹H signal shows the most intense correlations in the 2D D-HMQC spectra (Fig. 3K and Fig. S2, ESI†). Weaker ¹H–³⁵Cl heteronuclear correlations were observed in the 2D D-HQMC spectra for the amine ¹H NMR signal at 12.7 ppm and ammonium ¹H NMR signal at 17.2 ppm because of longer H–Cl internuclear distances and lower heteronuclear dipolar couplings (2.84 Å, b/2π = 514 Hz and 3.84 Å, b/2π = 208 Hz, respectively). Weak heteronuclear dipolar interactions will lead to smaller ratios of correlated magnetization to uncorrelated magnetization, which was predicted above to lead to increased t₁-noise. Consequently, with conventional D-HMQC it is very challenging, if not impossible, to observe the correlations between ³⁵Cl and the ¹H NMR signals at 12.7 ppm and 17.2 ppm with reasonable SNR (Fig. 3K and top slice in Fig. 3M). These correlations are even more challenging to observe at higher static magnetic fields due to the increase in ¹H CSA (Fig. S8, ESI†). Notably, as shown in Fig. 3L and Fig. S2 (ESI†), the ¹H–³⁵Cl correlations at a ¹H shift of 12.7 ppm and 17.2 ppm can be clearly observed with TONE D-HMQC-2–4, with TONE D-HMQC-4 providing the best resolution of the ³⁵Cl site. These results demonstrate the value of proton detected TONE D-HMQC sequences for indirectly detecting high resolution quadrupolar powder patterns of half-integer quadrupolar nuclei and extracting meaningful spatial proximity information from 2D HETCOR spectra.

The sensitivity of the TONE D-HMQC sequences can be further improved using the population transfer (PT) scheme.⁶⁷ In PT D-HMQC experiments, saturation pulses are applied to the satellite transitions of the quadrupolar spin concurrent with the ¹H recoupling scheme. The RAPT pulses⁶⁸ are easily incorporated into the TONE D-HMQC pulse sequences as shown in Fig. S9 and S10 (ESI†) providing further improvements in sensitivity by a factor 1.5–2. The ‘TONE’ concept can also be extended to D-HSQC experiments.^6,27 Fig. S11 (ESI†) shows that 1D ¹H{³⁵Cl} TONE D-HSQC has 10% higher signal in comparison to conventional D-HMQC. Notably, the ³⁵Cl NMR spectra obtained using TONE D-HSQC show similar resolution to those obtained with D-HMQC, suggesting the time constant for ¹H spin diffusion is similar to the ¹H T₂′ (Fig. S11 and S12, ESI†). Notably, the ³⁵Cl slice extracted from the 2D TONE D-HSQC spectrum has a sensitivity of 4.4 min^−1/2, which is comparable to the sensitivities obtained with the various TONE D-HMQC sequences (Fig. S11, ESI† and Fig. 3G–J). Therefore, the ideas presented in this article will also aid the further development of D-HSQC pulse sequences in the future.

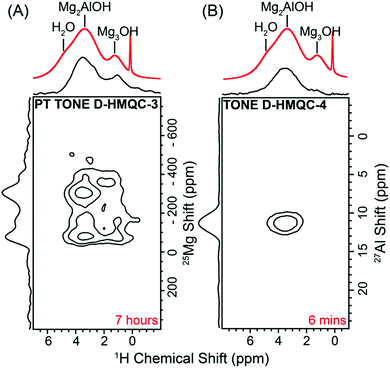
²⁵Mg solid-state NMR spectroscopy has been used for the characterization of metal–organic frameworks (MOFs),⁶⁹ layered double hydroxides,⁷⁰ and a number of other organic/inorganic compounds.⁷¹ Unfortunately, ²⁵Mg is a spin-5/2 quadrupolar nucleus with a low natural abundance of 10% and a low Larmor frequency (ca. 2.6 MHz T⁻¹), which makes observation of its NMR spectra at natural abundance very challenging. The development of natural abundance 2D ¹H{²⁵Mg} proton detected HETCOR methods to improve sensitivity and probe ¹H–²⁵Mg spatial proximities would be helpful for the characterization of magnesium containing materials. Fig. 4A shows the application of 2D ¹H{²⁵Mg} HETCOR solid-state NMR to Mg–Al layered double hydroxides.^72–74 The 1D ¹H spectrum (Fig. 4A, red trace) of the MgAl-27.8-NO₃⁻ sample (the molar percentage of Al³⁺ was determined using ICP) shows three signals corresponding to the Mg₃OH (1.2 ppm), Mg₂AlOH (3.3 ppm) and water sites (4.8 ppm), in good agreement with previous reports (Fig. S13, ESI†).^72–74 The ¹H signals at 1.2 and 3.3 ppm are both correlated to broad MAS ²⁵Mg second-order quadrupolar powder patterns. Simulations of these patterns give C_Q values of 4.5–4.8 MHz in agreement with previous studies (Fig. S14, ESI†).⁷³ Upon reducing the total dipolar recoupling from 1.732 to 0.8 ms, the correlation between the ¹H at 1.2 ppm and the expected brucite-like ²⁵Mg site becomes clearer (Fig. S14, ESI†). The observed correlations suggests an even mixing of Mg and Al rather than the formation of domains, in agreement with 2D ¹H SQ-DQ correlations experiments.⁷³ The result is further corroborated with ¹H{²⁷Al} TONE D-HMQC-4 experiments that show an intense correlation between the ¹H site at 3.3 ppm and the single ²⁷Al site (Fig. 4B). Notably, TONE D-HMQC-4 provides the highest resolution in the ²⁷Al spectrum amongst the D-HMQC and D-HSQC pulse sequences, while the best absolute ²⁷Al resolution is provided by ²⁷Al → ¹H D-RINEPT because ¹H heteronuclear decoupling can be applied during t₁ evolution (Fig. S15 and S16, ESI†). These results demonstrate the utility of fast MAS, proton detected TONE D-HMQC methods for the precise characterization of local structure in heterogeneous materials.

Fig. 4 (A) 2D ¹H{²⁵Mg} population transfer TONE D-HMQC-3 and (B) 2D ¹H{²⁷Al} TONE D-HMQC-4 spectra of MgAl-27.8-NO₃⁻ layered double hydroxide. The 1D ¹H spin echo spectrum is overlaid on top of both spectra (red traces). Spectra were acquired at 60 kHz MAS and B₀ = 9.4 T. The experiment times are indicated for each spectrum (bottom, red).

Due to efficient suppression of t₁-noise, the application of PT TONE DHMQC-3 results in a gain in sensitivity in the ²⁵Mg dimension by a factor 2.5 compared to ¹H{²⁵Mg} PT D-HMQC, while TONE D-HMQC-1 and 2 provide less sensitivity gain (Fig. S17, ESI†). TONE D-HMQC-4 produced a low quality spectrum due to a short ¹H T_1ρ under the LG spin-lock pulse (Fig. S18, ESI†). While it was not tested, TONE D-HMQC-5 would probably work well for this sample. TONE D-HMQC-4 provided a well-resolved ²⁵Mg quadrupolar pattern for magnesium hydroxide (Fig. S19, ESI†). These results suggest that judicious choice of TONE D-HMQC-2, -3 or -4 should be made based on the lifetime of the TONE D-HMQC signal under the LG spin-lock pulse. The lifetime can be easily determined by varying the LG spin-lock pulse and monitoring the 1D TONE D-HMQC signal intensities. While TONE D-HMQC-4 is a valuable experiment that can provide increased resolution in the indirect dimension, TONE D-HMQC-3 appears to provide the highest sensitivity (Fig. 4 and Fig. S17, ESI†). As explained in the previous section, TONE D-HMQC-4 is susceptible to signal losses due to residual spin-diffusion during the LG spin-lock pulse. This problem is exacerbated when the fraction of uncorrelated spins is higher and/or when the heteronuclear dipolar coupling constant is weaker.⁵⁹ Therefore, differences in the residual ¹H spin diffusion rate under the LG spin-lock pulse may explain the more negative impact on the TONE D-HMQC-4 experiments with ²⁵Mg than ²⁷Al (Fig. S18, ESI†). TONE D-HMQC-4 requires a LG spin-lock lifetime that is long enough to capture the decay of the indirect dimension signals and will only be effective in samples where the loss of signal due to this residual ¹H spin-diffusion is minimal. In cases, where TONE D-HMQC-4 is ineffective, TONE D-HMQC-3 or TONE D-HMQC-2 may work more efficiently as observed here. Based on the high efficiency of TONE D-HSQC observed with ¹H{³⁵Cl} experiments described earlier, we expect TONE D-HSQC to also be a suitable alternative.

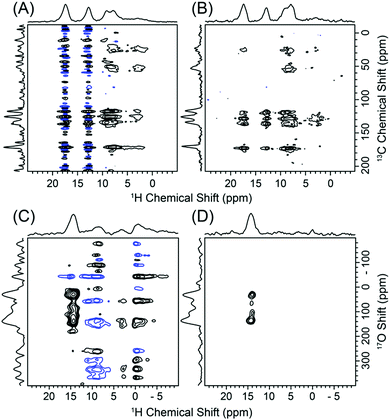
¹³C has a natural abundance of 1.1% which means that approximately 1% of protons in the sample may participate in the D-HMQC experiment and approximately 99% of the ¹H NMR signal must be canceled out through phase cycling.^27,75 Furthermore, the ca. 50% maximum efficiency of the dipolar recoupling induces further losses. Therefore, there is a high probability for the observation of t₁-noise in a natural abundance ¹H{¹³C} D-HMQC experiment, even with slight MAS instabilities of a few Hz. We note that ¹H{¹³C} idHETCOR pulse sequences that use efficient CP blocks for ¹H–¹³C magnetization transfer and saturation pulses to eliminate uncorrelated ¹H magnetization are preferred for proton-detected natural abundance ¹³C SSNMR.^11,13 However, as a proof-of-concept, ¹H{¹³C} D-HMQC experiments were performed with natural isotopic abundance histidine. As expected, there is considerable t₁-noise in the conventional 2D ¹H{¹³C} D-HMQC spectrum (Fig. 5A). The amine and ammonium ¹H NMR signals at 12.7 and 17.2 ppm display the most t₁ noise because both these sites also have the largest ¹H CSA. This result is consistent with the simulations presented above. Fig. 5B shows a TONE D-HMQC-3 spectrum that is essentially devoid of t₁-noise, similar to the ¹H–³⁵Cl data shown in Fig. 2. As shown in Fig. S20 (ESI†) while setting the relaxation delay according to Perras⁴⁵ also improves the signal to noise ratio, a far more successful approach is to simply eliminate t₁-noise at the source, demonstrating the value of TONE D-HMQC.

Fig. 5 (A and B) 2D ¹H{¹³C} spectra of histidine and (C and D) ¹H{¹⁷O} spectra of 20% ¹⁷O labeled fmoc-alanine obtained using (A) conventional D-HMQC, (B) TONE D-HMQC-3, (C) PT D-HMQC and (D) TONE D-HMQC-3 pulse sequences.

Fig. 5C shows a ¹H{¹⁷O} population transfer (PT) D-HMQC spectrum of 20% ¹⁷O labeled fmoc-alanine.⁷⁶ The t₁-noise arising from the large fraction of uncorrelated low-frequency ¹H signals in the D-HMQC spectrum is easily eliminated with the use of the TONE D-HMQC-3 method (Fig. 5D). Owing to the large ¹H–¹⁷O dipolar coupling (ca. 13.5 kHz) for the carboxylic acid proton at 14 ppm, each block is only 40 μs in duration in the D-HMQC experiments. Despite the fact that only a short recoupling time was required, TONE D-HMQC-3 still increases the sensitivity of ¹⁷O column at a ¹H chemical shift of 14 ppm by a factor of 1.5 as compared to PT D-HMQC. TONE D-HMQC-4 did not improve the ¹⁷O sensitivity further, likely because the correlated HMQC signal has a short lifetime under the LG spin-lock pulse, as was discussed earlier.

Conclusions

In conclusion, a series of modified D-HMQC pulse sequences, dubbed t₁-noise eliminated (TONE) D-HMQC were shown to reduce t₁-noise, permitting the acquisition of fast MAS, ¹H detected 2D HETCOR SSNMR spectra with ¹³C, ¹⁷O, ²⁷Al, ³⁵Cl and ²⁵Mg. The TONE sequences should offer better performance than conventional D-HMQC when there are experimental MAS frequency instabilities, the samples are dilute, the ¹H spins have large CSA, when the nuclei of interest have low abundance and/or have weak dipolar couplings to protons. The reduction of t₁-noise has been a long-standing challenge for ¹H detected D-HMQC SSNMR experiments. The application of TONE D-HMQC for the indirect detection of ³⁵Cl provided a gain in sensitivity by a factor 3 which results in a savings in time up to an order of magnitude, whereas, in case of ¹⁷O an enhancement of 1.5 was obtained. Notably, we have demonstrated that TONE D-HMQC can be used to obtain ¹H{²⁵Mg} heteronuclear correlation spectra of Mg–Al layered double hydroxides at natural abundance and provide a gain in sensitivity by a factor 2.5 in comparison to conventional D-HMQC.

Based upon the observations made here there are some general considerations to guide the selection of pulse sequence for ¹H detected fast MAS HMQC/HSQC experiments. The only disadvantage of the TONE D-HMQC-2 or TONE D-HSQC sequences as compared to conventional D-HMQC is that a π inversion pulse is required on the X channel. Hence, TONE D-HMQC-2 or TONE D-HSQC experiments are recommended in place of D-HMQC for indirect detection of spin-1/2 and half-integer quadrupolar nuclei. TONE D-HMQC-3, -4 and -5 pulse sequences utilize LG spin-lock pulses to eliminate t₁-noise and enhance indirect dimension resolution and were found to give better performance than TONE D-HMQC-2. The downside of the TONE D-HMQC-3, -4 and -5 pulse sequences is that LG pulse durations need to be optimized and the rf-field should be correctly selected. The LG spin-lock pulse ν₁ should be more than 2.5 × ν_r or between 0.1 × ν_r and 0.25 × ν_r to avoid rotary resonance conditions in fast MAS experiments.⁵⁹ LG trim pulses with durations between 250 μs and 1 ms were found to be sufficient to reduce the uncorrelated signal in the TONE D-HMQC-3–5 pulse sequences. Unfortunately the decay rate of spin-locked anti-phase magnetization (I_yS_z) during the LG spin-lock pulse is sample dependent, therefore the LG pulse duration should be experimentally optimized with both high- and low-rf field LG pulses to identify the best conditions. The LG pulse duration in the TONE D-HMQC-4 pulse sequence must be set to a duration greater than t_1,max, hence, this sequence is only applicable to samples which exhibit a slow decay of spin-locked anti-phase magnetization. For the TONE D-HMQC-5 pulse sequence, the duration of the first LG spin-lock pulse is set in the same way as TONE D-HMQC-3, whereas the second LG pulse block is applied throughout t₁ in an incremented fashion. Therefore, a slow decay of spin-locked anti-phase magnetization is also required for TONE D-HMQC-5 as well, although it will likely provide higher sensitivity than TONE D-HMQC-4. For experiments with half-integer quadrupolar nuclei, all the pulse sequences reported here can be performed with the population transfer (PT) scheme^67,77 (Fig. 1 and Fig. S7, S9 and S11, ESI†). In all cases PT was found to improve sensitivity. The use of PT necessitates optimization of the recoupling duration and the power and offset of satellite transition saturation pulses, although we have found that the same parameters for PT generally work well for a given nucleus. Finally, in cases where the ¹H T₁ is long or if the t₁-noise elimination by TONE is still insufficient, X → ¹H D-RINEPT experiments work well.³¹

The TONE D-HMQC and D-HSQC sequences presented here will allow the acquisition of HETCOR spectra with unreceptive and exotic nuclei, thereby widening the applicability of SSNMR. For instance, the techniques described here for ¹³C, ¹⁷O and ³⁵Cl should be applicable for the characterization of pure and formulated active pharmaceutical ingredients. ²⁵Mg and ²⁷Al experiments should be applicable to characterize a variety of inorganic materials or heterogeneous catalysts. It should also be possible to combine the sequences presented in this paper with other sensitivity enhancement techniques, such as dynamic nuclear polarization (DNP), where fast-MAS was recently introduced.^78,79 As pointed out previously, fast MAS DNP probes from Bruker may induce higher t₁-noise due to instabilities caused by the VT and Venturi gas flows.⁴⁵ TONE D-HMQC may enable correlation spectroscopy under DNP conditions with challenging nuclei. Such a combination would be of tremendous use for the characterization of materials and isotopes that were previously inaccessible using conventional solid-state NMR.

Experimental

NMR spectroscopy

Fast MAS experiments at 9.4 T were performed on a Bruker double resonance 1.3 mm HX probe, with a Bruker Avance III HD spectrometer and a wide-bore NMR magnet. 18.8 T ¹H{³⁵Cl} experiments were performed using a Bruker 1.3 mm HCN probe, a Bruker Avance III HD spectrometer and a 63 mm mid-bore magnet at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, Florida.

All samples were handled under ambient conditions and packed into zirconia rotors that were spun using N₂ gas for NMR experiments. ¹H rf calibrations were performed using a simple 90°-spin-lock sequence by determining the 0^th and 2^nd order rotary resonance conditions. The ²⁵Mg rf fields were calibrated using the Bloch–Siegert shift method reported by Hung et al.⁸⁰ The π/2 pulses used for ¹H, ¹³C, ¹⁷O, ²⁵Mg, ²⁷Al and ³⁵Cl were 2.5 μs, 2.5 μs, 4.75 μs, 10 μs, 13.0 μs and 4.75 μs, respectively. For the 18.8 T experiments, a ³⁵Cl π/2 pulse duration of 5.25 μs was used. Pulses on half-integer quadrupolar nuclei ¹⁷O, ²⁵Mg, ²⁷Al and ³⁵Cl were central-transition selective. A pulse duration of 1 μs was used for the 35° ¹H pulses that sandwich the LG spin-lock pulses. In all cases, the LG spin-lock pulses were applied off-resonance to satisfy the LG condition (Δν₀ = ν₁/√2, where Δν₀ is the calculated transmitter offset and ν₁ is the applied rf field).⁵⁹¹H–X heteronuclear dipolar recoupling was performed using the SR4²₁ dipolar recoupling sequence³³ at the 2^nd order rotary resonance condition in all cases. ¹H heteronuclear decoupling (in case of D-RINEPT experiments) was performed using pulses applied at the 0^th order rotary resonance condition (HORROR condition). ¹H pre-saturation was performed using a train of 90° pulses in all ¹H excitation experiments to equilibrate the ¹H magnetization before each scan. All 2D spectra were acquired using the States-TPPI method. 2D spectra are presented with skyline projects on the F₂ and F₁ axes unless mentioned otherwise. Further details for all experiments are provided below or in the respective figure captions.

¹H chemical shifts were indirectly referenced to neat tetramethylsilane by using adamantane (δ_iso(¹H) = 1.82 ppm). Topspin 3.6.1 was used to process all experimental NMR spectra. The average of four signal-to-noise ratio (SNR) measurements was considered while measuring SNR and calculating sensitivities. Care was taken to acquire and process spectra consistently before making comparisons.

¹H{³⁵Cl} experiments

L-Histidine·HCl·H₂O was used as received from Sigma Aldrich. All experiments were performed at 50 kHz MAS. The 9.4 T 2D ¹H{³⁵Cl} experiments were performed with 16 scans, a 3.1 s recycle delay (¹H T₁ is approximately 2.9 s) and 64 t₁ increments with an F₁ spectral width of 25 kHz. Optimal dipolar recoupling durations of 1.84 and 1.92 ms were used in the conventional and TONE D-HMQC experiments, respectively. The 2D ¹H{³⁵Cl} TONE D-HMQC-3 and 4 spectra were acquired with total LG spin-lock pulse durations of 25 rotor cycles and 66 rotor cycles, respectively. Note that the total duration of the LG spin-lock pulses in TONE D-HMQC-4 is set to a value greater than the maximum t₁ duration. The implementation of LG spin-lock pulses under fast MAS is described in detail in our previous report.⁵⁹ WURST pulses 38.0 μs in duration (followed by 2 μs of delay) with an rf field of 36 kHz were applied repeatedly in the RAPT blocks^68,81 used in PT D-HMQC experiments.^31,67,77 The frequency sweep width of the RAPT pulses was equal to the MAS frequency in all cases. The frequency offset of the WURST pulses was alternated between ±450 kHz.

In case of the 18.8 T 2D ¹H{³⁵Cl} experiments, optimal total dipolar recoupling durations of 1.52 and 1.76 ms were used in the conventional D-HMQC and TONE D-HMQC experiments, respectively. Total LG spin-lock pulses of durations 100 rotor cycles and 130 rotor cycles were applied at 150 kHz rf for the TONE D-HMQC-3 and 4 experiments, respectively. 38.0 μs WURST pulses were applied at an rf field of ca. 26 kHz on the ³⁵Cl to achieve population transfer. The frequency offset of the WURST pulses was alternated between ±200 kHz.

¹H{²⁵Mg} and ¹H{²⁷Al} experiments on the layered double hydroxide (LDH)

The magnesium LDH sample was synthesized using a previously reported procedure.⁷⁰ ICP indicated that the Al and Mg contents of the sample are ca. 27.8 and 33.9%, respectively. The powder X-ray diffraction (PXRD) pattern of the MgAl-27.8-NO₃⁻ sample is provided in Fig. S13 (ESI†). All solid-state NMR experiments were performed with a 60 kHz MAS frequency and a 9.4 T static magnetic field. A ¹H T₁ relaxation constant of 1 s was measured using a saturation recovery experiment. ¹H{²⁵Mg} (TONE) D-HMQC 2D spectra were acquired with 128 or 256 scans, 1.1 s recycle delay and 64 t₁ increments with a 60 kHz F₁ spectral width. The short recoupling time PT TONE D-HMQC-3 spectrum shown in Fig. S14 (ESI†) was obtained using 896 scans. Population transfer was performed using 31.34 μs WURST pulses with a 27 kHz rf field. The frequency offset of the WURST pulse was alternated between ±350 kHz. Total dipolar recoupling durations of 1.732–1.8 ms were used in the optimal (long) recoupling time experiments whereas 0.8 ms was used in the short recoupling time experiments (Fig. S14, ESI†). LG spin-lock pulses 60–75 rotor cycles in duration were applied in case of TONE D-HMQC-3 experiments whereas the total LG pulse duration was set to 120 rotor cycles in case of TONE D-HMQC-4. The rf field for the LG spin-lock pulses was 150 kHz in both cases.

¹H{²⁷Al} (TONE) D-HMQC and TONE D-HSQC 1Ds were obtained with 128 scans and 1.1 s recycle delay whereas the 2Ds were obtained with 8 scans, 1.1 s recycle delay and 40 t₁ increments with a 6 kHz F₁ spectral width. The 2D D-RINEPT experiment differed only in the recycle delay and the number of scans which were set to 0.2 s and 40 (512 scans for the 1D), respectively. Optimal dipolar recoupling durations of 0.532–0.932 ms were used. LG spin-lock pulses were applied at 150 kHz rf for durations of 15 and 204 rotor cycles in TONE D-HMQC-3 and TONE D-HMQC-4, respectively.

¹H{²⁵Mg} experiments on magnesium hydroxide

Experiments were performed with a 60 kHz MAS frequency and a 9.4 T static magnetic field. An optimal recycle delay of 4.42 s (¹H T₁ = 3.4 s), 48 scans, 48 t₁ increments with a F₁ spectral width of 30 kHz was used to acquire the 2D ¹H{²⁵Mg} spectra. An optimal total recoupling duration of 1.2 ms was used in all D-HMQC experiments. The total LG spin-lock pulse durations was set to 15 and 50 rotor cycles in TONE D-HMQC-3 and 4, respectively and the applied rf field was 150 kHz. 31.34 μs WURST pulses with a 27 kHz rf field were used for population transfer. The frequency offset of the WURST pulses was alternated between ±350 kHz.

¹H{¹³C} experiments

Experiments were performed with a 50 kHz MAS frequency and a 9.4 T static magnetic field. Some experimental details are provided in the figure caption of Fig. S20 (ESI†). The LG spin-lock duration in TONE D-HMQC-3 was set to 1 ms (50 rotor cycles) and applied at a rf field of 150 kHz, without the use of 35° pulses sandwiching the LG spin-lock. An optimized total dipolar recoupling duration of 1.28 ms was used in all experiments.

¹H{¹⁷O} experiments

Experiments were performed with a 50 kHz MAS frequency and a 9.4 T static magnetic field. ¹⁷O labeled fmoc-alanine obtained as described previously.⁷⁶ 2D spectra were acquired with 32 scans, 6.11 s recycle delay (1.3 × T₁), 64 t₁ increments with a 50 kHz F₁ spectral width. The total duration of the SR4²₁ recoupling was 80 μs and 160 μs for PT D-HMQC and TONE D-HMQC-3, respectively. For the TONE D-HMQC-3 spectrum the LG spin-lock trim pulse with a duration of 100 rotor cycles was applied with a 130 kHz rf field. Population transfer was performed using 38.0 μs WURST pulses with a 44 kHz rf field. The frequency offset of the WURST pulses was alternated between ±400 kHz.

Simulations of MAS frequency profiles

Numerical simulations were performed using SIMPSON v4.1.1.^62–64 The SIMPSON input files used for the D-HMQC and TONE D-HMQC-2 simulations are provided with the ESI.† All pulses in the simulations were of finite duration except the ¹H refocusing (π) pulses which were ideal. The rep 168 (α, β) crystal file was used and the gamma angles was set to 32. The correlated and uncorrelated signals were selected by filtering the density matrix for coherence orders 1 and −1 (uncorrelated intensity) or 2, 0 and −2 (correlated intensity). The filter was applied after the first 90° pulse on the ¹³C channel. The MAS frequency was varied systematically from 49 800 Hz to 50 200 Hz in steps of 20 Hz to obtain the profiles shown in Fig. 2A–D. Simulations with a finer 1 Hz stepping of the MAS frequency yielded similar profiles. The simulated profiles were fit to Lorentz/Gauss functions as described in the main text. ¹H CSA values derived from CASTEP correspond to the anisotropy (Δδ) in the Haeberlen convention and the corresponding reduced anisotropy (δ = 2Δδ/3) was input into SIMPSON.

Monte Carlo simulations of t₁-noise

MATLAB 9.8.0 (R2020a) was used to perform the Monte-Carlo simulations shown in Fig. 2. Examples of the MATLAB code used are provided with the ESI.† The X T₂* and ¹H T₂′ were set to 250 μs and 500 μs in all simulations based on estimates from experimental ³⁵Cl and ¹H spectra of histidine at 9.4 T and 50 kHz MAS. RMN 2.0.2⁸² was used to process the simulated FIDs and measure SNR. The simulated FIDs were zero-filled up to 1024 points prior to addition of thermal noise and Fourier transformation. Care was taken to ensure that the standard deviation of the added thermal noise was proportional to the maximum signal value in the FID.

Plane-wave DFT calculations

DFT calculations on the histidine and fmoc-alanine were performed using CASTEP⁸³ with the PBE-GGA functional,⁸⁴ TS dispersion correction scheme⁸⁵ and ultra-soft pseudopotentials.⁸⁶ Hydrogen atom positions were optimized prior to performing the NMR calculations. The GIPAW method⁸⁷ with the Zero-Order Relativistic Approximation (ZORA)⁸⁸ was used to calculate the magnetic shielding tensors. A k-point spacing of 0.07 Å⁻¹ was used for the Monkhorst–Pack grid.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The Ames Laboratory is operated for the U.S. DOE by Iowa State University under contract # DE-AC02-07CH11358. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-1644779 and the State of Florida.

References

1. D. D. Laws, H. M. L. Bitter and A. Jerschow, Solid-state NMR spectroscopic methods in chemistry, Angew. Chem., Int. Ed., 2002, 41(17), 3096–3129.
2. C. Dybowski and S. Bal, Solid-state NMR spectroscopy, Anal. Chem., 2008, 80(12), 4295–4300.
3. A. Lesage, Recent advances in solid-state NMR spectroscopy of spin I = 1/2 nuclei, Phys. Chem. Chem. Phys., 2009, 11(32), 6876–6891.
4. S. E. Ashbrook and S. Sneddon, New Methods and Applications in Solid-State NMR Spectroscopy of Quadrupolar Nuclei, J. Am. Chem. Soc., 2014, 136(44), 15440–15456.
5. M. Deschamps, Ultrafast Magic Angle Spinning Nuclear Magnetic Resonance, Annu. Rep. NMR Spectrosc., 2014, 81, 109–144.
6. Y. Nishiyama, Fast magic-angle sample spinning solid-state NMR at 60–100 kHz for natural abundance samples, Solid State Nucl. Magn. Reson., 2016, 78, 24–36.
7. R. C. Zhang, K. H. Mroue and A. Ramamoorthy, Proton-Based Ultrafast Magic Angle Spinning Solid-State NMR Spectroscopy, Acc. Chem. Res., 2017, 50(4), 1105–1113.
8. Y. Ishii and R. Tycko, Sensitivity Enhancement in Solid State ¹⁵N NMR by Indirect Detection with High-Speed Magic Angle Spinning, J. Magn. Reson., 2000, 142(1), 199–204.
9. I. Schnell, B. Langer, S. H. M. Sontjens, M. H. P. van Genderen, R. P. Sijbesma and H. W. Spiess, Inverse Detection and Heteronuclear Editing in ¹H-¹⁵N Correlation and ¹H–¹H Double-Quantum NMR Spectroscopy in the Solid State under Fast MAS, J. Magn. Reson., 2001, 150(1), 57–70.
10. E. K. Paulson, C. R. Morcombe, V. Gaponenko, B. Dancheck, R. A. Byrd and K. W. Zilm, Sensitive High Resolution Inverse Detection NMR Spectroscopy of Proteins in the Solid State, J. Am. Chem. Soc., 2003, 125(51), 15831–15836.
11. J. W. Wiench, C. E. Bronnimann, V. S. Y. Lin and M. Pruski, Chemical Shift Correlation NMR Spectroscopy with Indirect Detection in Fast Rotating Solids: Studies of Organically Functionalized Mesoporous Silicas, J. Am. Chem. Soc., 2007, 129(40), 12076–12077.
12. D. H. Zhou, G. Shah, M. Cormos, C. Mullen, D. Sandoz and C. M. Rienstra, Proton-detected solid-state NMR Spectroscopy of fully protonated proteins at 40 kHz magic-angle spinning, J. Am. Chem. Soc., 2007, 129(38), 11791–11801.
13. T. Kobayashi; Y. Nishiyama and M. Pruski, Heteronuclear Correlation Solid-state NMR Spectroscopy with Indirect Detection under Fast Magic-Angle Spinning, in Modern Methods in Solid-state NMR: A Practitioner's Guide, ed. P. Hodgkinson, The Royal Society of Chemistry, 2018, pp. 1–38.
14. A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Dynamic Nuclear Polarization Surface Enhanced NMR Spectroscopy, Acc. Chem. Res., 2013, 46(9), 1942–1951.
15. A. S. L. Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102, 120–195.
16. K. O. Tan, S. Jawla, R. J. Temkin and R. G. Griffin, Pulsed Dynamic Nuclear Polarization, eMagRes, 2019, 8(3), 339–351.
17. A. Pines, M. G. Gibby and J. S. Waugh, Proton-Enhanced NMR of Dilute Spins in Solids, J. Chem. Phys., 1973, 59(2), 569–590.
18. A. J. Vega, MAS NMR Spin Locking of Half-Integer Quadrupolar Nuclei, J. Magn. Reson., 1992, 96(1), 50–68.
19. F. A. Perras, T. Kobayashi and M. Pruski, PRESTO polarization transfer to quadrupolar nuclei: implications for dynamic nuclear polarization, Phys. Chem. Chem. Phys., 2015, 17(35), 22616–22622.
20. A. Bax, R. H. Griffey and B. L. Hawkins, Sensitivity-Enhanced Correlation of N-15 and H-1 Chemical-Shifts in Natural-Abundance Samples Via Multiple Quantum Coherence, J. Am. Chem. Soc., 1983, 105(24), 7188–7190.
21. D. Iuga, C. Morais, Z. H. Gan, D. R. Neuville, L. Cormier and D. Massiot, NMR heteronuclear correlation between quadrupolar nuclei in solids, J. Am. Chem. Soc., 2005, 127(33), 11540–11541.
22. S. Cavadini, S. Antonijevic, A. Lupulescu and G. Bodenhausen, Indirect Detection of Nitrogen-14 in Solids via Protons by Nuclear Magnetic Resonance Spectroscopy, J. Magn. Reson., 2006, 182(1), 168–172.
23. Z. H. Gan, Measuring amide nitrogen quadrupolar coupling by high-resolution N-14/C-13 NMR correlation under magic-angle spinning, J. Am. Chem. Soc., 2006, 128(18), 6040–6041.
24. Z. H. Gan, J. P. Amoureux and J. Trebosc, Proton-detected N-14 MAS NMR using homonuclear decoupled rotary resonance, Chem. Phys. Lett., 2007, 435(1–3), 163–169.
25. S. Cavadini, S. Antonijevic, A. Lupulescu and G. Bodenhausen, Indirect Detection of Nitrogen-14 in Solid-State NMR Spectroscopy, ChemPhysChem, 2007, 8(9), 1363–1374.
26. J. Trebosc, B. Hu, J. P. Amoureux and Z. Gan, Through-Space R³-HETCOR Experiments between Spin-1/2 and Half-Integer Quadrupolar Nuclei in Solid-State NMR, J. Magn. Reson., 2007, 186(2), 220–227.
27. O. Lafon, Q. Wang, B. W. Hu, F. Vasconcelos, J. Trebosc, S. Cristol, F. Deng and J. P. Amoureux, Indirect Detection via Spin-1/2 Nuclei in Solid State NMR Spectroscopy: Application to the Observation of Proximities between Protons and Quadrupolar Nuclei, J. Phys. Chem. A, 2009, 113(46), 12864–12878.
28. G. Tricot, J. Trebosc, F. Pourpoint, R. Gauvin and L. Delevoye, The D-HMQC MAS-NMR Technique: An Efficient Tool for the Editing of Through-Space Correlation Spectra Between Quadrupolar and Spin-1/2 (P-31, Si-29, H-1, C-13) Nuclei, Annu. Rep. NMR Spectrosc., 2014, 81, 145–184.
29. K. C. Szeto, N. Merle, J. Trebosc, M. Taoufik, R. M. Gauvin, F. Pourpoint and L. Delevoye, Caveat on the Actual Robustness of Heteronuclear NMR Methods for Probing the Surface of gamma-Alumina and Related Catalysts, J. Phys. Chem. C, 2019, 123(20), 12919–12927.
30. A. J. Rossini, M. P. Hanrahan and M. Thuo, Rapid Acquisition of Wideline MAS Solid-State NMR Spectra with Fast MAS, Proton Detection, and Dipolar HMQC Pulse Sequences, Phys. Chem. Chem. Phys., 2016, 18(36), 25284–25295.
31. A. Venkatesh, M. P. Hanrahan and A. J. Rossini, Proton detection of MAS solid-state NMR spectra of half-integer quadrupolar nuclei, Solid State Nucl. Magn. Reson., 2017, 84, 171–181.
32. A. V. Wijesekara, A. Venkatesh, B. J. Lampkin, B. VanVeller, J. W. Lubach, K. Nagapudi, I. Hung, P. L. Gor'kov, Z. Gan and A. J. Rossini, Fast Acquisition of Proton-Detected HETCOR Solid-State NMR Spectra of Quadrupolar Nuclei and Rapid Measurement of NH Bond Lengths by Frequency Selective HMQC and RESPDOR Pulse Sequences, Chem. – Eur. J., 2020, 26(35), 7881–7888.
33. A. Brinkmann and A. P. M. Kentgens, Proton-Selective ¹⁷O–¹H Distance Measurements in Fast Magic Angle Spinning Solid-State NMR Spectroscopy for the Determination of Hydrogen Bond Lengths, J. Am. Chem. Soc., 2006, 128(46), 14758–14759.
34. A. F. Mehlkopf, D. Korbee, T. A. Tiggelman and R. Freeman, Sources of t1 Noise in Two-Dimensional NMR, J. Magn. Reson., 1984, 58(2), 315–323.
35. N. T. Duong, F. Rossi, M. Makrinich, A. Goldbourt, M. R. Chierotti, R. Gobetto and Y. Nishiyama, Accurate H-1-N-14 distance measurements by phase-modulated RESPDOR at ultra-fast MAS, J. Magn. Reson., 2019, 308.
36. G. Otting, Chapter 8 Use of high power spin-lock purge pulses in high resolution NMR spectroscopy, in Analytical Spectroscopy Library, ed. G. Batta, K. E. Kövér and C. Szántay, Elsevier, 1997, vol. 8, pp. 149–171.
37. J. R. Garbow, D. P. Weitekamp and A. Pines, Bilinear Rotation Decoupling of Homonuclear Scalar Interactions, Chem. Phys. Lett., 1982, 93(5), 504–509.
38. A. Bax and S. Subramanian, Sensitivity-Enhanced Two-Dimensional Heteronuclear Shift Correlation Nmr-Spectroscopy, J. Magn. Reson., 1986, 67(3), 565–569.
39. R. E. Hurd and B. K. John, Gradient-Enhanced Proton-Detected Heteronuclear Multiple-Quantum Coherence Spectroscopy, J. Magn. Reson., 1991, 91(3), 648–653.
40. N. Manoleras and R. S. Norton, Spectral Processing Methods for the Removal of T1 Noise and Solvent Artifacts from Nmr-Spectra, J. Biomol. NMR, 1992, 2(5), 485–494.
41. A. Gibbs, G. A. Morris, A. G. Swanson and D. Cowburn, Suppression of T1 Noise in 2d-Nmr Spectroscopy by Reference Deconvolution, J. Magn. Reson., Ser. A, 1993, 101(3), 351–356.
42. J. M. Nuzillard and R. Freeman, Oversampling in 2-Dimensional Nmr, J. Magn. Reson., Ser. A, 1994, 110(2), 252–256.
43. H. P. Mo, J. S. Harwood, D. Z. Yang and C. B. Post, A simple method for NMR t(1) noise suppression, J. Magn. Reson., 2017, 276, 43–50.
44. L. Song, J. Wang, X. Su, X. Zhang, C. Li, X. Zhou, D. Yang, B. Jiang and M. Liu, REAL-t1, an Effective Approach for t1-Noise Suppression in NMR Spectroscopy Based on Resampling Algorithm, Chin. J. Chem., 2020, 38(1), 77–81.
45. F. A. Perras and M. Pruski, Reducing t(1) noise through rapid scanning, J. Magn. Reson., 2019, 298, 31–34.
46. A. J. Robertson, M. K. Pandey, A. Marsh, Y. Nishiyama and S. P. Brown, The use of a selective saturation pulse to suppress t(1) noise in two-dimensional H-1 fast magic angle spinning solid-state NMR spectroscopy, J. Magn. Reson., 2015, 260, 89–97.
47. H. Nagashima, A. S. L. Thankamony, J. Trebosc, F. Pourpoint, O. Lafon and J. P. Amoureux, gamma-Independent through-space hetero-nuclear correlation between spin-1/2 and quadrupolar nuclei in solids, Solid State Nucl. Magn. Reson., 2017, 84, 216–226.
48. B. Hu, J. Trebosc and J. P. Amoureux, Comparison of several hetero-nuclear dipolar recoupling NMR methods to be used in MAS HMQC/HSQC, J. Magn. Reson., 2008, 192(1), 112–122.
49. H. Nagashima, A. S. L. Thankamony, J. Trebosc, L. Montagne, G. Kerven, J. P. Amoureux and O. Lafon, Observation of proximities between spin-1/2 and quadrupolar nuclei in solids: Improved robustness to chemical shielding using adiabatic symmetry-based recoupling, Solid State Nucl. Magn. Reson., 2018, 94, 7–19.
50. J. A. Jarvis, I. M. Haies, P. T. F. Williamson and M. Carravetta, An efficient NMR method for the characterisation of N-14 sites through indirect C-13 detection, Phys. Chem. Chem. Phys., 2013, 15(20), 7613–7620.
51. I. Hung, P. Gor’kov and Z. H. Gan, Efficient and sideband-free H-1-detected N-14 magic-angle spinning NMR, J. Chem. Phys., 2019, 151(15), 154202.
52. I. Hung and Z. Gan, High-Resolution NMR of S = 3/2 Quadrupole Nuclei by Detection of Double-Quantum Satellite Transitions via Protons, J. Phys. Chem. Lett., 2020, 4734–4740.
53. O. W. Sorensen, G. W. Eich, M. H. Levitt, G. Bodenhausen and R. R. Ernst, Product Operator-Formalism for the Description of Nmr Pulse Experiments, Prog. Nucl. Magn. Reson. Spectrosc., 1983, 16, 163–192.
54. M. Carravetta, M. Eden, X. Zhao, A. Brinkmann and M. H. Levitt, Symmetry principles for the design of radiofrequency pulse sequences in the nuclear magnetic resonance of rotating solids, Chem. Phys. Lett., 2000, 321(3–4), 205–215.
55. J. M. Vinther, A. B. Nielsen, M. Bjerring, E. R. H. van Eck, A. P. M. Kentgens, N. Khaneja and N. C. Nielsen, Refocused continuous-wave decoupling: A new approach to heteronuclear dipolar decoupling in solid-state NMR spectroscopy, J. Chem. Phys., 2012, 137(21), 214202.
56. E. G. Keeler, K. J. Fritzsching and A. E. McDermott, Refocusing CSA during magic angle spinning rotating-frame relaxation experiments, J. Magn. Reson., 2018, 296, 130–137.
57. T. Parella, Towards perfect NMR: Spin-echo versus perfect-echo building blocks, Magn. Reson. Chem., 2019, 57(1), 13–29.
58. A. Brinkmann and M. H. Levitt, Symmetry principles in the nuclear magnetic resonance of spinning solids: Heteronuclear recoupling by generalized Hartmann-Hahn sequences, J. Chem. Phys., 2001, 115(1), 357–384.
59. A. Venkatesh, I. Hung, K. C. Boteju, A. D. Sadow, P. L. Gor’kov, Z. H. Gan and A. J. Rossini, Suppressing H-1 Spin Diffusion in Fast MAS Proton Detected Heteronuclear Correlation Solid-State NMR Experiments, Solid State Nucl. Magn. Reson., 2020, 105, 101636.
60. S. Cavadini, V. Vitzthum, S. Ulzega, A. Abraham and G. Bodenhausen, Line-narrowing in proton-detected nitrogen-14 NMR, J. Magn. Reson., 2010, 202(1), 57–63.
61. M. Shen, J. Trebosc, O. Lafon, F. Pourpoint, B. W. Hu, Q. Chen and J. P. Amoureux, Improving the resolution in proton-detected through-space heteronuclear multiple quantum correlation NMR spectroscopy, J. Magn. Reson., 2014, 245, 38–49.
62. M. Bak, J. T. Rasmussen and N. C. Nielsen, SIMPSON: A General Simulation Program for Solid-State NMR Spectroscopy, J. Magn. Reson., 2000, 147(2), 296–330.
63. Z. Tosner, T. Vosegaard, C. Kehlet, N. Khaneja, S. J. Glaser and N. C. Nielsen, Optimal Control in NMR Spectroscopy: Numerical Implementation in SIMPSON, J. Magn. Reson., 2009, 197(2), 120–134.
64. Z. Tosner, R. Andersen, B. Stevenss, M. Eden, N. C. Nielsen and T. Vosegaard, Computer-Intensive Simulation of Solid-State NMR Experiments using SIMPSON, J. Magn. Reson., 2014, 246, 79–93.
65. E. Mihaliuk and T. Gullion, Adding a lens Improves spinning speed characterization, Solid State Nucl. Magn. Reson., 2015, 72, 4–8.
66. J. Tegenfeldt and U. Haeberlen, Cross Polarization in Solids with Flip-Back of I-Spin Magnetization, J. Magn. Reson., 1979, 36(3), 453–457.
67. Q. Wang, Y. X. Li, J. Trebosc, O. Lafon, J. Xu, B. W. Hu, N. D. Feng, Q. Chen, J. P. Amoureux and F. Deng, Population transfer HMQC for half-integer quadrupolar nuclei, J. Chem. Phys., 2015, 142(9), 094201.
68. Z. Yao, H. T. Kwak, D. Sakellariou, L. Emsley and P. J. Grandinetti, Sensitivity enhancement of the central transition NMR signal of quadrupolar nuclei under magic-angle spinning, Chem. Phys. Lett., 2000, 327(1–2), 85–90.
69. J. Xu, V. V. Terskikh and Y. N. Huang, Mg-25 Solid-State NMR: A Sensitive Probe of Adsorbing Guest Molecules on a Metal Center in Metal-Organic Framework CPO-27-Mg, J. Phys. Chem. Lett., 2013, 4(1), 7–11.
70. P. J. Sideris, U. G. Nielsen, Z. H. Gan and C. P. Grey, Mg/Al ordering in layered double hydroxides revealed by multinuclear NMR spectroscopy, Science, 2008, 321(5885), 113–117.
71. L. S. Cahill, J. V. Hanna, A. Wong, J. C. C. Freitas, J. R. Yates, R. K. Harris and M. E. Smith, Natural Abundance Mg-25 Solid-State NMR of Mg Oxyanion Systems: A Combined Experimental and Computational Study, Chem. – Eur. J., 2009, 15(38), 9785–9798.
72. S. Cadars, G. Layrac, C. Gerardin, M. Deschamps, J. R. Yates, D. Tichit and D. Massiot, Identification and Quantification of Defects in the Cation Ordering in Mg/Al Layered Double Hydroxides, Chem. Mater., 2011, 23(11), 2821–2831.
73. P. J. Sideris, F. Blanc, Z. H. Gan and C. P. Grey, Identification of Cation Clustering in Mg-Al Layered Double Hydroxides Using Multinuclear Solid State Nuclear Magnetic Resonance Spectroscopy, Chem. Mater., 2012, 24(13), 2449–2461.
74. L. Zhao, Z. Qi, F. Blanc, G. Y. Yu, M. Wang, N. H. Xue, X. K. Ke, X. F. Guo, W. P. Ding, C. P. Grey and L. M. Peng, Investigating Local Structure in Layered Double Hydroxides with O-17 NMR Spectroscopy, Adv. Funct. Mater., 2014, 24(12), 1696–1702.
75. M. Shen, S. Wegner, J. Trebosc, B. Hu, O. Lafon and J. P. Amoureux, Minimizing the t(1)-noise when using an indirect H-1 high-resolution detection of unlabeled samples, Solid State Nucl. Magn. Reson., 2017, 87, 111–116.
76. S. L. Carnahan, B. J. Lampkin, P. Naik, M. P. Hanrahan, I. I. Slowing, B. VanVeller, G. Wu and A. J. Rossini, Probing O-H Bonding through Proton Detected H-1-O-17 Double Resonance Solid-State NMR Spectroscopy, J. Am. Chem. Soc., 2019, 141(1), 441–450.
77. Q. Wang, J. Trebosc, Y. Li, J. Xu, B. Hu, N. Feng, Q. Chen, O. Lafon, J.-P. Amoureux and F. Deng, Signal enhancement of J-HMQC experiments in solid-state NMR involving half-integer quadrupolar nuclei, Chem. Commun., 2013, 49(59), 6653–6655.
78. S. R. Chaudhari, D. Wisser, A. C. Pinon, P. Berruyer, D. Gajan, P. Tordo, O. Ouari, C. Reiter, F. Engelke, C. Coperet, M. Lelli, A. Lesage and L. Emsley, Dynamic Nuclear Polarization Efficiency Increased by Very Fast Magic Angle Spinning, J. Am. Chem. Soc., 2017, 139(31), 10609–10612.
79. M. M. Lu, M. Z. Wang, I. V. Sergeyev, C. M. Quinn, J. Struppe, M. Rosay, W. Maas, A. M. Gronenborn and T. Polenova, F-19 Dynamic Nuclear Polarization at Fast Magic Angle Spinning for NMR of HIV-1 Capsid Protein Assemblies, J. Am. Chem. Soc., 2019, 141(14), 5681–5691.
80. I. Hung, P. Gor’kov and Z. H. Gan, Using the heteronuclear Bloch-Siegert shift of protons for B-1 calibration of insensitive nuclei not present in the sample, J. Magn. Reson., 2020, 310, 106636.
81. S. Prasad, H.-T. Kwak, T. Clark and P. J. Grandinetti, A Simple Technique for Determining Nuclear Quadrupole Coupling Constants with RAPT Solid-State NMR Spectroscopy, J. Am. Chem. Soc., 2002, 124(18), 4964–4965.
82. RMN 2.0, 2.0; PhySy Ltd.: Grandview Heights, OH, USA, 2019, https://www.physyapps.com/rmn.
83. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First Principles Methods using CASTEP, Z. Kristallogr., 2005, 220(5–6), 567–570.
84. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
85. A. Tkatchenko and M. Scheffler, Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102(7), 073005.
86. J. R. Yates, C. J. Pickard and F. Mauri, Calculation of NMR Chemical Shifts for Extended Systems using Ultrasoft Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(2), 024401.
87. C. J. Pickard and F. Mauri, All-Electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(24), 245101.
88. T. F. G. Green and J. R. Yates, Relativistic Nuclear Ragnetic Resonance J-Coupling with Ultrasoft Pseudopotentials and the Zeroth-Order Regular Approximation, J. Chem. Phys., 2014, 140(23), 234106.

---

Footnote

† Electronic supplementary information (ESI) available: Additional tables, figures, pulse programs, SIMPSON input files, 2D NMR datasets and MATLAB scripts. See DOI: 10.1039/d0cp03511d

---