Elimination of fast variables in stochastic nonlinear kinetics

Abstract

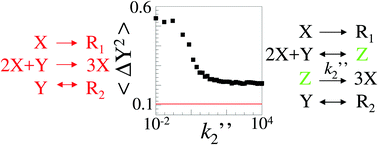
A reduced chemical scheme involving a small number of variables is often sufficient to account for the deterministic evolution of the concentration of the main species contributing to a reaction. However, its predictions are questionable in small systems used, for example in fluorescence correlation spectroscopy (FCS) or in explosive systems involving strong nonlinearities such as autocatalytic steps. We make precise dynamical criteria defining the validity domain of the quasi-steady-state approximation and the elimination of a fast concentration in deterministic dynamics. Designing two different three-variable models converging toward the same two-variable model, we show that the variances and covariance of the fluctuations of the slow variables are not correctly predicted using the two-variable model, even in the limit of a large system size. The more striking weaknesses of the reduced scheme are figured out in mesoscaled systems containing a small number of molecules. The results of two stochastic approaches are compared and the shortcomings of the Langevin equations with respect to the master equation are pointed out. We conclude that the description of the fluctuations and their coupling with nonlinearities of deterministic dynamics escape reduced chemical schemes.