Open Access Article
Open Access ArticleA statistical thermodynamics view of electron density polarisation: application to chemical selectivity
Frédéric
Guégan
 *a,
Vincent
Tognetti
*a,
Vincent
Tognetti
 b,
Jorge I.
Martínez-Araya
b,
Jorge I.
Martínez-Araya
 c,
Henry
Chermette
c,
Henry
Chermette
 d,
Lynda
Merzoud
d,
Alejandro
Toro-Labbé
e and
Christophe
Morell
d,
Lynda
Merzoud
d,
Alejandro
Toro-Labbé
e and
Christophe
Morell
 *d
*d
aIC2MP UMR 7285, Université de Poitiers - CNRS, 4, rue Michel Brunet TSA, 51106-86073 Cedex 9 Poitiers, France. E-mail: frederic.guegan@univ-poitiers.fr
bNormandy Univ., COBRA UMR 6014 - FR 3038, Université de Rouen, INSA Rouen, CNRS, 1 rue Tesniére, 76821 Mont St Aignan, Cedex, France
cDepartamento de Ciencias Químicas, Facultad de Ciencias Exactas, Universidad Andres Bello (UNAB), Av. República 498, Santiago, Chile
dUniversité de Lyon, Institut des Sciences Analytiques, UMR 5280, CNRS, Université Lyon 1 - 5, rue de la Doua, F-69100 Villeurbanne, France. E-mail: christophe.morell@univ-lyon1.fr
eLaboratorio de Química Teórica Computacional (QTC), Facultad de Química, Pontificia Universidad Católica de Chile, Santiago 7820436, Chile
First published on 21st September 2020
Abstract
A fundamental link between conceptual density functional theory and statistical thermodynamics is herein drawn, showing that intermolecular electrostatic interactions can be understood in terms of effective work and heat exchange. From a more detailed analysis of the heat exchange in a perturbation theory framework, an associated entropy can be subsequently derived, which appears to be a suitable descriptor for the local polarisability of the electron density. A general rule of thumb is evidenced: the more the perturbation can be spread, both through space and among the excited states, the larger the heat exchange and entropy.
1 Introduction
From the very beginning, density functional theory (DFT) and thermodynamics have been closely connected.1 This analogy very likely started with the treatment of a set of electrons as an inhomogeneous gas by Hohenberg and Kohn.2 It has been later reinforced by the development of a Gibbs–Duhem equation counterpart.3 The coining of the Lagrange multiplier associated with the energy minimization after the thermodynamics chemical potential pursued even further the connection.4Many macroscopic concepts have also found their analog in DFT. The definition of pressure5 and temperature6–8 of an electron system and the proposal of a maximum entropy principle9,10 are other examples.11 More recently, temperature-dependent conceptual DFT descriptors12–16 and temperature-dependent charge transfers have been paid a lot of attention, even though it has become quite clear that the temperatures required for tangible electron density modifications are much larger than the macroscopic temperatures used in routine experimental chemistry, ultimately suggesting that “electronic” and thermodynamic temperatures are two separate quantities.
It will be shown in this article that the interaction with an external perturbation may modify the electron density in such a way that it would be equivalent to a change in a well-defined electronic temperature. To prove it, we follow the traditional line by applying statistical physics concepts to DFT. Through this approach, the work and heat exchange between an electron system and its surroundings will be defined, and the definitions of the associated entropy and temperature will be subsequently provided. Interestingly, the temperatures calculated through this analogy are in agreement with the temperatures needed to make an electron density evolve.
Thus this paper is organized as follows. In the following section, we discuss some previous temperature and entropy definitions in conceptual theoretical chemistry, in order to unravel the differences between our approach and those already reported in the literature. In the third one, basic relations between statistical physics and thermodynamics are recalled. The fourth section then exploits the reminded concepts to devise the analogy with conceptual DFT17–19 and to define electronic work and heat counterparts, while section five more specifically deals with the concepts of entropy and temperature. Then, in section seven, these concepts are applied to a few molecular systems, such as acrolein, thiophene and pyrrole using the methodology outlined in section six. The article ends with some concluding remarks.
2 Temperature and entropy in theoretical chemistry
The purpose of this section is to highlight (without aiming at being comprehensive) some peculiarities of our approach by confronting it with some other conceptual schemes dealing with temperature. Note already that the aim here is not to define an exact explicit temperature-dependent density functional theory, but rather to use temperature as a probe for some specific property of interest. Saying otherwise, our aim here is conceptual and not computational DFT. Briefly (and with a little oversimplification), with this premise, two main objectives can be delineated for the use of temperature in DFT.The first one is mainly developing a computational tool targeted to improve or diagnose the methods. This is for instance the case of thermally-assisted-occupation DFT20,21 where a “fictitious” temperature is introduced in order to add flexibility for the design of accurate exchange–correlation functionals by involving virtual orbitals (VOs), while, in principle, the use of VOs is avoided in exact Kohn–Sham (KS) theory. Still within the KS framework, Grimme and Hansen considered finite-temperature DFT to characterise the multi-reference character of molecules and to assess the amount of static correlation.22 This is also usual in DFT solid state calculations.23
The second goal is related to the rationalisation of chemical behaviours and in particular of reactivity. For instance, Scheffler and co-workers introduced the change of the electron density due to the excitation of low-energy electron–hole pairs induced by an increased electronic temperature as a quantity that characterises the spatial distribution of the reactivity of metal surfaces.24 It illustrates Chermette's statement that “local reactivity indices may be introduced, taking into account variations with respect to variables […] such as the electron temperature, T, which induces electronic excitations”.19
There were thus several proposals for electronic temperature and electronic entropy based on the electron density. Among them, we should cite the Ghosh–Berkowitz–Parr (GBP) definition,1,25 which reads:
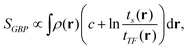 | (1) |
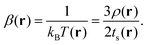 | (2) |
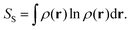 | (3) |
Accordingly, all these works intend to extract physico-chemical information from a given electron density. Our goal, here, is different: we do not aim to characterise the electron density by itself and as it is, but, rather, its propensity to be modified or distorted. Within the so-called canonical representation, two factors can make it evolve: either a variation of the electron number, or of the external potential.
Variations associated with the change of electron number have been the topic of many papers since the seminal Perdew–Parr–Levy–Balduz article.34 The prototypical case is that recently reviewed by Gázquez and collaborators:14 “the system under consideration is highly diluted in the solvent, which acts as an electron reservoir, so that the number of electrons in the system will fluctuate because it can exchange electrons with the solvent”. In the so-called three-state model, the fractional number of electrons around N0 is modelled by a mixing of the N0 − 1, N0, and N0 + 1 states. Then, the average number of electrons can be expressed by (see also Chapter 4 in Parr and Yang's textbook35):
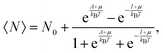 | (4) |
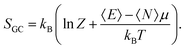 | (5) |
It it thus plain to see that this temperature T here controls the average fraction of electrons exchanged with the surroundings. As a consequence, to quote Franco-Pérez,13 “it is now well-accepted that the temperature that one uses when exploring chemical reactivity concepts is not the true temperature but an “effective” temperature that models in a qualitative way, interactions between reactants during a chemical reaction”, and, even more precisely, it is the charge transfer component of such a reaction.
Additionally, electron density variations due to the external potential can be split into two categories: those induced by displacements of nuclei associated with the atoms of the molecular system itself, and those triggered by an additional potential that does not belong to the initial system (this is the case for instance when a reaction partner approaches). The first category is closely related to molecular vibrations. In such cases, the relevant temperature is that associated with the nuclei kinetic energy, which, by virtue of the equipartition theorem, is directly linked to the thermodynamical temperature defined in the NVT ensemble. In a recent paper,36 molecular dynamics simulations (using classical nuclei) were performed to assess to what extent electron density-based reactivity descriptors are affected when structural breathing is described by thermal nuclei moves.
Here, we target the second category: the changes in the electron density associated with the addition of a new external potential, and we will show in Section 4 how a specific temperature can be associated with it. To this aim, some thermodynamical key concepts have to be preliminarly introduced.
3 Statistical physics background
It is textbook knowledge to retrieve thermodynamics from statistical physics.37 Through this approach, work, heat, entropy and temperature can be derived from probability distributions within the appropriate statistical ensemble.Take a closed system that can exchange heat (δQ) and work (δW) with its surroundings. The first principle of thermodynamics, which merely translates the energy conservation of the system, states that:
| dU = δW + δQ. | (6) |
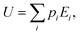 | (7) |
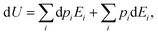 | (8) |
Now let λ be a parameter of the Hamiltonian describing the system. The associated force is:
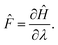 | (9) |
dEi = 〈Ψi|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) |Ψi〉dλ = −dWi, |Ψi〉dλ = −dWi, | (10) |
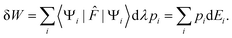 | (11) |
Hence the work exchange is clearly ascribed to the variation of energy levels at constant population. Therefore, the second right hand side term of eqn (8) can be identified with the heat exchange. This last result can actually be derived independently. Indeed, the corresponding Gibbs–Shannon entropy is given by:
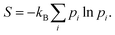 | (12) |
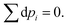 Hence,
Hence,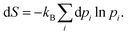 | (13) |
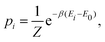 | (14) |
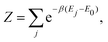 | (15) |
 | (16) |
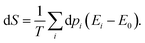 | (17) |
The associated heat is thus,
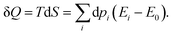 | (18) |
It is plain to see that, for a quantum system exchanging work and heat with its surroundings, on the one hand, the work exchange can be seen as a modification of the total energy due to a change in the state energy, while their populations remain unchanged. On the other hand, the heat exchange can be seen as an evolution of the total energy induced by a change in the state occupations.
We now apply these results to the fundamental equations of conceptual DFT.
4 Work and heat in conceptual DFT
For the sake of simplicity, one considers in the first stage a closed electron system that can only exchange energy with its surroundings. Systems able to exchange particles and therefore undergo chemical reactions will be the subject of another paper. The average electronic energy can be written as: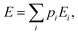 | (19) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K would be required to populate the first excited state of hydrogen by 1 percent of the total population. Therefore, the latter equation reduces to:
000 K would be required to populate the first excited state of hydrogen by 1 percent of the total population. Therefore, the latter equation reduces to:| E = E0. | (20) |
Let us now imagine that this system is perturbed by, for instance, an electrostatic external potential created by a point charge. The energy variation of the ground state is, up to the second order, given by:
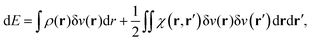 | (21) |
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) = Ĥ − Ĥ0 being the perturbation Hamiltonian, ρ(r) the electron density and χ(r,r′) the so-called static linear response kernel. The first right hand side term of the latter equation is the linear Stark effect energy. It actually corresponds to the first order energy correction in perturbation theory:
= Ĥ − Ĥ0 being the perturbation Hamiltonian, ρ(r) the electron density and χ(r,r′) the so-called static linear response kernel. The first right hand side term of the latter equation is the linear Stark effect energy. It actually corresponds to the first order energy correction in perturbation theory:| E(1) = 〈Ψ0|(Ĥ − Ĥ0)|ψ0〉, | (22) |
| E(1) = 〈Ψ0|(Ĥ − Ĥ0)|ψ0〉 = p0dE0. | (23) |
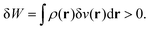 | (24) |
In a recent paper by the same authors,38 it has been shown that the second right hand side term of eqn (21), the polarisation energy, can be seen as an electron reconfiguration energy describing how the electron density is adapting to the new external potential. The perturbed wave-function can then be projected upon the basis set formed by the unperturbed eigenvectors,
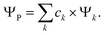 | (25) |
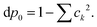 This polarisation energy can be expressed as:
This polarisation energy can be expressed as: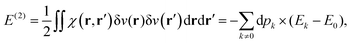 | (26) |
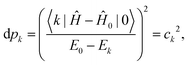 | (27) |
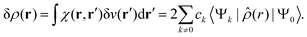 | (28) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) is the one-electron density operator. Thus, the second right-hand side term of eqn (8) can be identified with the heat exchange
is the one-electron density operator. Thus, the second right-hand side term of eqn (8) can be identified with the heat exchange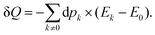 | (29) |
In summary:
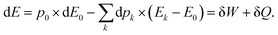 | (30) |
5 Entropy and temperature
The Gibbs–Shannon39 entropy of the unperturbed system is null (in analogy with Nernst's third law of thermodynamics)40 since only the ground state is populated (p0 = 1, and pi = 0 for i ≠ 0) and thus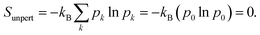 | (31) |
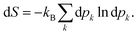 | (32) |
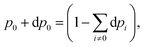 dpi being the population of the ith excited state. dS actually translates the spreading of the electron density over the excited states. It can be seen as a measure of how dispersed the electronic polarisation is, both in real space and among the energy states. Thus, a polarisation that leads to a wide electron density reshuffling would exhibit a large entropy. We stress that only static polarisation is considered here, i.e. the case of entropy of electromagnetic polarisation, more tricky,41–43 is not approached in this work.
dpi being the population of the ith excited state. dS actually translates the spreading of the electron density over the excited states. It can be seen as a measure of how dispersed the electronic polarisation is, both in real space and among the energy states. Thus, a polarisation that leads to a wide electron density reshuffling would exhibit a large entropy. We stress that only static polarisation is considered here, i.e. the case of entropy of electromagnetic polarisation, more tricky,41–43 is not approached in this work.
In Section 2, the connection between entropy, heat and temperature was done through the Boltzmann distribution in which the population of an excited state k depends on the ratio between the energy difference and the temperature. Thus, when one raises the temperature, the lowest excited states are populated first. In the problem at hand, the probability of having the level k populated is more intricate since it is given by:
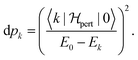 | (33) |
Should the numerator of the latter equation be the same for all the excited states, then a simple statistical distribution would be easily found. Indeed, the occupation would be a unique function of the inverse of excitation energies. Unfortunately, the numerator makes the connection between the ground state and the excited state through the perturbation potential. Therefore the numerator can be quite important for high excited states, and the population distribution may not be monotonic. Consequently, high excited states can be much more populated than lower ones. In this situation, a temperature can be hard to define rigorously. However, it will be shown in the next section that as an empirical relation exists between entropy and polarisation energy (heat), a temperature can be calculated. Indeed, one can use the macroscopic definition:
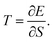 | (34) |
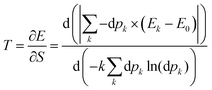 | (35) |
It is easily seen that if the perturbation is due to a point charge, the electric charge that generates the electrostatic potential will increase the population of every state. In that regard, the electrostatic charge can be seen as a temperature counterpart. It indicates how “hot” the point charge is. The dependence of temperature on the small electric charge δq of the point charge perturbation is not difficult to delineate. From eqn (33), the level occupations are proportional to δq2. This leads to the following dependence for the temperature:
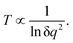 | (36) |
As a final remark for this section, let us notice that the gist of thermodynamics is essentially making averages. In the previous equation, a sum is made on all the considered perturbations of the external potential, which are independently imposed on the system. This can be compared with the other definitions presented in Section 2. Indeed, in eqn (1) and (3), the sum is made on all real space points where the electron density is evaluated. In eqn (5), the sum is carried out on the states featuring different electron number values. In the case where temperature controls the nucleus movements, the sum depends on the vibrational modes. This freedom on the choice of summation index accounts for the variety of possible temperature definitions in theoretical chemistry.
6 Computational details
All gas phase geometries and wavefunctions were obtained at the B3LYP/6-31+G* level of theory using ORCA 4.0 software.44 In all cases, the first 50 excited states were computed using the Tamm–Dancoff approximation (TDA). Transition densities for all 50 excited states were extracted in the cube file format using the orca_plot utility. They were used to evaluate the different descriptors analysed herein by a home made Fortran program that can be obtained from the authors upon request. Integration was performed by direct summation on the cube grids, whose spacing was in all cases less than 0.15 bohr. Potential perturbations were located at each nucleus of relevant atoms, which is in a way reminiscent of the H* method.45,46We would like to stress the fact that even if DFT was used here to generate all data, the post-Hartree–Fock (post-HF) methods could also have been used without any difficulty, since our approach only requires electron densities and transition densities that are in principle also available with the post-HF calculations. In that sense, the use of the “conceptual DFT” phrase should not be seen as restricting the method application to the sole DFT.
7 Polarisation entropy of selected molecular systems
In this section, the concepts previously defined are applied to several representative molecular systems, namely propenal (aka acrolein), thiophene and pyrrole.7.1 Acrolein
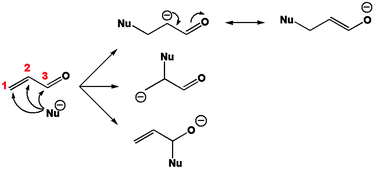
Propenal, more widely known as acrolein, is an enal (conjugated carbonyl system).It is well known that this molecule is prone to react with nucleophiles. The carbonyl carbon, hereafter numbered C3, reacts readily with “hard” (in the sense of Pearson's hard and soft acids and bases (HSAB) theory)47 nucleophiles. The conjugated carbon or β carbon, numbered C1, reacts better with “soft” nucleophiles leading for instance to the so-called Michael additions, which are among the most widespread techniques to form carbon–carbon bonds. On the other hand, the oxygen atom of the carbonyl group generally undergoes complexation with metal cations or protonation. The first stage of a nucleophilic attack on acrolein is represented in Fig. 1.
Carbon 1, the conjugated carbon, is considered as the most polarisable atom and therefore as softer. Within the HSAB principle, this atom reacts best with soft bases. On the other hand, carbon 3 is considered as the least polarisable, or the hardest. It is prone to combine with hard bases. Another way to explain the reactivity of C1 is to look at the reaction intermediate. In Fig. 1 it appears that the attack on carbon 1 leads to the most stable intermediate because the additional charge is best spread among the molecule.
To assess the polarisability of each carbon, a perturbation has been successively set on their nucleus. In Fig. 2 the density polarisation maps for the acroleine perturbed on C1(A), C2(B) and on C3(C) are represented.
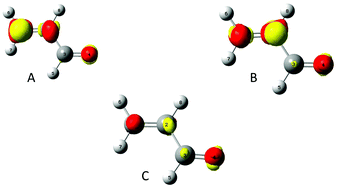 | ||
| Fig. 2 A, B and C indicate that perturbation is applied, respectively, on the nucleus of atoms C1, C2 and C3. Density polarisation maps. isovalue of 0.0005 e bohr−3. | ||
The density accumulation regions are colored in red, while the density depletion regions are in yellow. The perturbation by a negative point charge of q = −0.1 e successively located on each carbon induced a density depletion on the corresponding carbon. These density polarisation maps are a way to describe how the density is reshuffled or spread among the molecule, which atoms gain or lose electron density. The biggest reshuffling is reached when the perturbation is located on C1, which is consistent with the fact that it is the most polarisable amongst the carbon backbone. To get a more quantitative assessment, the polarisation energy and entropy have been calculated.
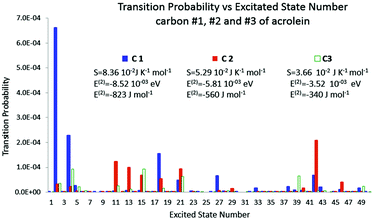
In Fig. 3, the polarisation spectrum for the 50 first excited states is represented along with the polarisation energy and the corresponding entropy for each carbon. The polarisation spectrum describes on the Y axis the transition probability dpk triggered by the perturbation with respect to the excited state number k on the X axis. The Gibbs–Shannon entropy has been computed for the three positions of the perturbation, namely on atoms C1, C2 and C3. It is plain to see that for carbon C1 fewer excited states are involved than those of the two other carbons. However the transition probabilities are about one order of magnitude higher. So even though the polarisation is distributed on fewer excited states, its magnitude is much higher. The entropy is therefore higher when the charge is located on C1 than on other carbons.
The polarisation energy, the second order correction to the energy, which is, according to Section 4, the heat exchange, was also calculated. The polarisation energy follows the same trend as the polarisation entropy. The polarisation energies are −8.52 × 10−3 eV, −5.81 × 10−3 eV, and −3.52 × 10−3 eV for carbons 1, 2 and 3, respectively. So, the bigger the entropy, the smaller the polarisation energy, and the larger the stabilization. As a consequence both the polarisation energy (heat exchange) and the polarisation entropy seem to be good candidates to indicate the most polarisable atom among the carbon backbone. Indeed, the results show a strong correlation between the polarisation energy and the polarisation entropy, which holds as far as our perturbative calculation remains valid.
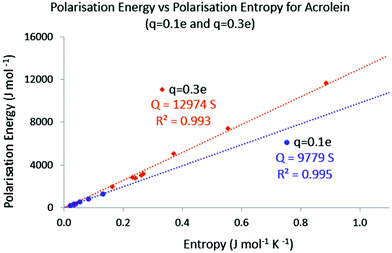
Finally, it might be interesting to assess the temperature associated with the different reshuffling. Provided that it is applicable, eqn (34) indicates that temperature can here be expressed as the slope of the E = f(S) plots. In Fig. 4, the absolute values of the polarisation energy with respect to the polarisation entropy for, respectively, a point charge perturbation of q = −0.1 e and q = −0.3 e applied on all the atoms of acrolein are represented. The (E = 0, S = 0) point was also added to the data sets, as the unperturbed system is expected to display both null polarisation energy and entropy.
It is believed that the number of E = f(S) points is large enough to draw some conclusions. In both cases the polarisation energy and the polarisation entropy are linearly connected. For a point charge perturbation of q = −0.1 e located at the nucleus of each atom, the corresponding temperature (slope) is about 9800 K. For a point charge perturbation of q = −0.3 e the equivalent temperature is about 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. These levels of temperature are in agreement with the temperature needed to distribute 1 percent of the total population of a molecule collection on the first excited state. As noted in other temperature-based developments, and as stated earlier, this temperature is also much higher than the “macroscopic” temperature used in chemical synthesis. Interestingly, even though the heat transfer and polarisation entropy values change with the location of the point charge perturbation, the global temperature remains the same and seems only dependent on the charge magnitude.
000 K. These levels of temperature are in agreement with the temperature needed to distribute 1 percent of the total population of a molecule collection on the first excited state. As noted in other temperature-based developments, and as stated earlier, this temperature is also much higher than the “macroscopic” temperature used in chemical synthesis. Interestingly, even though the heat transfer and polarisation entropy values change with the location of the point charge perturbation, the global temperature remains the same and seems only dependent on the charge magnitude.
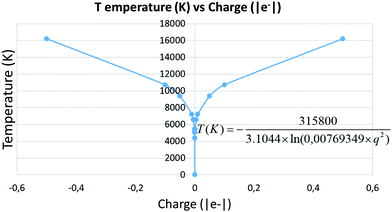
To evaluate the temperature dependence on charge, we considered again nuclei-centred perturbations, the point charge magnitude varying from −5 × 10−4 to −5 × 10−1e. Linearity of the S = f(E) plot is maintained in all cases (R2 being above 0.99 in all the cases). Moreover, the slope variation with the charge complies with the expected 1/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q2 dependence, as shown in Fig. 5, thus reinforcing confidence in the found results.
q2 dependence, as shown in Fig. 5, thus reinforcing confidence in the found results.
7.2 Thiophene and pyrrole
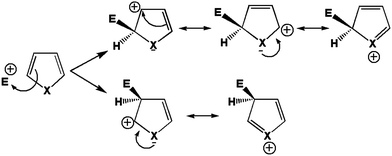
Reactivities of thiophene and pyrrole are very comparable. They generally undergo aromatic electrophilic substitution at the α carbon, the carbon neighbour to the heteroatom.48 The limiting step of this reaction is the addition of the electrophile on the aromatic system, which is indeed highly endothermic and thus, according to Hammond's postulate49 is associated with significant activation barriers. Because of the late character of the transition states of addition, selectivity is assumed to be better grasped through a study of the reaction intermediate, rather than of the starting reagent. From Fig. 6, one may indeed see that addition on the α carbon leads to the best dispersion of the positive charge over the molecule, and thus the associated intermediate (and transition state) should accordingly be the lowest in energy.However, it is noteworthy that in this particular case the driving force beneath the stabilisation of the reaction intermediate already manifests itself in the starting reagent. Indeed, the higher propensity to disperse the excess positive charge in the α intermediate can be traced back to the higher polarisability of this atom in the heterocycle. As such, we may expect to retrieve the regioselectivity of the electrophilic substitution on these heterocycles from a study of the polarisability of the carbon atoms on the ring.
Again, to check which atom is the most polarisable or soft, a perturbing positive point charge (+0.1 e) has been successively located on each nucleus. As the molecule is symmetrical, only two carbon positions have been tested, namely the α and β carbons. The density polarisation maps are represented in Fig. 7. The color code is unchanged, the electron density depletion regions are colored in yellow, while the regions that gain electrons are in red. Qualitatively, the same maps are obtained for both pyrrole and thiophene. The depletion regions for a perturbation located on the α carbon are the neighbour β and opposite α carbons. This is in agreement with the Lewis structures represented in Fig. 6. The same goes for the perturbation positioned on the nucleus of the β carbon. In this case the electron density depletion is principally located on the alpha carbon and the heteroatom, once again in full compliance with the Lewis structures in Fig. 6.
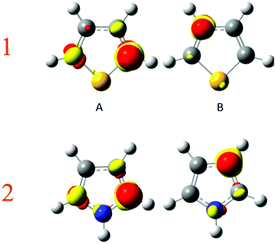 | ||
| Fig. 7 Density polarisation map for perturbation on carbon (A) α and (B) β of thiophene (1) and pyrrole (2). Isovalue of 0.0005 e bohr−3. | ||
It is now important to assess polarisation energy and polarisation entropy for both cases to check whether they are good indicators of the stabilization of the additional charge. The decomposition spectra for both molecules and both perturbation locations are represented in Fig. 8 and 9.
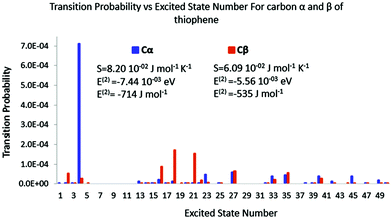
In the case of thiophene, it is striking how the polarisation spectra are different between α and β positions. Very few excited states are triggered in the former, while many are in the latter. The intensities are also quite different. Indeed, the transition probabilities are four times higher in the former than in the latter. The polarisation entropy and polarisation energies follow the same trends as for acrolein: stronger intensities lead to strong entropy and an important stabilization energy. Polarisation entropy and polarisation energy therefore are accordingly remarkable indices to describe the stability of the late reaction intermediate formed by the attack of an electrophile on thiophene.
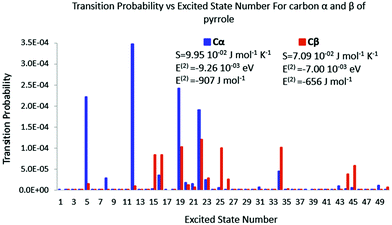
The same trend is also observed for pyrrole. When the perturbation is located in carbon α, fewer excited states are triggered than that of carbon β. The transition probabilities are nevertheless bigger for the former than for the latter leading to a larger polarisation entropy and a stronger polarisation energy stabilisation. Again the polarisation energy and the polarisation entropy are good descriptors of the stability of the late reaction intermediate.
Finally the temperature has been calculated using the same protocol. In Fig. 10 the polarisation energy with respect to the polarisation entropy for the perturbation point charge located successively on each nucleus is represented. Just like for acrolein, a linear relationship connects the polarisation energy to the polarisation entropy, with a temperature close to 8600 K. This procedure done on pyrrole leads to a temperature of 9100 K. Again these ranges of temperature are in agreement with the calculated temperature needed to excite 1 percent of the total population of a collection of molecules in the first excited state.
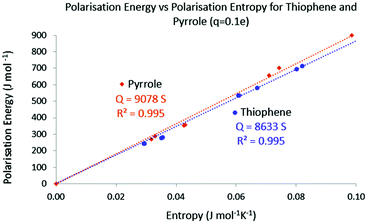 | ||
| Fig. 10 Absolute polarisation energy with respect to the polarisation entropy for thiophene and pyrrole. q = 0.1 e. | ||
8 Concluding remarks
The main goal of this paper was to show that a close analogy can be drawn between conceptual DFT and statistical thermodynamics. This analogy has led to the proposal of a new perspective on work, heat, entropy and also temperature associated with the electron system. It must be noted that their calculations come with quite a heavy price. Indeed, lots of excited states must be computed. An assessment of their added values with respect to more traditional DFT descriptors has to be undertaken. However, they thus complement the standard temperature defined and used in molecular dynamics, which is related to kinetic energy of the nuclei, and thus to the nuclear moves. In this contribution, we gave compelling evidence that the application of this concept to the electron density provides useful hints on chemical reactivity. More precisely, when an isolated molecule undergoes a perturbation of the potential it is submitted to, the electronic energy variation can be seen in terms of electronic work and electronic heat exchange, the latter being invoked when an electron density polarisation is induced.This density reshuffling can be further approached as a cooling (heat exchange) and is translated by a modification of the energy level occupations. It follows that an electron distribution entropy can be defined along with an electronic temperature. The polarisation entropy thus defined is able to characterize the stabilization due to the reshuffling and can be used to predict the stability of a chemical reaction intermediate. Many articles have recently focused upon the variation of DFT descriptors with temperature. In many of them, this latter concept remains elusive. It is believed that this approach may pave the way of the definition of temperature-dependent conceptual DFT descriptors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the GENCI/CINES (Project cpt2130) for HPC resources/computer time and the LABEX SynOrg (ANR-11-2ABX-0029) for funding.Notes and references
- S. K. Ghosh, M. Berkowitz and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 8028–8031 CrossRef CAS
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef
.
- J. F. Capitani, R. F. Nalewajski and R. G. Parr, J. Chem. Phys., 1982, 76, 568 CrossRef CAS
.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 69, 3801 CrossRef
.
- L. J. Bartoletti and R. G. Parr, J. Chem. Phys., 1980, 72, 1593–1596 CrossRef
.
- T. Gál and A. Nagy, Mol. Phys., 1997, 91, 873–880 CrossRef
.
- A. Nagy, R. G. Parr and S. Liu, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 3117–3121 CrossRef CAS
.
- P. Ayers, R. Parr and A. Nagy, Int. J. Quantum Chem., 2002, 90, 309–326 CrossRef CAS
.
- R. G. Parr, K. Rupnik and S. K. Ghosh, Phys. Rev. Lett., 1986, 56, 1555–1558 CrossRef CAS
.
- P. K. Chattaraj and S. Sengupta, J. Phys. Chem. A, 1997, 101, 7893–7900 CrossRef CAS
.
- S. Liu and R. Parr, J. Chem. Phys., 1997, 106, 5578–5586 CrossRef CAS
.
- M. Franco-Pérez, C. A. Polanco-Ramirez, J. L. Gazquez, P. W. Ayers and A. Vela, Theor. Chem. Acc., 2020, 139, 44 Search PubMed
.
- M. Franco-Pérez, J. Chem. Phys., 2019, 151, 074105 CrossRef
.
- J. L. Gazquez, M. Franco-Pérez, P. W. Ayers and A. Vela, Int. J. Quantum Chem., 2019, 119, e25797 CrossRef
.
- R. A. Miranda-Quintana, M. Franco-Perez, J. L. Gazquez, P. W. Ayers and A. Vela, J. Chem. Phys., 2018, 149, 124110 CrossRef
.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, J. Phys. Chem. A, 2020, 124(26), 5465–5473 CrossRef
.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gazquez, S. Liu, C. Morell, A. Toro-Labbe, A. Vela and P. Ayers, Theoretical Chemical Accounts, 2020, 139, 36 CrossRef CAS
.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS
.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS
.
- J.-D. Chai, J. Chem. Phys., 2012, 136, 154104 CrossRef
.
- J.-D. Chai, J. Chem. Phys., 2014, 140, 18A521 CrossRef
.
- S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313 CrossRef CAS
.
-
N. W. Ashcroft and N. D. Mermin, Solid State Physics, Saunders College, 1976 Search PubMed
.
- S. Wilke, M. H. Cohen and M. Scheffler, Phys. Rev. Lett., 1996, 77, 1560–1563 CrossRef CAS
.
- C. Rong, T. Lu, P. K. Chattaraj and S. Liu, Indian J. Chem., 2014, 53A, 970–977 CAS
.
- S. Liu, J. Chem. Phys., 2007, 126, 191107 CrossRef
.
- S. Liu, C. Rong and T. Lu, J. Phys. Chem. A, 2014, 118, 3698–3704 CrossRef CAS
.
- W. Wu, Z. Wu, C. Rong, T. Lu, Y. Huang and S. Liu, J. Phys. Chem. A, 2015, 119, 8216–8224 CrossRef CAS
.
- F. Heidar-Zadeh, I. Vinogradov and P. W. Ayers, Theor. Chem. Acc., 2017, 136, 54 Search PubMed
.
- F. Heidar-Zadeh, P. W. Ayers, T. Verstraelen, I. Vinogradov, E. Vöhringer-Martinez and P. Bultinck, J. Phys. Chem. A, 2018, 122, 4219–4245 CrossRef CAS
.
- R. F. Nalewajski, Int. J. Mol. Sci., 2002, 3, 237–259 CrossRef CAS
.
- R. F. Nalewajski, Found. Chem., 2014, 16, 27–62 CrossRef
.
- Á. Nagy, Chem. Phys. Lett., 2013, 556, 355–358 CrossRef
.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS
.
-
R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989 Search PubMed
.
- G. Hoffmann, V. Tognetti and L. Joubert, Chem. Phys. Lett., 2019, 724, 24–28 CrossRef CAS
.
-
P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 8th edn, 2006 Search PubMed
.
- F. Guégan, T. Pigeon, F. De Proft, V. Tognetti, L. Joubert, H. Chermette, P. W. Ayers, D. Luneau and C. Morell, J. Phys. Chem. A, 2020, 124, 633–641 CrossRef
.
- C. E. Shannon, Bell Syst. Tech. J., 1948, 27, 379–423 CrossRef
.
- W. Nernst, Sitzungsberichte der Koniglich Preussischen Akademie der Wissenschaften, 1906, 933–940 CAS
.
- Y. Zimmels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 036146 CrossRef CAS
.
- Y. Zimmels, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3173–3191 CrossRef CAS
.
- Y. Zimmels, J. Magn. Magn. Mater., 2005, 292, 433–439 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- E. Dumont and P. Chaquin, Chem. Phys. Lett., 2007, 435, 354–357 CrossRef CAS
.
- E. Dumont and P. Chaquin, J. Mol. Struct.: THEOCHEM, 2004, 680, 99–106 CrossRef CAS
.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS
.
-
F. Carey and R. Sundberg, Advanced Organic Chemistry: Part A: Structure and Mechanisms, Springer US, 2007 Search PubMed
.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS
.
| This journal is © the Owner Societies 2020 |