Open Access Article
Open Access ArticleInsight into the diffusion mechanism of sodium ion–polaron complexes in orthorhombic P2 layered cathode oxide NaxMnO2
Huu Duc
Luong
 ab,
Van An
Dinh
ab,
Van An
Dinh
 *cd,
Hiroyoshi
Momida
*cd,
Hiroyoshi
Momida
 be and
Tamio
Oguchi
be and
Tamio
Oguchi
 *be
*be
aDepartment of Precision Science & Technology and Applied Physics, Graduate School of Engineering, Osaka University, 2-1 Yamadaoka, Suita, Osaka, 565-0871, Japan
bDepartment of Theoretical Nanotechnology, Institute of Scientific and Industrial Research, Osaka University, Ibaraki, Osaka 567-0047, Japan. E-mail: oguchi@sanken.osaka-u.ac.jp
cNanotechnology Program, Vietnam-Japan University, National University of Hanoi, Luu Huu Phuoc Street, Nam Tu Liem District, 1000, Vietnam. E-mail: dv.an@vju.ac.vn
dCentre of Atomistic and Molecular Technologies, Graduate School of Engineering, Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
eElements Strategy Initiative for Catalysts and Batteries, Kyoto University, Kyoto, 615-8245, Japan
First published on 6th August 2020
Abstract
Using the density functional theory, we investigated the geometric, electronic structure, phase stability and electrochemical properties of a potential P2 layer orthorhombic cathode material NaxMnO2 (0 ≤ x ≤ 1) applied for sodium-ion batteries. Herein, we shed the light on the undeniable effect of the polaron formation and polaron migration on the diffusion of Na+ ions in the orthorhombic P2 layered oxides. Both GGA+U and HSE06 methods agree that, when a Na+ ion is removed from the fully charged state of NaMnO2, the accompanying polaron preferably forms at one of the third nearest Mn (3NN) octahedra to the Na vacancy, implying the oxidization of the Mn3+ ion at one of these 3NN sites to Mn4+. The positive polaron migrates simultaneously with the Na vacancy and would hinder the diffusion of Na ions. Two kinds of elementary diffusion processes, named parallel and crossing, have been explored which required almost same activation energy of about 423 meV (518 meV) by GGA+U (HSE06). In the fully discharged state, GGA+U and HSE06 methods indicate that the negative polaron forms at one of the second nearest Mn neighbours (2NN). The activation energy of 273 meV (327 meV) is needed for diffusion in a structure with a low Na concentration, which is much lower than that required for diffusion in the Na-rich regime. Consequently, Na+ ions can diffuse easier at lower Na concentrations. With the overall activation energy of 423 meV (518 meV), this material exhibits a faster ion diffusion in comparison with the prevailing lithium-based materials such as olivine phosphate.
Introduction
In recent decades, secondary lithium-ion batteries (LIBs) have emerged as crucial energy storage components of electronic portable devices and vehicles.1 However, the Li abundance is just 0.0017% of the Earth's crust.2 With the ever-increasing energy demand and the limited availability of Li element in the Earth's crust, it has been predicted that the Li abundance will be inadequate to the raw materials consumption for the LIBs productions. As a consequence, it has been anticipated that the world's energy storage market would experience a quick upturn in LIBs’ prices. In order to meet the highly increasing energy storage applications, several alternative elements such as Na, K, and Mg, have been used as charge carriers in the ion batteries. Among them, Na element is well-known as possessing the innate electrochemical affinity with Li, and recognized as the sixth order in the most plentiful elements, which contributes to 2.3% of the Earth's crust and 1.1% of the ocean.3 Therefore, sodium-based compounds have attracted a great deal of attention and expected to become the next generation of rechargeable batteries, named sodium-ion batteries (SIBs). Various materials such as NASICON, olivine phosphate, have been suggested to be promising candidates with similar electrochemical properties as Li analogous compounds. The apparent explanation is that sodium ions can diffuse easily inside the materials even though it possesses a larger ionic radius and atomic weight (rNa = 0.98 Å, mNa = 23 g mol−1) compared with those of lithium (rLi = 0.69 Å, mLi = 6.9 g mol−1).4In structure, three indispensable components of any rechargeable batteries are cathode,5–18 anode19,20 and electrolyte,21,22 in which the cathode primarily determines the overall cell voltage. Among the materials for cathode, layered oxides AxMO2 (where A stands for alkali metal with concentration of x, and M represents transition metals such as Mn, Fe, Ni, and Co) are in the spotlight as the most promising alternatives with high voltage (2.0–3.5 V) and capacity (150–210 mA h g−1) for both LIBs and SIBs.23–32 Among several types of layered oxides classified by Delmas et al.,33 O3 and P2 layered oxides, in which sodium ions locate at octahedral sites (denoted as O) and prismatic sites (denoted as P), respectively; the numbers 3 and 2 stand for the number of MO2 layers in a unit cell, are two most prevailing synthesized layered oxides groups. Although O3 layered oxides deliver a higher capacity, the better electrochemical performance with lower diffusion barrier and higher ionic conductivity was recorded in P2 layered oxides.34,35 In addition, O3 materials often exhibit hygroscopic property while P2 materials are more stable in ambient condition.36
Amid the P2 layered transition metals based oxides (Mn, Co, Ni), the sodium manganese oxide NaxMnO2 holds scientists spellbound more due to its cheaper cost and easier for synthesis.37–40 Two single-phase samples reported in experiments by slow cooling and quenching methods show hexagonal (space group P63/mmc, denoted by P2) and orthorhombic (space group Cmcm, denoted by P′2) phases.38 Both two phases exhibit a voltage window of 2.0–3.8 V. Even though the P2 phase samples exhibit a little higher cycle number (120 cycles), the P′2 phase materials deliver a significantly higher specific capacity of 210 mA h g−1 than the P2 phase (140 mA h g−1).41–43 Since the concentration of Na reaches more than 0.67 (x > 0.67), P2 layered phase shows a phase transformation to P′2, while P′2 layered material also experiences a phase transformation to OP4 at low concentration (x < 0.25).41 The phase transformation causes a rough discharging voltage profile over the capacity. An idea of doping other metals such as Fe, Co, Ni, Li, Mg, and Zn, has been indicated in many previous experimental and theoretical investigations to improve the stability and obtain better electrochemical properties.44–47 Even though the smoother voltage lines have been reported, the phase transformation has been also observed in those doped materials.46,47 Although there are many investigations of layered oxides for cathode materials, the Jahn–Teller effect and diffusion mechanism have not been addressed clearly so that more profound investigations are essential to perform.
In previous reports,5,48–51 many scientists pointed out the importance of a quasi-particle, named small polaron, to the diffusion of Li+/Na+ ion inside the transition-metal-based materials. The small polaron is formed due to the local distortion after the oxidation/reduction of transition metals. With a strong binding energy of 500 meV between the alkali vacancy/ion and the positive/negative polaron,48 the polaron migrates simultaneously with the diffusion of Li/Na vacancy/ion, and the polaron migration generally lowers the diffusion of those charge carriers inside the materials. The arrangement of the geometric structure and the polaron effect are incontrovertible during charging/discharging processes and would be clearly depicted for a better diffusion prediction. Several types of elementary diffusion paths might require different activation energies.5 Herein, we present a comprehensive density functional theory (DFT) investigation of the geometrical and electronic structures, the polaron formation and diffusion mechanism of Na ions. Especially, based on the model of polaron–Na ion/vacancy diffusion complex, we shed a light on how the Jahn–Teller polaron formation and polaron migration affect the diffusion of Na+ ions inside the orthorhombic manganese layered oxides NaxMnO2 (0 ≤ x ≤ 1).
Calculation schemes
All DFT energy calculations were performed using the Vienna Ab initio Simulation Package (VASP) within the projector augmented wave (PAW) pseudopotentials.52 Spin polarized calculations were accomplished with an energy cutoff of 700 eV and the 16 × 8 × 4 k-point mesh for unit cell (4 formula units) and 4 × 4 × 2 k-point mesh for 2 × 1 × 1 supercell (8 formula units). Since the Perdew–Burke–Ernzerhof (PBE)53 generalized gradient approximation (GGA) over-estimates the delocalization of 3d orbitals of transition metals, hence fails in describing the small polaron formation, a Hubbard like term U = 4.0 eV54 (GGA+U) of the Dudarev55 scheme was added. The hybrid functional method HSE0656 was also employed for comparison. Previously, DFT functionals combined with the van der Waals of vdW-D3 correction yield better agreement with the experimental results of the layered structure,57 thus the vdW interaction wdW-D3 correction scheme58 was introduced. The structure optimization calculations were converged until the residual atomic force was smaller than 1 × 10−2 eV Å−1. Structural stability, Na+–Mn3+–Mn4+ ordering, voltages, densities of states (DOS) and band structure were calculated by both GGA+U and HSE06 methods.The diffusion mechanism of Na+ ion in the charging and discharging processes inside the 4 × 2 × 1 (32 formula units) supercell was explored by using the nudged elastic band (NEB) approximation59 employing both GGA+U and HSE06 methods combined with vdW-D3 correction scheme. The spring force between images is set at −5 eV Å−1. The NEB calculation was converged when the residual force was smaller than 0.03 eV Å−1.
Results and discussion
The crystal structure
The geometric orthorhombic structure of NaxMnO2 (0 ≤ x ≤ 1) is shown in Fig. 1. In the unit cell, two MnO2 layers, formed by sharing six edges of each MnO6 octahedron with six nearest MnO6 octahedrons, contain four oxygen layers alternating an arrangement of A–B–B–A. In the full-unoccupied Na structure MnO2 (x = 0), the GGA+U (HSE06) results, as shown in Table 1, indicate that each Mn ion is surrounded by six oxygen ions with a same bond length of 1.96 Å (1.91 Å) to create a regular MnO6 octahedron. The slab distance between two MnO2 layers is 2.88 Å (2.88 Å).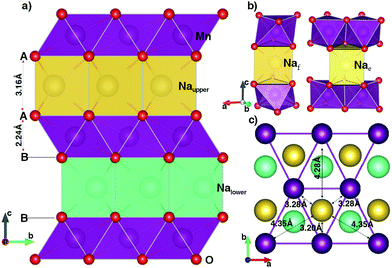 | ||
| Fig. 1 The geometric structure of P2 orthorhombic NaMnO2. The violet, red, yellow and cyan balls stand for Mn, O, Naupper and Nalower atoms, respectively. The data is obtained from GGA+U method. | ||
| MnO2 | NaMnO2 | ||||
|---|---|---|---|---|---|
| GGA+U | HSE06 | GGA+U | HSE06 | ||
| Lattice constant (Å) | a | 2.9595 | 2.8672 | 2.9414 | 2.8661 |
| b | 5.1254 | 4.9574 | 5.7184 | 5.6007 | |
| c | 9.6246 | 9.5440 | 10.8204 | 10.6499 | |
| Volume (Å3) | 145.99 | 135.66 | 182.01 | 170.96 | |
| Mn–O bond (Å) | 1.96 (×6) | 1.91 (×6) | 1.99 (×4) | 1.94 (×4) | |
| 2.41 (×2) | 2.37 (×2) | ||||
| Average (Å) | 1.96 | 1.91 | 2.13 | 2.08 | |
| Magnetic moment (μB) | 3.229 | 3.032 | 3.856 | 3.734 | |
Since Na+ ions are inserted in an empty space between MnO2 layers, they create a sandwich-liked structure. As illustrates in Fig. 1b, sodium ions can locate at atomic environments of edge-shared prisms (Nae), where each NaO6 prism shares six edges of two bottom faces with six MnO6 octahedrons; or of face-shared prisms (Naf), in which NaO6 prism shares two bottom faces with two MnO6 octahedrons in upper and lower MnO2 layers. In the full Na-occupied sites, our DFT calculations point out that the Na+ ions prefer locating at the Nae sites with the lower total energy of 220 meV f.u.−1 than that at the Naf site. The insertion of Na atoms to the MnO2 layered structure also results in the reduction reaction of Mn4+ (d3) to Mn3+ (d4). As a result, both GGA+U and HSE06 methods unanimously witness a sizable elongation in the bond length of the Mn–O bonds along the [010] direction from 1.96 Å to 2.41 Å by GGA+U (from 1.91 Å to 2.37 Å by HSE06), while four other bonds increase slightly. On average, the bond length increases by approximately 0.17 Å. In addition, the magnetic moments are 3.856 μB and 3.229 μB obtained by GGA+U (3.734 μB and 3.032 μB by HSE06) for Mn3+ and Mn4+ ions, respectively. The significant elongation in bond lengths along the [010] direction leads to the increase of the lattice constant b by approximately 11.5% (13.0%). Similarly, inserted positive Na+ ions expand the distance between two MnO2 layers so that the lattice constant c expands by about 12.4% (11.6%). In the case of all Na+ ions fully intercalated, the volume of the unit cell increases 19.8% (20.6%).
An important point is the distance relationship between each Na+ ion and its nearest Mn3+ ions. The distances from each Na+ ion to the first, second, and third nearest Mn3+ neighbours (1NN, 2NN and 3NN) are 3.28, 4.35, 4.82 Å (3.22, 4.26, 4.72 Å) obtained from GGA+U (HSE06) method, respectively. With the considerable difference in distance, the oxidation/reduction reactions of those Mn groups do not equivalently happen by their nearest Na+ ions deintercalation/intercalation.
Phase stability and Na+–Mn3+–Mn4+ ordering
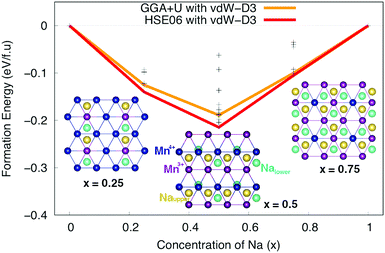
Subsequently, Na+–Mn3+–Mn4+ ordering structures of Na different concentrations, phase stability and voltage were carefully considered. Nearly 100 configurations of different Na+ ion concentrations (x = 0.25, 0.50, and 0.75) were investigated. The formation energy E can be estimated from the following formula:| E = ENaxMnO2 − xENaMnO2 − (1 − x)EMnO2 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to create a zigzag line along [100] direction. At x = 0.25 and 0.75, the most stable structures are the ones in which all of the Na+ ions locate at Nae sites. The Mn ions in the lower layer and their symmetrically equivalent Mn ions in the upper layer along [001] direction tends to be oxidized/reduced concurrently. Obviously, the stable orderings of Na+ ions at different concentrations are related to orderings of Mn4+–Mn3+ ions in MnO2 layers.
1 to create a zigzag line along [100] direction. At x = 0.25 and 0.75, the most stable structures are the ones in which all of the Na+ ions locate at Nae sites. The Mn ions in the lower layer and their symmetrically equivalent Mn ions in the upper layer along [001] direction tends to be oxidized/reduced concurrently. Obviously, the stable orderings of Na+ ions at different concentrations are related to orderings of Mn4+–Mn3+ ions in MnO2 layers.
Electronic structure
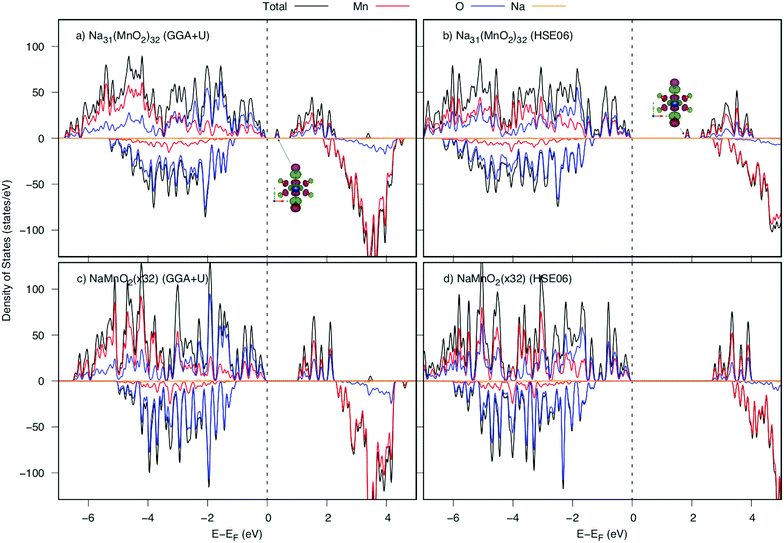
The density of states (DOS) and the band structures of the most stable structures of NaxMnO2 (x = 0, 0.25, 0.50, 0.75 and 1) are illustrated in Fig. 3. At x = 0, both the valence band and conduction bands are mainly contributed by 2p O states and 3d Mn states. The states near the Fermi level come from 2p states dominantly. The estimated up/down-spin gap is 0.82/2.30 eV (2.72/3.10 eV) by GGA+U (HSE06). Since x = 0.25, 0.50, and 0.75, new peaks in the upper valence band of DOS, contributed mainly by a combination of 2py O states with 3dyz and 3dx2−y2 Mn states, appear next to the Fermi levels. From the GGA+U (HSE06) method, the up/down-spin gaps are shortened significantly to 0.25/2.66, 0.14/2.68, and 0.17/2.74 eV (1.87/3.69, 1.64/3.76, and 1.71/3.91 eV), for x = 0.25, 0.50, and 0.75, respectively. Obviously, during the intercalation/deintercalation processes, the band gap almost remains so that it likely keeps the electronic conductivity persist. At the concentration of Na+ ion of x = 1, the 3dxz Mn states predominate the conduction band of NaMnO2 while the hybrid states of 2py O states, 3dyz and 3dx2−y2 Mn states hold the lion's share at states near Fermi level. The up/down-spin band gap estimated by GGA+U (HSE06) is enlarged to 0.81/3.11eV (2.48/4.31 eV), which is equivalent to those of full Na-unoccupied structure (x = 0). Understandably, the hybrid states of 2py O states, 3dyz and 3dx2−y2 Mn states play the crucial contribution to the electronic structure of the material.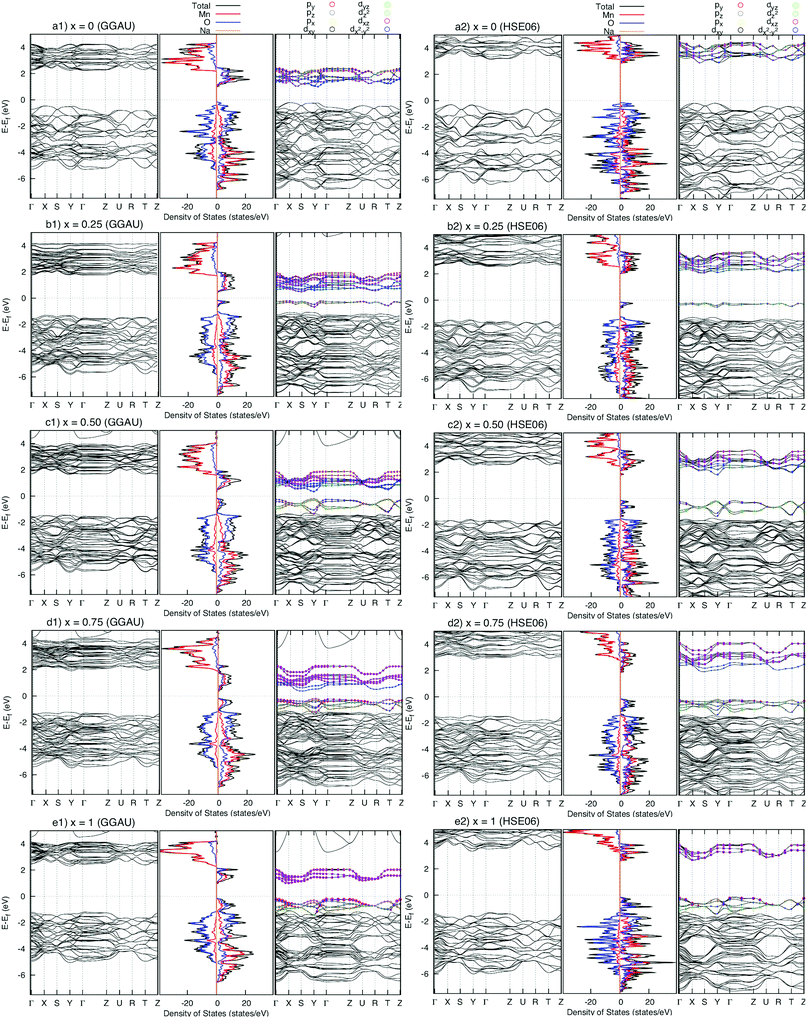 | ||
| Fig. 3 Density of states (centre) and band structure of up-spin (right) and down-spin (left) of NaxMnO2 (x = 0, 0.25, 0.50, 075, and 1). The energy origin is set to be the valence band top energy. | ||
Voltage
The calculated total energies of the most stable structures are used for voltage estimation. The voltage would be obtained by the formula below: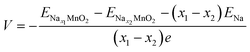 | (2) |
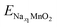 ;
; 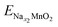 ; ENa are total energy of Nax1MnO2, Nax2MnO2, Na metal, respectively. x1 and x2 are Na concentration corresponded to Nax1MnO2, Nax2MnO2. e is the absolute electron charge. The GGA+U (HSE06) estimated voltages at specific capacities of 72, 135, and 191 mA h g−1 are 2.82, 2.60, and 1.97V (3.00, 2.73, and 1.99 V), respectively. Those results are well-agreed with experimental results (2.81, 2.26, and 1.86V).45
; ENa are total energy of Nax1MnO2, Nax2MnO2, Na metal, respectively. x1 and x2 are Na concentration corresponded to Nax1MnO2, Nax2MnO2. e is the absolute electron charge. The GGA+U (HSE06) estimated voltages at specific capacities of 72, 135, and 191 mA h g−1 are 2.82, 2.60, and 1.97V (3.00, 2.73, and 1.99 V), respectively. Those results are well-agreed with experimental results (2.81, 2.26, and 1.86V).45
Diffusion at high Na concentration
Now, we investigate the Na+ diffusion mechanism in the full charging/discharging states. As discussed in the previous article,5 two factors, the so-called quasi-particle named small polaron and geometric arrangement of the framework structure, affect considerably to the diffusion mechanism. Several types of elementary diffusion processes were proposed, including single, parallel and crossing processes. In this work, we carefully analyzed the geometrical structure and polaron migration in the defect structures.As a Na atom is deintercalated from the full-occupied Na structure, a positive hole is introduced to the structure. Surrounding the Na vacancy, there are six 1NN, four 2NN and two 3NN Mn3+ ions. Due to the hole introduced, one of those Mn3+ ions would be oxidized to be Mn4+. As a result, significant shrinkage of Mn–O bonds at Mn site would be observed. Our DFT calculations indicate that the structure possessing a 3NN Mn3+ ion oxidized is the most stable one by its lowest energy (approximately 140 meV lower than those of 1NN and 2NN Mn sites). As shown in Table 2, at the Mn3NNO6 octahedron, two Mn–O5 and Mn–O6 bond lengths along [010] direction significantly decrease from 2.41 Å (2.37 Å) to 2.07 Å and 2.10 Å (1.96 Å and 2.03 Å) after Na deintercalation. Overal, the average bond length is shrunk by approximately 0.13 Å (0.12 Å). Thereby, the magnetic moment at 3NN site reduces from 3.852 to 3.299 μB by GGA+U (3.734 to 3.056 μB by HSE06). The considerable shortened Mn–O bond length along the [010] direction results in a significant change in electronic structure. The DOSs of the structures before and after a Na deintercalation are shown in Fig. 4. Compared DOSs of those structures, it is understandable that the newborn bound state appearing right after the Fermi level is contributed mainly by a combination of O's 2py states with Mn's 3dyz and 3dx2−y2 states. The Mn4+ ion at 3NN sites surrounded by Mn3+ ions creates a defect structure in which a local polarized distortion prefers to appear around 3NN sites. It is concluded that a positive polaron is formed at one of the 3NN Mn sites.
| Mn3NN–O | O1 | O2 | O3 | O4 | O5 | O6 | Average |
|---|---|---|---|---|---|---|---|
| Before | 1.99 (1.94) | 1.99 (1.94) | 1.99 (1.94) | 1.99 (1.94) | 2.41 (2.37) | 2.41 (2.37) | 2.13 (2.08) |
| After | 1.97 (1.91) | 1.97 (1.91) | 1.97 (1.92) | 1.97 (1.92) | 2.03 (1.96) | 2.10 (2.03) | 2.00 (1.94) |
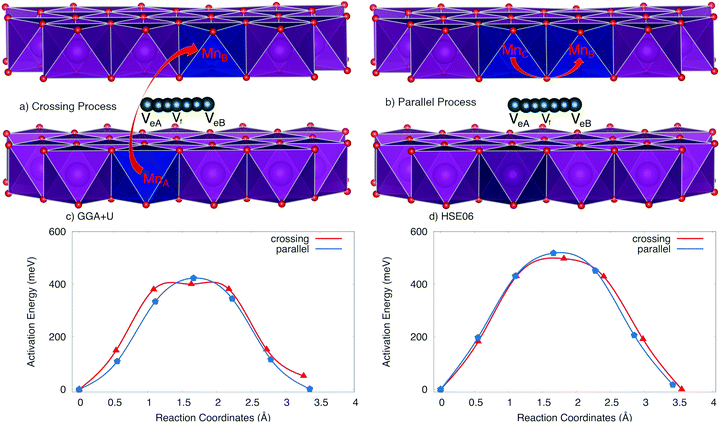
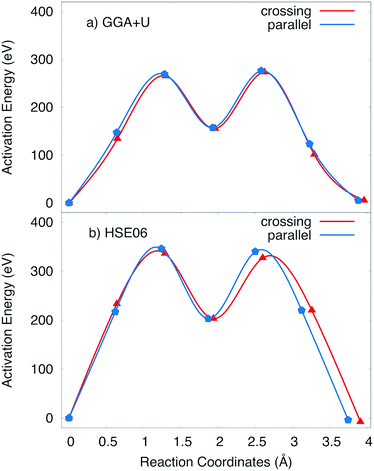
The positive polaron binds to the Na vacancy to form a Na vacancy–positive polaron complex. In the layer structure with the arrangement of MnO6 octahedron as shown in Fig. 1, the single process, which often requires the lowest activation energy, can not occur. Two types of elementary diffusion processes along the [010] direction were explored as shown in Fig. 5.
(i) The crossing process occurs if the positive polaron hops between the adjacent MnO2 layers. As illustrated in Fig. 5a, polaron leaps from the MnO2 lower layer to the upper one; explicitly from MnA to its Mn neighbour MnB while Na vacancy moves from an edged-share site VeA to another edged-shared site VeB. The reaction coordinate of this process is 3.264 Å by GGA+U (3.55 Å by HSE06).
(ii) On the other hand, the parallel process occurs if the positive polaron jumps inside the MnO2 layer; explicitly from MnC to MnB while the Na vacancy diffuses from an edged-share site VeA to another edged-shared site VeB as shown in Fig. 5b. The reaction coordinate is 3.30 Å by GGA+U (3.41 Å by HSE06).
The activation energy profiles obtained from GGA+U and HSE06 methods are shown in Fig. 5c and d. Both the GGA+U and HSE06 methods give the result indicating that the parallel process requires a little higher activation energy than crossing one; they are 423 meV and 400 meV by GGA+U (518 meV and 497 meV by HSE06) for the parallel and the crossing processes, respectively. The path from edged-shared vacancy site to its neighbour edged-share vacancy site (Ve–Ve) would be a sum of two sub-paths: the edge-shared vacant site to the face-shared vacant site (Ve–Vf) and then the face-shared vacant site to the edge-shared vacant site (Vf–Ve). With a scrap of difference, both parallel and crossing processes equivalently occur. Consequently, the overall activation energy is 423 meV (518 meV) obtained by GGA+U (and by HSE06). The influence of the positive polaron migration on the different diffusion paths of Na ion is equivalent.
Diffusion at low Na concentration
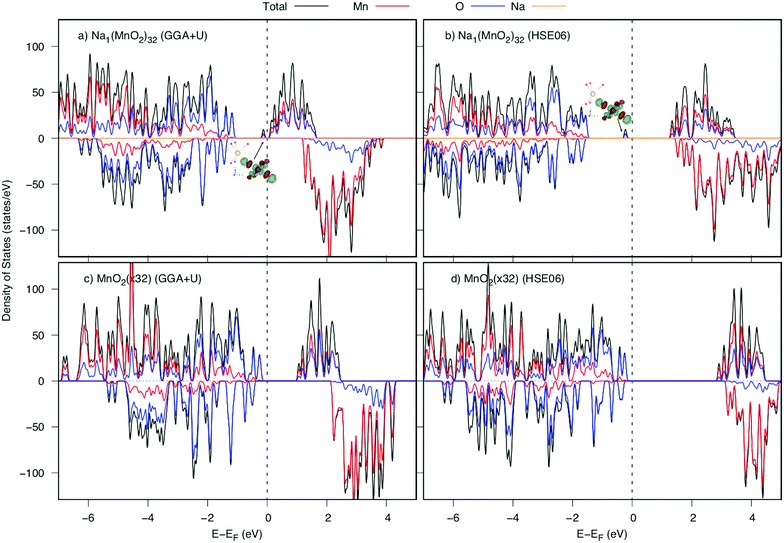
Next, we depict the fully discharged state. After the intercalation of the Na atom to MnO2 layered structure, an electron is also introduced to the structure to make a reduction reaction of Mn4+ to Mn3+. Because of creating from almost perfect MnO6 octahedrons, the Na+ ion is surrounded by six 1NN and six 2NN Mn ions. Among those, the Mn ion at the 2NN site prefers to be reduced first. As shown in Table 3, both GGA+U and HSE06 methods agree that there is a significant elongation in the average Mn–O bond length from 1.96 Å (1.91 Å) to 2.02 Å (2.00 Å) by GGA+U (HSE06), along with an increase magnetic moment from 3.299 μB (3.056 μB) to 3.856 μB (3.734 μB) by GGA+U (HSE06). That implies the Mn4+ ion at 2NN sites would be reduced first to be Mn3+ ion. The change in the bond length results in a new peak appeared right next to the Fermi level in DOS as shown in Fig. 6. This bound state comes from a hybrid orbital predominantly of O's 2py states and Mn's 3dyz and 3dx2−y2 states. As different as in the fully charged state, a negative small polaron is formed at the 2NN Mn site.| Mn3NN–O | O1 | O2 | O3 | O4 | O5 | O6 | Average |
|---|---|---|---|---|---|---|---|
| Before | 1.96 (1.91) | 1.96 (1.91) | 1.96 (1.91) | 1.96 (1.91) | 1.96 (1.91) | 1.96 (2.91) | 1.96 (1.91) |
| After | 1.98 (1.93) | 1.98 (1.93) | 1.99 (1.94) | 1.99 (1.94) | 2.07 (2.12) | 2.10 (2.13) | 2.02 (2.00) |
Since the negative polaron arises in the Na inserted structure, two elementary diffusion processes, including parallel and crossing processes, of Na+ ion–negative polaron complexes were explored by employing the GGA+U and HSE06 methods in NEB calculations. As illustrated in Fig. 7, both GGA+U and HSE06 methods agree that the activation energies are almost same for the parallel and crossing processes, which also points toward that the effect of small polaron hopping might be analogous. Obviously, both parallel and crossing processes equivalently occurred. Similar to the Na vacancy diffusion at high Na concentration, the Nae–Nae path is also a combination of the two small paths Nae–Naf and Naf–Nae. Evidently, the Naf site is the meta-stable position of Na+ ion. Two summits in the activation energy profile correspond to Na+ positions at the intermediate place between Nae site and Naf site. The barriers estimated by GGA+U and HSE06 methods are 273 and 327 meV, respectively.
 | ||
| Fig. 7 Activation energy profile of Na+ ion–negative polaron complex obtained by (a) GGA+U and (b) HSE06 method. | ||
Overall, the energy required for Na diffusion is in the range from 273 meV (327 meV) to 423 meV (518 meV) during the charging/discharging process by GGA+U (HSE06). Both parallel and crossing processes require an approximately same activation energy. Unlike polyanion cathode materials,5–10 the effect of polaron migration to overall activation energy is insignificant so that it benefits the diffusion of Na vacancy/ion inside the cathode material. Polaron can jump in the plane of MnO2 layer, or jump interplane from the upper layer to lower layer or contrariwise required an equivalent energy. Consequently, both processes might occur during the diffusion of Na+ ion inside the material. Compared with other common materials such as olivine phosphate (LiFePO4) with an activation energy of 630 meV,5 it is obvious that the activation energy of the orthorhombic P2 layered NaxMnO2 is considerably smaller, which benefits the Na+ diffusion.
Conclusions
For the sake of brevity, the crystal and electronic structures, stability diagram, voltage as well as diffusion of Na vacancy/ion–polaron complex in an auspicious cathode material NaxMnO2 (0 ≤ x ≤ 1) were dissected using GGA+U and HSE06 methods. The most stable structures having different concentrations of Na were explored. At high or low Na concentrations, Na+ ions prefer locating only at the edge-shared prism. The material is more stable at x = 0.5. During the charging/discharging process, a conspicuous change in lattice constant b and volume would be observed due to the significant shrinkage/elongation of bonds along the [010] direction. As a result, the hybrid orbital, combined by O's 2py states, Mn's 3dyz and 3dx2−y2 states, plays a crucial pivot in the electronic structure of the material during the intercalation/deintercalation. Also, the electric conductivity is better at the intermediate structures. The voltages against capacity obtained from the most stable structures using GGA+U and HSE06 methods are well-agreed with the experimental result. When a Na+ ion is deintercalated from the full-occupied Na structure, the positive small polaron is formed at one of the third nearest neighbours Mn to the Na vacancy. The polaron simultaneously escorts and would hinder the Na vacancy diffusion. Two elementary diffusion processes, including parallel and crossing process would occur equivalently and require an activation energy of 423 meV (518 meV) by GGA+U (HSE06). In the fully discharged state, the insertion of Na+ ion leads to the formation of a negative small polaron. Without Na+–Na+ repulsion, the significantly lower activation energy of 273 meV (327 meV) by GGA+U (HSE06) is required. At low Na concentration regime, Na+ ions can diffuse easier than at high Na concentration ones. Unlike polyanion based materials, the effect of polaron hopping is equivalent on the different diffusion paths in NaxMnO2. Compared to olivine phosphate, the Na+ ion would diffuse in NaxMnO2 better than in polyanion framework like LiFePO4.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Japanese Government Scholarship from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan and the ESICB project of MEXT, Japan. The numerical calculations of this work were performed using Supercomputer at the Institute for Solid State Physics, University of Tokyo.Notes and references
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS PubMed.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636 CrossRef CAS PubMed.
- Q. Sun, Y. Yang and Z.-W. Fu, Electrochem. Commun., 2012, 16, 22 CrossRef CAS.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. C. Gonzálezb and T. Rojo, Energy Environ. Sci., 2012, 5, 5884 RSC.
- V. A. Dinh, J. Nara and T. Ohno, Appl. Phys. Express, 2012, 5, 045801 CrossRef.
- K. M. Bui, V. A. Dinh and T. Ohno, Appl. Phys. Express, 2012, 5, 125802 CrossRef.
- K. M. Bui, V. A. Dinh and T. Ohno, J. Phys.: Conf. Ser., 2013, 454, 012061 CrossRef.
- D. M. Duong, V. A. Dinh and T. Ohno, Appl. Phys. Express, 2013, 6, 115801 CrossRef.
- K. M. Bui, V. A. Dinh, S. Okada and T. Ohno, Phys. Chem. Chem. Phys., 2015, 17, 30433 RSC.
- K. M. Bui, V. A. Dinh, S. Okada and T. Ohno, Phys. Chem. Chem. Phys., 2016, 18, 27226 RSC.
- A. Kitajou, Y. Ishado, T. Yamashita, H. Momida, T. Oguchi and S. Okada, Electrochim. Acta, 2017, 245, 424 CrossRef CAS.
- M. Debbichi, L. Debbichi, V. A. Dinh and S. Lebe’gue, J. Phys. D: Appl. Phys., 2017, 50, 045502 CrossRef.
- M. Hamaguchi, H. Momida and T. Oguchi, J. Phys. Soc. Jpn., 2018, 87, 044805 CrossRef.
- H. D. Luong, T. D. Pham, Y. Morikawa, Y. Shibutani and V. A. Dinh, Phys. Chem. Chem. Phys., 2018, 20, 23625 RSC.
- A. Kitajou, H. Momida, T. Yamashita, T. Oguchi and S. Okada, ACS Appl. Energy Mater., 2019, 2, 5968 CrossRef CAS.
- H. Kotaka, H. Momida, A. Kitajou, S. Okada and T. Oguchi, Chem. Rec., 2019, 19, 811 CrossRef CAS PubMed.
- M. Hamaguchi, H. Momida and T. Oguchi, Electrochim. Acta, 2020, 330, 135286 CrossRef CAS.
- H. Momida, A. Kitajou, S. Okada and T. Oguchi, J. Phys. Soc. Jpn., 2019, 88, 124709 CrossRef.
- T. Yamashita, H. Momida and T. Oguchi, Electrochim. Acta, 2016, 195, 1 CrossRef CAS.
- T. D. Pham, H. D. Luong, K. Sato, Y. Shibutani and V. A. Dinh, Phys. Chem. Chem. Phys., 2019, 21, 24326 RSC.
- K. M. Abraham and Z. Jiang, J. Electrochem. Soc., 1996, 143, 1 CrossRef CAS.
- K. M. Bui, V. A. Dinh, S. Okada and T. Ohno, Phys. Chem. Chem. Phys., 2016, 18, 27226 RSC.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680 RSC.
- N. Ortiz-Vitoriano, N. E. Drewett, E. Gonzaloa and T. Rojo, Energy Environ. Sci., 2017, 10, 1051 RSC.
- N. Yabuuchi, H. Yoshida and S. Komaba, Electrochemistry, 2012, 80, 716 CrossRef CAS.
- S. Komaba, N. Yabuuchi, T. Nakayama, A. Ogata, T. Ishikawa and I. Nakai, Inorg. Chem., 2012, 51, 6211 CrossRef CAS PubMed.
- K. Takada, H. Sakurai, E. Takayama-Muromachi, F. Izumi, R. A. Dilanian and T. Sasaki, Nature, 2003, 422, 53 CrossRef CAS PubMed.
- J. Deng, W.-B. Luo, X. Lu, Q. Yao, Z. Wang, H.-K. Liu, H. Zhou and S.-X. Dou, Adv. Energy Mater., 2018, 8, 1701610 CrossRef.
- K. Kubota, T. Asari, H. Yoshida, N. Yabuuchi, H. Shiiba, M. Nakayama and S. Komaba, Adv. Funct. Mater., 2016, 26, 6047 CrossRef CAS.
- F. Schipper, E. M. Erickson, C. Erik, J.-Y. Shin, F. F. Chesneau and D. Aurbach, J. Electrochem. Soc., 2017, 164, A6220 CrossRef CAS.
- K. Kubota, S. Kumakura, Y. Yoda, K. Kuroki and S. Komaba, Adv. Energy Mater., 2018, 8, 1703415 CrossRef.
- R. J. Clement, P. G. Bruce and C. P. Grey, J. Electrochem. Soc., 2015, 162, A2589 CrossRef CAS.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81 CrossRef CAS.
- M. H. Han, E. Gonzalo, G. Singh and T. A. Rojo, Energy Environ. Sci., 2015, 8, 81 RSC.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okyuyama, R. Usui, Y. Yamada and S. Kobama, Nat. Mater., 2012, 11, 512 CrossRef CAS PubMed.
- J. Billaud, R. J. Clément, A. R. Amstrong, J. C. Vázquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243 CrossRef CAS PubMed.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512 CrossRef CAS PubMed.
- J. Billaud, G. Singh, A. R. Amstrong, E. Gonzalo, V. Roddatis, M. Armand, T. Rojo and P. G. Bruce, Energy Environ. Sci., 2014, 7, 1387 RSC.
- Q. Liu, Z. Hu, M. Chen, C. Zou, H. Jin, S. Wang, S.-L. Chou and S.-H. Dou, Small, 2019, 15, 1805381 CrossRef PubMed.
- K. Zhang, D. Kim, Z. Hu, M. Park, G. Noh, Y. Yang, J. Zhang, V. W. Lau, S.-L. Chou, M. Cho, S.-Y. Choi and Y.-M. Kang, Nat. Commun., 2019, 10, 5302 CrossRef PubMed.
- A. Caballero, L. Hernán, J. Morales, L. Sánchez, J. S. Pena and M. A. G. Aranda, J. Mater. Chem., 2002, 12, 1142 RSC.
- S. Kumakura, Y. Tahara, K. Kubota, K. Chihara and S. Komaba, Angew. Chem., Int. Ed., 2016, 55, 12760 CrossRef CAS PubMed.
- M.-S. Kwon, S. G. Lim, Y. Park, S.-M. Lee, K. Y. Chung, T. J. Shin and K. T. Lee, ACS Appl. Mater. Interfaces, 2017, 9, 14758 CrossRef CAS PubMed.
- S. Kumakura, Y. Tahara, S. Sato, K. Kubota and S. Komaba, Chem. Mater., 2017, 29, 8958 CrossRef CAS.
- J.-Y. Hwang, J. Kim, T.-Y. Yu and Y.-K. Sun, Adv. Energy Mater., 2019, 9, 1803346 CrossRef.
- Y.-J. Park, J. U. Choi, J. H. Jo, C.-H. Jo, J. Kim and S.-T. Myung, Adv. Funct. Mater., 2019, 29, 1901912 CrossRef.
- J. U. Choi, C. S. Yoon, Q. Zhang, P. Kaghazchi, Y. H. Jung, K.-S. Lee, D.-C. Anh, Y.-K. Sun and S.-T. Myung, J. Mater. Chem. A, 2019, 7, 202 RSC.
- T. Maxisch, F. Zhou and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301 CrossRef.
- T. L. Tran, H. D. Luong, D. M. Duong, N. T. Dinh and V. A. Dinh, ACS Omega, 2020, 5(10), 5429 CrossRef CAS PubMed.
- L. Zheng, Z. Wang, M. Wu, B. Xu and C. Ouyang, J. Mater. Chem. A, 2019, 7, 6053 RSC.
- Z. Zhu, H. Peelaers and C. G. Van de Walle, Chem. Mater., 2019, 31, 5224 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- M. Aykol, S. Kim and C. Wolverton, J. Phys. Chem. C, 2015, 119, 19053 CrossRef CAS.
- S. Grimmea, J. Antony, S. Ehrlich and H. Krieg, J. Comput. Chem., 2011, 32, 1456 CrossRef PubMed.
- G. Henkelman and H. J. Jonsson, Chem. Phys., 2000, 113, 9978 CAS.
| This journal is © the Owner Societies 2020 |