Open Access Article
Open Access ArticleSolvent effects on Li ion transference number and dynamic ion correlations in glyme- and sulfolane-based molten Li salt solvates†
Keisuke
Shigenobu
a,
Kaoru
Dokko
 a,
Masayoshi
Watanabe
a,
Masayoshi
Watanabe
 b and
Kazuhide
Ueno
b and
Kazuhide
Ueno
 *a
*a
aDepartment of Chemistry and Life Science, Yokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama 240-8501, Japan. E-mail: ueno-kazuhide-rc@ynu.ac.jp; Fax: +81-45-339-3951; Tel: +81-45-339-3951
bInstitute of Advanced Sciences, Yokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama 240-8501, Japan
First published on 29th June 2020
Abstract
The Li+ transference number of electrolytes is one of the key factors contributing to the enhancement in the charge–discharge performance of Li secondary batteries. However, a design principle to achieve a high Li+ transference number has not been established for liquid electrolytes. To understand the factors governing the Li+ transference number tLi, we investigated the influence of the ion–solvent interactions, Li ion coordination, and correlations of ion motions on the Li+ transference number in glyme (Gn, n = 1–4)- and sulfolane (SL)-based molten Li salt solvate electrolytes with lithium bis(trifluoromethansulfonyl)amide (LiTFSA). For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 tetraglyme-LiTFSA molten complex, [Li(G4)][TFSA], the Li+ transference number estimated using the potentiostatic polarisation method (tPPLi = 0.028) was considerably lower than that estimated using the self-diffusion coefficient data with pulsed filed gradient (PFG)-NMR (tNMRLi = 0.52). The dynamic ion correlations (i.e., cation–cation, anion–anion, and cation–anion cross-correlations) were determined from the experimental data on the basis of Roling and Bedrov's concentrated solution theory, and the results suggest that the strongly negative cross-correlations of the ion motions (especially for cation–cation motions) are responsible for the extremely low tPPLi of [Li(G4)][TFSA]. In contrast, tPPLi is larger than tNMRLi in the SL-based electrolytes. The high tPPLi of the SL-based electrolytes was ascribed to the substantially weaker anti-correlations of cation–cation and cation–anion motions. Whereas the translational motions of the long-lived [Li(glyme)]+ and [TFSA]− dominate the ionic conduction for [Li(G4)][TFSA], Li ion hopping/exchange conduction was reported to be prevalent in the SL-based electrolytes. The unique Li ion conduction mechanism is considered to contribute to the less correlated cation–cation and cation–anion motions in SL-based electrolytes.
1 tetraglyme-LiTFSA molten complex, [Li(G4)][TFSA], the Li+ transference number estimated using the potentiostatic polarisation method (tPPLi = 0.028) was considerably lower than that estimated using the self-diffusion coefficient data with pulsed filed gradient (PFG)-NMR (tNMRLi = 0.52). The dynamic ion correlations (i.e., cation–cation, anion–anion, and cation–anion cross-correlations) were determined from the experimental data on the basis of Roling and Bedrov's concentrated solution theory, and the results suggest that the strongly negative cross-correlations of the ion motions (especially for cation–cation motions) are responsible for the extremely low tPPLi of [Li(G4)][TFSA]. In contrast, tPPLi is larger than tNMRLi in the SL-based electrolytes. The high tPPLi of the SL-based electrolytes was ascribed to the substantially weaker anti-correlations of cation–cation and cation–anion motions. Whereas the translational motions of the long-lived [Li(glyme)]+ and [TFSA]− dominate the ionic conduction for [Li(G4)][TFSA], Li ion hopping/exchange conduction was reported to be prevalent in the SL-based electrolytes. The unique Li ion conduction mechanism is considered to contribute to the less correlated cation–cation and cation–anion motions in SL-based electrolytes.
1. Introduction
The Li+ transference number, i.e., the ratio of Li ion mobility to the total ionic mobility, is one of the important parameters characterising the transport properties of electrolyte materials used in Li secondary batteries. With a growing demand for high-energy-density batteries with rapid charge–discharge capability, the significance of Li+ transference number has been revisited and emphasised upon for designing a highly Li ion conducting electrolytes, as recent studies on Li-ion battery modelling suggested a high-Li+ transference number electrolyte enables a fast charge–discharge capability even with relatively low ionic conductivity,1 and suppression of the lithium dendrite growth at the Li metal anode.2 All solid state batteries using sulphide-based solid electrolytes with Li+ transference number of unity demonstrated very fast charge–discharge within a few minutes3 and high-energy long-cycling with lithium metal anode.4Molten Li salt solvates or liquid electrolytes with nearly saturated Li salt concentrations are also regarded as a prospective electrolyte material for Li secondary batteries; this is because various types of highly concentrated electrolyte systems, ranging from aqueous to non-aqueous and ionic liquid (IL), have shown improved rate capability, long-term cycling stability, and high Coulombic efficiency.5–13 In previous studies, we investigated the Li ion coordination structure and ionic transport properties of two types of molten Li salt solvates:oligoether glyme (CH3O(CH2CH2O)nCH)-14–16 and sulfolane (SL)-based electrolytes.17,18 In the former case, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of tetraglyme (G4) and lithium bis(trifluoromethanesulfonyl)amide (LiTFSA) forms a thermally-stable molten Li salt solvate ([Li(G4)][TFSA]) comprising a crown-ether like [Li(G4)]+ complex cation and a TFSA− anion, and it behaves like ILs. [Li(G4)][TFSA] was found to exhibit a Li+-limiting current density one order of magnitude higher than that of a binary mixture electrolyte of IL and Li salt, leading to the enhanced rate capability of the Li/LiCoO2 cell.14,19 In the latter case, i.e., for SL-based molten Li salt solvates, the Li ion is observed to diffuse faster than SL and the anion; this indicates that the Li ion hopping/exchange conduction mechanism contributes significantly to the ionic conduction. A unique chain-like ⋯SL⋯Li+⋯SL⋯Li+⋯ coordination structure was suggested to be involved in the extraordinary Li ion conduction.17 The SL-based molten Li salt solvates showed a better rate capability of the Li/S cell compared with the cell using [Li(G4)][TFSA].18,20
1 molar mixture of tetraglyme (G4) and lithium bis(trifluoromethanesulfonyl)amide (LiTFSA) forms a thermally-stable molten Li salt solvate ([Li(G4)][TFSA]) comprising a crown-ether like [Li(G4)]+ complex cation and a TFSA− anion, and it behaves like ILs. [Li(G4)][TFSA] was found to exhibit a Li+-limiting current density one order of magnitude higher than that of a binary mixture electrolyte of IL and Li salt, leading to the enhanced rate capability of the Li/LiCoO2 cell.14,19 In the latter case, i.e., for SL-based molten Li salt solvates, the Li ion is observed to diffuse faster than SL and the anion; this indicates that the Li ion hopping/exchange conduction mechanism contributes significantly to the ionic conduction. A unique chain-like ⋯SL⋯Li+⋯SL⋯Li+⋯ coordination structure was suggested to be involved in the extraordinary Li ion conduction.17 The SL-based molten Li salt solvates showed a better rate capability of the Li/S cell compared with the cell using [Li(G4)][TFSA].18,20
The higher Li+ transference number of the concentrated electrolytes has been considered to be the key reason for the enhanced rate capability of Li secondary batteries. Nevertheless, the relationship between the molecular structure and Li+ transference number remains to be clarified. Furthermore, there is no established guideline for designing liquid electrolytes with a high Li+ transference number. For solid polymer electrolytes, Balsara and Newman systematically studied cross-correlations of ion motions by introducing Stefan–Maxwell diffusion coefficients and their relevance to the Li+ transference number.21–23 Woolf and Harris have also investigated the correlated ion motions in terms of velocity cross-correlation functions for aqueous electrolyte solutions.24 Although a few studies have focused on the ion correlations for Li ion conducting organic electrolyte solutions, recent seminal works based on Onsager reciprocal relations combined with the linear response theory by Roling and Bedrov has revealed the importance of the interionic correlations to the Li+ transference number for molten Li salt solvates.25–27 For [Li(G4)][TFSA], Roling and Bedrov suggested that the strongly anti-correlated ion dynamics were due to the constraint of momentum conservation for the long-lived [Li(G4)]+ complex cation and the TFSA− anion, resulting in an extremely low Li+ transference numbers under anion-blocking conditions.
Here, we studied effect of ion–solvent interactions and Li ion coordination structure on the Li+ transference number for the glyme- and SL-based molten Li salt solvates. The dynamic correlations of ions were also experimentally determined on the basis of Roling and Bedrov's concentrated electrolyte theory.26,27 The relationship between the ionic correlations and Li+ transference number was discussed in relation to Li ion coordination structure and possible ion transport mechanism.
2. Experimental
2.1 Materials
Purified diglyme (G2), triglyme (G3), and tetraglyme (G4) (water content <50 ppm) were supplied by Nippon Nyukazai. Monoglyme (G1, battery grade <50 ppm) and sulfolane (SL, battery grade <50 ppm) were purchased from Kishida Chemical. Lithium bis(trifluoromethanesulfonyl)amide (Li[TFSA], >99.9%, water content <100 ppm) was provided by Solvay Japan. All molten Li salt solvates were prepared in an inert argon-filled glove box ([H2O] < 1 ppm; [O2] < 1 ppm).2.2 Measurements
Two different Li+ transference numbers were determined by either potentiostatic polarisation method or self-diffusion coefficients obtained from PFG-NMR. For the potentiostatic polarisation method, the experiments were performed using an Li symmetric cell. A porous glass filter paper (Advantec, GA55, 17 mm in diameter) impregnated with the liquid electrolyte was placed between two Li foil electrodes (Honjo Metal, 16 mm in diameter) in a 2032-coin-type cell. Impedance spectra were measured in the frequency range of 100 mHz–1 MHz with a perturbation voltage amplitude of 10 mV, using a potentiostat (Solartron Analytical, ModuLab XM ECS). The impedance measurements were preliminarily performed every hour prior to the potentiostatic polarisation to ensure the stabilisation of Li electrode interface. The time dependence of current was monitored during the potentiostatic polarisation, with a potential step of 10 mV. After the current reached the steady state, impedance spectra were measured again, as prescribed in the literature.28,29 The experimental details for PFG-NMR are available in our previous report.15 The salt diffusion coefficients (Dsalt) used for calculating Onsager transport coefficients were determined using the same Li symmetric coin cell, as described in the literature.22 The cell was polarised to 10 mV in the potentiostatic mode and the relaxation of the cell potential was recorded after the applied potential was removed. The potential relaxation was fitted using a single exponential decay function to determine Dsalt (see ESI,† in detail). The electrode potentials of Li/Li+ were measured with the help of the reference electrode (Li/Li+ in 1 mol dm−3 Li[TFSA]/G3) using a multi-compartment concentration cell.30 Vycor glass was used for the junction between the reference electrolyte and the sample electrolytes. The potential was recorded using a multi-channel potentiostat (Bio-Logic, VSP300). A slope dφ/dln(c) at given concentration was obtained from the slope of the concentration dependence of the concentration cell potential (Fig. S1, ESI†).26 All the above measurements were performed at 30 °C, unless otherwise noted.3. Results and discussion
3.1 Estimation of Li+ transference number
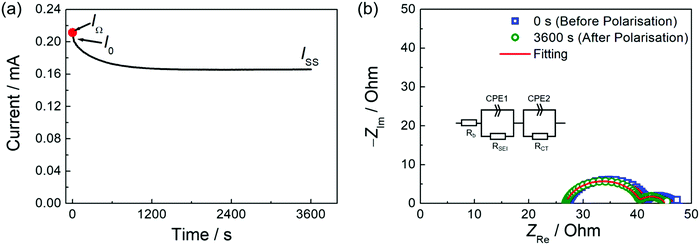
Several methods have been proposed for estimating Li+ transference number of Li ion conducting electrolytes, such as potentiostatic polarisation, galvanostatic polarisation, very-low-frequency impedance spectroscopy, concentration cell method, PFG-NMR, and electrophoretic NMR, although there are inherent restrictions for each method (e.g., sample limitations and cumbersome procedures).25,31,32 In previous publications, we reported the apparent Li+ transference number derived from PFG-NMR (tNMRLi) for the glyme- and SL-based molten Li salt solvates electrolytes.15,18 Here, tNMRLi is simply defined as the ratio of self-diffusion coefficients of Li ion (DLi) and TFSA anion (Danion),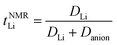 | (1) |
The PFG-NMR method relies on Nernst–Einstein equation, assuming that the ions are completely dissociated and move independently, as postulated for ideal dilute electrolyte solutions. This would not rigorously hold for the molten Li salt solvate electrolytes with extremely high salt concentrations, and therefore, tNMRLi may be dissimilar to the realistic Li+ transference number.
The potentiostatic polarisation combined with electrochemical impedance spectroscopy28,29 is facile and a relatively versatile method, and has been adopted for various electrolytes, ranging from polymeric to liquid systems. The Li+ transference number based on this method (tPPLi) was obtained as follows:
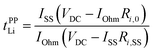 | (2) |
With the results of polarisation current curves (IOhm and ISS) and impedance spectra (Ri,0 and Ri,SS) for the Li symmetric cell as shown in Fig. 1, tPPLi was found to be 0.68 for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar mixture of LiTFSA and SL ([Li(SL)2][TFSA]). Similarly, tPPLi for [Li(G4)][TFSA] was found to be 0.028. These values reasonably agree with the reported tLi values for [Li(SL)2][TFSA] (0.71
2 molar mixture of LiTFSA and SL ([Li(SL)2][TFSA]). Similarly, tPPLi for [Li(G4)][TFSA] was found to be 0.028. These values reasonably agree with the reported tLi values for [Li(SL)2][TFSA] (0.71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) and for [Li(G4)][TFSA] (0.026 25 and 0.03 20) determined by very-low-frequency impedance method, confirming the validity of tPPLi measured by the potentiostatic polarisation method.
20) and for [Li(G4)][TFSA] (0.026 25 and 0.03 20) determined by very-low-frequency impedance method, confirming the validity of tPPLi measured by the potentiostatic polarisation method.
Here, we studied the influence of ion–solvent interaction and Li ion coordination structure on the Li+ transference numbers for the glyme- and SL-based molten Li salt solvate electrolytes. For the glyme systems, we examined the molten Li salt solvates with different glyme chain lengths (G1 to G4), while adjusting the molar ratio of oxygen atoms of the solvent molecules to Li ions ([O]/[Li+]) to be 4 or 5.16 [Li(SL)2][TFSA] and [Li(SL)3][TFSA] showing a unique Li ion transport via a dominant Li ion hopping/exchange mechanism17,18 were also studied for comparison.
The Li+ transference numbers (tNMRLi and tPPLi) of the molten Li salt solvates are listed in Table 1. Whereas the glyme-based electrolytes showed a relatively high tNMRLi of roughly 0.5–0.6, irrespective of the chain length of the glyme molecules, tPPLi was one order of magnitude lower for [Li(G3)][TFSA] and [Li(G4)][TFSA] with longer glymes compared with those for [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA] with shorter glymes. This dependence of tPPLi on the chain length appears to be relevant to the classification of the molten Li salt solvates into solvate ionic liquids. [Li(G3)][TFSA] and [Li(G4)][TFSA] were regarded as good solvate ionic liquids considering aspects such as the formation of crown ether-like, long-lived [Li(glyme)]+ complex cation and negligible amounts of uncoordinated glyme; in contrast, the molten Li salt solvates with the shorter glyme, such as [Li(G1)2][TFSA], were classified into concentrated solutions in which the complex cations are not stable owing to a weaker chelate effect.16
| Sample | t NMRLi | t PPLi | t MDLi |
|---|---|---|---|
| [Li(G3)][TFSA] | 0.61 | 0.028 | 0.10 |
| [Li(G4)][TFSA] | 0.52 | 0.028 | 0.06 |
| [Li(G1)2][TFSA] | 0.54 | 0.35 | 0.30 |
| [Li(G1)(G2)][TFSA] | 0.48 | 0.31 | 0.26 |
| [Li(SL)2][TFSA] | 0.61 | 0.68 | — |
| [Li(SL)3][TFSA] | 0.57 | 0.69 | — |
Molecular dynamics (MD) simulations by Bedrov et al. demonstrated a good correlation between the glyme chain length and the Li+ transference number (tMDLi) of the glyme-based molten Li salt solvates under anion-blocking conditions.26 The tMDLi value decreases with increasing chain length of the glyme from G1 to G4 as seen in Table 1. The general tendency observed in our experimental tPPLi is in accordance with the glyme chain length dependence of tMDLi estimated by Bedrov et al.
Both tNMRLi and tPPLi for the SL-based electrolytes were higher than those of the glyme-based electrolytes. The high tPPLi suggests that the Li salt concentration gradient develops to a lesser extent in the SL-based electrolytes. In the SL-based molten Li salt solvates, the two oxygen atoms of one SL coordinates to two different neighbouring Li ions forming an SL-bridged, chain-like Li ion coordination structure (⋯SL⋯Li+⋯SL⋯Li+⋯).17,18 The unique Li ion coordination structure may play a pivotal role in displaying the high tPPLi as well as the unusual self-diffusion behaviour of Li ions (diffusing faster than SL and TFSA anions).
Another noteworthy aspect in Table 1 is a discrepancy between tNMRLi and tPPLi for each electrolyte. tPPLi was considerably lower than tPPLi for [Li(G3)][TFSA] and [Li(G4)][TFSA]. The recent studies25,26,33,34 suggested that the extremely low tPPLi as compared with tNMRLi for the solvate ionic liquids, [Li(G3)][TFSA] and [Li(G4)][TFSA], is attributable to the remarkable anti-correlated motions of the ions, which is a consequence of the constraint of momentum conservation for the long-lived [Li(glyme)]+ complex cation and TFSA− anion under the anion blocking conditions. The momentum conservation of the ions is achieved solely by the momentum exchange of the ions, as with the cases for solvent-free molten salts and ionic liquids.35,36 The previous MD simulation study also suggested that the anti-correlated motions of the ions can be mitigated in the shorter glyme systems since a more frequent solvent exchange between the unstable [Li(glyme)] complex cations contributes to the momentum conservation.26 This would result in tPPLi being a little lower than tNMRLi for [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA]. In contrast, the tPPLi was higher than tNMRLi for [Li(SL)2][TSFA] and [Li(SL)3][TFSA]. The same trend was also observed for the SL-based concentrated electrolytes with lithium bis(fluorosulfonyl)amide.34,37 This implies that the dynamic ion correlations positively affected the Li+ transference number under anion blocking conditions (tPPLi) in the SL-based electrolytes. The effects of the dynamic ion correlations on the Li+ transference numbers are investigated in detail in the following section.
3.2 Dynamic correlations of the ions
The dynamic ion correlations in the molten Li salt solvates were experimentally determined to understand their contribution to ionic conductivity and to clarify the difference in ionic transport behaviour in the molten Li salt solvates. In this work, the Onsager transport coefficients were employed to evaluate the interionic correlations according to Roling and Bedrov et al.25,26 In the Onsager transport formalism, the ionic conductivity σion is described as| σion = σ++ + σ−− − 2σ+− | (3) |
Two transport coefficients for cation and anion, σ++ and σ−−, can be further divided into self-terms and distinct terms, respectively, and the ionic conductivity σion is given as follows:
| σion = σself+ + σdistinct+ + σself− + σdistinct−− − 2σ+− | (4) |
All the Onsager transport coefficients (σ++, σ−− and σ+−) can be estimated from experimentally determined quantities, σion, tPPLi, Dsalt and dΔφ/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(c) and these experimental data were listed in Table S1 (ESI†). The self-terms, σself+ and σself−, are obtained from the Nernst–Einstein equation using self-diffusion coefficients of Li ions (DLi), and the anions (Danion),26 and the distinct terms can be calculated by simply subtracting σself+ (and σself−) from σ++ (and σ−−). The detailed procedure for estimating the transport coefficients is described in Supplementary Information. The sign of σdistinct++, σdistinct−−, and σ+− is closely related to the dynamic cross-correlations of cation–cation, anion–anion, and cation–anion, respectively. The sign of the cross-correlations becomes positive and negative for correlated and anti-correlated ion motions, respectively, while the cross-correlations of zero represent non-correlated interionic dynamics as assumed in ideal electrolyte solutions.
ln(c) and these experimental data were listed in Table S1 (ESI†). The self-terms, σself+ and σself−, are obtained from the Nernst–Einstein equation using self-diffusion coefficients of Li ions (DLi), and the anions (Danion),26 and the distinct terms can be calculated by simply subtracting σself+ (and σself−) from σ++ (and σ−−). The detailed procedure for estimating the transport coefficients is described in Supplementary Information. The sign of σdistinct++, σdistinct−−, and σ+− is closely related to the dynamic cross-correlations of cation–cation, anion–anion, and cation–anion, respectively. The sign of the cross-correlations becomes positive and negative for correlated and anti-correlated ion motions, respectively, while the cross-correlations of zero represent non-correlated interionic dynamics as assumed in ideal electrolyte solutions.
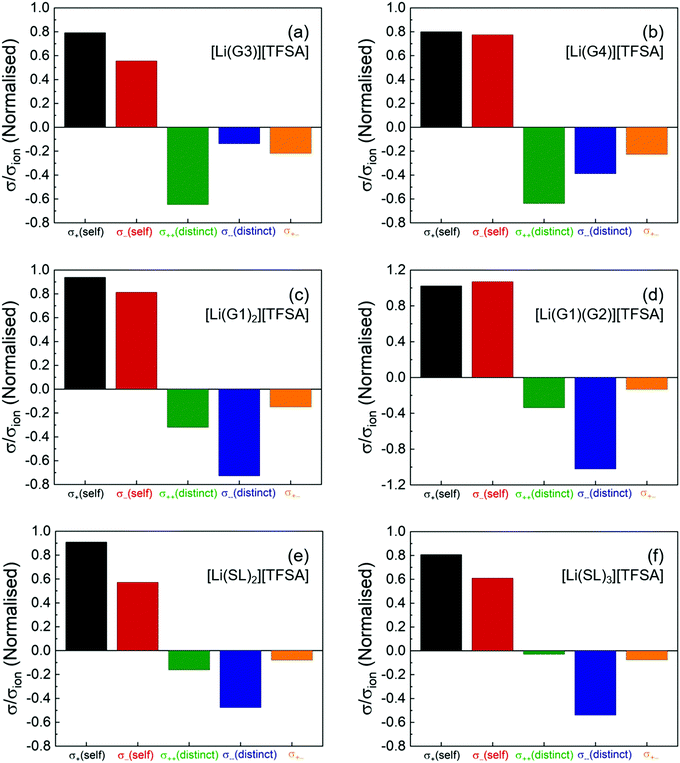
Fig. 2 shows the normalised coefficients (σself+, σself−, σdistinct++,σdistinct−−, and σ+− divided by σion) to illustrate the contribution of the dynamic correlations to the total ionic conductivity. The numeric data for these coefficients are also listed in Table S2 (ESI†). As shown in the Fig. 2a and b, for the solvate ionic liquids, [Li(G3)][TFSA] and [Li(G4)][TFSA], all the cross-correlations (σdistinct++/σion, σdistinct−−/σion, and σ+−/σion) are negative, indicating that the cation–cation, anion–anion, and cation–anion motions are anti-correlated (i.e., the movement of the ions in opposite directions). Therefore, as suggested by eqn (4), the cation–cation and anion–anion anti-correlations negatively contributed to the ionic conductivity, whereas the cation–anion anti-correlation contributed positively to the ionic conductivity. The negatively large value of σdistinct++/σion for [Li(G3)][TFSA] and [Li(G4)][TFSA] indicates that the momentum conservation of the vehicular-type translational motions of a long-lived [Li(glyme)]+ complex cation was preserved mainly by other [Li(glyme)]+ complex cations. Hence, σself+ is significantly offset by the negative σdistinct++, leading to a small contribution of σ++ to σion. Furthermore, the negative value of σ+−/σion suggests that [Li(glyme)]+ complex cations and [TFSA]− anions are generally well-dissociated, and most of the ions do not form persistent ion-pairs, even at high Li salt concentrations.
Although our experiments demonstrated the most negatively large value for σdistinct++/σion among the cross-correlations, σdistinct++/σion was comparable to σdistinct−−/σion for [Li(G4)][TFSA] in the reported MD simulations.33 Nevertheless, our experimental results on the transport coefficients are in reasonable agreement with the results in the MD simulations. All the distinct terms were found to be negative, and the dynamic cross-correlations of the ions with the same sign was negatively larger than the cation–anion cross-correlations for [Li(G4)][TFSA]. The anti-correlations of [Li(G4)]+ and [TFSA]− in [Li(G4)][TFSA] was also experimentally verified by the electrophoretic NMR study.38 Significant anti-correlations of the ion motions derived from the momentum conservation have been reported for solvent-free ionic liquids and molten salts.35 Hence, the strongly anti-correlated motions found in [Li(G3)][TFSA] and [Li(G4)][TFSA] corroborate our previous classification of these molten Li salt solvates into a good solvate ionic liquid on the basis of the robustness of [Li(glyme)]+ complex cations (i.e., long-term coupled motions of Li ion and glyme by diffusivity measurement15 and MD simulations39) and the scarcity of uncoordinated glyme estimated by Raman analysis.40
The σdistinct++/σion and σ+−/σion of [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA] with shorter glymes are less negative than those of [Li(G3)][TFSA] and [Li(G4)][TFSA] (Fig. 2c and d). This may be due to the occurrence of much faster ligand (glyme) exchange in the shorter glyme-based molten Li salt solvates.16 Shorter glymes with a high exchange rate (or a short residence time with the Li ion) enables the momentum exchange between the ions and the ligands to satisfy the momentum conservation, and thus the cation–cation and cation–anion correlations are less anti-correlated.26 Interestingly, σdistinct++/σion and σ+−/σion of the SL-based electrolytes are even less negative than those of [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA] and approach zero with a small increase in the SL content from [Li(SL)2][TFSA] to [Li(SL)3][TFSA] (Fig. 2e and f). This means that, despite high Li salt concentrations similar to the glyme systems, the cation–cation and cation–anion motions are found to be less anti-correlated for [Li(SL)2][TFSA] and nearly non-correlated for [Li(SL)3][TFSA]. The postulated Li ion hopping/exchange conduction mechanism through the unique SL-bridged, chain-like Li-ion coordination structure may be responsible for the insignificant anti-correlations even at high Li salt concentrations as well as a large contribution of σself+ to σion.17,18
In addition, the σdistinct−−/σion of the shorter glyme-based and the SL-based electrolytes is more negative than that of [Li(G3)][TFSA] and [Li(G4)][TFSA]. This suggests that the momentum of bulky TFSA anions is predominantly self-compensated in these molten Li salt solvates with the labile Li ion coordination structures. The negative contribution of σdistinct−− significantly offsets the positive contribution of σself−, and thus, σ−− has only a minor effect on σion in these molten Li salt solvates.
3.3 Effects of dynamic correlations of the ions on Li+ transference number
Herein, we discuss the influence of the dynamic ion correlations in the molten Li salt solvates on the Li+ transference number. The Li+ transference number determined from the potentiostatic polarisation method (tPPLi) is considered to be equivalent to that estimated from the MD simulations under anion-blocking conditions (tMDLi) and is rationalised with the Onsager transport coefficients as follows,25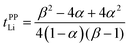 | (5) |
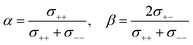 | (6) |
The parameter α must be equal to tNMRLi for non-correlated ideal systems, but is greatly affected by the cation–cation cross-correlation for the molten Li salt solvates, whereas the parameter β is dependent on the cation–anion cross-correlation. The parameters α and β for the molten Li salt solvates are listed in Table 2. Based on eqn (5), tPPLi was simulated versus β for different α values, as in Fig. 3; in this figure, the experimental values of [Li(G4)][TFSA], [Li(G1)(G2)][TFSA] and [Li(SL)3][TFSA] are also plotted.
| Sample | α | β |
|---|---|---|
| [Li(G3)][TFSA] | 0.25 | −0.78 |
| [Li(G4)][TFSA] | 0.29 | −0.83 |
| [Li(G1)2][TFSA] | 0.88 | −0.43 |
| [Li(G1)(G2)][TFSA] | 0.93 | −0.37 |
| [Li(SL)2][TFSA] | 0.89 | −0.19 |
| [Li(SL)3][TFSA] | 0.92 | −0.18 |
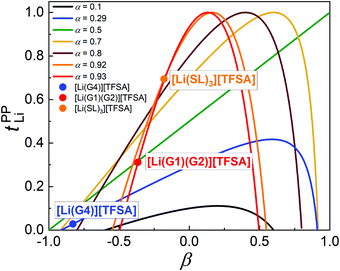 | ||
| Fig. 3 Plots of tPPLiversus β with different α. The data for [Li(G4)][TFSA], [Li(G1)(G2)][TFSA] and [Li(SL)3][TFSA] are also plotted in the figure. | ||
For the glyme-based electrolytes, the α value of [Li(G3)][TFSA] and [Li(G4)][TFSA] is significantly lower than that of [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA]. This is mainly attributed to the stronger anti-correlated motions of Li ions in the molten Li solvates with longer glymes (Fig. 2a and b). The decreased σ−− due to the highly negative σdistinct−− also contributes to higher α values for [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA]. The strength of the cation–anion anti-correlations are well manifested in the order of β values – [Li(G4)][TFSA] with the most pronounced cation–cation anti-correlations has the lowest β value of −0.83. Similar β values (−0.87 for [Li(G4)][TFSA] and ∼−0.5 for [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA]) were reported in the MD simulation study.26,33 As seen in Fig. 3, both low α and β values are responsible for the extremely low tPPLi for [Li(G4)][TFSA]. Consequently, we experimentally confirmed Bedrov's notion that tPPLi can increase for shorter glyme systems with the weaker Li ion–solvent interaction, in which the momentum conservation-derived ionic anti-correlations of cation–cation and cation–anion motions were suppressed to some extent by the fast solvent (momentum) exchange, leading to the higher α and β values.
For the SL-based electrolytes, the α values are comparable to that of the shorter glyme-based electrolytes, but the β values are higher than that of the shorter glyme-based electrolytes. The high α value arises from not only the large contribution of σself+ (due to higher DLi than Danion), but also the significantly less-pronounced cation–cation anti-correlations. In a comparison between the shorter glyme based electrolytes and the SL-based electrolytes with the high α values of ∼0.9 (Fig. 3), the higher β value (due to weaker cation–anion anti-correlations) for the SL-based electrolytes exerts an efficient contribution to tPPLi becoming high. As a result, the Li ion hopping/exchange mechanism through the labile SL-bridged, chain-like Li-ion coordination structure may reduce the cation–cation and cation–anion anti-correlations, and impart the high α value and the β value closer to zero, enabling a high tPPLi.
The simulation of tPPLi with different parameters of α and β (Fig. 3) provides an important guideline for designing liquid electrolytes with high tPPLi, and suggests that single ion conductors (tPPLi ∼ 1) can be prepared even with low molecular weight solvents and Li salts when liquid electrolytes have appropriate values of α (> 0.5) and β. For instance, one can expect an even higher tPPLi for the SL-based electrolytes if the β parameter approaches zero. This might be achieved either by decreasing the interactions between Li ions and SL solvents to facilitate solvent-derived momentum exchange (e.g., partial fluorination of SL), or by increasing the cation–anion interactions to some extent (e.g., use of more associative Li salt than LiTFSA). Both would contribute to an increase in β. Indeed, tPPLi increased from 0.68 for [Li(SL)2][TFSA] to 0.77 for [Li(SL)2][BF4]17 with reprising weakly coordinating, bulky TFSA anions by more strongly Lewis basic, smaller BF4 anions.
4. Conclusions
t PPLi of the glyme- and SL-based molten solvates was determined by potentiostatic polarisation method. The dynamic ion correlations of each electrolyte were also experimentally studied on the basis of Rolling and Bedrov's concentrated solution theory, and the effects of these correlations on tPPLi were discussed. For [Li(G3)][TFSA] and [Li(G4)][TFSA], the negatively large value of σdistinct++/σion and σ+−/σion indicates strong anti-correlations of cation–cation and cation–anion motions, and may be attributed to the momentum conservation of the [Li(glyme)]+ complex cation and TFSA− anions, preserved solely by the momentum exchange of the ions. These results verified that [Li(G3)][TFSA] and [Li(G4)][TFSA] showed ionic liquid-like ionic transport behaviour, which in turn led to the extremely low value of tPPLi. For [Li(G1)2][TFSA] and [Li(G1)(G2)][TFSA], σdistinct++/σion and σ+−/σion were found to be less negative, and the tPPLi values was higher than those of [Li(G3)][TFSA] and [Li(G4)][TFSA]. This was probably due to the more frequent solvent exchange between the unstable [Li(glyme)]+ complex cations. Overall, our experimental results on tPPLi and the dynamic ion correlations agreed reasonably with the results obtained from the MD simulations. For the SL-based electrolytes, σdistinct++/σion and σ+−/σion were even less negative and approached zero, indicative of the insignificant anti-correlations of cation–cation and cation–anion motions. It was suggested that the Li ion hopping/exchange conduction mechanism through the SL-bridged, chain-like Li-ion coordination structure plays an important role in suppressing the cation–cation and cation–anion anti-correlations and displaying a high tPPLi. As a result, the difference in the ion–solvent interactions and the Li ion coordination structure of the molten Li salt solvates has a significant impact on the cross-correlations of ion motions, which in turn become a critical determinant for tPPLi. The present study on dynamic ion correlations unveiled the difference in the ion conduction mechanism in some of the molten Li salt solvate electrolytes and its relevance to Li+ transference number. Further systematic studies on the ion dynamics in different electrolyte systems would offer insight into a rational design concept for single ion conducting liquid electrolytes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported in part by the JSPS KAKENHI (Grant No. 16H06053, 19K22216 and 20H02837 to K. U., 18H03926 to K. D. and 15H05758 to M. W.) from the Japan Society for the Promotion of Science (JSPS), and by JST ALCA-SPRING Grant Number JPMJAL1301, Japan.References
- K. M. Diederichsen, E. J. McShane and B. D. McCloskey, ACS Energy Lett., 2017, 2, 2563–2575 CrossRef CAS.
- P. Barai, K. Higa and V. Srinivasan, J. Electrochem. Soc., 2018, 165, A2654–A2666 CrossRef CAS.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- Y.-G. Lee, S. Fujiki, C. Jung, N. Suzuki, N. Yashiro, R. Omoda, D.-S. Ko, T. Shiratsuchi, T. Sugimoto, S. Ryu, J. H. Ku, T. Watanabe, Y. Park, Y. Aihara, D. Im and I. T. Han, Nat. Energy, 2020, 5, 299–308 CrossRef CAS.
- Y. Yamada, M. Yaegashi, T. Abe and A. Yamada, Chem. Commun., 2013, 49, 11194–11196 RSC.
- Y. Yamada, K. Furukawa, K. Sodeyama, K. Kikuchi, M. Yaegashi, Y. Tateyama and A. Yamada, J. Am. Chem. Soc., 2014, 136, 5039–5046 CrossRef CAS PubMed.
- J. Qian, W. A. Henderson, W. Xu, P. Bhattacharya, M. Engelhard, O. Borodin and J.-G. Zhang, Nat. Commun., 2015, 6, 6362 CrossRef CAS PubMed.
- L. Suo, W. Xue, M. Gobet, S. G. Greenbaum, C. Wang, Y. Chen, W. Yang, Y. Li and J. Li, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1156–1161 CrossRef CAS PubMed.
- H. Yoon, P. Howlett, A. S. Best, M. Forsyth and D. R. Macfarlane, J. Electrochem. Soc., 2013, 160, A1629 CrossRef CAS.
- X. Gao, F. Wu, A. Mariani and S. Passerini, ChemSusChem, 2019, 12, 4185–4193 CrossRef CAS PubMed.
- L. Suo, Y.-S. Hu, H. Li, M. Armand and L. Chen, Nat. Commun., 2013, 4, 1481 CrossRef PubMed.
- D. W. McOwen, D. M. Seo, O. Borodin, J. Vatamanu, P. D. Boyle and W. A. Henderson, Energy Environ. Sci., 2014, 7, 416–426 RSC.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943 CrossRef CAS PubMed.
- K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121–13129 CrossRef CAS PubMed.
- K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331 CrossRef CAS PubMed.
- C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, H. Moon, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2014, 118, 5144–5153 CrossRef CAS PubMed.
- K. Dokko, D. Watanabe, Y. Ugata, M. L. Thomas, S. Tsuzuki, W. Shinoda, K. Hashimoto, K. Ueno, Y. Umebayashi and M. Watanabe, J. Phys. Chem. B, 2018, 122, 10736–10745 CrossRef CAS PubMed.
- A. Nakanishi, K. Ueno, D. Watanabe, Y. Ugata, Y. Matsumae, J. Liu, M. L. Thomas, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2019, 123, 14229–14238 CrossRef CAS.
- K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Electrochem. Soc., 2012, 159, A1005–A1012 CrossRef CAS.
- M. Yanagi, K. Ueno, A. Ando, S. Li, Y. Matsumae, J. Liu, K. Dokko and M. Watanabe, J. Electrochem. Soc., 2020, 167, 070531 CrossRef CAS.
- D. M. Pesko, K. Timachova, R. Bhattacharya, M. C. Smith, I. Villaluenga, J. Newman and N. P. Balsara, J. Electrochem. Soc., 2017, 164, E3569–E3575 CrossRef CAS.
- I. Villaluenga, D. M. Pesko, K. Timachova, Z. Feng, J. Newman, V. Srinivasan and N. P. Balsara, J. Electrochem. Soc., 2018, 165, A2766–A2773 CrossRef CAS.
- M. D. Galluzzo, J. A. Maslyn, D. B. Shah and N. P. Balsara, J. Chem. Phys., 2019, 151, 020901 CrossRef PubMed.
- L. A. Woolf and K. R. Harris, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 933–947 RSC.
- F. Wohde, M. Balabajew and B. Roling, J. Electrochem. Soc., 2016, 163, A714–A721 CrossRef CAS.
- D. Dong, F. Sälzer, B. Roling and D. Bedrov, Phys. Chem. Chem. Phys., 2018, 20, 29174–29183 RSC.
- N. M. Vargas-Barbosa and B. Roling, ChemElectroChem, 2020, 7, 367–385 CrossRef CAS.
- P. G. Bruce, J. Evans and C. A. Vincent, Solid State Ionics, 1988, 28, 918–922 CrossRef.
- M. Watanabe, S. Nagano, K. Sanui and N. Ogata, Solid State Ionics, 1988, 28-30, 911–917 CrossRef.
- H. Moon, R. Tatara, T. Mandai, K. Ueno, K. Yoshida, N. Tachikawa, T. Yasuda, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 20246–20256 CrossRef CAS.
- S. Zugmann, M. Fleischmann, M. Amereller, R. M. Gschwind, H. D. Wiemhöfer and H. J. Gores, Electrochim. Acta, 2011, 56, 3926–3933 CrossRef CAS.
- M. Gouverneur, J. Kopp, L. van Wüllen and M. Schönhoff, Phys. Chem. Chem. Phys., 2015, 17, 30680–30686 RSC.
- D. Dong and D. Bedrov, J. Phys. Chem. B, 2018, 122, 9994–10004 CrossRef CAS PubMed.
- O. Borodin, J. Self, K. A. Persson, C. Wang and K. Xu, Joule, 2020, 4, 69–100 CrossRef CAS.
- H. K. Kashyap, H. V. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221 CrossRef CAS PubMed.
- K. R. Harris and M. Kanakubo, J. Chem. Eng. Data, 2016, 61, 2399–2411 CrossRef CAS.
- J. Alvarado, M. A. Schroeder, M. Zhang, O. Borodin, E. Gobrogge, M. Olguin, M. S. Ding, M. Gobet, S. Greenbaum, Y. S. Meng and K. Xu, Mater. Today, 2018, 21, 341–353 CrossRef CAS.
- F. Schmidt and M. Schönhoff, J. Phys. Chem. B, 2020, 124, 1245–1252 CrossRef CAS PubMed.
- W. Shinoda, Y. Hatanaka, M. Hirakawa, S. Okazaki, S. Tsuzuki, K. Ueno and M. Watanabe, J. Chem. Phys., 2018, 148, 193809 CrossRef PubMed.
- K. Ueno, R. Tatara, S. Tsuzuki, S. Saito, H. Doi, K. Yoshida, T. Mandai, M. Matsugami, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 8248–8257 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Plots of the Li/Li+ electrode potential against the natural logarithm of the Li salt concentration in the mixture of LiTFSA in the solvents, numerical data of the six experimentally obtained parameters for the calculation of Onsager transport coefficients, and the normalised transport coefficients. See DOI: 10.1039/d0cp02181d |
| This journal is © the Owner Societies 2020 |