Open Access Article
Open Access ArticleA close view of the organic linker in a MOF: structural insights from a combined 1H NMR relaxometry and computational investigation†
Silvia
Pizzanelli
 *a,
Susanna
Monti
*a,
Susanna
Monti
 a,
Larisa G.
Gordeeva
bc,
Marina V.
Solovyeva
bc,
Angelo
Freni
a and
Claudia
Forte
a,
Larisa G.
Gordeeva
bc,
Marina V.
Solovyeva
bc,
Angelo
Freni
a and
Claudia
Forte
 a
a
aCNR-ICCOM, Institute of the Chemistry of Organometallic Compounds, via G. Moruzzi 1, 56124 Pisa, Italy. E-mail: silvia.pizzanelli@cnr.it
bBoreskov Institute of Catalysis, Ac. Lavrentiev av. 5, Novosibirsk 630090, Russia
cNovosibirsk State University, Pirogova str. 1, Novosibirsk 630090, Russia
First published on 17th June 2020
Abstract
The organic linker in a metal organic framework (MOF) affects its adsorption behavior and performance, and its structure and dynamics play a role in the modulation of the adsorption properties. In this work, the combination of 1H nuclear magnetic resonance (NMR) longitudinal relaxometry and theoretical calculations allowed details of the structure and dynamics of the organic linker in the NH2-MIL-125 MOF to be obtained. In particular, fast field cycling (FFC) NMR, applied here for the first time on MOFs, was used to disclose the dynamics of the amino group and its electronic environment through the analysis of the 14N quadrupole relaxation peaks, observed in the frequency interval 0.5–5 MHz, at different temperatures from 25 to 110 °C. The line width of the peaks allowed a lower boundary on the rotational correlation time of the N–H bonds to be set, whereas relevant changes in the amplitudes were interpreted in terms of a change in the orientation of the 14N averaged electric field gradient tensor. The experimental findings were complemented by quantum chemistry calculations and classical molecular dynamics simulations.
Introduction
Over the last two decades, metal organic frameworks (MOFs), also known as coordination polymers, have aroused increasing interest because of their high potential for applications in diverse fields, such as gas separation and storage,1,2 energy storage,3 catalysis,4 and thermal energy conversion.5–7 These hybrid crystalline solids are made of metal clusters linked by organic multidentate ligands that form extended three-dimensional porous frameworks with tunable pore size and shape through suitable chemical functionalities. Distinctive features of these versatile materials are extraordinarily large porosity and surface area, and unique adsorption properties.8The functionalization of the organic ligand may induce a modulation of the adsorption properties.9 Although the role of the functionalization has been disclosed in many applications, very little attention has been paid to the dynamics and the environment of the functional groups, which might contribute to rationalizing the adsorption behavior.
This study is focused on NH2-MIL-125, a microporous MOF composed of Ti8O8(OH)4-(BDC-NH2)6 (BDC = benzene-1,4-dicarboxylate) units, with a cyclic inorganic octamer structure built from TiO5(OH) octahedra and connected to other 12 octamers through NH2-BDC linkers.10 This MOF exhibited promising properties in the field of gas separation,11 liquid phase separation of hydrocarbons,12 adsorption heat transformation, and storage.13,14 A previous Nuclear Magnetic Resonance (NMR) investigation on the rotational motion of the amino group bound to the BDC ligand and of the aromatic ring in a Zn-based MOF, IRMOF-3, showed that the correlation time for both processes is on the order of microseconds in the 25–100 °C temperature range.15 Values of the same order of magnitude were found for the rotational motion of the aromatic ring in NH2 functionalized UiO-66(Zr).16
Here, we applied 1H FFC relaxometry to characterize the dynamics and the electronic environment of the amino group bound to the BDC unit, exploiting the quadrupolar relaxation enhancement (QRE) of the 1H longitudinal relaxation rate. Indeed, when the dynamics is relatively slow, the 1H spin lattice relaxation rate increases at 1H frequencies matching the 14N quadrupole spin transition. This effect was observed in some solids,17–19 and in biological systems,20–22 but, to the best of our knowledge, it was never reported for a MOF. The positions of the quadrupolar peaks were used to derive the quadrupolar coupling constant and the asymmetry parameter of the electric field gradient (EFG) acting on the 14N nucleus, whereas the relative intensities and widths of the peaks were related to the orientation of the N–H vectors with respect to the averaged EFG principal axes and to their rotational correlation and 14N relaxation times through simple analytical expressions.23 Differently from 2H NMR spectroscopy, which is a well established technique for probing molecular mobility, applied by Kolokolov et al. to linkers and guest molecules adsorbed in MOFs,24–28 the method used here does not require deuteration of the sample, but it is restricted to systems containing a quadrupolar nucleus, such as 14N. The flip of the BDC units was excluded to occur within a time scale of tens of microseconds at room temperature by estimating the 1H–13C dipolar interaction through a two-dimensional Lee-Goldburg cross-polarization technique (2D LG-CP);29,30 this finding is in agreement with previous studies on a variety of MOFs.27,28,31,32 The temperature dependence of the observables in the 25–110 °C range was discussed in connection with the predictive results of atomistic molecular dynamics simulations (MD), which were combined with quantum chemistry (QC) calculations to obtain a picture of the amino group geometry and dynamics, and of the EFG tensor at the nitrogen centers.
Materials and methods
NMR measurements
NH2-MIL-125 was synthesized according to the procedure reported in ref. 14. The as-synthesized product was dried at 150 °C in vacuo for 20 hours.1H longitudinal relaxation times, T1, were measured in the 0.01–35 MHz Larmor frequency range on a SpinMaster FFC-2000 Fast Field-Cycling NMR relaxometer (Stelar srl, Mede, Italy) using the pre-polarized and non-polarized pulse sequences below and above 12 MHz, respectively.33 The polarizing and detection fields were 0.6 T and 0.5 T, which correspond to 1H Larmor frequencies of 25.0 and 21.5 MHz, respectively. The switching time was 3 ms and the 90° pulse duration was 9.8 μs. A single scan was acquired. All the other experimental parameters were optimized for each measurement. All the 1H magnetization curves vs. time were mono-exponential within experimental error and the errors in the relaxation rate R1 (=1/T1) fitting were always less than 1%. The experiments were performed at three temperatures, i.e. at 25, 80 and 110 °C; the temperature was controlled within ±0.1 °C with a Stelar VTC90 variable temperature controller.
1H–13C dipolar interactions were estimated at room temperature using a Bruker Avance Neo-300 WB spectrometer equipped with a 4 mm probe. The operating frequencies were 300.13 and 75.47 MHz for 1H and 13C, respectively. The 90° pulses on 1H and 13C were 3.0 and 4.0 μs, respectively. The 2D LG-CP experiment was conducted using the sequence reported in Fig. 2a of ref. 29. For the LG-CP period, the 1H effective field strength was 50 kHz and the 13C spin-lock field strength was adjusted to the first order sideband conditions. The LG-CP contact time was incremented in 41.7 μs steps with 100 steps. The spinning speed was 12 kHz, the recycle delay was set to 1.2 s and the number of scans was 2000. Only cosine-modulated data were collected. The t1 time signals were processed using a baseline correction mode “qfil” in Bruker TopSpin 3.5 software, which subtracts a constant intensity before performing a real Fourier transformation, to eliminate the zero-frequency peak.
Analysis of the R1 profile: theoretical basis
14N is a quadrupolar nucleus with spin quantum number equal to 1. In the low field regime, i.e. when the magnetic field B0 is smaller than 0.1 T, the Zeeman coupling of the 14N spin is much weaker than its electrostatic interaction with the local EFG and can be neglected. Therefore, the 14N energy levels are determined by the interaction between the nuclear quadrupole moment and the EFG. The frequencies associated to the possible transitions between these levels are
 and
and 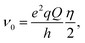 with
with  and η representing the 14N quadrupolar coupling constant and the asymmetry parameter, respectively. In the 1H R1 profile a local maximum may occur when the 1H Zeeman transition energy matches one of the transition frequencies ν+, ν−, or ν0. In the case of a 14N nucleus belonging to a slowly tumbling entity (i.e.,
and η representing the 14N quadrupolar coupling constant and the asymmetry parameter, respectively. In the 1H R1 profile a local maximum may occur when the 1H Zeeman transition energy matches one of the transition frequencies ν+, ν−, or ν0. In the case of a 14N nucleus belonging to a slowly tumbling entity (i.e.,  with τrot representing the N–H rotational correlation time), the following simple analytical expression of the 1H longitudinal QRE, RHN1, was reported:23
with τrot representing the N–H rotational correlation time), the following simple analytical expression of the 1H longitudinal QRE, RHN1, was reported:23 | (1) |
 where r represents the internuclear N–H distance, γ1H and γ14N are the gyromagnetic ratios of 1H and 14N nuclei, respectively, and μ0 is the permittivity. In eqn (1)τeff is an effective correlation time dependent on τrot and on the 14N relaxation time T1N due to spin–flip fluctuations, according to the equation:
where r represents the internuclear N–H distance, γ1H and γ14N are the gyromagnetic ratios of 1H and 14N nuclei, respectively, and μ0 is the permittivity. In eqn (1)τeff is an effective correlation time dependent on τrot and on the 14N relaxation time T1N due to spin–flip fluctuations, according to the equation: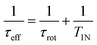 | (2) |
 | (3) |
 | (4a) |
 | (4b) |
 | (4c) |
 | (5a) |
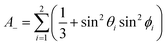 | (5b) |
 | (5c) |
Analysis of the R1 profile: data treatment
The measured 1H longitudinal relaxation rate consists of a homonuclear dipolar contribution, RHH1, due to 1H–1H dipole–dipole interactions, and a QRE contribution, RHN1, due to 1H–14N dipole–dipole interactions. The overall relaxation R1(ν) is the sum of the two contributions:| R1(ν) = RHH1(ν) + RHN1(ν) | (6) |
In order to obtain RHN1, RHH1 was subtracted from the measured R1 at each frequency using the baseline correction tool in the Origin software.34 We did not attempt to analyze the RHH1 contribution, as carried out by other authors,21 because the data did not show distinctive features capable of unambiguously defining the dynamic processes modulating the 1H–1H dipolar interactions. For a given temperature, the experimental RHN1 data were fitted using eqn (1) within the Mathematica 10 programming environment.35 The fitting parameters relative to each peak i, with i = +, −, 0, were νi, and cAi, besides the common τeff.
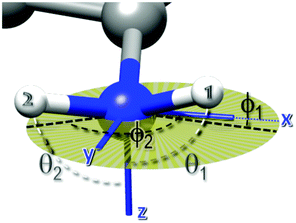
The values of the four angles defining the orientation of the two N–H bonds, namely θ1, ϕ1, θ2, ϕ2, were derived from the relative amplitudes of the ν0 and ν− peaks with respect to that of the ν+ peak, using eqn (5). We imposed the constraint that the angle between the two N–H bonds was between 105 and 125 degrees, the most populated region according to MD simulations (Fig. S1 of ESI†), and looked for numerical solutions by varying the polar and the azimuthal angles on a grid in the range 0–π and 0–2π, respectively. We rejected those angular sets that produced deviations of the calculated rescaled amplitudes from the experimental values larger than 5%. It should be noticed that, given the symmetry of the trigonometric functions appearing in eqn (5), we were not able to distinguish among the possible solutions θi, −θi, π − θi and −π + θi, the same holding for ϕi.
Quantum chemistry calculations and classical simulations
The atomic coordinates and unit cell parameters (18.7028 × 18.7028 × 18.2028 Å3) of NH2-MIL-125 were obtained from the Cambridge Crystallographic Data Centre36 and optimized at the density functional (DFT) level, after adding the hydrogen atoms, using the Quantum Espresso package,37 ultrasoft pseudopotentials and the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.38 Periodic boundary conditions were applied in all directions and a cutoff energy of 600 eV was employed to obtain convergent results. The Gauge Including Projector Augmented Wave (GIPAW) approach39,40 was used to calculate and fully characterize the traceless EFG tensor for each nitrogen nucleus (that is, the quadrupolar coupling constant, the asymmetry parameter and the orientation of the PAS with respect to the molecular frame).To explore the dynamics of the MOF at 25 and 110 °C and generate a reasonable variety of geometries for predicting and explaining the experimental data, classical reactive molecular dynamics simulations based on the ReaxFF methodology were carried out. This approach was selected because an appropriate parametrization for this type of system is available in the literature.41 The DFT optimized geometry was energy minimized at the classical level and then gradually heated to 25 °C (or 110 °C). Equilibration was carried out for about 50 ps. After equilibration, the sampling simulations were performed in the NVT ensemble for about one nanosecond. System configurations were collected every 0.1 ps. The temperature was controlled through the Berendsen's thermostat42 with a relaxation constant of 0.05 ps, and the time step was set to 0.2 fs. The analysis of the production trajectories was focused on the orientation of the NH2 group relative to the ring system, the degree of pyramidalization of the nitrogen atom, the H–N–H angles, the C–C–N–H dihedral angles, and the length of the hydrogen bond between the amino and carboxyl group. Representative configurations were extracted from the two trajectories and EFG-GIPAW calculations were carried out to predict the orientations of the EFG tensors in the molecular frame (Fig. S2 of ESI†).
Results and discussion
The R1 dispersion curves of dry NH2-MIL-125, recorded at 25, 80 and 110 °C, are shown in Fig. 2a. The profiles at 25 and 80 °C are very similar, and only minor changes could be observed upon further heating to 110 °C. This indicated that, in the investigated temperature domain, no major dynamic process was activated in the 10 kHz–35 MHz frequency range. Moreover, the profiles display three quadrupolar peaks (Fig. 2b), due to the level crossing with the 14N quadrupole frequencies, which indicated that all the 14N nuclei are characterized by very similar EFGs, in line with the theoretical predictions, and provided important information on the very slow dynamics of the NH2 group.The quadrupolar contribution to R1, after subtraction of the background curve mainly due to RHH1, is shown in Fig. 3. The small frequency shifts of the maxima suggested that the quadrupole parameters  and η slightly changed with the temperature. Fig. 3 clearly shows that the peaks sharpened upon increasing the temperature from 25 °C to 80 °C, whereas a further temperature increase to 110 °C did not result in a significant variation. Furthermore, increasing the temperature determined a change in the relative amplitudes of the three signals, which was most evident for the 25 °C to 80 °C variation.
and η slightly changed with the temperature. Fig. 3 clearly shows that the peaks sharpened upon increasing the temperature from 25 °C to 80 °C, whereas a further temperature increase to 110 °C did not result in a significant variation. Furthermore, increasing the temperature determined a change in the relative amplitudes of the three signals, which was most evident for the 25 °C to 80 °C variation.
 | ||
| Fig. 3 1H RHN1 NMRD curves of NH2-MIL-125 at the indicated temperatures, obtained from the R1 data after subtraction of the background contribution mainly due to RHH1. The solid lines represent the fits to the quadrupolar peaks using eqn (1). The values of the fitting parameters are reported in Table 1. | ||
For a quantitative analysis, the shape of the peaks, after subtraction of the background, was reproduced using the fitting function reported in eqn (1), with fitting parameters τeff, and νi and cAi relative to each peak i, with i = +, −, 0.
Fig. 3 shows the fitting curve at the investigated temperatures and Table 1 reports the best fit values. It is worth noting that the quadrupolar parameters are close to those determined for anthranilic acid with 14N quadrupole resonance spectroscopy.43
| T (°C) | (MHz) | η | τ eff (μs) | cA +; cA−; cA0a (s−2) | ν +; ν−; ν0a (MHz) |
|---|---|---|---|---|---|
| a Values obtained by fitting RHN1 data, as described in the section Materials and methods. Uncertainty on the last digit is given in parenthesis. | |||||
| 25 | 3.52 (1) | 0.41 (1) | 0.90 (2) | 25 (1); | 3.00 (1); |
| 21 (1); | 2.28 (1); | ||||
| 8 (1) | 0.67 (4) | ||||
| 80 | 3.55 (1) | 0.38 (1) | 2.2 (1) | 14 (1); | 3.00 (1); |
| 6 (1); | 2.33 (1); | ||||
| 7 (1) | 0.65 (2) | ||||
| 110 | 3.54 (1) | 0.39 (1) | 2.2 (1) | 13 (1); | 3.00 (1); |
| 8 (1); | 2.31 (1); | ||||
| 10 (1) | 0.64 (1) | ||||
A first theoretical estimate of the nuclear quadrupole constants and anisotropy parameters was obtained through the full optimization of the experimental crystal structure of the MOF at the QC level and subsequent calculations of the EFG tensor at the nitrogen nuclei. Inspection of the QC optimized geometry indicated that in NH2-MIL-125 all the 14N nuclei occupy positions characterized by similar electric field gradients with sp2 hybridized nitrogen atoms hydrogen-bonded to the carboxyl oxygens. The best agreement of the theoretical nuclear quadrupole coupling constant with the experimental result was obtained with a 14N nuclear quadrupole moment of 1.94 × 10−30 m2, chosen in line with the studies of Bailey,44 that produced a quadrupolar coupling constant of −3.79 ± 0.04 MHz and an asymmetry parameter around 0.31 (±0.03) for all the nitrogen nuclei. This ideal situation satisfactorily compares with the experimental results.
Information on the dynamics of the amino group could be obtained from the τeff values determined from the fitting of the experimental data (Table 1). Of relevance is the fact that τeff increased from 0.9 to 2.2 μs upon heating from 25 to 80 °C, as determined from the linewidth of the peaks using eqn (3); a further increase in temperature up to 110 °C did not give rise to any additional change. Since τrot should decrease with increasing the temperature, the observed increase in τeff suggests that τeff is mainly determined by T1N (see eqn (2)). A similar behavior was previously reported for the solid [C(NH2)3]3Bi2I9 and was indeed explained taking into account the longitudinal relaxation time of 14N, T1N, associated with a fast fluctuation of an EFG component, i.e., on the time scale of 1 ns.18 In immobilized proteins, T1N values on the order of microseconds were ascribed to fast fluctuations of the EFG about its average value, probably due to a rocking motion on a 10 ns time scale.23 In our case, we could suppose that T1N significantly contributed to τeff at all the investigated temperatures, with T1N < τrot. Indeed, the detection of the quadrupolar peaks is evidence for a slow N–H bond dynamics, with the condition that the slow dynamics is characterized by a correlation time τrot ≥ 1/2πν0 ≈ 0.2 μs.23 On the other hand, T1N values can be very short, especially at low fields, and in the extreme narrowing limit.23,45 The extreme narrowing regime predicts an increase in T1N upon heating, which results in the sharpening of the peaks with increasing the temperature. The observed temperature trend of τeff and the values determined indicated that τrot must be longer than 2.2 μs at 110 °C, a condition which also holds at 25 °C a fortiori. Therefore, the lower boundary obtained for τrot is longer than 0.2 μs, the low limit which was determined based on the conditions τrot ≥ 1/2πν0. Long τrot values were consistent with the absence of BDC flips at room temperature within a time scale of tens of microseconds, as revealed by the estimate of the 1H–13C dipolar interactions by means of the 2D LG-CP experiment (Fig. S3 of ESI†). In fact, aromatic carbon atoms carrying a hydrogen atom were found to be subject to a 1H–13C dipolar interaction close to the static value (see caption of Fig. S3 of the ESI†).
Other features of relevance for characterizing the changes that occur in the system upon heating were the absolute and relative peak amplitudes (see Table 1). The significant decrease in the amplitudes of the quadrupolar peaks, observed upon heating from 25 to 80 °C, indicated that the effective H–N dipole–dipole interaction leading to the QRE effect became weaker on increasing the temperature; this can be attributed to the pre-averaging of this interaction by a relatively fast dynamic process. Also, the relative values of the amplitudes changed upon heating from 25 to 80 °C, with the peaks centered at ν0 and ν− assuming larger and smaller amplitude values, respectively. Only minor changes were observed upon further heating up to 110 °C, with a slight increase in amplitude of the ν− and ν0 peaks and a decrease for the ν+ one. We ascribed the variation of the relative amplitudes to a change in the orientation of the EFG tensor, according to eqn (5). These equations were used to fit the three amplitudes A+, A−, A0 with the constraint that the angle between the two N–H bonds could assume values between 105 and 125 degrees, which is the most populated region according to the MD simulations discussed afterwards, and with variable parameters the angles θ1, ϕ1, θ2, ϕ2 defining the direction of the two N–H bonds in the averaged EFG PAS (Fig. 1).
At 25 °C, it was found that the set of angles {θ1 = 90 ± 6, ϕ1 = 115 ± 3, θ2 = 90 ± 6, ϕ2 = 0 ± 10 degrees} was compatible with the observed relative amplitudes. This set implies that the EFG z-axis is approximately perpendicular to the H–N–H plane. This is in line with other studies,46,47 which found that the principal axis associated with the largest EFG component, Vzz, is oriented along the direction of the nitrogen lone pair. The two hydrogen atoms do not occupy symmetric positions with respect to the EFG x and y axes, and this could be ascribed to the formation of a hydrogen bond between the carboxylate oxygen and one of the hydrogen atoms.
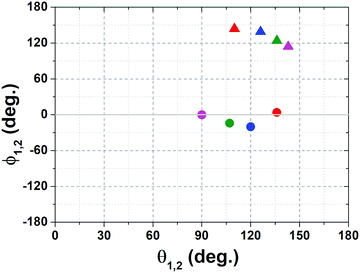
At higher temperatures, since no major differences were observed between the amplitudes at 80 and 110 °C, we focused only on those at 110 °C. Several sets of angles were compatible with the experimental amplitudes, with θ values spread in the range 80–150 degrees and ϕ values clustered around −10 and 130 degrees (Fig. 4). For the sake of clarity, the figure shows only four compatible sets, out of the possible values found. Among these sets, the corresponding value of the H–N–H angle was in the interval 105–125 degrees.
In order to better understand the experimental data and, possibly, confirm the analysis, an MD study was performed on the system at 25 and 110 °C. Examination of the conformational tendency of the BDC-NH2 units at the two extreme temperatures revealed that the nitrogen atom could be both trigonal planar (sp2 hybridization) or tetrahedral (sp3 hybridization) due to a rapid umbrella inversion that became more marked at a higher temperature. Given the inequivalence of the nitrogen substituents, the motion was slightly asymmetric and influenced by the relatively tight intramolecular hydrogen bond between one of the amine hydrogens and the nearby carboxyl oxygen. The MD results indicated that this hydrogen bond is strong enough to induce a moderate pyramidalization with a preferential direction, which is apparent in Fig. S1 of the ESI,† where the distributions of the distance of the nitrogen from the C–H(N)–H(N) plane are displayed. This distance represents the displacement of the nitrogen above and below the substituents plane and can be correlated with the degree of pyramidalization of the atom. From inspection of these data it is apparent that the peaks of both curves are shifted to negative values and centered at approximately −0.03 Å. Further evidence of the nature of the nitrogen was provided by the H–N–H angle distribution (Fig. S1 of ESI†) which indicated that the most probable values were in the 110°–120° range, corresponding to characteristic tetrahedral and planar arrangements of the hydrogen atoms. This angular range was indeed the one considered, although slightly extended, in the analysis of the experimental data.
The asymmetry of the motion at both temperatures is clearly visible in Fig. 5 which shows the probabilities of the dihedral angles defining the positions of the amine hydrogens relative to the ring plane at the two temperatures investigated. At 110 °C the higher propensity of the amino group to explore the outer regions of the range mentioned above was confirmed by the widening of the contours. Furthermore, the vibrations of the various portions of the MOF were faster and accompanied by modest deformations of the BDC-NH2 rings and occasional rotations of both the NH2 group (around the C–N bond) and the COO moiety (around the C–C bond). In particular, in the MD data displayed in Fig. S4 (ESI†), the NH2 rotation occurred only once over a trajectory of 1 ns.
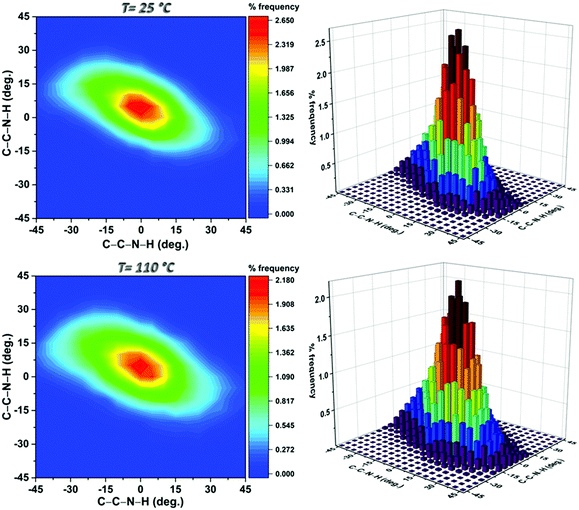 | ||
| Fig. 5 Contour plots of the distributions of the C–C–N–H torsional angles and their respective three-dimensional histograms obtained from the configurations sampled at the selected temperatures. | ||
Representative configurations at the two temperatures were extracted for the calculation of the EFG tensor through the GIPAW approach; the one at 25 °C is shown in Fig. 6a where the BDC-NH2 unit and the local EFG PAS are highlighted. It is apparent that the calculated 14N EFG tensor orientations are identical for all the planar BDC-NH2 units, with Vzz perpendicular to the C–H(N)–H(N) plane (in this case, the plane of the molecule), oriented as the N lone pair, Vyy in the plane of the molecule almost aligned to the H–N–H angle bisector and Vxx in the plane of the molecule perpendicular to the Vyy axis. This static picture became more complex when the effect of the temperature was applied and the local configurations of the BDC-NH2 units were sampled as a function of time. In fact, a great variety of nitrogen pyramidalizations were identified and the EFG descriptors estimated in each case. The simplest cases were those where the hybridization of the nitrogen was not accompanied by a rotation of the NH2 group around the C–N axis. In these cases, the hydrogens remained close to the molecular plane and the EFG PAS maintained an orientation typical of the flat sp2 arrangement. Fig. 6b shows the EFG tensor orientation for pyramidalized nitrogen with hydrogens almost perpendicular to the O–C–O plane. Vzz is again in the direction of the lone pair, Vyy is aligned with the bisector of the H–N–H angle and Vxx is roughly perpendicular to the molecular plane. Therefore, the trait common to all the situations is the alignment of Vzz with the lone pair direction. Moreover, local effects did not drastically perturb the environment of the nitrogen. Even though the values of  and η were different in each unit, their average was close to the values found for the QC optimized structure and from the experiments.
and η were different in each unit, their average was close to the values found for the QC optimized structure and from the experiments.
 | ||
| Fig. 6 Principal components of the 14N EFG tensor (blue lines) in two different local structures of the BDC-NH2 unit of NH2-MIL-125. (a) Planar unit extracted from the MOF structure optimized at the QC level. (b) Deformed unit, extracted from the MD trajectory at 110 °C, where the nitrogen is pyramidalized and rotated (before the exchange of the NH2 hydrogens). The plane of the three N substituents is depicted with a cyan disk (on the right-hand side, the transparent effect mitigates the color of the disk) to highlight the perpendicular orientation of Vzz (lone pair direction). The representation of EFG tensors as surfaces obtained by means of TensorView is shown in Fig. S5 of the ESI.† | ||
At 25 °C, where the main tendency of the NH2 group was to adopt an almost flat arrangement with only a slight pyramidalization, the GIPAW calculations on the DFT-optimized structure and on geometries extracted from the MD simulations gave the angular values {θ1 = 85 ± 12, ϕ1 = 132 ± 7, θ2 = 85 ± 12, ϕ2 = 19 ± 14 degrees} for the two amine hydrogen atoms in the EFG PAS, in fairly good agreement with the values determined from the fitting of the experimental peak amplitudes. MD simulations did not predict significant changes in the static EFG tensor when the temperature was increased from 25 to 110 °C. Therefore, the change in the relative amplitudes of the QRE peaks could not be ascribed to a modification of the orientation of the static EFG tensor. However, the observed amplitudes were compatible with sets of angles {θ1, ϕ1, θ2, ϕ2} (see Fig. 4) implying a significant deviation of the Vzz component from the lone pair direction. Such deviation was quantified through the angle between the normal to the plane defined by H–N–H and the EFG z-axis for our compatible sets, which was 65 ± 10°, to be compared with the values of 0 and 35° for an sp2 and an sp3 hybridization, respectively. We thus speculated that the tensor is subject to a fast motion that modifies its orientation, and consequently the angles {θ1, ϕ1, θ2, ϕ2} at 110 °C. Considering the relative amplitudes of the peaks and the observed  and η values, we excluded that the motion could be simply modelled as a two-site rotation of the NH2 group around the C2 axis with jump angles ranging from 0 to 180° or as a rocking motion about an axis perpendicular to the NH2 plane. A more complex motional process might occur, possibly involving a different dynamic behavior of the two H–N bonds, as hinted by the MD data. At 25 °C this motion is probably more restricted so that the static tensor satisfactorily accounts for the amplitude values. This motion would be responsible for the decrease of T1N and for the slight change in the quadrupolar parameters upon heating.
and η values, we excluded that the motion could be simply modelled as a two-site rotation of the NH2 group around the C2 axis with jump angles ranging from 0 to 180° or as a rocking motion about an axis perpendicular to the NH2 plane. A more complex motional process might occur, possibly involving a different dynamic behavior of the two H–N bonds, as hinted by the MD data. At 25 °C this motion is probably more restricted so that the static tensor satisfactorily accounts for the amplitude values. This motion would be responsible for the decrease of T1N and for the slight change in the quadrupolar parameters upon heating.
Conclusions
For the first time we have applied 1H FFC NMR relaxometry to study a metal organic framework, disclosing important details of the amino group dynamics in the specific environment constituted by NH2-MIL-125, and of its EFG tensor at different temperatures. From the linewidth of the QRE peaks we could set a lower boundary on the rotational correlation time of the N–H bonds, which was 2.2 μs at 110 °C, whereas from the relative amplitudes we could estimate the orientation of the N–H bonds with respect to the averaged EFG principal axes system. It was found that at 25 °C the averaged EFG tensor orientation coincides with the static picture, identified by QC calculations, where the z EFG component, aligned with the lone pair, is perpendicular to the BDC-NH2 unit and the dynamics is quite restricted. This was not the case at 110 °C, where larger fast fluctuations modulate the static interaction and are responsible for a change in the orientation of the averaged EFG.Besides the structural and dynamic details obtained, this study demonstrates the applicability and usefulness of FFC NMR, hitherto applied to aqueous solutions, soft matter or fluids in porous materials, also in the study of MOFs, unveiling information of relevance for their technological application. Furthermore, the combination with theoretical calculations, on the one hand, guides the data analysis, and, on the other, validates and at the same time complements the information obtained.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to acknowledge the contribution of the COST Action CA15209 (Eurelax: European Network on NMR Relaxometry). This work was partially supported by the Tuscany Region (POR FESR 2014-2020 FELIX project) and by Beneficentia Stiftung. The Russian authors thank the Russian Foundation of Basic Research (grant no. 18-29-04033) for partial financial support of this work.Notes and references
- R.-B. Lin, S. Xiang, H. Xing, W. Zhou and B. Chen, Coord. Chem. Rev., 2019, 378, 87–103 CrossRef CAS
.
- H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Mater. Today, 2018, 21, 108–121 CrossRef CAS
.
- V. Shrivastav, S. Sundriyal, P. Goel, H. Kaur, S. K. Tuteja, K. Vikrant, K.-H. Kim, U. K. Tiwari and A. Deep, Coord. Chem. Rev., 2019, 393, 48–78 CrossRef CAS
.
- C. Xu, R. Fang, R. Luque, L. Chen and Y. Li, Coord. Chem. Rev., 2019, 388, 268–292 CrossRef CAS
.
- M. F. de Lange, K. J. F. M. Verouden, T. J. H. Vlugt, J. Gascon and F. Kapteijn, Chem. Rev., 2015, 115, 12205–12250 CrossRef CAS PubMed
.
- S. K. Henninger, F. Jeremias, H. Kummer and C. Janiak, Eur. J. Inorg. Chem., 2012, 2625–2634 CrossRef CAS
.
- S. Cui, M. Qin, A. Marandi, V. Steggles, S. Wang, X. Feng, F. Nouar and C. Serre, Sci. Rep., 2018, 8, 15284 CrossRef PubMed
.
- H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed
.
- C. Zlotea, D. Phanon, M. Mazaj, D. Heurtaux, V. Guillerm, C. Serre, P. Horcajada, T. Devic, E. Magnier and F. Cuevas,
et al.
, Dalton Trans., 2011, 40, 4879–4881 RSC
.
- M. Dan-Hardi, C. Serre, T. Frot, L. Rozes, G. Maurin, C. Sanchez and G. Férey, J. Am. Chem. Soc., 2009, 131, 10857–10859 CrossRef CAS PubMed
.
- S. Vaesen, V. Guillerm, Q. Yang, A. D. Wiersum, B. Marszalek, B. Gil, A. Vimont, M. Daturi, T. Devic, P. L. Llewellyn, C. Serre, G. Maurin and G. De Weireld, Chem. Commun., 2013, 49, 10082–10084 RSC
.
- F. Vermoortele, M. Maes, P. Z. Moghadam, M. J. Lennox, F. Ragon, M. Boulhout, S. Biswas, K. G. M. Laurier, I. Beurroies, R. Denoyel, M. Roeffaers, N. Stock, T. Düren, C. Serre and D. E. De Vos, J. Am. Chem. Soc., 2011, 133, 18526–18529 CrossRef CAS PubMed
.
- F. Jeremias, V. Lozan, S. K. Henninger and C. Janiak, Dalton Trans., 2013, 42, 15967–15973 RSC
.
- L. G. Gordeeva, M. V. Solovyeva and Y. I. Aristov, Energy, 2016, 100, 18–24 CrossRef CAS
.
- W. Morris, R. E. Taylor, C. Dybowski, O. M. Yaghi and M. A. Garcia-Garibay, J. Mol. Struct., 2011, 1004, 94–101 CrossRef CAS
.
- S. Devautour-Vinot, G. Maurin, C. Serre, P. Horcajada, D. P. da Cunha, V. Guillerm, E. de Souza Costa, F. Taulelle and C. Martineau, Chem. Mater., 2012, 24, 2168–2177 CrossRef CAS
.
- W. Masierak, M. Florek-Wojciechowska, I. Oglodek, R. Jakubas, A. F. Privalov, B. Kresse, F. Fujara and D. Kruk, J. Chem. Phys., 2015, 142, 204503 CrossRef CAS PubMed
.
- M. Florek-Wojciechowska, M. Wojciechowski, R. Jakubas, Sz. Brym and D. Kruk, J. Chem. Phys., 2016, 144, 054501 CrossRef CAS PubMed
.
- M. Florek-Wojciechowska, R. Jakubas and D. Kruk, Phys. Chem. Chem. Phys., 2017, 19, 11197–11205 RSC
.
- F. Winter and R. Kimmich, Biochim. Biophys. Acta, 1982, 719, 292–298 CrossRef CAS
.
- E. P. Sunde and B. Halle, J. Magn. Reson., 2010, 203, 257–273 CrossRef CAS PubMed
.
- D. Kruk, E. Masiewicz, A. M. Borkowska, P. Rochowski, P. H. Fries, L. M. Broche and D. J. Lurie, Biomolecules, 2019, 9, 652 CrossRef CAS PubMed
.
- P. H. Fries and E. Belorizky, J. Chem. Phys., 2015, 143, 044202 CrossRef PubMed
.
- A. E. Khudozhitkov, S. S. Arzumanov, D. I. Kolokolov, D. Freude and A. G. Stepanov, Phys. Chem. Chem. Phys., 2020, 22, 5976–5984 RSC
.
- D. I. Kolokolov, A. G. Stepanov and H. Jobic, J. Phys. Chem. C, 2015, 119, 27512–27520 CrossRef CAS
.
- A. Knebel, B. Geppert, K. Volgmann, D. I. Kolokolov, A. G. Stepanov, J. Twiefel, P. Heitjans, D. Volkmer and J. Caro, Science, 2017, 358, 347–351 CrossRef CAS PubMed
.
- D. I. Kolokolov, H. Jobic, A. G. Stepanov, V. Guillerm, T. Devic, C. Serre and G. Férey, Angew. Chem., Int. Ed., 2010, 49, 4791–4794 CrossRef CAS PubMed
.
- D. I. Kolokolov, A. G. Stepanov and H. Jobic, J. Phys. Chem. C, 2014, 118, 15978–15984 CrossRef CAS
.
- B.-J. van Rossum, C. P. de Groot, V. Ladizhansky, S. Vega and H. J. M. de Groot, J. Am. Chem. Soc., 2000, 122, 3465–3472 CrossRef CAS
.
- M. Hong, X. Yao, K. Jakes and D. Huster, J. Phys. Chem. B, 2002, 106, 7355–7364 CrossRef CAS
.
- S. L. Gould, D. Tranchemontagne, O. M. Yaghi and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2008, 130, 3246–3247 CrossRef CAS PubMed
.
- J. Gonzalez, R. N. Devi, D. P. Tunstall, P. A. Cox and P. A. Wright, Microporous Mesoporous Mater., 2005, 84, 97–104 CrossRef CAS
.
- D. Kruk, A. Herrmann and E. A. Rössler, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 63, 33–64 CrossRef CAS PubMed
.
-
Origin(Pro), Version 8.6.0. OriginLab Corporation, Northampton, MA, USA Search PubMed
.
-
Wolfram Research, Inc. MATHEMATICA, (Version 10.0), Wolfram Research Inc., Champaign, IL, 2014 Search PubMed
.
- A. P. Smalley, D. G. Reid, J. C. Tan and G. O. Lloyd, CrystEngComm, 2013, 15, 9368–9371 RSC
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo,
et al.
, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef
.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef
.
- S. Monti, A. C. T. van Duin, S.-Y. Kim and V. Barone, J. Phys. Chem. C, 2012, 116, 5141–5150 CrossRef CAS
.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS
.
- D. A. d’Avignon and T. L. Brown, J. Phys. Chem., 1981, 85, 4073–4079 CrossRef
.
- W. C. Bailey, Chem. Phys., 2000, 252, 57–66 CrossRef CAS
.
-
A. Carrington and A. D. McLachlan, Introduction to Magnetic Resonance: With Applications to Chemistry and Chemical Physics, Chapman & Hall, London, UK, 1979 Search PubMed
.
- J. Autschbach, S. Zheng and R. W. Schurko, Concepts Magn. Reson., 2010, 36a, 84–126 CrossRef CAS
.
- B. Kleibömer and D. H. Sutter, Z. Naturforsch., 1988, 43a, 561–571 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Distributions of H–N–H angles and N distances to the plane of the ligands obtained from sampled configurations extracted from the MD simulations. Representative configuration of NH2-MIL-125 extracted from the MD simulations at 25 °C used to predict the EFG PAS orientation on the different nitrogen sites. 13C–1H Lee-Goldburg – cross polarization spectrum of NH2-MIL-125. Evolution of the hydrogen bond distance during the first 300 ps of the MD simulation at 110 °C. Principal components of the 14N EFG tensor in two different local structures of the BDC-NH2 unit of NH2-MIL-125 (PDF). See DOI: 10.1039/d0cp01863e |
| This journal is © the Owner Societies 2020 |