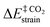Evaluation and understanding the performances of various derivatives of carbonyl-stabilized phosphonium ylides in CO₂ transformation to cyclic carbonates

Abstract

The kinetic and mechanism evaluations of the formation of cyclic carbonates by carbonyl-stabilized phosphonium ylides as an efficient and new class of organocatalysts are the main purposes of this research. Recently, it has been reported that tetraarylphosphonium salts play the role of organocatalysts in carbon dioxide conversion to cyclic carbonates. However, in this research, the oxygen atom of the carbonyl-stabilized phosphonium ylides was treated as the nucleophilic atom for the carbon dioxide activation. Two probable mechanisms were considered and analyzed by the energetic span model. The kinetic behavior of the carbonyl-stabilized phosphonium ylides in the carbon dioxide or ethylene oxide activation was justified by the molecular electrostatic potential (ESP) analysis at the nuclear position. However, it was confirmed that the activation strain model (ASM) was a more efficient tool in explaining the kinetic behaviors in the carbon dioxide or ethylene oxide activation. A change in the ESP value of the donor–acceptor interacting system (ΔΔV_n) and distortion energy at the transition states (ΔE_strain(ζ)) were the outcomes of the ESP and ASM models, respectively, which showed a linear correlation. The electron localization function (ELF) concept was used to justify the kinetic behavior of the second step of the preferred mechanism, revealing that the electron-donating/withdrawing groups substituted on the organocatalysts have a remarkable effect on the electron density of the involved basin at the transition states. On the basis of different analyses, it was proposed that carbonyl-stabilized phosphonium ylides having electron-donating substituents are the best candidates for carbon dioxide conversion to cyclic carbonates.

---

1. Introduction

Global warming is related to an increment in the carbon dioxide concentration in the atmosphere, which is due to the thermal use of fossil fuels. Because of the increasing greenhouse gas levels due to human activities, reducing the CO₂ emission has become a remarkable and challenging research issue as it is the most critical reason in the global warming phenomenon. Hence, these concerns need various approaches to reduce atmospheric CO₂ levels. The capture and transformation of CO₂ as a highly plentiful, cost-efficient, nontoxic, nonflammable and readily available C1 source to value-added chemicals, such as methane,¹ methanol,² carbon monoxide,³ and sugar,⁴ have received considerable interest as an alternative feedstock for the chemical industry by researchers in recent decades.^5–7

The conversion of CO₂ to a cyclic carbonate is a common reaction, which is well-known as an important pathway for the cyclic carbonate and polycarbonate production on an industrial scale.^8,9 Because of the broad applications of the cyclic carbonates as solvents, electrolytes, monomers for polymer syntheses, synthetic building blocks, fine chemicals, and industrial lubricants,^10,11 cyclic carbonate production is one area of particular interest in the scientific community. The first synthesis method of the cyclic carbonates was reported by Nemirowsky,¹² in which the reaction occurs between extremely toxic phosgene and ethylene glycol, producing ethylene carbonate. Afterward, many pathways have been reported for the synthesis of cyclic carbonates by various starting materials, such as dimethyl carbonate,^13,14 urea,^15,16 CO,¹⁷ CO₂,^18,19 halohydrins,²⁰ and propargyl alcohols.^21,22 However, the synthesis of cyclic carbonate from CO₂, with regards to green and sustainable chemistry, is the newest noteworthy method.²³ Several catalyst, including organocatalysts,^24,25 ionic liquids,^25–29 metal–organic frameworks,³⁰ hydroxyl-based organocatalysts,^31,32 and homogeneous metal-based catalysts,^33,34 have been reported for this conversion.

Notably, according to the reported studies, it can be concluded that the type of catalyst applied has a significant effect on the polymerization of the cyclic carbonate formation. Indeed, most of the applied catalysts in polymerization are metal-complex catalysts, such as zinc-,³⁵ cobalt-,³⁶ and chromium-based systems.³⁷ It can be related to the strong interactions between the oxygen lone pairs of the epoxide ring and the unoccupied d orbital of the metal, which reinforces the suitable conditions for polymerization. Also, commonly linked ligands in the metal-complex catalysts are porphyrins, salens, phenoxides, and diiminates.³⁸ However, nucleophilic organocatalysts have a greater selectivity against cyclic carbonate.²⁴ In addition, experimental conditions and lab techniques are important factors in polymerization or cyclic carbonate formation. It has been reported that the high pressure of CO₂ increases the selectivity of polymerization. Moreover, since the activation energy for the synthesis of polycarbonates is usually lower than that for cyclic carbonates, a lower temperature leads to the kinetic control towards polycarbonate formation.³⁹

Phosphonium ylides, as essential intermediates in the Wittig reaction, are composed of a phosphorus center as a cationic site bonded to the negatively charged atom and classified as a particular type of zwitterionic compound.⁴⁰ A new generation of the phosphonium ylides is the carbonyl-stabilized types, playing an essential role in modern organic synthesis.^41,42 Byrne and Mayr investigated the nucleophilic behavior of the carbon or oxygen atoms of the formyl- and acetyl-stabilized phosphonium ylides.⁴³ In these ylides, they showed that O-attack to the electrophile carbon such as alkyl halides and acyl chlorides is kinetically more favorable than C-attack. In comparison with the metal-based catalysts, phosphonium ylides are organocatalysts, which catalyse a typical reaction without any metal. Applied metal-based catalysts in the conversion of CO₂ to cyclic carbonate have advantages, such as suitable catalytic activity and selectivity.^44,45 These conversions were performed in the presence of an additive, such as tetrabutylammonium salts, in which the anion part behaves as a nucleophile in the reaction. However, the catalytic conversion of CO₂ by phosphonium ylides is accomplished without any additive. Moreover, the application of the organic molecule as the organocatalyst has some benefits, such as low-cost, low toxicity, metal-free reaction, and sustainability.⁴⁶

Zhou et al. used the triphenyl phosphonium ylide for CO₂ activation, in which PPh₃CH₂CO₂ adducts are efficient organocatalysts for the CO₂ transformation to cyclic α-alkylidene carbonates, oxazolidinone, N-methylated, and N-formylated amines.⁴⁷ Toda et al. introduced carbonyl-stabilized phosphonium ylides (phosphonium-phenolate) (Compound I in Fig. 1) in primary alcohol acylation.⁴⁸ The inherent nucleophilicity of the oxygen atom of these compounds was considered to develop an ionic nucleophilic catalyst. The aryl group bonded to the phosphorous atom prevents the undesired C-attack. Moreover, tetraarylphosphonium salts (Compound II in Fig. 1) were applied for the coupling reaction of the atmospheric pressure carbon dioxide with epoxides, in which a halide ion acts as the nucleophile.⁴⁹ However, in this research, the oxygen atom of carbonyl-stabilized phosphonium ylides was investigated as a potent nucleophile in carbon dioxide transformation to cyclic carbonate, instead of the counter ion (X⁻) of tetraarylphosphonium salts (Fig. 1).

Fig. 1 Chemical structures of the carbonyl-stabilized phosphonium ylides (Compound I) and tetraarylphosphonium salts (Compound II).

Therefore, on the basis of our previous experiences in carbon dioxide conversion,^50–53 the investigation of the mechanism and performance of various derivatives of carbonyl-stabilized phosphonium ylides, as efficient organocatalysts in the carbon dioxide reaction with ethylene oxide (oxirane) and its transformation to a cyclic carbonate (Fig. 2) were the main purposes of this study. Furthermore, the catalytic behavior of the studied organocatalysts along the reaction paths was justified by various quantum chemistry descriptors, such as the activation strain model (ASM), molecular electrostatic potential (MESP), quantum theory of atoms in molecules (QTAIM), and electron localized function (ELF) analyses.

Fig. 2 The studied carbonyl-stabilized phosphonium ylides as the organocatalysts in the carbon dioxide reaction with ethylene oxide.

2. Computational details

Geometry optimization and vibrational frequency calculations were performed at the M06-2X/6-31G(d,p) level^54–56 by using the Gaussian 09 software.⁵⁷ Schlegel's synchronous transit-guided quasi-Newton method (STQN) was applied to locate the structures of the transition states (TSs), and their accuracy was checked via the intrinsic reaction coordinate (IRC) calculations.⁵⁸ Thermodynamic and kinetic parameters were calculated within the zero-point vibrational energy, and thermal corrections based on the harmonic oscillator approximations and solvation corrections at 298.15 K and 1 atm. All calculations were performed using dichloromethane as the solvent in cyclic carbonate synthesis.⁵⁹ The conductor-like polarisable continuum model (CPCM) was applied to calculate the solvent effects on the kinetic and thermodynamic parameters of the reaction.⁶⁰

In order to increase the accuracy level of the theoretical data, single-point energies were calculated at the MPW1PW91/6-311++G(d,p) level of the theory^61,62 because the experimental data reveal that the MPW1PW91 function provides a good agreement with the several tested post-HF methods, such as MP2⁶³ and ELF analysis. The electron density of atoms at the bond critical points (BCPs), the electron density of the basins, and the molecular electrostatic potential MESP at the nuclear position were obtained by MultiWFN 3.1 package.⁶⁴

3. Results and discussion

Two probable mechanisms can be considered for the reaction of CO₂ and ethylene oxide (Fig. 3). In step 1 of mechanism A, the oxygen atom of the organocatalyst as a nucleophile, attacks the carbon atom of the carbon dioxide, yielding In1A. In step 2, In2A was produced due to another nucleophilic attack of the oxygen atom of In1A to ethylene oxide. Finally, in step 3, In2A as an unstable intermediate dissociated with the initial organocatalyst and cyclic carbonate. However, in the first step of mechanism B, instead of carbon dioxide, the carbon atom of the ethylene oxide was involved in the nucleophilic attack of the oxygen atom of the organocatalyst, which leads to In1B formation. The O atom linkage of In1B to carbon dioxide occurred in step 2 of this mechanism, yielding In2B. Finally, in step 3, due to the intermolecular nucleophilic attack of the oxygen atom of In2B, cyclic carbonate was formed and the organocatalyst was reproduced. Table 1 shows the thermodynamic and kinetic parameters of the reaction in the presence of different organocatalysts.

Table 1 Thermodynamic and kinetic parameters of the reaction in the presence of different organocatalysts

Substituent (G)	Steps	Mechanism A				Mechanism B
		ΔG (kcal mol^−1)	ΔH (kcal mol^−1)	ΔS (cal mol^−1 K^−1)	ΔG^≠ (kcal mol^−1)	ΔG (kcal mol^−1)	ΔH (kcal mol^−1)	ΔS (cal mol^−1 K^−1)	ΔG^≠ (kcal mol^−1)
Me	1	9.60	−2.98	−42.21	13.59	17.80	4.25	−45.45	40.01
	2	32.36	19.97	−41.58	42.07	−26.66	−36.25	−32.18	—
	3	−54.14	−41.02	44.00	—	−3.32	7.96	37.85	29.07
CF3	1	12.99	1.47	−38.62	15.06	20.77	7.89	−43.19	42.15
	2	35.70	22.83	−43.16	45.67	−23.33	−34.39	−37.10	—
	3	−60.87	−48.34	42.00	—	−9.62	2.46	40.51	24.25
OMe	1	9.48	−5.23	−49.33	14.47	18.19	2.81	−51.57	40.83
	2	33.49	22.76	−36.01	44.01	−23.96	−34.41	−35.06	—
	3	−55.15	−41.57	45.56	—	−6.41	7.56	46.85	27.78
Br	1	11.64	−0.57	−40.95	15.02	20.00	6.45	−45.46	40.94
	2	34.49	22.05	−41.72	45.32	−24.11	−34.98	−36.46	—
	3	−69.14	−45.52	42.884	—	−8.072	4.49	42.14	25.52
Cl	1	11.44	−0.78	−40.97	14.42	22.07	9.88	−40.87	41.35
	2	33.93	21.87	−40.46	44.52	−27.25	−38.50	−37.74	—
	3	−57.55	−45.13	41.65	—	−7.00	4.58	38.83	26.78
CO2Me	1	13.82	1.96	−39.79	16.23	21.55	8.36	−44.23	42.99
	2	35.49	22.51	−43.55	45.31	−23.85	−34.66	−40.28	—
	3	−61.49	−48.51	43.56	—	−9.88	2.26	40.72	24.81
CHO	1	15.25	3.260	−40.22	16.37	22.22	9.082	−44.06	42.71
	2	34.89	22.66	−41.00	44.45	−23.49	−34.30	−36.27	—
	3	−62.32	−49.96	41.43	—	−10.91	1.18	40.54	24.77
CN	1	16.29	3.87	−41.63	16.74	22.84	9.45	−44.90	43.70
	2	35.23	23.35	−39.85	43.80	−23.40	−33.65	−34.38	—
	3	−63.69	−51.25	41.70	—	−11.61	0.16	39.50	24.84
NMe2	1	15.25	3.26	−40.22	16.37	14.71	2.35	−41.45	40.12
	2	34.89	22.66	−41.00	44.45	−9.32	−36.77	−42.745	—
	3	−50.49	−36.92	45.50	—	−2.86	10.38	44.41	20.35

---

Fig. 3 Two possible mechanisms for the carbon dioxide reaction with ethylene oxide.

The energetic span model (ESM)⁶⁵ was applied for the investigation of the most probable paths of the catalytic mechanisms A and B. The energy profile describes each catalytic reaction by illustrating the energy of all species relative to the primary reactants. The ESM concept^66,67 as a useful tool was developed to connect the energy profile derived from the electronic-structure calculations to the turnover frequency (TOF) as an experimentally accessible quantity. TOF is defined as the number of productive cycles (N) per catalyst unit [C_t] and time (t), as illustrated in eqn (1).

Kozuch and Shaik developed a kinetic model by considering the energy balance of the reaction at the end of the catalytic cycle.⁶⁵ Based on their report, eqn (2) was derived from eqn (1)

where ΔG_r is the energy of the general reaction, T_i and I_j are the calculated Gibbs energies of the ith transition state and the jth intermediate, respectively. k_B and h are the Boltzmann and Planck constants, respectively. R is the gas constant (1.98 cal mol⁻¹ K⁻¹), and T is the absolute temperature (298.15 K). δG_i,j′ is specified according to eqn (3).

The degree of the TOF control (X_TOF) was used to identify the influence of each intermediate and transition state on the TOF in the energetic span model to evaluate the TOF determining intermediate (TDI) and the TOF determining transition state (TDTS). It was developed based on the Campbell's degree of rate control,^68,69 which measures the extent of the TOF changes by a small variation in TS or the intermediate energy. X_TOF can be calculated by eqn (4).⁶⁵

It is noticeable that the sum of all the X_TOF,Ij or X_TOF,Ti was equal to one. After that TDI and TDTS were evaluated, the TOF equation (eqn (2)) can be simplified as eqn (5). δE, as the energetic span, is the apparent activation energy of the cycle.

A corrected calculation of the energetic span for a specific pathway needs the calculation of several δE. Indeed, TDI and TDTS are the pairs of states that maximize the energy span quantity within the operative reaction pathway. Table S1 (ESI†) shows the degree of the TOF control (X_TOF) of the reaction for all functional groups in both mechanisms. Fig. 4 depicts four energy potential diagrams (PED) for the electron-withdrawing (CF₃ and CO₂Me) and electron-donating (Me and NMe₂) substituted organocatalysts, in which the TDI and TDTS states are shown for the studied mechanisms at the M062X/6-31G(d,p) and MPW1PW91/6-311++G(d,p) levels of theory. Fig. S1 (ESI†) shows the PED diagrams for other studied organocatalysts.

Fig. 4 Energy potential diagrams of the substituted organocatalysts (G = CF₃, CO₂Me, Me and NMe₂).

As shown in Fig. 4, TDTS for mechanism A occurs in step 2, in which the nucleophilic attack of the oxygen atom of In1A to ethylene oxide forms In2A. Therefore, TDTS appeared after the TDI and δE were calculated from eqn (5a). In the case of mechanism B, the TS of step 1 was the TDTS and In2B was considered as the TDI of the mechanism. As a result, δE was calculated from eqn (5b) because TDTS appeared before TDI.

Table 2 shows the TDI, TDTS, δE (in kcal mol⁻¹), and TOF (s⁻¹) values of the studied organocatalysts at the M062X/6-31G(d,p) and MPW1PW91/6-311++G(d,p) levels. According to Table 2, in both levels, the δE and TOF values in mechanism A were significantly lower and higher than mechanism B, respectively. It can be concluded that mechanism A was a preferred mechanism for the reaction progress, which was initiated by the reaction of the nucleophilic attack of the oxygen atom of the organocatalysts to carbon dioxide. This means that O-attack to CO₂ was a more probable path than O-attack to the carbon atom of the ethylene oxide.

Table 2 TDI, TDTS, δE (in kcal mol⁻¹) and TOF (s⁻¹) values of the studied organocatalysts at M062X/6-31G(d,p) and MPW1PW91/6-311++G(d,p) levels

Level	G	Mechanism A				Mechanism B
		TDI (kcal mol^−1)	TDTS (kcal mol^−1)	δE (kcal mol^−1)	TOF (s^−1)	TDI (kcal mol^−1)	TDTS (kcal mol^−1)	δE (kcal mol^−1)	TOF (s^−1)
M062X6-31G(d,p)	Me	−4.96	25.82	30.78	1.79 × 10^−10	−36.48	27.14	36.84	6.20 × 10^−14
	CF3	0.00	32.61	32.61	5. 50 × 10^−12	−30.83	30.48	34.54	3.00 × 10^−12
	OMe	−7.13	26.37	33.50	1.70 × 10^−12	−35.95	27.52	36.69	7.90 × 10^−14
	Br	−1.64	30.03	31.68	3.50 × 10^−11	−32.88	29.28	35.38	7.20 × 10^−13
	Cl	−1.92	29.01	30.93	1.30 × 10^−10	−33.07	29.09	35.39	7.20 × 10^−13
	CO2Me	0.00	32.84	32.84	4.40 × 10^−12	−30.75	30.62	34.60	2.70 × 10^−12
	CHO	0.00	34.34	34.34	4.10 × 10^−13	−29.59	31.54	34.35	3.80 × 10^−12
	CN	0.00	35.43	35.43	6.60 × 10^−14	−28.52	31.87	33.61	9.30 × 10^−12
	NMe2	−7.72	22.24	29.96	6.80 × 10^−10	−39.21	26.57	39.00	1.60 × 10^−15
MPW1PW916-311++G(d,p)	Me	5.69	33.66	27.96	2.05 × 10^−8	−23.29	24.64	41.71	1.76 × 10^−18
	CF3	11.43	40.79	29.36	1.96 × 10^−9	−17.42	27.27	38.47	4.13 × 10^−16
	OMe	3.64	34.47	30.83	1.64 × 10^−10	−22.75	24.98	41.51	2.46 × 10^−18
	Br	8.82	37.62	28.80	5.01 × 10^−9	−19.90	26.09	39.77	4.65 × 10^−17
	Cl	8.40	37.46	29.06	3.23 × 10^−9	−20.30	26.07	40.15	2.44 × 10^−17
	CO2Me	11.74	41.01	29.27	2.26 × 10^−9	−17.46	27.21	38.45	4.30 × 10^−16
	CHO	13.38	43.02	29.64	1.21 × 10^−9	−15.90	28.55	38.23	6.25 × 10^−16
	CN	13.38	43.34	29.96	7.03 × 10^−10	−15.44	28.26	37.48	2.22 × 10^−15
	NMe2	2.50	29.64	27.14	8.22 × 10^−8	−26.46	23.86	44.09	3.16 × 10^−20

---

The kinetic behaviors of step 1 in the studied mechanisms were substantially different. Indeed, the O-attack of the substituted organocatalysts to carbon dioxide in the step 1 of mechanism A passed via a lower barrier energy than the nucleophilic attack to ethylene oxide in the first step of mechanism B. The analysis of MESP at the involved nucleus (V_n) at TS was a good criterion to understand the kinetic aspects of step 1.

MESP was a useful quantum chemistry descriptor, which was used for the justification and quantification of the substituent properties, topographical, and surface features in the molecular systems.^70–72 This descriptor was derived from the electron density data from the X-ray diffraction or calculated with high accuracy by theoretical methods implemented in many of the standard ab initio/DFT program packages. Theoretically obtained MESP was used to understand the molecular reactivity in various investigations.^73,74 At a specific point, r, eqn (6) was the standard equation to calculate the molecular electrostatic potential (V(r)).

Mohan and Suresh investigated various electrostatic dominated interacting systems, such as hydrogen, halogen, and dihydrogen bonds. These interactions were classified as the electron donor–acceptor interactions, where the donor stands for a electron-rich moiety (Lewis base), while the acceptor was an electron-deficient moiety (Lewis acid).⁷³ At the nuclear positions, ΔΔV_n was a quantity based on ESP, as described by eqn (7). V_n-D′ is ESP at the nuclear position of the donor atom in the donor–acceptor interacting system, in which the nucleus contribution of this donor atom was ignored. The definition of V_n-D is the same as V_n-D′, which was related to the donor atom of the monomer state in the absence of the acceptor monomer. Therefore, ΔV_n-D = V_n-D′ − V_n-D can be considered as the variation of ESP at the nuclear position of the donor atom due to the presence of another molecule, V_n-A′ and V_n-A quantities are similar to V_n-D′ and V_n-D, respectively, but they are calculated for the acceptor atom.

The ESP analysis on the nucleophilic oxygen atom of the organocatalyst and carbon atoms of carbon dioxide and ethylene oxide in the step 1 of the mechanisms A and B reveals a valuable correlation between ΔE^≠ and ΔΔV_n.

Two strategies were considered for the ESP analysis in the nuclear position. In the first strategy, the studied TSs were considered as the donor–acceptor interacting system, applied for the V_n-D′ and V_n-A′ calculations. To calculate V_n-D and V_n-A, the optimized structures at a global minimum of the species, including organocatalysts, as the donor monomer, and carbon dioxide in mechanism A and ethylene oxide in mechanism B, as the acceptor monomers were used. In the second strategy, the V_n-D′ and V_n-A′ values were calculated at TSs, as the donor–acceptor interacting system. However, V_n-D was calculated for the distorted organocatalysts from the equilibrium geometry as the donor monomer at TSs, in which the carbon dioxide and ethylene oxide were eliminated. Also, V_n-A was obtained from the distorted carbon dioxide and ethylene oxide from the equilibrium geometry as the acceptor monomers, when the organocatalysts were eliminated. Table S2, ESI,† and Table 3 represent ESP at the nuclear positions and the obtained ΔE^≠ values at two levels for the first and second strategies, respectively. Fig. 5 illustrates two applied strategies in the ESP calculation in the nuclear position.

Fig. 5 Two applied strategies in the ESP analysis at the nuclear position calculation.

In all studied donor–acceptor interacting systems, ΔV_n-D was positive and ΔV_n-A was negative, indicating that the donor monomer donates electron density to the acceptor monomer during the bond formation at TSs. ΔΔV_n was an important criterion to measure the donor–acceptor strength in the interacting systems. Based on the obtained results, the ΔΔV_n values for the step 1 of mechanism B was higher than that of mechanism A, showing a more powerful donor–acceptor interaction at the TS of the nucleophilic attack to ethylene oxide. However, the ΔΔV_n values were not the only determining factor in the obtained ΔE^≠ values of the studied mechanisms.

A large negative character of ΔV_n-A represents a higher tendency of electron-acceptance in the donor–acceptor interacting systems. As shown in Table 3, the average value of ΔV_n-A for the nucleophilic attack of the organocatalysts to carbon dioxide (step 1 in mechanism A) had a more significant negative character than the nucleophilic attack to ethylene oxide (step 1 in mechanism B). As a good result, carbon dioxide is a more powerful electron acceptor from the organocatalysts than ethylene oxide, which can be considered as a good reason for the lower ΔE^≠ values in the nucleophilic attack to carbon dioxide than that of ethylene oxide. The relationship between ΔΔV_n and ΔE^≠ was different in the studied strategies.

Table 3 ESP quantities at the nuclear positions (in a.u.), electron densities (ρ) and their Laplacian (∇²ρ) for the critical point of developing bond at TSs (in a.u.) and the obtained ΔE^≠ values (in kcal mol⁻¹) for the second strategy

	G	V n-D′	V n-A′	V n-D	V n-A	ΔVn-D	ΔVn-A	ρ	∇^2ρ	ΔΔVn	ΔE^≠ M062X	ΔE^≠ MPW1PW91
Step 1 of mechanism A	Me	−22.4233	−14.6273	−22.4706	−14.5302	0.0473	−0.0970	0.0632	0.1432	0.1444	1.75	9.47
	CF3	−22.3932	−14.6239	−22.4484	−14.5276	0.0552	−0.0963	0.0797	0.1485	0.1516	4.08	12.46
	OMe	−22.4195	−14.6260	−22.4674	−14.5302	0.0479	−0.0958	0.0639	0.1441	0.1437	1.79	9.89
	Br	−22.4036	−14.6235	−22.4546	−14.5288	0.0510	−0.0947	0.0721	0.1475	0.1458	3.03	10.92
	Cl	−22.4046	−14.6240	−22.4557	−14.5287	0.0511	−0.0953	0.0720	0.1472	0.1463	2.94	10.68
	CO2Me	−22.3939	−14.6270	−22.4480	−14.5272	0.0541	−0.0997	0.0817	0.1483	0.1540	4.44	12.93
	CHO	−22.3860	−14.6241	−22.4403	−14.5267	0.0544	−0.0974	0.0850	0.1480	0.1518	5.24	13.97
	CN	−22.3778	−14.6203	−22.4346	−14.5263	0.0568	−0.0939	0.0877	0.1470	0.1507	5.34	13.93
	NMe2	−22.4291	−14.6271	−22.4739	−14.5309	0.0448	−0.0962	0.0597	0.1404	0.1410	1.13	9.01
Step 1 of mechanism B	Me	−22.3717	−14.7599	−22.4590	−14.6641	0.0804	−0.0958	0.0935	0.1385	0.1831	27.14	24.64
	CF3	−22.3553	−14.7510	−22.4357	−14.6628	0.0804	−0.0881	0.0971	0.1351	0.1685	30.48	27.27
	OMe	−22.3681	−14.7581	−22.4558	−14.6640	0.0877	−0.0941	0.0938	0.1384	0.1818	27.52	24.98
	Br	−22.3553	−14.7510	−22.4428	−14.6633	0.0874	−0.0876	0.0959	0.1364	0.1751	29.28	26.09
	Cl	−22.3561	−14.7513	−22.4438	−14.6604	0.0877	−0.0910	0.0957	0.1364	0.1787	29.09	26.07
	CO2Me	−22.3469	−14.7487	−22.4343	−14.6629	0.0875	−0.0858	0.0973	0.1354	0.1732	30.62	27.21
	CHO	−22.3419	−14.7454	−22.4273	−14.6623	0.0854	−0.0831	0.0982	0.1338	0.1686	31.54	28.55
	CN	−22.3334	−14.7405	−22.4209	−14.6623	0.0875	−0.0782	0.0989	0.1332	0.1657	31.87	28.26
	NMe2	−22.3787	−14.7624	−22.4650	−14.6647	0.0863	−0.0978	0.0923	0.1398	0.1840	26.57	23.86

---

Fig. 6 depicts a linear relationship between these quantities. As shown in this figure, in the first strategy, mechanism B shows a linear correlation between ΔE^≠ and ΔΔV_n, which is in contrast to mechanism A. However, in the second strategy, a good linear correlation was obtained in both mechanisms. As a result, in the investigation of the correlation between ΔE^≠ and ΔΔV_n, the second strategy in considering the V_n-D and V_n-A values of monomers was more efficient.

Fig. 6 Graphical representation of ΔE^≠ as a function of ΔΔV_n.

In addition to ESP quantities at the nuclear positions, Table 3 depicts the electron density (ρ) and Laplacian (∇²ρ) of the critical point of the developing bond at TSs of step 1. Fig. 7 illustrates the ρ values of the developing bond critical point (BCP) at the TSs of the step 1 of the studied mechanisms for the selected substituted organocatalysts. As illustrated in Table 3 and Fig. 7, the ρ values of the BCP of the nucleophilic attack to ethylene oxide were substantially higher than those in the case of carbon dioxide. The higher ρ values for developing the BCP of the TS in mechanism B reveal a significant donor–acceptor interaction than that of the nucleophilic attack to carbon dioxide. This result was according to the achieved ΔΔV_n values. However, the obtained values of ΔΔV_n and ρ for developing the BCP of TSs were not effective factors in the ΔE^≠ values of step 1 in the studied mechanisms. The distortion of carbon dioxide and ethylene oxide from the equilibrium geometry at the TSs has a determining factor in the ΔE^≠ values. Hence, the ASM model is a unique analysis in the activation strain measurement at the TSs of a typical reaction.

Fig. 7 Molecular graph and ρ values (a.u.) of the developing BCP of the selected substituted organocatalysts in step 1 of the studied mechanisms.

The fundamental assumption of the ASM model is based on the concept that the energy of the reacting system is illustrated and figured out regarding the initial situation of the reactants.^75,76 This model evaluates the reactant rigidity and the amount of the reactant deformation during the reaction plus their facility to interact together as the reaction proceeds. Therefore, the total energy, ΔE(ζ), can be divided into the strain (ΔE_strain(ζ)) and the interaction (ΔE_int(ζ)) energies. These values are projected onto the bond stretch of the activated bond (eqn (8)).

ΔE(ζ) = ΔE_strain(ζ) + ΔE_int(ζ) (8)

where ΔE_strain(ζ), as the strain energy, is the required energy for the deformation of the starting materials from their equilibrium structure to the necessary geometry in the reacting system at the point ζ of the reaction coordinate. Moreover, ΔE_int(ζ) is the interaction energy between the deformed species during the reaction. According to this model, the sum of the activation strain (ΔE^‡_strain = ΔE_strain(ζ^TS)) and the interaction energy at the TS (ΔE^‡_int = ΔE_int(ζ^TS)) was equal to the activation energy of the reaction (ΔE^‡ = ΔE(ζ^TS)) (eqn (9)).

ΔE^‡ = ΔE^‡_strain + ΔE^‡_int (9)

Table 4 represents the distortion/interaction parameters of the investigated organocatalysts at the TSs of step 1 of both mechanisms, and Fig. 8 depicts the correlation between ΔE^‡_reaction and ΔE^‡_strain of the involved species. The obtained values of the ΔE^‡_strain of carbon dioxide in mechanism A was remarkably lower than that of ethylene oxide (ΔE^{‡ oxirane}_strain). Moreover, the obtained values of the ΔE^‡_strain of carbon dioxide and ethylene oxide, in which the organocatalysts having the electron-withdrawing substituents, such as CN and CHO were higher than that of the electron-donating groups. Also, significant linear correlations were distinguishable between the ΔE^‡_reactionvs. ΔE^‡_strain of carbon dioxide, ethylene oxide, and the total activation strain of the involved components (ΔE^‡ total_strain) at TSs. As a result, during step 1, carbon dioxide bore a lower distortion from its equilibrium geometry than ethylene oxide at the TS. This factor was a more effective agent in ΔE^‡_reaction than the ΔΔV_n values in the donor–acceptor interactions. In the second strategy, a linear correlation can be observed between the and ΔΔV_n values in mechanism A, and ΔE^{‡ Oxirane}_strain and ΔΔV_n values in mechanism B (Fig. 9). It is worth mentioning that the values of ΔΔV_n depend on the extent of distortion from the equilibrium geometry.

Table 4 Calculated distortion/interaction parameters (kcal mol⁻¹) at the TSs of step 1 of both mechanisms

Level	G	Step 1 of mechanism A				Step 1 of mechanism B
			ΔE^‡ Orgstrain	ΔE^‡ totalstrain	ΔE^‡i	ΔE^‡ Oxiranestrain	ΔE^‡ Orgstrain	ΔE^‡ totalstrain	ΔE^‡i
M062X6-31G(d,p)	Me	9.62	8.07	17.69	−15.94	40.30	2.19	42.48	−15.35
	CF3	13.41	9.01	22.42	−18.34	42.61	2.50	45.11	−14.63
	OMe	9.72	8.26	17.97	−16.18	40.46	2.28	42.74	−15.22
	Br	11.66	8.63	20.29	−17.26	41.75	2.36	44.10	−14.83
	Cl	11.64	8.32	19.96	−17.02	41.75	2.47	44.22	−15.12
	CO2Me	13.87	8.83	22.69	−18.25	42.59	2.09	44.69	−14.06
	CHO	14.54	9.38	23.92	−18.68	43.38	2.75	46.13	−14.59
	CN	15.12	9.14	24.26	−18.91	43.61	2.33	45.94	−14.07
	NMe2	8.79	7.97	16.76	−15.63	39.27	2.54	41.81	−15.25
MPW1PW916-311++G(d,p)	Me	10.34	5.93	16.27	−6.70	34.27	1.20	35.48	−10.79
	CF3	14.27	6.74	21.01	−8.45	36.22	1.52	37.74	−10.43
	OMe	10.44	6.38	16.82	−6.82	34.40	1.27	35.68	−10.66
	Br	12.45	6.32	18.77	−7.75	35.49	1.24	36.74	−10.60
	Cl	12.44	6.16	18.59	−7.81	35.50	1.43	36.92	−10.81
	CO2Me	14.74	6.88	21.62	−8.59	36.21	1.43	37.64	−10.43
	CHO	15.44	7.16	22.60	−8.52	36.86	1.94	38.80	−10.21
	CN	16.03	6.99	23.03	−9.00	37.07	1.55	38.62	−10.32
	NMe2	9.48	6.10	15.58	−6.47	33.41	1.14	34.55	−10.65

---

Fig. 8 Linear correlation of ΔE^‡_reactionvs. ΔE^‡_strain of the involved species and ΔE^‡ total_strain.

Fig. 9 The linear correlation between ΔE^‡_strain of the carbon dioxide and ethylene oxide and the obtained ΔΔV_n values.

On the basis of the energetic span, the δE analysis, mechanism A was more probable in the carbon dioxide conversion to cyclic carbonate. This conclusion is compatible with the experimental results of Zhou's report.⁴⁷ In step 2 of this mechanism, In2A was produced due to the nucleophilic attack of the oxygen atom of In1A to ethylene oxide. This step had a higher activation energy barrier than step 1.

The electron localization function (ELF) concept as a useful molecular descriptor, can be applied to explain the nucleophilic attack of In1A to ethylene oxide. The capability of the ELF analysis as a valuable descriptor for the evaluation of the critical bonds along the reaction path, has been emphasized in many reports.^77–79 The basins of the attractors were essential issues in the topological section of the ELF gradient field analysis, which can be related to the atomic cores, bonds, and lone pairs. In a typical molecule, two kinds of basins can be recognized: (i) core basins surrounding nuclei with the atomic number Z > 2 denoted by C(A), where A is the atomic symbol of the element; (ii) valence basins that are identified based on a number of the participated atomic valence shells.⁸⁰ In a typical molecule, the number of core basins that share a boundary is called the synaptic order. Based on this definition, it can be identified as monosynaptic, disynaptic, trisynaptic basins, and so on. The lone pairs of the Lewis type or non-bonding regions are classified as monosynaptic basins, V(A). If a basin corresponds to a bonding region between A and X, and connects the core of two nuclei A and X, then it is a disynaptic basin which is denoted by V(A,X). A trisynaptic basin, V(A,B,C), refers to a three-center bond and so on. Based on the ELF analysis, a single C_x–C_y bond formation was a result of V(C_x) and V(C_y) merging into a new disynaptic basin V(C_x,C_y).

On the basis of the ELF terminology, along with step 2 in mechanism A, the disynaptic basin of the ethylene oxide C–O bond, V(C,O), diminishes, and electron density of monosynaptic basin oxygen atom of In1A (V(O_In1A)) was transferred to a developing vacant orbital of an ethylene oxide carbon atom. Fig. 10 depicts the electron density of the V(O_In1A) basin and ΔE^‡ of step 2 at the M062X/6-31G(d,p) (Red color) and MPW1PW91/6-311++G(d,p) (Green color) levels. Based on the ΔE^‡ values, there are two categories for the substituted organocatalysts. In one category, in which the substituents are electron-donating groups (ERG), such as OMe and NMe₂, the ΔE^‡ values were lower than another category having the electron-withdrawing groups (EWG), such as CF₃ and CN. Moreover, the electron density of the V(O_In1A) basin in the case of the ERG category was remarkably higher than that in the case of the EWG category. The average values of V(O_In1A) electron densities were 1.3747 and 1.3573 a.u. for the ERG and EWG categories, respectively. As a result, the electron-withdrawing character decreases the electron density of the V(O_In1A) basin, leading to an increment in the ΔE^‡ values in the case of the EWG category. Finally, as a logical result, carbonyl-stabilized phosphonium ylides, having the electron-donating groups, were the preferred candidates in the carbon dioxide reaction with ethylene oxide and its conversion to cyclic carbonates.

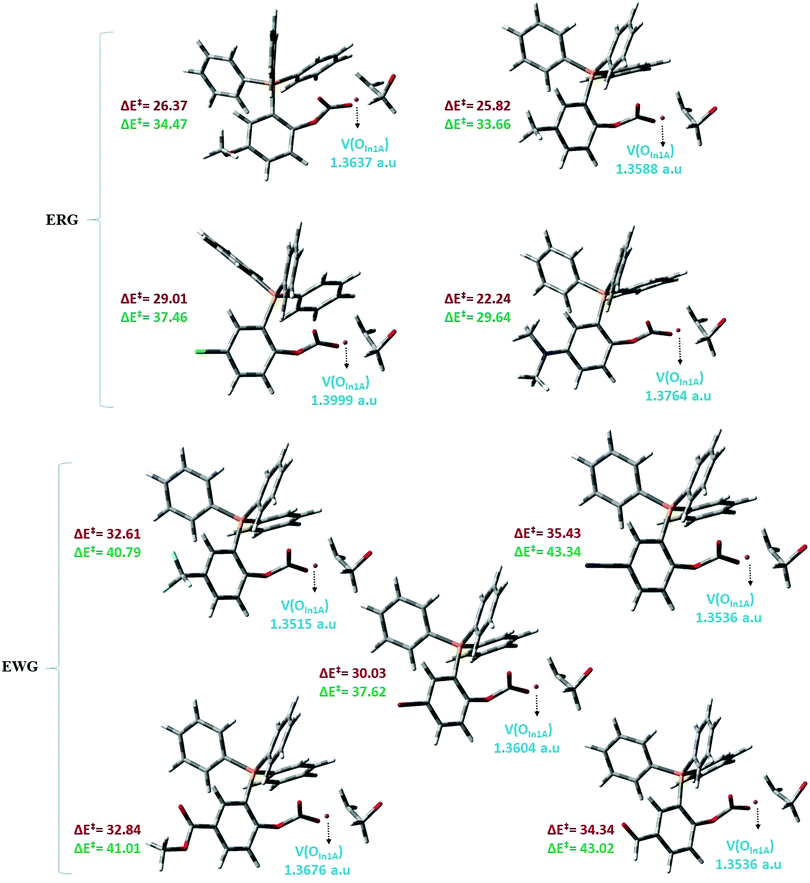Fig. 10 Electron density of the V(O_In1A) basin and ΔE^‡ (kcal mol⁻¹) of step 2 in mechanism A; M062X/6-31G(d,p) (Red color) and MPW1PW91/6-311++G(d,p) (Green color).

4. Conclusion

The kinetic investigation of carbon dioxide reaction and ethylene oxide, and their conversion to cyclic carbonate in the presence of various derivatives of the carbonyl-stabilized phosphonium ylides as the organocatalyst, were the main purposes of this research. All calculations were performed by using the M062X/6-31G(d,p) and MPW1PW91/6-311++G(d,p) levels of theory. Two mechanisms were proposed for this conversion. The first mechanism was initiated by the nucleophilic attack of the O-atom of the organocatalyst to the carbon atom of carbon dioxide (mechanism A), while another one was started by the O-attack to the carbon atom of ethylene oxide (mechanism B). On the basis of the energetic span model, the δE and TOF values in mechanism A were significantly lower and higher than mechanism B, respectively. Therefore, mechanism A was a preferred path for the reaction progress. The kinetic behaviors of the first step of both mechanisms were studied by ESP at the nuclear position by two strategies. The results showed that the evaluation of V_n-D and V_n-A by the distorted species from the equilibrium geometry at TSs (second strategy) led to a better linear correlation than the considering values of V_n-D and V_n-A by the optimized structures in the global minimum of the energies. However, the ASM analysis showed that the ΔE^‡_strain values were more effective factors in ΔE^‡ of the reaction than ΔΔV_n. On the other hand, a good linear correlation between the ΔE^‡_strain and ΔΔV_n values was obtained, which confirms that the ΔΔV_n values are dependent on the molecular distortion from the equilibrium geometry. The ELF analysis was used to justify the kinetic behavior of step 2 in mechanism A. Based on the results, the electron-withdrawing group decreases the electron density of the V(O_In1A) basin, which increases the ΔE^‡ values of the substituted organocatalysts. Finally, carbonyl-stabilized phosphonium ylides having electron-donating groups were proposed as the more efficient organocatalysts in carbon dioxide conversion to cyclic carbonates in the presence of ethylene oxide.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Research Council of the Ferdowsi University of Mashhad is gratefully acknowledged for the financial support of this project (Grant No 2/46908). Also, we hereby acknowledge that some parts of this computation were performed in the HPC center of the Ferdowsi University of Mashhad.

References

1. Y. Zhu, S. Zhang, Y. Ye, X. Zhang, L. Wang, W. Zhu, F. Cheng and F. Tao, ACS Catal., 2012, 2, 2403–2408.
2. H. Sabet-Sarvestani, H. Eshghi, M. Izadyar, N. Noroozi-Shad, M. Bakavoli and F. Ziaee, Int. J. Hydrog. Energy, 2016, 41, 11131–11140.
3. S. Sarfraz, A. T. Garcia-Esparza, A. Jedidi, L. Cavallo and K. Takanabe, ACS Catal., 2016, 6, 2842–2851.
4. J. Lin, Z. Ding, Y. Hou and X. Wang, Sci. Rep., 2013, 3, 1056–1060.
5. J. Klankermayer, S. Wesselbaum, K. Beydoun and W. Leitner, Angew. Chem., Int. Ed., 2016, 55, 7296–7343.
6. Q. Liu, L. Wu, R. Jackstell and M. Beller, Nat. Commun., 2015, 6, 5933.
7. A. Otto, T. Grube, S. Schiebahn and D. Stolten, Energy Environ. Sci., 2015, 8, 3283–3297.
8. V. Besse, F. Camara, C. Voirin, R. Auvergne, S. Caillol and B. Boutevin, Polym. Chem., 2013, 4, 4545–4561.
9. P. P. Pescarmona and M. Taherimehr, Catal. Sci. Technol., 2012, 2, 2169–2187.
10. C. M. Alder, J. D. Hayler, R. K. Henderson, A. M. Redman, L. Shukla, L. E. Shuster and H. F. Sneddon, Green Chem., 2016, 18, 3879–3890.
11. M. Philipp, R. Bhandary, F. J. Groche, M. Schönhoff and B. Rieger, Electrochim. Acta, 2015, 173, 687–697.
12. J. Nemirowsky, J. Prakt. Chem., 1883, 28, 439–440.
13. R. Khusnutdinov, N. Shchadneva and Y. Y. Mayakova, Russ. J. Org. Chem., 2014, 50, 948–952.
14. M. Selva, A. Caretto, M. Noè and A. Perosa, Org. Biomol. Chem., 2014, 12, 4143–4155.
15. V. P. Indran, A. S. H. Saud, G. P. Maniam, M. M. Yusoff, Y. H. Taufiq-Yap and M. H. A. Rahim, RSC Adv., 2016, 6, 34877–34884.
16. M. Pena-López, H. Neumann and M. Beller, Eur. J. Org. Chem., 2016, 3721–3727.
17. B. Gabriele, R. Mancuso, G. Salerno, L. Veltri, M. Costa and A. Dibenedetto, ChemSusChem, 2011, 4, 1778–1786.
18. F. D. Bobbink, W. Gruszka, M. Hulla, S. Das and P. J. Dyson, Chem. Commun., 2016, 52, 10787–10790.
19. Y. N. Lim, C. Lee and H. Y. Jang, Eur. J. Org. Chem., 2014, 1823–1826.
20. T. Hirose, S. Shimizu, S. Qu, H. Shitara, K. Kodama and L. Wang, RSC Adv., 2016, 6, 69040–69044.
21. K. Chen, G. Shi, R. Dao, K. Mei, X. Zhou, H. Li and C. Wang, Chem. Commun., 2016, 52, 7830–7833.
22. J. Hu, J. Ma, Q. Zhu, Q. Qian, H. Han, Q. Mei and B. Han, Green Chem., 2016, 18, 382–385.
23. P. Anastas and N. Eghbali, Chem. Soc. Rev., 2010, 39, 301–312.
24. M. Cokoja, M. E. Wilhelm, M. H. Anthofer, W. A. Herrmann and F. E. Kuehn, ChemSusChem, 2015, 8, 2436–2454.
25. R. S. Kalb, E. N. Stepurko, V. N. Emel'yanenko and S. P. Verevkin, Phys. Chem. Chem. Phys., 2016, 18, 31904–31913.
26. S. Yue, P. Wang and X. Hao, Fuel, 2019, 251, 233–241.
27. A. A. Chaugule, A. H. Tamboli and H. Kim, Fuel, 2017, 200, 316–332.
28. J. Peng, S. Wang, H.-J. Yang, B. Ban, Z. Wei, L. Wang and B. Lei, Fuel, 2018, 224, 481–488.
29. M. Liu, K. Gao, L. Liang, F. Wang, L. Shi, L. Sheng and J. Sun, Phys. Chem. Chem. Phys., 2015, 17, 5959–5965.
30. M. H. Beyzavi, C. J. Stephenson, Y. Liu, O. Karagiaridi, J. T. Hupp and O. K. Farha, Front. Energy Res., 2015, 2, 63.
31. P. Yingcharoen, C. Kongtes, S. Arayachukiat, K. Suvarnapunya, S. V. Vummaleti, S. Wannakao, L. Cavallo, A. Poater and V. D'Elia, Adv. Synth. Catal., 2019, 361, 366–373.
32. J.-Q. Wang, J. Sun, W.-G. Cheng, K. Dong, X.-P. Zhang and S.-J. Zhang, Phys. Chem. Chem. Phys., 2012, 14, 11021–11026.
33. X. Wu, J. A. Castro-Osma and M. North, Symmetry, 2016, 8, 4.
34. V. D'Elia, J. D. Pelletier and J. M. Basset, ChemCatChem, 2015, 7, 1906–1917.
35. M. R. Kember, P. D. Knight, P. T. Reung and C. K. Williams, Angew. Chem., Int. Ed., 2009, 48, 931–933.
36. J. Y. Jeon, J. J. Lee, J. K. Varghese, S. J. Na, S. Sujith, M. J. Go, J. Lee, M.-A. Ok and B. Y. Lee, Dalton Trans., 2013, 42, 9245–9254.
37. L. Guo, C. Wang, W. Zhao, H. Li, W. Sun and Z. Shen, Dalton Trans., 2009, 5406–5410.
38. S. Klaus, M. W. Lehenmeier, C. E. Anderson and B. Rieger, Coord. Chem. Rev., 2011, 255, 1460–1479.
39. P. P. Pescarmona and M. Taherimehr, Catal. Sci. Technol., 2012, 2, 2169–2187.
40. P. A. Byrne and D. G. Gilheany, Chem. Soc. Rev., 2013, 42, 6670–6696.
41. C. S. Shanahan, P. Truong, S. M. Mason, J. S. Leszczynski and M. P. Doyle, Org. Lett., 2013, 15, 3642–3645.
42. V. Cachatra, A. Almeida, J. o. Sardinha, S. D. Lucas, A. Gomes, P. D. Vaz, M. H. Florêncio, R. Nunes, D. Vila-Viçosa and M. J. Calhorda, Org. Lett., 2015, 17, 5622–5625.
43. P. A. Byrne, K. Karaghiosoff and H. Mayr, J. Am. Chem. Soc., 2016, 138, 11272–11281.
44. C. A. Montoya, C. F. Gómez, A. B. Paninho, A. V. Nunes, K. T. Mahmudov, V. Najdanovic-Visak, L. M. Martins, M. F. C. G. da Silva, A. J. Pombeiro and M. N. da Ponte, J. Catal., 2016, 335, 135–140.
45. A. B. Paninho, A. L. Ventura, L. C. Branco, A. J. Pombeiro, M. F. C. G. da Silva, M. N. da Ponte, K. T. Mahmudov and A. V. Nunes, J. Supercrit. Fluids, 2018, 132, 71–75.
46. G. Fiorani, W. Guo and A. W. Kleij, Green Chem., 2015, 17, 1375–1389.
47. H. Zhou, G.-X. Wang, W.-Z. Zhang and X.-B. Lu, ACS Catal., 2015, 5, 6773–6779.
48. Y. Toda, T. Sakamoto, Y. Komiyama, A. Kikuchi and H. Suga, ACS Catal., 2017, 7, 6150–6154.
49. Y. Toda, Y. Komiyama, A. Kikuchi and H. Suga, ACS Catal., 2016, 6, 6906–6910.
50. H. Sabet-Sarvestani, H. Eshghi and M. Izadyar, RSC Adv., 2017, 7, 1701–1710.
51. H. Sabet-Sarvestani, M. Izadyar and H. Eshghi, Energy, 2017, 134, 493–503.
52. H. Sabet-Sarvestani, M. Izadyar and H. Eshghi, J. CO2 Util., 2017, 21, 459–466.
53. H. Sabet-Sarvestani, M. Izadyar, H. Eshghi, N. Noroozi-Shad and M. Bakavoli, Fuel, 2018, 221, 491–500.
54. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
55. J. Kona and W. M. Fabian, J. Chem. Theory Comput., 2011, 7, 2610–2616.
56. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
57. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
58. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
59. M. North, R. Pasquale and C. Young, Green Chem., 2010, 12, 1514–1539.
60. G. S. Heverly-Coulson and R. J. Boyd, J. Phys. Chem. A, 2010, 114, 10706–10711.
61. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
62. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
63. C. A. Bayse and S. Antony, Main Group Chem., 2007, 6, 185–200.
64. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
65. S. Kozuch and S. Shaik, Acc. Chem. Res., 2010, 44, 101–110.
66. R. Kheirabadi, M. Izadyar and M. R. Housaindokht, J. Phys. Chem. A, 2017, 122, 364–374.
67. L. Falivene, S. M. Kozlov and L. Cavallo, ACS Catal., 2018, 8, 5637–5656.
68. C. T. Campbell, J. Catal., 2001, 204, 520–524.
69. C. Stegelmann, A. Andreasen and C. T. Campbell, J. Am. Chem. Soc., 2009, 131, 8077–8082.
70. M. J. Ajitha and C. H. Suresh, J. Org. Chem., 2012, 77, 1087–1094.
71. B. Galabov, S. Ilieva and H. F. Schaefer, J. Org. Chem., 2006, 71, 6382–6387.
72. P. Politzer and J. S. Murray, Theor. Chem. Acc., 2002, 108, 134–142.
73. N. Mohan and C. H. Suresh, J. Phys. Chem. A, 2014, 118, 1697–1705.
74. B. A. Anjali, F. B. Sayyed and C. H. Suresh, J. Phys. Chem. A, 2016, 120, 1112–1119.
75. L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343.
76. H. Sabet-Sarvestani, M. Izadyar, H. Eshghi and N. Noroozi-Shad, Energy, 2018, 145, 329–337.
77. V. Polo, J. Andres, S. Berski, L. R. Domingo and B. Silvi, J. Phys. Chem. A, 2008, 112, 7128–7136.
78. J. Andres, S. Berski, L. R. Domingo, V. Polo and B. Silvi, Curr. Org. Chem., 2011, 15, 3566–3575.
79. J. Andrés, S. Berski, L. R. Domingo and P. González-Navarrete, J. Comput. Chem., 2012, 33, 748–756.
80. B. Silvi, J. Mol. Struct., 2002, 614, 3–10.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary tables and Cartesian coordinates of the molecules. See DOI: 10.1039/c9cp05211a

---