 Open Access Article
Open Access ArticleHow size ratio and segregation affect the packing of binary granular mixtures†
Salvatore
Pillitteri
 *,
Eric
Opsomer
,
Geoffroy
Lumay
and
Nicolas
Vandewalle
*,
Eric
Opsomer
,
Geoffroy
Lumay
and
Nicolas
Vandewalle

Quartier Agora, allée du six Août 19, Liège, Belgium. E-mail: s.pillitteri@uliege.be; Tel: +32 4 366 3633
First published on 11th September 2020
Abstract
For reaching high packing fractions, grains of various sizes are often mixed together allowing the small grains to fill the voids created by the large ones. However, in most cases, granular segregation occurs leading to lower packing fractions. We performed a wide set of experiments with different binary granular systems, proving that two main parameters are respectively the volume fraction f of small beads and the grain size ratio α. In addition, we show how granular segregation affects the global packing fraction. We propose a model with a strong dependency on α that takes into account possible granular segregation. Our model is in good agreement with both earlier experimental and simulation data.
1 Introduction
Granular and powdered systems are ubiquitous in nature. Their peculiar behaviours are strongly linked to the packing fraction η, being the ratio between the true volume V and the apparent volume Va of a granular assembly. Indeed, voids left by the grains allow rearrangements in the structure such that η triggers both flowing and jamming behaviours.1–3 Therefore, increasing the packing fraction of a granular medium is of great interest in several sectors of applications such as construction, pharmaceutical industry and many other fields where powders are manipulated.4–9Granular materials are out of equilibrium systems.10 Consequently, if one pours granular material into a recipient, the measured packing fraction corresponds to a metastable state.11 Indeed, the initial configuration is often a Random Loose Packing (RLP) which corresponds to a mechanical stable assembly, far from minimizing the gravity potential. For monodisperse spherical particles under normal gravity conditions, the RLP is found around ηRLP ≈ 0.60.2,12,13 If one gently vibrates the granular medium, the packing fraction will increase because of the grain reorganizations. When η increases, the mobility of grains rapidly decreases and the system becomes jammed.14 A monodisperse sphere packing can reach at most ηRCP ≈ 0.64, being the Random Close Packing (RCP).15 One should note that this value is far below the packing fraction of an ordered monodisperse sphere packing 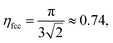 corresponding to a face centered cubic (fcc) lattice.15
corresponding to a face centered cubic (fcc) lattice.15
In granular materials, binary mixtures are systems made of particles with two different sizes. For the case of spherical particles, one can define the size ratio 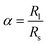 as control parameter,16Rl and Rs being respectively the radii of large and small particles. Binary mixtures of spheres with low size ratio 1 < α < 1.4 are commonly used by experimental and numerical scientists to avoid crystallization phenomena.17–19 However, for larger size ratios, these mixtures are known to reach higher packing fraction values than monodisperse systems. Both experimental and numerical studies have been performed on these systems16,20–25 and methods to predict the density of a bidisperse granular medium have been proposed.26–30 These approaches are based on a model proposed by Furnas et al.26 It considers two extreme mixing scenarios: the first (I) being dominated by large particles and the second (II) being dominated by small ones, as sketched in Fig. 1 for three different grain size ratios.
as control parameter,16Rl and Rs being respectively the radii of large and small particles. Binary mixtures of spheres with low size ratio 1 < α < 1.4 are commonly used by experimental and numerical scientists to avoid crystallization phenomena.17–19 However, for larger size ratios, these mixtures are known to reach higher packing fraction values than monodisperse systems. Both experimental and numerical studies have been performed on these systems16,20–25 and methods to predict the density of a bidisperse granular medium have been proposed.26–30 These approaches are based on a model proposed by Furnas et al.26 It considers two extreme mixing scenarios: the first (I) being dominated by large particles and the second (II) being dominated by small ones, as sketched in Fig. 1 for three different grain size ratios.
The latter model is only valid for mixtures with large difference in size between both granular species. For this reason, analytical models27–30 have been proposed to take into account the size ratio in binary mixtures. Stovall et al.27 introduced the concepts of the loosening and the wall effects as an explanation for the dependency of the packing fraction with the size ratio. Both effects are modelized by interaction functions which are added as correction terms to Furnas model. Yu et al.28 and de Larrard et al.31 proposed different interaction functions. Despite data agreement, these functions are experimentally adjusted and their physical meaning is not easily seen.32 Moreover, these models consider homogeneous mixtures while granular segregation often occurs in packing experiments.
Experimentally, granular mixtures are rarely homogeneous.33 Indeed, when there is a difference in size between particles, mechanical manipulations such as vibrations or flowing lead to segregation. Different effects such as the well known “Brazil Nuts effect”34 or percolation35,36 may be the cause. When the size ratio is large enough, small particles naturally percolate due to gravity. We often observed this phenomenon during our experiments.
One can see in Fig. 2 examples of segregated small beads due to percolation. When the size ratio is higher than 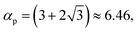 37 gravity systematically leads to percolation of small particles through an ordered porous medium made by large ones. Indeed, three kissing large particles define the minimum pore size of
37 gravity systematically leads to percolation of small particles through an ordered porous medium made by large ones. Indeed, three kissing large particles define the minimum pore size of 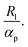 Any small bead with a radius
Any small bead with a radius 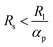 can then percolate. The segregation for the size ratio α ≈ 9 is consequently obvious. Moreover, percolation can happen even for lower size ratios because the random structure leads to larger pores than expected for a fcc lattice. For this reason, one can observe percolation for α ≈ 5 and α ≈ 3. During experiments, mechanical agitation of the granular pile helps the percolation of small grains. Moreover, the pouring procedure may lead to inhomogeneities in the horizontal direction since segregation also occurs during flow.38
can then percolate. The segregation for the size ratio α ≈ 9 is consequently obvious. Moreover, percolation can happen even for lower size ratios because the random structure leads to larger pores than expected for a fcc lattice. For this reason, one can observe percolation for α ≈ 5 and α ≈ 3. During experiments, mechanical agitation of the granular pile helps the percolation of small grains. Moreover, the pouring procedure may lead to inhomogeneities in the horizontal direction since segregation also occurs during flow.38
 | ||
| Fig. 2 Example of three mixtures, α ≈ 3, α ≈ 5 and α ≈ 9 with percolation after few taps. One observes the inhomogeneity of the mixtures. Glass containers are only used for this illustration. | ||
The objective of the present paper is to study binary mixtures and the impact of inhomogeneity on the packing fraction. We propose an original model which takes into account the size ratio and the inhomogeneity of the mixture. Our approach is based on physical arguments, corroborated by literature. We collected and analysed data from experimental and numerical works in order to test our model. Some experimental data come from our previous work S. Pillitteri et al.16 In this article, we will demonstrate that taking into account inhomogeneities allows to conciliate numerical and experimental results with a single model.
2 Experimental results
For collecting our data, we prepared several granular mixtures made of spherical glass beads with two different radii Rl and Rs, giving different size ratio α. For each mixture with a specific α, the relative composition of large and small beads can be tuned. The volume fraction of small beads is defined as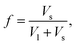 where Vl and Vs are respectively the true volumes of large and small beads. Please note that in our mixtures, a small polydispersity exists for each species. This means that α should be considered in a range giving a relative error of at most 12%.
where Vl and Vs are respectively the true volumes of large and small beads. Please note that in our mixtures, a small polydispersity exists for each species. This means that α should be considered in a range giving a relative error of at most 12%.
We performed measurements for various size ratios α and volume fractions f of small beads. The relative humidity of the laboratory was kept constant at RH = 35 ± 5%. Indeed, previous studies have shown that humidity affects the packing of granular media.39,40 Initially, the system is expected to be in a loose configuration and is gently vibrated to increase the packing fraction.16 This process is called compaction and is performed with GranuPack instrument from GranuTools.8 The dynamic of this phenomenon is well described by the logarithmic law41
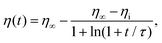 | (1) |
Typical experimental results for η∞ are plotted in Fig. 3 as a function of f and for various size ratios α. A complete data set for α ranging from 3 to 35 has been collected. Each point of η∞, indexed by the pair of parameters f and α, is averaged over 10 experiments. The error bar of each point corresponds to the standard deviation around the mean. The color code is used to distinguish different α values throughout this paper. The plot shows that for each size ratio, one can define a fraction fmax ∈ [0.2,0.4] for which the packing fraction is optimal. Increasing the size ratio enhances this optimal packing fraction ηmax = η∞(fmax).
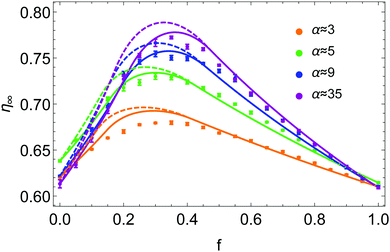 | ||
| Fig. 3 Asymptotic packing fraction η∞ as a function of the volume fraction of small beads f in the mixture for different size ratios α. Experimental data are represented by points with specific colors related to their size ratio. Each set of data is fitted by eqn (6), with a step distribution Ψl = D1(z,p*) and a gradient distribution Ψs = D2(z,f) respectively defined by eqn (7) and (8). The dashed curves are obtained with p* forced to 0 (zero free fitting parameter) while the plain ones are obtained with p* = 0.12 being a free fitting parameter. | ||
3 Model
Our model stems from Furnas' approach which considers both extreme cases (I) and (II) cited before. Furnas model assumes that the mixture is homogeneous. Consequently, for each case, a global apparent volume, respectively VI and VII, can be computed. The global apparent volume of the mixture Va is defined as the maximum between VI and VII and consequently depends on which phase is dominant. Then, the global packing fraction is obtained by the ratio between the total true volume (Vl + Vs) and Va.In our case, the packing fraction is however computed differently. Since the inhomogeneity of the mixture can affect the packing fraction,42–44 and consequently the global apparent volume, one has to compute the local apparent volume Vloca instead of Va for each case. Indeed, when the distributions of large and small particles are inhomogeneous, the dominant phase depends on the position in the granular pile. Under these conditions, Va = max{VI,VII} is no longer valid. One has to take into account Ψl(r) and Ψs(r), respectively the distribution functions of the large and small beads in the normalized unit volume V* of the granular pile. These functions follow the constraints
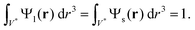 | (2) |
In the first case (I), when f → 0, the system is mainly made of large beads. The apparent volume only depends on the structure of the large beads when α → ∞. Indeed, the small beads just fill the remaining voids, as illustrated on the top of Fig. 1 for α = 5 and α = 9. On the contrary, if α → 1, the remaining voids are broadened by small particles as illustrated for α = 3. The local apparent volume VlocI is expected to be proportional to 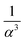 for an ordered cubic binary system. Indeed, any variation of the radius of the small particle will lead to a displacement in the three directions of space of the surrounding large beads, as illustrated in Fig. 1, in the case (I) with α = 3. However, when the size ratio is large enough, a small bead cannot be in contact with more than two large beads. Indeed, it has been numerically observed that the average number of contacts of a small bead with large ones is below 3 for random packings of binary mixtures,20,45 even when the size ratio α is low. Consequently, the displacement of large particles takes place only in one direction. This results in a decrease of VlocI in
for an ordered cubic binary system. Indeed, any variation of the radius of the small particle will lead to a displacement in the three directions of space of the surrounding large beads, as illustrated in Fig. 1, in the case (I) with α = 3. However, when the size ratio is large enough, a small bead cannot be in contact with more than two large beads. Indeed, it has been numerically observed that the average number of contacts of a small bead with large ones is below 3 for random packings of binary mixtures,20,45 even when the size ratio α is low. Consequently, the displacement of large particles takes place only in one direction. This results in a decrease of VlocI in 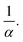 If one assumes that both species take a random packing arrangement, each weighted by its corresponding distribution function Ψl and Ψs, one can write the local apparent volume as
If one assumes that both species take a random packing arrangement, each weighted by its corresponding distribution function Ψl and Ψs, one can write the local apparent volume as
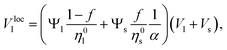 | (3) |
In the second case (II), when f → 1, the mixture is in a random packing configuration dominated by small beads. However, one has to add an effective volume Veff coming from the large ones. Indeed, if one places a large bead in this granular medium, the small spheres on its surface are locally at a lower packing fraction, as illustrated in Fig. 1. The effective volume Veff takes into account the volume of the added particles and this disturbing effect. In Furnas model, this effective volume is strictly equal to the real volume of the large particles. In the extreme case, when α → ∞, one assumes that the effective volume tends indeed to Vl. We propose to develop the effective volume as the contribution of the volume Vl and a shell with the thickness of a small sphere radius. As the small particles in contact with the large one do not fill completely its surrounding space, one should multiply this shell volume by the local packing fraction ϕ at the surface. Using first order approximation, one can reduce the volume of the shell to the first term in 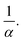 One has
One has
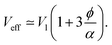 | (4) |
If one assumes that the maximum number of small spheres that can be randomly placed at the surface of a large one is equivalent to a parking problem,50 one can estimate ϕ. We simulated the random placement of small particles at the surface of a large sphere with various size ratios and systematically obtained 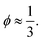 We compared the number of small beads at the surface to the mean number of contacts between large and small beads and found similar results in the literature.20,50–52 Accordingly, we propose to fix the local packing fraction with the value
We compared the number of small beads at the surface to the mean number of contacts between large and small beads and found similar results in the literature.20,50–52 Accordingly, we propose to fix the local packing fraction with the value 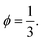 Finally, the local apparent volume for the case II can be written
Finally, the local apparent volume for the case II can be written
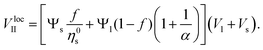 | (5) |
The local apparent volume Vloca is determined in the same way as for the Furnas model and is defined as the maximum between eqn (3) and (5). The global apparent volume is calculated by integration of Vloca over the unitary volume V*. Dividing the total true volume (Vl + Vs) by this global apparent volume, one has consequently for the global packing fraction
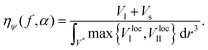 | (6) |
One should note that both regimes of the Furnas model are recovered by taking the limit α → ∞ in eqn (3) and (5) for homogeneous mixtures. With this model, the packing fraction ηψ(f) increases with α, in agreement with experiment. This increase is however limited. Indeed for the special case Ψl = Ψs = 1, one obtains the Furnas model when α → ∞. When the packing is not homogeneous with Ψl ≠ Ψs ≠ 1, the packing fraction is lower, as we will show later in this article.
4 Discussion
Experimental and numerical data can be fitted by eqn (6), after fixing η0l and η0s by the values obtained for monodisperse cases, respectively at f = 0 and f = 1. The simplest case that can be considered is the homogeneous mixture. The distribution functions can be defined as uniform distributions Ψl(r) = Ψs(r) = 1. We report our fit of eqn (6) on numerical data obtained from various simulations in Fig. 4(a). Since simulations consider generaly homogeneous packings, one can observe a good agreement between the model and the data from various numerical studies.20–23 The dependency with α is well reproduced. Furthermore, the higher the size ratio, the better the fit. When the size ratio is low, as for α = 3, one notes smooth behaviour of the data close to the optimum at fmax, quite different from the pointed shape predicted by the model. Indeed, this sharp peak at fmax appears only when the size ratio is large enough, as pointed out by Prasad et al.22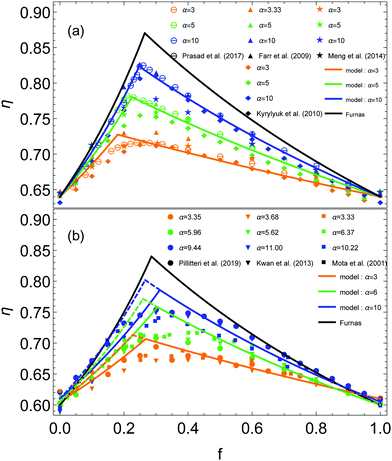 | ||
| Fig. 4 (a) Packing fractions η obtained in earlier simulations as a function of the volume fraction of small beads f in the mixture. The data are taken from previous works.20–23 The distribution functions Ψl = Ψs = 1 are uniform since the mixture is assumed to be homogeneous. (b) Packing fractions η experimentally obtained as a function of the volume fraction of small beads f in the mixture. The data are taken from previous works.16,24,25 The plain curves represent the model with Ψl = D1(z,p) and Ψs = 1, and the dashed ones the predictions for homogeneous mixtures. (a and b) Three different size ratios α are considered. The color code remains the same as Fig. 3. Each set of data is fitted by eqn (6), represented by a curve of the same color. The black curve is obtained with the Furnas' model. | ||
The numerical results differ from experiments. Indeed, one can compare the simulations data to our experimental results and some data taken from other experimental works,24,25 presented in Fig. 4(b). The smooth optimum is always observed even for large α. Moreover, the slope in the left part of the curve is lower than for the simulations. On the contrary, the right parts of the experimental curves seem to have behaviours similar to the simulations data. We report our fit of eqn (6) on experimental data in Fig. 4, represented by dashed curves. If one considers homogeneous mixtures, the model reproduces the dependency with α, in agreement with experimental data. However, it seems unable to fit the left part of the experimental data. The slope is overestimated for the left part while the right part remains in agreement with the data. One has to take into account the inhomogeneity of the mixture to explain this difference.
Since percolation is observed experimentally, one assumes as a first approximation the existence of a monodisperse phase for the small beads in any mixture. The rest of small particles is supposed homogeneously mixed with the large ones. We propose to keep the uniform distribution Ψs = 1, and to define Ψl as a step function along the vertical axis z, represented by the black plain curve in Fig. 5. We simplify the distribution to a one dimensional problem because the segregation occurs essentially in the direction of the height of the granular pile.
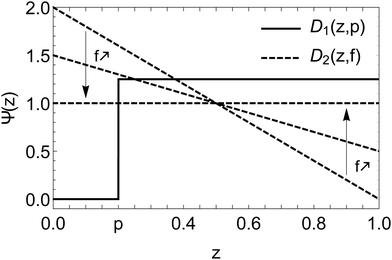 | ||
| Fig. 5 Distributions D1(z,p) and D2(z,f) as a function of the normalised height z of the granular pile. The functions are respectively defined by eqn (7) and (8). The slope of D2(z,f) decreases with f in order to reach an uniform distribution in the limit f → 1. | ||
One has a step distribution Ψl = D1(z,p) with
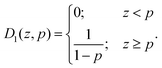 | (7) |
The parameter p is called the segregation parameter. When Ψl = D1(z,p) and Ψs = 1, it directly corresponds to the relative proportion of small particles in a monodisperse phase at the bottom of the packing (z < p), while large particles are still mixed with the rest of small particles for z > p. Indeed, integrating Ψs = 1 between 0 and p gives the portion of monodisperse small particles since the distribution of large ones is null in this range. On average, we obtained p ≈ 0.20 ± 0.05 as best adjustment parameter of experimental data of Fig. 4.
The results of such modelling are shown in Fig. 4(b). The plain curves represent the model with Ψl = D1(z,p) defined by eqn (7) and p = 0.20 fixed. One can observe the difference compared to a homogeneous system, when p = 0, represented by the dashed curves. The existence of a monodisperse phase leads to a higher global apparent volume Va. This results in a lower packing fraction ηψ (ESI†). Consequently, the slope of the plain curves is lower than for the dashed ones, in the left part of the model. This effect can explain the difference between numerical and experimental data. Indeed, there is systematically inhomogeneities in mixtures for experiments while simulations are expected to generate homogeneous mixtures.
Unexpectedly, the monodisperse phase of small beads has no influence on the right part of the curves. Actually, the model predicts that the latter would be affected by the presence of a monodisperse phase of large particles. Indeed, with a small amount of unmixed large beads, one can define Ψs = D1(1 − z,p) and Ψl = 1. With these distributions, p corresponds to the proportion of large particles segregated in a monodisperse phase. In this case, the slope of the right part will decrease while the left part will be unchanged. This can happen, for example, when the Brazil Nuts effect occurs. However, during our experiments, the compaction procedure was not able to create convection or sufficient shakes in the granular pile to generate this phenomenon.
Nevertheless, it remains possible to control the fraction of large particles in a monodisperse phase. Indeed, one can divide the large particles into two parts, the first mixed with small particles and the second kept unmixed. After pouring the mixture, one can place on top of the granular pile the rest of large particles. In this way, one obtain a monodisperse phase of large beads. In addition, the proportion of segregated large particles is known. We did so for different controlled proportions of segregated large particles p. The experimental results are presented in Fig. 6, in black, for the size ratio α ≈ 9. They are compared to the model, using the corresponding parameter p with the distributions Ψl = 1 and Ψs = D1(1 − z,p). One observes for experimental data the decrease of the right part of the curve when the proportion of segregated large particles increases while the left part remains unchanged as predicted by the model.
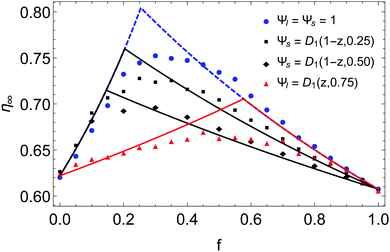 | ||
| Fig. 6 Comparison between the model and experimental data for mixtures with different proportions of segregated large (in black) or small (in red) particles for α ≈ 9. It this particular case, p is known and corresponds to the proportion of segregated particles in the monodisperse phase. The blue data are the mixtures with no control on the segregation, as presented in Fig. 3 and 4. | ||
We performed the same kind of experiment for small particles by pouring an unmixed proportion p at the bottom of the cell before pouring the mixture with the rest of small beads. Since percolation can occur in the mixture itself, a large proportion of unmixed small particles p = 0.75 was chosen in order to control as much as possible the segregated part. Indeed, even if a small quantity of small beads percolates in the mixture, this supplement can be negligible compared to the part already unmixed. One can see the results in red in Fig. 6. The data are also compared to the model with Ψl = D1(z,0.75) and Ψs = 1. One effectively observes in this case that the slope of the left part is greatly decreased while the right one remains unchanged.
The agreement between the model and experimental data seems good at first approximation. However, one should point out the large deviations close to fmax. The experimental optimum value ηmax is lower than expected. Moreover the smooth shape at the optimum is still absent.
Let us investigate more deeply the model. We observed that small beads tend to percolate for low values of f and are preferentially distributed at the bottom of the granular pile. On the contrary, for large values of f, they represent the dominant phase and are homogeneously distributed. One assumes that under gravity the small beads are distributed according to a gradient along z when f → 0. When f → 1, Ψs must tend to a uniform distribution. We propose to define Ψs = D2(z,f) with
| D2(z,f) = f + 2(1 − z)(1 − f). | (8) |
This empirical behavior is represented in Fig. 5 by dashed lines. The distribution Ψl = D1(z,p*), as defined by the eqn (7), is used. We obtained p* ≈ 0.12 ± 0.02 as the best adjustment of data in Fig. 3. One notes that p* < p. This can be understood as follows: if one integrates Ψs = D2(z,0) between 0 and 0.12, one obtains a proportion of monodisperse small particles about 0.23, close to the previous value p = 0.20 obtained in Fig. 4(b). One can understand that for a same proportion of unmixed small particles, p* ≤ p when Ψs is a decreasing law. Unfortunately, p* does not correspond directly to the proportion of segregated small particles, even if it is strongly related. The results of such modelling are reported in Fig. 3 (ESI†). The plain curves are obtained with p* = 0.12. One can see the good agreement with the experimental results. One notes that the smooth shape can be obtained close to the optimum at fmax when the inhomogeneous distribution Ψs = D2(z,f) is used in eqn (6). Indeed, a step function just affects the slopes of the right and left parts, as it has been demonstrated in Fig. 4 and 6, since the distribution is null below p and uniform beyond. On the contrary, the presence of a non uniform distribution, such as a gradient, generates a smooth shape at the optimum.
One figures out that the smooth shape at the optimum of experimental data may be due to the non uniform distribution of small particles in the mixture. Indeed, because of the granular segregation coming from percolation of small particles, Brazil Nuts effect or other phenomena, mixtures made of different particles sizes are rarely homogeneous. Moreover, it is probable that segregation leads to complex distributions of particles, like gradients, rather than a simple separation into monodisperse phases. Therefore, one should take into account the distributions of small and large particles in the granular medium to obtain the smooth curve at the optimum. Moreover, one notes that for numerical data in Fig. 4(a), where the packing is generated homogeneously, the smooth peak is absent when the size ratio is large enough.
In Fig. 3, the dashed curves are obtained with the segregation parameter p* = 0. In this case, no small beads is considered in a monodisperse phase. One notes that better fits are obtained considering a small amount of unmixed small particles, with p* = 0.12.
5 Conclusion
In summary, we have experimentally and theoretically studied the packing fraction η in the case of binary mixtures. We proposed a model that takes into account the size ratio α between two kinds of particles and the distributions Ψl and Ψs of both species in the granular pile. This model captures the behavior of experimental and numerical data, with the segregation parameter p as a single free adjustment parameter.However, we used p as a free parameter because the distributions Ψl and Ψs are unknown. If one imagines knowing these distributions, no adjustment parameter would be needed. Indeed, we intentionally segregated different proportions of large or small particles in the granular pile in order to fix Ψl and Ψs. We observed good agreement with experimental data using directly these distributions, without any adjustment parameter. It remains however difficult to control everything in the mixture since natural segregation often occurs in granular media during manipulation.
Future numerical study should investigate more deeply the dependence of the distributions Ψl and Ψs on the packing fraction η. Indeed, in this case, more complex distributions could be fixed and no adjustment parameter will be needed. One could compare the numerical results with the model, knowing exactly the distributions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is conducted in the framework of the “PowderReg” project, funded by the European program Interreg VA GR within the priority axis 4 “Strengthen the competitiveness and the attractiveness of the Grande Région/Groβregion”. We thank M. Marck for helping us to realize all the measurements.Notes and references
- A. Ikeda, L. Berthier and P. Sollich, Phys. Rev. Lett., 2012, 109, 018301 CrossRef.
- C. Song, P. Wang and H. A. Makse, Nature, 2008, 453, 629–632 CrossRef.
- T. K. Haxton, M. Schmiedeberg and A. J. Liu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031503 CrossRef.
- L. Li and A. Kwan, Powder Technol., 2014, 253, 514–521 CrossRef CAS.
- M. Jones, L. Zheng and M. Newlands, Mater. Struct., 2002, 35, 301–309 Search PubMed.
- P. Stroeven, H. He, Z. Guo and M. Stroeven, Mater. Charact., 2009, 60, 1088–1092 CrossRef.
- G. Fu and W. Dekelbab, Powder Technol., 2003, 133, 147–155 CrossRef.
- G. Lumay, F. Boschini, K. Traina, S. Bontempi, J.-C. Remy, R. Cloots and N. Vandewalle, Powder Technol., 2012, 224, 19–27 CrossRef.
- F. Boschini, V. Delaval, K. Traina, N. Vandewalle and G. Lumay, Int. J. Pharm., 2015, 494, 312–320 CrossRef.
- P. Richard, M. Nicodemi, R. Delannay, P. Ribiere and D. Bideau, Nat. Mater., 2005, 4, 121–128 CrossRef.
- M. Nicolas, P. Duru and O. Pouliquen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 309–314 CrossRef.
- J. G. Berryman, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 27, 1053 CrossRef.
- G. Y. Onoda and E. G. Liniger, Phys. Rev. Lett., 1990, 64, 2727 CrossRef.
- G. Lumay and N. Vandewalle, Phys. Rev. Lett., 2005, 95, 028002 CrossRef.
- D. Weaire and T. Aste, The pursuit of perfect packing, CRC Press, 2008 Search PubMed.
- S. Pillitteri, G. Lumay, E. Opsomer and N. Vandewalle, Sci. Rep., 2019, 9, 1–7 CrossRef.
- P. Pusey, E. Zaccarelli, C. Valeriani, E. Sanz, W. C. Poon and M. E. Cates, Philos. Trans. R. Soc., A, 2009, 367, 4993–5011 CrossRef.
- S. Williams, I. Snook and W. Van Megen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021506 CrossRef.
- S. R. Williams, C. P. Royall and G. Bryant, Phys. Rev. Lett., 2008, 100, 225502 CrossRef.
- L. Meng, P. Lu and S. Li, Particuology, 2014, 16, 155–166 CrossRef.
- R. S. Farr and R. D. Groot, J. Chem. Phys., 2009, 131, 244104 CrossRef.
- I. Prasad, C. Santangelo and G. Grason, Phys. Rev. E, 2017, 96, 052905 CrossRef.
- A. V. Kyrylyuk, A. Wouterse and A. P. Philipse, Trends in Colloid and Interface Science XXIII, Springer, 2010, pp. 29–33 Search PubMed.
- A. K. H. Kwan, K. W. Chan and V. Wong, Powder Technol., 2013, 237, 172–179 CrossRef.
- M. Mota, J. A. Teixeira, W. R. Bowen and A. Yelshin, Trans. Filtr. Soc., 2001, 1, 101–106 CAS.
- C. Furnas, Ind. Eng. Chem., 1931, 23, 1052–1058 CrossRef CAS.
- T. Stovall, F. De Larrard and M. Buil, Powder Technol., 1986, 48, 1–12 CrossRef CAS.
- A.-B. Yu, R. Zou and N. Standish, Ind. Eng. Chem. Res., 1996, 35, 3730–3741 CrossRef CAS.
- G. Roquier, Powder Technol., 2016, 302, 247–253 CrossRef CAS.
- K. Chan and A. Kwan, Particuology, 2014, 16, 108–115 CrossRef.
- F. De Larrard, Concrete mixture proportioning: a scientific approach, CRC Press, 1999 Search PubMed.
- C. S. Chang, J.-Y. Wang and L. Ge, Eng. Geol., 2015, 196, 293–304 CrossRef.
- B. Andreotti, Y. Forterre and O. Pouliquen, Les milieux granulaires: Entre fluide et solide, EDP sciences, 2012 Search PubMed.
- A. Rosato, K. J. Strandburg, F. Prinz and R. H. Swendsen, Phys. Rev. Lett., 1987, 58, 1038 CrossRef.
- A. K. Jha and V. M. Puri, Powder Technol., 2009, 195, 73–82 CrossRef CAS.
- S. Savage and C. Lun, J. Fluid Mech., 1988, 189, 311–335 CrossRef CAS.
- F. Soddy, Nature, 1936, 137, 1021 CrossRef.
- B. Marks, P. Rognon and I. Einav, J. Fluid Mech., 2012, 690, 499–511 CrossRef.
- J. Fiscina, G. Lumay, F. Ludewig and N. Vandewalle, Phys. Rev. Lett., 2010, 105, 048001 CrossRef CAS.
- N. Vandewalle, G. Lumay, F. Ludewig and J. E. Fiscina, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 031309 CrossRef CAS.
- J. B. Knight, C. G. Fandrich, C. N. Lau, H. M. Jaeger and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 3957–3963 CrossRef CAS.
- Z.-R. Liu, W.-M. Ye, Z. Zhang, Q. Wang, Y.-G. Chen and Y.-J. Cui, Powder Technol., 2019, 351, 92–101 CrossRef CAS.
- T. J. Fiske, S. B. Railkar and D. M. Kalyon, Powder Technol., 1994, 81, 57–64 CrossRef CAS.
- L. Woollacott, Miner. Eng., 2019, 131, 98–110 CrossRef CAS.
- N. B. Schade, M. C. Holmes-Cerfon, E. R. Chen, D. Aronzon, J. W. Collins, J. A. Fan, F. Capasso and V. N. Manoharan, Phys. Rev. Lett., 2013, 110, 148303 CrossRef.
- A. Mughal, H. Chan, D. Weaire and S. Hutzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051305 CrossRef CAS.
- G. Scott and D. Kilgour, J. Phys. D: Appl. Phys., 1969, 2, 863 CrossRef.
- N. Vandewalle, G. Lumay, O. Gerasimov and F. Ludewig, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 22, 241–248 CrossRef CAS.
- F. Ludewig, S. Dorbolo and N. Vandewalle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051304 CrossRef CAS.
- M. L. Mansfield, L. Rakesh and D. A. Tomalia, J. Chem. Phys., 1996, 105, 3245–3249 CrossRef CAS.
- D. W. Cooper, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 522 CrossRef.
- D. W. Cooper, J. Colloid Interface Sci., 1987, 119, 442–450 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: “AnimFig4bAnd5.mov”, “AnimFig3And5.mov”. See DOI: 10.1039/d0sm00939c |
| This journal is © The Royal Society of Chemistry 2020 |

