Open Access Article
Open Access ArticleStudy of the magnetic interface and its effect in Fe/NiFe bilayers of alternating order†
Sagarika
Nayak
a,
Sudhansu Sekhar
Das
 a,
Braj Bhusan
Singh
a,
Timothy R.
Charlton
a,
Braj Bhusan
Singh
a,
Timothy R.
Charlton
 b,
Christy J.
Kinane
c and
Subhankar
Bedanta
b,
Christy J.
Kinane
c and
Subhankar
Bedanta
 *a
*a
aLaboratory for Nanomagnetism and Magnetic Materials (LNMM), School of Physical Sciences, National Institute of Science Education and Research (NISER), HBNI, P.O. Bhimpur Padanpur, Via-Jatni, 752050, India. E-mail: sbedanta@niser.ac.in
bOak Ridge National Laboratory, 1 Bethel Valley Rd, Oak Ridge, TN 37830, USA
cISIS, Harwell Science and Innovation Campus, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Didcot, Oxon OX11 0QX, UK
First published on 15th September 2020
Abstract
We present a comprehensive study on the magnetization reversal in the Fe/NiFe bilayer system by alternating the order of the magnetic layers. All the samples show growth-induced uniaxial magnetic anisotropy due to the oblique angle deposition technique. Strong interfacial exchange coupling between the Fe and NiFe layers leads to single-phase hysteresis loops in the bilayer system. The strength of coupling being dependent on the interface changes upon alternating the order of magnetic layers. The magnetic parameters such as coercivity HC, and anisotropy field HK become almost doubled when a NiFe layer is grown over the Fe layers. This enhancement in the magnetic parameters is primarily dependent on the increase of the thickness and magnetic moment of the Fe–NiFe interfacial layer as revealed from the polarized neutron reflectivity (PNR) data of the bilayer samples. The difference in the thickness and magnetization of the Fe–NiFe interfacial layer indicates the modification of the microstructure by alternating the order of the magnetic layers of the bilayers. The interfacial magnetic moment increased by almost 18% when the NiFe layer was grown over the Fe layer. In spite of the different values of anisotropy fields and modified interfacial exchange coupling, the Gilbert damping constant values of the ferromagnetic bilayers remain similar to the single NiFe layer.
1 Introduction
In exchange-coupled soft/hard bilayers, one can find a high energy product (BH)max value as the soft magnetic layer provides high saturation magnetization MS and the hard one provides intermediate coercivity HC.1 This soft–hard combination of the magnetic bilayers provides an excellent research opportunity not just for their potential application in the field of permanent magnets1 but also for the sake of fundamental understanding of various magnetization reversal processes. A hard magnetic layer gives a large HC due to its high magnetic anisotropy which is not desired in the application of the write head. Further, the switching field of the hard layer can be reduced by fabricating soft/hard magnetic bilayers which fulfills the requirement of write-head and simultaneously provides excellent temperature stability.2,3 The interface plays a very important role in tuning the HC of the bilayers by modifying the interfacial exchange coupling. In literature, several techniques have been employed for modifications of the interfacial layer. Different deposition techniques and subsequent post-deposition annealing at different temperatures have been widely employed for modification of the interface.2–4 Varying the thickness of the soft layer and using the materials of different crystallographic structures have also been considered to study the role of interfacial exchange coupling in a soft/hard bilayer system.1,2,5 The interfacial exchange coupling between the hard and soft layers can be enhanced by interdiffusion.6 Although there are several reports on various techniques for modification of the interface, there is still a continuous focus to understand the interface properties.7,8In order to account the role of interdiffusion on the magnetic properties, several experiments and simulations have been performed. Conversion electron Mössbauer spectroscopy has been used to find the presence of interdiffusion in hard (FePt)/soft (Fe or Co/Fe) bilayers.9 The presence of a graded interface has been observed in SmCo/Fe system from synchrotron X-ray scattering and electron microscopy elemental mapping measurements.10 Transmission electron microscopy and magnetic measurements show an enhanced epitaxy in the postannealed Co/CoPt system.11 Depth and element resolved X-ray resonant magnetic scattering (XRMS) measurements on SmCo/Fe bilayer show the presence of diffused Co-atoms from Sm–Co layer in Fe magnetic layer.12 Despite several experimental techniques for studying the magnetic properties of the individual layers, a quantitative knowledge about the interface of a layered system always remains challenging due to the very complex nature of the interface.13 In this context, polarized neutron reflectivity (PNR) is a very promising tool for a quantitative structural and magnetic information about the interface.
In addition to the above study, materials with lower Gilbert damping constant α are being studied extensively for their application in spin-transfer torque-based oscillators,14 and also in spintronics devices.15 Intrinsic Gilbert damping in materials has its origin on the spin–orbit coupling.16 Extrinsic contributions can enhance this damping. Several deposition methodologies such as different oblique angle of deposition,17 deposition pressure18etc. have been employed for tuning of the damping constant. It is desired to fabricate hard/soft magnetic bilayers where anisotropy gets enhanced keeping the damping value of the same order as that of the reference soft layer.
In the present paper, we report tuning of the interfacial exchange coupling by alternating the order of magnetic layers in the hard/soft Fe/NiFe bilayers. We show that by alternating the order of layers the interface changes which results in tuning of the magnetic properties of the bilayers. In order to quantify the interface thickness and moment, we have performed polarized neutron reflectometry on the bilayer samples. We also made a comparative study on the damping constants of the samples through FMR analysis.
2 Experimental details
All the samples are deposited by combination of dc magnetron sputtering and e-beam deposition in a high vacuum chamber on naturally oxidized Si (100) substrate. The base pressure was ∼6 × 10−8 mbar. Prior to the deposition, the substrates were annealed for a period of 2 h at 150 °C. The samples were prepared on to the Si-substrates kept at 150 °C at an Ar pressure of ∼5 × 10−3 mbar. A capping layer of Au (3 nm) was further deposited by e-beam evaporation to protect the samples from oxidation. The rate of deposition of Fe, NiFe and Au were kept at 0.22, 0.17 and 0.1 Å s−1, respectively. Table 1 shows the list of sample nomenclature, and structure.| Sample name | Sample structure |
|---|---|
| S1 | Si (100)/NiFe (10 nm)/Au (3 nm) |
| S2 | Si (100)/Fe (5 nm)/Au (3 nm) |
| S3 | Si (100)/Fe (5 nm)/NiFe (10 nm)/Au (3 nm) |
| S4 | Si (100)/NiFe (10 nm)/Fe (5 nm)/Au (3 nm) |
We performed X-ray reflectivity (XRR) measurements to evaluate the thickness, density and roughness of each individual layers by using X-ray diffractometer from Rigaku with CuKα radiation (λ = 0.154 nm). We have performed PNR measurements at room temperature at POLREF neutron reflectometer, at Rutherford Appleton Laboratory, UK. In the PNR measurements, magnetic field was applied along the easy axis (EA) and experiments were performed at saturation and near to coercive field of the bilayer samples. POLREF is a white beam instrument and we have used a pulse of length 2–15 Å's with several varying angles. We plotted the experimental data of reflectivity vs. perpendicular scattering vector QZ = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ where QZ is the component of momentum transfer perpendicular to the sample surface, thus, giving sample's layer-by-layer information.19,20 We always applied positive saturation field and then reverse the field to the measurement fields. The guiding field was −1 mT. Neutron reflectivity can be spin flipped or non-spin flipped. We measured two non-spin flipped scattering cross sections namely R++ and R−−.19,20 In R++, the first + sign is for the incident neutron with up-spin polarization and the second + sign is for the reflected neutron with up-spin polarization. Similarly, we can explain R−− (down–down). The XRR and PNR data were fitted using GenX software.21 We have performed longitudinal magneto-optic Kerr effect based microscopy to simultaneously measure hysteresis loops and image the magnetic domains. Magnetic dynamic properties were studied using ferromagnetic resonance (FMR) setup manufactured by NanoOsc.
θ/λ where QZ is the component of momentum transfer perpendicular to the sample surface, thus, giving sample's layer-by-layer information.19,20 We always applied positive saturation field and then reverse the field to the measurement fields. The guiding field was −1 mT. Neutron reflectivity can be spin flipped or non-spin flipped. We measured two non-spin flipped scattering cross sections namely R++ and R−−.19,20 In R++, the first + sign is for the incident neutron with up-spin polarization and the second + sign is for the reflected neutron with up-spin polarization. Similarly, we can explain R−− (down–down). The XRR and PNR data were fitted using GenX software.21 We have performed longitudinal magneto-optic Kerr effect based microscopy to simultaneously measure hysteresis loops and image the magnetic domains. Magnetic dynamic properties were studied using ferromagnetic resonance (FMR) setup manufactured by NanoOsc.
3 Results and discussion
3.1 PNR analysis
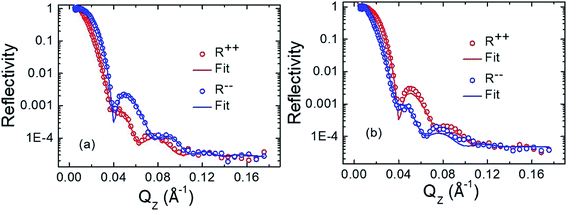
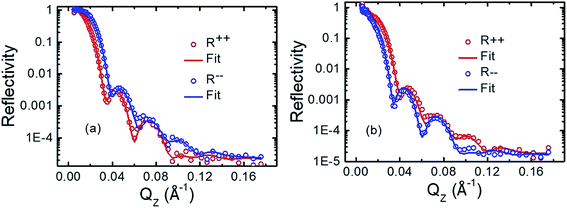
We have evaluated the quantitative structural information such as density, roughness and thickness of the samples from X-ray reflectivity (XRR) measurement (data are not shown). The layer thickness and roughness obtained from XRR and PNR measurements are similar for the bilayer samples.In order to get quantitative information from the layers and interfaces in the sample stack, we have performed polarized neutron reflectivity (PNR) measurement on the samples. PNR has been proven to be an ideal technique for providing layer-by-layer magnetization profile in a multilayer stack. Fig. 2(a) and (b) show the PNR data along with the fits for sample S3 measured at the saturation field of −50 mT and near to coercivity of −4 mT, respectively. Similarly, Fig. 3(a) and (b) show the PNR data along with the fits for sample S4 measured at saturation field of −50 mT and near to coercivity of −1.2 mT, respectively. We have fitted the PNR data by considering different interface models to find the best figure of merit (FOM). Considering all other interface models other than the three interface model, we found less value of FOM and the fitting is not good. We found that best FOM is achieved by considering a three interface model in samples S3 and S4. The interfaces are named as NiFe–Au, Fe–NiFe and SiO2–Fe for sample S3. Similarly the interfaces are named as Fe–Au, NiFe–Fe and SiO2–NiFe for sample S4. The interfaces taken to fit the neutron reflectivity data are shown in Fig. 1. FOMs of 4.60 × 10−2 and 5.04 × 10−2 are found in samples S3 and S4. Here, we have used LOG type of FOM. Using this type of FOM, we fitted the data more easily and robustly. LOG type of FOM takes into account the average of the difference between the logarithms of the data and the simulation. Structural and magnetic parameters, obtained from PNR fit, are shown in Tables 2 and 3 for samples S3 and S4, respectively. The magnetic moment of Fe and NiFe obtained from the PNR data of the sample S3 are 1.57 μB per atom and 0.7 μB per atom, respectively. The observed deviation in the magnetic moment of Fe and NiFe from their bulk value is due to the transfer of magnetic moment to the interface caused by interdiffusion. Similarly, the Fe–NiFe interface of sample S3 has a magnetic moment of 0.90 μB per atom which is intermediate between Fe and NiFe layers, and has a thickness of 2.3 nm. The SiO2–Fe interface has lesser magnetic moment of 1.00 μB per atom than Fe itself due to interdiffusion in sample S3.22 Interface roughness of the order of 1 nm might also be a reason for lesser magnetic moment at Fe–SiO2 interface.22 In contrast to the SiO2–Fe interface, the NiFe–Au interface in the sample S3 has a relatively smaller values of magnetic moment (0.10 μB per atom) and thickness (2.99 nm), indicating high amount of interdiffusion. Thus, a dead layer is formed at the NiFe–Au interface of sample S3. Our XRR data also suggests different roughness values of Fe and NiFe which are in direct contact with SiO2 and Au layers, respectively. Thus, we can conclude that interface roughness might be a reason for the different values of magnetic moment at SiO2–Fe and NiFe–Au interfaces than the parent layers in sample S3. Interdiffusion and/or alloying at the interfaces are the result of high temperature (150 °C) deposition of the studied films. The formation of a magnetic dead layer is also reported in the case of Fe/Ge system when Fe is grown on Ge at 150 °C.22 In contrast to the sample S3, the magnetic moment of the Fe layer, NiFe layer and the NiFe–Fe interfacial layer in the sample S4, are 1.26 μB per atom, 0.75 μB per atom, and 0.76 μB per atom, respectively. This indicates that the sample S3 has relatively higher magnetic moment values of its constituent layers Fe, NiFe and Fe–NiFe interface as compared to that of the S4. This is further confirmed from the SQUID data of the samples where the S3 has a higher saturation magnetization value (762 emu cc−1) in comparison to that of S4 (636 emu cc−1). We observed that all magnetic layers including SiO2–Fe interface are reversed completely at −4 mT of magnetic field in sample S3. 88% of Fe–NiFe interface magnetic moments are reversed from positive saturation state at −4 mT field in sample S3. Further, 92% of magnetic moments of Fe have reversed their direction near to coercive field (−1.2 mT) from positive saturation state in sample S4. Again, 38% of the magnetic moment at the Fe–Au interface has reversed direction in sample S4 whereas all other layers has reversed completely. Further, the thicknesses of all the interdiffused interface layers of sample S3 are higher than that of sample S4. Thus, larger interdiffusion might be a reason for the difference in magnetic properties of samples S3 and S4. We found from Tables 2 and 3 that the roughness of Fe in sample S3 is higher than sample S4 whereas the magnetic moment of Fe is higher in sample S3. Similarly, Fe–NiFe interface of sample S3 has higher roughness and magnetic moment than sample S4. The thickness of NiFe magnetic layer is higher in sample S4, and hence, higher roughness in comparison to sample S3.
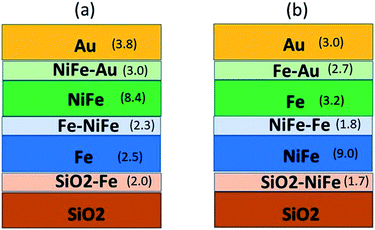 | ||
| Fig. 1 Schematic of all the interfaces and thin film layers in samples (a) S3 and (b) S4 with the estimated thicknesses in nm obtained from PNR fits are given in the bracket. | ||
| Layer description | Thickness (nm) | Roughness (nm) | Magnetic moment (μB per atom) at −50 mT | Magnetic moment (μB per atom) at −4 mT |
|---|---|---|---|---|
| Au | 3.79 | 1.99 | — | — |
| NiFe–Au | 2.99 | 0.94 | −0.10 | −0.003 |
| NiFe | 8.39 | 1.09 | −0.79 | 0.78 |
| Fe–NiFe | 2.31 | 1.20 | −0.90 | 0.8 |
| Fe | 2.48 | 1.56 | −1.57 | 1.57 |
| SiO2–Fe | 1.99 | 0.99 | −1.00 | 0.99 |
| Layer description | Thickness (nm) | Roughness (nm) | Magnetic moment (μB per atom) at −50 mT | Magnetic moment (μB per atom) at −1.2 mT |
|---|---|---|---|---|
| Au | 3.00 | 1.37 | — | — |
| Fe–Au | 2.66 | 1.19 | −0.52 | 0.20 |
| Fe | 3.24 | 0.85 | −1.26 | 1.17 |
| NiFe–Fe | 1.79 | 1.10 | −0.76 | 0.76 |
| NiFe | 8.99 | 1.29 | −0.75 | 0.75 |
| SiO2–NiFe | 1.66 | 0.9 | −0.75 | 0.75 |
The high roughness observed here is probably due to the growth conditions which we have observed for other thin films grown in the same sample.19 The roughness values extracted from the PNR analysis are comparable to the XRR data analysis. Unfortunately, AFM is not very useful in this case as it is a surface sensitive technique and our samples have a 3 nm thick Au capping layer.
From the PNR data analysis, we found the thickness of interface between Fe–NiFe (S3) and NiFe–Fe (S4) are 2.31 and 1.79 nm, respectively. The magnetic moments evaluated from the PNR fit at saturation for the interfaces Fe–NiFe (S3) and NiFe–Fe (S4) are 0.90 and 0.76 μB per atom, respectively. It is also observed that a dead layer is created at the NiFe–Au interface in sample S3 whereas no dead layer is formed in the Fe–Au interface in sample S4. These observations indicate that the order of Fe and NiFe layers has noticeable effect on the HC and HK. Further, the presence of high exchange coupling may be a possible reason for the higher value of coercivity and anisotropy field HK in sample S3 than S4 (see Table 4).
| Sample name | H C (EA) (mT) | H C (HA) (mT) | H K (mT) |
|---|---|---|---|
| S1 | 0.80 | 0.38 | 4.28 |
| S2 | 0.74 | 0.32 | 2.44 |
| S3 | 5.10 | 1.47 | 7.10 |
| S4 | 1.45 | 0.79 | 4.00 |
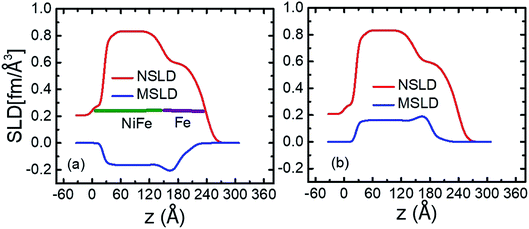
The nuclear scattering length density (NSLD) is found to be of 0.2 fm Å−3 near to SiO2–Fe interface whereas zero NSLD is found above NiFe–Au interface in sample S3. However, we found zero magnetic scattering length density (MSLD) near to SiO2–Fe and NiFe–Au interfaces of sample S3. Similar trends of NSLD and MSLD is found near to the interfaces SiO2–NiFe and Fe–Au. Also, we found the similar trend of the NSLD and MSLD profiles near to saturation and HC field values for the samples S3 and S4. Comparing the SLD profiles of samples S3 and S4, we found a sharp drop in NSLD for Fe magnetic layer of sample S4 whereas SLD is almost constant for Fe and NiFe layers of sample S3. Also, we found the change in sign of the MSLD's for the samples S3 and S4 near to the coercive field HC and this is due to magnetic field history. We can not say that depolarisation is responsible for the sign change of MSLD because the PNR measurement fields (shown in the Fig. 6(c) and (d) with green coloured square symbols) and guide field are along the same direction.
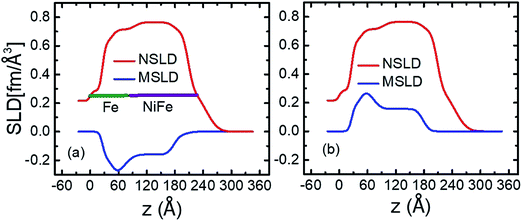 | ||
| Fig. 4 Nuclear and magnetic scattering length densities (NSLD and MSLD) vs. layer thickness (z) of the sample S3 at saturation field of −50 mT (a) and near to HC at −4 mT (b). | ||
We can calculate the MSLD from the MS obtained from SQUID using the relation MSLD = C.MS, where C = 2.853 × 10−9 (Å−2) (cm3 emu−1). We found MSLD of 0.22 and 0.18 fm Å−3 for the samples S3 and S4. These MSLD values obtained from SQUID match well with the values found from PNR (see Fig. 4 and 5).
 | ||
| Fig. 5 Nuclear and magnetic scattering length densities (NSLD and MSLD) vs. layer thickness (z) of the sample S4 at saturation field of −50 mT (a) and near to HC at −1.2 mT (b). | ||
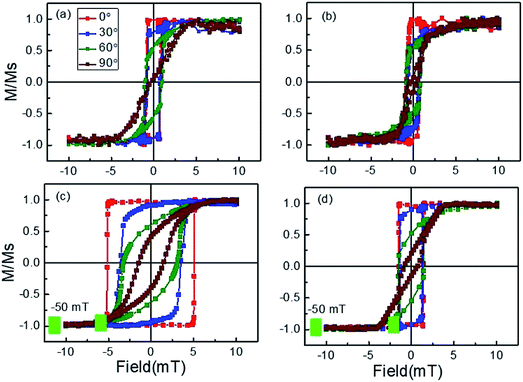 | ||
| Fig. 6 (a)–(d) Hysteresis loops measured by LMOKE at room temperature along ϕ = 0°, 30°, 60°, and 90° for samples S1–S4. | ||
Every material possess nuclear and magnetic potentials with respect to the neutrons. If the magnetic moment of the neutron is parallel or antiparallel with the magnetic moment of the sample, the refractive index can be written as;
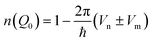 | (1) |
3.2 Kerr microscopy and magnetometry analysis
Hysteresis loops were measured using longitudinal magneto optic Kerr effect (LMOKE) based magnetometry at room temperature along ϕ = 0° (EA), 30°, 60°, 90° wrt EA for all the samples, which are shown in Fig. 6. We first saturated the sample with a field of 10 mT. Then we have reversed the field towards negative saturation and measured the hysteresis loop. Simultaneously at each field point we have recorded the domain images. We found that no domains present at H = 0 i.e. remanent magnetization state. However during the reversal we have observed domains nucleating and domain wall propagation at fields close to the coercive value. Also, it should be noted that the linearly polarized light and the external magnetic field H were also aligned to the direction with ϕ angle.We observed square-shaped loops along EA and s-shaped loops along HA for all the samples. This indicates, magnetization reversal is occurring via domain wall motion along EA and coherent rotation along HA. From the hysteresis loops, it is also concluded that the samples exhibit uniaxial magnetic anisotropy due to oblique angle of deposition. It is reported in the literature that anisotropic samples give high energy product value (BH)max than the isotropic samples.23 This is because sample with magnetocrystalline anisotropy gives high coercivity with square shaped loop, and thus, high (BH)max value. Although the thickness of sample S1 is twice of S2, we found similar coercivity and different anisotropy field values in samples S1 and S2. We found the enhancement of coercivity in magnetic bilayers than the reference single magnetic layers. Interfacial exchange coupling might be a reason for this enhancement of coercivity. Also, we found the tuning of coercivity by alternating the order of magnetic layers. This indicates the presence of different interfacial exchange coupling strength in the samples S3 and S4. The magnetization reversal behaviour of samples S3 and S4 is like a rigid magnetic system because the soft and hard phases reverse with a single coercive field.
Magnetic domain images of samples S1 ((a)–(d)), S2 ((e)–(h)), S3 ((i)–(l)) and S4 ((m)–(p)) along ϕ = 0° (EA), 30°, 60° and 90° (HA) are shown in Fig. 7. We found big branch domains along EA for all the samples. Further, magnetization reversal is occurring via 180° domain wall motion. We found the nucleation and propagation of domain walls in all the samples. Magnetization reversal of samples S1, S2 and S4 away from EA occurs via big domains indicating the presence of anisotropy inhomogeneity.24 However, magnetization reversal of sample S3 occurs via small domains indicating strong uniaxial anisotropy in this sample. The absence of magnetic domains is found along HA in all the samples, thus, the magnetization reversal occurs via coherent rotation.
 | ||
| Fig. 7 Magnetic domain images of samples S1 ((a)–(d)), S2 ((e)–(h)), S3 ((i)–(l)), and S4 ((m)–(p)) along ϕ = 0° (EA), 30°, 60° and 90° (HA) recorded in LMOKE based microscopy at room temperature. | ||
3.3 FMR analysis
In order to understand the anisotropy symmetry, we have performed in-plane angle (ϕ) dependent FMR measurements at an interval of 10°.We can write the magnetic free energy density as the equation given below;24,25
E = HMS[sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θH θH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ − ϕH) + cos cos(ϕ − ϕH) + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θH θH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] − 2π(MS)2(sin θ] − 2π(MS)2(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 + KP(sin θ)2 + KP(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2 + Kin(sin θ)2 + Kin(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2(sin(ϕ − ϕ0)2 θ)2(sin(ϕ − ϕ0)2 | (2) |
It should be noted that the magnetic field was applied in the film plane. Therefore we have used the following dispersion relation to fit the angle dependent Hres in order to find the values of HK and hu.24
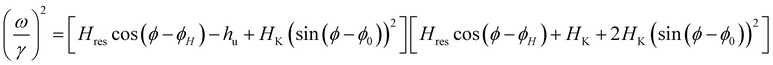 | (3) |
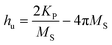 and
and 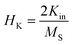 .
.
In-plane angle dependent FMR measurements are performed at a fixed frequency of 9 GHz. FMR measurement confirms the presence of uniaxial magnetic anisotropy in all the samples. Fig. 8 shows the plot of in-plane angle dependent Hres. The solid scattered data points are the experimental data whereas the solid continuous line is the fitted data using eqn (2). We could not find the ferromagnetic resonance signal of sample S2, therefore the plot of Hresvs. ϕ of this sample has not been shown. HK values of 0.0036 T, 0.0082 T and 0.0041 T are evaluated for samples S1, S3 and S4, respectively, by fitting the experimental data (Fig. 8) using eqn (2). Fig. 9 shows the FMR frequency (fFMR) vs. Hres and line width (ΔH), respectively. The effective demagnetization field (4πMeff), effective anisotropy field (HKeff) and the gyromagnetic ratio 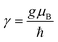 values have been extracted by fitting experimental data (Fig. 9(a)) using the following Kittel equation:26,27
values have been extracted by fitting experimental data (Fig. 9(a)) using the following Kittel equation:26,27
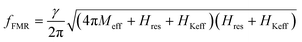 | (4) |
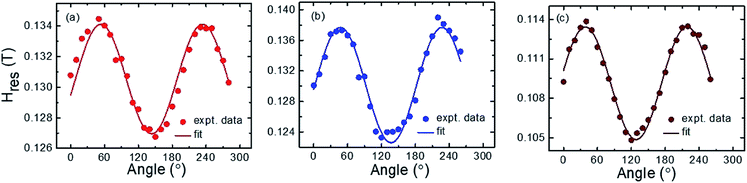 | ||
| Fig. 8 (a)–(c) The plot of resonance magnetic field (Hres) vs. in-plane angle ϕ for samples S1, S3 and S4, respectively. Solid symbols are the experimental data while solid lines are the best fit using eqn (2). | ||
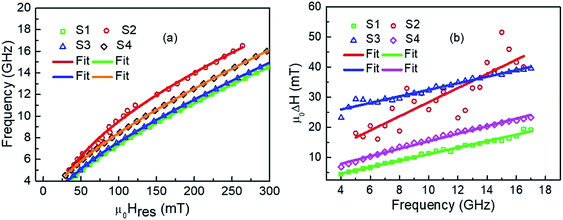 | ||
| Fig. 9 (a) Hres, (b) ΔH versus fFMR plot and their fits using eqn (3) and (4) for the samples S1, S2, S3 and S4. | ||
Similarly, the Gilbert damping constant value α is obtained by fitting the line width (ΔH) vs. fFMR (Fig. 9(b)) using the following equation;27,28
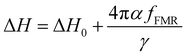 | (5) |
The thickness and crystalline structure of Fe affects the ferromagnetic resonance spectra. We have experienced with our FMR setup (NanoOsc) that if the thickness of polycrystalline Fe film is less than 10 nm then the data becomes very noisy. Nevertheless we have remeasured the sample with more data averaging for the sample S2 which is shown as a new Fig. R1 in ESI.† It is theoretically reported that line width value depends on anisotropy field HK and the interlayer exchange coupling of two ferromagnetic layers separated by a non-magnetic layer.29 We found different values of HK in the bilayer samples S3 and S4 from Kerr microscopy measurements. This result indicates different interfacial exchange coupling strength from the ferromagnetic bilayers. The large increase in the linewidth value of sample S3 in comparison to S4 may be due to the change in interfacial exchange coupling of the bilayers. Also, little deviation in the Hres value from all other samples is observed in sample S4 and this may be due to modified exchange coupling at the interface of the ferromagnetic layers. We reported earlier that direct exchange coupling between magnetic layer leads to the enhancement of the Gilbert damping constant α value.30 We are getting simultaneously high coercivity and less α values in sample S3 which is good for FMR applications. Omelchenko et al., reported the tuning of damping by alternating the order of Py/Fe bilayers deposited on Si substrate with Ta as seed layer.31 However, in this study, damping remains similar by alternating the order of magnetic layers which is useful for potential applications. Table 5 shows the list of values of g, 4πMeff, HKeff, α, ΔH0, and KS of all the samples.
| Sample name | g | μ 04πMeff (mT) | μ 0 H Keff (mT) | α | μ 0ΔH0 (mT) | K S (erg cm−2) |
|---|---|---|---|---|---|---|
| S1 | 1.956 ± 0.007 | 636.25 ± 8.69 | 8.44 ± 0.34 | 0.0160 ± 0.0005 | 0.31 ± 0.41 | −0.042 ± 0.002 |
| S2 | 1.291 ± 0.005 | 2962.56 ± 23.58 | 9.48 ± 0.74 | 0.0211 ± 0.0003 | 4.89 ± 3.33 | — |
| S3 | 2.032 ± 0.016 | 630.47 ± 15.83 | 2.35 ± 0.47 | 0.0150 ± 0.0006 | 21.59 ± 0.48 | −0.148 ± 0.007 |
| S4 | 2.060 ± 0.002 | 731.63 ± 2.73 | 2.43 ± 0.05 | 0.0180 ± 0.0003 | 2.92 ± 0.28 | −0.025 ± 0.001 |
In a crystalline material, due to symmetry in crystal lattice, average value of orbital angular momentum is zero. But, the orbital contribution of magnetic moment μL is non-zero leading to the g-factor greater than 2 following the relation g ≃ 2 (1 + (μL/μS)).32 As the surfaces and interfaces break inversion symmetry, that leads to crystal field no longer symmetric. Therefore, g-factor is less than 2 and follows the relation g ≃ 2 (1 − (μL/μS)).32 We observed large value of the inhomogeneous linewidth broadening ΔH0 in sample S3 and this value is higher than sample S4.
We evaluated the volume anisotropy field HK for all the samples using Kerr measurements. However, using FMR spectroscopy, we can evaluate surface induced anisotropy known as perpendicular surface anisotropy constant KS. The effective demagnetization field (4πMeff) and saturation magnetization MS values follow the below relation;
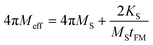 | (6) |
We have not calculated the KS value of sample S2 as unphysical value of 4πMeff is found in this sample.
We found MS value of 762 emu cc−1 in sample S3 which is higher than sample S1 (639 emu cc−1). Thus, direct exchange coupling between the magnetic layers results higher value of MS. Also, we found MS value of 860 emu cc−1 in sample S2. Again, samples S3 and S4 (636 emu cc−1) have dissimilar MS values indicating the tailoring of the interfacial exchange coupling by alternating the order of magnetic layers.
Therefore it is observed that in sample S3 i.e. when NiFe layer is grown on top of Fe, the sample exhibits high coercive field and anisotropy. Further this sample also exhibits damping value comparable to the reference single NiFe film.
4 Conclusions
We have studied the role of interface modification on the magnetization reversal of the Fe/NiFe bilayer system fabricated by magnetron sputtering. Kerr Microscopy data showed single-phase hysteresis loops, indicating strong interfacial exchange coupling. Quantitative analysis of the Kerr loops revealed the enhancement of the magnetic parameters such as coercive field HC and anisotropy field HK which get almost doubled when NiFe layer grows over the Fe layer. Further, this bilayer sample showed smaller domains away from the EA, confirming the presence of high uniaxial magnetic anisotropy in it. The presence of uniaxial magnetic anisotropy was also revealed from the in-plane angle-dependent FMR study. By comparing the PNR results of the bilayer samples, we observed the modification of the Fe–NiFe interfacial layer upon changing the order of the magnetic layers. The strength of the interfacial exchange coupling was higher when the NiFe layer is grown over the Fe layer. Despite different values of the anisotropy field and modified interfacial exchange coupling, the Gilbert damping constant of the bilayer systems remains similar to single NiFe layer. In summary, interchanging the order of magnetic layers plays a key role in tuning the interfacial exchange coupling through modification of interdiffusion layer thickness and magnetic moment. In this respect PNR has been proven to be an ideal technique to reveal the interface magnetic properties. Tuning of fundamental magnetic properties is possible by this methodology whereas the Gilbert damping constant remains similar which is good for applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from Department of Atomic Energy (DAE), Department of Science and Technology - Science and Engineering Research Board (SB/S2/CMP-107/2013) and Department of Science and Technology (DST) Nanomission (SR/NM/NS-1018/2016(G)), Government of India for providing the financial support. SB and SSD acknowledge the financial support from Newton Fund to carry out the PNR experiments at Rutherford Appleton Laboratory. BBS acknowledges DST for INSPIRE faculty fellowship. ISIS DOI for the data set along with the RB number of the experiment is 10.5286/ISIS.E.RB1520249.References
- L. Wei, L. Xiong-Hua, C. Wei-Bin, G. Wen-Jie and Z. Zhi-Dong, Exchange couplings in magnetic films, Chin. Phys. B, 2013, 22, 027104 CrossRef.
- F. Wang, X. Xu, Y. Liang, J. Zhang and H. Wu, FeAu/FePt exchange-spring media fabricated by magnetron sputtering and postannealing, Appl. Phys. Lett., 2009, 95, 022516 CrossRef.
- V. Alexandrakis, D. Niarchos, K. Mergia, J. Lee, J. Fidler and I. Panagiotopoulos, Magnetic properties of graded A1/L10 films obtained by heat treatment of FePt/CoPt multilayers, J. Appl. Phys., 2010, 107, 013903 CrossRef.
- D. C. Crew, J. Kim, L. H. Lewis and K. Barmark, Interdiffusion in bilayer CoPt/Co films: potential for tailoring the magnetic exchange spring, J. Magn. Magn. Mater., 2001, 233, 257–273 CrossRef CAS.
- J. Wang, B. Yang, W. Pei, G. Qin, Y. Zhang, C. Esling, X. Zhao and L. Zuo, Structural and magnetic properties of L10-FePt/Fe exchange coupled nano-composite thin films with high energy product, J. Magn. Magn. Mater., 2013, 345, 165–170 CrossRef CAS.
- V. Alexandrakis, D. Niarchos, M. Wolff and I. Panagiotopoulos, Magnetization reversal in CoPt(111) hard/soft bilayers, J. Appl. Phys., 2009, 105, 063908 CrossRef.
- N. Behera, A. Kumarab, S. Chaudhary and D. K. Pandya, Two magnon scattering and anti-damping behavior in a two-dimensional epitaxial TiN/Py(tPy)/β-Ta(tTa) system, RSC Adv., 2017, 7, 8106–8117 RSC.
- M. Tang, W. Li, Y. Ren, Z. Zhang, S. Lou and Q. Y. Jin, Magnetic damping and perpendicular magnetic anisotropy in Pd-buffered [Co/Ni]5 and [Ni/Co]5 multilayers, RSC Adv., 2017, 7, 5315–5321 RSC.
- V. R. Reddy, O. Crisan, A. Gupta, A. Banerjee and V. Kuncser, Tuning exchange spring effects in FePt/Fe(Co) magnetic bilayers, Thin Solid Films, 2012, 520, 2184–2189 CrossRef.
- J. S. Jiang, J. E. Pearson, Z. Y. Liu, B. Kabius, S. Trasobares, D. J. Miller and S. D. Bader, Improving exchange-spring nanocomposite permanent magnets, Appl. Phys. Lett., 2004, 85, 5293 CrossRef CAS.
- J. Kim, K. Barmak, M. De Graef, L. H. Lewis and D. C. Crew, Effect of annealing on magnetic exchange coupling in CoPt/Co bilayer thin films, J. Appl. Phys., 2000, 87, 6140 CrossRef CAS.
- Y. Choi, J. S. Jiang, Y. Ding, R. A. Rosenberg, J. E. Pearson, S. D. Bader, A. Zambano, M. Murakami, I. Takeuchi, Z. L. Wang and J. P. Liu, Role of diffused Co atoms in improving effective exchange coupling in Sm-Co/Fe spring magnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104432 CrossRef.
- Y. Liu, S. G. E. te Velthuis, J. S. Jiang, Y. Choi, S. D. Bader, A. A. Parizzi, H. Ambaye and V. Lauter, Magnetic structure in Fe/Sm-Co exchange spring bilayers with intermixed interfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174418 CrossRef.
- A. Conca, J. Greser, T. Sebastian, S. Klingler, B. Obry, B. Leven and B. Hillebrands, Low spin-wave damping in amorphous Co40Fe40B20 thin films, J. Appl. Phys., 2013, 113, 213909 CrossRef.
- S. Pal, B. Rana, O. Hellwig, T. Thomson and A. Barman, Tunable magnonic frequency and damping in [Co/Pd]8 multilayers with variable Co layer thickness, Appl. Phys. Lett., 2011, 98, 082501 CrossRef.
- M. C. Hickey and J. S. Moodera, Origin of Intrinsic Gilbert Damping, Phys. Rev. Lett., 2009, 103, 239702 CrossRef.
- N. N. Phuoc, F. Xu and C. K. Ong, Tuning magnetization dynamic properties of Fe-SiO2 multilayers by oblique deposition, J. Appl. Phys., 2009, 105, 113926 CrossRef.
- F. Xu, Q. Huang, Z. Liao, S. Li and C. K. Ong, Tuning of magnetization dynamics in sputtered CoFeB thin film by gas pressure, J. Appl. Phys., 2012, 111, 07A304 CrossRef.
- S. Mallik, A. S. Mohd, A. Koutsioubas, S. Mattauch, B. Satpati, T. Brückel and S. Bedanta, Tuning spinterface properties in iron/fullerene thin films, Nanotechnology, 2019, 30, 435705 CrossRef CAS.
- S. Mallik, S. Mattauch, M. K. Dalai, T. Brückel and S. Bedanta, Effect of magnetic fullerene on magnetization reversal created at the Fe/C60 interface, Sci. Rep., 2018, 8, 5515 CrossRef.
- https://genx.sourceforge.io/index.html .
- S. Singh, S. Basu, M. Gupta, M. Vedpathakz and R. H. Kodama, Investigation of interface magnetic moment of Fe/Ge multilayer: A neutron reflectivity study, J. Appl. Phys., 2007, 101, 033913 CrossRef.
- J. Zhang, Y. K. Takahashi, R. Gopalan and K. Hono, Sm(Co,Cu)5/Fe exchange spring multilayer films with high energy product, Appl. Phys. Lett., 2005, 86, 122509 CrossRef.
- S. Mallick, S. Mallik, B. B. Singh, N. Chowdhury, R. Gieniusz, A. Maziewski and S. Bedanta, Tuning the anisotropy and domain structure of Co films by variable growth conditions and seed layers, J. Phys. D: Appl. Phys., 2018, 51, 275003 CrossRef.
- S. Mallik and S. Bedanta, Study of anisotropy, magnetization reversal and damping in ultrathin Co films on MgO (0 0 1) substrate, J. Magn. Magn. Mater., 2018, 446, 270–275 CrossRef CAS.
- C. Kittel, On the Theory of Ferromagnetic Resonance Absorption, Phys. Rev., 1948, 73, 155 CrossRef CAS.
- B. B. Singh, S. K. Jena and S. Bedanta, Study of spin pumping in Co thin film vis-à-vis seed and capping layers using ferromagnetic resonance spectroscopy, J. Phys. D: Appl. Phys., 2017, 50, 345001 CrossRef.
- S. S. Kalarickal, P. Krivosik, M. Wu and C. E. Patton, Ferromagnetic resonance linewidth in metallic thin films: Comparison of measurement methods, J. Appl. Phys., 2006, 99, 093909 CrossRef.
- A. Layadi, A theoretical investigation of Ferromagnetic Resonance Linewidth and damping constants in coupled trilayer and spin valve systems, AIP Adv., 2015, 5, 057113 CrossRef.
- S. Nayak, B. B. Singh, S. Mallick and S. Bedanta, Tuning of magnetic properties by alternating the order of hard/soft bilayers with various thicknesses, J. Phys. D: Appl. Phys., 2019, 52, 305301 CrossRef CAS.
- P. Omelchenko, E. A. Montoya, C. Coutts, B. Heinrich and E. Girt, Tunable magnetization and damping of sputter-deposited, exchange coupled Py/Fe bilayers, Sci. Rep., 2017, 7, 4861 CrossRef PubMed.
- J. P. Nibarger, R. Lopusnik, Z. Celinski and T. J. Silva, Variation of magnetization and the Landé g factor with thickness in Ni-Fe films, Appl. Phys. Lett., 2003, 83, 93–95 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05429a |
| This journal is © The Royal Society of Chemistry 2020 |