Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling mass transport in hierarchically porous catalysts†
Mark A.
Isaacs
 a,
Neil
Robinson
a,
Neil
Robinson
 b,
Brunella
Barbero
c,
Lee J.
Durndell
d,
Jinesh C.
Manayil
c,
Christopher M. A.
Parlett
b,
Brunella
Barbero
c,
Lee J.
Durndell
d,
Jinesh C.
Manayil
c,
Christopher M. A.
Parlett
 ef,
Carmine
D'Agostino
ef,
Carmine
D'Agostino
 *e,
Karen
Wilson
*e,
Karen
Wilson
 g and
Adam F.
Lee
g and
Adam F.
Lee
 *g
*g
aDepartment of Chemistry, University College London, Kings Cross, London WC1H 0AJ, UK
bDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Cambridge, CB3 0AS, UK
cEuropean Bioenergy Research Institute, Aston University, Birmingham B4 7ET, UK
dSchool of Geography, Earth and Environmental Sciences, University of Plymouth, Plymouth PL4 8AA, UK. E-mail: carmine.dagostino@manchester.ac.uk
eSchool of Chemical Engineering and Analytical Science, University of Manchester, Manchester M13 9PL, UK
fUniversity of Manchester at Harwell, Diamond Light Source, Harwell Science and Innovation Campus, Didcot OX11 0DE, UK
gSchool of Science, RMIT University, Melbourne VIC3000, Australia. E-mail: adam.lee2@rmit.edu.au
First published on 24th April 2019
Abstract
Bio-derived platform chemicals and fuels are important for the development of sustainable manufacturing. However, their efficient production from biomass necessitates new catalysts and processes optimised for the selective transformation of large molecules. Mesoporous and hierarchically porous functional materials are promising catalyst candidates for biomass valorisation, but quantitative relationships between pore dimensions/connectivity, mass transport, and corresponding catalytic performance are poorly defined. A family of hierarchical macroporous–mesoporous SBA-15 sulfonic acids were prepared with tunable macropore diameters for carboxylic acid esterification. Turnover frequencies for long-chain (palmitic and erucic) acids were proportional to macropore diameter (≤370 nm), whereas propanoic acid esterification was independent of macropore size. Pulsed field gradient NMR diffusion experiments reveal that larger macropores enhance esterification of bulky carboxylic acids by conferring superior pore interconnectivity and associated mass transport.
Introduction
Porous solids find widespread practical application in catalysis, sorption, and separation science wherein pore dimensions and network connectivity control the attendant internal surface area and accessibility.1,2 Micro- and mesopores (0.5–50 nm diameter) confer high areas that can maximise the density of surface chemical functions such as catalytically active sites, while macropores (>50 nm) enhance the rate and extent of fluid permeation through a pore network. Hierarchical porous solids, typically comprising interpenetrating bimodal mesopore–micropore or macropore–mesopore networks, extend control over molecular transport, adsorption, and reaction.3 For example, the introduction of mesoporosity into zeolites improves their lifetime,4,5 and activity and selectivity for (bio)fuels6,7 or fine chemicals8 production, while macropores promote esterification9 and selective alcohol oxidation10 over sulfonic acid and Pd mesoporous SBA-15 silicas respectively, CO2 hydrogenation over Cu alumina,11 and transesterification over Mg–Al hydrotalcites.12 This is conceptually akin to fractal networks in Nature,13 wherein the transport of matter is optimised by rapid convective flow through large channels, that in turn supply a network of smaller channels through which diffusion is constrained. Although chemical transport through hierarchical pore networks is extensively modelled, nature-inspired design principles14 have yet to be implemented to synthesise materials with architectures ‘tailored for purpose’.Considering heterogeneous catalysis, simulations suggest that in the Knudsen diffusion regime, where reactants/products can enter/exit mesopores but experience attendant diffusion limitation, hierarchical bimodal pore networks can significantly improve active site accessibility, with larger pores acting as ‘molecular superhighways’15 to accelerate transport from the bulk media to mesopore domains.16–19 In practice, such enhanced accessibility is also facilitated by truncation of mesopore channels in ordered hierarchical porous solids (commonly prepared by dual-templating routes) compared with their mesoporous counterparts;20,21 shorter mesopores may mitigate any attendant diffusional resistance. The interdependence of pore hierarchy and individual pore dimensions in experimental studies hampers validation of transport models and necessitates direct measurement of diffusion and reaction in systematically related families of hierarchical porous solids.
Routes to interpenetrating bimodal macro-mesopore networks using microemulsion colloidal polystyrene microspheres or co-surfactant templating routes are particularly attractive for liquid phase heterogeneous catalysis using bulky substrates. Hierarchical macroporous–mesoporous silicas offer great flexibility in pore size and connectivity through the choice of soft/hard surfactant template, use of porogens, and hydrothermal processing.20,22–25 However, in the context of catalysis, systematic studies of porosity are largely confined to mesoporous silicas, wherein e.g. pore-expansion increased the turnover frequency (TOF) of sulfonic acid functionalised SBA-15 and KIT-6 for carboxylic acid esterification,26 or hierarchically porous silicas in which only the mesopore diameter was varied for Fischer–Tropsch synthesis.27 In all cases, improved mass transport is inferred from superior catalytic performance. Nevertheless, very few experimental studies have correlated molecular diffusion through mesopores and corresponding reactivity,28,29 and to our knowledge diffusion has never been experimentally measured for an ordered hierarchical porous catalyst. The mechanism by which macropores improve reactivity in hierarchically porous catalysts remains unclear, but is amenable to interrogation by pulsed field gradient (PFG) NMR, widely applied to elucidate transport phenomena within liquid-saturated porous media.30–32
Here we assess the impact of macropore size on molecular diffusion and carboxylic acid esterification for propylsulfonic acid functionalised, hierarchical macroporous–mesoporous SBA-15 (PrSO3H/MM-SBA-15) catalysts. PFG NMR is used to probe diffusive restriction and pore connectivity within these catalyst frameworks. Larger macropores reduce pore network tortuosity and increase diffusion through mesopore channels, accounting for the >4-fold increase in TOF observed for palmitic and erucic acid esterification with methanol.
Experimental
Polystyrene nanosphere synthesis
A family of monodispersed polystyrene nanospheres (200, 300, 400, 500, and 600 nm diameter) were prepared using a modified literature protocol.33 Styrene (50 cm3 for 200 nm beads increasing linearly to 150 cm3 for 600 nm, Aldrich 99%) was washed five times with aqueous NaOH (0.1 M, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) and five times with deionized water (1
1 by volume) and five times with deionized water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) to remove the 4-tert butylcatechol polymerisation inhibitor; larger styrene volumes yielded larger beads (Fig. S1†). Washed styrene was then added to N2 degassed, deionised water (1000 cm3) at 80 °C, to which aqueous K2S2O8 (0.24 M, 50 cm3, Aldrich ≥99%) was added dropwise with stirring (300 rpm). Reactions were stopped after 22 h, the resulting solid products recovered by filtration, and colloidal crystal assembly induced by centrifugation (Heraeus Multifuge X1 with Thermo Fiberlite F15-8x50cy Fixed-Angle Rotor, operated at 8000 rpm/7441 g for 1 h). The resulting highly ordered, polystyrene nanosphere crystalline matrices were ground to fine powders.
1 by volume) to remove the 4-tert butylcatechol polymerisation inhibitor; larger styrene volumes yielded larger beads (Fig. S1†). Washed styrene was then added to N2 degassed, deionised water (1000 cm3) at 80 °C, to which aqueous K2S2O8 (0.24 M, 50 cm3, Aldrich ≥99%) was added dropwise with stirring (300 rpm). Reactions were stopped after 22 h, the resulting solid products recovered by filtration, and colloidal crystal assembly induced by centrifugation (Heraeus Multifuge X1 with Thermo Fiberlite F15-8x50cy Fixed-Angle Rotor, operated at 8000 rpm/7441 g for 1 h). The resulting highly ordered, polystyrene nanosphere crystalline matrices were ground to fine powders.
Hierarchically porous SBA-15
Hierarchically porous silicas were prepared by a modified true liquid crystal templating technique incorporating a range of polystyrene nanospheres as macropore-directing hard templates.34 Pluronic P123 (2 g, Aldrich average Mn ∼ 5800) was sonicated with HCl-acidified deionised water (2 g, pH 2) at 40 °C to form a homogeneous gel. Tetramethoxysilane (4.08 cm3, Acros 99%) was added to the gel and rapidly stirred for 5 min (800 rpm) until a homogeneous liquid formed. Immediately following this phase change, polystyrene nanospheres of a particular size (6 g, independent of bead diameter, as a fine powder) were added with agitation (100 rpm) for 1 min. The resulting viscous, homogeneous mixtures were heated in vacuo (100 mbar) at 40 °C for 2 h to remove reactively-formed methanol. The solids thus obtained were exposed to air at room temperature for 24 h to complete condensation of the silicate precursor, and then calcined at 550 °C for 6 h (ramp rate 5 °C min−1) to remove organic templates.Acid functionalisation
The preceding hierarchically porous silicas were functionalised with propylsulfonic acid by an alkoxide grafting method. In each case, silica (1 g) was added to a 100 mL round-bottomed flask with anhydrous toluene (30 mL) under N2 at 90 °C with stirring (700 rpm). A (3-mercaptopropyl)trimethoxysilane thiol precursor (1 mL) was subsequently added and the reaction mixture stirred for 24 h. The resulting solid was filtered, washed with ethanol, and dried at 80 °C overnight. Surface thiols were then oxidised to sulfonic acids (1 g solid in 20 mL of 30 vol% H2O2) with stirring (400 rpm) overnight. Propylsulfonic acid functionalised materials were recovered, washed with deionised water and ethanol, and dried overnight at 80 °C.Material characterisation
Powder XRD was performed on a Bruker D8 ADVANCE fitted with a Cu Kα X-ray source with a Ni filter and LynxEYE 192-channel high speed strip detector. Wide angle scans were performed between 10–80° with a step size of 0.02° and dwell time of 0.6 s, and low angle scans between 0.5–8° with a step size of 0.01° and a dwell time of 1 s. Crystalline phases were determined by Rietveld refinement using Profex v3.11.1, and crystallite sizes determined using the Scherrer equation. N2 adsorption isotherms were measured using a Quantachrome 4000 surface area analyser. Surface areas and pore size distributions were determined through application of the BET and BJH equations respectively to the recorded isotherms. XPS analysis was performed using a Kratos Axis HSi spectrometer equipped with a monochromated Al Kα (1486.8 eV) X-ray source and charge neutraliser, operating <10−9 Torr. Survey spectra were recorded with a pass energy of 160 eV, and high-resolution spectra with a pass energy of 40 eV. Spectra were Shirley background-subtracted, calibrated to adventitious carbon (284.8 eV), and fitted using Casa v2.3.15. S 2p peaks were fitted using a Gaussian–Lorentzian (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30) lineshape and a doublet separation of 1.16 eV. Sulfur loadings were determined by CHNS analysis using a Thermo Flash 2000 organic elemental analyser calibrated against a sulphanilamide standard. SEM was performed using a JEOL 7800F Prime FEG SEM fitted with a BSE and SE detector. Samples were affixed to carbon tape, and images recorded at a probe current of 3 mA and an accelerating voltage between 1–15 kV. STEM images were recorded using an aberration-corrected JEOL 2100F STEM with an accelerating voltage of 200 kV, a HAADF detector and Gatan bright field camera. Electron micrographs were processed with ImageJ 1.46r, and particle sizes determined from samples of >200 particles.
30) lineshape and a doublet separation of 1.16 eV. Sulfur loadings were determined by CHNS analysis using a Thermo Flash 2000 organic elemental analyser calibrated against a sulphanilamide standard. SEM was performed using a JEOL 7800F Prime FEG SEM fitted with a BSE and SE detector. Samples were affixed to carbon tape, and images recorded at a probe current of 3 mA and an accelerating voltage between 1–15 kV. STEM images were recorded using an aberration-corrected JEOL 2100F STEM with an accelerating voltage of 200 kV, a HAADF detector and Gatan bright field camera. Electron micrographs were processed with ImageJ 1.46r, and particle sizes determined from samples of >200 particles.
Catalytic testing
Esterification reactions were performed in a 50 mL round-bottomed flask at 90 °C with stirring (700 rpm). 25 mg of catalyst was tested with 5 mmol of propanoic acid, palmitic acid, or erucic acid, and 12.5 mL methanol with 0.1 mmol dihexylether as an internal standard. 0.25 mL aliquots were periodically removed, diluted with methanol, and analysed using a Varian 450 GC with 8400 autosampler fitted with a ZB-50 column.PFG NMR
Pulsed-field gradient (PFG) NMR diffusion measurements were performed to assess the diffusive behaviour of liquids in the unrestricted bulk and within PrSO3H/MM-SBA-15 catalysts. Samples for NMR analysis were prepared according to the following procedure: PrSO3H/MM-SBA-15 exhibiting 150 nm and 430 nm macropores were pressed into 1 cm diameter pellets. The pellets were broken apart into approximately 4 mm × 4 mm × 2 mm pieces and dried at 105 °C for 12 h. The catalysts were soaked in excess cyclohexane (Sigma Aldrich, ≥99.5%) or dodecane (Fischer Scientific, ≥99%) for at least 48 h under ambient conditions, with each liquid absorbed through capillary imbibition. Prior to NMR analysis the saturated materials were removed from the liquids and rolled over pre-soaked filter paper; this process removed any excess liquid on the outer surface of the pellets without drawing liquid from the pores. The saturated materials were then transferred to sealed 5 mm NMR tubes to a sample depth of ∼10 mm.1H PFG NMR experiments were performed using a Bruker DMX 300 NMR spectrometer equipped with a 7.1 T magnet (300.13 MHz for 1H) and a Bruker Diff30 diffusion probe capable of producing pulsed magnetic field gradients up to 11.6 T m−1. Samples were placed at the centre of the radiofrequency coil and left for at least 15 minutes to thermally equilibrate. Diffusion of unrestricted liquids was analysed using the pulsed gradient stimulated echo (PGSTE) sequence (Fig. 1a).35 To minimise the effects of background magnetic field gradients (so-called internal gradients36) the diffusion of liquids confined to the porous catalysts was analysed using the alternating pulsed gradient stimulated echo (APGSTE) pulse sequence (Fig. 1b).37 In each case, measurements were performed by holding the gradient pulse duration δ constant and linearly varying the magnetic field gradient strength g. Trapezoidal gradient pulses were used to ensure reproducible pulse shapes across all values of g. The recycle time was 2T1 (as measured using the inversion recovery method) and 2 dummy scans were used to equilibrate the sample magnetisation before the acquisition of each data point. All measurements were performed at 20 ± 0.1 °C and under ambient pressure. A summary of the typical PFG NMR acquisition parameters used is reported in Table 1.
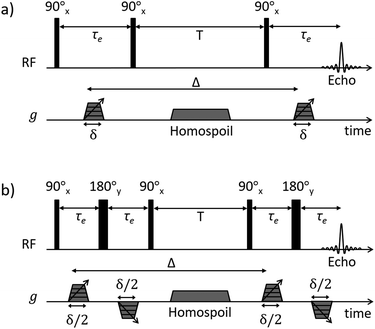 | ||
| Fig. 1 NMR diffusion pulse sequence diagrams for (a) PGSTE and (b) APGSTE experiments. Radiofrequency (RF axis) pulses are indicated by vertical bars; thin and thick bars represent 90° and 180° RF pulses respectively. Gradient pulse timings (g axis) are specified according to the notation of Tanner.38 Trapezoidal gradient pulses of incremental magnitude g are shown with effective pulse durations δ and δ/2 for the PGSTE and APGSTE sequences, respectively. Homospoil gradients are also shown and are applied during the longitudinal storage period T to remove any residual transverse magnetisation. The observation time is Δ. | ||
| PFG NMR parameters | Unrestricted liquids | Liquids in hierarchical catalysts |
|---|---|---|
| Pulse sequence | PGSTE | APGSTE |
| Observation time, Δ/ms | 50 | 25–200 |
| Effective gradient pulse duration, δ/ms | 1 | 1 |
| Maximum gradient strength/G cm−1 | 140 | 900 |
| Spin echo time, τe/ms | 3.2 | 2.7 |
| Homospoil gradient duration/ms | 10 | 5 |
| No. of gradient steps | 16 | 32 |
| No. of scans | 16 | 64 |
Results and discussion
Synthesis of macroporous SBA-15
Macropore size control was achieved through the synthesis of monodispersed polystyrene nanospheres of tunable diameter (200 to 580 nm) as sacrificial hard templates and their subsequent compaction into a colloidal crystal assembly. Ordered, hexagonal close-packed mesoporous SBA-15 silica networks were subsequently formed throughout the crystal assembly by a true liquid crystal templating method.34 Calcination resulted in hierarchically macroporous–mesoporous silicas (MM-SBA-15) with uniform macropore diameters of 150 to 430 nm (proportional to template size) shown in Fig. 2; macropore shrinkage relative to the polystyrene template was consistent with previous reports for hierarchically porous alumina.39 N2 porosimetry of the as-prepared porous frameworks revealed a common type-IV isotherm with H1 hysteresis indicative of mesoporous SBA-15, with common BJH mesopore diameters of 4 nm (Fig. S2†). Low angle XRD confirmed the d10 reflection characteristic of p6mm SBA-15 was present for all materials (Fig. S3†).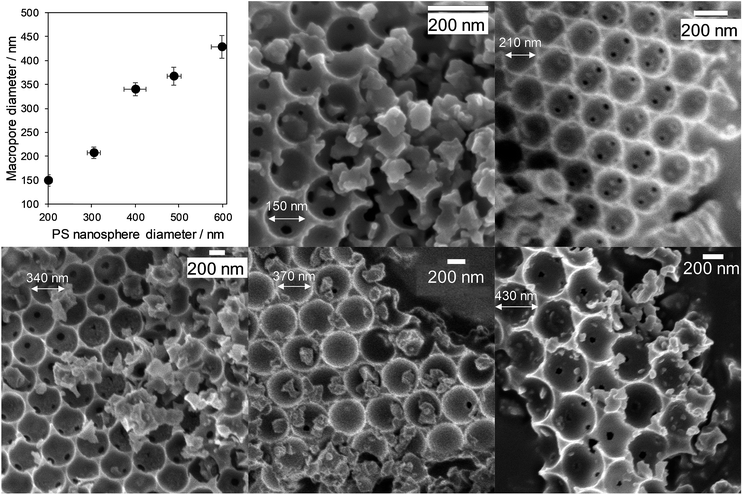 | ||
| Fig. 2 Hierarchically porous SBA-15 frameworks of tunable macropore diameter: relationship between macropore and polymer template diameters, and representative SEM images. | ||
The preceding silica frameworks were functionalised with a common, and uniformly distributed, propylsulfonic acid (PrSO3H) loading (∼1 wt% S, Table S1†) to yield a family of hierarchically porous solid acid catalysts (PrSO3H/MM-SBA-15). S 2p XP spectra (Fig. S4†) confirmed complete oxidation of the thiol precursor, and N2 porosimetry confirmed retention of the parent mesopore networks following PrSO3H functionalisation (Fig. S5†). The density of sulfonic acid groups was approximately independent of macropore diameter (0.69 nm−2 ± 0.05), and in a regime where the strongest acidity obtains due to lateral interactions between neighbouring sulfonic acid head groups.40 HAADF-STEM showed that mesopores were highly ordered in all cases, with a common mesopore diameter and macropore/mesopore interface (Fig. S6†).
Catalytic enhancement through macropore tuning
The impact of macropore diameter on the activity of PrSO3H/MM-SBA-15 catalysts was studied for free fatty acid (FFA) esterification with methanol as a function of chain length. In the case of propanoic acid, turnover frequencies (TOFs) per sulfonic acid site were independent of macropore size (and similar to that reported for mesoporous PrSO3H/SBA-15),26 whereas those for bulky palmitic (C16:0) and erucic (C22:1) acids both significantly increased with macropore size (Fig. 3). For palmitic acid, per site activities increased four-fold as the macropores expanded from 150 to 430 nm, while negligible activity was observed for the unsaturated, bent erucic acid for 150 nm macropores. Although erucic acid can readily access 150 nm macropores, only 2–8% of all active sites reside in the macropores (Table S1†) and hence negligible catalysis occurs within them. The question arises as to why increasing the macropore size promotes erucic acid esterification. A plausible explanation is that the increased pore connectivity for larger macropores (observed by PFG NMR below) is at least partially associated with break-up of the mesopore channel network,20,21 which in turn increases the number of mesopore openings and opportunities for the carboxylate group to react over active sites at mesopore entrances. This is akin to the mechanism invoked for the oxidation of n-alkanes (up to C12) over molecular sieves, in which an end-on approach into small pore entrances favours terminal methyl attack.41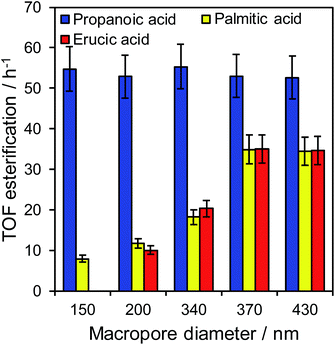 | ||
| Fig. 3 Turnover frequencies for propanoic acid, palmitic acid, and erucic acid esterification over PrSO3H/MM-SBA-15 as a function of macropore diameter. | ||
The maximum TOFs for propanoic and palmitic acids are in accordance with those reported for PrSO3H/SBA-15 and PrSO3H/MM-SBA-15 with 340 nm macropores and a similar acid loading.21,26 The influence of macropore diameter on esterification activity is solely attributable to internal pore architecture, since particle size distributions across the hierarchical catalysts were essentially constant (modal values ∼12 μm, Fig. S7†). This sensitivity of TOF to macropore and molecular size suggests that in-pore diffusion may be rate-limiting for bulky reactants; indeed the linear relationship between palmitic acid esterification and macropore diameter (Fig. S8†) is reminiscent of that for anticipated for Knudsen diffusion through porous media. Direct evidence of in-pore transport limitations for palmitic acid esterification was obtained from mechanical grinding of the 210 nm macropore catalyst. This reduced the mean particle size (and implicitly diffusion pathlength) approximately 3-fold without changing the porosity (Fig. S9 and Table S2†), resulting in a corresponding two-fold increase in TOF from 12 to 22 h−1. Apparent activation energies for palmitic acid esterification over the 210 and 430 nm macropore hierarchical catalysts also indicate a switchover from diffusion limited to reaction-rate limited esterification with increasing macropore size, rising from 34 ± 3 kJ mol−1 (210 nm) to 45 ± 3 kJ mol−1 (430 nm). The latter barrier is in fair agreement with the homogeneous acid catalysed value of 56 kJ mol−1,42 suggesting that esterification over the 430 nm macropore catalyst is largely free from mass transport limitations.
PFG NMR diffusion studies
Insight into the preceding dependence of TOF on catalyst structure and carboxylic acid size was subsequently derived by investigating the changes in pore connectivity with macropore diameter. PFG NMR experiments are uniquely suited to such studies, enabling the direct and non-invasive evaluation of molecular self-diffusion coefficients within liquid-saturated catalyst structures.43 For long observation times Δ, the effective diffusion coefficient of the restricted liquid Deff is reduced from that of the unrestricted liquid D0 (in the bulk media) by the tortuosity of the porous network τ. This parameter defines the overall interconnectivity of accessible pore structures and may be estimated from:31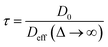 | (1) |
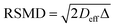 ), which are significantly greater than the modal pore sizes present. Eqn (1) holds for small, non-viscous, weakly-interacting liquids, and has been used to quantify the tortuosity of various mesoporous catalysts.44–48 For liquids exhibiting non-negligible interactions with the porous matrix, τ will vary with molecular structure and functionality, giving an effective tortuosity factor that may no longer represent the pore connectivity.28,46,48
), which are significantly greater than the modal pore sizes present. Eqn (1) holds for small, non-viscous, weakly-interacting liquids, and has been used to quantify the tortuosity of various mesoporous catalysts.44–48 For liquids exhibiting non-negligible interactions with the porous matrix, τ will vary with molecular structure and functionality, giving an effective tortuosity factor that may no longer represent the pore connectivity.28,46,48
In the present work, the diffusivities of cyclohexane and dodecane were explored for the preceding 150 nm and 430 nm macroporous sulfonic acid silicas. The significant difference in molecular size between these probe molecules is an approximate analogue for the structural differences between the short- and long-chain carboxylic acids in Fig. 3. The use of alkanes was necessitated by the relatively high melting points of erucic and palmitic acids (33.8 °C and 62.9 °C respectively) which prohibited self-diffusion measurements using our diffusion probe. Solubilising the acids in methanol is problematic due to: (i) competitive in-pore diffusion between methanol and the acid (diffusion of 2-component systems depends on their molar fraction); (ii) strong hydrogen bonding networks throughout the imbibed methanol/acid mixture and with the pore surfaces, which prevent determination of the true tortuosity of the porous catalyst (only possible when probe molecules do not chemically interact with pore surfaces or each other); and (iii) catalytic reaction resulting in changing molecule populations which is not congruent to obtaining useful diffusion information.46 Ideal probe molecules should therefore be chemically inert, free of polar functional groups, exhibit sufficiently high diffusivities that the long-time diffusion limit can be accessed (wherein probe molecules can access multiple pores during a sensible observation time of ∼100 ms), and express long relaxation times; criteria which favour relatively ‘small’ probe molecules, with dodecane the largest such probe typically investigated.
Self-diffusion coefficients D0 and Deff(Δ → ∞) are readily obtained through appropriate PFG NMR diffusion experiments.31 Log-attenuation plots for unrestricted liquids were obtained using the PGSTE pulse sequence (Fig. 4); D0 was determined by fitting the acquired data points to the Stejskal–Tanner equation:35
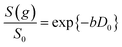 | (2) |
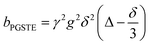 | (3) |
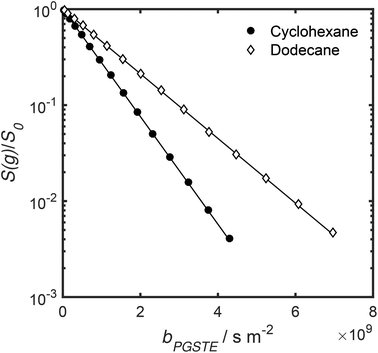 | ||
| Fig. 4 PGSTE data for unrestricted cyclohexane and dodecane self-diffusion. Solid lines are a fit to eqn (2) and (3). | ||
Log-attenuation data for the self-diffusion of cyclohexane and dodecane when restricted within PrSO3H/MM-SBA-15 catalysts possessing 150 nm and 430 nm macropores were subsequently obtained (Fig. 5); these materials were selected as limiting small and large pore solid acid catalysts. The APGSTE data points were acquired using four different observation times ranging from 25–200 ms. It is apparent that these signal attenuations do not follow a simple exponential decay of the form described in eqn (2). Indeed, the attenuation data exhibit significant curvature on a log-scale, which is qualitatively independent of the observation time over the range of Δ values explored. Extracting physically meaningful diffusion coefficients from these data requires careful consideration of the origin of this complex signal. Curved log-attenuation data are typically attributed to multicomponent exponential behaviour of the form 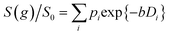 . Here, the diffusion coefficients Di describe the mobility of different molecular ensembles i with effective populations pi. Such an approach is generally valid if the mean lifetime of molecules within each population exceeds the observation time over which diffusion is measured (the so-called slow exchange condition),31 and if appropriate molecular environments exhibiting different length scales and connectivity exist throughout the sample to generate multiple diffusion coefficients. Normal (or Fickian) self-diffusion must be assumed within each environment, such that a Gaussian distribution of molecular displacements evolves over time.43,50 Typical examples include the long- and short-range behaviour of gases and volatile liquids imbibed in microporous crystalline solids, wherein different diffusion coefficients may be assigned to inter- and intracrystalline diffusion.51 Differentiation between these transport phenomena primarily depends on the RMSD of the diffusing probe molecules, and hence the observation times and experimental temperatures employed. Relevant studies in which multicomponent exponential data fittings of this form have been applied include investigations of diffusion within hierarchical meso/microporous zeolites52–55 and aggregates of mesoporous SBA-15.56 Galarneau et al. examined n-hexane diffusion in zeolite FAU-Y and mesoporous Al-MCM-41,57 demonstrating that self-diffusion within a mechanical mixture of these materials could be described as a simple superposition of the diffusivities within the individual materials, whereas the self-diffusion coefficient from a hierarchical combination of these materials lay in an intermediate regime between that characteristic of mesopores or micropores. Furthermore, Adem et al. investigated the self-diffusion of n-hexane during the pseudomorphic synthesis of MCM-41
. Here, the diffusion coefficients Di describe the mobility of different molecular ensembles i with effective populations pi. Such an approach is generally valid if the mean lifetime of molecules within each population exceeds the observation time over which diffusion is measured (the so-called slow exchange condition),31 and if appropriate molecular environments exhibiting different length scales and connectivity exist throughout the sample to generate multiple diffusion coefficients. Normal (or Fickian) self-diffusion must be assumed within each environment, such that a Gaussian distribution of molecular displacements evolves over time.43,50 Typical examples include the long- and short-range behaviour of gases and volatile liquids imbibed in microporous crystalline solids, wherein different diffusion coefficients may be assigned to inter- and intracrystalline diffusion.51 Differentiation between these transport phenomena primarily depends on the RMSD of the diffusing probe molecules, and hence the observation times and experimental temperatures employed. Relevant studies in which multicomponent exponential data fittings of this form have been applied include investigations of diffusion within hierarchical meso/microporous zeolites52–55 and aggregates of mesoporous SBA-15.56 Galarneau et al. examined n-hexane diffusion in zeolite FAU-Y and mesoporous Al-MCM-41,57 demonstrating that self-diffusion within a mechanical mixture of these materials could be described as a simple superposition of the diffusivities within the individual materials, whereas the self-diffusion coefficient from a hierarchical combination of these materials lay in an intermediate regime between that characteristic of mesopores or micropores. Furthermore, Adem et al. investigated the self-diffusion of n-hexane during the pseudomorphic synthesis of MCM-41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58) to explore time-dependent pore structures. Multicomponent exponential fittings distinguished between long-range interparticle displacement and intraparticle displacement within the resulting pore structures, revealing a notable dependence of the intraparticle effective self-diffusion coefficient on both pore size and connectivity.
58) to explore time-dependent pore structures. Multicomponent exponential fittings distinguished between long-range interparticle displacement and intraparticle displacement within the resulting pore structures, revealing a notable dependence of the intraparticle effective self-diffusion coefficient on both pore size and connectivity.
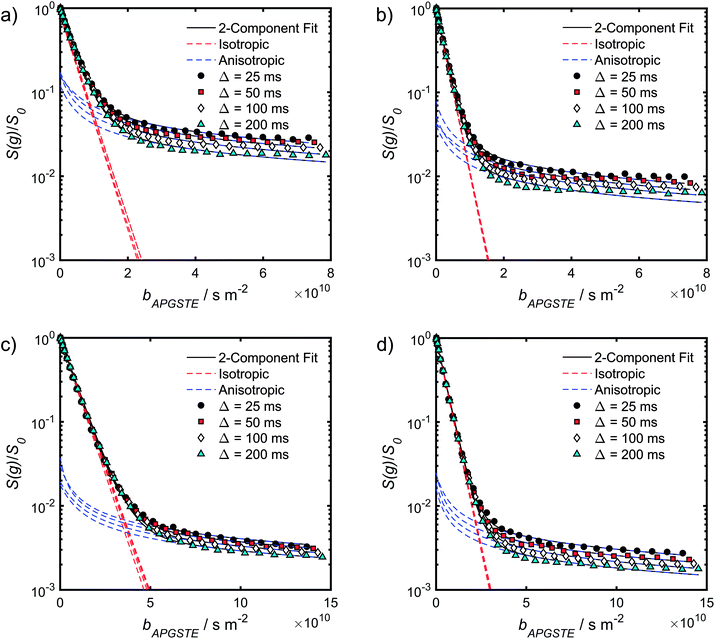 | ||
| Fig. 5 APGSTE data for PrSO3H/MM-SBA-15 catalysts: PFG NMR signal attenuation curves for (a and b) cyclohexane saturated and (c and d) dodecane-saturated PrSO3H/MM-SBA-15 catalysts with respective 150 nm and 430 nm macropores. Two-component fits to the acquired data points utilised eqn (6); isotropic and anisotropic fitted components are shown in red and blue respectively. | ||
A biexponential fitting of the form S(g)/S0 = pfastexp{−bDfast} + pslowexp{−bDslow} provided good agreement with our acquired attenuation data (Fig. S10†), where Dfast describes the initial, steep signal decay at low b, while Dslow describes the limiting gradient of the shallow decay observed at high b. Recalling the APGSTE sequence for the observation of restricted self-diffusion, the relevant b-factor is:37
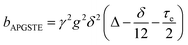 | (4) |
The slowly decaying signal attenuation at high b in Fig. 5 is more difficult to assign. Biexponential fitting yields Dslow ∼ 10−12 m2 s−1 for both the cyclohexane- and dodecane-saturated catalysts. Considering the above discussion of RMSDs and the assignment of Dfast to diffusion through the entire pore network, it is rather surprising to identify a small spin population exhibiting such a significantly different diffusion coefficient. Such an observation might imply the existence of configurational diffusion, where liquid mobility is dominated by interactions with the pore walls within one of the domains.43 However, in the present materials mesopore diameters are too large for configurational diffusion to occur, and no micropore population was identified by N2 porosimetry t-plot analysis (data not shown), suggesting this slow component cannot be attributed to configurational diffusion through structural micropores. Previous studies of self-diffusion within an adsorbed surface layer reported similar PFG NMR attenuation curves to the present data.59,60 However, covalent modification of the surface with alkyl groups removed this component from the attenuation data.60 The existence of a slowly diffusing surface component can therefore be discounted in this work due to presence of surface propyl sulfonic acid groups. Furthermore, the aforementioned studies required thousands of repeat scans to observe the slowly diffusing surface layer,59,60 and hence such a population is unlikely to be detected by the limited repeat scans in this work. It is pertinent then to consider the isotropy of the pore structures under study. Kärger and co-workers have demonstrated that diffusion through mesoporous SBA-15 and MCM-41 silicas may result in curved PFG log-attenuation plots due to their anisotropic pore structure.61–63 For a powder-average of saturated anisotropic pores, the PFG signal is expected to attenuate according to:63
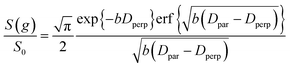 | (5) |
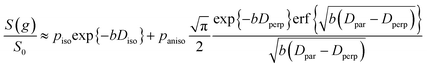 | (6) |
It is appropriate here to highlight the recent development by Splith et al.66 of a complex model to address diffusive exchange between isotropic and anisotropic environments. The authors considered the diffusion and exchange of water within and between crystals of the anisotropic microporous metal–organic-framework Al fumarate. The resulting model improved fitting of PFG echo attenuation data relative to that achieved using eqn (5) but required that population of the isotropic environment was negligible. Such an approximation is appropriate for systems containing saturated anisotropic materials with only vapour phase within the intercrystalline voids, but is clearly not valid for our hierarchical catalysts which comprise fully-saturated isotropic and anisotropic pores. A different approach was therefore adopted in which APGSTE data for liquid-saturated PrSO3H/MM-SBA-15 pellets were fit to eqn (4) and (6) using a non-linear least squares fitting. The resulting two-component fit is in good agreement with the acquired data; representative curves are shown in Fig. 5, where the isotropic and anisotropic contributions of eqn (6) are deconvoluted for clarity. This deconvolution visualises the slowly decaying signal at high b resulting from a small spin population exhibiting anisotropic diffusion. A small decrease in the signal obtained from this population (paniso) is evident with increasing Δ. There are two possible explanations for this decrease: (i) nuclear spin T1 relaxation during the longitudinal storage period T = Δ − 2τe, facilitating additional signal attenuation with increasing Δ; (ii) diffusive exchange, reducing the number of spins experiencing purely anisotropic self-diffusion during Δ. Since longitudinal relaxation time constants T1 (Table S4†) were at least an order of magnitude greater than the maximum Δ value employed, molecular exchange appears the dominant mechanism underpinning the decrease in paniso. A decrease in paniso with increasing macropore size is also apparent, as would be expected from the concomitant increase in piso. The inherent differences in paniso for the two probe liquids may be rationalised by considering the enhanced T1 relaxation rates (1/T1) exhibited by the dodecane-versus cyclohexane saturated catalysts (Table S4†).
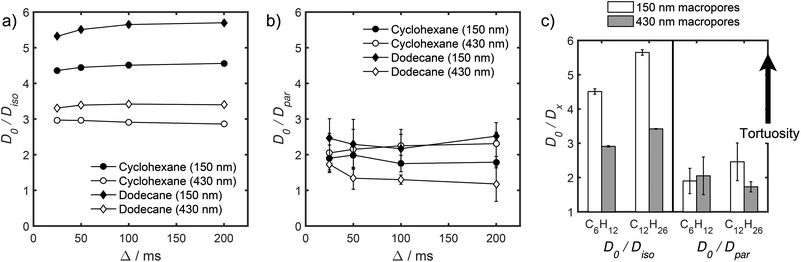
Unfortunately, the fits in Fig. 5 are of insufficient quality to robustly estimate Dperp; we attribute this to dominance of the acquired data by isotropic signal attenuation at small b, and hence focus discussion on Diso and Dpar. These diffusion coefficients (Table S5†) are shown as a function of observation time in Fig. 6, and are of equivalent orders of magnitude (∼10−10 m2 s−1) in contrast to the diffusion coefficients assigned through the preceding biexponential fitting (Table S3†). Self-diffusion coefficients obtained from the isotropic component of eqn (6) appear in Fig. 6a. For the dodecane-saturated catalysts, and cyclohexane-saturated analogue with 150 nm macropores, a small decrease in Diso occurs with increasing Δ over the range 25–100 ms. Since the observed Diso values are all significantly reduced from D0, we interpret these diffusivities as indicative of an intermediate regime between unrestricted and restricted diffusion.31 Molecules therefore experience significant interactions with the pore walls but do not displace through a large enough sample of the pore space to be considered within the long-time diffusion limit. Above Δ = 100 ms Diso is invariant, with dodecane presenting asymptotic Diso(Δ → ∞) ≅ Diso(Δ = 100 ms) values of ∼1.37 × 10−10 m2 s−1 and ∼2.27 × 10−10 m2 s−1 within the 150 nm and 430 nm macropore catalysts respectively, and cyclohexane presenting an asymptotic value of ∼2.86 × 10−10 m2 s−1 within the 150 nm macropore catalyst. These diffusivities may therefore be interpreted as a probe of pore connectivity. It is interesting to note that we do not observe the same trend when considering cyclohexane-saturated PrSO3H/MM-SBA-15 with 430 nm macropores, which exhibits by far the largest Diso of the alkane/silica systems investigated (measurements were conducted multiple times to confirm this anomaly). In this latter case, a slight but steady increase in Diso with increasing Δ was observed suggesting that Diso observed at small Δ is already indicative of the long-time diffusion limit. The small increase in Diso with increasing Δ suggests an increased propensity for the imbibed cyclohexane to diffuse out of the particles and into the intercrystalline voids during large observation times. For the purposes of assigning a long-time diffusion limit value to this system we take a Diso(Δ → ∞) ≅ Diso(Δ = 25 ms) value of ∼4.35 × 10−10 m2 s−1.
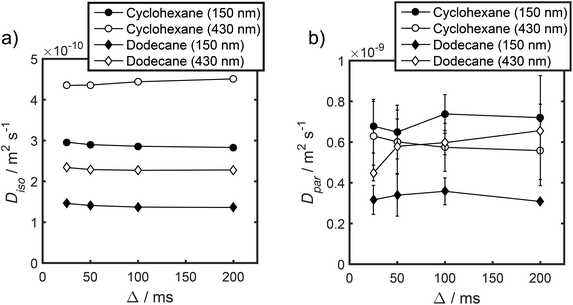 | ||
| Fig. 6 (a) Diso and (b) Dpar values obtained by fitting APGSTE data to eqn (6). Macropore diameters are indicated in parentheses. Errors represent ±1 standard deviation of three measurements of three different samples and are too small to be observed in (a). | ||
Values of the anisotropic diffusion coefficient Dpar are presented in Fig. 6b. Despite greater uncertainty in these Dpar values, fitting clearly reveals that Dpar > Diso, suggesting diffusion is faster through the mesopore network than the overall hierarchical pore structure. This finding is in agreement with Adem et al., who reported a distinct decrease in the effective self-diffusivity of n-hexane imbibed within MCM-41 upon the addition of large, secondary mesopores embedded in the structure which create ‘stagnation zones’.58 More detailed insight is obtained from the ratios D0/Diso and D0/Dpar (Table S6†), which we interpret as providing direct insight into pore connectivity within the catalyst structures studied. In particular, D0/Diso reflects the pore connectivity of the overall catalyst structure, while D0/Dpar reflects that of the anisotropic mesopores. These ratios are plotted as a function of observation time in Fig. 7. The ratio D0/Diso is shown in Fig. 7a and b for each catalyst/alkane combination, and is invariant at Δ ≥ 100 ms, consistent with the preceding analysis of their effective self-diffusion coefficients. These values are therefore considered indicative of the long-time diffusion limit, and hence a probe of pore connectivity. The anomalous behaviour of cyclohexane within PrSO3H/MM-SBA-15 with 430 nm macropores is no longer apparent when interpreted as a D0/Diso ratio and is essentially invariant to increasing observation time (Fig. 7a). Values of this ratio for the four alkane/catalyst systems are summarised in Table 2 and reveal two notable features. First, D0/Diso is greater for the catalyst with 150 nm macropores than that with 430 nm macropores, irrespective of the probe molecule considered, i.e. overall pore network tortuosity decreases with increasing macropore size. Second, D0/Diso values for cyclohexane and dodecane are significantly different for the same macropore size; dodecane values are approximately 20% larger for both macropore sizes. A consequence of the latter is that these values represent an effective tortuosity which is influenced by molecular size and/shape. However, since the change in D0/Diso with macropore size is qualitatively independent of the probe liquid, we can remain confident that an increase in macropore size is indeed associated with a decrease in overall tortuosity.
| Probe molecule | Macropore diameter/nm | D 0/10−10 m2 s−1 | D iso(Δ → ∞)/10−10 m2 s−1 | D 0/Diso(Δ → ∞) |
|---|---|---|---|---|
| Cyclohexane | 150 | 12.91 ± 0.02 | 2.86 ± 0.05 | 4.51 ± 0.08 |
| 430 | 4.35 ± 0.02 | 2.97 ± 0.01 | ||
| Dodecane | 150 | 7.76 ± 0.01 | 1.37 ± 0.02 | 5.65 ± 0.08 |
| 430 | 2.27 ± 0.01 | 3.42 ± 0.02 |
Fig. 7b also shows D0/Dpar as a function of observation time. The uncertainty in these values is significant, and stems from errors in assigning Dpar during fitting (Table S5†). Nevertheless, there is clearly substantial overlap between the four datasets, particularly clear at short observation times, where the RMSD is significantly less than the modal catalyst particle size (Table S5†). This overlap strongly suggests that the interconnectivity (and pore diameter and curvature) of the mesopores is similar in both catalysts, as expected given that the only difference in their syntheses was the size of sacrificial polymeric bead used to form the macropores, and further evidences that the tortuosity of our PrSO3H/MM-SBA-15 catalysts is solely controlled by macropore size. General agreement (within experimental error) between cyclohexane and dodecane D0/Dpar values (Fig. 7b and c) indicates that diffusive displacement within the mesopores of both catalysts is largely independent of molecular size/shape.
Structure-reactivity correlations
We first note that macropores were varied independently of the size or tortuosity of mesopores (Fig. S5, S6† and 7c), enabling the influence of macropores on carboxylic acid esterification by the hierarchical catalysts to be rationalised. For propanoic acid, esterification was independent of macropore size, as may be anticipated from its small kinetic diameter (∼0.48 nm) and hence minimal diffusive restriction by the pore network. A recent PFG NMR study on organic acid diffusion through mesoporous SBA-15 and KIT-6 silicas47 reported that the effective tortuosity increased with acid chain length, and that pore walls enhanced diffusion possibly by disrupting the dynamic hydrogen bonding network present throughout the liquid mixture (as has previously observed for polyols and polyol/methanol mixtures41–44). It follows that propanoic acid self-diffusion may be dominated by hydrogen-bonding dynamics, rather than by pore network tortuosity, consistent with the present findings that propanoic acid TOF and D0/Diso (equated here to macropore size) are uncorrelated. Conversely, the preceding SBA-15 and KIT-6 PFG-NMR study showed that long-chain acid diffusion was dominated by (meso)pore tortuosity and molecular size.45 We might therefore expect the TOFs for palmitic and erucic acids to follow the tortuosity of our hierarchical PrSO3H/MM-SBA-15 catalysts, as indeed is observed; long-chain acids TOFs are inversely correlated with D0/Diso.PFG NMR analysis of the diffusion of solvated acids was not possible due to competing catalytic esterification. It is therefore insightful to consider the difference in effective tortuosity experienced by cyclohexane and dodecane within the small and large macropore catalysts (Table 2). Dodecane exhibits greater D0/Diso values than the smaller cyclohexane probe molecule, irrespective of macropore size. It follows that a secondary, size-dependent transport resistance must be present, which further reduces the mobility of large molecules in addition to restrictions imposed by the inherent pore network tortuosity. Since dodecane lacks any polar functionality, this secondary transport resistance cannot be attributed to e.g. enhanced interactions with surface sulfonic acid groups or hydroxyls, but rather reflects topological constraints of the pore system. This finding agrees with pore-scale diffusion simulations,67,68 which reveal that the effective tortuosity of mesoporous SBA-15 and KIT-6 silicas depends on the size of the probe molecule. Note that this contrasts with simulations67,68 and PFG-NMR studies of amorphous mesoporous silicas, for which effective tortuosity is independent of molecular size.46 Relative D0/Diso values for cyclohexane versus dodecane through PrSO3H/MM-SBA-15 also depend on macropore size, being 23% greater for 150 nm macropores and 15% greater for 430 nm macropores (Table 2), i.e. the secondary transport resistance identified above decreases with increasing macropore size. This observation manifests our chemical intuition that larger macropores do indeed enhance mass transport of long-chain acids through hierarchically porous catalysts. In contrast D0/Dpar, which reflects diffusion through only the mesopores, is approximately independent of probe molecule. This suggests that the size-dependent transport resistance seen for D0/Diso arises from: (i) topological effects at the macropore/mesopore interface, i.e. bulkier molecules (dodecane, palmitic or erucic acid) struggle to enter mesopores, but once correctly oriented can diffuse relatively freely along mesopore channels (recall that Dpar > Diso); and/or (ii) stagnation zones created by small macropores that are embedded in the silica framework and hinder transport through the mesopore network. Constricted pore openings are reported for mesoporous MCM-41 and SBA-15.67,69 A detailed analysis of secondary transport resistances within these hierarchically porous catalysts is the subject of future studies.
Conclusions
The synthesis and characterisation of hierarchical macroporous–mesoporous SBA-15 sulfonic acid catalysts exhibiting tunable macropore sizes is reported, facilitating new insight into transport phenomena through hierarchically porous materials. Catalytic performance of the resulting PrSO3H/MM-SBA-15 family towards the liquid phase esterification of short and long-chain carboxylic acids with methanol revealed that turnover frequencies for propanoic acid were structure invariant, whereas those for palmitic and erucic acids exhibit striking increases with macropore size. Complementary PFG NMR diffusion measurements enable the non-invasive assessment of pore connectivity and diffusive restrictions for liquids imbibed within these catalysts. Effective self-diffusion of cyclohexane and dodecane within PrSO3H/MM-SBA-15 catalysts containing 150 nm and 430 nm macropores reveals complex signal attenuation data, attributed to a superposition of isotropic and anisotropic contributions. Diffusivities extracted from these measurements provide an estimate of the structural tortuosity through comparison with bulk self-diffusion coefficients. Tortuosity of the overall pore network decreases with increasing macropore size, indicating that larger macropores improve pore connectivity throughout the hierarchical framework. Larger macropores enhance long-chain carboxylic acid esterification by improving pore structure connectivity and hence active site accessibility. Propanoic acid esterification is indifferent to the tortuosity of our hierarchically porous catalysts, consistent with the diffusive behaviour of short-chain carboxylic acids in SBA-15,47 and presumably reflecting its small kinetic diameter. Molecular size is an important factor in determining the extent of diffusive restriction imposed by the hierarchical pore networks, and increased for larger probe molecules resulting in larger effective tortuosities for dodecane than cyclohexane. This additional restriction was more pronounced for smaller macropores exacerbating the poor catalytic turnover for palmitic and erucic acids within small (150 nm) macropore PrSO3H/MM-SBA-15 catalysts.In summary, PFG-NMR analysis shows that diffusion limitations are not related to a single textural parameter, but rather depend on a convolution of molecular size, pore connectivity, and pore diameter. Pore size and connectivity are themselves not mutually exclusive, since we have shown that altering the macropore diameter also change the effective tortuosity throughout hierarchical pore networks (a measure of connectivity). Trends in catalytic esterification are explicable by considering the enhanced mass transport attainable through tailoring macropore size (and attendant pore connectivity) to the reactant size. This work highlights the significant capability of PFG NMR experiments for elucidating pore structure and connectivity within complex porous solids, and more specifically as a powerful tool to guide the design of hierarchically porous catalysts for maximal activity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to acknowledge the EPSRC for funding this work (grants EP/G007594/4 and EP/F063423/2). N. R. acknowledges the Catalysis@Cambridge initiative, University of Cambridge, for the award of a PhD studentship. C. D. A. would like to acknowledge Wolfson College, Cambridge, for supporting his research activities. The authors also thank Prof Lynn F. Gladden, University of Cambridge, for access to the NMR equipment.References
- A. G. Slater and A. I. Cooper, Science, 2015, 348, aaa8075 CrossRef PubMed.
- M. E. Davis, Nature, 2002, 417, 813 CrossRef CAS PubMed.
- X.-Y. Yang, L.-H. Chen, Y. Li, J. C. Rooke, C. Sanchez and B.-L. Su, Chem. Soc. Rev., 2017, 46, 481–558 RSC.
- J. Kim, M. Choi and R. Ryoo, J. Catal., 2010, 269, 219–228 CrossRef CAS.
- M. Milina, S. Mitchell, P. Crivelli, D. Cooke and J. Perez-Ramirez, Nat. Commun., 2014, 5, 10 Search PubMed.
- J. A. Hunns, M. Arroyo, A. F. Lee, J. M. Escola, D. Serrano and K. Wilson, Catal. Sci. Technol., 2016, 6, 2560–2564 RSC.
- L. Y. Jia, M. Raad, S. Hamieh, J. Toufaily, T. Hamieh, M. M. Bettahar, G. Mauviel, M. Tarrighi, L. Pinard and A. Dufour, Green Chem., 2017, 19, 5442–5459 RSC.
- M. Linares, C. Vargas, A. Garcia, C. Ochoa-Hernandez, J. Cejka, R. A. Garcia-Munoz and D. P. Serrano, Catal. Sci. Technol., 2017, 7, 181–190 RSC.
- J. C. Manayil, A. Osatiashtiani, A. Mendoza, C. M. A. Parlett, M. A. Isaacs, L. J. Durndell, C. Michailof, E. Heracleous, A. Lappas, A. F. Lee and K. Wilson, ChemSusChem, 2017, 10, 3506–3511 CrossRef CAS PubMed.
- C. M. Parlett, P. Keshwalla, S. G. Wainwright, D. W. Bruce, N. S. Hondow, K. Wilson and A. F. Lee, ACS Catal., 2013, 3, 2122–2129 CrossRef CAS.
- T. Witoon, S. Bumrungsalee, M. Chareonpanich and J. Limtrakul, Energy Convers. Manage., 2015, 103, 886–894 CrossRef CAS.
- J. J. Woodford, J.-P. Dacquin, K. Wilson and A. F. Lee, Energy Environ. Sci., 2012, 5, 6145–6150 RSC.
- J. Lynch, Plant Physiol., 1995, 109, 7 CrossRef CAS PubMed.
- P. Trogadas, M. M. Nigra and M.-O. Coppens, New J. Chem., 2016, 40, 4016–4026 RSC.
- S. Gheorghiu and M.-O. Coppens, AIChE J., 2004, 50, 812–820 CrossRef CAS.
- M.-O. Coppens and G. F. Froment, Chem. Eng. Sci., 1995, 50, 1013–1026 CrossRef CAS.
- G. Wang and M.-O. Coppens, Chem. Eng. Sci., 2010, 65, 2344–2351 CrossRef CAS.
- P. Zeigermann, S. Naumov, S. Mascotto, J. Kärger, B. M. Smarsly and R. Valiullin, Langmuir, 2012, 28, 3621–3632 CrossRef CAS PubMed.
- M. A. Sadeghi, M. Aghighi, J. Barralet and J. T. Gostick, Chem. Eng. J., 2017, 330, 1002–1011 CrossRef CAS.
- F. Li, Z. Wang, N. S. Ergang, C. A. Fyfe and A. Stein, Langmuir, 2007, 23, 3996–4004 CrossRef CAS PubMed.
- J. Dhainaut, J.-P. Dacquin, A. F. Lee and K. Wilson, Green Chem., 2010, 12, 296–303 RSC.
- D. Kuang, T. Brezesinski and B. Smarsly, J. Am. Chem. Soc., 2004, 126, 10534–10535 CrossRef CAS PubMed.
- T. Sen, G. J. T. Tiddy, J. L. Casci and M. W. Anderson, Chem. Mater., 2004, 16, 2044–2054 CrossRef CAS.
- B. H. Jones and T. P. Lodge, Chem. Mater., 2011, 23, 4824–4831 CrossRef CAS.
- G. Lee, E. Choi, S. Yang and E.-B. Cho, J. Phys. Chem. C, 2018, 122, 4507–4516 CrossRef CAS.
- C. Pirez, J.-M. Caderon, J.-P. Dacquin, A. F. Lee and K. Wilson, ACS Catal., 2012, 2, 1607–1614 CrossRef CAS.
- H. Li, B. Hou, J. Wang, X. Huang, C. Chen, Z. Ma, J. Cui, L. Jia, D. Sun and D. Li, Catal. Sci. Technol., 2017, 7, 3812–3822 RSC.
- C. D'Agostino, M. D. Mantle and L. F. Gladden, Microporous Mesoporous Mater., 2018, 269, 88–92 CrossRef.
- C. D'Agostino, Y. Ryabenkova, P. J. Miedziak, S. H. Taylor, G. J. Hutchings, L. F. Gladden and M. D. Mantle, Catal. Sci. Technol., 2014, 4, 1313–1322 RSC.
- M. P. Hollewand and L. F. Gladden, Chem. Eng. Sci., 1995, 50, 309–326 CrossRef CAS.
- W. S. Price, NMR studies of translational motion: principles and applications, Cambridge University Press, 2009 Search PubMed.
- P. T. Callaghan, Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin Echo NMR, Oxford University Press, 2011 Search PubMed.
- T. Sen, G. Tiddy, J. Casci and M. Anderson, Chem. Mater., 2004, 16, 2044–2054 CrossRef CAS.
- C. M. Parlett, M. A. Isaacs, S. K. Beaumont, L. M. Bingham, N. S. Hondow, K. Wilson and A. F. Lee, Nat. Mater., 2016, 15, 178–182 CrossRef CAS PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- J. Mitchell, T. Chandrasekera, M. Johns, L. Gladden and E. Fordham, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 026101 CrossRef CAS PubMed.
- R. Cotts, M. Hoch, T. Sun and J. Markert, J. Magn. Reson., 1989, 83, 252–266 CAS.
- J. E. Tanner, J. Chem. Phys., 1970, 52, 2523–2526 CrossRef CAS.
- Y. Zhang, H. Liang, C. Y. Zhao and Y. Liu, J. Mater. Sci., 2009, 44, 931–938 CrossRef CAS.
- J.-P. Dacquin, H. E. Cross, D. R. Brown, T. Düren, J. J. Williams, A. F. Lee and K. Wilson, Green Chem., 2010, 12, 1383–1391 RSC.
- J. M. Thomas and R. Raja, Chem. Commun., 2001, 675–687, 10.1039/b100369k.
- C. Beula and P. S. T. Sai, Int. J. Chem. Eng. Appl., 2013, 4, 388–392 CAS.
- F. Stallmach and J. Kärger, Adsorption, 1999, 5, 117–133 CrossRef CAS.
- C. D'Agostino, T. Kotionova, J. Mitchell, P. J. Miedziak, D. W. Knight, S. H. Taylor, G. J. Hutchings, L. F. Gladden and M. D. Mantle, Chem.–Eur. J., 2013, 19, 11725–11732 CrossRef PubMed.
- C. D'Agostino, G. L. Brett, P. J. Miedziak, D. W. Knight, G. J. Hutchings, L. F. Gladden and M. D. Mantle, Chem.–Eur. J., 2012, 18, 14426–14433 CrossRef PubMed.
- C. D'Agostino, J. Mitchell, L. F. Gladden and M. D. Mantle, J. Phys. Chem. C, 2012, 116, 8975–8982 CrossRef.
- T. J. Rottreau, C. M. Parlett, A. F. Lee and R. Evans, J. Phys. Chem. C, 2017, 121, 16250–16256 CrossRef CAS.
- M. D. Mantle, D. I. Enache, E. Nowicka, S. P. Davies, J. K. Edwards, C. D'Agostino, D. P. Mascarenhas, L. Durham, M. Sankar and D. W. Knight, J. Phys. Chem. C, 2010, 115, 1073–1079 CrossRef.
- M. Holz, S. R. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- F. Stallmach and P. Galvosas, Annu. Rep. NMR Spectrosc., 2007, 61, 51–131 CrossRef CAS.
- J. Kärger, D. M. Ruthven and D. N. Theodorou, Diffusion in Nanoporous Materials, 2012, pp. 347–394 Search PubMed.
- P. Kortunov, S. Vasenkov, J. Kärger, R. Valiullin, P. Gottschalk, M. Fé Elía, M. Perez, M. Stöcker, B. Drescher, G. McElhiney, C. Berger, R. Gläser and J. Weitkamp, J. Am. Chem. Soc., 2005, 127, 13055–13059 CrossRef CAS PubMed.
- D. Mehlhorn, R. Valiullin, J. Kärger, K. Cho and R. Ryoo, Microporous Mesoporous Mater., 2012, 164, 273–279 CrossRef CAS.
- A. Menjoge, S. A. Bradley, D. B. Galloway, J. J. Low, S. Prabhakar and S. Vasenkov, Microporous Mesoporous Mater., 2010, 135, 30–36 CrossRef CAS.
- D. Mehlhorn, A. Inayat, W. Schwieger, R. Valiullin and J. Kärger, ChemPhysChem, 2014, 15, 1681–1686 CrossRef CAS PubMed.
- A. R. Menjoge, Q. Huang, B. Nohair, M. Eic, W. Shen, R. Che, S. Kaliaguine and S. Vasenkov, J. Phys. Chem. C, 2010, 114, 16298–16308 CrossRef CAS.
- A. Galarneau, F. Guenneau, A. Gedeon, D. Mereib, J. Rodriguez, F. Fajula and B. Coasne, J. Phys. Chem. C, 2016, 120, 1562–1569 CrossRef CAS.
- Z. Adem, F. Guenneau, M.-A. Springuel-Huet, A. Gédéon, J. Iapichella, T. Cacciaguerra and A. Galarneau, J. Phys. Chem. C, 2012, 116, 13749–13759 CrossRef CAS.
- T. G. A. Youngs, D. Weber, L. F. Gladden and C. Hardacre, J. Phys. Chem. C, 2009, 113, 21342–21352 CrossRef CAS.
- D. Weber, A. J. Sederman, M. D. Mantle, J. Mitchell and L. F. Gladden, Phys. Chem. Chem. Phys., 2010, 12, 2619–2624 RSC.
- F. Stallmach, J. Kärger, C. Krause, M. Jeschke and U. Oberhagemann, J. Am. Chem. Soc., 2000, 122, 9237–9242 CrossRef CAS.
- F. Stallmach, A. Gräser, J. Kärger, C. Krause, M. Jeschke, U. Oberhagemann and S. Spange, Microporous Mesoporous Mater., 2001, 44, 745–753 CrossRef.
- S. Naumov, R. Valiullin, J. Kärger, R. Pitchumani and M.-O. Coppens, Microporous Mesoporous Mater., 2008, 110, 37–40 CrossRef CAS.
- M. Dvoyashkin, J. Zang, G. I. Yucelen, A. Katihar, S. Nair, D. S. Sholl, C. R. Bowers and S. Vasenkov, J. Phys. Chem. C, 2012, 116, 21350–21355 CrossRef CAS.
- M. Dvoyashkin, A. Wang, A. Katihar, J. Zang, G. I. Yucelen, S. Nair, D. S. Sholl, C. R. Bowers and S. Vasenkov, Microporous Mesoporous Mater., 2013, 178, 119–122 CrossRef CAS.
- T. Splith, D. Fröhlich, S. K. Henninger and F. Stallmach, J. Magn. Reson., 2018, 291, 40–46 CrossRef CAS PubMed.
- S.-J. Reich, A. Svidrytski, A. Höltzel, J. Florek, F. Kleitz, W. Wang, C. Kübel, D. Hlushkou and U. Tallarek, J. Phys. Chem. C, 2018, 122, 12350–12361 CrossRef CAS.
- S.-J. Reich, A. Svidrytski, D. Hlushkou, D. Stoeckel, C. Kübel, A. Höltzel and U. Tallarek, Ind. Eng. Chem. Res., 2018, 57, 3031–3042 CrossRef CAS.
- H. Tüysüz, C. W. Lehmann, H. Bongard, B. Tesche, R. Schmidt and F. Schüth, J. Am. Chem. Soc., 2008, 130, 11510–11517 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional materials characterisation and NMR data. See DOI: 10.1039/c9ta01867k |
| This journal is © The Royal Society of Chemistry 2019 |