Open Access Article
Open Access ArticleDoping and phase segregation in Mn2+- and Co2+-doped lead halide perovskites from 133Cs and 1H NMR relaxation enhancement†
Dominik J.
Kubicki
 ab,
Daniel
Prochowicz
ab,
Daniel
Prochowicz
 bc,
Arthur
Pinon
a,
Gabriele
Stevanato
a,
Albert
Hofstetter
a,
Shaik M.
Zakeeruddin
bc,
Arthur
Pinon
a,
Gabriele
Stevanato
a,
Albert
Hofstetter
a,
Shaik M.
Zakeeruddin
 b,
Michael
Grätzel
*b and
Lyndon
Emsley
b,
Michael
Grätzel
*b and
Lyndon
Emsley
 *a
*a
aLaboratory of Magnetic Resonance, Institute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland. E-mail: lyndon.emsley@epfl.ch
bLaboratory of Photonics and Interfaces, Institute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015 Lausanne, Switzerland. E-mail: michael.graetzel@epfl.ch
cInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland
First published on 15th January 2019
Abstract
Lead halide perovskites belong to a broad class of compounds with appealing optoelectronic and photovoltaic properties. Doping with transition metal ions such as Mn2+ and Co2+ has recently been reported to substantially enhance luminescence and stability of these materials. However, so far atomic-level evidence for incorporation of the dopants into perovskite phases has been missing. Here, we introduce a general and straightforward method for confirming the substitutional doping of bulk perovskite phases with paramagnetic dopants. Using 133Cs and 1H solid-state MAS NMR relaxation measurements we provide for the first time direct evidence that, consistent with current understanding, Mn2+ is incorporated into the perovskite lattice of CsPbCl3 and CsPbBr3 and does not form clusters. We also show that, contrary to current conviction, Co2+ is not incorporated into the perovskite lattice of MAPbI3.
Introduction
Lead halide perovskites are highly promising semiconducting materials for optoelectronic and photovoltaic applications.1 All-inorganic cesium lead halide (CsPbX3, X = Cl, Br, I) nanocrystals have recently emerged as a viable alternative to classical II–VI metal chalcogenides used in LED and solar cell applications.2–6 Similarly, multi-component organic–inorganic lead halide perovskites (APbX3, A = methylammonium (CH3NH3+, MA), formamidinium (CH3(NH2)2+, FA), (X = Cl, Br, I)) applied as light absorbers in solar cells, currently provide power conversion efficiencies of over 22%.7,8All-inorganic lead halide perovskite quantum dots (QDs) doped with transition metal and lanthanide ions show particularly advantageous optoelectronic properties such as strongly sensitized luminescence9,10 and improved thermal and air stability.11,12 The most widely investigated materials are CsPbCl3,10,13–22 CsPbBr3,23–26 and CsPbI3,9,12 as well as mixed-halide compositions10,27–29 doped with Mn2+ and very recently Ce3+.30 The strategy of transition metal ion doping has also been proposed as a means of fine tuning of photovoltaic parameters in organic–inorganic lead halide perovskites.31,32 Incorporation of transition metal ions into the perovskite lattice is typically evidenced using XRD, UV-VIS, PL, and in some instances by EPR10,11,18 and HAADF-STEM.11,30,33 While some of these methods provide atomic-level resolution (HAADF-STEM, EPR) and others provide insight into phase composition (XRD), none of them achieves both. Cesium lead halides form a variety of non-perovskite phases with different stoichiometries34–36 but there are currently no experimental protocols that can confirm which phase of interest is doped with transition metals. On the other hand, NMR is capable of providing atomic-level resolution by utilizing local nuclear probes such as 1H, 13C, 14N, 133Cs, 87Rb, 39K and 207Pb.37–45 In particular, 207Pb is a good probe of the halide composition38 but is far less sensitive to other changes in composition.46,47 Solid-state NMR spectra are acquired by placing a powder sample inside a strong homogeneous magnetic field (typically between around 10 and 20 T) and then recording spectra of the transitions between nuclear spin states which occur in the radiofrequency region. The resulting spectra contain peaks at distinct frequencies for each type of nucleus, and where very small variations (so-called chemical shifts) within a given nucleus type report very precisely on the local chemical environments of the nucleus in all its chemically inequivalent sites. For solids, the sample is usually rapidly spun at the magic angle (54.7° with respect to the magnetic field), which yields a very significant improvement in spectral resolution. This makes magic angle spinning (MAS) NMR one of the most powerful tools available to probe the local atomic-level structure of solids.48
Spectra are obtained from Fourier transformation of time domain signals recorded after a radiofrequency pulse that perturbs the system from equilibrium. The return to equilibrium after excitation by the pulse is referred to as longitudinal relaxation. Most transition metal and lanthanide ions are paramagnetic and therefore are expected to induce large paramagnetic relaxation enhancements (PRE) in otherwise diamagnetic perovskite materials.49 PREs arise as a consequence of the electron spin-nuclear spin interactions between NMR active nuclei (e.g.133Cs or 1H) and unpaired electrons of the metal ion, and lead to significant (up to 3–4 orders of magnitude) shortening of longitudinal relaxation times, T1, of nuclei in close proximity to paramagnetic centers. PRE is a short-range effect and scales as 1/r,6 where r is the distance between the nucleus and the paramagnetic species, and typically can be observed for distances up to ∼20 Å from the unpaired electron. The sensitivity limit for the detection of PREs is on the order of 0.1 s−1.50 In solids, another process, known as spin diffusion (SD)51 can transport the magnetization to nuclei farther away from the paramagnetic centres, leading to substantially shorter apparent T1 in the bulk of the material.
Here, using solid-state NMR relaxation measurements we provide for the first time atomic-level evidence that Mn2+ can dope CsPbCl3 and CsPbBr3 perovskite phases, consistent with replacing Pb2+ on the B site. We also show that, contrary to current belief, Co2+ is not capable of doping MAPbI3. Our study establishes a straightforward and general method for confirming incorporation of paramagnetic dopants into perovskite lattices.
Experimental
Materials
The following materials were used: methylammonium iodide (DyeSol), PbI2 (TCI, 99.99%), PbBr2 (TCI), PbCl2 (TCI), CsBr (Sigma, 99.999%), CsCl (Sigma, 99.999%), CoI2 (abcr, 99.999%), MnBr2 (abcr, 99%, anhydrous), MnCl2 (abcr, 99.999%, ultra dry).Perovskite mechanosynthesis
Starting materials were stored inside a glove box under argon. Perovskite powders were synthesized by grinding the reactants in an electric ball mill (Retsch Ball Mill MM-200) using a grinding jar (10 ml) and a ball (Ø 10 mm) for 30 min. at 25 Hz. The resulting perovskite powders were annealed at 250 °C for 10 minutes. The amounts of reagents taken into the synthesis were as follows: CsPbBr3: 212.8 mg CsBr (1 mmol), 367.0 mg PbBr2 (1 mmol), CsPb0.995Mn0.005Br3: 212.8 mg CsBr (1 mmol), 1.1 mg MnBr2 (0.005 mmol) 365.2 mg PbBr2 (0.995 mmol), CsPb0.97Mn0.03Br3: 212.8 mg CsBr (1 mmol), 6.4 mg MnBr2 (0.03 mmol) 356.0 mg PbBr2 (0.97 mmol), CsPb0.92Mn0.08Br3: 212.8 mg CsBr (1 mmol), 17.2 mg MnBr2 (0.08 mmol) 337.6 mg PbBr2 (0.92 mmol), CsMnBr3: 212.8 mg CsBr (1 mmol), 214.8 mg MnBr2 (1 mmol), CsPbCl3: 168.4 mg CsCl (1 mmol), 278.0 mg PbCl2 (1 mmol), CsPb0.97Mn0.03Cl3: 168.4 mg CsCl (1 mmol), 3.8 mg MnCl2 (0.03 mmol) 269.7 mg PbCl2 (0.97 mmol), CsMnCl3: 168.4 mg CsCl (1 mmol), 125.8 mg MnCl2 (1 mmol), MAPbI3: 159.0 mg MAI (1 mmol), 461.0 mg PbI2 (1 mmol), MA2CoI4: 318.0 mg MAI (2 mmol), 312.7 mg CoI2 (1 mmol), MAPb0.97Co0.03I3: 159.0 mg MAI (1 mmol), 9.4 mg CoI2 (0.03 mmol), 447.1 mg PbI2 (0.97 mmol).NMR measurements
Solid-state MAS NMR spectra of 1H (900 MHz at 21.1 T) and 133Cs (52.5 MHz at 9.4 T), were recorded on Avance IV 21.1 T and Bruker Avance III 9.4 T spectrometers, respectively, equipped with 3.2 mm CPMAS probes. Solid samples were packed into 3.2 mm diameter zirconia rotors and closed off using Vespel caps. The samples were spun at 20 kHz MAS (unless stated otherwise) using dry nitrogen gas. The rotation rate was controlled using a PID controller and its stability was ±1 Hz. Radiofrequency (RF) field strengths were calibrated directly on the samples of interest by acquiring an on-resonance nutation curve. 1H chemical shifts were referenced to solid adamantane (δ = 1.91 ppm). 133Cs shifts were referenced to 1 M aqueous solutions of cesium chloride, using solid CsI (δ = 271.05 ppm) as a secondary reference.52 For the saturation-recovery experiments, saturation was achieved by applying a train of 30 π/2 pulses spaced by 3 ms.Results and discussion
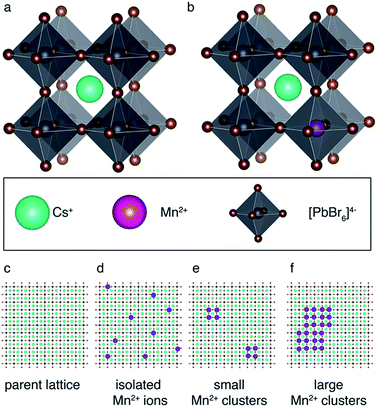
Fig. 1 schematically shows how paramagnetic metal ions can be incorporated into perovskite lattices. Analysis of XRD and TEM data of Mn2+-doped cesium lead halides has suggested lattice contraction consistent with homovalent B-site substitution (ionic radii: Pb2+: 133 pm, Mn2+: 97 pm).9,11 Heterovalent A-site replacement with concomitant formation of A-site vacancies has never been considered as highly unlikely owing to even larger mismatch of ionic radii (Cs+: 167 pm). In our analysis, we assume that homovalent B-site substitution is the dominant substitution mechanism. Since the Cs–Pb distance in the parent CsPbBr3 lattice (Fig. 1a) is about 5 Å, replacing Pb2+ by Mn2+ is expected to cause substantial PRE. An important question associated with manganese doping is whether or not it is uniformly dispersed inside the perovskite lattice (Fig. 1c and d) or whether it forms larger manganese-rich domains (Fig. 1e and f). Since sensitised luminescence relies on the exchange of energy between the host lattice and the dopant, it is crucial to know if the dopant forms large aggregates. To answer these questions, we carried out 133Cs relaxation measurements on mechanochemically53,54 synthesized CsPbBr3 undoped and stoichiometrically doped with 0.5, 3 and 8 mol% of Mn2+ (see Fig. S4† for the 133Cs spectra). The corresponding saturation-recovery curves (Fig. 2a) show significantly faster recovery (shorter T1) of 133Cs nuclei in the perovskite phase of the Mn2+-doped samples and indicate incorporation of the paramagnetic dopant into the perovskite lattice.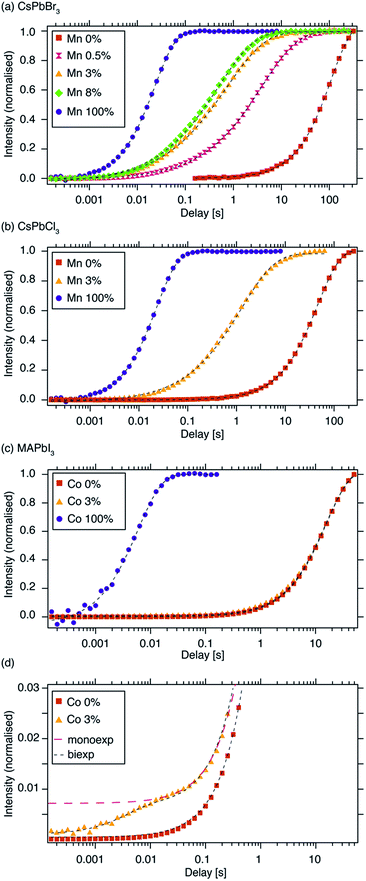 | ||
| Fig. 2 133Cs T1 build-up curves measured using a saturation-recovery sequence (shorthand legend labels are given in parentheses): (a) CsPbBr3, (“Mn 0%”) CsPb0.995Mn0.005Br3 (“Mn 0.5%”), CsPb0.97Mn0.03Br3 (“Mn 3%”), CsPb0.92Mn0.08Br3 (“Mn 8%”) and CsMnBr3 (“Mn 100%”), (b) 133Cs T1 of CsPbCl3, (“Mn 0%”), CsPb0.97Mn0.03Cl3 (“Mn 3%”) and CsMnCl3 (“Mn 100%”), (c) 1H T1 of MAPbI3, (“Co 0%”), MAPb0.97Co0.03I3 (“Co 3%”) and MA2CoI4 (“Co 100%”), (d) a vertical zoom of the initial recovery period from panel “c”. Experimental conditions: (a, b) at 9.4 T and 20 kHz MAS, (c) at 21.1 T and 20 kHz MAS. Dashed lines are fits: (a, b) stretched exponential, (c, d) mono-exponential (Co 0%, Co 100%), bi-exponential (black marker, Co 3%), mono-exponential (red marker, Co 3%). The curves were normalized to the fully recovered intensity. Raw data are given in the ESI.† | ||
Since paramagnetic doping leads to a distribution of apparent relaxation times, the curves are best fitted using a stretched exponential function:
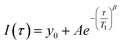 | (1) |
| Material | 133Cs T1 [s] | Stretching parameter β |
|---|---|---|
| CsPbBr3 | 109 ± 1 | 0.999 ± 0.007 |
| CsPb0.995Mn0.005Br3 | 4.00 ± 0.02 | 0.585 ± 0.002 |
| CsPb0.97Mn0.03Br3 | 0.73 ± 0.01 | 0.541 ± 0.006 |
| CsPb0.92Mn0.08Br3 | 0.49 ± 0.01 | 0.569 ± 0.006 |
| CsMnBr3 | 0.0233 ± 0.0001 | 1.000 ± 0.009 |
| CsPbCl3 | 45.9 ± 0.1 | 0.941 ± 0.002 |
| CsPb0.97Mn0.03Cl3 | 1.27 ± 0.02 | 0.633 ± 0.008 |
| CsMnCl3 | 0.0388 ± 0.0002 | 0.976 ± 0.005 |
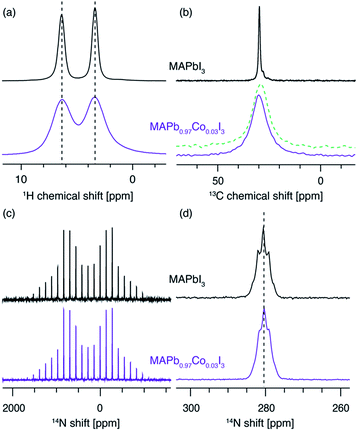
B-site Co2+ incorporation has recently been reported and its effects studied for MAPbI3, the widely used standard photovoltaic material.34,48Fig. 2c shows 1H saturation-recovery curves of MAPbI3 undoped and stoichiometrically doped with 3 mol% Co2+, corresponding to the composition “MAPb0.97Co0.03I3”, that is assuming homovalent replacement of Pb2+ with Co2+. High-spin cobalt(II) in octahedral (Oh) symmetry at a distance of 5 angstroms from a proton is expected to lead to 1H PRE on the order of 30 s−1, or more if the symmetry is lower.50 The relaxation behaviour observed here is significantly different from the previous cases. 1H T1 relaxation of undoped MAPbI3 is best described using a mono-exponential function with a T1 of (15.89 ± 0.04) s (Table 2). Upon doping with Co2+, no stretching is observed. Instead, a clear biexponential behaviour is evident (Fig. 2d), and a satisfactory fit is obtained by constraining the slowly relaxing component using the T1 of the reference diamagnetic MAPbI3 phase while fitting the small, fast relaxing component. This procedure yields a T1 of (10 ± 10) ms for the fast relaxing component, with the large error being due to the very large intensity difference between the two components. This suggests the presence of undoped MAPbI3 and a separate, purely paramagnetic phase (Fig. 2d). A mono-exponential fit yields a T1 of (15.3 ± 0.2) s and does not provide a satisfactory description of the early phase of the recovery, as shown in Fig. 2d in the trace labelled “monoexp”. The reference paramagnetic phase, MA2CoI4, has a T1 of (6.7 ± 0.1) ms. The clear bi-exponential relaxation behaviour and no shortening of T1of the MAPbI3perovskite phase provides compelling evidence that in this case Co2+is not incorporated into the perovskite lattice. We note that, in principle, the two components could be quantified to give the relative amounts of the two phases. However, since the T1 measurements were carried out using an echo saturation-recovery sequence to remove the probe background, a sizeable portion of the cobalt-rich phase loses spin coherence due to fast T2 relaxation during the 0.2 ms echo delay,71–73 which in turn makes its signal intensity lower. On the other hand, the diamagnetic phase has a comparatively long T′2, hence its coherence decays less in the spin echo experiment. The difference in coherence lifetimes of protons in the two phases makes the quantification of these saturation-recovery curves unreliable, as it underestimates the amount of the cobalt-rich phase. Using numerical simulations (vide infra), we demonstrate that the bi-exponential behaviour corresponds to the formation of cobalt-rich phases with a radius larger than 100 nm (see the ESI† for details).
| Material | 1H T1 [s] | |
|---|---|---|
| Component 1 | Component 2 | |
| MAPbI3 | 15.89 ± 0.04 | — |
| MAPb0.97Co0.03I3 | 15.3 ± 0.2 | — |
| MAPb0.97Co0.03I3 | 15.89 (constraint) | 0.01 ± 0.01 |
| MA2CoI4 | 0.0067 ± 0.0001 | — |
We corroborate this result by comparing the 1H, 13C and 14N MAS NMR spectra of the two materials (Fig. 4). The 1H (Fig. 3a) and 13C (Fig. 3b) isotropic chemical shifts as well as the 14N shift (Fig. 3c and d) are, to within error, identical for both materials. The presence of paramagnetic ions should lead to hyperfine shifts of the neighbouring nuclei. For protons at a distance of 5 angstroms from a high-spin Co2+ ion in octahedral (Oh) symmetry, shifts on the order of 10 ppm are expected.50,74,75 For example, the H–Co2+ distance of about 3.5 angstroms76 in the MA2CoI4 paramagnetic reference phase leads to an isotropic 1H shift of 24.7 ppm (Fig. S5,† a relative shift of about 20 ppm compared to the diamagnetic MAPbI3). We have previously shown that 14N spectral envelopes are a sensitive probe of cation incorporation into perovskites, as they indicate changes in the symmetry of the cubooctahedral cavity in which the picosecond time scale cation reorientation takes place.43–45 The 14N spectral envelopes of both materials are identical, indicating that the reorientation symmetry of the MA cation did not change upon Co2+ doping, consistent with no change in the crystallographic symmetry of the main perovskite phase (Fig. 3c). The significant broadening present in the sample doped with Co2+ is due to bulk magnetic susceptibility effects caused by the presence of a secondary paramagnetic phase leading to inhomogeneity of the magnetic field inside the sample volume.77,78 This effect can be reproduced by simply mixing MAPbI3 with 3 mol% of CoI2, without mechanochemical grinding and annealing (Fig. 3b, green dashed line). Notably, beside pronounced broadening, bulk magnetic susceptibility effects can also cause small shifts, depending on the homogeneity of mixing of the two phases. These shifts can potentially be misinterpreted as a change in the underlying molecular structure. This effect is also visible here (Fig. 3b, green dashed line vs. violet solid line) and it highlights the key advantage of the relaxation-based methodology. No EPR spectra could be detected from MAPbI3 doped with Co2+ and MA2CoI4, consistent with the very large exchange interaction expected in cobalt-rich phases. The XRD patterns of the materials are shown in Fig. S3.† All these observations are thus consistent with no incorporation of Co2+ into the perovskite lattice.
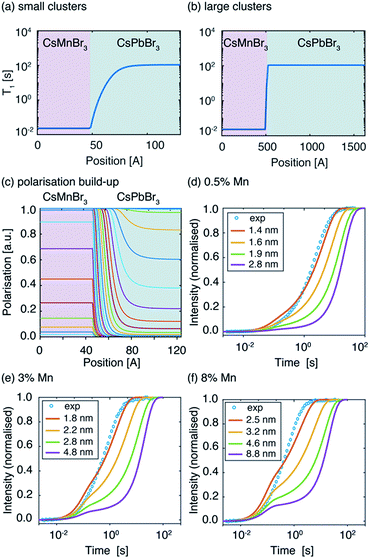
In order to further probe Mn2+ aggregation inside the perovskite lattice, we modelled the spatial distribution of polarisation in the presence of Mn-induced PRE by describing polarisation dynamics using a heat transfer equation.51 The full procedure is described in the SI. As described in the introduction, the PRE effect can in some cases propagate through spin diffusion. We use a pseudopotential defined by De Gennes79 to describe the competition between PRE and SD and demonstrate that in the case of Mn-doped CsPbBr3 the PRE effect is not relayed by spin diffusion (see the ESI† for full derivation). To model domain formation, we consider spherical clusters of CsMnBr3 surrounded by a CsPbBr3 lattice. Inside the cluster, the 133Cs spin-lattice relaxation time was measured to be T1,cluster = 23 ms. Outside the cluster, the 133Cs T1 depends on the distance between the cesium atom and the nearest manganese atom from the CsMnBr3 cluster and follows an r−6 dependence. We consider paramagnetic clusters with a radius of between 1.4 and 8.8 nm, schematically shown in Fig. 4a and b.
The resulting polarisation dynamics can then be plotted as a function of position, for different time steps in a saturation recovery experiment (Fig. 4c). As expected, the polarisation is predicted to build up quickly inside the CsMnBr3 region due to strong PRE, and more slowly in the diamagnetic CsPbBr3 region. The simulation is then performed for increasing cluster radii while adjusting the diamagnetic volume so that the doping percentage is respected. The build-up curves obtained in this way are shown in Fig. 4d–f. For the largest cluster radii, the simulated build-up behaviour is clearly bi-exponential. By fitting the curves one obtains a component corresponding to cesium atoms located inside the paramagnetic cluster with a T1,fit = 23 ms and representing 0.5%, 3%, and 8% of the total build-up, while the second component represents 99.5%, 97%, and 92%, respectively, of the total build-up with a T1,fit = 108 s. These results demonstrate that for large clusters, the PRE effect in the diamagnetic CsPbBr3 lattice is negligible given the comparatively low surface area of the cluster. However, as the radius of the paramagnetic cluster decreases, the surface area increases and the PRE effect in the diamagnetic part of the lattice becomes more pronounced, leading to stretched exponential behaviour. Comparing this simulation with the experimental curves allows us to conclude that the manganese dopant does not form manganese-rich clusters larger than 1.6 nm (2 unit cells), 2.2 nm (3 unit cells), and 3.2 nm (5 unit cells) for 0.5%, 3% and 8% Mn2+doping, respectively. Finally, we note that the numerical simulation does not perfectly reproduce the experimentally observed recovery curve. This is caused by the fact that the simulation, based on the heat transfer equation, describes the flow of polarization in the spin system as being continuous. In reality, the lattice is composed of discrete unit cells which renders this approach approximate when the involved length scale is on the order of the lattice parameters, as it is the case here for the smallest clusters. Finally, we note that this approach yields information on the cluster size but not the homogeneity or spatial distribution of the clusters.
Conclusions
In conclusion, we have shown that the introduction of paramagnetic dopants into perovskite phases leads to substantial shortening of their nuclear relaxation times. This approach is a straightforward and general method for evidencing substitutional doping of perovskites with paramagnetic transition metal or lanthanide ions. Specifically, we have shown that Mn2+ is readily incorporated into CsPbBr3 and CsPbCl3 up to at least 8 mol% and 3%, respectively and that if it forms any clusters they are not larger than 2 to 5 unit cells, depending on the doping level. Conversely, we show that Co2+ is not capable of doping the MAPbI3 perovskite phase. We believe that this simple, relaxation-based approach should become a routine tool for the characterization of perovskites doped with paramagnetic ions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Moreno Lelli for helpful discussions. This work was supported by Swiss National Science Foundation Grant No. 200021_160112. D. P. acknowledges financial support from the HOMING programme of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund (POIR.04.04.00-00-5EE7/18-00). S. M. Z. and M. G acknowledge funding from the EU Horizon 2020 programme, through the FET Open Research and Innovation Action, grant agreement no. 687008. M. G. and S. M. Z thank the King Abdulaziz City for Science and Technology (KACST) and the SNSF for a joint research project (IZLRZ2_164061) under Scientific & Technological Cooperation Programme Switzerland-Russia.Notes and references
- W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099 CrossRef.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- G. Nedelcu, L. Protesescu, S. Yakunin, M. I. Bodnarchuk, M. J. Grotevent and M. V. Kovalenko, Nano Lett., 2015, 15, 5635–5640 CrossRef CAS PubMed.
- Q. A. Akkerman, V. D'Innocenzo, S. Accornero, A. Scarpellini, A. Petrozza, M. Prato and L. Manna, J. Am. Chem. Soc., 2015, 137, 10276–10281 CrossRef CAS PubMed.
- S. Sun, D. Yuan, Y. Xu, A. Wang and Z. Deng, ACS Nano, 2016, 10, 3648–3657 CrossRef CAS PubMed.
- D. Zhang, S. W. Eaton, Y. Yu, L. Dou and P. Yang, J. Am. Chem. Soc., 2015, 137, 9230–9233 CrossRef CAS PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. I. Seok, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- W. Liu, Q. Lin, H. Li, K. Wu, I. Robel, J. M. Pietryga and V. I. Klimov, J. Am. Chem. Soc., 2016, 138, 14954–14961 CrossRef CAS PubMed.
- D. Parobek, B. J. Roman, Y. Dong, H. Jin, E. Lee, M. Sheldon and D. H. Son, Nano Lett., 2016, 16, 7376–7380 CrossRef CAS PubMed.
- S. Zou, Y. Liu, J. Li, C. Liu, R. Feng, F. Jiang, Y. Li, J. Song, H. Zeng, M. Hong and X. Chen, J. Am. Chem. Soc., 2017, 139, 11443–11450 CrossRef CAS PubMed.
- Q. A. Akkerman, D. Meggiolaro, Z. Dang, F. De Angelis and L. Manna, ACS Energy Lett., 2017, 2, 2183–2186 CrossRef CAS PubMed.
- K. Xu, C. C. Lin, X. Xie and A. Meijerink, Chem. Mater., 2017, 29, 4265–4272 CrossRef CAS PubMed.
- X. Yuan, S. Ji, M. C. De Siena, L. Fei, Z. Zhao, Y. Wang, H. Li, J. Zhao and D. R. Gamelin, Chem. Mater., 2017, 29, 8003–8011 CrossRef CAS.
- D. Rossi, D. Parobek, Y. Dong and D. H. Son, J. Phys. Chem. C, 2017, 121, 17143–17149 CrossRef CAS.
- D. Gao, B. Qiao, Z. Xu, D. Song, P. Song, Z. Liang, Z. Shen, J. Cao, J. Zhang and S. Zhao, J. Phys. Chem. C, 2017, 121, 20387–20395 CrossRef CAS.
- J. Zhu, X. Yang, Y. Zhu, Y. Wang, J. Cai, J. Shen, L. Sun and C. Li, J. Phys. Chem. Lett., 2017, 8, 4167–4171 CrossRef CAS PubMed.
- W. J. Mir, M. Jagadeeswararao, S. Das and A. Nag, ACS Energy Lett., 2017, 2, 537–543 CrossRef CAS.
- Q. Wang, X. Zhang, Z. Jin, J. Zhang, Z. Gao, Y. Li and S. F. Liu, ACS Energy Lett., 2017, 2, 1479–1486 CrossRef CAS.
- F. Meinardi, Q. A. Akkerman, F. Bruni, S. Park, M. Mauri, Z. Dang, L. Manna and S. Brovelli, ACS Energy Lett., 2017, 2, 2368–2377 CrossRef CAS.
- H. Liu, Z. Wu, J. Shao, D. Yao, H. Gao, Y. Liu, W. Yu, H. Zhang and B. Yang, ACS Nano, 2017, 11, 2239–2247 CrossRef CAS PubMed.
- T. He, J. Li, C. Ren, S. Xiao, Y. Li, R. Chen and X. Lin, Appl. Phys. Lett., 2017, 111, 211105/1–211105/4 CAS.
- J.-H. Cha, J. H. Han, W. Yin, C. Park, Y. Park, T. K. Ahn, J. H. Cho and D.-Y. Jung, J. Phys. Chem. Lett., 2017, 8, 565–570 CrossRef CAS PubMed.
- M. Lorenzon, L. Sortino, Q. Akkerman, S. Accornero, J. Pedrini, M. Prato, V. Pinchetti, F. Meinardi, L. Manna and S. Brovelli, Nano Lett., 2017, 17, 3844–3853 CrossRef CAS PubMed.
- C. Zhou, Y. Tian, O. Khabou, M. Worku, Y. Zhou, J. Hurley, H. Lin and B. Ma, ACS Appl. Mater. Interfaces, 2017, 9, 40446–40451 CrossRef CAS PubMed.
- D. Parobek, Y. Dong, T. Qiao and D. H. Son, Chem. Mater., 2018, 30, 2939–2944 CrossRef CAS.
- D. Chen, G. Fang and X. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 40477–40487 CrossRef CAS PubMed.
- H. Wu, S. Xu, H. Shao, L. Li, Y. Cui and C. Wang, Nanoscale, 2017, 9, 16858–16863 RSC.
- P. Wang, B. Dong, Z. Cui, R. Gao, G. Su, W. Wang and L. Cao, RSC Adv., 2018, 8, 1940–1947 RSC.
- J.-S. Yao, J. Ge, B.-N. Han, K.-H. Wang, H.-B. Yao, H.-L. Yu, J.-H. Li, B.-S. Zhu, J.-Z. Song, C. Chen, Q. Zhang, H.-B. Zeng, Y. Luo and S.-H. Yu, J. Am. Chem. Soc., 2018, 140, 3626–3634 CrossRef CAS PubMed.
- M. T. Klug, A. Osherov, A. A. Haghighirad, S. D. Stranks, P. R. Brown, S. Bai, J. T.-W. Wang, X. Dang, V. Bulovic, H. J. Snaith and A. M. Belcher, Energy Environ. Sci., 2017, 10, 236–246 RSC.
- S. T. Williams, A. Rajagopal, S. B. Jo, C.-C. Chueh, T. F. L. Tang, A. Kraeger and A. K.-Y. Jen, J. Mater. Chem. A, 2017, 5, 10640–10650 RSC.
- R. Beaulac, P. I. Archer, J. van Rijssel, A. Meijerink and D. R. Gamelin, Nano Lett., 2008, 8, 2949–2953 CrossRef CAS PubMed.
- S. Kondo, K. Amaya and T. Saito, Journal of Physics-Condensed Matter, 2002, 14, 2093–2099 CrossRef CAS.
- K. -H. Wang, L. Wu, L. Lei, H. -B. Yao, H. -S. Qian and S. -H. Yu, Angew. Chem., Int. Ed., 2016, 55, 8328–8332 CrossRef CAS PubMed.
- Q. A. Akkerman, S. Park, E. Radicchi, F. Nunzi, E. Mosconi, F. De Angelis, R. Brescia, P. Rastogi, M. Prato and L. Manna, Nano Lett., 2017, 17, 1924–1930 CrossRef CAS PubMed.
- O. Knop, R. E. Wasylishen, M. A. White, T. S. Cameron and M. J. M. Van Oort, Can. J. Chem., 1990, 68, 412–422 CrossRef CAS.
- B. A. Rosales, L. Men, S. D. Cady, M. P. Hanrahan, A. J. Rossini and J. Vela, Chem. Mater., 2016, 28, 6848–6859 CrossRef CAS.
- B. A. Rosales, M. P. Hanrahan, B. W. Boote, A. J. Rossini, E. A. Smith and J. Vela, ACS Energy Lett., 2017, 2, 906–914 CrossRef CAS.
- C. Roiland, G. Trippe-Allard, K. Jemli, B. Alonso, J.-C. Ameline, R. Gautier, T. Bataille, L. Le Polles, E. Deleporte, J. Even and C. Katan, Phys. Chem. Chem. Phys., 2016, 18, 27133–27142 RSC.
- W. M. J. Franssen, S. G. D. van Es, R. Dervisoglu, G. A. de Wijs and A. P. M. Kentgens, J. Phys. Chem. Lett., 2017, 8, 61–66 CrossRef CAS PubMed.
- A. Senocrate, I. Moudrakovski, G. Y. Kim, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Angew. Chem., Int. Ed., 2017, 56, 7755–7759 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Péchy, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10055–10061 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 14173–14180 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, M. Saski, P. Yadav, D. Bi, N. Pellet, J. Lewiński, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2018, 140, 3345–3351 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2018, 140, 7232–7238 CrossRef CAS PubMed.
- A. Karmakar, A. M. Askar, G. M. Bernard, V. V. Terskikh, M. Ha, S. Patel, K. Shankar and V. K. Michaelis, Chem. Mater., 2018, 30, 2309–2321 CrossRef CAS.
- T. Polenova, R. Gupta and A. Goldbourt, Anal. Chem., 2015, 87, 5458–5469 CrossRef CAS PubMed.
- I. Solomon, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, NMR of Paramagnetic Molecules, Elsevier Science, 2017 Search PubMed.
- N. Bloembergen, Physica, 1949, 15, 386–426 CrossRef CAS.
- S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1990, 63, 913–919 CrossRef CAS.
- D. Prochowicz, M. Franckevicius, A. M. Cieslak, S. M. Zakeeruddin, M. Gratzel and J. Lewinski, J. Mater. Chem. A, 2015, 3, 20772–20777 RSC.
- D. Prochowicz, P. Yadav, M. Saliba, M. Saski, S. M. Zakeeruddin, J. Lewinski and M. Gratzel, Sustainable Energy Fuels, 2017, 1, 689–693 RSC.
- M. GORDON and M. HOCH, Journal of Physics C-Solid State Physics, 1978, 11, 783–795 CrossRef CAS.
- W. E. Blumberg, Phys. Rev., 1960, 119, 79–84 CrossRef CAS.
- I. J. Lowe and D. Tse, Phys. Rev., 1968, 166, 279–291 CrossRef CAS.
- D. Tse and S. R. Hartmann, Phys. Rev. Lett., 1968, 21, 511–514 CrossRef CAS.
- P. M. Henrichs, M. Linder and J. M. Hewitt, J. Chem. Phys., 1986, 85, 7077–7086 CrossRef CAS.
- A. Narayanan, J. S. Hartman and A. D. Bain, J. Magn. Reson., Ser. A, 1995, 112, 58–65 CrossRef CAS.
- M. H. Alaimo and I. E. Roberts, Solid State Nucl. Magn. Reson., 1997, 8, 241–250 CrossRef CAS PubMed.
- J. S. Hartman, A. Narayanan and Y. Wang, J. Am. Chem. Soc., 1994, 116, 4019–4027 CrossRef CAS.
- H. -J. Seifert and E. Dau, Z. Anorg. Allg. Chem., 1972, 391, 302–312 CrossRef CAS.
- K. Keller, M. Zalibera, M. Qi, V. Koch, J. Wegner, H. Hintz, A. Godt, G. Jeschke, A. Savitsky and M. Yulikov, Phys. Chem. Chem. Phys., 2016, 18, 25120–25135 RSC.
- R. E. Taylor, P. A. Beckmann, S. Bai and C. Dybowski, J. Phys. Chem. C, 2014, 118, 9143–9153 CrossRef CAS.
- Q. Xu, E. Taro, H. Nakayama, N. Nakamura and K. Michihiko, Z. Naturforsch., 2014, 46, 240 Search PubMed.
- A. Senocrate, I. Moudrakovski and J. Maier, Phys. Chem. Chem. Phys., 2018, 20, 20043–20055 RSC.
- D. L. Bryce, G. D. Sward and S. Adiga, J. Am. Chem. Soc., 2006, 128, 2121–2134 CrossRef CAS PubMed.
- C. M. Widdifield, R. P. Chapman and D. L. Bryce, in Annual Reports on NMR Spectroscopy, Academic Press, 2009, vol. 66, pp. 195–326 Search PubMed.
- C. M. Widdifield and D. L. Bryce, J. Phys. Chem. A, 2010, 114, 10810–10823 CrossRef CAS PubMed.
- C. Marichal, J. Hirschinger, P. Granger, M. Menetrier, A. Rougier and C. Delmas, Inorg. Chem., 1995, 34, 1773–1778 CrossRef CAS.
- V. Ladizhansky and S. Vega, J. Phys. Chem. B, 2000, 104, 5237–5241 CrossRef CAS.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc. DOI:10.1016/j.pnmrs.2018.05.001.
- S. Balayssac, I. Bertini, M. Lelli, C. Luchinat and M. Maletta, J. Am. Chem. Soc., 2007, 129, 2218–2219 CrossRef CAS PubMed.
- I. Bertini, A. Bhaumik, G. De Paëpe, R. G. Griffin, M. Lelli, J. R. Lewandowski and C. Luchinat, J. Am. Chem. Soc., 2010, 132, 1032–1040 CrossRef CAS PubMed.
- M. Daub, R. Stroh and H. Harald, Z. Anorg. Allg. Chem., 2016, 642, 268–274 CrossRef CAS.
- N. Bloembergen and W. C. Dickinson, Phys. Rev., 1950, 79, 179–180 CrossRef CAS.
- A. Kubo, T. P. Spaniol and T. Terao, J. Magn. Reson., 1998, 133, 330–340 CrossRef CAS PubMed.
- P.-G. de Gennes, J. Phys. Chem. Solids, 1958, 7, 345–350 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta11457a |
| This journal is © The Royal Society of Chemistry 2019 |