Bifunctional OER/ORR catalytic activity in the tetrahedral YBaCo₄O_7.3 oxide

Abstract

Transition metal oxides, mostly perovskites, have received attention as effective catalysts for the oxygen evolution reaction (OER) and oxygen reduction reaction (ORR) in alkaline media. However, despite the numerous reaction mechanisms and descriptors proposed, the understanding of the nature of their electrochemical activity is still far from complete. Herein, we present YBaCo₄O_7.3 oxide with tetrahedrally coordinated Co²⁺/Co³⁺ as a fundamentally new bifunctional catalyst, which demonstrates OER activity of 1.18 mA cm⁻² at an overpotential of 400 mV and ORR activity of 2.76 mA cm⁻² at an overpotential of −537 mV, exceeding that of the LaNiO₃ benchmark catalyst. The electrochemical activity of YBaCo₄O_7.3 was rationalized in terms of the Zaanen–Sawatzky–Allen model using DFT-based calculations. According to the results, overstoichiometric oxygen induces octahedral Co positions as active sites in the OER, while large Coulomb on-site repulsion energy for Co in the tetrahedral coordination makes these sites active in the ORR.

---

Introduction

The practical deployment of low-temperature regenerative alkaline fuel cells is impeded by significant energy loss due to the sluggish kinetics of the oxygen reduction (ORR, O₂ + 2H₂O + 4e⁻ → 4OH⁻) and oxygen evolution (OER, 4OH⁻ → O₂ + 2H₂O + 4e⁻) reactions.¹ Transition metal oxides are considered as promising catalysts for the OER and ORR with fair potential of bifunctionality (i.e. activity for both OER and OER),^2–4 resistance to corrosion in alkaline media, moderate cost and low environmental hazard. Precious group metals (PGMs) and their oxides are generally used for benchmarking the catalytic activity in the OER/ORR, but their scarcity and high cost have motivated the extensive search for possible alternatives. Transition metal (TM) oxides are known for their stability in alkaline solutions and ability to catalyze both reactions. The most common non-PGM bifunctional catalysts include the binary oxides M_xO_y (M = Mn, Co, Ni), oxyhydroxides (M′M′′OOH, particularly with M′, M′′ = Fe, Ni), spinels, conventional perovskites AMO_3±δ, and quadruple perovskites (AMn₇O₁₂ (A = Ca and La)).^5–7

Although recent studies on specific perovskites have demonstrated the ability of lattice oxygen to play a role in the OER,^8,9 generally the ORR/OER electrocatalytic activity of a material can be rationalized in terms of its surface reaction mechanism, which presents a complex problem requiring knowledge of intermediate steps, associated Gibbs free energies and activation barriers.^10–13 However, due to the linear correlation of activation barriers with reaction free energies^14–16 and linear relationships between the adsorption energies of intermediates preserved for a wide range of catalyst chemistry, crystal and surface and electronic structures,^11,17,18 the qualitative understanding of catalytic activity trends can be achieved in a less sophisticated manner.^11,14 For example, Rossmeisl et al. showed that the adsorption energy ΔE(O*(ads)) is a good descriptor of OER activity for rutile-type oxides.¹⁶ For perovskites in OER conditions, ΔE(O*(ads)) − ΔE(HO*(ads)) strongly correlates with activity, while for the ORR the ΔE(HO*(ads)) energy is the preferred descriptor.¹⁴ The calculation of surface binding energies is complicated by the choice of surface orientation, its termination, and identification of active sites. This type of information is also difficult to obtain both from experimental and computational studies. Hence, to simplify the situation even further, instead of adsorption energies, the electronic structure features of the bulk material are used as effective descriptors of catalytic activity. This fairly crude approach has shown to be useful due to the linear relationships between O*, OO*, HO*, and HOO* adsorption energies, and the relation of the adsorption energies to the surface electronic structure, which in turn inherits the electronic structure of the bulk material. The examples of the discussed electronic structural features are the number of electrons on the d shells¹⁹ and on the e_g* orbital of the transition metal,^20,21 the d-band center of the transition metal,²² the O p-band center,²³ and the charge-transfer energy (Δ).^24,25

The electronic structure of TM oxide catalysts is generally discussed in terms of the Zaanen–Sawatzky–Allen (ZSA) three-band model,²⁶ in which the TM d-manifold is split due to Coulomb repulsion into two bands (upper and lower Hubbard bands, UHB and LHB, respectively) with the energy difference U, the anionic O2p band is separated from UHB by the charge transfer energy Δ, and the band overlap is controlled by the one-electron bandwidth W. The ZSA model has been demonstrated to be universal, being applicable to oxide materials with various crystal structures and transition metals. Considering ionic bonding, the band positioning with respect to each other and to the Fermi level depends on the ionization energies of the Mⁿ⁺/M⁽ⁿ⁺¹⁾⁺ cations and Madelung site potentials, taking into account the effect of coordination of the M cations with oxygen.²⁷ However, this strongly simplified approach can fail in accounting for the changing coordination geometry of the TM cations (for instance, from octahedral to tetrahedral) in prediction of the true band structure,²⁸ which may be related to the stronger hybridization of the M3d and O2p orbitals in the tetrahedral MO₄ unit compared to that in MO₆ octahedra.²⁹

The crystal structures of most TM oxide catalysts are based on octahedral MO₆ units (with the exception of spinels and some anion-deficient³⁰ and hexagonal perovskites³¹). Considering that pure tetrahedral structures (i.e. comprised exclusively of MO₄ units) have never been considered as potential catalysts for the OER and ORR in alkaline media, the investigation of their activity toward these reactions is of significant fundamental interest and may provide new insight into the relationships between the electronic structure and catalytic activity and verify the applicability of certain descriptors for materials outside the conventional field of research. Thus, herein, we suggest the complex transition metal oxide YBaCo₄O_7+δ as a potential bifunctional catalyst.

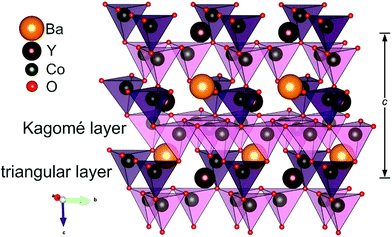
The crystal structure of YBaCo₄O_7+δ consists of two types of corner-sharing CoO₄ tetrahedra in a 1 : 3 ratio linked into a framework by corner sharing (Fig. 1). The tetrahedra are distinguished by different bond lengths and are located in alternating Kagomé and triangular layers. YBaCo₄O_7+δ can adopt a wide range of oxygen nonstoichiometries with δ varying from 0 to 1.5,^32,33 which corresponds to a change in the cobalt average oxidation state from +2.25 to +3. YBaCo₄O_7+δ demonstrates the ability to reversibly intercalate impressive amounts of oxygen at temperatures ranging from 270–350 °C,³² making it a promising oxygen storage material as well. The oxygen-storage capacity (OSC) of YBaCo₄O_7+δ (OSC ≈ 2450 μmol-O g⁻¹) substantially exceeds that reported for conventional oxygen-storage materials, e.g. CeO₂–ZrO₂ (OSC ≈ 1500 μmol-O g⁻¹).^34,35 The oxidation capacity of YBaCo₄O_7+δ has been intensively studied in many works^34,36 by thermogravimetric measurements under an O₂ flow and under anodic and cathodic polarization in alkaline aqueous solution.³⁷ YBaCo₄O_7+δ possesses mixed ionic and electronic conductivity with a dominant contribution from p-type electronic conduction, demonstrating conductivity of ∼2.5 S cm⁻¹ at 50 °C.^38,39

Fig. 1 Crystal structure of YBaCo₄O₇. The triangular and Kagomé layers alternate along the c-axis.

Herein, we report the investigation of the activity of YBaCo₄O_7+δ toward the OER and ORR in alkaline media and attempt to trace the origin of its activity using the intrinsic features of its electronic structure.

Experimental

Synthesis

YBaCo₄O_7+δ samples were synthesized via an ethylenediaminetetraacetic acid (EDTA)-complexing method followed by high temperature annealing. Stoichiometric amounts of Y(NO₃)₃·6H₂O (Sigma-Aldrich), Ba(NO₃)₂ (Ruskhim) and Co(CH₃COO)₂·4H₂O (Sigma-Aldrich) were mixed with EDTA (Sigma-Aldrich) and dissolved in a minimum volume of distilled water (∼5 mL per 1 g of metal salts) under vigorous stirring for 10–15 min. The molar ratio between the total amount of metal ions and EDTA was 1 : 1.5, and 20 wt% ammonia was used to adjust the pH value between 9 and 10. The solution was heated over a burner to form a very viscous mass. After evaporation of water, the product ignited spontaneously to turn into a raw ash, which was placed in an alumina crucible and calcined in air at 650 °C for 5 h. The obtained black-colored precursor was reground in an agate mortar, pressed into a pellet, heated at 1100 °C in air for 4–8 h and then quenched to ambient temperature in air.

Powder X-ray diffraction

The phase purity and the lattice parameters were determined by powder X-ray diffraction (PXRD) using a Huber G670 Guinier camera (transmission geometry, curved primary Ge (111) monochromator, CoKα₁ radiation (λ = 1.78896 Å), image plate detector). The Rietveld refinement was performed using the JANA2006 software.⁴⁰

Oxygen content analysis

The oxygen content was measured via a standard iodometric titration. About 15 mg of sample was placed into a glass flask and 20 mL of 20 wt% KI solution was added. Thereafter, several drops of concentrated HCl were added to dissolve the powder. The flask was tightly closed and kept in the dark for 10 minutes followed by the addition of 50 mL of distilled water. The solution was titrated with 0.0022 M sodium thiosulfate and several drops of starch were added at the very end of the titration to form a transparent violet solution. The procedure was continued until a straw-coloured solution was formed. The calculation of the Co³⁺ fraction was performed according to the equations:

2Co³⁺(aq) + 3I⁻(aq) = 2Co²⁺(aq) + I₃⁻(aq)

I₃⁻(aq) + 2S₂O₃²⁻(aq) = 3I⁻(aq) + S₄O₆²⁻(aq)

Electron microscopy

The morphology of the YBaCo₄O_7+δ crystallites was characterized via scanning electron microscopy (SEM) with a JEOL JSM-6490LV microscope at 30 kV. Electron diffraction (ED) patterns, high-angle annular dark field scanning transmission electron microscopy (HAADF-STEM) images, annular bright-field STEM (ABF-STEM) images and energy dispersive X-ray (EDX) compositional maps were obtained with an aberration-corrected Titan G3 transmission electron microscope operated at 200 kV and equipped with a Super-X EDX system. The sample for the TEM study was prepared by crushing the material under anhydrous ethanol in an agate mortar and depositing a few drops of the suspension onto a holey carbon grid mounted on a Cu support.

Surface area analysis

Nitrogen sorption analysis was performed with a Quantachrome Instruments NOVA 2000 high-speed surface area analyzer at a temperature of 77 K. Prior to the measurements, the samples were degassed in vacuum for at least 12 h at room temperature. The specific surface area was calculated using the Brunauer–Emmett–Teller (BET) method from the nitrogen adsorption data in the relative pressure range (P/P₀) of 0.05 to 0.30.

Electrochemical characterization

YBaCo₄O_7+δ samples were tested for the OER and ORR and oxygen diffusion rates within the bulk material. LaNiO₃ and IrO₂ were used as benchmarks. For the OER and ORR comparison, LaNiO₃ was tested on Vulcan carbon (VC) at 30 wt%, while IrO₂ supported on VC at 20 wt% was tested for the OER only. For OER and ORR testing, the YBaCo₄O_7.3 sample was supported with 30 wt% catalyst on XC-72 VC via ball milling for 3 min using a Wig-L-Bug ball mill. Catalyst inks were prepared by dispersing 2 mg of the supported catalyst in 2 mL of ethanol containing 0.05 wt% Na-substituted Nafion, followed by bath sonication for 2 h. The catalyst inks were dropcast onto 5 mm glassy carbon electrodes (GCE) with 51 μg cm⁻² catalyst/carbon composite, yielding 15.3 μg_oxide cm_geo⁻². Prior to dropcasting, the electrodes were cleaned via sonication in a 1 : 1 deionized (DI) water : ethanol solution followed by polishing using 0.05 μm alumina powder. The powder was removed by sonication in DI water : ethanol solution and dried in air. Oxygen diffusion rate tests were performed on 5 mm GCEs prepared in the same manner described above but with the catalyst supported at 85 wt% on VC.

Electrochemical testing was performed on a Metrohm Autolab PGSTAT302N potentiostat equipped with high speed rotators from Pine Instruments. All OER and ORR measurements were performed in 0.1 M KOH at room temperature. Current interrupt and positive feedback methods were used to determine the electrolyte resistance, which was 46 Ω in 0.1 M KOH and 6 Ω in 1 M KOH. All data for the OER and ORR was iR compensated after testing. Testing was performed in a standard three electrode cell using a CH Instruments Hg/HgO (1 M KOH) reference electrode, Au wire counter electrode, and film of catalyst ink on glassy carbon as the working electrode. All potentials are reported versus the Hg/HgO (1 M KOH) reference electrode or versus the regular hydrogen electrode (RHE), which were determined experimentally to be +0.8976 V vs. Hg/HgO (1 M KOH). Cyclic voltammetry (CV) for both OER and ORR testing was performed in O₂ saturated 0.1 M KOH at a rotation rate of 1600 rpm. For OER testing, the scan rate was 10 mV s⁻¹, while 5 mV s⁻¹ was used for ORR testing. Activities were measured at 1.63 V vs. RHE-iR for the OER and 0.693 V for the ORR. Oxygen diffusion rates were measured following an adapted method reported previously using chronoamperometry at a potential of 50 mV positive of the Co^2+/Co³⁺ redox wave, while being rotated at 1600 rpm to ensure the experiment was performed at a high enough potential that the measured current was due to a diffusion-limited process.^41–43 All OER and ORR stability experiments were performed under the same conditions and in the same experimental setup described above.

DFT calculations

Total energies and optimized geometries were calculated with the Vienna Ab Initio Simulation Package (VASP), which implemented the widely established density-functional theory (DFT).^44–46 The Perdew–Burke–Ernzerhof (PBE) flavor of the generalized gradient approximation (GGA) and projected augmented wave (PAW) method were employed.^47,48 The standard library potentials “Y_sv”, “Ba_sv”, “Co”, and “O”, were used. To consider the strongly correlated character of the d-electrons of cobalt, a Hubbard-like correction was added within the Dudarev scheme and U–J value of 4.2 eV.^49,50 All calculations were performed with spin polarization with the antiferromagnetic ground state (AFM) and tetrahedron method with Blöchl corrections for partial occupancies. The initial crystal structures for YBaCo₄O₇ with P6₃mc (26 atoms) and YBaCo₄O₈ with Pbc2₁ (112 atoms) space groups were taken from the ICSD database.^51,52 The ground state AFM configuration for YBaCo₄O₇ was found by checking all possible configurations (70 in total). For YBaCo₄O₈, the AFM configuration with the lowest energy was chosen from 10 random configurations. The convergence study showed that the energy cut-off of 400 eV and k-point grids of 4 × 4 × 3 and 2 × 2 × 3 were sufficient for the reliable description of lattice constants and formation energies. The relaxation was performed until the forces acting on atoms were smaller than 0.05 eV Å⁻¹. The (001) surface and adsorption energies were calculated using the slab model within the periodic boundary conditions and vacuum thickness of 11 Å. For the slab calculations, only one k-point and dipole correction in the [001] direction, as well as relaxation of all atomic position were chosen. The convergence of adsorption energies was checked with respect to the increase in slab thickness in the [001] direction, increase in surface area, fixing of bottom atomic layers, and increase in k-point density and energy cut-off. The resulting precision for the calculated adsorption energies was in the order of ∼0.3 eV improvement in energy differences. The projected density of states (PDOS) was calculated using the increased k-point density of 8 × 8 × 5 and 4 × 4 × 5 for YBaCo₄O₇ and YBaCo₄O₈, respectively. To make the correct t₂ and e separation of d-orbitals on Co atoms, we rotated the simulation cells in such a way that the oxygen tetrahedra coincided with the tetrahedral crystal field splitting. An effective O p-band center was determined by taking the centroid of the projected density of states of the O 2p states relative to the Fermi level.

Results and discussion

Compositional and crystallographic characterization

The EDX compositional maps of the YBaCo₄O_7+δ crystallites showed a homogeneous distribution of Y, Ba and Co (Fig. S1 of ESI†). Iodometric titration revealed the oxygen non-stoichiometry index δ = 0.3. The PXRD pattern of YBaCo₄O_7.3 was indexed on a hexagonal lattice with the unit cell parameters a = 6.30038(3) Å and c = 10.24280(6) Å and refined by the Rietveld method (Fig. 2, Tables S1 and S2 in ESI†). The unit cell parameters and the c/a ratio of 1.626 correspond well to the δ = 1/3 material prepared by annealing at the partial oxygen pressure P(O₂) = 0.2 bar.⁵³ The PXRD pattern could be fitted with the highest P6₃mc symmetry, but the electron diffraction patterns of YBaCo₄O_7.3 (Fig. 3) demonstrated the presence of satellite reflections corresponding to the modulation vector q = 1/3(a* + b*) + c*. This modulation vector reduces the crystal symmetry down to trigonal, corresponding to the superspace group P31c(1/3,1/3,γ)000. Indeed, a distortion from P6₃mc to P31c has been reported for the room temperature structure of slightly overstoichiometric YBaCo₄O_7+δ.⁵³ However, the refinement of the complete modulated structure requires synchrotron PXRD data as the satellites are too weak to be detected in the laboratory PXRD pattern. The [010] and [11̄0] high resolution HAADF-STEM images confirm that the cation arrangement well-fits the basic P31c structure (Fig. S2 in ESI†). The [11̄0] ABF-STEM image (Fig. S3†) provides a clue on the origin of the superstructure. The ABF intensity profile along the Ba/Y/Co1 triangular layers demonstrates a tripled periodicity along the {110} direction. This tripled periodicity is due to the systematic increase in ABF intensity at the positions between two neighboring Ba/Y/Co1 columns, where two out of three positions show a decrease in scattering density compared to the third (marked with arrowheads in Fig. S3,† bottom). This may be associated with the insertion of overstoichiometric oxygens into the Ba/Y/Co1 triangular layers in an ordered manner. The Kagomé layers stay intact at the given oxygen overstoichiometry index δ = 0.3.

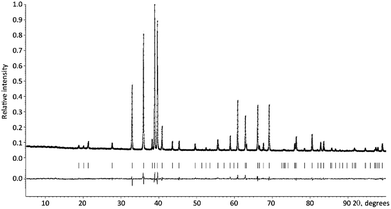Fig. 2 Experimental, calculated and difference PXRD patterns of YBaCo₄O_7.3 after Rietveld refinement. The Bragg positions are indicated with the vertical lines.

Fig. 3 Electron diffraction patterns of YBaCo₄O_7.3. Weak satellite reflections are visible in the [001] and [11̄0] ED patterns.

Microstructural characterization

Since YBaCo₄O_7.3 was prepared via high-temperature calcination, the obtained material consisted of relatively large crystallites with a size of 2–5 μm, as visualized by scanning electron microscopy (ESI, Fig. S4a†). Thus, to decrease the particle size and increase the surface area, the sample was milled in a SPEX 8000M high-energy ball mill for 20 min in ethanol. Ball milling reduced the average particle size by a factor of two (ESI, Fig. S4b†). The BET surface area measured through N₂ adsorption in the milled sample was 3.3 m² g⁻¹ (ESI, Fig. S5†). The ABF-STEM images demonstrate that the surface of the YBaCo₄O_7.3 crystallites retained a high degree of crystallinity (ESI, Fig. S6†).

Electrochemical characterization

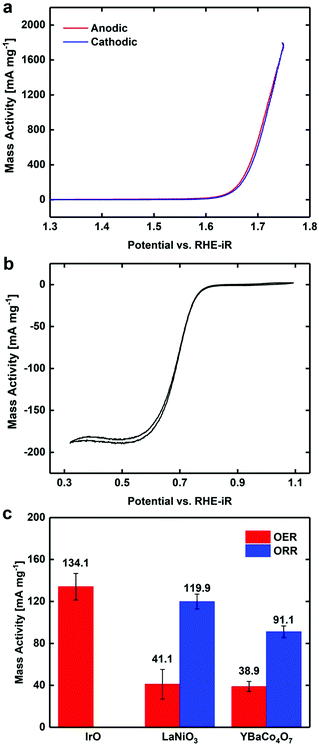
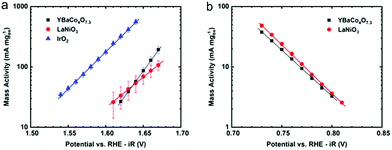
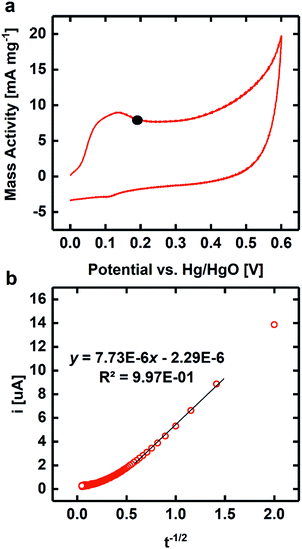
CV was used to quantify the bifunctional capabilities of YBaCo₄O_7.3 in the OER and ORR. The representative CVs for both OER and ORR in O₂-saturated 0.1 M KOH are shown in Fig. 4. The catalyst was supported at 30 wt% on VC because without the carbon support, the catalyst itself is much less conductive than other metallic systems and only contacts the GCE through point contacts. Mixing the catalyst material with VC increased the electrical contact between adjacent catalyst particles and between the catalyst and the electrode, leading to higher conductivity. The activity of YBaCo₄O_7.3 towards the OER at 1.63 V vs. RHE-iR was 39 mA mg⁻¹, which is similar to that of the benchmark catalysts in this field, such as IrO₂ and LaNiO₃ perovskite (see ESI Fig. S7†). Furthermore, its activity towards the ORR was measured to be −91 mA mg⁻¹ at 0.693 V, which also compares well with the abovementioned benchmark catalysts. Although the mass activity of YBaCo₄O_7.3 seems to be moderate, its low surface area of 3.3 m² g⁻¹ has to be considered due to sintering of the metal oxide precursor particles during calcination at high temperature. The specific activities of YBaCo₄O_7.3 calculated with the given surface area scale were determined to be 1.18 mA cm⁻² (OER) and 2.76 mA cm⁻² (ORR). As the surface of the LaNiO₃ sample used here for benchmarking is almost 3 times higher (11.1 m² g⁻¹), the specific activity of YBaCo₄O_7.3 in both the OER and ORR significantly exceeds that of LaNiO₃ (0.37 mA cm⁻² and 1.08 mA cm⁻², respectively). The bifunctional window or the potential difference between the voltage at which 10 mA cm_ox⁻² is generated for the OER and −3 mA cm_ox⁻² for the ORR is 1.00 V. The OER Tafel slope for YBaCo₄O_7.3 is 58 mV dec⁻¹ (Fig. 5), which is significantly lower than the 82 mV dec⁻¹ measured for the benchmark precious metal catalyst IrO₂. The ORR Tafel slope for YBaCo₄O_7.3 is 66 mV dec⁻¹, which is similar to the Tafel slope measured for Pt. The comparisons to other well-studied TM oxides studied by our group in the same experimental setup are shown in the ESI, Table S3.†

Fig. 4 OER and ORR performances. (a) OER polarization curve for YBaCo₄O_7.3 in O₂-saturated 0.1 M KOH. Catalyst was supported at 30 wt% on VC and rotated at 1600 rpm. (b) ORR polarization curve tested under the same conditions as above. (c) Activities of YBaCo₄O_7.3 for the OER and ORR compared to LaNiO₃ and IrO₂ tested in the same experimental setup. OER activities were measured at 1.63 V vs. RHE-iR and ORR activities were measured at 0.693 V. All measurements were performed in triplicate on fresh electrodes.

Fig. 5 Tafel analysis for YBaCo₄O_7.3 and LaNiO₃ for both the (a) OER and (b) ORR as well as IrO₂ for the OER. All samples were supported at 30 wt% on VC XC-72 and dropcast on 5 mm glassy carbon electrodes at a mass loading of 51 μg cm⁻² and tested in O₂-saturated 0.1 M KOH while rotating at 1600 rpm. OER testing was performed at a scan rate of 10 mV s⁻¹ while ORR testing was performed at a scan rate of 5 mV s⁻¹. All measurements were performed in triplicate.

Previous studies have demonstrated that YBaCo₄O_7+δ can absorb and store significant amounts of oxygen upon heated in a relatively low temperature range of 270–350 °C in an O₂-containing atmosphere,^32,33 making it interesting as a possible pseudocapacitor material in basic electrolyte. CV was performed in Ar-saturated 1 M KOH to determine the Co redox features concomitant with oxygen intercalation. By consulting the Pourbaix diagram for cobalt, as shown in Fig. 6, Co²⁺ is oxidized to Co³⁺ at 0.2 V on the anodic scan, which is in agreement with the results reported by Dan et al.³⁷ against an Ag/AgCl reference electrode (−0.1 V). To measure the oxygen diffusion rate within YBaCo₄O_7.3, chronoamperometry was performed at a potential 50 mV positive of the peak potential to ensure a diffusion-limited process and the current was plotted as a function of t^−1/2. The oxygen diffusion rate was calculated by extrapolating the linear portion of the data to find the intercept with the t^−1/2 axis (Fig. 6b) and then using a bounded diffusion model to calculate the diffusion rate coefficient. More details on the method used can be found elsewhere.^41–43 Using an average particle size of 1 μm, as calculated from the SEM images in Fig. S4,† the oxygen diffusion rate within YBaCo₄O_7.3 was measured to be 2.74 × 10⁻¹⁰ cm² s⁻¹, which is faster than that reported for LaMnO_3−δ in our previous work.⁵⁴

Fig. 6 Oxygen diffusion rate testing. (a) First CV of 85 wt% YBaCo₄O_7.3 in Ar-saturated 1 M KOH to find the Co^2+/3+ redox potential. (b) Chronoamperometry performed at a potential 50 mV positive of the peak potential for the Co^2+/3+ redox on the anodic scan in Ar-saturated 1 M KOH with the RDE rotating at 1600 rpm. The black circle on the CV in (a) shows the potential at which chronoamperometry was performed. Measurements were performed in triplicate on fresh electrodes.

To investigate the durability of YBaCo₄O_7.3 for the OER and ORR, both chronoamperometry and constant current stability experiments were performed under the same experimental conditions as the CV experiments described above. The chronoamperometry experiments were performed for hour periods at three potentials for both the OER and ORR. The potentials were chosen by consulting the CVs in Fig. 4 to ensure that the constant potentials were located in the OER or ORR regions. As can be seen in Fig. S8a,† YBaCo₄O_7.3 was able to maintain a steady potential while generating up to 180 mA mg⁻¹ for the ORR and 58 mA mg⁻¹ for the OER, although when a potential of 1.74 V vs. RHE was applied, there was a significant decrease in the amount of current generated over the hour-long period. This may be because the carbon support is not stable at these high potentials and may undergo significant oxidation, as has been previously shown.¹² Thus, to further examine the catalyst stability, both the OER and ORR were performed under the same conditions described above and the current generated was held constant at 10 mA mg⁻¹ while the potential necessary to generate that current was measured. As can be seen in Fig. S8b,† YBaCo₄O_7.3 was able to maintain this current for 12 h for both oxygen evolution and reduction, and although there was a slight increase in the potential for the OER over this time frame, we again attribute this to oxidation of the VC support.

DFT calculations of oxygen adsorption energies

To rationalize the observed bifunctional activity of the YBaCo₄O_7.3 material in terms of the surface reaction mechanism, we estimated the adsorption energies of the intermediates along the (001) surface, which provide transition metal-O termination. This type of termination was repeatedly studied for perovskites and proved its usefulness for rationalizing catalytic activity trends.^14,21 The calculations for the stoichiometric YBaCo₄O₇ (001) surface were performed using a 10.5 Å thick slab with a 1 × 1 surface area and vacuum region of 11 Å. Due to the lack of appropriate symmetry of the slab center, it had two non-equivalent surfaces. In total, seven different terminations were considered for the (001) surface. By calculating the energies, the most stable combination of two surfaces with an average surface energy (cleavage energy) of 0.8 J m⁻² was identified.⁵⁵ This relatively low value of energy for free surfaces proves that the found surface terminations were thermodynamically stable or close to stable. The two surfaces had Co–O and Y–Ba–Co–O terminations, respectively. The coordination of atoms at both surfaces conserved their bulk topology; however the surface O and Co atoms were shifted in opposite ways along the [001] direction, reducing the polarity of the surfaces. Further, we focused only on the first Co–O surface, which had more transition metal sites per unit area. The top-view of the optimized structure of Co–O surface is shown in Fig. 7.

Fig. 7 Structure of the (001) surface of YBaCo₄O₇ with Co–O termination. The adsorption sites are A1, A2, and A3. The Y atom is located deeper than the Co and O atoms. The ab mesh of the unit cell is outlined.

To find the most favorable adsorption sites for the intermediates, the surface was probed by placing an O atom with a 1 Å step along the surface plane, optimizing the distance between O and the surface, and calculating adsorption energy. The adsorption energies for O* and HO* were calculated as follows:

ΔE(O*(ads)) = E(O*(ads)) − E(*) − (E_H2O(g) − E_H2(g)),

ΔE(HO*(ads)) = E(HO*(ads)) − E(*) − (E_H2O(g) − 1/2E_H2(g)),

where, E(*), E(O*), and E(HO*) are the total energies of the bare surfaces and the surfaces with adsorbed O* and HO*, respectively. E_H2O and E_H2 are the total energies of H₂O and H₂ molecules in the gas phase, respectively (big box). Commonly, the ΔE values with zero-point energy corrections (ZPE) are amended. Here, we provide a comparison for only zero Kelvin results without ZPE.

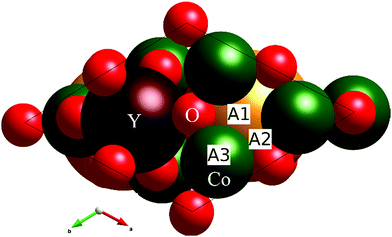
The most favorable adsorption sites for the oxygen atom are shown in Fig. 7 with labels A1, A2, and A3. The A1 position is located above the Co triangle with the Co–O distances of 2.1, 2.1, and 1.8 Å. The oxygen atom at this position forms a nearly linear O–Co–O fragment with one of the remaining lattice O atoms of the tetrahedral oxygen coordination of Co. The A2 position is located between two Co atoms, and the Co–O distances are 2 and 1.7 Å. The third position A3 is located just above the Co atom at a distance of 1.7 Å, completing its coordination back to tetrahedron. The corresponding adsorption energies ΔE(O*) of O for the A1, A2, and A3 positions are 1.8, 2.0, and 2.8 eV, respectively. The most favorable position for O adsorption is located near the center of the triangles formed by the Co atoms on the surface. This is different to that in perovskites, where their surface structures do not contain transition metal triangles, and oxygen prefers to be either above the metal site or between two metal sites. The local coordination of the most energetically favorable A1 position for the adsorbates is reminiscent to that of the oxygen position in the octahedral layers of LiCoO₂, i.e. due to the formation of the linear O–Co–O fragment, the A1 position looks more “octahedral” rather than “tetrahedral”. Surprisingly, the “tetrahedral” A3 position inherited from the regular YBaCo₄O₇ structure is the least energetically favorable.

The relation between electronic structure and catalytic activity

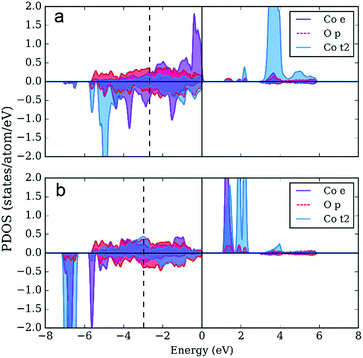
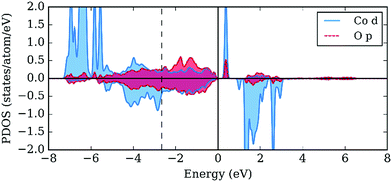
The distinct feature of the electronic structure of YBaCo₄O_7+δ is the charge disproportionation with the Co atoms in the Co²⁺ and Co³⁺ oxidation states. Thus, to gain more insight into the character of the bonding between Co and O, we investigated the partial density of electronic states (PDOS), such as t₂ and e orbitals in the tetrahedral field splitting for Co²⁺ and Co³⁺, as well as for the p orbitals on the O atoms. As expected, the local orbital projected PDOS for Co²⁺ and Co³⁺ are different (Fig. 8). First, the Co³⁺ atom is characterized by a lower density on the e orbitals, which serve as a source of electrons during oxidation. Second, the low-lying d peak is located 2 eV lower on Co³⁺ than that on Co²⁺. The local electronic structure of both atoms has a band gap, which is smaller in the case of Co³⁺. On the one hand, the DOS on Co²⁺ locally resembles the Mott–Hubbard insulator scenario (with U < Δ, where U is the difference between the centers of the occupied and unoccupied d-bands and Δ is the difference between the center of the valence p-band and unoccupied d band⁵⁶). On the other hand, the local electronic structure of Co³⁺ resembles that of a typical charge-transfer insulator, with U > Δ. The centers of the valence p-bands, shown with dashed vertical lines on the PDOS plots, usually correlate with the adsorption energies and consequently with catalytic activity.¹⁴ Since the observed adsorption can be considered too strong (using adsorption energies on perovskite surfaces as a reference¹⁴), the upshift of the p-band center should be accompanied with an increase in catalytic activity.

Fig. 8 Local PDOS for YBaCo₄O₇ on (a) Co²⁺ and (b) Co³⁺. e and t₂ are provided on the Co atoms according to tetrahedral crystal field splitting. The O p-orbitals are provided on the four oxygen atoms that form a tetrahedron around the corresponding Co atom (normalized). The solid vertical line shows the Fermi level. The dashed vertical line shows the p-band center.

As the next step, we calculated the PDOS for partially oxidized YBaCo₄O₈, where a fraction of the tetrahedrally coordinated Co acquires octahedral oxygen coordination.⁵¹ Oxidation results in the upshifting of the p-band center by 0.1 eV compared to the p-band center in YBaCo₄O₇ located 2.7 eV below the Fermi level, which indicates that the increase in oxygen concentration could be responsible for the weaker adsorption of the intermediates and corresponding increase in catalytic activity. Besides the upshift of the p-band center, the PDOSs for the tetrahedral Co²⁺ and Co³⁺ atoms in YBaCo₄O₈ (not shown) resemble that for YBaCo₄O₇. However, in YBaCo₄O₈, 1/4 of the Co atoms adopt a 6-fold oxygen octahedral coordination. The PDOS for the octahedrally coordinated Co (Fig. 9) has an additional peak above the Fermi level with significant contribution from both the Co3d and O2p states, which represent the σ* band characteristic of TM cations in the octahedral oxygen coordination. The appearance of the σ* band results in a very small band gap and increased p-density below the Fermi level (in agreement with the drastic conductivity increase in YBaCo₄O_7+δ upon increasing the oxygen content^32,39). The oxidation state is +3, locally resembling a charge-transfer insulator with a small Δ. According to Hong et al., the charge-transfer energy serves as a utility descriptor of the OER catalytic activity.^24,25 Moreover, in contrast to other descriptors that usually obey the volcano shape of activity, Δ has a simpler inverse linear relationship with activity. Thus, the octahedrally-coordinated atoms in YBaCo₄O₈ should serve as active catalytic centers for the OER reaction.

Fig. 9 PDOS of YBaCo₄O₈ separating the d orbital on Co³⁺ in the 6-fold oxygen octahedral coordination and p orbitals on six surrounding the O atoms (normalized). The solid vertical line shows the Fermi level. The dashed vertical line shows the p-band center.

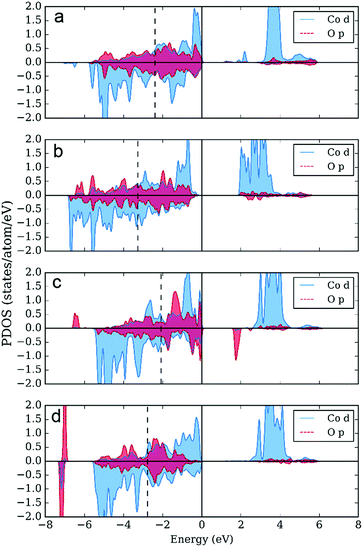
The drastic increase in the Co3d contribution to the PDOS near the Fermi level is not the sole effect of the oxygen insertion into the YBaCo₄O_7+δ crystal structure. The adsorbates at the “octahedral” A1 position provide a similar effect on the local PDOS at the surface Co atoms. A comparison of the local PDOS on the bulk Co and O atoms, bare surface Co and O atoms, and surface Co and adsorbed O atoms for O* and HO* is provided in Fig. 10. The d-PDOS on the Co atom at the surface resembles that obtained for the bulk Co, although more density is acquired in the −6 to −7 eV region in the case of Co at the surface (Fig. 10b). For both the bulk and surface Co atoms, there is an e-peak under the Fermi-level (Fig. 10a and b). The adsorption of O causes oxidation of the Co atom, removing the electrons from the e-orbital and forming a strongly hybridized p–d bond in a wide range of energies (Fig. 10c). The adsorption of O is accompanied by the formation of p–d hybridized σ* anti-bonding states right below the Fermi level. The p-band center of adsorbed oxygen surprisingly coincides with that of the bulk oxygen. In the case of HO*, oxygen forms s–p hybridized bonds with hydrogen, which are manifested around −7 eV as sharp peaks in Fig. 10d. The p–d hybridized band is also present in the case of HO*, but is shifted downwards from the Fermi level. Thus, the qualitative changes in the local band structure caused by oxygen insertion and surface adsorption are very similar, suggesting that the undercoordinated octahedral sites on the surfaces should be more active and responsible for the increase in OER catalytic activity.

Fig. 10 Local PDOS for (a) bulk on Co and neighboring O, (b) bare surface on Co and O, (c) surface with O on adsorbed O at A1 and surface Co, and (d) surface with HO on adsorbed O at A1 and surface Co. The solid vertical line shows the Fermi level. The dashed vertical line shows the p-band center.

Origin of bifunctional behavior in the frame of the ZSA model

If the OER activity of YBaCo₄O_7+δ can still be rationalized in the frame of the ZSA model, understanding the ORR activity in the same framework is much more challenging. This is due to the lack of systematic correlations between the ORR activity and the parameters of the ZSA band structure unequivocally established thus far. Thus, based on the knowledge on the perovskite OER and ORR activities from our own experiments and that extrapolated from the published data,^19–21,57 we attempted to establish the correlations between them and the U and Δ values for perovskites in the ZSA model determined within the configuration interaction method from the XPS spectra.^58–60 The correlations of the overpotentials (taken as a measure of the catalytic activity at the current density of 10 mA cm⁻² and 3 mA cm⁻² for the OER and ORR, respectively) with U and Δ are shown in Fig. 11.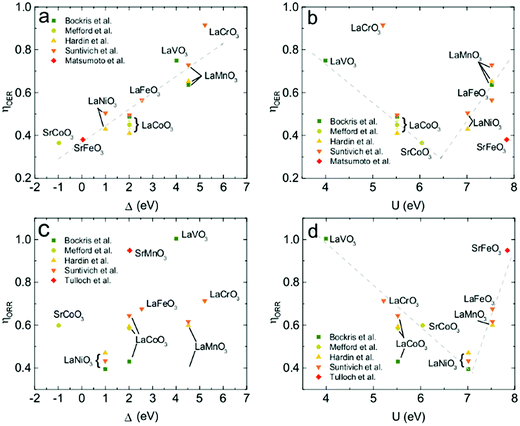

Fig. 11 Relationships of the OER (a and b) and ORR (c and d) overpotentials for perovskite oxides with the Coulomb on-site repulsion energy, U, and charge transfer energy, Δ. Dash lines shown on the plots are guides for the eye. Part of the data points are extrapolated from the published Tafel curves;^{12,21,57,64–67} thus they have no error bars.

The linear decrease in the OER overpotential with Δ (Fig. 11a) is strikingly similar to the latest observations by Hong et al. on a monotonic increase in the OER kinetic current with a decrease in Δ.²⁵ The volcano-like plot of the OER overpotential as a function of U with a minimum on SrCoO_3−δ (Fig. 11b), the most active OER catalyst reported to date,¹² suggests that U can be considered as a secondary descriptor for OER catalytic activity. Surprisingly, the ORR overpotential does not show any noticeable correlation with the charge transfer energy (Fig. 11c). However, the ORR overpotential demonstrates a strong volcano-type dependence on U with a minimum at 7.0 eV for LaNiO₃ (Fig. 11d). Thus, in terms of the ZSA model, the Coulomb on-site repulsion U may be considered as a primary descriptor governing the ORR activity of perovskites in alkaline solutions.

Different primary descriptors for the OER and ORR stems from the different rate determining steps (RDS) on the surface for two regimes. In the case of the OER, the RDS step is associated with electron-transfer energy, explaining its correlation with Δ. In the case of YBaCo₄O_7+δ, oxidation leads to the formation of octahedral Co with a small Δ, thus rendering this Co site more electrochemically active. In the case of the ORR, the RDS step is associated with the adsorption energies of the intermediates, making the on-site repulsion more important. Qualitatively, this can be understood from the correlation between U and the adsorption strength of the intermediates. On the one hand, the adsorption of surface intermediates weakens from early to late transition metals.⁶¹ On the other hand, the on-site Coulomb repulsion energy, which is a measure of d-orbital localization, increases from early to late transition metals since the spatial extent of the d orbital shrinks with atomic number.⁶² As a result, the higher U values correspond to weaker adsorption. The direct weakening of adsorption due to the increase in U value was shown using DFT+U calculations.⁶³ Comparing the Co atoms in the tetrahedral and octahedral coordination in YBaCo₄O₈, the former is characterized with more compact d orbitals and, therefore, a higher U value. This was confirmed from the calculated local PDOS on the tetrahedral and octahedral atoms (the d-peak separations are ∼7 and ∼5.5 eV, respectively). The larger value of U in the tetrahedral case weakens the adsorption strength towards the optimal value, corresponding to an increase in catalytic activity for the ORR and renders the tetrahedrally coordinated Co a catalytically active center.

Conclusions

The tetrahedral oxide YBaCo₄O_7.3 demonstrated bifunctional catalytic activity of 1.18 mA cm⁻² and 2.76 mA cm⁻² in the OER and ORR, respectively, similar to that of the benchmark LaNiO₃ perovskite. At the same time, this compound was chosen as an interesting object to study the correlations between the OER and ORR catalytic activity and the peculiarities of the bulk band structure. The bifunctional activity of YBaCo₄O_7.3 was rationalized in terms of the ZSA model with the parameters U (Coulomb on-site repulsion energy) and Δ (charge transfer energy). The Co²⁺ and Co³⁺ cations in the stoichiometric mixed-valent YBaCo₄O₇ are charge-ordered, with the local DOS on Co²⁺ being strongly reminiscent of a Mott–Hubbard insulator (U < Δ); whereas, the local electronic structure at Co³⁺ is typical for a charge transfer insulator (U > Δ). However, prior to the OER, YBaCo₄O_7.3 absorbs overstoichiometric oxygen, inducing octahedrally coordinated Co and giving rise to a narrow d–p σ* band near the Fermi level. This drastically reduces Δ and renders the octahedral Co positions active sites in the OER according to the established correlation between the OER catalytic activity and charge transfer energy. The analysis of the possible positions for the adsorbates on the model (001) Co–O terminated surface reflects that the most energetically favorable position is along the nearly linear O–Co–O bridges, introducing similar a d–p σ* band near the Fermi level and making the surface Co act more like an “octahedral” redox center rather than a “tetrahedral” one. In the ORR, the Coulomb on-site repulsion energy may serve as a descriptor of the catalytic activity scaling inversely with the binding energies of the adsorbates. Apparently, the comparative qualitative analysis of the U-overpotential trends in the OER and ORR demonstrated that the highest catalytic activity in the ORR requires a lower binding energy of the adsorbates compared to the OER, as reflected by ∼1 eV larger U. In YBaCo₄O₇, a larger U was realized for Co in the tetrahedral coordination due to its more compact coordination environment, thus making these sites active in the ORR.

Author contributions

M. A. K. and V. D. O. performed the synthesis, XRPD and iodometric titration. M. A. K. performed microstructural characterization. D. A. A. performed DFT modelling. R. P. F. performed electrochemical characterization. J. T. M. performed calculations for perovskite overpotentials in frame of ZSA model. A. M. A. performed the SAED, HAAFD-STEM, ABF-STEM and EDX measurements. K. J. S. planned the electrochemical measurements and analyzed the data. A. M. A. and K. J. S. conceived and guided the work. All authors contributed to the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. A. K. thanks Victoria Nikitina for fruitful discussion of electrochemical results.

References

1. W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Toward the Rational Design of Non-Precious Transition Metal Oxides for Oxygen Electrocatalysis, Energy Environ. Sci., 2015, 8, 1404–1427.
2. C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, Benchmarking Heterogeneous Electrocatalysts for the Oxygen Evolution Reaction, J. Am. Chem. Soc., 2013, 135, 16977–16987.
3. Y. Gorlin and T. F. Jaramillo, A Bifunctional Nonprecious Metal Catalyst for Oxygen Reduction and Water Oxidation, J. Am. Chem. Soc., 2010, 132, 13612–13614.
4. S. M. Jasem and A. C. C. Tseung, A Potentiostatic Pulse Study of Oxygen Evolution on Teflon-Bonded Nickel-Cobalt Oxide Electrodes, J. Electrochem. Soc., 1979, 126, 1353–1360.
5. M. P. Browne, C. Domínguez and P. E. Colavita, Emerging Trends in Metal Oxide Electrocatalysis: Bifunctional Oxygen Catalysis, Synergies and New Insights from in situ Studies, Curr. Opin. Electrochem., 2018, 7, 208–215.
6. H. Osgood, S. V. Devaguptapu, H. Xu, J. Cho and G. Wu, Transition Metal (Fe, Co, Ni, and Mn) Oxides for Oxygen Reduction And evolution Bifunctional Catalysts in Alkaline Media, Nano Today, 2016, 11, 601–625.
7. I. Yamada, et al., Bifunctional Oxygen Reaction Catalysis of Quadruple Manganese Perovskites, Adv. Mater., 2017, 29, 1603004.
8. W. G. Hardin, D. A. Slanac, X. Wang, S. Dai, K. P. Johnston and K. J. Stevenson, Highly Active, Nonprecious Metal Perovskite Electrocatalysts for Bifunctional Metal–Air Battery Electrodes, J. Phys. Chem. Lett., 2013, 4, 1254–1259.
9. R. P. Forslund, et al., Exceptional Electrocatalytic Oxygen Evolution via Tunable Charge Transfer Interactions in La_0.5Sr_1.5Ni_1−xFe_xO_4±δ Ruddlesden-Popper Oxides, Nat. Commun., 2018, 9, 3150.
10. J. K. Nørskov, et al., Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892.
11. I. C. Man, et al., Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165.
12. J. T. Mefford, et al., Water Electrolysis on La_1-xSr_xCoO_3-δ Perovskite Electrocatalysts, Nat. Commun., 2016, 7, 11053.
13. A. Grimaud, et al., Activating Lattice Oxygen Redox Reactions in Metal Oxides to Catalyse Oxygen Evolution, Nat. Chem., 2017, 9, 457–465.
14. Y.-L. Lee, M. J. Gadre, Y. Shao-Horn and D. Morgan, Ab Initio GGA+U Study of Oxygen Evolution and Oxygen Reduction Electrocatalysis on the (001) Surfaces of Lanthanum Transition Metal Perovskites LaBO₃ (B = Cr, Mn, Fe, Co and Ni), Phys. Chem. Chem. Phys., 2015, 17, 21643–21663.
15. J. K. Nørskov, et al., Universality in Heterogeneous Catalysis, J. Catal., 2002, 209, 275–278.
16. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of Water on Oxide Surfaces, J. Electroanal. Chem., 2007, 607, 83–89.
17. F. Calle-Vallejo, et al., Number of Outer Electrons as Descriptor for Adsorption Processes on Transition Metals and Their Oxides, Chem. Sci., 2013, 4, 1245–1249.
18. F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Introducing Structural Sensitivity into Adsorption–Energy Scaling Relations by Means of Coordination Numbers, Nat. Chem., 2015, 7, 403–410.
19. J. O. Bockris and T. Otagawa, The Electrocatalysis of Oxygen Evolution on Perovskites, J. Electrochem. Soc., 1984, 131, 290–302.
20. J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Design Principles for Oxygen-Reduction Activity on Perovskite Oxide Catalysts for Fuel Cells and Metal–Air Batteries, Nat. Chem., 2011, 3, 546–550.
21. J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, A Perovskite Oxide Optimized for Oxygen Evolution Catalysis from Molecular Orbital Principles, Science, 2011, 334, 1383–1385.
22. V. Stamenkovic, et al., Changing the Activity of Electrocatalysts for Oxygen Reduction by Tuning the Surface Electronic Structure, Angew. Chem., 2006, 118, 2963–2967.
23. A. Grimaud, et al., Double Perovskites as a Family of Highly Active Catalysts for Oxygen Evolution in Alkaline Solution, Nat. Commun., 2013, 4, 2439.
24. W. T. Hong, R. E. Welsch and Y. Shao-Horn, Descriptors of Oxygen-Evolution Activity for Oxides: A Statistical Evaluation, J. Phys. Chem. C, 2016, 120, 78–86.
25. W. T. Hong, et al., Charge-Transfer-Energy-Dependent Oxygen Evolution Reaction Mechanisms for Perovskite Oxides, Energy Environ. Sci., 2017, 10, 2190–2200.
26. J. Zaanen, G. A. Sawatzky and J. W. Allen, Band Gaps and Electronic Structure of Transition-Metal Compounds, Phys. Rev. Lett., 1985, 55, 418–421.
27. J. B. Torrance, P. Lacorre, C. Asavaroengchai and R. M. Metzger, Why are Some Oxides Metallic, While Most are Insulating?, Physica C, 1991, 182, 351–364.
28. A. A. Tsirlin, M. G. Rabie, A. Efimenko, Z. Hu, R. Saez-Puche and L. H. Tjeng, Importance of Tetrahedral Coordination for High-Valent Transition-Metal Oxides: YCrO₄ as a Model System, Phys. Rev. Lett., 2014, 90, 085106.
29. L. Qiao, et al., The Impact of Crystal Symmetry on the Electronic Structure and Functional Properties of Complex Lanthanum Chromium Oxides, J. Mater. Chem. C, 2013, 1, 4527–4535.
30. E. Tsuji, et al., Brownmillerite-Type Ca₂FeCoO₅ as a Practicable Oxygen Evolution Reaction Catalyst, ChemSusChem, 2017, 10, 2864–2868.
31. A. Grimaud, C. E. Carlton, M. Risch, W. T. Hong, K. J. May and Y. Shao-Horn, Oxygen Evolution Activity and Stability of Ba₆Mn₅O₁₆, Sr₄Mn₂CoO₉, and Sr₆Co₅O₁₅: The Influence of Transition Metal Coordination, J. Phys. Chem. C, 2013, 117, 25926–25932.
32. M. Karppinen, et al., Oxygen Nonstoichiometry in YBaCo₄O_7+δ: Large Low-Temperature Oxygen Absorption/Desorption Capability, Chem. Mater., 2006, 18, 490–494.
33. S. Räsänen, H. Yamauchi and M. Karppinen, Oxygen Absorption Capability of YBaCo₄O_7+δ, Chem. Lett., 2008, 37, 638–639.
34. T. Motohashi, S. Kadota, H. Fjellvåg, M. Karppinen and H. Yamauchi, Uncommon Oxygen Intake/Release Capability of Layered Cobalt Oxides, REBaCo₄O_7+δ: Novel Oxygen-Storage Materials, Mater. Sci. Eng., B, 2008, 148, 196–198.
35. Y. Nagai, et al., X-ray Absorption fine Structure Analysis of Local Structure of CeO₂–ZrO₂ Mixed Oxides With the Same Composition Ratio (Ce/Zr=1), Catal. Today, 2002, 74, 225–234.
36. E. V. Tsipis, D. D. Khalyavin, S. V. Shiryaev, K. S. Redkina and P. Núñez, Electrical and Magnetic Properties of YBaCo₄O_7+δ, Mater. Chem. Phys., 2005, 92, 33–38.
37. M. Dan, V. Pralong, N. Vaszilcsin, A. Kellenberger and N. Duteanu, Electrochemical Behaviour of YBaCo₄O₇ in Alkaline Aqueous Solution, J. Solid State Electrochem., 2011, 15, 1227–1233.
38. E. V. Tsipis, V. V. Kharton and J. R. Frade, Transport Properties and Electrochemical Activity of YBa(Co,Fe)₄O₇ Cathodes, Solid State Ionics, 2006, 177, 1823–1826.
39. H. Hao, Q. He, Y. Cheng and L. Zhao, Oxygen Adsorption and Electronic Transport Properties of Fe-Substituted YBaCo₄O₇ Compounds, Mater. Res. Bull., 2014, 53, 84–88.
40. V. Petricek, M. Dusek and L. Palatinus, Crystallographic Computing System JANA2006: General features, Z. Kristallogr., 2014, 229, 345–352.
41. F. R. van Buren, G. H. J. Broers, A. J. Bouman and C. Boesveld, An Electrochemical Method for the Determination_–xSr_xCoO_3–y Compounds: Theoretical Aspects of Oxygen Ion Diffusion Coefficients in La₁, J. Electroanal. Chem. Interfacial Electrochem., 1978, 87, 389–394.
42. F. R. van Buren, G. H. J. Broers, A. J. Bouman and C. Boesveld, The Electrochemical Determination of Oxygen Ion Diffusion Coefficients in La_0.50Sr_0.50CoO_3–y: Experimental Results and Related Properties, J. Electroanal. Chem. Interfacial Electrochem., 1978, 88, 353–361.
43. A. G. C. Kobussen, F. R. van Buren and G. H. J. Broers, The Influence of the Particle Size Distribution on the Measurement of Oxygen Ion Diffusion Coefficients in La_0.50Sr_0.50CoO_3–y, J. Electroanal. Chem. Interfacial Electrochem., 1978, 91, 211–217.
44. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
45. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev. B, 1964, 136, B864–B871.
46. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev. A, 1965, 140, A1133–A1138.
47. J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
48. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953.
49. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
50. S. Chatterjee and T. Saha-Dasgupta, Electronic and Magnetic Structure of the Mixed-Valence Cobaltite CaBaCo₄O₇, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 85116.
51. N. V Podberezskaya, A. I. Smolentsev, L. P. Kozeeva, M. Y. Kameneva and A. N. Lavrov, Yttrium Barium Heptaoxocobaltate YBaCo₄O_7+δ: Refinement of the Structure and Determination of the Composition, Crystallogr. Rep., 2013, 58, 682–686.
52. O. Chmaissem, H. Zheng, A. Huq, P. W. Stephens and J. F. Mitchell, Formation of Co³⁺ Octahedra and Tetrahedra in YBaCo₄O_8.1, J. Solid State Chem., 2008, 181, 664–672.
53. S. Avci, O. Chmaissem, H. Zheng, A. Huq, P. Manuel and J. F. Mitchell, J. F. Oxygen Stoichiometry in the Geometrically Frustrated Kagomé System YBaCo₄O_7+δ: Impact on Phase Behavior and Magnetism, Chem. Mater., 2013, 25, 4188–4196.
54. J. T. Mefford, W. G. Hardin, S. Dai, K. P. Johnston and K. J. Stevenson, Anion Charge Storage Through Oxygen Intercalation in LaMnO₃ Perovskite Pseudocapacitor Electrodes, Nat. Mater., 2014, 13, 726–732.
55. W. Sun and G. Ceder, Efficient Creation and Convergence of Surface Slabs, Surf. Sci., 2013, 617, 53–59.
56. C. Yang and A. Grimaud, Factors Controlling the Redox Activity of Oxygen in Perovskites: from Theory to Application for Catalytic Reactions, Catalysts, 2017, 7, 149.
57. J. Tulloch and S. W. Donne, Activity of Perovskite La_1−xSr_xMnO₃ Catalysts Towards Oxygen Reduction in Alkaline Electrolytes, J. Power Sources, 2009, 188, 359–366.
58. A. E. Bocquet, T. Mizokawa, T. Saitoh, H. Namatame and A. Fujimori, Electronic Structure of 3d-Transition-Metal Compounds by Analysis of the 2p Core-Level Photoemission Spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3771–3784.
59. A. E. Bocquet, et al., Electronic Structure of SrFe⁴⁺O₃ and Related Fe Perovskite Oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1561–1570.
60. A. E. Bocquet, et al., Electronic Structure of Early 3d-Transition-Metal Oxides by Analysis of the 2p Core-Level Photoemission Spectra, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1161–1170.
61. S. A. Akhade and J. R. Kitchin, Effects of Strain, d-Band Filling, and Oxidation State on the Surface Electronic Structure and Reactivity of 3d Perovskite Surfaces, J. Chem. Phys., 2012, 137, 084703.
62. M. Imada, A. Fujimori and Y. Tokura, Metal-Insulator Transitions, Rev. Mod. Phys., 1998, 70, 1039–1263.
63. Y.-L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Ab Initio Energetics of LaBO₃(001) (B = Mn, Fe, Co, and Ni) for Solid Oxide Fuel Cell Cathodes, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101.
64. J. O'M Bockris and T. Otagawa, Mechanism of Oxygen Evolution on Perovskites, J. Phys. Chem., 1983, 87, 2960–2971.
65. W. G. Hardin, et al., Tuning the Electrocatalytic Activity of Perovskites through Active Site Variation and Support Interactions, Chem. Mater., 2014, 26, 3368–3376.
66. Y. Matsumoto, J. Kurimoto and E. Sato, Oxygen Evolution on SrFeO₃ Electrode, J. Electroanal. Chem. Interfacial Electrochem., 1979, 102, 77–83.
67. J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Design Principles for Oxygen-Reduction Activity on Perovskite Oxide Catalysts for Fuel Cells and Metal–Air Batteries, Nat. Chem., 2011, 3, 546–550.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta09862j

---