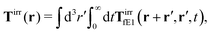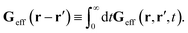DOI:
10.1039/C9SM01119F
(Paper)
Soft Matter, 2020,
16, 114-124
Diffusion and flow in complex liquids†
Received
4th June 2019
, Accepted 13th October 2019
First published on 8th November 2019
Abstract
Thermal motion of particles and molecules in liquids underlies many chemical and biological processes. Liquids, especially in biology, are complex due to structure at multiple relevant length scales. While diffusion in homogeneous simple liquids is well understood through the Stokes–Einstein relation, this equation fails completely in describing diffusion in complex media. Modeling, understanding, engineering and controlling processes at the nanoscale, most importantly inside living cells, requires a theoretical framework for the description of viscous response to allow predictions of diffusion rates in complex fluids. Here we use a general framework with the viscosity η(k) described by a function of wave vector in reciprocal space. We introduce a formulation that allows one to relate the rotational and translational diffusion coefficients and determine the viscosity η(k) directly from experiments. We apply our theory to provide a database for rotational diffusion coefficients of proteins/protein complexes in the bacterium E. coli. We also provide a database for the diffusion coefficient of proteins sliding along major grooves of DNA in E. coli. These parameters allow predictions of rate constants for association of proteins. In addition to constituting a theoretical framework for description of diffusion of probes and viscosity in complex fluids, the formulation that we propose should decrease substantially the cost of numerical simulations of transport in complex media by replacing the simulation of individual crowding particles with a continuous medium characterized by a wave-length dependent viscosity η(k).
1 Introduction
While all living—and many chemical systems of interest—dwell in liquid environments, hydrodynamics alone do not suffice to describe and predict all processes. This is because hydrodynamics assume that in the absence of external forces, a particle immersed in a liquid remains at rest. In reality thermal vibrations cause molecules and small particles to constantly move via erratic Brownian motion. The Brownian motion of an individual particle in a simple liquid has been described by Einstein and Smoluchowski.1,2 The diffusive motion of a particle can be described by its translation, the change of its position R(t), and its rotation, the change of its orientation û(t). The translational diffusion coefficient Dtr(a) is measured from the mean-square displacement 〈(R(t) − R(0))2〉 of the particle of interest, where t is time and the average 〈⋯〉 is taken over possible trajectories of the nanoparticle. For sufficiently long times3 the mean-square displacement of a single nanoparticle of hydrodynamic radius a increases linearly with time, 〈(R(t) − R(0))2〉 ∼ 6Dtr(a)t. Similarly linear dependence can be found for the mean square displacement of rotational degrees of freedom of the nanoparticle, 〈(û(t) − û(0))2〉 ∼ 4Drot(a)t, where Drot(a) is the rotational diffusion coefficient.4
For simple liquids comprising small molecules such as water, the diffusion coefficients are related to the solvent viscosity, particle size, and thermal energy kBT by the Stokes–Einstein equation, Dtr(a) = kBT/6πη0a, which is the standard in physics for the analysis of diffusion in liquids. The rotational diffusion coefficient follows from the relation Drot(a) = kBT/8πη0a3. In simple liquids the ratio of the diffusion coefficients, Dtr(a)/Drot(a) = 4a2/3, depends solely on the hydrodynamic radius of the nanoparticle.
In incompressible simple fluids the only coefficient that in practice characterizes their flow properties is the shear viscosity.5 In complex fluids, supramolecular particles introduce additional length and time scales. These other molecules and particles act as obstacles altering the motion of the diffusing nanoparticle. The diffusion coefficient defined by the mean square displacement of the probe diffusing in a complex liquid becomes time-dependent, and may no longer be proportional to the inverse of the particle radius.
If the tracer particle is much larger than all of the length scales that characterize the complex fluid, then the scaling of the diffusivity with size is the same as in the Stokes–Einstein formula. Additional time scales are taken into account by a frequency dependence of the diffusion coefficient, D(ω), in the generalized Stokes–Einstein relation, D(ω) = kBT/(6πaη(ω)) with a frequency-dependent bulk viscosity. This formula is the foundation of microrheological experiments.6,7 However, when a probe becomes small this formula has known shortcomings.8,9 For example, Gisler and Weitz noticed that for 3 μm tracer particles in a suspension of 20 μm long F-actin filaments, the frequency-dependent Stokes–Einstein relation is no longer valid.10 In this article we focus on the zero-frequency limit, which is equivalent to the observation of the mean square displacement for long times, but for probe sizes that sample the microstuctural length scales.
In this long time limit, different scaling of the diffusion coefficient with particle size is also observed in other complex fluids.11–17 Deviation from the Stokes–Einstein description can be significant. For example, a few orders of magnitude estimates have appeared in biological complex liquids inside E. coli cell cytoplasm16 and inside HeLa cell.17E. coli is a model system for microbiologists and computational biophysicists18 and HeLa is a model system of human cancer cells. Experiments on diffusion of probes in polymer solutions also show huge discrepancies from the Stokes–Einstein description.20 Moreover in complex liquids the ratio of the translational and the rotational diffusion coefficients Dtr(a)/Drot(a) depends on the particular type of the complex liquid and cannot be described by, Dtr(a)/Drot(a) = 4a2/3, which holds for simple liquids.19 Experiments such as these need a theoretical framework that explains and predicts the rates of diffusion. Such a theory is needed for understanding and engineering processes at the nanoscale not only in industrial complex fluids, but also in biological systems where diffusive motion lies at the heart of life processes. Diffusion of probes has been studied with different simplified theoretical approaches:21e.g., scaling theory,22 approaches based on a particular structure of a complex liquid23 or developed for simple fluids,24 or for non-Brownian suspensions.25,26
In this paper we use the framework of Brownian dynamics described by the generalized Smoluchowski equation27 to introduce expressions for translational and rotational diffusion coefficients in complex liquids. This framework takes into account different length scales in these complex liquids. In a cell interior the length scales are spanned by sizes of, for example, several hundred nanometers for actin filaments, a few nanometers for proteins, and a nanometer or less for small molecules and water. We include the effects of the structure of the liquid by using a generalized viscosity that is a function of the wave vector, η(k).28 On sufficiently small scales, all liquids are characterized by a wave-vector dependent shear viscosity.5 This quantity has been determined in numerical simulations by the Green–Kubo formula or by calculation of the decay of the transverse current autocorrelation function for different simple liquids and polymer fluids.29–33 The wave-vector dependent viscosity can be defined through the relation between stress and shear rate for sinusoidal velocity fields. As suggested by Wyart and de Gennes,28 it can be measured by applying a spatially sinusoidal shear rate, ∂vx/∂z ≡ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kz and measuring the corresponding shear stress, σxz = σ
kz and measuring the corresponding shear stress, σxz = σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kz, from the relation, σ = η(k)
kz, from the relation, σ = η(k)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
We demonstrate that, surprisingly, the whole spectrum of possible physical behaviors of various complex liquids can be captured by this single key quantity—the generalized viscosity function. We start from the Smoluchowski dynamics and discuss a general expression for the translational diffusion coefficient of a probe particle. It is based on rigorous results from the literature, but we reformulate relevant equations to emphasize the role of the wave-vector dependent viscosity. Using these rigorous expressions we introduce an approximation that allows us to obtain a formula for the diffusivity of the probe in terms of the wave-vector dependent viscosity. We also invert this relation to obtain the wave-vector dependent viscosity in terms of diffusivities of probes of different sizes. To our knowledge, this is the first time the wave-vector dependent viscosity is expressed in terms of the probe diffusivities. This approximate formula constitutes a new framework to measure the wave-vector dependent viscosity in terms of diffusivities that are experimentally available for different complex liquids. In a similar manner we derive an approximate expression for the rotational diffusion coefficient. By utilizing the translational and the rotational case, we also derive a relation between the translational and the rotational diffusion coefficients of the probes. This relation appears to be universal as it does not depend on the complex fluid. We use this relation to test our phenomenological framework. Using the above formulas we discuss the viscosity function and the translational and the rotational diffusion rates using literature data on micellar solutions, polymer solutions, and in cytoplasm of E. coli and HeLa cell. These examples show how our framework captures orders of magnitude deviations from the Stokes–Einstein formula in a single expression. As an application of our theory we provide a database for the rotational diffusion coefficients and the diffusion coefficients of the sliding of proteins along major grooves of DNA in E. coli.
2 Translational diffusion
We consider complex liquids that can be described by Smoluchowski dynamics. The Smoluchowski dynamics are stochastic and a reduced description of the motion of macromolecules in solution.27 Macromolecules are modelled by interacting beads. The Smoluchowski description includes the effects of Brownian motion, interactions of the beads through the solution (hydrodynamic interactions) and direct—such as van der Waals—forces between macromolecules. Because the interactions among the beads are to some extent arbitrary, the Smoluchowski equation can model a wide class of complex systems, e.g., suspensions of spherical particles, a complex liquid of polymer chains, suspensions of rod-like particles, or more complicated complex fluids made of multiple types of macromolecules which model a cell cytoplasm.18 The Smoluchowski description is valid on the Smoluchowski time scale, which is the characteristic time for the beads to change their velocities many times probing nearly a Maxwelian distribution. We give the detail description of the Smoluchowski dynamics in Appendix A.
Treating one of the beads as a probe particle, we determine the translational diffusion coefficient of the probe moving in such a complex fluid from the generalized Einstein relation, Dtr(a) = kBT/ζ(a),34 by calculating the friction coefficient, ζ(a). This is defined via the linear relation, F = ζ(a)〈U〉, between the average probe velocity, 〈U〉, and a drag force acting on the probe, F. Therefore, calculation of the friction coefficient requires solution of the Smoluchowski equation when a small force acts on the probe particle.
Similar situations have been considered, e.g., by Felderhof and Jones,34 and also recently by Szymczak and Cichocki.35 In their treatments they assumed that a small external force acts on all macromolecules. In the Appendix B we discuss how their analysis should be modified to the case when the external force acts only on one macromolecule, that is a probe particle in our case. Below we describe the most essential conclusions which we draw from their analysis (see the Appendix B for a more detailed description). In particular, the average velocity field, 〈v(r)〉, around the probe particle under action of an external force, F, on the particle is given as follows,
| | 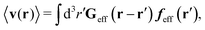 | (1) |
The average velocity field is represented
via the effective Green function, written in Fourier space,
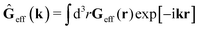
, by,
| | 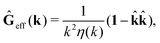 | (3) |
and the effective force density,
feff(
r′). The effective Green function depends solely on properties of the complex liquid through its shear wave-vector dependent viscosity
η(
k). In
eqn (2), the kernel,
Tirr(
r), determines the effective force density which appears as a result of the force
F acting on the probe. To give an example of the situation in which such forces appear, consider two non-Brownian spherical particles and an external force
F acting on one of the particles. Due to motion of the fluid around the particles they mutually affect their motion changing the distribution of forces on their surfaces. This example shows that the force
F on the first particle induces local forces acting on the surface of the second particle
via the fluid. In a general case, the effective force density includes effects of Brownian motion and hydrodynamic and electrostatic interactions between the probe particle and macromolecules in the surrounding complex liquid.
More details are given in Appendix B, where we also show that Newton's third law implies that the total effective force must be equal to the external force F, therefore,
| | 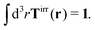 | (4) |
Eqn (1) and (2) are obtained within linear response regime. Therefore, the only assumptions needed to derive them from the Smoluchowski equation are that the external force F acting on the probe slightly disturbs the homogeneous and isotropic complex liquid from equilibrium. It is satisfied for any complex liquid which can be modeled by the Smoluchowski equation.
The average velocity field around the probe particle given by (1) must be consistent with the hydrodynamic boundary conditions which underlie the Smoluchowski dynamics.4 We consider stick boundary conditions and a rigid spherical particle,
The above boundary condition implies that
| | 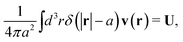 | (6) |
where
δ(
x) is the Dirac delta function in one dimension. Combining the above equation with the average velocity field in
(1) and (2) leads to relation between applied force
F and velocity of the particle
U in the form,
F =
ζ(
a)
U, with the friction coefficient,
ζ(
a), given by
| | 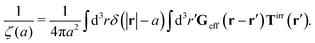 | (7) |
The friction coefficient can be determined in experiments either by measurements of velocity of the particle under action of a small drag force from the formula F = ζ(a)U, or by measurements of the rate of diffusion of a particle from the generalized Einstein relation, Dtr(a) = kBT/ζ(a).34 Measurements of the friction (or diffusion) coefficient show that the hydrodynamic radius of the probe particle is crucial. An example of such data is presented in Fig. 1 which shows measurements by Szymański et al.14 They measured diffusion coefficients of different probe particles in aqueous micellar solution of hexaethylene glycol monododecyl ether in phosphate buffer. Fig. 1 shows the friction coefficient ζmic(a)/(6πη0a) normalized by the friction in the buffer reconstructed from their experimental data for a complex liquid with macroscopic viscosity ηmacro = 500η0. Their experiments covered the full range of sizes of the probe particles. On the one hand the friction of the smallest probe particles is consistent with the viscosity of water. On the other hand the biggest probe particles experienced the macroscopic viscosity of the complex liquid. The probe size seems to be a factor which determines the friction of particles in these experiments.
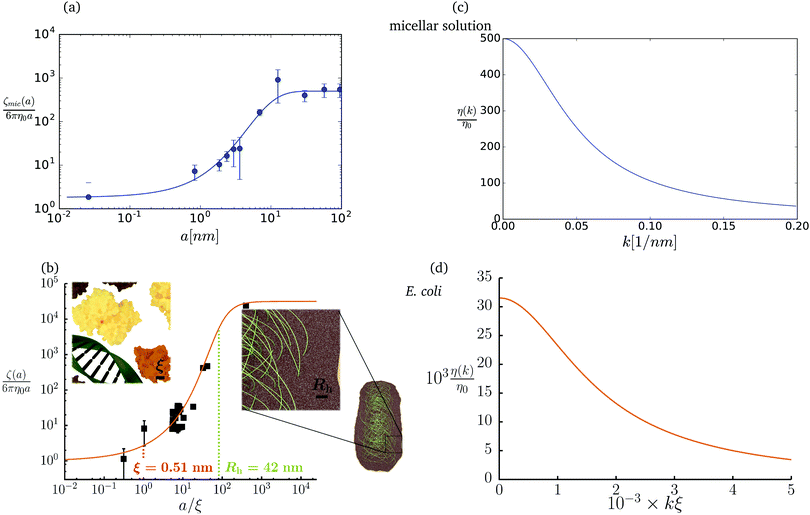 |
| | Fig. 1 (a) Data points show normalized friction coefficient, ζmic(a)/6πη0a, of different probe particles in a solution of hexaethylene glycol monododecyl ether in phosphate buffer reconstructed for the effective viscosity ηeff = 500η0 from Fig. 4b in ref. 14. The continuous line is the fitting formula log[ζmic(a)/(6πη0a)] = (1 + gmice−a/amic)ηmacro/η0 with parameters, gmic = −0.904 and amic = 4.455 nm. Figure (b): normalized friction coefficient, ζEC(a)/6πη0a, in E. coli cell cytoplasm from the literature data summarized in Table 1 of ref. 36. The continuous line corresponds to the phenomenological fit ζEC(a) = 6πη0a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(Reff(a)/ξEC)αEC], with Reff(a)−2 = REC−2 + a−2 and the fitting parameters ξEC = 0.51 nm, REC = 42 nm, and αEC = 0.53. (c and d) The wave-vector-dependent viscosity calculated from formula (11) from the fits of the friction coefficients presented in corresponding left panels. exp[(Reff(a)/ξEC)αEC], with Reff(a)−2 = REC−2 + a−2 and the fitting parameters ξEC = 0.51 nm, REC = 42 nm, and αEC = 0.53. (c and d) The wave-vector-dependent viscosity calculated from formula (11) from the fits of the friction coefficients presented in corresponding left panels. | |
Modelling the probes by spherical particles of hydrodynamic radii equal to the sizes of the probes we can interpret these results using eqn (7). Here, the hydrodynamic radius enters in two ways: by the hydrodynamic boundary condition with the Dirac delta function and by the kernel of the effective force density Tirr. If the hydrodynamic radius is a quantity determining diffusivity of different probes, it leaves a possibility that the integral 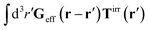 in eqn (7) for r on the surface of a particle, in a negligible way, depends on interactions of the probe with surrounding macromolecules. Motivated by this observation and keeping in mind that Tirr must be isotropic and satisfy Newton's third law, given by eqn (4), we introduce the following approximation
in eqn (7) for r on the surface of a particle, in a negligible way, depends on interactions of the probe with surrounding macromolecules. Motivated by this observation and keeping in mind that Tirr must be isotropic and satisfy Newton's third law, given by eqn (4), we introduce the following approximation
It assumes that the effective force density is distributed on the center of the probe. This approximation has phenomenological character and below we show its consequences and test them against experimental data. We expect that the above approximation is reasonable for a probe which does not strongly disturb the structure of surrounding complex fluid. In the opposite case of strong interactions between a probe and surrounding macromolecules we expect that this approximation is invalid. For example, when a probe particle attracts surrounding macromolecules so strongly that the probe, with the macromolecules nearby, forms a big conglomerate. In this case we expect that the effective force density is distributed at the border of the conglomerate which may be far from the probe particle.
We then apply the above phenomenological approximation in formula (7) to obtain the following expression for the friction coefficient
| | 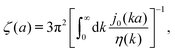 | (9) |
where
j0(
x) = sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x/
x is the zeroth order spherical Bessel function and appears as a result of the Fourier space representation of the Dirac delta function from
eqn (7) as follows,
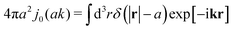
. We call formula
(9) the Stokes' law in complex liquids. Using the following property of the spherical Bessel function,
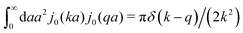
, we can invert the Stokes' law in complex liquids to obtain,
| | 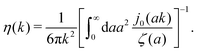 | (10) |
The original Stokes' law in simple liquids is recovered when we use
ζ(
a) = 6π
ηmacroa, which then gives
η(
k) =
ηmacro. This result is not straightforward because the integrand
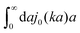
(which appears after utilizing
ζ(
a) = 6π
ηmacroa) is defined only in a distributional sense. Therefore we use a regularization procedure in
(10) as follows,
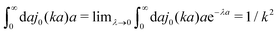
, which gives
η(
k) =
ηmacro, as expected for friction
ζ(
a) = 6π
ηmacroa. Because of the need for the regularization procedure we also give the following equivalent form of the inverse Stokes' law
(10),
| | 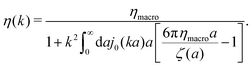 | (11) |
The macroscopic viscosity is defined by
ηmacro = lim
a→∞ζ(
a)/6π
a, which is the viscosity experienced by the largest particles.
The inverse Stokes' law in complex liquids given by (10) provides an experimental procedure to determine the wave-vector dependent viscosity η(k). The equation contains the integral over radius of a probe particle with corresponding friction coefficient ζ(a). Therefore, to determine η(k) we should measure friction coefficients of probe particles of different sizes in the complex liquid. We use data of Szymanski et al.14 from Fig. 1a to show how the procedure of the determination of the wave-vector dependent viscosity works.
We first fit their experimental data with the following fitting formula, log[ζmic(a)/(6πη0a)] = (1 + gmice−a/amic)ηmacro/η0 and the fitting parameters gmic = −0.904 and amic = 4.455 nm, which is shown in Fig. 1. The fit interpolates the experimental data for any radius of the probe, which is needed in the inverse Stokes' law (11) to obtain the wave-vector dependent viscosity. We use the above fit for the friction coefficient ζmic(a) in eqn (11) and numerically evaluate the integral. As a result we obtain the wave-vector dependent viscosity presented in Fig. 1c.
Diffusion of probe particles of different sizes has also been studied in biological systems. The literature data for diffusion inside E. coli cell cytoplasm have been combined in ref. 36 and are presented in Fig. 1b, along with the fitting formula (see caption for details). We use the analytical fit in the inverse Stokes' law (11) to determine the wave-vector dependent viscosity of E. coli cell cytoplasm. The result is presented in Fig. 1d. Here we assumed that from the perspective of long-time diffusion the cell cytoplasm can be treated as a fluid described by a wave-vector dependent viscosity and ignore life processes inside the cell. We also treat the probes as spherical particles. It is also worth mentioning that, as in the ref. 36, we assume that there is a saturation of the normalized friction in the curve of Fig. 1b for large hydrodynamic radii. In a similar way we determine the wave-vector dependent viscosity of HeLa cell cytoplasm in Fig. 2 and of aqueous solutions of polyethylene glycols of different molecular weight in the ESI.†
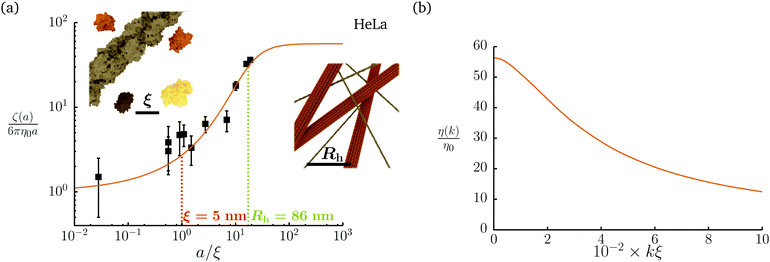 |
| | Fig. 2 Figure (a) shows normalized friction coefficient, ζ(a)/6πη0a, in HeLa cell cytoplasm calculated by phenomenological fit ζHeLa(a) = 6πη0a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(Reff(a)/ξHeLa)αHeLa], with Reff(a)−2 = RHeLa−2 + a−2 and the following parameters ξHeLa = 5 nm, RHeLa = 86 nm, and αHeLa = 0.49 for HeLa.17 The points following the curve correspond to the literature data used in reference17 supplemented by experimental data from.37–39 Insets represents the cell interior observed at different length-scales. In the left inset the exemplary proteins and the fragment of actin filament (7 nm in diameter) are visible. The right inset depicts actin filaments and microtubules (∼24 nm in diameter). (b) Wave-vector-dependent viscosity calculated from formula (11) for friction coefficient presented in panel (a). exp[(Reff(a)/ξHeLa)αHeLa], with Reff(a)−2 = RHeLa−2 + a−2 and the following parameters ξHeLa = 5 nm, RHeLa = 86 nm, and αHeLa = 0.49 for HeLa.17 The points following the curve correspond to the literature data used in reference17 supplemented by experimental data from.37–39 Insets represents the cell interior observed at different length-scales. In the left inset the exemplary proteins and the fragment of actin filament (7 nm in diameter) are visible. The right inset depicts actin filaments and microtubules (∼24 nm in diameter). (b) Wave-vector-dependent viscosity calculated from formula (11) for friction coefficient presented in panel (a). | |
3 Rotational diffusion and translation
We use the same approach as before to predict the rotational friction coefficient of the probe particle, ζrot(a), which is defined as the relation between the torque, T, and the angular velocity, Ω: T = ζrot(a)Ω. In this case the average velocity field around the rotating probe particle is given by 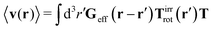 .35 Again, we apply the stick boundary condition, v(
.35 Again, we apply the stick boundary condition, v(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) a) = Ω ×
a) = Ω × ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) a and use the following phenomenological approximation for Tirrrot,
a and use the following phenomenological approximation for Tirrrot,| | 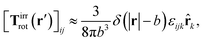 | (12) |
with summation over repeating Cartesian indices i, j, k and Levi-Civita symbol εijk. We assume that the effective force density is focused in the center of the particle so we will take the limit b → 0 in eqn (12). The total effective torque is preserved, 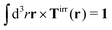 , which corresponds to Newton's third law. These equations lead to the following Stokes' law in complex liquids for rotational motion,
, which corresponds to Newton's third law. These equations lead to the following Stokes' law in complex liquids for rotational motion,| | 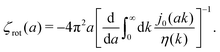 | (13) |
Combination of the Stokes' law for rotational motion (13) with the inverse Stokes' law for translation (9) leads to the following formula
| | 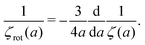 | (14) |
Rotational diffusion coefficients calculated from the above equation for
E. coli cell cytoplasm are presented in
Fig. 3. In the ESI
† there are also rotational diffusion coefficients obtained with the relation
(14) for aqueous solutions of polyethylene glycols, aqueous micellar solutions and HeLa cell. Both sides of
eqn (14) are measurable and below we give several tests of this equation for various complex liquids.
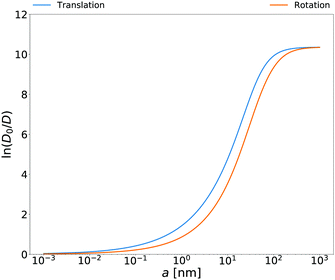 |
| | Fig. 3 Translational and rotational diffusion coefficients inside E. coli cell cytoplasm as a function of the hydrodynamic radius of the probe particle. Continuous blue line: natural logarithm of the inverse of the normalized translational diffusion coefficient, D0/D = ζEC(a)/6πη0a, with translational friction coefficient ζEC(a) described in the caption of Fig. 1b. Continuous orange line: natural logarithm of the inverse of normalized rotational diffusion coefficient, D0/D = ζrotEC(a)/8πη0a3 with ζrotEC(a) calculated from the formula (14) with ζEC(a) as an input. | |
McGuffee and Elcock40 performed Brownian dynamics (BD) simulations of protein diffusion in solution of various proteins designed to resemble the crowding of the cytoplasm of an E. coli cell. The authors performed simulations of long-time translational and short-time rotational diffusion of proteins using two models: one with steric interactions only, and the full model including steric, electrostatic and short-range attractive hydrophobic interactions. In our previous work36 we used the translational diffusion data of McGuffee and Elcock40 and introduced a fit, ζsteric/full(a) = 6πη0a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(Reff(a)/ξsteric/full)αsteric/full], with Reff(a)−2 = Rsteric/full−2 + a−2 to calculate the long-time translational friction ζsteric/full(a)ζ0 ratio for both models; here ζ0 = 6πη0a. The model parameters were equal to ξsteric = 3.6 nm, Rsteric = 17 nm, αsteric = 0.59, ξfull = 0.2 nm, Rfull = 20 nm, αfull = 0.32. Here we use that phenomenological fit in the formula (14) to find ζrot(a)/ζ0,rot ratio with ζ0,rot = 8πη0a3, and compare our prediction with the short-time rotational diffusion data of McGuffee and Elcock.40 Predictions made according to eqn (14) give the long-time rotational friction. Comparison of the data revealed that short-time friction from BD was systematically shifted by a factor of 2/3 with respect to the predicted values of ζrot(a)/ζ0,rot. Data are shown in Fig. 4.
exp[(Reff(a)/ξsteric/full)αsteric/full], with Reff(a)−2 = Rsteric/full−2 + a−2 to calculate the long-time translational friction ζsteric/full(a)ζ0 ratio for both models; here ζ0 = 6πη0a. The model parameters were equal to ξsteric = 3.6 nm, Rsteric = 17 nm, αsteric = 0.59, ξfull = 0.2 nm, Rfull = 20 nm, αfull = 0.32. Here we use that phenomenological fit in the formula (14) to find ζrot(a)/ζ0,rot ratio with ζ0,rot = 8πη0a3, and compare our prediction with the short-time rotational diffusion data of McGuffee and Elcock.40 Predictions made according to eqn (14) give the long-time rotational friction. Comparison of the data revealed that short-time friction from BD was systematically shifted by a factor of 2/3 with respect to the predicted values of ζrot(a)/ζ0,rot. Data are shown in Fig. 4.
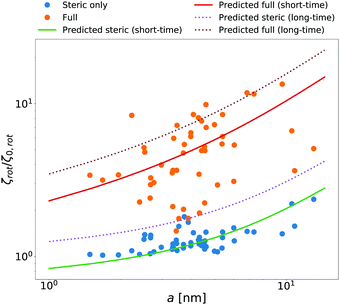 |
| | Fig. 4 Comparison of simulated40 and predicted data of relative rotational friction ζrot(a)/ζ0,rot. The circles correspond to the short-time friction obtained from the BD simulations by McGuffee and Elcock.40 Dotted lines correspond to the predicted values of the long-time rotational friction predicted on the basis of long-time translational friction using eqn (14). Solid lines were obtained by shifting the corresponding long-time friction values by the factor of 2/3 to match the simulated short-time data. | |
We additionally applied eqn (14) to predict rotational friction experienced by the globular protein—aldolase—in solutions of poly(ethylene glycol) (PEG). In our previous work41 we obtained the model of long-time translational friction ζ(a,c) in solutions with different concentrations c of PEG (see caption of Fig. 5 for details). We use this model in eqn (14) to predict the long-time rotational friction ζrot(aaldolase,c)/ζ0,rot ratio. In Fig. 5 we compare the short-time friction experienced by aldolase in the polymer solutions obtained by means of fluorescence correlation spectroscopy (FCS) with the predicted values of short-time rotational friction (the long-time friction obtained from eqn (14) and reduced by the factor of 2/3).
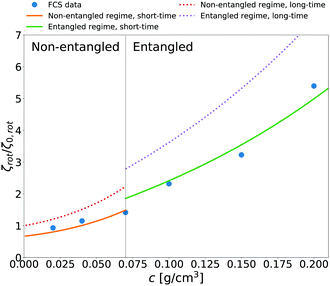 |
| | Fig. 5 The relative short-time rotational friction ζrot(aaldolase,c)/ζ0,rot experienced by the aldolase diffusing in the poly(ethylene glycol) solutions obtained by means of fluorescence correlation spectroscopy (FCS); circles. Experimental data are compared with the predictions made for two concentration regimes—non-entangled and entangled. The prediction (solid lines) were made on the basis of eqn (14) reduced by the factor of 2/3 and with translational friction from the ref. 41 as follows ζ(aaldolase,c) = 6πη0aaldolase![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[γ(Reff(aaldolase)/ξ(c))αRT]; here Reff−2(aaldolase) = RPEG−2 + aaldolase−2, ξ(c) = Rg(c/c*)−0.75, c* = 3M/(4πRg3NA), M = 24 exp[γ(Reff(aaldolase)/ξ(c))αRT]; here Reff−2(aaldolase) = RPEG−2 + aaldolase−2, ξ(c) = Rg(c/c*)−0.75, c* = 3M/(4πRg3NA), M = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 g mol−1 denotes average molecular weight of the polymer, NA is the Avogadro constant, Rg = 7.6 nm is the gyration radius of polymer, RPEG = 4.6 nm denotes hydrodynamic radius of the polymer, R is the gas constant, T = 298 K is absolute temperature, γ = 3.7 kJ mol−1, aaldolase = 4.5 nm, α equals to 0.78 and 695 g mol−1 denotes average molecular weight of the polymer, NA is the Avogadro constant, Rg = 7.6 nm is the gyration radius of polymer, RPEG = 4.6 nm denotes hydrodynamic radius of the polymer, R is the gas constant, T = 298 K is absolute temperature, γ = 3.7 kJ mol−1, aaldolase = 4.5 nm, α equals to 0.78 and 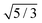 for entangled and non-entangled regime, respectively. The long-time rotational friction is shown as dotted lines. Following the work of Wisniewska et al.41 the crossover between both regimes was assumed at Reff(aaldolase)/ξ(c) = 1. for entangled and non-entangled regime, respectively. The long-time rotational friction is shown as dotted lines. Following the work of Wisniewska et al.41 the crossover between both regimes was assumed at Reff(aaldolase)/ξ(c) = 1. | |
In both of the analyzed types of complex liquids the measured short-time rotational friction is given by 2/3 of the long-time rotational friction predicted by eqn (14). This relation between short and long-time diffusion—the factor 3/2—is only a rough approximation. In the limit of low concentrations the 2/3 factor should approach 1. Nevertheless, the agreement of our prediction with the simulated and experimental values is pronounced.
4 Application to biological systems
We provide two practical applications of our predictions. For example, descriptions of protein–protein association rates require information about both translational and rotational diffusion coefficients of reactants.42 Based on eqn (14) and the model describing the ζ(a)/ζ0 ratio for cytoplasm of E. coli we provide a database of rotational diffusion coefficients for all proteins and their possible oligomers; see Table S1 from the ESI.†
Another example, also related to the diffusion in the cytoplasm of E. coli, is the motion of the transcription factors along a DNA strand described by the model of Blainey et al.43 The model was introduced to describe experiments on interactions of DNA with proteins.44,45 According to the model, the transcription factor during the search of the target DNA sequence performs three types of motion: three dimensional translation, rotational and sliding. Therefore all three types of friction need to be included in calculations of the effective diffusion coefficient D1 describing one dimensional sliding of protein along DNA. Tabaka et al.46 calculated the D1 values for all transcription factors in E. coli using the constant value of rotational friction assuming that it was ten times higher than the friction of pure solvent. Our study shows that the rotational friction is not a constant and is dependent on the size of particles in motion. We therefore recalculated the values of D1 provided by Tabaka et al.46 (new data are given in Table S2 from the ESI†). We compared the predicted values of D1 with those provided by Tabaka et al.46 (D1(ηrot = const.)). We found that the D1/D1(ηrot = const.) ratio takes values from 0.87 to 1.41, with median equal to 1.11.
5 Summary and conclusions
We did not find more experimental or numerical simulation data in the literature to systematically test the relation (14) between translational and rotational friction. The available data presented in Fig. 4 and 5 validate formula (14) because they show that this relation unifies roughly one hundred different friction coefficients taken from numerical simulations and experiments. Proper tests of the relation require comparing the rotational and translational friction of particles of similar hydrodynamic radii to calculate the derivative in formula (14) for the same complex liquid. Moreover, the frictions should be determined on the same time-scales. This should be readily achievable in numerical simulations. In experiments on friction or diffusion of probe particles in complex liquids it is easier to focus on one probe particle in different complex liquids. Different complex liquids can be obtained, e.g., by taking different concentration of polymers in polymer solution. To change the size of the probe particles in the same complex liquid is more challenging and often requires different experimental techniques for different probes.14 Experiments with probes of different sizes are also necessary in our method to determine a wave-vector dependent viscosity.
Our theoretical framework quantitatively captures diffusion in complex liquids. To the best of our knowledge, we offer the first framework to measure the viscosity function and to predict diffusivities of various probes in complex media. This is also the first time the viscosity function of complex liquids has been determined from experimental data and a relation between the translational and rotational diffusion coefficients in complex liquids has been given. Our framework allows predictions of a viscosity function, translational diffusion and rotational diffusion as a function of probe size when one of these functions is known. We used the theory to provide a database for rotational diffusion and sliding along a DNA strand in E. coli, which gives parameters necessary for a quantitative description of protein association rates.42
Another effect which modifies nanoparticle diffusion is related to its interactions (e.g., electrostatics) with surrounding macromolecules.47,48 This effect can be included in the governing equations used in this article but was neglected in our phenomenological assumptions. It thus remains an open question to include the interactions within the presented formalism. Knowledge about the wave-vector dependent viscosity opens a new door in simulations of complex liquids. Numerical simulations are very challenging because of multiple-sized objects and their complicated, long-range hydrodynamic interactions. Instead of simulations of many multicomponent objects such as proteins in a liquid, it is tempting to simulate only one or a few multicomponent proteins but immersed in a liquid with a wave-vector-dependent viscosity determined by our method. This approach can be achieved by modification of the Green function in the hydrodynamic equations. In this situation η(k) will represent the liquid and other surrounding macromolecules. We hope that our theoretical approach can be generalized to the case of diffusion of probe particles of different shapes. That would allow diffusivity predictions of, e.g., rod-like particles, in a complex liquid with the wave-vector dependent viscosity measured by our method. Another possible application would be to predict Stokesian flow of complex fluids in micro and especially nano-fluidic systems where flow is affected by small length-scales.
Conflicts of interest
There are no conflicts to declare.
Appendix A: Smoluchowski dynamics
Within the Smoluchowski dynamics,27 we model all macromolecules by N spherical beads, with interparticle potential forces, Finti(X), and the external forces, Ej(Rj), acting on the beads. The forces depend on the configuration of the particles, X ≡ R1,…,RN. The macromolecules are immersed in a solution with ambient velocity field, v0(r). In the generalized Smoluchowski description of complex liquids, the evolution of the probability distribution of configuration, P(X,t), is described by the generalized Smoluchowski equation,| | 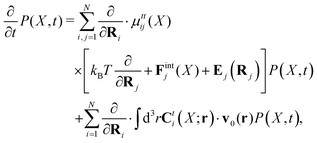 | (15) |
with configuration dependent Smoluchowski flow velocity in the whole complex liquid,49| | 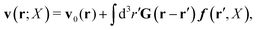 | (16) |
given by the Smoluchowski force density,| | 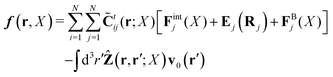 | (17) |
and the thermodynamic, Brownian forces, FBj(X) = −kBT∂/∂Rj![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(X,t).
P(X,t).
In the above equations, the matrix, μttij(X), and the kernels, Cti(X;r), G(r − r′), ![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) tij(r;X), and, Ẑij(r,r′;X), are purely hydrodynamical quantities. They are defined for N beads immersed in an incompressible and Newtonian fluid described by the stationary Stokes equations,50 −∇p(r) + η0Δv(r) = 0, and ∇·v(r) = 0, which determine fluid pressure, p(r), and the fluid velocity field, v(r). The beads are immersed in the fluid with initial velocity field, v0(r). We assume that there is no external torque, but there are external forces acting on the beads, Fhydj. We also assume no-slip boundary conditions on their surfaces. Presence of the beads and the external forces modify the ambient flow, v0(r), and lead to the velocity field, v(r). This velocity field must be found by solving the Stokes equations in the situation described above. It is a difficult task,50 but for our purpose we need to know that the velocity field in the whole space may be represented by the Green function of the Stokes equations as follows,
tij(r;X), and, Ẑij(r,r′;X), are purely hydrodynamical quantities. They are defined for N beads immersed in an incompressible and Newtonian fluid described by the stationary Stokes equations,50 −∇p(r) + η0Δv(r) = 0, and ∇·v(r) = 0, which determine fluid pressure, p(r), and the fluid velocity field, v(r). The beads are immersed in the fluid with initial velocity field, v0(r). We assume that there is no external torque, but there are external forces acting on the beads, Fhydj. We also assume no-slip boundary conditions on their surfaces. Presence of the beads and the external forces modify the ambient flow, v0(r), and lead to the velocity field, v(r). This velocity field must be found by solving the Stokes equations in the situation described above. It is a difficult task,50 but for our purpose we need to know that the velocity field in the whole space may be represented by the Green function of the Stokes equations as follows, 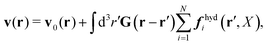 where, fhydi(r,X), is the hydrodynamic force density acting on fluid on the surface of the ith bead.35 The Green function in Fourier space,
where, fhydi(r,X), is the hydrodynamic force density acting on fluid on the surface of the ith bead.35 The Green function in Fourier space, 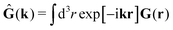 , is given by the Oseen tensor,
, is given by the Oseen tensor,
| | 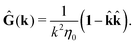 | (18) |
The above representation of the velocity field in terms of the Green function shifts the problem of calculating,
v(
r), to the task of finding the hydrodynamic force densities,
fhydi(
r,
X).
Because the Stokes equations are linear, the hydrodynamic force density must also be linear in external forces acting on the particles, Fj, and in the ambient velocity field, v0(r),
| | 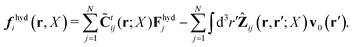 | (19) |
The above expression is a definition of the matrix,
![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) tij
tij(
r;
X), and the matrix kernel,
Ẑij(
r,
r′;
X). The velocities of the particles are also linear in the external forces and the ambient flow,
| | 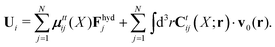 | (20) |
which defines the mobility matrix,
μttij(
X), and the kernel,
Ctij(
X;
r). In the generalized Smoluchowski equation we use the kernel,
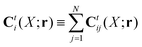
. We closely follow the notation of Szymczak and Cichocki,
35 where they describe those quantities in detail.
Appendix B: linear response theory for Smoluchowski dynamics
We consider motion of a probe particle in the system described by the Smoluchowski eqn (15) under action of a small external force on the probe. A proper tool in this situation is linear response theory, which has already been applied to the case of the Smoluchowski equation.34,51 A particularly useful result in the context of our work was derived by Szymczak and Cichocki.35 The difference between their and our case lies in the external force, that in their case acts on all particles, while in our case it acts only on the probe. Before discussing our case, in the next paragraph we summarize those elements of their work that we found particularly useful for our analysis.
Szymczak and Cichocki use the Smoluchowski eqn (15). Assuming that the external force field, E(r,t), which determines external forces, Ej(Rj) = E(Rj,t), and the ambient flow, v0(r,t), are small, they apply linear response theory to predict evolution of the probability distribution function, P(X,t), for the configuration of the interacting Brownian beads. Initially, for time, t0 = −∞, the system is in equilibrium, P(X,t0) = Peq(X), then the time dependent force field, E(r,t), acting on the beads and the ambient flow, v0(r,t), appear. The distribution function, P(X,t) = Peq(X) + δP(X,t), deviates from equilibrium and evolves according to the Smoluchowski equation. Neglecting in the Smoluchowski equation the terms that are quadratic in δP(X,t), E(r,t), or v0(r,t), Szymczak and Cichocki perform rigorous analysis within this linear response assumption. They obtain expression for the average Smoluchowski force density (17) in the following form,
| | 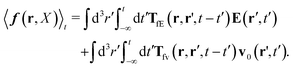 | (21) |
It has a form that is typical to the linear response theory. The response of the system is given by response kernels, here denoted by
TfE and
Tfv, which linearly take into account the ‘history’ of the ‘external forces’. Szymczak and Cichocki also obtain statistical expressions for the response kernels
TfE and
Tfv, the details of which are not relevant here. We will need the general form of the
TfE(
r,
r′,
t −
t′) kernel, that is,
| | 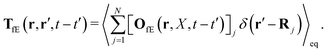 | (22) |
The index
j is the index of the particle on which the external force acts. The kernels
TfE and
Tfv along with
OfE(
r,
X,
t −
t′) can be inferred from the formulae (9.14)–(9.17) in
ref. 35. There is also analysis of
TfE and
Tfv in the language of diagrams. It leads to identification of two classes of diagrams: irreducible and reducible diagrams, that allows to represent the above response kernels by,
| | 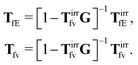 | (23) |
The above formulae should be understood as a series of convolutions in the following sense,
e.g.,
| | 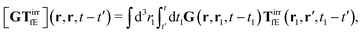 | (24) |
where we use the following extended definition of the Oseen tensor,
G(
r,
r′,
t −
t′) =
δ(
t −
t′)
G(
r,
r′), with the Dirac delta function. Formulas
(23) can be treated as definitions of the irreducible kernels,
Tirrfv, and
TirrfE.
Using the above expressions by Szymczak and Cichocki, below we calculate the average velocity field for the case with vanishing ambient velocity field, v0(r) = 0. By averaging the velocity field (16) over the probability distribution at time t and utilizing the formula (21) we obtain,
| | 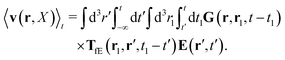 | (25) |
Using expression
(23) in the above equation we additionally get,
| | 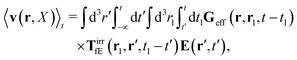 | (26) |
with the effective Green function
Geff(
r,
r′,
t −
t′) defined by,
| | | Geff = G(1 − TirrfvG)−1. | (27) |
It is called the effective Green function, because it gives the average velocity field of a complex fluid in terms of the force density acting on the fluid,
f0. For a simple fluid it is given by the Green function as follows,
| | 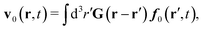 | (28) |
To obtain the average velocity field for a complex liquid we average
eqn (16) and utilize
eqn (21), (23), (27) and (28) for the case of no external forces,
E = 0, which leads to the following expression,
| | 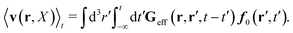 | (29) |
We return to the case when the force acts on the probe only. Calculation of the average velocity field around the probe requires only minor change of Szymczak and Cichocki's approach. Assuming that the probe is the particle with the index 1, it is sufficient to repeat their analysis leaving in the formula (22) only term with j = 1. Therefore in our problem the force density is given by,
| | 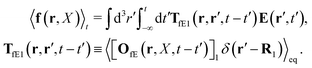 | (30) |
Moreover we would like to know what is the average velocity field around the probe particle. For given configuration it is defined by,
| | | v1(r,X) ≡ v(r − R1,X). | (31) |
In terms of the force density, according to
eqn (16), it can be given by
| | 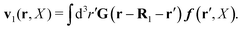 | (32) |
Changing the integration variable,
r′ →
r′ +
R1, and averaging of the above equation over the probability distribution at time
t gives,
| | 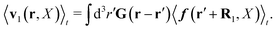 | (33) |
The Smoluchowski force density 〈
f(
r′ +
R1,
X)〉
t can be calculated from
eqn (30) by replacing
r →
r +
R1 under the average, which gives,
| | 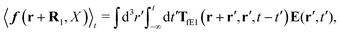 | (34) |
where we used the fact that in
eqn (30) we can use
r′ =
R1, because of the Dirac delta function. The above expression can be further analyzed as it is in Szymczak and Cichocki's paper. Therefore, we can represent the kernel,
TfE1, in terms of its irreducible part,
| | | TfE1 = [1 − TirrfvG]−1TirrfE1. | (35) |
Moreover, as follows from their analysis, the probe particle appears only in
TirrfE1, not in
Tirrfv. Similarly to expressions
(25) and (26), for the external force acting only on the probe we also get two equivalent expressions for the average velocity field around the probe,
| | 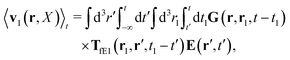 | (36) |
and
| | 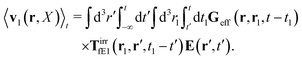 | (37) |
The above analysis can be generalized to the case of beads of different sizes. Because of a wide applicability of the Smoluchowski equation for modeling of different complex fluids, eqn (36) and (37) give important insight into the mechanism of dragging a probe through a complex liquid. Both expressions for the average velocity field, (36) and (37), are equivalent. However, they give two different interpretations of the situation when a probe is dragged by the external force in a complex fluid. According to eqn (36), the external force induces force density given by, 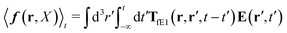 , which acts on the solution—because it is followed by the Oseen tensor which propagates the velocity field in the solution. On the other hand, the interpretation of eqn (37) is that the external force on the probe induces effective force density defined by,
, which acts on the solution—because it is followed by the Oseen tensor which propagates the velocity field in the solution. On the other hand, the interpretation of eqn (37) is that the external force on the probe induces effective force density defined by, 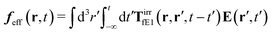 , which acts on the complex liquid—because it is followed by the effective Green function, Geff. It is worth emphasizing the local character of the induced effective force density. Contrary to the kernel TfE1, the irreducible kernel TirrfE1, is a local quantity which means that its integral,
, which acts on the complex liquid—because it is followed by the effective Green function, Geff. It is worth emphasizing the local character of the induced effective force density. Contrary to the kernel TfE1, the irreducible kernel TirrfE1, is a local quantity which means that its integral, 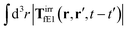 , is finite. The long range character of the kernel TfE1(r,r′,t − t′) produces force densities acting on the solution far from the probe, because it can be shown that,
, is finite. The long range character of the kernel TfE1(r,r′,t − t′) produces force densities acting on the solution far from the probe, because it can be shown that, 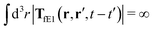 . The effective force density form around the probe a local ‘cloud’, contrary to a much wider ‘cloud’ of the force density.
. The effective force density form around the probe a local ‘cloud’, contrary to a much wider ‘cloud’ of the force density.
The effective force density preserves Newton's third law in the following sense,
| | 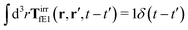 | (38) |
where 1 is a unit 3 × 3 matrix. It means that the total effective induced force acting on the complex liquid is equal to the external force acting on the probe. This is consistent with Szymczak and Cichocki's analysis of the integral
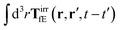
given by formulas (13.11)–(13.23) in the
ref. 35.
In our paper we confine ourselves to the case of constant force acting on the probe particle, E(r,t) = F, in homogeneous, isotropic and incompressible complex fluid. In this case the formula (37) is reduced to eqn (1) and (2) with
| | 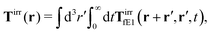 | (39) |
and
| | 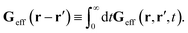 | (40) |
For a homogeneous fluid the effective Green function must depend on the difference of positional variables, Geff(r − r′, t − t′) = Geff(r,r′,t − t′). Moreover, for isotropic complex fluid, because the flow is incompressible, the effective Green function must also be isotropic and incompressible. It follows that the above time-integrated effective Green function is given in Fourier space by eqn (3). Eqn (38) and (39) imply that preservation of Newton's third law by Tirr is represented by eqn (4).
Acknowledgements
KM acknowledges discussion with P. Malgaretti. We are grateful to Ahmad Omar and Austin Dulaney for their comments on the manuscript. KM has received funding from the National Science Centre, Poland (2016/21/D/ST3/00988). PG was supported by the European Research Council Starting (Grant No. 279647). RH was supported by the National Science Centre, Poland within the grant Maestro UMO-2016/22/A/ST4/00017.
Notes and references
- A. Einstein, Zur theorie der brownschen bewegung, Ann. Phys., 1906, 324(2), 371–381 CrossRef.
- M. Von Smoluchowski, Zur kinetischen theorie der brownschen molekularbewegung und der suspensionen, Ann. Phys., 1906, 326(14), 756–780 CrossRef.
- R. Huang, I. Chavez, K. M. Taute, B. Lukić, S. Jeney, M. G. Raizen and E.-L. Florin, Direct observation of the full transition from ballistic to diffusive brownian motion in a liquid, Nat. Phys., 2011, 7(7), 576 Search PubMed.
-
J. K. G. Dhont, An introduction to dynamics of colloids, vol. 2, Elsevier, 1996 Search PubMed.
-
J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier, 2006 Search PubMed.
- T. G. Mason, K. Ganesan, J. H. Van Zanten, D. Wirtz and S. C. Kuo, Particle tracking microrheology of complex fluids, Phys. Rev. Lett., 1997, 79(17), 3282 CrossRef CAS.
- T. G. Mason and D. A. Weitz, Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids, Phys. Rev. Lett., 1995, 74(7), 1250 CrossRef CAS PubMed.
- C. D. Chapman, K. Lee, D. Henze, D. E. Smith and R. M. Robertson-Anderson, Onset of non-continuum effects in microrheology of entangled polymer solutions, Macromolecules, 2014, 47, 1181–1186 CrossRef CAS.
- L. Maldonado-Camargo and C. Rinaldi, Breakdown of the Stokes–Einstein relation for the rotational diffusivity of polymer grafted nanoparticles in polymer melts, Nano Lett., 2016, 16(11), 6767–6773 CrossRef CAS.
- T. Gisler and D. A. Weitz, Scaling of the microrheology of semidilute f-actin solutions, Phys. Rev. Lett., 1999, 82(7), 1606 CrossRef CAS.
- Z. Bu and P. S. Russo, Diffusion of dextran in aqueous (hydroxypropyl) cellulose, Macromolecules, 1994, 27(5), 1187–1194 CrossRef CAS.
- J. Van der Gucht, N. A. M. Besseling, W. Knoben, L. Bouteiller and M. A. Cohen Stuart, Brownian particles in supramolecular polymer solutions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67(5), 051106 CrossRef CAS.
- S. S. Jena and V. A. Bloomfield, Probe diffusion in concentrated polyelectrolyte solutions: effect of background interactions on competition between electrostatic and viscous forces, Macromolecules, 2005, 38(25), 10551–10556 CrossRef CAS.
- J. Szymański, A. Patkowski, A. Wilk, P. Garstecki and R. Holyst, Diffusion and viscosity in a crowded environment: from nano- to macroscale, J. Phys. Chem. B, 2006, 110(51), 25593–25597 CrossRef PubMed.
- G. H. Koenderink, H. Zhang, D. G. A. L. Aarts, M. P. Lettinga, A. P. Philipse and G. Nägele, On the validity of Stokes–Einstein–Debye relations for rotational diffusion in colloidal suspensions, Faraday Discuss., 2003, 123, 335–354 RSC.
- F. Trovato and V. Tozzini, Diffusion within the cytoplasm: a mesoscale model of interacting macromolecules, Biophys. J., 2014, 107(11), 2579–2591 CrossRef CAS.
- T. Kalwarczyk, N. Ziebacz, A. Bielejewska, E. Zaboklicka, K. Koynov, J. Szymanski, A. Wilk, A. Patkowski, J. Gapinski and H.-J. Butt,
et al., Comparative analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale, Nano Lett., 2011, 11(5), 2157–2163 CrossRef CAS PubMed.
- J. Skolnick, Perspective: on the importance of hydrodynamic interactions in the subcellular dynamics of macromolecules, J. Chem. Phys., 2016, 145(10), 100901 CrossRef.
- D. Lavalette, M. A. Hink, M. Tourbez, C. Tetreau and A. J. Visser, Proteins as micro viscosimeters: Brownian motion revisited, Eur. Biophys. J., 2006, 35(6), 517–522 CrossRef CAS.
- G. D. J. Phillies, Probe dynamics constraints on theoretical models for polymer dynamics, J. Chem. Phys., 2012, 137(22), 224905 CrossRef.
- L. Masaro and X. X. Zhu, Physical models of diffusion for polymer solutions, gels and solids, Prog. Polym. Sci., 1999, 24(5), 731–775 CrossRef CAS.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Mobility of nonsticky nanoparticles in polymer liquids, Macromolecules, 2011, 44(19), 7853–7863 CrossRef CAS PubMed.
- V. Ganesan, V. Pryamitsyn, M. Surve and B. Narayanan, Noncontinuum effects in nanoparticle dynamics in polymers, J. Chem. Phys., 2006, 124(22), 221102 CrossRef PubMed.
- T. Keyes, Self-diffusion in a binary critical fluid, J. Chem. Phys., 1975, 62(5), 1691–1692 CrossRef CAS.
- C. W. J. Beenakker, The effective viscosity of a concentrated suspension of spheres (and its relation to diffusion), Phys. A, 1984, 128(1–2), 48–81 CrossRef.
- K. F. Freed and M. Muthukumar, On the Stokes problem for a suspension of spheres at finite concentrations, J. Chem. Phys., 1978, 68, 2088 CrossRef CAS.
-
P. N. Pusey, Liquids, freezing and the glass transition, North-Holland, Amsterdam, 1991 Search PubMed.
- F. Brochard Wyart and P. G. De Gennes, Viscosity at small scales in polymer melts, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 1(1), 93–97 CrossRef.
- R. M. Puscasu, B. D. Todd, P. J. Daivis and J. S. Hansen, An extended analysis of the viscosity kernel for monatomic and diatomic fluids, J. Phys.: Condens. Matter, 2010, 22(19), 195105 CrossRef CAS PubMed.
- B. J. Palmer, Transverse-current autocorrelation-function calculations of the shear viscosity for molecular liquids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 49(1), 359 CrossRef CAS PubMed.
- D. Bertolini and A. Tani, Stress tensor and viscosity of water: molecular dynamics and generalized hydrodynamics results, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52(2), 1699 CrossRef CAS.
- R. M. Puscasu, B. D. Todd, P. J. Daivis and J. S. Hansen, Viscosity kernel of molecular fluids: butane and polymer melts, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82(1), 011801 CrossRef CAS.
- A. Furukawa and H. Tanaka, Nonlocal nature of the viscous transport in supercooled liquids: complex fluid approach to supercooled liquids, Phys. Rev. Lett., 2009, 103(13), 135703 CrossRef PubMed.
- B. U. Felderhof and R. B. Jones, Linear response theory of sedimentation and diffusion in a suspension of spherical particles, Phys. A, 1983, 119(3), 591–608 CrossRef.
- P. Szymczak and B. Cichocki, A diagrammatic approach to response problems in composite systems, J. Stat. Mech.: Theory Exp., 2008, P01025 Search PubMed.
- T. Kalwarczyk, M. Tabaka and R. Holyst, Biologistics-diffusion coefficients for complete proteome of Escherichia coli, Bioinformatics, 2012, 28(22), 2971–2978 CrossRef CAS PubMed.
- M. Kloster-Landsberg, G. Herbomel, I. Wang, J. Derouard, C. Vourc'h, Y. Usson, C. Souchier and A. Delon, Cellular response to heat shock studied by multiconfocal fluorescence correlation spectroscopy, Biophys. J., 2012, 103(6), 1110–1119 CrossRef CAS PubMed.
- M. K. Daddysman and C. J. Fecko, Revisiting point frap to quantitatively characterize anomalous diffusion in live cells, J. Phys. Chem. B, 2013, 117(5), 1241–1251 CrossRef CAS.
- Y. Nakane, A. Sasaki, M. Kinjo and T. Jin, Bovine serum albumin-coated quantum dots as a cytoplasmic viscosity probe in a single living cell, Anal. Methods, 2012, 4(7), 1903–1905 RSC.
- S. R. McGuffee and A. H. Elcock, Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm, PLoS Comput. Biol., 2010, 6(3), e1000694 CrossRef.
- A. Wiśniewska, K. Sozański, T. Kalwarczyk, K. Kedra-Królik, C. Pieper, S. A. Wieczorek, S. Jakieła, J. Enderlein and R. Hołyst, Scaling of activation energy for macroscopic flow in poly(ethylene glycol) solutions: entangled-non-entangled crossover, Polymer, 2014, 55(18), 4651–4657 CrossRef.
-
J. Qing, A. Chen and N. Zhao, Effect of crowding on protein–protein association in diffusion-limited regime, in Journal of Physics: Conference Series, IOP Publishing, 2018, vol. 1035, p. 012006 Search PubMed.
- B. Bagchi, P. C. Blainey and X. S. Xie, Diffusion constant of a nonspecifically bound protein undergoing curvilinear motion along dna, J. Phys. Chem. B, 2008, 112(19), 6282–6284 CrossRef CAS.
- P. C. Blainey, A. M. van Oijen, A. Banerjee, G. L. Verdine and X. Sunney Xie, A base-excision DNA-repair protein finds intrahelical lesion bases by fast sliding in contact with dna, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(15), 5752–5757 CrossRef CAS PubMed.
- P. C. Blainey, G. Luo, S. C. Kou, W. F. Mangel, G. L. Verdine, B. Bagchi and X. Sunney Xie, Nonspecifically bound proteins spin while diffusing along DNA, Nat. Struct. Mol. Biol., 2009, 16(12), 1224 CrossRef CAS PubMed.
- M. Tabaka, T. Kalwarczyk and R. Hołyst, Quantitative influence of macromolecular crowding on gene regulation kinetics, Nucleic Acids Res., 2013, 42(2), 727–738 CrossRef.
- F. Etoc, E. Balloul, C. Vicario, D. Normanno, D. Liße, A. Sittner, J. Piehler, M. Dahan and M. Coppey, Non-specific interactions govern cytosolic diffusion of nanosized objects in mammalian cells, Nat. Mater., 2018, 17(8), 740–746 CrossRef CAS.
- A. Wisniewska, K. Sozanski, T. Kalwarczyk, K. Kedra-Krolik and R. Holyst, Scaling equation for viscosity of polymer mixtures in solutions with application to diffusion of molecular probes, Macromolecules, 2017, 50(11), 4555–4561 CrossRef CAS.
- B. U. Felderhof, Brownian motion and creeping flow on the smoluchowski time scale, Phys. A, 1987, 147(1–2), 203–218 CrossRef.
-
S. Kim and S. J. Karrila, Microhydrodynamics: principles and selected applications, Courier Corporation, 2013 Search PubMed.
- B. U. Felderhof and R. B. Jones, Linear response theory of the viscosity of suspensions of spherical brownian particles, Phys. A, 1987, 146(3), 417–432 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01119f |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Robert
Hołyst
*ab,
Robert
Hołyst
 *a,
Tomasz
Kalwarczyk
*a,
Tomasz
Kalwarczyk
 a,
Piotr
Garstecki
a,
Piotr
Garstecki
 a and
John F.
Brady
b
a and
John F.
Brady
b
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kz and measuring the corresponding shear stress, σxz = σ
kz and measuring the corresponding shear stress, σxz = σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kz, from the relation, σ = η(k)
kz, from the relation, σ = η(k)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.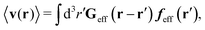
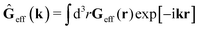 , by,
, by,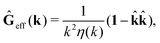
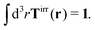
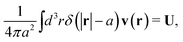
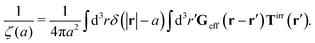

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(Reff(a)/ξEC)αEC], with Reff(a)−2 = REC−2 + a−2 and the fitting parameters ξEC = 0.51 nm, REC = 42 nm, and αEC = 0.53. (c and d) The wave-vector-dependent viscosity calculated from formula (11) from the fits of the friction coefficients presented in corresponding left panels.
exp[(Reff(a)/ξEC)αEC], with Reff(a)−2 = REC−2 + a−2 and the fitting parameters ξEC = 0.51 nm, REC = 42 nm, and αEC = 0.53. (c and d) The wave-vector-dependent viscosity calculated from formula (11) from the fits of the friction coefficients presented in corresponding left panels.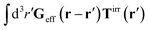 in eqn (7) for r on the surface of a particle, in a negligible way, depends on interactions of the probe with surrounding macromolecules. Motivated by this observation and keeping in mind that Tirr must be isotropic and satisfy Newton's third law, given by eqn (4), we introduce the following approximation
in eqn (7) for r on the surface of a particle, in a negligible way, depends on interactions of the probe with surrounding macromolecules. Motivated by this observation and keeping in mind that Tirr must be isotropic and satisfy Newton's third law, given by eqn (4), we introduce the following approximation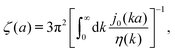
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x/x is the zeroth order spherical Bessel function and appears as a result of the Fourier space representation of the Dirac delta function from eqn (7) as follows,
x/x is the zeroth order spherical Bessel function and appears as a result of the Fourier space representation of the Dirac delta function from eqn (7) as follows, 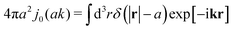 . We call formula (9) the Stokes' law in complex liquids. Using the following property of the spherical Bessel function,
. We call formula (9) the Stokes' law in complex liquids. Using the following property of the spherical Bessel function, 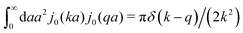 , we can invert the Stokes' law in complex liquids to obtain,
, we can invert the Stokes' law in complex liquids to obtain,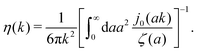
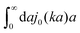 (which appears after utilizing ζ(a) = 6πηmacroa) is defined only in a distributional sense. Therefore we use a regularization procedure in (10) as follows,
(which appears after utilizing ζ(a) = 6πηmacroa) is defined only in a distributional sense. Therefore we use a regularization procedure in (10) as follows, 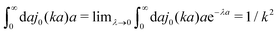 , which gives η(k) = ηmacro, as expected for friction ζ(a) = 6πηmacroa. Because of the need for the regularization procedure we also give the following equivalent form of the inverse Stokes' law (10),
, which gives η(k) = ηmacro, as expected for friction ζ(a) = 6πηmacroa. Because of the need for the regularization procedure we also give the following equivalent form of the inverse Stokes' law (10),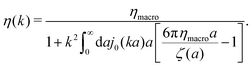
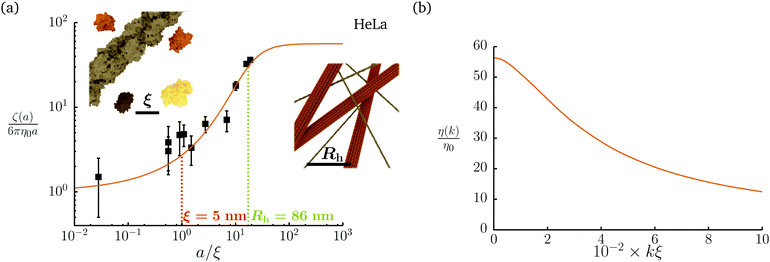
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(Reff(a)/ξHeLa)αHeLa], with Reff(a)−2 = RHeLa−2 + a−2 and the following parameters ξHeLa = 5 nm, RHeLa = 86 nm, and αHeLa = 0.49 for HeLa.17 The points following the curve correspond to the literature data used in reference17 supplemented by experimental data from.37–39 Insets represents the cell interior observed at different length-scales. In the left inset the exemplary proteins and the fragment of actin filament (7 nm in diameter) are visible. The right inset depicts actin filaments and microtubules (∼24 nm in diameter). (b) Wave-vector-dependent viscosity calculated from formula (11) for friction coefficient presented in panel (a).
exp[(Reff(a)/ξHeLa)αHeLa], with Reff(a)−2 = RHeLa−2 + a−2 and the following parameters ξHeLa = 5 nm, RHeLa = 86 nm, and αHeLa = 0.49 for HeLa.17 The points following the curve correspond to the literature data used in reference17 supplemented by experimental data from.37–39 Insets represents the cell interior observed at different length-scales. In the left inset the exemplary proteins and the fragment of actin filament (7 nm in diameter) are visible. The right inset depicts actin filaments and microtubules (∼24 nm in diameter). (b) Wave-vector-dependent viscosity calculated from formula (11) for friction coefficient presented in panel (a).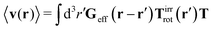 .35 Again, we apply the stick boundary condition, v(
.35 Again, we apply the stick boundary condition, v(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) a) = Ω ×
a) = Ω × ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) a and use the following phenomenological approximation for Tirrrot,
a and use the following phenomenological approximation for Tirrrot,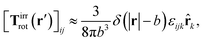
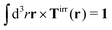 , which corresponds to Newton's third law. These equations lead to the following Stokes' law in complex liquids for rotational motion,
, which corresponds to Newton's third law. These equations lead to the following Stokes' law in complex liquids for rotational motion,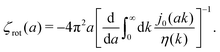
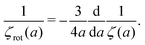

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(Reff(a)/ξsteric/full)αsteric/full], with Reff(a)−2 = Rsteric/full−2 + a−2 to calculate the long-time translational friction ζsteric/full(a)ζ0 ratio for both models; here ζ0 = 6πη0a. The model parameters were equal to ξsteric = 3.6 nm, Rsteric = 17 nm, αsteric = 0.59, ξfull = 0.2 nm, Rfull = 20 nm, αfull = 0.32. Here we use that phenomenological fit in the formula (14) to find ζrot(a)/ζ0,rot ratio with ζ0,rot = 8πη0a3, and compare our prediction with the short-time rotational diffusion data of McGuffee and Elcock.40 Predictions made according to eqn (14) give the long-time rotational friction. Comparison of the data revealed that short-time friction from BD was systematically shifted by a factor of 2/3 with respect to the predicted values of ζrot(a)/ζ0,rot. Data are shown in Fig. 4.
exp[(Reff(a)/ξsteric/full)αsteric/full], with Reff(a)−2 = Rsteric/full−2 + a−2 to calculate the long-time translational friction ζsteric/full(a)ζ0 ratio for both models; here ζ0 = 6πη0a. The model parameters were equal to ξsteric = 3.6 nm, Rsteric = 17 nm, αsteric = 0.59, ξfull = 0.2 nm, Rfull = 20 nm, αfull = 0.32. Here we use that phenomenological fit in the formula (14) to find ζrot(a)/ζ0,rot ratio with ζ0,rot = 8πη0a3, and compare our prediction with the short-time rotational diffusion data of McGuffee and Elcock.40 Predictions made according to eqn (14) give the long-time rotational friction. Comparison of the data revealed that short-time friction from BD was systematically shifted by a factor of 2/3 with respect to the predicted values of ζrot(a)/ζ0,rot. Data are shown in Fig. 4.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[γ(Reff(aaldolase)/ξ(c))αRT]; here Reff−2(aaldolase) = RPEG−2 + aaldolase−2, ξ(c) = Rg(c/c*)−0.75, c* = 3M/(4πRg3NA), M = 24
exp[γ(Reff(aaldolase)/ξ(c))αRT]; here Reff−2(aaldolase) = RPEG−2 + aaldolase−2, ξ(c) = Rg(c/c*)−0.75, c* = 3M/(4πRg3NA), M = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 g mol−1 denotes average molecular weight of the polymer, NA is the Avogadro constant, Rg = 7.6 nm is the gyration radius of polymer, RPEG = 4.6 nm denotes hydrodynamic radius of the polymer, R is the gas constant, T = 298 K is absolute temperature, γ = 3.7 kJ mol−1, aaldolase = 4.5 nm, α equals to 0.78 and
695 g mol−1 denotes average molecular weight of the polymer, NA is the Avogadro constant, Rg = 7.6 nm is the gyration radius of polymer, RPEG = 4.6 nm denotes hydrodynamic radius of the polymer, R is the gas constant, T = 298 K is absolute temperature, γ = 3.7 kJ mol−1, aaldolase = 4.5 nm, α equals to 0.78 and 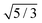 for entangled and non-entangled regime, respectively. The long-time rotational friction is shown as dotted lines. Following the work of Wisniewska et al.41 the crossover between both regimes was assumed at Reff(aaldolase)/ξ(c) = 1.
for entangled and non-entangled regime, respectively. The long-time rotational friction is shown as dotted lines. Following the work of Wisniewska et al.41 the crossover between both regimes was assumed at Reff(aaldolase)/ξ(c) = 1.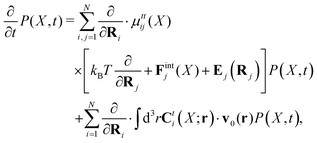
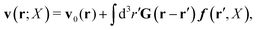
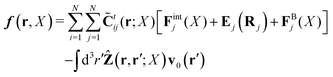
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(X,t).
P(X,t).
![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) tij(r;X), and, Ẑij(r,r′;X), are purely hydrodynamical quantities. They are defined for N beads immersed in an incompressible and Newtonian fluid described by the stationary Stokes equations,50 −∇p(r) + η0Δv(r) = 0, and ∇·v(r) = 0, which determine fluid pressure, p(r), and the fluid velocity field, v(r). The beads are immersed in the fluid with initial velocity field, v0(r). We assume that there is no external torque, but there are external forces acting on the beads, Fhydj. We also assume no-slip boundary conditions on their surfaces. Presence of the beads and the external forces modify the ambient flow, v0(r), and lead to the velocity field, v(r). This velocity field must be found by solving the Stokes equations in the situation described above. It is a difficult task,50 but for our purpose we need to know that the velocity field in the whole space may be represented by the Green function of the Stokes equations as follows,
tij(r;X), and, Ẑij(r,r′;X), are purely hydrodynamical quantities. They are defined for N beads immersed in an incompressible and Newtonian fluid described by the stationary Stokes equations,50 −∇p(r) + η0Δv(r) = 0, and ∇·v(r) = 0, which determine fluid pressure, p(r), and the fluid velocity field, v(r). The beads are immersed in the fluid with initial velocity field, v0(r). We assume that there is no external torque, but there are external forces acting on the beads, Fhydj. We also assume no-slip boundary conditions on their surfaces. Presence of the beads and the external forces modify the ambient flow, v0(r), and lead to the velocity field, v(r). This velocity field must be found by solving the Stokes equations in the situation described above. It is a difficult task,50 but for our purpose we need to know that the velocity field in the whole space may be represented by the Green function of the Stokes equations as follows, 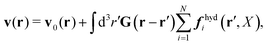 where, fhydi(r,X), is the hydrodynamic force density acting on fluid on the surface of the ith bead.35 The Green function in Fourier space,
where, fhydi(r,X), is the hydrodynamic force density acting on fluid on the surface of the ith bead.35 The Green function in Fourier space, 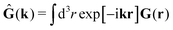 , is given by the Oseen tensor,
, is given by the Oseen tensor,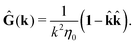
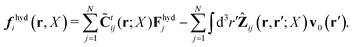
![[C with combining tilde]](https://www.rsc.org/images/entities/b_char_0043_0303.gif) tij(r;X), and the matrix kernel, Ẑij(r,r′;X). The velocities of the particles are also linear in the external forces and the ambient flow,
tij(r;X), and the matrix kernel, Ẑij(r,r′;X). The velocities of the particles are also linear in the external forces and the ambient flow,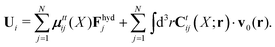
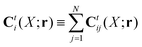 . We closely follow the notation of Szymczak and Cichocki,35 where they describe those quantities in detail.
. We closely follow the notation of Szymczak and Cichocki,35 where they describe those quantities in detail.
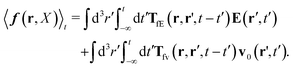
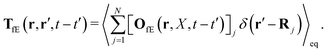
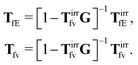
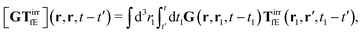
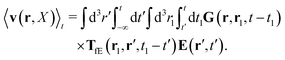
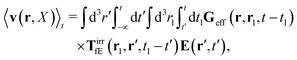
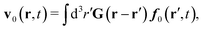
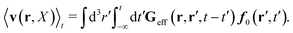
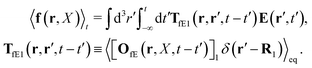
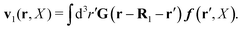
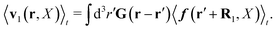
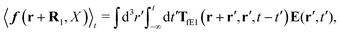
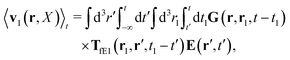
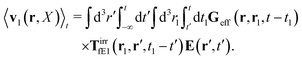
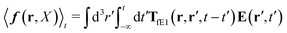 , which acts on the solution—because it is followed by the Oseen tensor which propagates the velocity field in the solution. On the other hand, the interpretation of eqn (37) is that the external force on the probe induces effective force density defined by,
, which acts on the solution—because it is followed by the Oseen tensor which propagates the velocity field in the solution. On the other hand, the interpretation of eqn (37) is that the external force on the probe induces effective force density defined by, 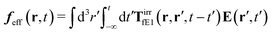 , which acts on the complex liquid—because it is followed by the effective Green function, Geff. It is worth emphasizing the local character of the induced effective force density. Contrary to the kernel TfE1, the irreducible kernel TirrfE1, is a local quantity which means that its integral,
, which acts on the complex liquid—because it is followed by the effective Green function, Geff. It is worth emphasizing the local character of the induced effective force density. Contrary to the kernel TfE1, the irreducible kernel TirrfE1, is a local quantity which means that its integral, 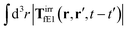 , is finite. The long range character of the kernel TfE1(r,r′,t − t′) produces force densities acting on the solution far from the probe, because it can be shown that,
, is finite. The long range character of the kernel TfE1(r,r′,t − t′) produces force densities acting on the solution far from the probe, because it can be shown that, 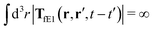 . The effective force density form around the probe a local ‘cloud’, contrary to a much wider ‘cloud’ of the force density.
. The effective force density form around the probe a local ‘cloud’, contrary to a much wider ‘cloud’ of the force density.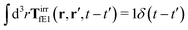
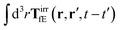 given by formulas (13.11)–(13.23) in the ref. 35.
given by formulas (13.11)–(13.23) in the ref. 35.