DOI:
10.1039/C8SM01851K
(Paper)
Soft Matter, 2019,
15, 22-29
Molecular ejection transition in liquid crystal columns self-assembled from wedge-shaped minidendrons†
Received
10th September 2018
, Accepted 31st October 2018
First published on 2nd November 2018
Abstract
Fan-shaped molecules with aromatic head-groups and two or more flexible pendant chains often self-assemble into columns that form columnar liquid crystals by packing on a 2d lattice. Such dendrons or minidendrons are essential building blocks in a large number of synthetic self-assembled systems and organic device materials. Here we report a new type of phase transition that occurs between two hexagonal columnar phases, Colh1 and Colh2, of Na-salt of 3,4,5-tris-dodecyloxy benzoic acid. Interestingly, the transition does not change the symmetry, which is p6mm in both phases, but on heating it involves a quantised drop in the number of molecules 〈n〉 in the cross-section of a column. The drop is from 4 to 3.5, with a further continuous decrease toward 〈n〉 = 3 as temperature increases further above Tc. The finding is based on evidence from X-ray diffraction. Using a transfer matrix formulation for the interactions within a column, with small additional mean field terms, we describe quantitatively the observed changes in terms of intermolecular forces responsible for the formation of supramolecular columns. The driving force behind temperature-induced molecular ejection from the columns is the increase in conformational disorder and the consequent lateral expansion of the alkyl chains. The asymmetry of the transition is due to the local order between 4-molecule discs giving extra stability to purely 〈n〉 = 4 columns.
Introduction
Taper-shaped molecules such as the tree-like “dendrons” have been shown to exhibit rich phase behavior by self-assembly into supramolecular sheets, columns or spheres. Dendrons displaying such liquid crystal (LC) phases usually comprise an aromatic core with flexible chains at the periphery.1–4 In many fan-shaped molecules the 2d-ordered columnar phase that appears at lower temperatures transforms on heating to one or a series of 3d spherical micellar phases. These have their counterparts in metals and are either cubic such as Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n (A15)5 and body-centered cubic (BCC),6 or tetragonal (α-phase)7 or even quasicrystalline.8,9 Interestingly, all phases observed so far in these series of compounds can be seen in the simplest of them, known as ‘minidendrons’10–12 (see e.g.Fig. 1a). Taper-shaped mesogens, including minidendrons, are some of the most fundamental and widespread building blocks in supramolecular chemistry.13 They have been attached to moieties such as organic semiconductors,14,15 ionic conductors,16–20 crown ether selective chelators,21–23 donor–acceptor complexes and polymers,24,25 peptides,26 nanoparticles,27,28 quantum dots29etc. In this way, “dendronized” functional materials may be created, useful in a variety of applications.30
n (A15)5 and body-centered cubic (BCC),6 or tetragonal (α-phase)7 or even quasicrystalline.8,9 Interestingly, all phases observed so far in these series of compounds can be seen in the simplest of them, known as ‘minidendrons’10–12 (see e.g.Fig. 1a). Taper-shaped mesogens, including minidendrons, are some of the most fundamental and widespread building blocks in supramolecular chemistry.13 They have been attached to moieties such as organic semiconductors,14,15 ionic conductors,16–20 crown ether selective chelators,21–23 donor–acceptor complexes and polymers,24,25 peptides,26 nanoparticles,27,28 quantum dots29etc. In this way, “dendronized” functional materials may be created, useful in a variety of applications.30
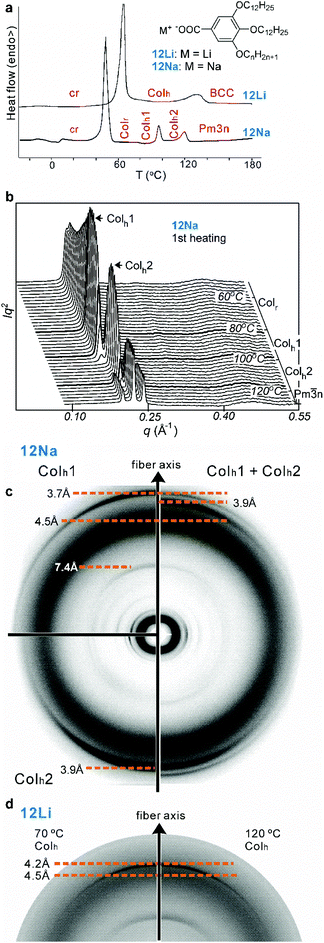 |
| | Fig. 1 (a) The compounds and their first DSC heating scans (5 K min−1). Phase abbreviations: cr = crystal; Colr = rectangular columnar phase (c2mm symmetry); Colh, Colh1, Colh2 = hexagonal columnar phases (p6mm); BCC and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n = body-centered and A15 cubic phases, respectively. (b) Temperature evolution of SAXS curve of 12Na on 1st heating at 5 K min−1. (c) WAXS patterns of an extruded 12Na fiber in the Colh1 phase at 85 °C (top left), Colh2 phase at 105 °C (bottom left) and the mixture of phases (Colh1 + Colh2) at 95 °C (right). (d) Part of WAXS pattern of an extruded fiber of 12Li in the Colh phase at 70 °C (left) and 120 °C (right). n = body-centered and A15 cubic phases, respectively. (b) Temperature evolution of SAXS curve of 12Na on 1st heating at 5 K min−1. (c) WAXS patterns of an extruded 12Na fiber in the Colh1 phase at 85 °C (top left), Colh2 phase at 105 °C (bottom left) and the mixture of phases (Colh1 + Colh2) at 95 °C (right). (d) Part of WAXS pattern of an extruded fiber of 12Li in the Colh phase at 70 °C (left) and 120 °C (right). | |
Besides displaying an impressive array of complex 2d and 3d nanostructures, wedge-shaped and other “unusual” mesogens undergo numerous phase transitions. However, studies giving a theoretical basis of such phenomena are surprisingly rare in such systems.31,32 In more traditional LC's, i.e. nematic and smectic, structures and transitions have been described theoretically in a number of cases by “borrowing” models from other areas of condensed matter and understood in the framework of the same physical principles. Well known examples include the nematic to smectic-A transition,33 the twist-grain-boundary (TGB) smectic phase34 and the hexatic phases,35 the latter being real-life examples of the Kosterlitz–Thouless theory of 2d melting.36 The present work describes an unusual transition, one that happens within the same p6mm hexagonal columnar phase. We show that the ordering of an LC column may be described using the formalism of a magnetic spin chain. Interestingly, an approach linking magnetism and another type of complex soft self-assembly, i.e. multicolour tiling in a honeycomb LC,37,38 is to our knowledge so far the only other example in complex LC's.
In the hexagonal columnar phase (Colh) wedge-shaped molecules assemble to form supramolecular discs which in turn stack to form columns.39 With increasing temperature these columns show typically a continuous lateral shrinkage while maintaining positive bulk expansion.10,11,40 This has been attributed to continuous shedding of dendrons along the supramolecular column. An optimal average number of molecules per disc, 〈n〉, exists at a given temperature such that the overall system free energy is minimized. With increasing temperature, the dendrons expand sideways due to the increased entropy of the terminal chains, resulting in a decreasing optimal 〈n〉, and shedding of surplus dendrons. Similar behavior is observed in the cubic phases where spherical micelles shed their conically shaped dendrons continuously, thus shrinking with increasing temperature,10 in some cases down to half their size at low temperatures.41
All cases so far show continuous thermal shrinkage. Herein we report a special case where the lateral shrinkage of the columns is discontinuous, involving a new type of first-order transition between two columnar LC phases of the same hexagonal symmetry but with a quantised change in the average number of molecules in a supramolecular disc. We present experimental evidence and a quantitative statistical model of this unique LC phenomenon.
Experimental results
X-ray diffraction and calorimetry
The compounds used in this study are Na and Li salts of 3,4,5-tris-dodecyl benzoic acid. They are labeled 12Na and 12Li and are shown in Fig. 1a, together with their calorimetry (DSC) scans. Powder small-angle X-ray scattering (SAXS) curves recorded on heating are shown in Fig. 1b. While 12Li shows only two LC phases, a hexagonal columnar (Colh) and a body-centered cubic (BCC), 12Na displays a sequence of four LC phases. Crystals melt into a centered rectangular columnar phase (Colr), symmetry c2mm, which gradually transforms into Colh, plane group p6mm, around 82 °C (see Fig. 2a). Above 120–125 °C the columnar transforms into the cubic A15 phase, symmetry Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n. At the same time crystalline compound 12Li melts directly into the Colh phase which subsequently transforms into BCC.
n. At the same time crystalline compound 12Li melts directly into the Colh phase which subsequently transforms into BCC.
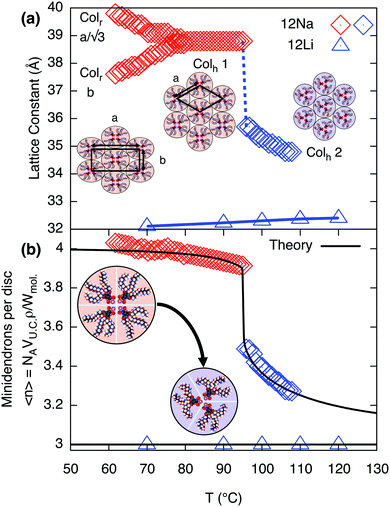 |
| | Fig. 2 (a) Intercolumnar distance in compounds 12Na and 12Li on heating, along with schematic drawings of each structure: Colr, Colh1 and Colh2. (b) Calculated number of minidendrons per supramolecular disc, 〈n〉, for both compounds, along with the best-fit curve from model for 12Na. Fitting parameters are discussed in the subsequent section. | |
Whilst in most other salts the hexagonal lattice parameter, ah, i.e. the distance between column axes, decreases continuously with increasing T,10,11 both 12Li and 12Na are exceptional. In 12Li ah is virtually independent of temperature42 – see Fig. 2. Even more interestingly, in 12Na a clear first order transition is observed between two columnar hexagonal phases, labeled Colh1 and Colh2, as shown in Fig. 1 and 2.
Changes in lattice parameters with temperature for 12Na and 12Li are given in Fig. 2a. The first hexagonal phase of 12Na (Colh1) forms at around 82 °C at the convergence of 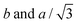 of the Colr phase. In the Colh1 phase the intercolumnar distance ah remains constant at 39 Å, and at about 95 °C it suddenly decreases by approximately 3 Å to 36 Å, signifying the transition to the Colh2 phase. After that in the Colh2 phase ah decreases gradually with increasing temperature. The transition is reversible, albeit with a considerable hysteresis.
of the Colr phase. In the Colh1 phase the intercolumnar distance ah remains constant at 39 Å, and at about 95 °C it suddenly decreases by approximately 3 Å to 36 Å, signifying the transition to the Colh2 phase. After that in the Colh2 phase ah decreases gradually with increasing temperature. The transition is reversible, albeit with a considerable hysteresis.
Determining the number of minidendrons 〈n〉
To determine the average number of molecules 〈n〉 in a supramolecular disc, or stratum of a column we need, besides the cross-section area of the column, also the height of the stratum c and the density ρ. While there is no true 3d long-range order, the wide-angle X-ray scattering (WAXS) pattern of a partially oriented extruded fiber of 12Na shows a relatively sharp meridional arc corresponding to a spacing of 3.7 Å in Colh1 and 3.9 Å in Colh2 phase (Fig. 1c). These correspond to the π−π stacking distance of benzene rings along the column axis and are taken as c values. The density was measured at room temperature10,11 and then corrected, factoring in thermal expansion (see ESI† and Table S3). 〈n〉, thus obtained, is plotted against temperature in Fig. 2b. In the Colh1 phase of 12Na 〈n〉 is nearly constant at 4 molecules per stratum, dropping abruptly to 3.5 at the Colh1–Colh2 transition and further decreasing continuously toward 3 as T is increased further. In 12Li, on the other hand, 〈n〉 is constant at 3 within the T-range of stability of the Colh phase (Fig. 2 and Fig. S1, ESI†).
Theory
Outline
Fig. 3 shows a simplified schematic of the proposed statistical model of a column consisting of interacting supramolecular discs. Each disc may contain either 3 or 4 minidendrons which are held together by an attractive energy Un (n is the number of minidendrons in each disc), assumed to be dominated by Coulomb interactions at the center of the disc. There are also temperature dependent free energy terms of the end chains Fn(T), mainly entropic due to confinement of the molecule in a slice (1/3 or 1/4) of the disc. Interaction energy Jmn between two neighboring discs in a column is also included, and again considered to be dominated by Coulomb interactions. The model Hamiltonian describing a single column, in eqn (1), is constructed in terms of these interaction energies and the projection operators, P(3)i and P(3)i which correspond to an arbitrary disc, i, containing 3 or 4 minidendrons respectively (P(3)i + P(4)i = 1).| | 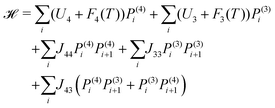 | (1) |
Equilibrium properties of a single column are calculated from eqn (1), assuming that molecules are in a heatbath and a reservoir of free molecules. Weak inter-columnar interactions are included later to take into account long-ranged interactions both along and across columns.
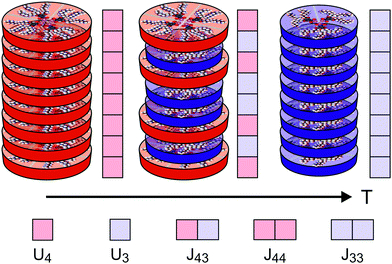 |
| | Fig. 3 Model of interacting supramolecular discs of 3 or 4 minidendrons per disc showing the pure (4), mixed (43) and pure (3) phases with increasing temperature. The intra-disc interactions Un, and inter-disc interactions Jmn are also indicated. | |
Calculating the chain free energy Fn(T)
Calculating the free energy of the three end chains Fn(T) for a single minidendron presents an interesting problem since there are interactions with other molecules both within and between the supramolecular columns. Two important factors govern the shapes adopted by the chains at a given temperature; these are the number of gauche defects ng and the extent of crystallisation with surrounding monomers. To simulate this effect, the minidendrons were confined within a segment with vertex angle θ and thickness d where the chains are restricted to only those conformations which contain discrete trans (t) or gauche (g) bonds, according to the Rotational Isomeric State model43 – see Fig. 4(a). The diamond lattice is therefore chosen as a suitable lattice upon which the end chains may arrange themselves. The [111] direction of the lattice is oriented along the axis of the segment, to ensure a symmetric distribution. The core boundary radius, R, is fixed such that volume is kept constant hence 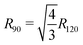 , where R90 = 10 Å. For three free chains of length l in unrestricted space, the number of possible conformations N is described by eqn (2).This is of the order 1017 for l = 12 but for self-avoiding chains in confined space this number falls dramatically, in our case down to 107. The simulations have been run for vertex angles θ = 90° and 120°, to approximate the confinement of 4 or 3 molecules per disc respectively, at a thickness d = 3.6 Å, the closest allowed by the experimental thickness on a diamond lattice. It should be noted that the conformers are self-avoiding such that no two H atoms may come closer than the first nearest neighbor distance. Successive gg' bonds are disallowed in the simulation to avoid H–H conflicts from 5th nearest neighbor monomer units, otherwise known as “pentane interference”. All possible conformations are enumerated and the ensemble is then weighted according to eqn (3).Here η is the energy cost of introducing a gauche defect, ncc is the number of close contacts between first nearest neighboring H atoms and γ represents the energy drop of crystallisation and allows for freezing. In this case, η is taken to be 4141 (J mol−1) with and the expected increase in ng and decrease in ncc with increasing temperature was found for γ = 0.4, see Fig. 4(b). The partition function can then be written as eqn (4) and the free energy Fn(T) calculated.
, where R90 = 10 Å. For three free chains of length l in unrestricted space, the number of possible conformations N is described by eqn (2).This is of the order 1017 for l = 12 but for self-avoiding chains in confined space this number falls dramatically, in our case down to 107. The simulations have been run for vertex angles θ = 90° and 120°, to approximate the confinement of 4 or 3 molecules per disc respectively, at a thickness d = 3.6 Å, the closest allowed by the experimental thickness on a diamond lattice. It should be noted that the conformers are self-avoiding such that no two H atoms may come closer than the first nearest neighbor distance. Successive gg' bonds are disallowed in the simulation to avoid H–H conflicts from 5th nearest neighbor monomer units, otherwise known as “pentane interference”. All possible conformations are enumerated and the ensemble is then weighted according to eqn (3).Here η is the energy cost of introducing a gauche defect, ncc is the number of close contacts between first nearest neighboring H atoms and γ represents the energy drop of crystallisation and allows for freezing. In this case, η is taken to be 4141 (J mol−1) with and the expected increase in ng and decrease in ncc with increasing temperature was found for γ = 0.4, see Fig. 4(b). The partition function can then be written as eqn (4) and the free energy Fn(T) calculated.| | 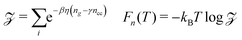 | (4) |
The generated free energy curves are shown in Fig. 4. Both geometries appear identical at low temperature and gradually diverge as temperature is increased. Hence for the chains alone a mixed (43) phase is preferred at low temperature with an increasing preference for (3) at higher temperatures.
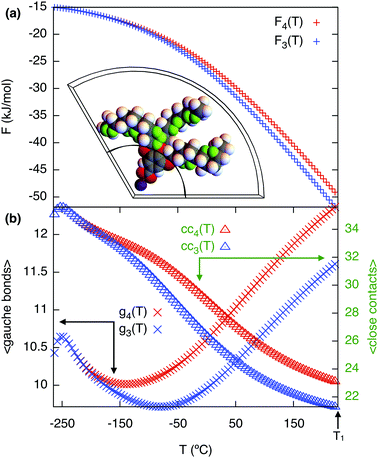 |
| | Fig. 4 (a) Chain free energy curves with a confined minidendron in a 120° segment shown in the inset, close contacts are shown in green. (b) Gauche bonds gn and close contacts ccnvs. temperature in respective geometries. 90° (red) and 120° (blue) from the simulation with η = 4141 (J mol−1), γ = 0.4 as defined in eqn (3). | |
Estimating Coulomb interactions Un and Jmn
Coulomb interactions inside the supramolecular core, namely Un and Jmn, are difficult to calculate since the exact arrangement is unknown. However this can be estimated by considering an idealised symmetric ring of alternating cations and anions, see Fig. 5b and Fig. S2 (ESI†). This serves as an order of magnitude estimate, the intra-disc interactions U4 and U3, were calculated to be −479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 (J mol−1) and −479
289 (J mol−1) and −479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 (J mol−1) respectively. Inter-disc interactions were estimated by rotating these rings in plane around an axis perpendicular to their respective centres at the experimentally-determined inter-disc separation of 3.8 Å. The interaction parameter for like rings Jnn were always found to have an attractive minimum whereas unlike rings Jmn are always repulsive. This can be seen in Fig. 5a, where the minima correspond to J44 = −11241.2 (J mol−1) and J33 = −10090.2 (J mol−1) at 45° or 60° respectively.
198 (J mol−1) respectively. Inter-disc interactions were estimated by rotating these rings in plane around an axis perpendicular to their respective centres at the experimentally-determined inter-disc separation of 3.8 Å. The interaction parameter for like rings Jnn were always found to have an attractive minimum whereas unlike rings Jmn are always repulsive. This can be seen in Fig. 5a, where the minima correspond to J44 = −11241.2 (J mol−1) and J33 = −10090.2 (J mol−1) at 45° or 60° respectively.
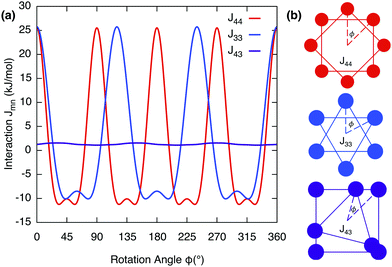 |
| | Fig. 5 (a) Inter-disc Coulomb potentials Jmn as a function of rotation angle ϕ for rings in plane rotated around an axis perpendicular to their respective centres at the experimentally determined inter-disc separation of 3.8 Å. (b) Simplified rings of cations rotating about their respective centres, for the three separate configurations considered. Anions are not shown but included in the calculations, see Fig. S2 (ESI†). | |
Solving the 1D column & introducing a mean field
To solve the model we draw analogy with the spin 1/2 Ising model,44 by writing the projection operator, P(n)i, in terms of σi = ±1.| | 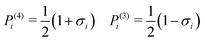 | (5) |
The Hamiltonian takes a convenient form| | 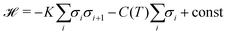 | (6) |
Here| | 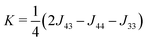 | (7) |
| | 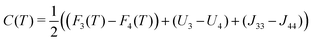 | (8) |
This is then solved via the transfer matrix method.44 The expectation value of 〈σ〉 can be expressed exactly in terms of the parameters K and C(T), where Tc occurs at C(T) = 0.| | 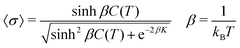 | (9) |
Only nearest neighbor interactions along a single column are considered above, but a mean field interaction, standing for long range (intra- and inter-columnar) interactions, is crucial to achieve long range ordering and a first order transition between phases. Therefore, two additional energy parameters, λ and μ, are introduced; the first disfavours mixing of unlike discs/columns and the second reduces impurities in the region T < Tc. This changes eqn (8)–(10) and this means that the solution must be obtained numerically.| | | C′(T) = C(T) − λ〈σ〉 − μ〈σ〉2 | (10) |
Discussion
The free energy of the chains Fn(T) is evaluated by examining their conformations on a diamond lattice in the confinement of the segment (1/3 or 1/4 of the disc) as described above. The intra-disc Coulomb interactions U3 − U4 were calculated assuming a near circular arrangement of alternating anions/cations in the core of the disc, see Fig. 5 and Fig. S2 (ESI†). The interactions between neighboring cores that were obtained from the fitting, see Table 1, J33 − J44 and K, were smaller than those calculated from the Coulomb interactions between the cores. Several important interactions were not included in the calculation: these include the interactions between the benzene rings and between the chains. The mean field interaction terms, λ = 115 J mol−1 and μ = 190 J mol−1, which are significantly smaller than the nearest neighbor interaction K, are additional fitting parameters. Note that K is equivalent to the χ parameter in the theory of polymer solutions and blends. The reason that such small additional terms are so important here is because even in their absence, there are very long regions of order along the chains because K/kBTc ∼ 1.8 which is greater than unity. Fig. 6 depicts the effect of each of the above described interactions on the shape of the phase transition. Panel (i) shows how a supramolecular column might behave without interaction between its constituent discs: the free energy of the end chains Fn(T) alone would prefer a mixed (43) phase with increasing preference for (3) at higher temperatures; and introducing the intra-disc interactions Un stabilizes the (4) phase at lower temperatures. This clearly shows a competition between the entropy-driven end chains and energy-driven core interactions. Panel (ii) describes the behavior of the column with nearest neighbor interactions Jmn. In this case, an ordered column in the (4) phase is stable over a considerable T-range and may then continuously transform to the (3) phase via the mixed (43) phase. Comparing (i) and (ii), it is clear that core–core interactions are responsible for the stable formation of columns. The effect of long range (intra- and inter-columnar) interactions are shown in (iii) and (iv): λ is responsible for the sharpness of the transition, and μ for the imbalance in tolerance to impurities in (4) and (3) phases. This allows us to produce the characteristic transition shape seen experimentally in Fig. 2b.
Table 1 Calculated vs. fitted parameters for the model fit shown in Fig. 2, all values stated are in J mol−1 unless otherwise indicated and T1 is indicated in Fig. 4 at 227 °C
|
|
U
3
|
U
4
|
J
33
|
J
44
|
J
43
|
U
3 − U4 |
J
33 − J44 |
K
|
F
3(T1) − F4(T1) |
λ
|
μ
|
| Calculated |
−479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
−479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 198 |
−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090 090 |
−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
1096 |
−91 |
−1151 |
5881 |
−2746 |
— |
— |
| Fitted |
−479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
−479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 198 |
−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985 985 |
0 |
−91 |
−1855 |
5529 |
−2746 |
115 |
190 |
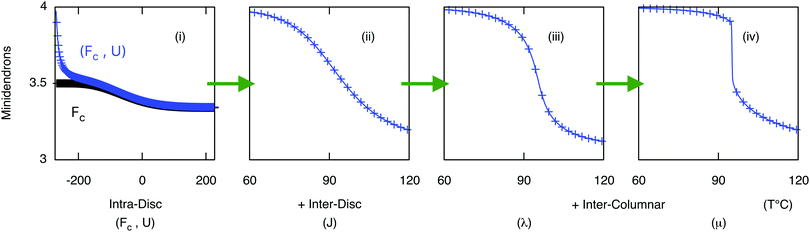 |
| | Fig. 6 Average number of molecules per disc as a function of temperature as different interactions are introduced, parameter values can be found in Table 1. (i) using core free energy Fc and intra-disc interactions Un alone (ii) inter-disc interactions Jmn added, and (iii/iv) long range inter-columnar interaction parameters λ and μ included. Note the temperature range in (i) is significantly larger than (ii), (iii) and (iv). | |
Our results demonstrate that the observed transition is driven predominantly by the entropy of the end chains. In our quantitative fitting, the only explicitly temperature dependent term is the free energy of the chains. With increasing temperature the entropy of the end chains of the minidendrons increases due to the growing number of gauche defects, see Fig. 4. This leads to the expulsion of minidendrons from the disc, which are now able to overcome the attractive energies holding them together.
The size of the inter-disc J33 − J44 in comparison to the intra-disc U3 − U4 would suggest that discs of 4 minidendrons cannot exist without forming a column to stabilise their structure. Once a column is formed the discs are effectively locked into the column by the attraction between their head groups. By increasing temperature, the free energy of the end chains eventually allows for expulsion of a minidendron; when this occurs the entire column is destabilised leading to a sudden runaway expulsion of minidendrons down the column. This is true for an isolated column where K is the only parameter responsible for the continuity/discontinuity of the transition. Further increasing K would lead to a completely symmetric strongly first order transition effectively destroying the characteristic tail seen experimentally. The discontinuity and asymmetry in the transition must result from the attractive energy between the columns themselves. As we approach the critical point from low T, any supramolecular disc which transitions would break the long range order between columns, triggering this energetic transition to occur. The λ and μ terms are then absolutely necessary. Long range interactions are responsible for the discontinuity in the transition, as well as the temperature range over which the (4) phase remains stable.
A clear asymmetry is present in the transition which suggests the supramolecular columns in the (4) phase are able to tolerate the pressure due to the lateral expansion of the end chains with increasing temperature. The characteristic high-temperature tail would suggest that, once shedding has occurred, some (4) discs still exist due to the free space made available by the transition. However, even these remaining discs are then gradually lost at higher temperatures. The resilience of the pure (4)-columns below the transition may be, at least partially, due to additional intra-columnar interactions that develop in (4)-columns, reflected in the appearance of a weak 7.4 Å near-meridional diffraction feature (Fig. 1c). While the main meridional diffraction at 3.7 Å comes from the stacking of individual discs, the weak 7.4 Å arc indicates pairing of adjacent discs. Most likely, the successive discs are rotated in plane by 45°, minimizing repulsion between alkyl chains and making the column a quadruple 81 helix (see Fig. 5 and Coulomb energy calculations in ESI†). It should be noted that neither the 3.7 Å nor the 7.4 Å reflect true long-range order. Upon the Colh1–Colh2 transition the 3.7 Å peak shifts to 3.9 Å indicating some tilting of the benzene rings away from the xy plane. At the same time the 7.4 Å feature disappears, meaning that the extra intra-columnar order is lost in the mixed (43) columns.
In contrast to 12Na, 12Li maintains 3-dendron columns in the entire temperature range of the Colh phase from 70 °C to above 120 °C. The smaller number of dendrons in 12Li discs is attributed to the tight-binding small Li+ ions drawing the dendron cores closer to the column centre thereby effectively increasing the molecular taper compared to that of 12Na. We also note that the fiber pattern of the purely (3)-columns of 12Li (Fig. 1d) again contains a clear 7.4 Å arc, suggesting relatively high intra-columnar order, this time possibly of a triple 61 helical type (60° rotation between successive discs). Shrinkage of the purely (3)-columns of 12Li appears to be completely prevented, at least up to the temperature at which columns turn into spheres that form the cubic phase (Fig. 2).
This strong resistance to shrinkage and the raising of Tc beyond the range of stability of the columnar phase is primarily due to a weaker intra-disc cohesion U2 of the (2)-disc. In addition to the lower Coulomb energy of (2)-discs, the ample volume left empty by the removal of the third molecule and the resulting breaking of van der Waals bonds between alkyl chains must contribute significantly to raising the energy of the (2) phase. The extra conformational entropy achieved by turning 120° segments into 180° is clearly insufficient to offset the energy penalty at these moderate temperatures.
However it has been shown recently that addition of free alkane overcomes this obstacle and allows continuous thermal shrinkage of the (3)-columns in 12Li at moderate temperatures.42 It was established, using labeled alkane and neutron scattering that, following dendron expulsion, the alkane collects preferentially in the resulting (2)-columns replacing the missing dendrons, effectively increasing U2 by re-establishing the missing van der Waals bonds. Furthermore we noted the transition in 12Li starts continuous. Interestingly, the (3)-columns and the (2)-columns were found to occupy defined positions on a 2D superlattice with a three-column hexagonal unit cell. By analogy, it is expected that addition of alkane could turn the shrinkage of (4)-columns in 12Na from discontinuous to continuous.
Experimental methods
The synthesis has been described previously.10,11 Powder SAXS experiments were conducted on beamline I22 of the Diamond synchrotron, and the fiber patterns on a Rigaku rotating anode source with multilayer mirrors and a MAR 345 image-plate detector. DSC was recorded on a Perkin-Elmer Pyris instrument at 5 K min−1. Prior to the experiments the samples were vacuum dried for 24 hours and kept in sealed capillaries during the X-ray experiments.
Conclusions
We have reported the first example of a transition between two columnar phases of the same symmetry. To our knowledge, this is also the first case of a transition based entirely on a change in the number of molecules in a self-assembled aggregate. We have described the transition quantitatively. The model is quasi one-dimensional because the largest interactions are along the columns and only small long range interactions are needed to cause the phase transition. The transition is driven by the end chains of the minidendrons that expand as the temperature is raised. This work is another demonstration of the principle of universality, which explains why similar behavior is seen in disparate physical systems with the same dimensionality and number of degrees of freedom. In the original magnetic system the increase in temperature causes disorder along the spin chain; while in the system that is described here it also changes the sign of the ordering field.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
For help with synchrotron SAXS and fiber WAXS experiments we thank, respectively, Prof. Nick Terrill at I22, Diamond, and Dr Patrick Baker at Sheffield University. Simulations were performed using the Sheffield Advanced Research Computer (ShARC) hosted by the University of Sheffield. Financial support is acknowledged from EPSRC (EP/K034308, EP/P002250), Leverhulme Trust (RPG-2012-804) and NSFC China (21274132).
References
- H. J. Sun, S. Zhang and V. Percec, Chem. Soc. Rev., 2015, 44, 3900–3923 RSC.
- B. Donnio, S. Buathong, I. Bury and D. Guillon, Chem. Soc. Rev., 2007, 36, 1495–1513 RSC.
- C. Tschierske, Angew. Chem., Int. Ed., 2013, 52, 8828–8878 CrossRef CAS PubMed.
- T. Kato, N. Mizoshita and K. Kishimoto, Angew. Chem., Int. Ed., 2006, 45, 38–68 CrossRef CAS PubMed.
- V. Balagurusamy, G. Ungar, V. Percec and G. Johansson, J. Am. Chem. Soc., 1997, 119, 1539–1555 CrossRef CAS.
- D. J. Yeardley, G. Ungar, V. Percec, M. N. Holerca and G. Johansson, J. Am. Chem. Soc., 2000, 122, 1684–1689 CrossRef CAS.
- G. Ungar, Y. Liu, X. Zeng, V. Percec and W.-D. Cho, Science, 2003, 299, 1208–1211 CrossRef CAS PubMed.
- X. Zeng, G. Ungar, Y. Liu, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157 CrossRef CAS.
- R. Zhang, X. Zeng and G. Ungar, J. Phys.: Condens. Matter, 2017, 29, 414001 CrossRef PubMed.
- G. Ungar, V. Percec, M. N. Holerca, G. Johansson and J. A. Heck, Chem. – Eur. J., 2000, 6, 1258–1266 CrossRef CAS.
- V. Percec, M. N. Holerca, S. Uchida, W.-D. Cho, G. Ungar, Y. Lee and D. J. Yeardley, Chem. – Eur. J., 2002, 8, 1106–1117 CrossRef CAS.
- M. A. Shcherbina, A. V. Bakirov, A. N. Yakunin, U. Beginn, L. Yan, M. Möller and S. N. Chvalun, Soft Matter, 2014, 10, 1746–1757 RSC.
- S. Hecht and J. M. Fréchet, Angew. Chem., Int. Ed., 2001, 40, 74–91 CrossRef CAS.
- F. Würthner, C. Thalacker, S. Diele and C. Tschierske, Chem. – Eur. J., 2001, 7, 2245–2253 CrossRef.
- Z. An, J. Yu, B. Domercq, S. C. Jones, S. Barlow, B. Kippelen and S. R. Marder, J. Mater. Chem., 2009, 19, 6688–6698 RSC.
- G. Ungar, S. Batty, V. Percec, J. Heck and G. Johansson, Adv. Funct. Mater., 1994, 4, 303–313 CAS.
- T. Ichikawa, M. Yoshio, A. Hamasaki, T. Mukai, H. Ohno and T. Kato, J. Am. Chem. Soc., 2007, 129, 10662–10663 CrossRef CAS.
- M. Peterca, V. Percec, A. E. Dulcey, S. Nummelin, S. Korey, M. Ilies and P. A. Heiney, J. Am. Chem. Soc., 2006, 128, 6713–6720 CrossRef CAS PubMed.
- C. S. Pecinovsky, E. S. Hatakeyama and D. L. Gin, Adv. Funct. Mater., 2008, 20, 174–178 CrossRef CAS.
- B. Soberats, M. Yoshio, T. Ichikawa, X. Zeng, H. Ohno, G. Ungar and T. Kato, J. Am. Chem. Soc., 2015, 137, 13212–13215 CrossRef CAS.
- G. Johansson, V. Percec, G. Ungar and D. Abramic, J. Chem. Soc., Perkin Trans. 1, 1994, 447–459 RSC.
- A. Schultz, S. Laschat, A. Saipa, F. Gießelmann, M. Nimtz, J. L. Schulte, A. Baro and B. Miehlich, Adv. Funct. Mater., 2004, 14, 163–168 CrossRef CAS.
- Y. Luo, N. Marets and T. Kato, Chem. Sci., 2018, 9, 608–616 RSC.
- V. Percec, M. Glodde, T. Bera, Y. Miura, I. Shiyanovskaya, K. Singer, V. Balagurusamy, P. Heiney, I. Schnell and A. e. a. Rapp, Nature, 2002, 419, 384 CrossRef CAS.
- T. T. Steckler, X. Zhang, J. Hwang, R. Honeyager, S. Ohira, X.-H. Zhang, A. Grant, S. Ellinger, S. A. Odom and D. e. a. Sweat, J. Am. Chem. Soc., 2009, 131, 2824–2826 CrossRef CAS.
- V. Percec, A. E. Dulcey, M. Peterca, P. Adelman, R. Samant, V. S. Balagurusamy and P. A. Heiney, J. Am. Chem. Soc., 2007, 129, 5992–6002 CrossRef CAS PubMed.
- B. Donnio, P. Garca-Vázquez, J.-L. Gallani, D. Guillon and E. Terazzi, Adv. Funct. Mater., 2007, 19, 3534–3539 CrossRef CAS.
- K. Kanie, M. Matsubara, X. Zeng, F. Liu, G. Ungar, H. Nakamura and A. Muramatsu, J. Am. Chem. Soc., 2011, 134, 808–811 CrossRef.
- M. Matsubara, W. Stevenson, J. Yabuki, X. Zeng, H. Dong, K. Kojima, S. F. Chichibu, K. Tamada, A. Muramatsu and G. e. a. Ungar, Chem, 2017, 2, 860–876 CAS.
- X. Feng, M. E. Tousley, M. G. Cowan, B. R. Wiesenauer, S. Nejati, Y. Choo, R. D. Noble, M. Elimelech, D. L. Gin and C. O. Osuji, ACS Nano, 2014, 8, 11977–11986 CrossRef CAS.
- Y. Li, S.-T. Lin and W. A. Goddard, J. Am. Chem. Soc., 2004, 126, 1872–1885 CrossRef CAS.
- P. Ziherl and R. D. Kamien, J. Phys. Chem. B, 2001, 105, 10147–10158 CrossRef CAS.
-
P. G. de Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1995, vol. 83, pp. 507–527 Search PubMed.
- S. John and T. Lubensky, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 4815 CrossRef.
- D. R. Nelson and B. Halperin, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 5312 CrossRef CAS.
- J. Kosterlitz, J. Phys. C: Solid State Phys., 1973, 6, 1181 CrossRef CAS.
- X. Zeng, R. Kieffer, B. Glettner, C. Nürnberger, F. Liu, K. Pelz, M. Prehm, U. Baumeister, H. Hahn and H. Lang,
et al.
, Science, 2011, 331, 1302–1306 CrossRef CAS.
- S. George, C. Bentham, X. Zeng, G. Ungar and G. A. Gehring, Phys. Rev. E, 2017, 95, 062126 CrossRef CAS.
- B. Mu, X. Hao, J. Chen, Q. Li, C. Zhang and D. Chen, Polym. Chem., 2017, 8, 3286–3293 RSC.
- Y. K. Kwon, S. N. Chvalun, J. Blackwell, V. Percec and J. A. Heck, Macromolecules, 1995, 28, 1552–1558 CrossRef CAS.
- X. Yao, L. Cseh, X. Zeng, M. Xue, Y. Liu and G. Ungar, Nanoscale Horiz., 2017, 2, 43–49 RSC.
- M.-H. Yen, J. Chaiprapa, X. Zeng, Y. Liu, L. Cseh, G. H. Mehl and G. Ungar, J. Am. Chem. Soc., 2016, 138, 5757–5760 CrossRef CAS.
-
P. J. Flory and M. Volkenstein, Statistical mechanics of chain molecules, 1969 Search PubMed.
- H. A. Kramers and G. H. Wannier, Phys. Rev., 1941, 60, 252 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. (1) Spacing and average number of molecules per disc n in the Colh phase, (2) details of calculation of Coulomb energies, (3) details of chain free energy simulations, including data file of configurations. See DOI: 10.1039/c8sm01851k |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
Ming-Huei
Yen
c,
Xiangbing
Zeng
ab,
Ming-Huei
Yen
c,
Xiangbing
Zeng
 c,
Liliana
Cseh
c,
Liliana
Cseh
 d,
Yongsong
Liu
a,
Gillian A.
Gehring
d,
Yongsong
Liu
a,
Gillian A.
Gehring
 *b and
Goran
Ungar
*b and
Goran
Ungar
 *ac
*ac
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n (A15)5 and body-centered cubic (BCC),6 or tetragonal (α-phase)7 or even quasicrystalline.8,9 Interestingly, all phases observed so far in these series of compounds can be seen in the simplest of them, known as ‘minidendrons’10–12 (see e.g.Fig. 1a). Taper-shaped mesogens, including minidendrons, are some of the most fundamental and widespread building blocks in supramolecular chemistry.13 They have been attached to moieties such as organic semiconductors,14,15 ionic conductors,16–20 crown ether selective chelators,21–23 donor–acceptor complexes and polymers,24,25 peptides,26 nanoparticles,27,28 quantum dots29etc. In this way, “dendronized” functional materials may be created, useful in a variety of applications.30
n (A15)5 and body-centered cubic (BCC),6 or tetragonal (α-phase)7 or even quasicrystalline.8,9 Interestingly, all phases observed so far in these series of compounds can be seen in the simplest of them, known as ‘minidendrons’10–12 (see e.g.Fig. 1a). Taper-shaped mesogens, including minidendrons, are some of the most fundamental and widespread building blocks in supramolecular chemistry.13 They have been attached to moieties such as organic semiconductors,14,15 ionic conductors,16–20 crown ether selective chelators,21–23 donor–acceptor complexes and polymers,24,25 peptides,26 nanoparticles,27,28 quantum dots29etc. In this way, “dendronized” functional materials may be created, useful in a variety of applications.30
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n. At the same time crystalline compound 12Li melts directly into the Colh phase which subsequently transforms into BCC.
n. At the same time crystalline compound 12Li melts directly into the Colh phase which subsequently transforms into BCC.
 of the Colr phase. In the Colh1 phase the intercolumnar distance ah remains constant at 39 Å, and at about 95 °C it suddenly decreases by approximately 3 Å to 36 Å, signifying the transition to the Colh2 phase. After that in the Colh2 phase ah decreases gradually with increasing temperature. The transition is reversible, albeit with a considerable hysteresis.
of the Colr phase. In the Colh1 phase the intercolumnar distance ah remains constant at 39 Å, and at about 95 °C it suddenly decreases by approximately 3 Å to 36 Å, signifying the transition to the Colh2 phase. After that in the Colh2 phase ah decreases gradually with increasing temperature. The transition is reversible, albeit with a considerable hysteresis.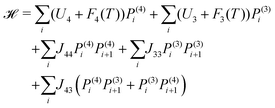
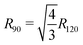 , where R90 = 10 Å. For three free chains of length l in unrestricted space, the number of possible conformations N is described by eqn (2).
, where R90 = 10 Å. For three free chains of length l in unrestricted space, the number of possible conformations N is described by eqn (2).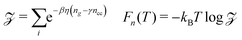

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 (J mol−1) and −479
289 (J mol−1) and −479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 (J mol−1) respectively. Inter-disc interactions were estimated by rotating these rings in plane around an axis perpendicular to their respective centres at the experimentally-determined inter-disc separation of 3.8 Å. The interaction parameter for like rings Jnn were always found to have an attractive minimum whereas unlike rings Jmn are always repulsive. This can be seen in Fig. 5a, where the minima correspond to J44 = −11241.2 (J mol−1) and J33 = −10090.2 (J mol−1) at 45° or 60° respectively.
198 (J mol−1) respectively. Inter-disc interactions were estimated by rotating these rings in plane around an axis perpendicular to their respective centres at the experimentally-determined inter-disc separation of 3.8 Å. The interaction parameter for like rings Jnn were always found to have an attractive minimum whereas unlike rings Jmn are always repulsive. This can be seen in Fig. 5a, where the minima correspond to J44 = −11241.2 (J mol−1) and J33 = −10090.2 (J mol−1) at 45° or 60° respectively.

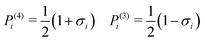
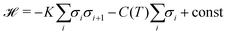
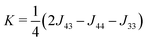
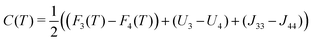
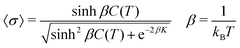
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289
289![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198
198![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090
090![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241
241![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289
289![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198
198![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130
130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985
985



