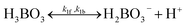Membrane-less photoelectrochemical devices for H2O2 production: efficiency limit and operational constraint
Shu
Hu
 *ab
*ab
aDepartment of Chemical and Environmental Engineering, Yale University, New Haven, Connecticut 06520, USA. E-mail: Shu.Hu@yale.edu; Tel: +1-203-737-6521
bEnergy Sciences Institute, Yale University, 810 West Campus Drive, West Haven, CT 06516, USA
First published on 1st November 2018
Abstract
Three types of membrane-less photoelectrochemical (PEC) devices for solar-driven hydrogen peroxide (H2O2) production have been proposed, including (a) a H2O2 electrolyzer; (b) a photoelectrode-based PEC device; and (c) particulate photocatalysts in a suspension reactor. These devices can produce H2O2 from sunlight, water, and oxygen in air as the only inputs. Their respective efficiency limits were calculated by using the measured performance of H2O2 evolving electrocatalysts and by assuming idealized 100% selectivity for H2O2 accumulation, and by using the energy-conversion performance of light absorbers at their Shockley–Queisser limit. Multi-physics models for the three device configurations were employed for evaluating their electrochemical polarization behaviour as a function of the operating current density and for quantifying the respective contribution from the catalyst overpotential loss, the resistive loss between the cathode and anode, and the Nernstian potential loss due to pH gradients across the electrolyte. For particulate photocatalysts in a suspension, the concept of a non-zero light intensity threshold was for the first time applied to account for net positive H2O2 accumulation, which implies that the most efficient photocatalyst suspension should not fully absorb sunlight. The maximum solar-to-H2O2 conversion efficiency for a photoelectrode-based device was found to be 20.0%, fundamentally limited by the photocurrent density that is matched by dual absorbers in tandem series under 1-sun illumination. The maximum solar-to-H2O2 conversion efficiency for a particulate photocatalyst suspension can achieve 24.5–27.5% with a single-absorber band gap of 1.5–1.7 eV, depending on particle sizes. The modelling outcomes emphasize the importance of water-oxidation selectivity for achieving H2O2 accumulation towards molar concentration levels, and should guide the PEC H2O2 device implementation as the activity and selectivity of H2O2-evolving electro-catalysts continue to improve.
1. Introduction
Photoelectrochemical (PEC) production of hydrogen peroxide (H2O2) is an emerging pathway for converting solar energy to commodity chemicals, which requires only sunlight, oxygen in air, and water as inputs. H2O2 is an environmentally friendly commodity chemical with an estimated global gross production of 3 million metric tons per year.1 It has been widely used in advanced oxidation processes for water and wastewater treatment.2–5a So far, photoelectrode-based PEC devices have only achieved 0.12–0.66% solar-to-H2O2 conversion efficiency, and particulate photocatalysts in a suspension have only achieved 0.15–0.22%.6–10 There remains a big gap in the demonstrated efficiencies for PEC H2O2 production vs. PEC water splitting devices: various models of PEC water splitting devices reported that a solar-to-hydrogen conversion efficiency of 25% is achievable with a tandem light absorber of 1.7/1.1 band gap, coupled with earth-abundant H2 and O2 evolving electro-catalysts;11–13 and to date, the demonstrated solar-to-H2 conversion device has a record efficiency of 16%.14,15 However, an analysis for the efficiency limits of PEC H2O2 devices and their corresponding operational constraints is lacking. Such an analysis should guide the continuing improvement of new materials or components for PEC H2O2 production.This work is focused on modelling the solar-to-H2O2 conversion process in the context of design principles and performance limits under various device configurations. The reported performance of H2O2 electro-catalysts will input to the model. Therefore, before constructing PEC H2O2 prototypes, one can use this model to understand the operational constraints and to implement sound design choices.
H2O2 can be directly produced from H2O and O2 through either of the following two routes:
| Route 1: O2 + 2H2O → 2H2O2Ecell = 1.083 V |
| Cathode: O2 + 2H+ + 2e− → H2O2 0.680 V vs. RHE (I) |
| Anode: 2H2O → H2O2 + 2H+ + 2e− 1.763 V vs. RHE (II) |
| Route 2: O2 + H2O → H2O2 + 1/2O2Ecell = 0.549 V |
| Cathode: O2 + 2H+ + 2e− → H2O2 0.680 V vs. RHE (I)′ |
| Anode: H2O → 1/2O2 + 2H+ + 2e− 1.229 V vs. RHE (II)′ |
For both routes, the cathodic side should perform 2-electron (2-e−) reduction of O2 to H2O2, and should be selective over 4-electron O2 reduction to H2O. Route 1 is a preferred pathway, not only because it produces twice the amount of cell potentials as Route 2 does which means storing twice amount of energy, but also because H2O2 produced by cathodes can become the reactant (reducing reagent) and get consumed in the anodic half-reaction of water oxidation to O2 in Route 2. To achieve H2O2 accumulation to molar quantities in any (photo-)electrochemical pathways, H2O-to-H2O2 oxidative selectivity is crucial and should become a criterion for catalyst benchmarking. But only recently, the literature reported the possibility of selective water oxidation to produce H2O2, thereby promising Route 1.16–18 For the purpose of finding the efficiency limits of PEC H2O2 devices, 100% selectivity for water oxidation to H2O2 is assumed and should be a key performance target for any H2O2-producing (photo)-anodes that are being developed. Facile electro-catalytic kinetics even with a small overpotential has been shown to enable the desired H2O-to-H2O2 selectivity.19,20 In fact, efficient oxygen-evolution catalysts almost always over-oxidize H2O2 into O2. With the thermodynamic energetics considered, efficient water oxidation usually does not favour H2O2 selectivity because the H2O-to-H2O2 pathway in Route 1 exhibits an excess overpotential of 0.534 V (1.763 V vs. RHE to 1.229 V vs. RHE) compared to a non-selective H2O-to-O2 pathway. Nonetheless, there are emerging reports about oxidative H2O2 selectivity and tuning branching ratios of different water oxidation pathways is a viable route: various H2O2 producing (photo-)electrodes, such as g-C3N4 materials/Ni mesh composite photoanodes, have been shown to produce H2O2 oxidatively but have not yet accumulated H2O2 beyond milli-molar concentrations.18
Route 1 synthesis is chosen in this modelling study also because it can simplify device designs. With Route 1 synthesis, a membrane for product separation is no longer necessary because both reductive and oxidative products are the same, H2O2. This membrane-less design is unique to essentially any proposed PEC devices so far because of the disproportionation chemistry of H2O2: unlike H2O2 cells, a water-splitting cell requires separation of H2 and O2 products; and a CO2 reduction cell requires elimination of cross-over of water-soluble products such as oxygenates to anode compartments.21
H2O2 is also considered as an alternative liquid fuel with comparable energy density to compressed H2 gas. Concentrated H2O2 (usually 70% in aqueous solution with a stabilizing reagent) has been used as a liquid fuel for propulsion22 and actuation.23 Its energy density reaches up to 0.75 kW h L−1 which rivals that of compressed H2 gas (350 bar), useful for stationary energy storage. Chemical energy stored in H2O2 can be converted to (i) electricity via a H2O2 fuel cell24–26 or (ii) H2 gas on-demand by applying a small voltage (∼0.6 V). Up to 0.8 V open-circuit voltage has been achieved by H2O2 fuel cells, which rival state-of-the-art H2 fuel cells.25 Notably, H2O2 is one of the very few chemicals that interface applications in both energy and environment with growing interest in both sectors. Such an integration of energy production and water remediation shall be a great example of solar-powered, sustainable, and green chemistry at the nexus of energy and water. Therefore, the PEC H2O2 device offers two advantages over existing solar-fuel technologies: (i) not costing additional energy for product separation, provided H2O2 (aq.) fuels can accumulate to molar concentration; and (ii) not requiring membrane separators, thus reducing system complexity and cost.
2. Types of photoelectrochemical H2O2 devices
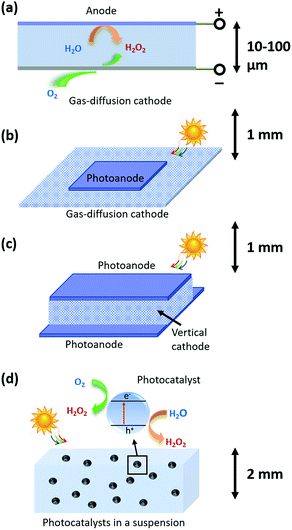
As shown in Fig. 1, three types of devices can be implemented, including (a) a H2O2 electrolyzer; (b) a photoelectrode-based PEC device; and (c) photocatalysts in a particle suspension reactor. The taxonomy of photocatalysts is defined as such: that photocatalysts host co-existing, reductive and oxidative reactions at their electrolyte interfaces.27 The terminology, photocatalysis, in following the convention, refers to light-driven thermodynamically up-hill reactions; although strictly speaking, photocatalysis should only refer to thermodynamically down-hill reactions. PEC, in following the convention, refers to photoelectrode processes exclusively; although by definition, PEC should be inclusive of photocatalyst-based processes. It is noted that under 1-sun solar illumination, the local pH near cathode surfaces becomes basic as protons are consumed during the 2-e− reduction of O2 to make H2O2, and by the same reason the local pH near anodes becomes acidic as protons are liberated via water oxidation to make H2O2. This phenomenon motivates the multi-physics modelling of electrochemical polarization losses.2.1 H2O2 electrolyzers coupled to solar cells
Fig. 1a shows the light-harvesting components, such as a Si photovoltaic module, which provides the electrical energy needed to drive a separately built, H2O2-synthesizing electrolyzer. A simple parallel-plate design can readily achieve H2O2 electrolysis at high throughput: all the pairs of cathodes and anodes in a H2O2 electrolyzer are stacked back-to-back, and a laminar flow plate of μm-length distances is placed in-between the cathodes and anodes. H2O2 is produced from both cathodes and anodes, and then collected by a laminar flow electrolyte that travels inside the flow plate parallel with the electrodes and removes the H2O2 products. The electrolyzer can operate with neutral pH electrolytes and the cathodes and anodes can be as close as manufacturing allows.28,29 The H2O2 products gradually accumulate in the electrolyte, and eventually get separated and concentrated for delivery.Different from water-splitting devices, porous gas diffusion electrodes (GDE) as cathodes may be employed for enhancing O2 transport. Because the O2 reactant for O2-reduction half-reactions has limited solubility in water (2.4 × 10−4 M under standard conditions), the cathodic O2-reduction current is limited to only −2.5 mA cm−2.30 GDEs create a triple phase boundary of air, electrodes, and electrolytes, and the electrolyte/catalyst contact in GDEs ensures sufficient supply of O2 reactants for the cathodic half-reactions. Typically, the photon flux under 1-sun solar illumination produces a current density of 10–20 mA cm−2 per geometric area. Electrolyzers can operate at 100–2000 mA cm−2 current densities. Therefore, both PEC and electrolysis devices require the use of GDEs as cathodes.
2.2 Photoelectrode-based PEC H2O2 devices
This device scheme, as illustrated in Fig. 1b and c, consists of PEC anode and cathode components which couple the processes of light absorption, charge separation, and catalysis in one device. In this case, direct solar-to-H2O2 conversion processes occur at the electrode/electrolyte interface. Fig. 1b schematically illustrates a parallel PEC electrode configuration, which is extended from the electrolyzer's parallel-plate design (Fig. 1a). For example, the upper photoelectrodes facing the sun can be light absorbing photoanodes; and the lower electrodes can be GDE cathodes or photocathodes. A thin electrolyte surrounds the upper photoelectrode and resides above the lower electrode for minimizing solution losses.It is preferred for a design to utilize a maximum of light harvesting area. Because GDE cathodes can operate in the dark, alternatively, vertical O2 reduction GDE cathodes can be arranged perpendicular with the upper and lower photoanodes that face illumination for light harvesting (shown in Fig. 1c). The merit of this vertical design is that these GDEs neither obstruct light absorption nor take up the light harvesting area: most reported selective O2-to-H2O2 electro-catalysts are optically opaque and can be readily applied to such GDE configurations by anchoring onto porous carbon supports.10,31,32
2.3 Particle-based H2O2 photocatalysts
In our model, particulate photocatalysts are treated as mono-disperse spheres that are suspended in pure water, as shown in Fig. 1d. Reactants of O2 will be initially saturated in water, and as the reaction takes place, O2 will be consumed and replenished via passive exchange with air or active bubbling with air. Both reductive and oxidative sites on individual particles produce the same product, H2O2. According to our numerical calculations, O2 transport can match with the rate of O2 reduction per particle; and furthermore, particles do not need a supporting electrolyte for lossless ion transport (see Section 3.6). It is also assumed that the reductive and oxidative sites do not further reduce H2O2 to water, and do not further oxidize H2O2 to O2, respectively, which is consistent with the required selectivity for Route 1 synthesis, i.e. O2 reduction to H2O2 and water oxidation to H2O2. If so, particulate photocatalysts can produce and accumulate, in pure water, a high concentration of H2O2 (aq) solution under solar illumination (UV filtered, >400 nm). Through simple filtration, the photocatalysts are easily separated from the as-produced H2O2 (aq) concentrate.2.4 Strategies for H2O2 accumulation at molar concentrations
Both thermal instability and photo-decomposition of H2O2 are potential concerns for H2O2 accumulation at molar concentrations. H2O2 accumulation is certainly achievable but needs to be managed carefully.17,18 A stability benchmark is decomposition by <0.3% over 1000 hours as set by the US Department of Energy.33 First, H2O2 self-decomposes at elevated temperatures: at 65 °C, its concentration reduces by 0.3% over 1000 hours; whereas at 25 °C, the same concentration reduction takes 3 years.34 Therefore, both type (a) electrolyzer and type (b)–(d) PEC devices are recommended to operate at room temperatures with active cooling, but not at elevated temperatures where commercial electrolyzers typically operate for improved catalytic kinetics. Furthermore, metal impurities are known to catalytically decompose H2O2via an OH˙ radical mediated mechanism. Metal-free components are thus desirable components for constructing H2O2 devices, and OH˙ binding reagents such as Lewis acids25 and sodium stannate34 should help stabilize H2O2 molecules for their accumulation.PEC production and accumulation of H2O2 by type (b)–(d) devices is also possible because H2O2 can remain stable with the UV portion (λ < 420 nm) of solar spectra filtered, thereby preventing photo-decomposition of H2O2.35 Last but not the least, both catalytic and electro-catalytic decomposition of H2O2 at the electrodes should be avoided. A platinum-group catalyst, for example, can catalyse H2O2's disproportion reactions with a first-order rate law with respect to its molar concentration. For electro-catalytic decomposition, a non-unity Faradaic efficiency for either the O2 reduction to H2O2 pathway or the water oxidation to H2O2 pathway implies the formation of H2O by H2O2 reduction or the formation of O2 by H2O2 oxidation, respectively, just by running non-selective catalysts.
3. Modelling methods
3.1 Performance and modelling of H2O2 electrocatalysts
The electro-catalytic behaviour for O2 reduction to H2O2 and H2O oxidation to H2O2 is taken directly from the literature reported, experimentally measured values.17,31 Although selectivity was not available for the J–E performance of each reported catalyst, 100% selectivity is assigned to all catalytic performances used in efficiency calculations. It is very optimistic to assign both reductive and oxidative catalysts to operate at 100% Faradaic efficiency. It remains appropriate for calculating the upper bound of solar-to-H2O2 conversion efficiencies. For cathodic half-reactions, electro-catalysts of nitrogen-doped carbon,31 oxidized carbon,30 platinum or palladium–gold composites,37 and graphitic carbon nitrides8,36 and photo-catalysts of titanium oxides38–40 and carbon nitrides9,10 have been surveyed, and the best performing nitrogen-doped carbon electro-catalysts were chosen as modelling inputs.31 Because oxygen transport usually affects the current density–potential (J–E) behaviour during O2 reduction experiments, we used the kinetic limiting current densities (jkin) extracted from the reported Koutecky–Levich plots. These jkin–E data reasonably describe the behaviour of GDEs when they are loaded with the respective catalysts which can achieve operating current densities of ca. 20 mA cm−2 or even above. For anodic half-reactions, catalysts such as bismuth vanadium oxides, manganese oxides, tungsten oxides, and niobates have been evaluated,5a,17,41–43 and the anodic J–E behaviour of manganese-alloyed titanium oxides was chosen for modelling.5Butler–Volmer kinetics was used to fit the J–E behaviour of chosen catalysts.12,44,45 The fitted kinetic parameters were used to describe the reductive and oxidative kinetics of catalyst-loaded cathodes and anodes, respectively, as listed in Table 1. It is noted that the Faradaic efficiency for O2 reduction to H2O2 is often less than unity and that the selectivity of water oxidation catalysis to H2O2 is much less explored. Further understanding and improvement of H2O2 selectivity should be an area of active investigation.
| Materials | Exchange current density | Transfer coefficient αcathode | Transfer coefficient αanode | Ref. |
|---|---|---|---|---|
| O 2 -reduction-to-H 2 O 2 catalysts | ||||
| Nitrogen-doped carbon | 0.3078 mA cm−2 | 0.3811 | 0.50 | Fellinger31 |
| Oxidized carbon | 0.2497 mA cm−2 | 0.3942 | 0.50 | Lu30 |
| Graphitic carbon nitrides | 0.1953 mA cm−2 | 0.2105 | 0.78 | Kofuji36 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| H 2 O-oxidation-to-H 2 O 2 catalysts | ||||
| (Ti, Mn)Ox | 0.03895 mA cm−2 | 0.50 | 0.35 | Siddiqi5 |
| BiVO4 | 0.00497 mA cm−2 | 0.50 | 0.2235 | Shi17 |
3.2 Optical absorption of light-absorbing photoelectrodes
The photovoltage of light absorbers, or the quasi Fermi level splitting between photo-generated electrons and holes, provides the driving force for solar-to-H2O2 conversion and will be calculated by applying the detailed-balance principle at the Shockley–Queisser limit. The same method had been used elsewhere for estimating efficiency limits of PEC water splitting and CO2 reduction devices.46,47 Detailed balance refers to the net flux of incoming photons through the thin electrolyte layer and photon dissipation due to radiative recombination in the light absorbers. Mathematically, the net carrier flux is calculated from the gain of generating electron–hole pairs by optical absorption, and the loss of charge carriers due to outgoing radiative recombination and black-body thermal emission. Then, the net outgoing flux of electron–hole pairs determines the H2O2 production rates, where the quantum yield of photon-to-charge conversion is assumed to be 100%.For PEC photoelectrode devices, a dual-absorber configuration should achieve a maximum efficiency during solar-to-H2O2 conversion, because (i) dual absorbers provide sufficient up-hill driving force for light-driven H2O2 production; (ii) the matching photocurrent flux of more than two absorbers decreases and reduces H2O2 production rates; and (iii) dual absorbers offer a two-electrode design necessary for PEC H2O2 devices which is not possible with single absorbers. The thickness of electrolytes above the tandem light absorbers was chosen to be 2 mm, which is thick enough to ensure effective ion transport thereby minimizing solution losses (see Fig. 6a), but not too thick to absorb the infrared photons of 1.0–1.3 eV energy thereby limiting the bottom absorber's photocurrent.48
During operation, the respective photocurrent densities, jtop(V1) and jbottom(V2), of the top and bottom absorbers are equal, jph(Vph) = jtop(V1) = jbottom(V2). The tandem absorber photovoltage at jph is Vph = V1 + V2. To make realistic modelling of dual absorbers, an effective series resistance, Rs, was introduced to adjust the jph–Vph behavior comparable to the reported record efficiency solar cells. Typically, calculations at the Shockley–Queisser limit usually give a fill-factor of ca. 0.90, which will be adjusted to 0.85 to match with record efficiency solar cells.49
3.3 Electrolyte modelling
A buffer electrolyte was used for both H2O2 electrolyzers and PEC photoelectrode devices but not for photocatalysts, which are suspended in pure water. The borate buffer was chosen for modelling with their literature parameters listed in Table 2.21,44 Both electrolytes of phosphates (pKa = 7.21) and borates (pKa = 9.23) buffered at near neutral pH were considered and both resulted in similar behaviour of ion transport and pH gradient in solution modelling (see Section 3.4). To illustrate the benefits of the high ionic strength of buffered electrolytes, a weak electrolyte of pH = 2 sulfuric acid was also used for comparison.In a 1-D model for parallel-plate H2O2 electrolyzers, the local current density is identical across the electrode surface because of the translational symmetry. In a 2-D model of PEC devices, the local current densities and the electrolyte potentials vary spatially across the electrode surface. The potential of the electrode is set constant so that the operating voltage of PEC devices is quoted as the anode–cathode potential difference.
3.4 Electrochemical load behaviour at the device level
In the COMSOL Multi-physics model, the boundary conditions were set for identical total currents, I, while sweeping the total current and monitoring the anode–cathode potential difference, V. The total current is equal to the integration of local current densities over the electrode surface. The electrochemical load behaviour is represented by the modelled I–V performance under a specific device configuration, and will be used in conjunction with the light absorber optoelectronic modelling (Section 3.2) to determine the device operation point and solar-to-H2O2 conversion efficiency (see Section 3.5).For both electrolyzers and PEC devices, the potential difference, V, or the operating voltage, consists of the thermodynamic cell potential (E0), kinetic overpotentials for reduction and oxidation half-reactions (ηC and ηA, respectively), ion transport losses in electrolytes (Δϕtransport), and pH gradient losses (ΔϕpH).
| V = E0 + |ηA| + |ηC| + Δϕtransport + ΔϕpH, | (1) |
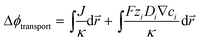 | (2) |
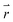 is the position vector of the 2-D and 3-D device models, F is Faraday's constant, Di is the diffusion coefficient for the ith species in the electrolyte, and zi is the charge number and ci is the molar concentration for the ith species (see Table 2 for modelling parameters). The major contribution to the ion transport losses is the ohmic resistance. Electrodialysis loss is negligible for all the membrane-less devices that operate with the current density and geometric parameters investigated herein.
is the position vector of the 2-D and 3-D device models, F is Faraday's constant, Di is the diffusion coefficient for the ith species in the electrolyte, and zi is the charge number and ci is the molar concentration for the ith species (see Table 2 for modelling parameters). The major contribution to the ion transport losses is the ohmic resistance. Electrodialysis loss is negligible for all the membrane-less devices that operate with the current density and geometric parameters investigated herein.
The loss due to pH gradient, ΔϕpH, was obtained by the Nernstian term:
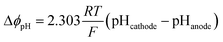 | (3) |
3.5 Efficiency and operation point of PEC devices
The operation point of PEC photoelectrode H2O2 devices determines the device efficiency.46,52 Under steady-state illumination, the device will settle at a single operation point where the dual-absorber photovoltage should match with the operating voltage for electrochemical catalysis under the same operating photocurrent density, i.e. Vph(jop) = V(jop). Generally, one combination of top and bottom absorbers, one set of electrocatalysts, and one device configuration determine one efficiency number. As the absorber performance reaches its Shockley–Queisser limit and as the catalyst selectivity approaches 100%, this calculation represents the upper limit of solar-to-H2O2 conversion efficiencies. The operation point at any time is given by intersecting the electrochemical load curve (I–V behaviour) and the light-absorber drive curve (jph–Vph behaviour) as illustrated in Fig. 2. The solar-to-H2O2 efficiency limit is defined as: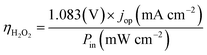 | (4) |
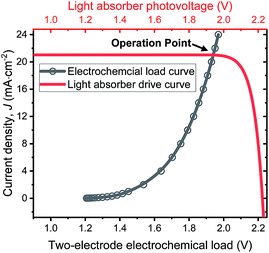 | ||
| Fig. 2 Illustration of operation points for PEC H2O2 devices operating at the optimal efficiency point as shown in Fig. 6d. The specific calculation presented involves the photovoltaic performance of tandem dual absorbers of 1.75 eV/1.15 eV band gaps adjusted to a realistic fill factor of 0.85 (red curve), and electrochemical load (black curve) of the lower photoanode + vertical GDE cathode device configuration. | ||
Photovoltaic-coupled electrolyzers can use the same intersection method to obtain operation points. In this case, the solar-to-H2O2 conversion efficiency is the product of the solar-cell efficiency at the maximum power point, the electrolyzer efficiency determined by the operating currents voltages of the electrolyzer, and power transmission efficiency from the solar cell to the electrolyzer. The areal ratio of PV cells and electrolyzer electrodes strongly affects the operation point: for example, a small area PV cell driving a large surface area electrode will skew the conversion efficiency to a high efficiency number. Practical engineering and economic considerations will settle the combined PV–H2O2 electrolyzer efficiency on a reasonable number, which is not the subject of this study.
3.6 Detailed-balance modelling of particulate absorbers
For particles made of one type of absorber, the detailed balance formalism remains applicable. Individual particles are treated as geometric points despite their realistic shapes are often aggregated spheres. For each particle, the net current flux, Jph, is proportional to the rate of H2O2 production, ṅH2O2:| 2FṅH2O2 = Jph/q = Gy + ṙth − ṙrad(Vph), | (5) |
For simplicity, we use an average volumetric optical generation rate by assigning a particle as a geometric point, the centre point of a particle. This assumption is reasonable for efficiency bound calculations because it captures the physics of position dependent light intensity as a function of the particle-centre depth, y. The volumetric optical generation rate, gy, taking units of # cm−3, is the photons absorbed per unit volume at the depth, y, in units of cm, following the Beer–Lambert Law of light absorption:
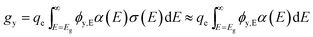 | (6) |
| ϕy,E = ϕAM1.5,ET(y,E)exp[−fparα(E)y] | (7) |
For baseline values of modelling, α(E) is taken as a constant, α, of 5 × 103 cm−1 because typical direct band gap absorbers like GaAs have a value of 104 cm−1 for absorbed photons and typical indirect band gap absorbers like Si have a value of 102–103 cm−1. To simplify the calculation of particle efficiency limits and to account for realistic water absorption, T(y,E) is taken as depth-independent values at y = 2 mm.11 Using Si's materials property, the bulk density of semiconductor particles, ρpar, is 2.3 g cm−3; and the particle concentration, cpar, is 10.5 g L−1, which is a reasonable value for particle loading in a suspension.
The radiative emission rate of ṙrad(Vph) adopts the formalism by Henry54 and its calculation may incorporate the term for the Mie resonance according to the reciprocity of optics.
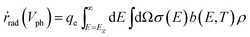 | (8) |
The total optical generation rate of individual particles, Gy, can be approximated by multiplying the particle volume, Vpar, and the position-dependent, average volumetric optical generation rate, i.e. Gy = gyVpar.55 In this study, we do not consider the size-dependent effects of light scattering and Mie resonance at individual particles, i.e. σ(E) ≈ 1. The enhancement due to the Mie resonance is at most 4n2 where n is the refractive index of particle absorbers.53
Notably, the rate of particulate photocatalysis depends on particle sizes, because optical absorption scales with particle volume and radiative emission rate scales with surface area. At each particle, the net outgoing current of electron/hole pairs for photocatalytic H2O2 production is
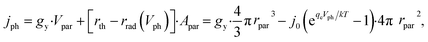 | (9) |
3.7 Efficiency of particulate photocatalyst suspension
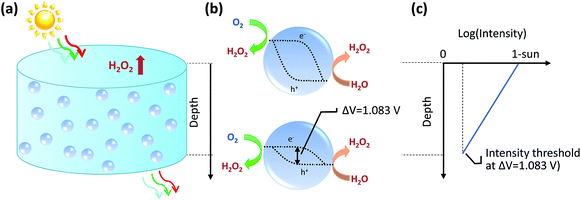
We will first analyse the operation points of individual particles and then sum up H2O2 production rates of all the particles in the reactor. For particulate photocatalysts of <1 μm diameter, the equivalent photocurrent densities at particle surfaces are typically two orders of magnitude smaller than those of planar photoelectrodes. Thus, the total polarization losses including the overpotential losses and solution transport losses (see Section 4.3) at individual particles are negligible under 1-sun illumination.Another distinction with photoelectrodes is that each individual particle is simultaneously in contact with both O2/H2O2 and H2O2/H2O redox levels in the same electrolyte. It requires an additional consideration of a light intensity threshold, at which a minimal photovoltage is required for the net accumulation of H2O2 products in the electrolyte surrounding the particles. According to Shreve and Lewis, a non-zero quasi Fermi-level splitting at photoelectrode/electrolyte interfaces is a necessary condition for net accumulation of chemical products.56 In this case, the threshold photovoltage is the cell potential, i.e. 1.083 V, to achieve the microscopic reversibility of forward H2O2 reactions (photo-electrolysis) and H2O2 recombination back-reactions (fuel–cell reactions). With particles in complete darkness, H2O2 can disproportionate back to oxygen and water via cathodic and anodic backward half-reactions, which is identical to running a H2O2 fuel cell.24–26 The particles recombine their excess electrons and holes to emit light or to generate heat, thereby catalysing H2O2's disproportionation. In this case, one does need to separate solid particles from H2O2 containing water when there is no illumination.
Once the photovoltage threshold is met, the H2O2 production rates by individual particles (typically μm size, under 1-sun illumination) are essentially determined by the outgoing currents, jph because of particles' negligible polarization losses. The operating point of each particle, therefore, is at jph = jph(Vph = 1.083 V).
The bottom of a photocatalytic reactor should not be completely dark: the light intensity at the reactor bottom is just enough to produce 1.083 V. In other words, a well-designed particle reactor should not fully absorb the incident solar illumination, as illustrated in Fig. 3. As the intensity of light impinging onto particles attenuates from top to bottom of the particle reactor, the particle photovoltage, or quasi Fermi level splitting, decreases down to the threshold voltage of 1.083 V.
For individual particles under various illumination intensities, their jph (jph > 0) is taken at Vph = 1.083 V using eqn (9), because the outgoing current flux is equivalent to 10−2 mA or less, which is so small that Vph is poised at ca. 1.083 V. Specifically, particles at the reactor bottom give a net zero H2O2 production rate, mathematically expressed as,
| jph(Vph = 1.083 V) = 0 | (10) |
The minimal intensity at the reactor bottom, gy,min, is obtained by solving the above equation. The depth to achieve the minimal intensity is defined as ymin, which is the maximum height of the reactor. Combining eqn (6) and (7), ymin can be solved. ymin is a function of the critical variables of particle radius rpar, and band gap, Eg, according to eqn (6)–(9).
According to eqn (9), jph varies with the optical generate rate, gy, radiative emission dark currents, j0, and particle sizes, rpar. To calculate the efficiency of a particle suspension, we define a volumetric H2O2 production rate, in units of # cm−3, which is expressed by normalizing with the particle volume because each particle is assigned as a geometric point:
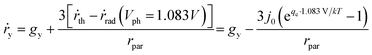 | (11) |
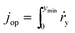 | (12) |
4. Results and discussion
4.1 Parallel-plate H2O2 electrolysis
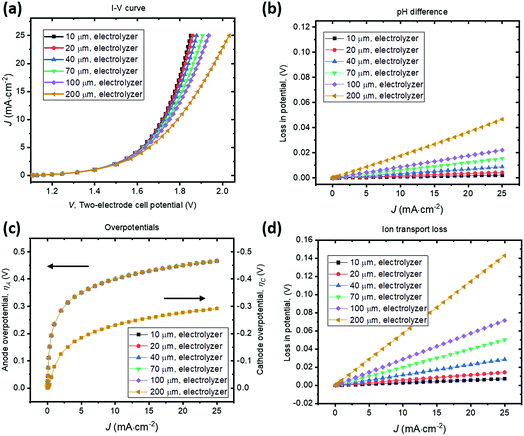
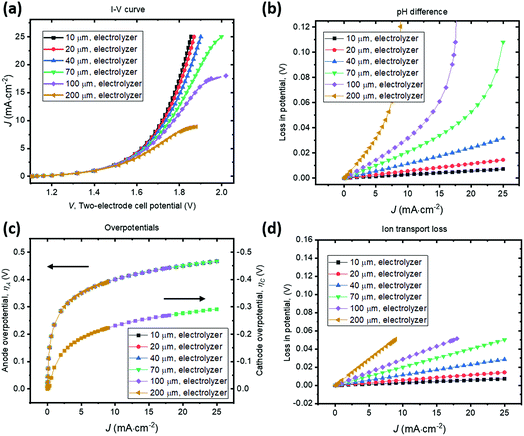
A parallel-plate H2O2 electrolyzer employing the state-of-the-art, reductive and oxidative H2O2 evolving electrocatalysts (their kinetic parameters are listed in Table 1) was modelled in 1-D. The gas-diffusion cathode of nitrogen-doped carbon31 and the water oxidation anodes of manganese-alloyed titanium oxides5a simultaneously produce H2O2 across a thin-layer electrolyte of a thickness of w (μm). The anode is assumed to selectively produce H2O2 from water at 100% Faradaic efficiency.5b We use this simple 1-D model to illustrate the electro-catalytic production of H2O2 in a membrane-less electrolyzer and to quantify the various polarization losses during its operation. Despite a laminar flow of thin electrolytes, they are modelled as stagnant layers because the ion transport across the thin electrolyte should not be affected by the traversing flow field.Fig. 4 shows the current density–voltage (J–V) behaviour and polarization-loss breakdown of parallel-plate H2O2 electrolyzers that operate in a borate buffer with an initial pH = 9.2. A current density of 20 mA cm−2 is obtained at an applied two-electrode potential of 1.85 V for electrode distances of less than 50 μm. With the cathode–anode distance of w < 50 μm, the sum of the ion transport loss (Fig. 4d) and pH gradient loss (Fig. 4b) consist of less than 10% of overall polarization losses. Fig. 4c exhibits the identical current density–overpotential behaviour of anodes and cathodes irrespective of various electrode distances, which validates our 1-D model.
We found that the catalyst overpotentials contribute to the major polarization losses for any reasonable electrode distances of w < 100 μm. The loss of (1.850–1.083) V = 0.767 V at 20 mA cm−2 mostly consists of overpotential losses, i.e. 0.450 V for anodic and 0.277 V for cathodic overpotentials, respectively. At a shorter distance of w < 50 μm, both the ion transport loss and pH gradient become negligible, and appears to be in a linear relationship with the electrolyzer's operating currents. For proper operation of the H2O2 electrolyzer, a cathode–anode distance should be 100 μm or less and this operational constraint is consistent with typical designs of membrane-based water-splitting electrolyzers.29
To illustrate the necessity of buffered electrolytes, we further assessed the polarization losses during the H2O2 electrolysis in a weak acid with a low ionic strength (weak base is known to gradually decompose H2O2 and was not chosen34). Fig. 5 shows the J–V and loss behaviour of the same set of electrolyzer configurations as in Fig. 4, but in a diluted sulfuric acid of pH = 2. As shown in Fig. 5b, the loss due to pH gradient becomes significant at a jop of above 20 A cm−2 for intermediate electrode distances of w > 70 μm. Without buffer, the concentration polarization of local H+ or OH− ions at high current densities can dominate over the overpotential losses and become the major contributor to the overall polarization losses. Beyond this point, the loss due to pH gradient could increase so dramatically that no further increments in electrolysis currents can be made even with operating voltages, V, continuously increased. Fig. 5c shows that the catalyst overpotential losses at various operating current densities are identical with the case of buffered electrolytes (Fig. 4c) which further validated our model. The ion transport losses in a weak acid (Fig. 5d) are comparable with those calculated for a buffered electrolyte (Fig. 4d).
With no buffer or with weak ionic strength, losses due to pH gradient can become significant at high current densities (>20 mA cm−2). This phenomenon of concentration polarization is very sensitive to the electrode distance. With weak electrolytes, the cathode–anode distance becomes a major operational constraint for membrane-less electrolysis. This is because H+ and OH− ion mobility is finite and they do not effectively transport across the thin-layer electrolyte by drift under a small electrical field and/or across a large distance. When jop increases to the magnitude of 1 A cm−2, which is the typical operating current density of a commercial water electrolysis unit, both losses of ion transport resistance and pH difference can become significant. With weak electrolytes, the cathode–anode distance needs to be small. In a pH = 2 acid, it is still possible to operate efficiently, but the electrode distance needs to be <50 μm for a jop of ca. 20 mA cm−2. For a jop of 1 A cm−2, the electrode distance needs to be <2 μm.
4.2 Photoelectrode-based H2O2 devices under illumination
The design principles and operational constraints that have been studied for H2O2 electrolysis are expandable to PEC H2O2 production with the photoelectrode-based devices and photocatalyst-based suspension. For photoelectrodes, we will apply the same Butler–Volmer kinetics for the cathodic and anodic catalysis using a 2-D device model, and additionally couple the light-driven electro-catalysis with light absorption and charge separation using the operation point analysis outlined in Section 3.5.While the 1-D electrolyzer model shows identical current densities across the electrode surface due to a translational symmetry, the 2-D PEC device model only exhibits a mirror symmetry.
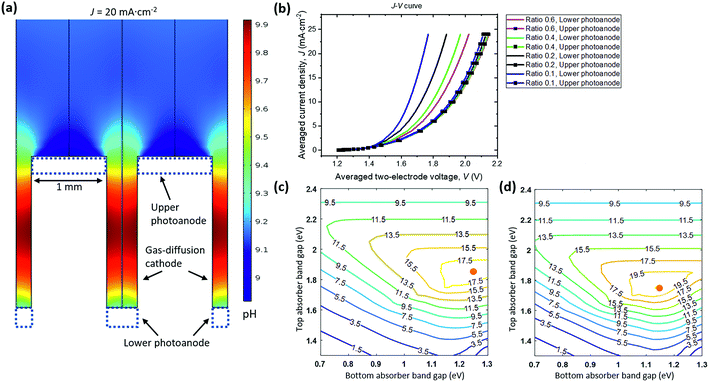
Fig. 6a shows the pH distribution under a steady-state, average operating current density of 20 mA cm−2, which is consistent with the expected mirror symmetric distribution of local current densities and electrolyte potentials. The widths of top and bottom photoanodes are 1 mm and 0.4 mm, respectively. The dual absorber tandem by adjusting their band gaps can provide an upper limit of matching photocurrent densities at ca. 20 mA cm−2 under 1-sun illumination. The pH gradient between photoanodes and vertical GDE cathodes under this limiting photocurrent density is less than 1 pH unit with buffered electrolytes.
To survey the design space, two geometric parameters including the upper anode width and the width ratios of lower/upper anodes were varied in the 2-D PEC model. Their effects on the light-driven electrolysis performance and associated solution losses were evaluated. The I–V behaviour of upper photoanode/vertical cathode and lower photoanode/vertical cathode pairs is plotted in Fig. 6b as a function of average operating current densities. The solar-to-H2O2 conversion efficiency can be improved with less polarization losses, because the electro-catalytic component of the photoelectrodes is coupled to the dual absorber tandem (see Section 3.5). An upper anode width of 1 mm and a width ratio of 0.4 were chosen as the optimized configuration, because the calculated total polarization losses in this case had already matched with the Shockley–Queisser limit of tandem absorbers, i.e. a photovoltage of 1.8 V at a photocurrent density of 20 mA cm−2. Further reducing width ratios to less than 0.2 only marginally improves the cell J–V performance but with increased manufacturing complexity. In principle, the upper anode width and lower anode width can be 10s of μm as long as manufacturing allows57 but its complexity and cost render this geometry impractical.
There will be an optimal combination of band gaps for each parameter set of catalyst performance and device geometry. Fig. 6c and d show solar-to-H2O2 iso-efficiency contour plots for the upper photoanode + vertical GDE cathode and for the lower photoanode + vertical GDE cathode configurations, respectively. The two-electrode I–V curves at a width ratio of 0.4 were quoted from Fig. 6b and used for generating both iso-efficiency plots. The upper photoanode component can achieve an optimal solar-to-H2O2 efficiency of 19.3% at a band gap combination of 1.85 eV/1.25 eV for the upper photoanode tandem absorber. The lower photoanode can achieve an optimal solar-to-H2O2 efficiency of 21.7% at a band gap combination of 1.75 eV/1.15 eV for the lower photoanode tandem absorber. Photoelectrode-based PEC H2O2 devices can reach an overall solar-to-H2O2 efficiency of 20.0%.† Because the maximum photocurrent density at the Shockley–Queisser limit is ca. 20 mA cm−2 at 1-sun, 20.0% is near the solar-to-H2O2 efficiency upper limit.
The iso-efficiency plots exhibit three characteristic regions of efficiency contour lines: (i) the upper region: top-absorber band gaps are too large to limit photocurrents in series; (ii) the lower left region: band gaps of both top and bottom absorbers are so small that the total output photovoltage is not sufficient to drive H2O2 electrolysis; and (iii) the central high-efficiency plateau: the device at the given parameter set achieves optimal conversion efficiencies at an operating point of sufficient photovoltage matching with the modelled electrochemical polarization behaviour.
The geometric parameter space can be further explored under the trade-off between the catalyst overpotential losses and the solution transport losses. Improving the catalyst performance will relax many operational constraints such as the PEC electrode width (wider than 1 mm), GDE cathode height (lower anode/cathode aspect-ratio), and optical concentration (brighter than 1-sun). Mild optical concentration (10×) can effectively utilize the real-estates of electrode area without complex optics. We had fixed the height of the vertical GDE cathode to be 4 times the width of top photoanodes: in principle, an increase in the height length of GDE cathodes can further relieve the turn-over-frequency limitation of current O2-reduction electro-catalysts; however too tall of vertical cathodes may easily shadow the bottom photoelectrode making manufacturing impractical. Other configurations may help reduce solution losses, such as an angled arrangement of photoanodes and GDE cathodes but at a cost of increased light absorber area.
4.3 Efficiency limits of photocatalytic H2O2 production
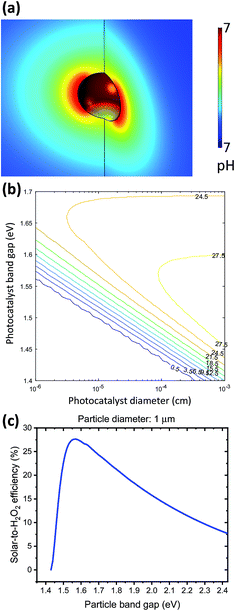
A particle at mesoscopic sizes (<10 μm diameter) effectively reduces both catalyst overpotential and solution transport losses by shortening distances between cathodic and anodic catalytic sites. First, a 3-D multi-physics model was employed to verify the nuance variation in the pH gradient of electrolytes surrounding a 1 μm diameter, strongly absorbing particle (e.g. GaAs) under 1-sun illumination. As shown in Fig. 7a, the local pH difference between any cathodic and anodic sites is less than 10−3 pH units, negligible as compared to the electrolysis and photoelectrode devices (see Sections 4.1 and 4.2). Similar analysis has been applied to O2 transport, indicating that the solubility of O2 (2.4 × 10−4 M, aerated with 1 atm and 25 °C air under standard conditions) does not limit the photocatalytic rates either.Fig. 7a shows the upper bound of pH difference, at the maximum optical generation rate of particles by using the most absorbing materials and most efficient band gaps: optical absorption coefficient is taken as 105 cm−1, which is GaAs's absorption coefficient at 600 nm (much greater than α = 5 × 103 cm−1 used for particle efficiency calculations); particles are assumed to be perfect spheres of 1 μm diameter; and the band gap of particles is taken as 1.55 eV, which will be presented below as the optimal band gap for solar-to-H2O2 conversion. The estimated upper bound of optical generation rates for individual particles has an upper bound of 1.69 × 1022 cm−3 s−1, because as light penetrates deeper through the particle suspension in the reactor, the light intensity is effectively decreased, and so are optical generation rates. Even when the generation rate increases by two orders of magnitude, e.g. by considering light trapping under Mie resonance and under 10× mild concentration, the local polarization losses at individual particles are still negligible. As particle diameters become comparable with the wavelength of incident visible light, the size-dependent Mie resonance can enhance both optical absorption and photon emission. This effect will be subject to future analysis and modelling.
Because both the overpotential losses and solution transport losses are negligible for particles, the detailed-balance principle is sufficient for modelling the efficiency limits of photocatalytic H2O2 production. During particle operation, the splitting between electron and hole quasi-Fermi levels at individual particles is very close to the thermodynamic cell potential. Under the principle of detailed balance, the operation points of individual particles are taken as jph at which Vph = 1.083 V (see Sections 3.6 and 3.7). According to eqn (9) and (10), the particle size and the particle band gap determine the minimal light intensity at the reactor bottom, for the particles at which the detailed balance of light absorption and emission gives a net zero photocatalytic rate. We note that for realistic photocatalysts, the Shockley-Read-Hall surface recombination is usually dominant due to the slow catalytic kinetics, but it is not considered here for estimating the efficiency limits of particle-based solar-to-H2O2 conversion.
Fig. 7b shows the limiting particle efficiency as a function of band gaps and particle diameter, which is expected from the mathematics. With the same band gap, as particles become smaller, the efficiency limit reduces monotonically. Fig. 7c presents a trade-off between the efficiency and band gaps when the particle diameter is fixed to 1 μm. A maximum efficiency of 27.5% is achievable at a band gap of 1.55 eV, above which the reduced photon absorption limits the efficiency and below which the reduced photovoltage results in insufficient driving force for H2O2 photocatalysis. As expected, the iso-efficiency contour plots exhibit a “nose” shape: with particle diameters >100 nm, it's possible to achieve >25% solar-to-H2O2 efficiency. When particle diameters are reduced to 50 nm, the maximum efficiency reduces to 24.5% at a different band gap of 1.65 eV.
4.4 Device applications at the energy–water nexus
H2O2 produced from renewable energy sources, e.g. solar, wind, and nuclear, can have an immediate impact on energy and environment at once: H2O2 can be converted to electricity in a fuel cell, and can be used for water treatment at the same location. PEC and photocatalytic devices enable a distributed approach for chemical and energy production, irrespective of the local infrastructure. If H2O2 can be accumulated to molar concentration levels, it can be considered as an energy-storage medium in a flow battery: electrolysis stores electrical energy in the chemical energy of H2O2, and a separate fuel cell will convert the stored chemical energy back to electricity. Under an idealized condition of 100% selectivity, one would not need to run a flow system to constantly remove H2O2 products but rather let H2O2 molecules accumulate.In the long term, photocatalysts offer the biggest potential for cost effective solar-to-H2O2 conversion. A simple filtration can separate photocatalysts from H2O2-containing water. At the Shockley–Queisser limit where radiative recombination is the only loss mechanism, model spherical particles of 50 nm to 1 μm diameter can achieve a maximum conversion efficiency of 24.5–27.5% with a single band gap ranging from 1.5 to 1.7 eV. Numerous efficient semiconductor absorbers of this band gap range are readily available. However, challenges of poor charge separation, rapid surface recombination, and instability against photo-corrosion remain to be addressed. These aspects of challenges are common not just for H2O2 photocatalysis but also for particle-based water splitting.58–60
Integrated, photoelectrode-based PEC devices can find their niche applications in portable H2O2 production and water treatment, by flowing water across the active surfaces of these flat-panel devices under sunlight. So far these PEC devices hold the record efficiency because photoelectrodes employ semiconductor/liquid junctions or heterojunction interfaces to separate and collect light-excited charge effectively.7 Surface coatings over photoelectrodes have shown multi-functionalities of protecting light absorbers against photo-corrosion and facilitating effective charge separation.5a,61,62 Hybrids of photovoltaics or photoelectrodes in conjunction with parallel-plate electrolyzers can also have immediate impacts: one can directly stack a photovoltaic cell or a photoanode over a thin electrolyte channel with a parallel counter electrode just like the H2O2 electrolyzer (see Fig. 1a). Our break-down analysis of electrolysis polarization losses is equally applicable to such hybrid devices.
5. Conclusions
A modelling approach was primarily used to evaluate the efficiency limits and operational constraints of three types of H2O2-evolving photoelectrochemical (PEC) devices using the measured and reported performance of H2O2-evolving catalyst materials. Both cathodic O2 reduction and anodic water oxidation should be close-to-100% selective towards H2O2 production for H2O2 accumulation at molar concentrations, and if so, efficient solar-to-H2O2 conversion can be realized taking advantage of membrane-less configurations. The membrane-free design can afford operational conditions where catalyst overpotentials are the major loss for H2O2 electrolysis, and where total polarization losses in photoelectrode PEC devices should not limit the maximum photocurrent density of ca. 20 mA cm−2 that is offered by a current-matching, tandem light absorber under 1-sun illumination. Manageable solution losses (<100 mV at 20 mA cm−2) can be achieved both in strong borate buffer (1 M, pH = 9.2) and in a diluted acid (pH = 2) but with thin-layer electrolytes across the cathode and anode (distance <50 μm). For particulate H2O2 photocatalysts, both the overpotential losses and solution transport losses are negligible. Therefore, the detailed-balance principle is sufficient for modelling their solar-to-H2O2 conversion efficiency as a function of absorber band gaps and particle sizes. A non-zero light intensity threshold was for the first time applied to account for the net accumulation of cathodic and anodic co-evolved H2O2, which means that the most efficient particle suspension should not be fully opaque.The efficiency limits of photoelectrode PEC devices are found to be ca. 20.0% with an upper anode width of 1 mm, a lower anode width of 0.4 mm, and the upper and lower absorber band gap pairs of 1.85 eV/1.25 eV and 1.75 eV/1.15 eV, respectively. A single band gap for model spherical absorbers can achieve a solar-to-H2O2 conversion efficiency of 27.5% in their suspension, and particle sizes of 50 nm–1 μm diameter can achieve a maximum conversion efficiency of 24.5–27.6% with a band gap of 1.5–1.7 eV. It is concluded that within the boundary of reported, realistic parameters of light absorbers, electro-catalysts, and electrolyte properties, H2O2 (aq.) can be considered as a promising energy carrier for long-term storage of renewable energy and for water remediation. The model will be useful for guiding the development of sunlight-driven H2O2-production devices, and for improving and benchmarking the materials and components for efficient H2O2 conversion.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author thanks William Rosenbluth and Brenna Hodges for participating in 1-D model validation, and would like to acknowledge Prof. Jaehong Kim, Prof. Owen Miller, Xi Chen, Jiahui Li, and Qianhong Zhu for very helpful discussions. The author also thanks the start-up support from Yale Energy Sciences Institute.Notes and references
- J. M. Campos-Martin, G. Blanco-Brieva and J. L. G. Fierro, Angew. Chem., Int. Ed., 2006, 45, 6962–6984 CrossRef CAS PubMed.
- C. B. C. Raj and H. L. Quen, Chem. Eng. Sci., 2005, 60, 5305–5311 CrossRef CAS.
- T. T. M. Nguyen, H. J. Park, J. Y. Kim, H. E. Kim, H. Lee, J. Yoon and C. Lee, Environ. Sci. Technol., 2013, 47, 13661–13667 CrossRef CAS PubMed.
- G. Ruppert and R. Bauer, Chemosphere, 1994, 28, 1447–1454 CrossRef CAS.
- (a) G. Siddiqi, Z. Luo, Y. Xie, Z. Pan, Q. Zhu, J. A. Röhr, J. J. Cha and S. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 18805–18815 CrossRef CAS PubMed; (b) Private communication with Jiahui Li regarding Mn-alloyed TiO2's electro-catalytic selectivity. In this modelling study, the selectivity of water oxidation to H2O2 is assumed to be 100%.
- K. Mase, M. Yoneda, Y. Yamada and S. Fukuzumi, ACS Energy Lett., 2016, 1, 913–919 CrossRef CAS.
- K. Mase, M. Yoneda, Y. Yamada and S. Fukuzumi, Nat. Commun., 2016, 7, 11470 CrossRef CAS PubMed.
- Y. Kofuji, S. Ohkita, Y. Shiraishi, H. Sakamoto, S. Ichikawa, S. Tanaka and T. Hirai, ACS Sustainable Chem. Eng., 2017, 5, 6478–6485 CrossRef CAS.
- G.-h. Moon, M. Fujitsuka, S. Kim, T. Majima, X. Wang and W. Choi, ACS Catal., 2017, 7, 2886–2895 CrossRef CAS.
- H.-i. Kim, Y. Choi, S. Hu, W. Choi and J.-H. Kim, Appl. Catal., B, 2018, 229, 121–129 CrossRef CAS.
- H. Doscher, J. F. Geisz, T. G. Deutsch and J. A. Turner, Energy Environ. Sci., 2014, 7, 2951–2956 RSC.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 RSC.
- L. C. Seitz, Z. Chen, A. J. Forman, B. A. Pinaud, J. D. Benck and T. F. Jaramillo, Chemsuschem, 2014, 7, 1372–1385 CrossRef CAS PubMed.
- J. L. Young, M. A. Steiner, H. Döscher, R. M. France, J. A. Turner and T. G. Deutsch, Nat. Energy, 2017, 2, 17028 CrossRef CAS.
- W.-H. Cheng, M. H. Richter, M. M. May, J. Ohlmann, D. Lackner, F. Dimroth, T. Hannappel, H. A. Atwater and H.-J. Lewerenz, ACS Energy Lett., 2018, 3, 1795–1800 CrossRef CAS.
- C. McDonnell-Worth and D. R. MacFarlane, RSC Adv., 2014, 4, 30551–30557 RSC.
- X. Shi, S. Siahrostami, G.-L. Li, Y. Zhang, P. Chakthranont, F. Studt, T. F. Jaramillo, X. Zheng and J. K. Nørskov, Nat. Commun., 2017, 8, 701 CrossRef PubMed.
- N. Liu, M. Han, Y. Sun, C. Zhu, Y. Zhou, Y. Zhang, H. Huang, V. Kremnican, Y. Liu, Y. Lifshitz and Z. Kang, Energy Environ. Sci., 2018, 11, 1841–1847 RSC.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Norskov, J. Phys. Chem. Lett., 2012, 3, 2948–2951 CrossRef CAS PubMed.
- S. Siahrostami, G.-L. Li, V. Viswanathan and J. K. Nørskov, J. Phys. Chem. Lett., 2017, 8, 1157–1160 CrossRef CAS PubMed.
- X. Zhou, R. Liu, K. Sun, Y. Chen, E. Verlage, S. A. Francis, N. S. Lewis and C. Xiang, ACS Energy Lett., 2016, 1, 764–770 CrossRef CAS.
- K. K. Kuo and M. J. Chiaverini, Fundamentals of Hybrid Rocket Combustion and Propulsion, American Institute of Aeronautics and Astronautics, 2007 Search PubMed.
- B. Mazzolai and V. Mattoli, Nature, 2016, 536, 400–401 CrossRef CAS PubMed.
- A. E. Sanli and A. Aytaç, Int. J. Hydrogen Energy, 2011, 36, 869–875 CrossRef CAS.
- Y. Yamada, M. Yoneda and S. Fukuzumi, Energy Environ. Sci., 2015, 8, 1698–1701 RSC.
- S.-i. Yamazaki, Z. Siroma, H. Senoh, T. Ioroi, N. Fujiwara and K. Yasuda, J. Power Sources, 2008, 178, 20–25 CrossRef CAS.
- A. C. Nielander, M. R. Shaner, K. M. Papadantonakis, S. A. Francis and N. S. Lewis, Energy Environ. Sci., 2015, 8, 16–25 RSC.
- M. R. Singh, K. Papadantonakis, C. Xiang and N. S. Lewis, Energy Environ. Sci., 2015, 8, 2760–2767 RSC.
- E. J. Park, C. B. Capuano, K. E. Ayers and C. Bae, J. Power Sources, 2018, 375, 367–372 CrossRef CAS.
- Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Nørskov and Y. Cui, Nat. Catal., 2018, 1, 156–162 CrossRef.
- T.-P. Fellinger, F. Hasché, P. Strasser and M. Antonietti, J. Am. Chem. Soc., 2012, 134, 4072–4075 CrossRef CAS PubMed.
- J. Park, Y. Nabae, T. Hayakawa and M.-a. Kakimoto, ACS Catal., 2014, 4, 3749–3754 CrossRef CAS.
- ARPA-E, Renewable Energy to Fuels Through Utilization of Energy Dense Liquids (REFUEL) Program Overview, 2017 Search PubMed.
- W. C. Schumb, Ind. Eng. Chem., 1949, 41, 992–1003 CrossRef CAS.
- J. P. Hunt and H. Taube, J. Am. Chem. Soc., 1952, 74, 5999–6002 CrossRef CAS.
- Y. Kofuji, Y. Isobe, Y. Shiraishi, H. Sakamoto, S. Tanaka, S. Ichikawa and T. Hirai, J. Am. Chem. Soc., 2016, 138, 10019–10025 CrossRef CAS PubMed.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- V. Diesen and M. Jonsson, J. Phys. Chem. C, 2014, 118, 10083–10087 CrossRef CAS.
- D. Tafalla and P. Salvador, J. Electroanal. Chem. Interfacial Electrochem., 1987, 237, 225–236 CrossRef CAS.
- D. Tsukamoto, A. Shiro, Y. Shiraishi, Y. Sugano, S. Ichikawa, S. Tanaka and T. Hirai, ACS Catal., 2012, 2, 599–603 CrossRef CAS.
- A. Izgorodin, E. Izgorodina and D. R. MacFarlane, Energy Environ. Sci., 2012, 5, 9496 RSC.
- O. C. Compton and F. E. Osterloh, J. Phys. Chem. C, 2009, 113, 479–485 CrossRef CAS.
- J. C. Hill and K.-S. Choi, J. Phys. Chem. C, 2012, 116, 7612–7620 CrossRef CAS.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 RSC.
- M. A. Modestino, S. M. H. Hashemi and S. Haussener, Energy Environ. Sci., 2016, 9, 1533–1551 RSC.
- M. R. Singh, E. L. Clark and A. T. Bell, Proc. Natl. Acad. Sci., 2015, 112, E6111–E6118 CrossRef CAS PubMed.
- S. Haussener, S. Hu, C. Xiang, A. Z. Weber and N. S. Lewis, Energy Environ. Sci., 2013, 6, 3605–3618 RSC.
- H. Döscher, J. F. Geisz, T. G. Deutsch and J. A. Turner, Energy Environ. Sci., 2014, 7, 2951–2956 RSC.
- M. A. Green, Y. Hishikawa, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger and A. W. Y. Ho-Baillie, Prog. Photovoltaics, 2018, 26, 3–12 Search PubMed.
- M. R. Singh, J. D. Goodpaster, A. Z. Weber, M. Head-Gordon and A. T. Bell, Proc. Natl. Acad. Sci., 2017, 114, E8812–E8821 CrossRef CAS PubMed.
- Y. Chen, N. S. Lewis and C. Xiang, Energy Environ. Sci., 2015, 8, 3663–3674 RSC.
- Y. Surendranath, D. K. Bediako and D. G. Nocera, Proc. Natl. Acad. Sci., 2012, 109, 15617–15621 CrossRef CAS PubMed.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley, 2008 Search PubMed.
- C. H. Henry, J. Appl. Phys., 1980, 51, 4494–4500 CrossRef CAS.
- R. Bala Chandran, S. Breen, Y. Shao, S. Ardo and A. Z. Weber, Energy Environ. Sci., 2018, 11, 115–135 RSC.
- G. A. Shreve and N. S. Lewis, J. Electrochem. Soc., 1995, 142(1), 112–119 CrossRef CAS.
- P. Gečys, G. Račiukaitis, E. Miltenis, A. Braun and S. Ragnow, Phys. Procedia, 2011, 12, 141–148 CrossRef.
- D. M. Fabian, S. Hu, N. Singh, F. A. Houle, T. Hisatomi, K. Domen, F. E. Osterlohf and S. Ardo, Energy Environ. Sci., 2015, 8, 2825–2850 RSC.
- S. Chen, T. Takata and K. Domen, Nat. Rev. Mater., 2017, 2, 17050 CrossRef CAS.
- K. Takanabe, ACS Catal., 2017, 7, 8006–8022 CrossRef CAS.
- S. Hu, M. R. Shaner, J. A. Beardslee, M. Lichterman, B. S. Brunschwig and N. S. Lewis, Science, 2014, 344, 1005–1009 CrossRef CAS PubMed.
- A. G. Scheuermann, J. P. Lawrence, K. W. Kemp, T. Ito, A. Walsh, C. E. D. Chidsey, P. K. Hurley and P. C. McIntyre, Nat. Mater., 2015, 15, 99 CrossRef PubMed.
Footnote |
| † This value is calculated by (i) following the optimal combinations for both upper and lower tandem absorbers, namely 19.3% for the upper photoanode/vertical cathode pair and 21.7% for the lower photoanode/vertical cathode pair; and (ii) taking the areal average following the width ratio of 0.4. |
| This journal is © The Royal Society of Chemistry 2019 |