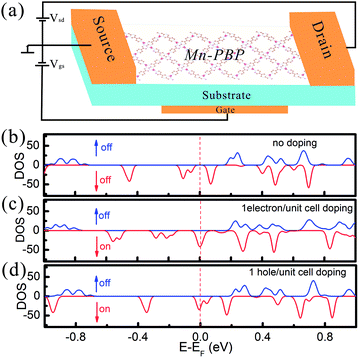
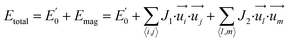Open Access Article
Open Access ArticleTwo-dimensional magnetic metal–organic frameworks with the Shastry-Sutherland lattice†
Li-Chuan
Zhang‡
abc,
Lizhi
Zhang‡
 d,
Guangzhao
Qin
d,
Guangzhao
Qin
 e,
Qing-Rong
Zheng
f,
Ming
Hu
*e,
Qing-Bo
Yan
e,
Qing-Rong
Zheng
f,
Ming
Hu
*e,
Qing-Bo
Yan
 *a and
Gang
Su
*fg
*a and
Gang
Su
*fg
aCenter of Materials Science and Optoelectronics Engineering, College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China. E-mail: yan@ucas.ac.cn
bPeter Grünberg Institut and Institute for Advanced Simulation, Forschungszentrum Jülich, JARA, 52425 Jülich, Germany
cDepartment of Physics, RWTH Aachen University, 52056 Aachen, Germany
dDepartment of Physics and Astronomy, University of Tennessee, Knoxville, Tennessee 37916, USA
eDepartment of Mechanical Engineering, University of South Carolina, Columbia, SC 29208, USA. E-mail: hu@sc.edu
fSchool of Physics, University of Chinese Academy of Sciences, Beijing 100049, China
gCAS Center for Excellence in Topological Quantum Computation, Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100190, China. E-mail: gsu@ucas.ac.cn
First published on 25th September 2019
Abstract
Inspired by the successful synthesis of Fe/Cu-5,5′-bis(4-pyridyl)(2,2′-bipirimidine) (PBP), a family of two-dimensional (2D) metal–organic frameworks (MOFs) with the Shastry-Sutherland lattice, i.e., transition metal (TM)-PBP (TM = Cr, Mn, Fe, Co, Ni, Cu, Zn) has been systematically investigated by means of first-principles density functional theory calculations and Monte Carlo simulations. Mn-PBP is discovered to be the first ferromagnetic 2D MOF with the Shastry-Sutherland lattice and the Curie temperature is predicted to be about 105 K, while Fe-PBP, TM-PBP (TM = Cr, Co, Ni) and TM-PBP (TM = Cu, Zn) are found to be stripe-order antiferromagnetic, magnetic-dimerized and nonmagnetic, respectively. The electronic structure calculations reveal that TM-PBP MOFs are semiconductors with band gaps ranging from 0.12 eV to 0.85 eV, which could be easily modulated by various methods. Particularly, Mn-PBP would exhibit half-metallic behavior under compressive strain or appropriate electron/hole doping and a Mn-PBP based spintronic device has been proposed. This study not only improves the understanding of the geometric, electronic and magnetic properties of the 2D TM-PBP MOF family, but also provides a novel spin lattice playground for the research of 2D magnetic systems, which has diverse modulating possibilities and rich potential applications.
Introduction
Two-dimensional (2D) metal–organic frameworks (MOFs)1–5 are novel 2D materials formed by metal atoms and polar organic molecules, and have aroused wide interest among researchers6–16 due to their advantages of low cost, chemical tenability, easy fabrication, and mechanical flexibility. Novel physical properties, such as ferromagnetic/antiferromagnetic ground states,17–20 superconductivity,21 and topological insulation,22–24 have also been discovered in 2D MOF systems. According to their geometrical structure, the lattice structures of 2D MOFs can be classified into hexagonal lattice,20,22,23,25 square lattice17,18 Kagome lattice,15,16,24etc. The Shastry-Sutherland (SS) lattice is a special type of distorted square lattice introduced by Shastry and Sutherland26 in 1981, and the typical materials are SrCu2(BO3)2 (ref. 27–30) and rare-earth-metal tetraborides RB4 (R = La-Lu),31,32 which have been drawing wide attention, especially on the magnetic order and fractional magnetization plateaus27–32 at low temperature. Recently, several 2D MOF materials with the SS lattice have also been synthesized, such as Cu-5,5′-bis(4-pyridyl)(2,2′-bipirimidine) (PBP)33 and Fe-PBP.34 Could any other transition metal (TM) elements also form MOFs with PBP? What are the electronic and magnetic properties of this 2D MOF material family with the SS lattice? These questions stimulate us to perform intensive theoretical research on them to extend the frontier of the 2D MOF field.In this work, the 2D TM-PBP (TM = Cr, Mn, Fe, Co, Ni, Cu, Zn) family of MOFs with the SS lattice has been systematically investigated by means of first-principles density functional theory (DFT) calculations and Monte Carlo simulations. It turns out that they have diverse ground state magnetic properties, i.e., Mn-PBP and Fe-PBP are found to be ferromagnetic (FM) and antiferromagnetic (AFM), while TM-PBP (TM = Cr, Co, Ni) and TM-PBP (TM = Cu, Zn) are found to be magnetic-dimerized and nonmagnetic, respectively. Especially, to the best of our knowledge, Mn-PBP should be the first FM 2D MOF with the SS lattice, the Curie temperature of which is predicted to be about 105 K. The novel low-symmetry coordination bonds caused by hybridization of the pz orbital from PBP molecules and the dxz and dyz orbitals from Mn atoms play a very important role in the formation of TM-PBP. The electronic structure calculations reveal that TM-PBP MOFs are semiconductors with band gaps ranging from 0.12 eV to 0.85 eV, which could be easily modulated by various methods, such as strain or hole/electron doping. A spin-field-effect transistor device model has been proposed and potential applications have been discussed.
Methods
The first-principles calculations were performed using the Vienna ab initio simulation package (VASP)35 with the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)36 for the exchange–correlation potential. The interaction between the electron and nuclei was expressed with the projector-augmented wave (PAW) method.37 The planewave function kinetic energy cutoff is 800 eV and the energy convergence threshold is 10−6 eV. The Brillouin zone was sampled with the 5 × 5 × 1 Γ-centred Monkhorst–Pack grid.38 The cell shape and volume were fully optimized and the maximum force for each atom was less than 0.01 eV Å−1. Coulomb and exchange interactions of the localized d orbitals in TM elements were treated with the DFT + U method proposed by Dudarev et al.,39,40 where only the Ueff = U(correlation energy) − J(exchange energy) value is meaningful. Referring previous work on other 2D MOFs15,16,41–43 with the DFT + U method, the same value Ueff = 3 eV for TM elements was adopted in our calculations. To confirm the FM ground state of Mn-PBP, we also used the linear response theory developed by Cococcioni44,45 to evaluate Ueff and the obtained value was 4.2 eV (see Fig. S1†), which does not change the FM ground state of Mn-PBP. Moreover, to further check the effect of the Ueff value on magnetic properties, a series of Ueff values ranging from 1.0 eV to 4.2 eV have also been tested, and the ground state of Mn-PBP is always FM. Thus, the finding of the FM ground state of Mn-PBP is reliable. During the Monte Carlo simulation, the spins on all sites flip randomly. We employed a 2D 200 × 200 SS lattice with 109 flip steps for each temperature. A test on the 100 × 100 SS lattice with 108 steps was also performed, and almost the same results were obtained, verifying that the simulation converged. More calculation details can be found in the ESI.†Results and discussion
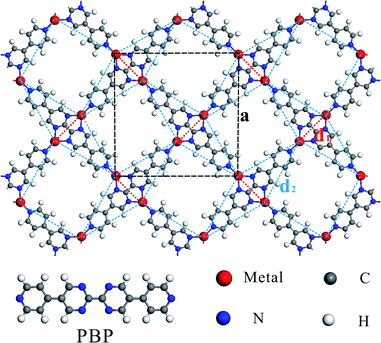
Fig. 1 shows the schematic structure of the TM-PBP framework and the black dashed lines outline the square unit cell. There are four TM atoms and two PBP molecules in each unit cell, and each TM atom bonds with three N atoms, marked as N1, N2, and N3. Focusing on the TM atoms, which are connected by red dotted lines (nearest neighbor) and blue dashed lines (second-nearest neighbor), the TM-PBP framework can be abstracted to a deformed square lattice and is topologically-equivalent to the standard Shastry-Sutherland (SS) lattice (see Fig. S2†). Table 1 lists the lattice parameters of TM-PBP, which generally decrease from Cr to Zn as the atomic numbers increase except Cu. The nearest neighboring TM atom distances (d1) are approximately 5–6 Å, while the second-nearest neighboring TM atom distances (d2) are about 10 Å. The binding energy between TM atoms and PBP molecules is generally about 3–4 eV per TM atom for most TM-PBP MOFs except that of Zn-PBP is only 1 eV. Detailed geometric parameters of TM-PBP are listed in Table S1.†| a | d 1 | d 2 | E b | E g | M | M cell | J 1 | J 2 | Magnetic | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cr | 18.17 | 5.91 | 10.33 | 3.4 | 0.73 | 4.36 | 0 | 0.1 | −3.3 × 10−5 | Dimerized |
| Mn | 17.79 | 5.50 | 10.21 | 3.5 | 0.12 | 4.33 | 16 | −1.86 | −0.31 | FM |
| Fe | 17.67 | 5.43 | 10.15 | 4.2 | 0.16 | 3.12 | 0 | 2.5 | 0.7 | Stripe-order AFM |
| Co | 17.62 | 5.46 | 10.11 | 4.4 | 0.53 | 1.96 | 0 | 0.4 | −3.5 × 10−2 | Dimerized |
| Ni | 17.49 | 5.33 | 10.06 | 4.3 | 0.73 | 0.96 | 0 | 0.9 | −2.0 × 10−2 | Dimerized |
| Cu | 17.55 | 5.44 | 10.07 | 3.6 | 0.85 | 0 | 0 | — | — | Nonmagnetic |
| Zn | 17.34 | 5.17 | 10.01 | 1.0 | 0.13 | 0 | 0 | — | — | Nonmagnetic |
To identify the magnetic ground states of 2D TM-PBP frameworks, three different typical magnetic state configurations, i.e., FM, Néel AFM and stripe AFM (see Fig. S2†) have been considered and investigated. Significantly, only the Mn-PBP framework is found to hold FM ground states; while Fe-PBP, TM-PBP (TM = Cr, Co, Ni) and TM-PBP (TM = Cu, Zn) are proved to be stripe-order AFM, magnetic-dimerized and nonmagnetic, respectively. To the best of our knowledge, Mn-PBP is the first 2D MOF material with the SS lattice discovered to present the FM ground state. As for the magnetic exchange interactions among TM atoms, considering that the nearest neighboring distances (d1) are much longer than the second-nearest neighboring distance (d2), the nearest neighboring magnetic exchange interactions should be much stronger than the second-nearest neighbouring interactions, which leads to complex magnetic states in TM-PBP systems.
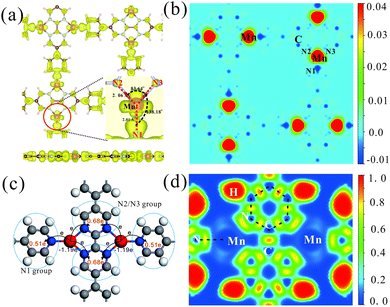
Electronic structures of all the above TM-PBP frameworks have been obtained, where the energy bands and projected density of states (PDOS) of Mn-PBP are shown in Fig. 2 and the energy bands of others are shown in Fig. S4.† All of them are found to be semiconductors and the band gaps range from 0.12 eV to 0.85 eV, as listed in Table 1. Cu-PBP has the largest energy gap, while Mn-PBP has the smallest gap. Only Mn-PBP has the FM ground state, which means that the spin-up and spin-down energy bands deviate from each other. As indicated in Fig. 2, spin-up electrons hold the semiconducting behavior with a band gap of 0.12 eV, while an almost 1 eV band gap is observed for the spin-down electrons. This means that the Mn-PBP framework is a FM semiconductor with a tiny band gap, resulting in that 100% spin-polarized carriers could be obtained under thermal, optical or electrical gating excitation. The calculated PDOS revealed that strong hybridization of pz orbitals from C and N atoms and the dxz and dyz orbitals from Mn atoms occurs near the Fermi level, while the s, dxy, and dz2 orbitals of Mn atoms are located about 0.4–0.8 eV above the Fermi level and correspond to the flat-band states with higher energy. This phenomenon could be rationalized as follows. As shown in Fig. 3(a), three Mn–N bonds around the same Mn atom do not hold C3 symmetry. The distance between Mn and N1 atoms is 2.01 Å, while the distance between Mn and N2/N3 atoms is 2.06 Å. The angle of N2–Mn–N3 and N1–Mn–N2 is 83.64° and 138.18°, respectively. The diverse bond lengths and angles reveal that asymmetric Mn–N coordinating bonds are formed. Under the non-equilateral triangle crystal field contributed by neighboring N atoms, the Mn d orbitals split, dxz and dyz orbitals shift down and dxy, dz2 and dx2−y2 orbitals shift up. The dxz and dyz orbitals of Mn are located around the Fermi level and hybridize with the pz orbitals of C and N atoms, which is responsible for the bonding between Mn and PBP molecules. The PDOS of Co-PBP and Cu-PBP is drawn in Fig. S5,† also indicating that the DOS near Fermi level mainly comes from the pz orbital of N/C atoms and the d orbital of TM atoms.
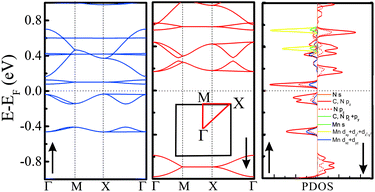 | ||
| Fig. 2 Electronic structure of Mn-PBP. Left panel: spin-up bands (blue lines); Middle panel: spin-down bands (red lines); Right panel: spin-up and spin-down projected density of states (PDOS). | ||
The electronic and spin properties in real space are also investigated. Fig. 3(a) manifests the partial charge density of Mn-PBP around the Fermi level. Consistent with the above deduction that d orbitals (Mn) strongly hybridize with pz (N and C atoms) orbitals, the partial charge density is mainly located around the Mn atom and its neighboring N atom. Fig. 3(b) shows the spin-polarized charge density of Mn-PBP. It is clear that the majority spin is located on Mn atoms, which should be provided by the dxz and dyz orbitals of Mn. Meanwhile, the minority spin is mainly on PBP molecules. Mn atoms and adjacent N atoms are oppositely polarized, and the polarization of the adjacent N1 atom is much stronger than N2 and N3 atoms. Interestingly, the carbon atoms in PBP molecules are alternately polarized, which is very similar to the phenomena described by the RKKY exchange mechanism.46 Similar phenomena can also be observed in some other MOF materials.16 Obviously, the spin-polarization on PBP molecules is very weak compared with Mn atoms, showing a FM spin lattice of Mn atoms (Fig. S6†). The spin polarization of the Fe-PBP framework is also investigated and shown in Fig. S6.† The nearest Fe atoms form AFM dimers and the whole framework exhibits stripe AFM order.
By means of Bader charge analysis,47,48 migrations of charge in Mn-PBP are obtained and shown in Fig. 3(c). The charge transfer from each Mn atom to whole PBP molecules is evaluated as 1.19e. Besides, the PBP molecules around each Mn atom can be viewed as three groups, i.e., the N1 group and N2/N3 group. Charges transferred from the Mn atom to the N1 group and the N2/N3 group are 0.51e and 0.68e, respectively, where each of the N1 and N2/N3 atoms accepts about 0.13e and 0.12e from nearby Mn atoms respectively. Fig. 3(d) presents the electron localization function (ELF) analysis. A high ELF area is found at C–C and C–N covalent bonds. There is also a large high ELF area between N and Mn atoms, which is apparently different from the C–C bond and should correspond to the N–Mn coordinated bond caused by the electron pair donation from the N atom to the Mn atom. Moreover, a bridge-like area between neighbouring N1, N2 and N3 atoms with low ELF can be observed, which may imply that neighbouring N atoms can interact with each other directly.
To further understand the magnetic properties and mechanism of TM-PBP frameworks, a 2D Ising model for the SS lattice30 is adopted,
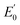 represent the energy of magnetic interaction and the total energy without the magnetic interaction respectively. J1 and J2 stand for the coupling coefficients of the nearest metal atoms and second nearest metal atoms,
represent the energy of magnetic interaction and the total energy without the magnetic interaction respectively. J1 and J2 stand for the coupling coefficients of the nearest metal atoms and second nearest metal atoms, 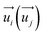 and
and 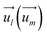 indicate the spin operators at the nearest sites i and j (second nearest sites l and m) respectively. Due to the small value of the magnetic anisotropic energy (∼0.034 meV, see Section 8 of ESI†), the magnetic anisotropic energy term is neglected.
indicate the spin operators at the nearest sites i and j (second nearest sites l and m) respectively. Due to the small value of the magnetic anisotropic energy (∼0.034 meV, see Section 8 of ESI†), the magnetic anisotropic energy term is neglected.
With the total energy of the TM-PBP framework with different magnetic configurations, the value of coupling coefficients J1 and J2 can be acquired (see Section 5 of ESI†), and the results are listed in Table 1. The exchange coupling coefficients of Mn-PBP and Fe-PBP are much larger than those of others. In fact, the values of J1 and J2 demonstrate the coupling types for the nearest and second-nearest TM atoms. For Mn-PBP, coupling coefficients J1 (−1.86 meV) and J2 (−0.31 meV) are both negative, which shows that the magnetic exchange interactions between the nearest and second-nearest TM atoms are both FM, and the whole system also exhibits FM behavior. For Fe-PBP, J1 (2.5 meV) and J2 (0.7 meV) are both positive, implying AFM interactions between neighboring Fe atoms and a stripe AFM ground state of the whole system. For TM-PBP (TM = Cr, Co, Ni), J1 values are positive, illustrating AFM interactions between the nearest neighboring TM atoms, however, J2 is lower than J1 by at least two orders of magnitude. Thus, we deduce that the magnetic ground state of TM-PBP (TM = Cr, Co, Ni) should be a dimer phase, in which the nearest TM atoms are bonded to AFM dimers, but the whole system doesn't exhibit macro magnetic order. Notably, the SS lattice systems normally display AFM ground states,30–32 whereas the FM ground state found in Mn-PBP here contributes a novel example of the FM SS spin lattice.
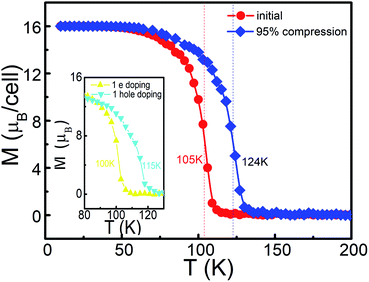
Based on the above Ising model and exchange coupling coefficients, the thermodynamical magnetic properties for the Mn-PBP framework are simulated using the Monte Carlo method.15,49,50 As shown in Fig. 4, the total magnetic moments per unit cell start to drop gradually from 16 μB at about 60 K, until at about 110 K the total magnetic movements become 0 μB. The second order phase transition point is located at about 105 K, which corresponds to the value of Tc. The effect of U on Tc has been calculated and the detailed results in Fig. S10† indicate that very small changes happen when the different value of U is selected for the calculation. Compared with recent experiments for 2D FM materials, e.g. 2D PTC-Fe MOFs51 and 2D CrI3,52 this material holds a much higher Tc. It is more likely that this result can be verified by experiments, although the Curie temperature could be overestimated from the Ising model.
As mentioned above, Mn-PBP is a FM semiconductor with a tiny band gap, which could be easily regulated by various methods. We have tried to apply strain on Mn-PBP, and it is uncovered that 95% compressive strain could turn Mn-PBP into a half metal (see Fig. S11†), which can act as a spin filter to obtain 100% spin-polarized carriers. The strain will also change the distance between Mn atoms and affect the exchange coupling coefficients, and thus would change the Curie temperature. As shown in Fig. 4, a 95% compressive strain will raise the Curie temperature from 105 K to 125 K. Furthermore, electron and hole doping can also increase the Curie temperature as shown in the inset of Fig. 4.
The effect of electron and hole doping on the electronic structure of Mn-PBP is investigated and shown in Fig. 5. Since the band gap is tiny and there are spin-polarized states below and above the Fermi level, when the system is doped with 1 hole/electron per unit cell, the Fermi level declines/inclines and crosses the spin-polarized energy band, giving rise to a half metal in which spin-up electrons behave as a metal, while spin-down electrons act like a semiconductor. According to this analysis, we proposed a spin-field-effect transistor (SFET) based on Mn-PBP, and its schematic structure is declared in Fig. 5(a). Since electron/hole doping can be controlled by the substrate materials and gate voltage Vgs, controllable spin ON/OFF switch can be realized in Mn-PBP SFET and 100% spin-polarization carriers could be observed. Although the concept of SFET was introduced more than two decades ago,53 it is still complicated to realize the functional SFET for information processing. Thus, Mn-PBP is a promising material for future spintronic devices.
Conclusions
A family of 2D TM-PBP MOFs with the SS lattice has been systematically studied by means of first-principles calculations and Monte Carlo simulations. In the TM-PBP framework, each TM atom bonds with its nearby three N atoms with asymmetric coordination bonds. Different magnetic arrangements have been investigated in TM-PBP frameworks, where the Mn-PBP framework holds the FM ground state with a Curie temperature of about 105 K, Fe-PBP possesses the stripe AFM ground state, TM-PBP (TM = Cr, Co, Ni) forms the magnetic dimerized ground state, and TM-PBP MOFs (TM = Cu, Zn) are non-magnetic. Their band gap ranges from 0.12 eV to 0.87 eV. The Mn-PBP framework is found to be a half semiconductor with a band gap of less than 0.15 eV, caused by the novel low-symmetry coordination bonds with the hybridization of the pz orbital from PBP molecules and the dxz and dyz orbitals from Mn atoms. Especially, it is demonstrated that strain will cause Mn-PBP to transit from semiconductor to metal. Furthermore, electron doping and hole doping of Mn-PBP are investigated, illustrating that the Mn-PBP framework can be easily regulated from half semiconductor to half-metal. As Cu-PBP and Fe-PBP systems have been already successfully synthesized, it is promising that Mn-PBP and other 2D MOFs TM-PBP we studied here can also be synthesized in the near future. These novel properties indicate that TM-PBP frameworks have promising applications in electronic devices, especially the Mn-PBP framework with the first predicted FM ground state with the SS lattice in MOFs is an excellent 2D candidate material for spintronic application.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Prof. S. S. Gong of Beihang University, Dr S. Y. Yue of University of California, Santa Barbara (UCSB), Prof. Y. Mokrousov and P. M. Buhl of IAS, Forschungszentrum, Jülich, Prof. Z.-G. Zhu, and Dr C. Peng of UCAS for helpful discussions. All calculations are performed in the Supercomputing centre of Chinese Academy of Sciences and Shanghai Supercomputing Centre, China. L.-C. Zhang acknowledges support from the China Scholarship Council (CSC) (No. [2016]3100). This work is supported in part by the National Key R&D Program of China (Grant No. 2018FYA0305800), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB28000000), the National Natural Science Foundation of China (Grant No. 11834014), and the Beijing Municipal Science and Technology Commission (Grant No. Z118100004218001).Notes and references
- S. Stepanow, N. Lin, D. Payer, U. Schlickum, F. Klappenberger, G. Zoppellaro, M. Ruben, H. Brune, J. V. Barth and K. Kern, Surface-Assisted Assembly of 2D Metal-Organic Networks That Exhibit Unusual Threefold Coordination Symmetry, Angew. Chem., Int. Ed., 2007, 46, 710–713 CrossRef CAS PubMed.
- U. Schlickum, R. Decker, F. Klappenberger, G. Zoppellaro, S. Klyatskaya, M. Ruben, I. Silanes, A. Arnau, K. Kern, H. Brune and J. V. Barth, Metal-organic honeycomb nanomeshes with tunable cavity size, Nano Lett., 2007, 7, 3813–3817 CrossRef CAS PubMed.
- X. Wu and X. C. Zeng, Double Metallocene Nanowires, J. Am. Chem. Soc., 2009, 131, 14246–14248 CrossRef CAS PubMed.
- M. Abel, S. Clair, O. Ourdjini, M. Mossoyan and L. Porte, Single Layer of Polymeric Fe-Phthalocyanine: An Organometallic Sheet on Metal and Thin Insulating Film, J. Am. Chem. Soc., 2011, 133, 1203–1205 CrossRef CAS PubMed.
- M. Hmadeh, Z. Lu, Z. Liu, F. Gándara, H. Furukawa, S. Wan, V. Augustyn, R. Chang, L. Liao, F. Zhou, E. Perre, V. Ozolins, K. Suenaga, X. Duan, B. Dunn, Y. Yamamto, O. Terasaki and O. M. Yaghi, New Porous Crystals of Extended Metal-Catecholates, Chem. Mater., 2012, 24, 3511–3513 CrossRef CAS.
- T. Kambe, R. Sakamoto, K. Hoshiko, K. Takada, M. Miyachi, J.-H. Ryu, S. Sasaki, J. Kim, K. Nakazato, M. Takata and H. Nishihara, π-Conjugated Nickel Bis(dithiolene) Complex Nanosheet, J. Am. Chem. Soc., 2013, 135, 2462–2465 CrossRef CAS PubMed.
- Z. F. Wang, N. Su and F. Liu, Prediction of a Two-Dimensional Organic Topological Insulator, Nano Lett., 2013, 13, 2842–2845 CrossRef CAS PubMed.
- D. Sheberla, L. Sun, M. A. Blood-Forsythe, S. Er, C. R. Wade, C. K. Brozek, A. Aspuru-Guzik and M. Dincă, High electrical conductivity in Ni3(2,3,6,7,10,11-hexaiminotriphenylene)2, a semiconducting metal-organic graphene analogue, J. Am. Chem. Soc., 2014, 136, 8859–8862 CrossRef CAS PubMed.
- T. Kambe, R. Sakamoto, T. Kusamoto, T. Pal, N. Fukui, K. Hoshiko, T. Shimojima, Z. Wang, T. Hirahara, K. Ishizaka, S. Hasegawa, F. Liu and H. Nishihara, Redox Control and High Conductivity of Nickel Bis(dithiolene) Complex π-Nanosheet: A Potential Organic Two-Dimensional Topological Insulator, J. Am. Chem. Soc., 2014, 136, 14357–14360 CrossRef CAS PubMed.
- A. J. Clough, J. W. Yoo, M. H. Mecklenburg and S. C. Marinescu, Two-dimensional metal-organic surfaces for efficient hydrogen evolution from water, J. Am. Chem. Soc., 2015, 137, 118–121 CrossRef CAS PubMed.
- M. G. Campbell, D. Sheberla, S. F. Liu, T. M. Swager and M. Dincă, Cu3(hexaiminotriphenylene)2: an electrically conductive 2D metal-organic framework for chemiresistive sensing, Angew. Chem., Int. Ed., 2015, 54, 4349–4352 CrossRef CAS PubMed.
- M. G. Campbell, S. F. Liu, T. M. Swager and M. Dincă, Chemiresistive Sensor Arrays from Conductive 2D Metal-Organic Frameworks, J. Am. Chem. Soc., 2015, 137, 13780–13783 CrossRef CAS PubMed.
- L. Sun, M. G. Campbell and M. Dincă, Electrically Conductive Porous Metal-Organic Frameworks, Angew. Chem., Int. Ed., 2016, 55, 3566–3579 CrossRef CAS PubMed.
- E. M. Miner, T. Fukushima, D. Sheberla, L. Sun, Y. Surendranath and M. Dincă, Electrochemical oxygen reduction catalysed by Ni3(hexaiminotriphenylene)2, Nat. Commun., 2016, 7, 10942 CrossRef CAS PubMed.
- J.-H. Dou, L. Sun, Y. Ge, W. Li, C. H. Hendon, J. Li, S. Gul, J. Yano, E. A. Stach and M. Dincă, Signature of Metallic Behavior in the Metal-Organic Frameworks M3(hexaiminobenzene)2 (M = Ni, Cu), J. Am. Chem. Soc., 2017, 139, 13608–13611 CrossRef CAS.
- A. J. Clough, J. M. Skelton, C. A. Downes, A. De la Rosa, J. W. Yoo, A. Walsh, B. C. Melot and S. C. Marinescu, Metallic Conductivity in a Two-Dimensional Cobalt Dithiolene Metal-Organic Framework, J. Am. Chem. Soc., 2017, 139, 10863–10867 CrossRef CAS PubMed.
- J. Zhou and Q. Sun, Magnetism of Phthalocyanine-Based Organometallic Single Porous Sheet, J. Am. Chem. Soc., 2011, 133, 15113–15119 CrossRef CAS PubMed.
- W. Li, L. Sun, J. Qi, P. Jarillo-Herrero, M. Dincă and J. Li, High temperature ferromagnetism in π-conjugated two-dimensional metal–organic frameworks, Chem. Sci., 2017, 8, 2859–2867 RSC.
- H. Xiang, J. Yang, J. G. Hou and Q. Zhu, One-Dimensional Transition Metal-Benzene Sandwich Polymers: Possible Ideal Conductors for Spin Transport, J. Am. Chem. Soc., 2006, 128, 2310–2314 CrossRef CAS PubMed.
- E. Kan, W. Hu, C. Xiao, R. Lu, K. Deng, J. Yang and H. Su, Half-Metallicity in Organic Single Porous Sheets, J. Am. Chem. Soc., 2012, 134, 5718–5721 CrossRef CAS PubMed.
- X. Zhang, Y. Zhou, B. Cui, M. Zhao and F. Liu, Theoretical Discovery of a Superconducting Two-Dimensional Metal-Organic Framework, Nano Lett., 2017, 17, 6166–6170 CrossRef CAS PubMed.
- Z. Liu, Z.-F. Wang, J.-W. Mei, Y.-S. Wu and F. Liu, Flat Chern Band in a Two-Dimensional Organometallic Framework, Phys. Rev. Lett., 2013, 110, 106804 CrossRef PubMed.
- L. Z. Zhang, Z. F. Wang, B. Huang, B. Cui, Z. Wang, S. X. Du, H.-J. Gao and F. Liu, Intrinsic Two-Dimensional Organic Topological Insulators in Metal-Dicyanoanthracene Lattices, Nano Lett., 2016, 16, 2072–2075 CrossRef CAS PubMed.
- L. Dong, Y. Kim, D. Er, A. M. Rappe and V. B. Shenoy, Two-Dimensional π-Conjugated Covalent-Organic Frameworks as Quantum Anomalous Hall Topological Insulators, Phys. Rev. Lett., 2016, 116, 096601 CrossRef.
- H. Hu, Z.-F. Wang and F. Liu, Half metal in two-dimensional hexagonal organometallic framework, Nanoscale Res. Lett., 2014, 9, 690 CrossRef PubMed.
- B. Sriram Shastry and B. Sutherland, Exact ground state of a quantum mechanical antiferromagnet, Physica B+C, 1981, 108, 1069–1070 CrossRef.
- H. Kageyama, K. Yoshimura, M. Kato, K. Kosuge, H. Kageyama, N. V. Mushnikov, K. Onizuka, T. Goto, Y. Ueda, K. Yoshimura, R. Stern and C. P. Slichter, Exact Dimer Ground State and Quantized Magnetization Plateaus in the Two-Dimensional Spin System SrCu2(BO3)2, Phys. Rev. Lett., 1999, 82, 3168 CrossRef CAS.
- A. Koga and N. Kawakami, Quantum Phase Transitions in the Shastry-Sutherland Model for SrCu2(BO3)2, Phys. Rev. Lett., 2000, 84, 4461 CrossRef CAS PubMed.
- K. Kodama, M. Takigawa, M. Horvatic, C. Berthier, H. Kageyama, Y. Ueda, S. Miyahara, F. Becca and F. Mila, Magnetic Superstructure in the Two-Dimensional Quantum Antiferromagnet SrCu2(BO3)2, Science, 2002, 298, 395–399 CrossRef CAS PubMed.
- S. Miyahara and K. Ueda, Theory of the orthogonal dimer Heisenberg spin model for SrCu2(BO3)2, J. Phys.: Condens. Matter, 2003, 15, R327 CrossRef CAS.
- A. Abendschein and S. Capponi, Effective Theory of Magnetization Plateaux in the Shastry-Sutherland Lattice, Phys. Rev. Lett., 2008, 101, 227201 CrossRef CAS PubMed.
- Y. I. Dublenych, Ground States of the Ising Model on the Shastry-Sutherland Lattice and the Origin of the Fractional Magnetization Plateaus in Rare-Earth-Metal Tetraborides, Phys. Rev. Lett., 2012, 109, 167202 CrossRef PubMed.
- S. L. Tait, A. Langner, N. Lin, R. Chandrasekar, O. Fuhr, M. Ruben and K. Kern, Assembling Isostructural Metal-Organic Coordination Architectures on Cu (100), Ag (100) and Ag (111) Substrates, ChemPhysChem, 2008, 9, 2495–2499 CrossRef CAS.
- D. Grumelli, B. Wurster, S. Stepanow and K. Kern, Bio-inspired nanocatalysts for the oxygen reduction reaction, Nat. Commun., 2013, 4, 2904 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- A. Calzolari, A. Ferretti and M. B. Nardelli, Ab initio correlation effects on the electronic and transport properties of metal (II)-phthalocyanine-based devices, Nanotechnology, 2007, 18, 424013 CrossRef PubMed.
- M. Bernien, J. Miguel, C. Weis, M. E. Ali, J. Kurde, B. Krumme, P. M. Panchmatia, B. Sanyal, M. Piantek, P. Srivastava, K. Baberschke, P. M. Oppeneer, O. Eriksson, W. Kuch and H. Wende, Tailoring the Nature of Magnetic Coupling of Fe-Porphyrin Molecules to Ferromagnetic Substrates, Phys. Rev. Lett., 2009, 102, 047202 CrossRef CAS PubMed.
- S. Lach, A. Altenhof, K. Tarafder, F. Schmitt, M. E. Ali, M. Vogel, J. Sauther, P. M. Oppeneer and C. Ziegler, Metal-Organic Hybrid Interface States of A Ferromagnet/Organic Semiconductor Hybrid Junction as Basis For Engineering Spin Injection in Organic Spintronics, Adv. Funct. Mater., 2012, 22, 989–997 CrossRef CAS.
- M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA+U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach, Phys. Rev. Lett., 2006, 97, 103001 CrossRef PubMed.
- K. Yosida, Magnetic Properties of Cu-Mn Alloys, Phys. Rev., 1957, 106, 893–898 CrossRef.
- M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- J. He, S. Ma, P. Lyu and P. Nachtigall, Unusual Dirac half-metallicity with intrinsic ferromagnetism in vanadium trihalide monolayers, J. Mater. Chem. C, 2016, 4, 2518–2526 RSC.
- E. Torun, H. Sahin, S. K. Singh and F. M. Peeters, Stable half-metallic monolayers of FeCl2, Appl. Phys. Lett., 2015, 106, 192404 CrossRef.
- R. Dong, Z. Zhang, D. C. Tranca, S. Zhou, M. Wang, P. Adler, Z. Liao, F. Liu, Y. Sun and W. Shi, et al., A coronene-based semiconducting two-dimensional metal-organic framework with ferromagnetic behavior, Nat. Commun., 2018, 9, 2637 CrossRef PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, et al., Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- S. Datta and B. Das, Electronic analog of the electro-optic modulator, Appl. Phys. Lett., 1990, 56, 665–667 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Calculation details, geometric information, magnetic configuration, electronic structures of TM-PBP, the influence of different effective U values, and the 2D Ising model for the Shastry-Sutherland lattice. See DOI: 10.1039/c9sc03816g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |