Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structures of bent lanthanide(III) complexes with two N-donor ligands†
Hannah M.
Nicholas
,
Michele
Vonci
 ,
Conrad A. P.
Goodwin
,
Conrad A. P.
Goodwin
 ,
Song Wei
Loo
,
Siobhan R.
Murphy
,
Daniel
Cassim
,
Richard E. P.
Winpenny
,
Song Wei
Loo
,
Siobhan R.
Murphy
,
Daniel
Cassim
,
Richard E. P.
Winpenny
 ,
Eric J. L.
McInnes
,
Nicholas F.
Chilton
,
Eric J. L.
McInnes
,
Nicholas F.
Chilton
 and
David P.
Mills
and
David P.
Mills
 *
*
Department of Chemistry, School of Natural Sciences, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: david.mills@manchester.ac.uk
First published on 18th September 2019
Abstract
Low coordinate metal complexes can exhibit superlative physicochemical properties, but this chemistry is challenging for the lanthanides (Ln) due to their tendency to maximize electrostatic contacts in predominantly ionic bonding regimes. Although a handful of Ln2+ complexes with only two monodentate ligands have been isolated, examples in the most common +3 oxidation state have remained elusive due to the greater electrostatic forces of Ln3+ ions. Here, we report bent Ln3+ complexes with two bis(silyl)amide ligands; in the solid state the Yb3+ analogue exhibits a crystal field similar to its three coordinate precursor rather than that expected for an axial system. This unanticipated finding is in opposition to the predicted electronic structure for two-coordinate systems, indicating that geometries can be more important than the Ln ion identity for dictating the magnetic ground states of low coordinate complexes; this is crucial transferable information for the construction of systems with enhanced magnetic properties.
Introduction
The remarkable optical, magnetic and catalytic properties of the lanthanides (Ln) have provided numerous technological applications,1 and design criteria now exist to build complexes with precise geometrical features that maximize these attributes.2–10 Highly axial Ln3+ complexes have recently become desirable targets for the single-molecule magnet (SMM) community as such geometries can provide maximum anisotropy for several Ln3+ ions;2–5,11–13 indeed, we have previously predicted that a hypothetical near-linear Dy3+ cation [Dy{N(SiiPr3)2}2]+ could exhibit a record energy barrier to the reversal of magnetization, providing the inspiration for this work.14 Some of us15–18 and others19,20 have recently shown that isolated axial Ln3+ metallocenium cations [Ln(CpR)2]+ (CpR = substituted cyclopentadienyl) can be prepared by halide abstraction from [Ln(CpR)2(X)] precursors by using the silylium reagent [H(SiEt3)2][B(C6F5)4].21 The axial [Dy(CpR)2]+ members of this family15,19,20 together with a linear Tb2+ metallocene22 exhibit the current highest blocking temperatures for SMMs.The isolation of low coordinate Ln complexes is often synthetically challenging, as the predominantly ionic bonding regimes in these systems favour high coordination numbers to maximize the number of electrostatic interactions between ligand donor atoms and relatively large Ln cations.8 Seminal work by Bradley in the early 1970s provided the trigonal pyramidal Ln complexes, [Ln{N(SiMe3)2}3], which exhibit additional Ln⋯Cγ–Siβ interactions that stabilize the coordinatively unsaturated Ln3+ centres.23,24 In the interim, numerous trigonal pyramidal and planar Ln3+ and Ln2+ complexes have been accessed by using a combination of sterically demanding ligands and strict anaerobic conditions.25,26 In contrast, there are only a handful of structurally characterised monomeric Ln2+ complexes with only two formally monodentate ligands; the majority contain intramolecular π-arene contacts,27–31 whilst bent [Ln{C(SiMe3)3}2] (Ln = Sm, Eu, Yb)32–34 and near-linear [Ln{N(SiiPr3)2}2] (1-Ln; Ln = Sm, Eu, Tm, Yb)14,35 have additional electrostatic interactions between the ligand σ-bonding frameworks and Ln2+ centres. Ln3+ complexes with only two monodentate ligands have remained elusive to date as more Lewis acidic Ln3+ centres favour higher coordination numbers.1
In 2018, some of us showed that 1-Sm can be easily oxidized by a variety of reagents to afford heteroleptic Sm3+ halide complexes [Sm{N(SiiPr3)2}2(X)] (X = F, Cl, Br, I).36 Herein we report the synthesis of the bent Ln3+ complexes [Ln{N(SiiPr3)2}2][B(C6F5)4] (2-Ln; Ln = Sm, Tm, Yb) by an analogous halide abstraction from [Ln{N(SiiPr3)2}2(X)], (3-Ln; X = Cl, Ln = Sm,36 Tm; X = F, Ln = Yb) using [H(SiEt3)2][B(C6F5)4]; 3-Tm and 3-Yb are prepared by the oxidation of [Ln{N(SiiPr3)2}2] (1-Ln; Ln = Tm, Yb) with tBuCl and [FeCp2][PF6], respectively. We have probed the electronic structures of these exotic yet structurally simple complexes by magnetic and EPR methods, supported by ab initio calculations. This allows us to probe the effect of approximately linear, bent or planar geometries on the ligand field splitting. Simple electrostatic arguments5 based on aspherical electron density distributions in the Russell Saunders sub-levels37 predict that 2-Ln and 3-Ln should have opposite senses of magnetic anisotropy for a given 4fn configuration: we find that this is not always the case, and in fact can vary markedly with the degree of bending of the N–Ln–N angle.
Results and discussion
Synthesis
Oxidation of the Ln2+ complexes 1-Ln with either tBuCl (Ln = Sm,36 Tm) or [FeCp2][PF6] (Yb) in toluene gave the heteroleptic Ln3+ complexes 3-Ln in good yields (58–72%) following recrystallization from hexane (Scheme 1); similar oxidative procedures on Ln2+ bis(silyl)amide complexes have recently been applied by Anwander and co-workers.38 The Eu3+ analogue 3-Eu could not be accessed by analogous methods, with crystals of 1-Eu the only isolable product from numerous attempts to oxidize 1-Eu with tBuCl, [FeCp2][PF6] and Ph3CCl. This can be attributed to the preference of Eu to exhibit the +2 oxidation state over all other Ln, as illustrated by standard reduction potentials, Eθ, Ln3+ → Ln2+: −0.35 V (Eu), −1.15 V (Yb), −1.55 V (Sm), −2.3 V (Tm).39 Halide abstraction of 3-Ln using [H(SiEt3)2][B(C6F5)4] in benzene (Sm, Tm) or toluene (Yb) yielded the bent Ln3+ complexes, 2-Ln, in moderate yields (46–70%) after recrystallization from DCM layered with hexane (Scheme 1). The silylium reagent was selected for its solubility in non-coordinating solvents and for the provision of a large thermodynamic driving force for the reaction.40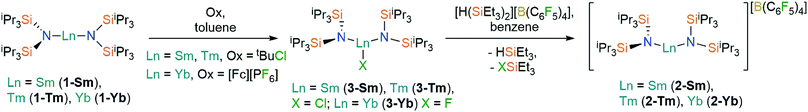 | ||
| Scheme 1 Synthesis of 2-Ln and 3-Ln. See ref. 36 for the synthesis of 3-Sm. | ||
NMR spectroscopy
The paramagnetic Ln3+ centres in 2-Ln and 3-Ln engender large pseudocontact shifts and significant signal broadening in NMR spectra;41,42 the spectra that exhibited signals are compiled in ESI Fig. S4–S13.†1H NMR spectra were recorded from +200 to −200 ppm and for 2-Sm peaks were observed at 0.43 ppm and −5.27 ppm, corresponding to the methyl and methine protons, respectively, of the bis(silyl)amide ligand. For both 2-Tm and 2-Yb only one broad peak was observed at 25.04 ppm and 11.02 ppm, respectively, which we tentatively assign to the methyl protons as these are more numerous than methine protons. No signals were observed for 2-Ln by 29Si{1H} and 13C{1H} NMR spectroscopy. Similarly, no signals were observed for the [B(C6F5)4]− anion in the 13C{1H} NMR spectra of 2-Ln; however for 2-Sm, 2-Tm and 2-Yb, the 11B{1H} NMR spectra displayed sharp peaks at −16.76, −12.35 and −14.67 ppm, respectively. The 19F{1H} NMR spectra of 2-Sm and 2-Yb each displayed three signals characteristic of the [B(C6F5)4]− anion (−133.17, −163.71 and −167.60 ppm for 2-Sm and −131.58, −162.00 and −165.15 ppm for 2-Yb), but only one signal was observed in the 19F{1H} NMR spectrum of 2-Tm (−128.51 ppm). No signals corresponding to 3-Ln could be seen in the 1H or 13C{1H} NMR spectra for all 3-Ln, with only diamagnetic impurities observed; no features were seen in the 19F NMR spectrum of 3-Yb. Given the paucity of information that could be extracted by NMR spectroscopy for 2-Ln and 3-Ln, we did not conduct variable temperature studies as these did not prove fruitful for 1-Ln previously;35 instead we have analysed metal–ligand interactions by computational methods (see below).Single crystal XRD
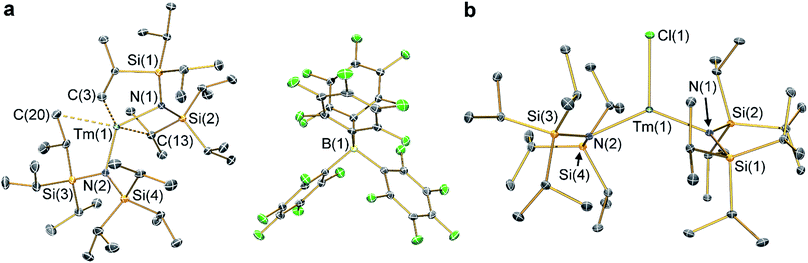
The solid state structures of 2-Ln and 3-Ln were determined by single crystal X-ray diffraction. Complexes 2-Tm and 3-Tm are depicted in Fig. 1 and selected metrical parameters are compiled in Table 1; see ESI Fig. S1–S3† and ref. 35 for the structures of other complexes. Complexes 2-Ln are structurally analogous, though 2-Sm and 2-Yb both adopt the P21/n space group and 2-Tm crystallizes in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , and one molecule of DCM was present in the crystal lattice for both 2-Tm and 2-Yb, but is absent in crystals of 2-Sm. The [Ln{N(SiiPr3)2}2]+ cations in 2-Ln exhibit bent geometries defined by the two Ln–N bonds, with N–Ln–N angles of 131.02(8)° for 2-Sm, 125.49(9)° for 2-Tm, and 127.7(2)° for 2-Yb, which are in contrast to the near-linear geometries seen for 1-Ln (range 166.01(14)–175.5(2)°).14,35 We attribute the bent geometries of 2-Ln to the Ln3+ cations being more Lewis acidic than the Ln2+ centres in 1-Ln,14,35 as this permits the more electron deficient Ln3+ centres to form additional stabilizing electrostatic contacts with methyl and methine groups of the {N(SiiPr3)2} ligands. A permanent dipole is formed between the two formally anionic N− centres and Ln3+ ion upon bending; such dipolar stabilization mechanisms have previously been used to explain the pyramidal geometries of some f-block tris-silylamides.43 Crystal packing forces and inter-ligand dispersion forces also likely make important contributions.44 This subtle interplay of forces is particularly apparent for 2-Yb (see below).
, and one molecule of DCM was present in the crystal lattice for both 2-Tm and 2-Yb, but is absent in crystals of 2-Sm. The [Ln{N(SiiPr3)2}2]+ cations in 2-Ln exhibit bent geometries defined by the two Ln–N bonds, with N–Ln–N angles of 131.02(8)° for 2-Sm, 125.49(9)° for 2-Tm, and 127.7(2)° for 2-Yb, which are in contrast to the near-linear geometries seen for 1-Ln (range 166.01(14)–175.5(2)°).14,35 We attribute the bent geometries of 2-Ln to the Ln3+ cations being more Lewis acidic than the Ln2+ centres in 1-Ln,14,35 as this permits the more electron deficient Ln3+ centres to form additional stabilizing electrostatic contacts with methyl and methine groups of the {N(SiiPr3)2} ligands. A permanent dipole is formed between the two formally anionic N− centres and Ln3+ ion upon bending; such dipolar stabilization mechanisms have previously been used to explain the pyramidal geometries of some f-block tris-silylamides.43 Crystal packing forces and inter-ligand dispersion forces also likely make important contributions.44 This subtle interplay of forces is particularly apparent for 2-Yb (see below).
| Complex | Ln–N/Å | N–Ln–N/° | Ln–X |
|---|---|---|---|
| 2-Sm | 2.257(3), 2.228(3) | 131.02(8) | — |
| 2-Tm | 2.156(2), 2.156(2) | 125.49(9) | — |
| 2-Yb | 2.152(4), 2.144(5) | 127.7(2) | — |
| 3-Sm 36 | 2.295(2), 2.317(2) | 128.24(7) | 2.5813(7) |
| 3-Tm | 2.219(2), 2.238(2) | 129.39(5) | 2.4832(5) |
| 3-Yb | 2.226(3), 2.235(3) | 138.71(9) | 1.983(2) |
As with the 1-Ln series,14,35 the heavier Ln3+ centres in 2-Ln exhibit more bent N–Ln–N angles, which we again ascribe to the greater charge density of smaller Ln3+ cations driving stronger electrostatic interactions with ligand C–H bonds. The {N(SiiPr3)2} ligands in 2-Ln are staggered with respect to each other, with the mean Ln–N bond lengths decreasing with Ln3+ atomic radii: 2.243(4) Å (Sm), 2.156(3) Å (Tm) and 2.148(6) Å (Yb). It may appear counterintuitive that the Ln–N bonds in 2-Ln are shorter than those in 1-Ln (2.483(6) Å, Sm; 2.373(2) Å, Tm; and 2.384(3) Å, Yb)14,35 given the decreased N–Ln–N angles in 2-Ln compared with 1-Ln, but shorter Ln–N bonds for 2-Ln are expected from an increase in Ln oxidation state. Three Si–C bonds are oriented towards the Ln3+ centre in each [Ln{N(SiiPr3)2}2]+ cation; these are assigned as Ln⋯Cγ–Siβ agostic-type interactions by analogy with those discussed for three-coordinate silyl-substituted Ln complexes.45–48 These interactions lead to three relatively long β-Si–C bonds, three short Ln⋯Si distances, six Ln⋯C and six Ln⋯H electrostatic contacts with methyl/methine groups [e.g. for 2-Tm: range Tm⋯C: 2.731(3)–3.051(3) Å; range Tm⋯H: 2.200–2.495 Å; range Tm⋯Si: 3.066(2)–3.178(2) Å; mean β-Si–C: 1.938(3) Å; range other Si–C: 1.889(3)–1.917(3) Å]. The [B(C6F5)4]− anions do not coordinate; the shortest Ln⋯F distance for 2-Yb is 4.627(4) Å, whereas for 2-Sm and 2-Tm the shortest Ln⋯F distances are longer at 7.957(2) Å and 7.715(2) Å, respectively. Using the IUPAC definition of coordination number as the number of metal–ligand σ-bonds,49 the cations of 2-Ln can be considered to be formally two-coordinate as they each exhibit two Ln–N bonds; we probed the numerous additional Ln⋯Cγ–Siβ electrostatic interactions further through calculations as these could affect the magnetic properties of the proposed [Dy{N(SiiPr3)2}2]+ cation (see below).12,14
The structure of 3-Sm has previously been reported,36 but will be discussed together with 3-Tm and 3-Yb as all three complexes are structurally similar. Complex 3-Yb crystallizes in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , whilst 3-Sm and 3-Tm are in the P21/c space group. Complexes 3-Ln all crystallize with distorted trigonal planar geometries, with the Ln3+ centres positioned out of the plane defined by the two nitrogen atoms and halide (distances of Ln from N2(X) plane: 0.245(2) Å for 3-Sm, 0.3292(9) Å for 3-Tm and 0.312(2) Å for 3-Yb). As expected the Yb–F bond length of 3-Yb [1.983(2) Å] is shorter than the Ln–Cl bond lengths of 3-Sm (2.5813(7) Å) and 3-Tm (2.4832(5) Å) due to the smaller size of the fluoride anion; this also leads to differing N–Ln–N angles (3-Sm: 128.24(7)°; 3-Tm: 129.39(5)°; 3-Yb: 138.71(9)°). The mean Sm–N bond length of 3-Sm (2.306(3) Å) is significantly longer than the mean Ln–N bond lengths of 3-Tm (2.229(3) Å) and 3-Yb (2.231(4) Å), which corresponds with earlier Ln3+ ions being larger.1 The Ln–N bond lengths in 3-Ln are longer than those in 2-Ln, as expected from increasing the formal coordination number from two to three. Finally, as with 2-Ln the coordination spheres of the Ln3+ centres of 3-Ln are completed by multiple electrostatic contacts with methine and methyl groups. These are also likely to arise from Ln⋯Cγ–Siβ agostic-type interactions, though in 3-Ln there are fewer, and the Tm⋯C/H/Si distances are generally longer due to the presence of a halide [e.g. for 3-Tm: range three Tm⋯C: 2.874(2)–3.261(2) Å; range three Tm⋯H: 2.324–2.467 Å; range three Tm⋯Si: 3.195(2)–3.354(2) Å; mean three β-Si–C: 1.928(3) Å; range other Si–C: 1.899(2)–1.913(2) Å].
, whilst 3-Sm and 3-Tm are in the P21/c space group. Complexes 3-Ln all crystallize with distorted trigonal planar geometries, with the Ln3+ centres positioned out of the plane defined by the two nitrogen atoms and halide (distances of Ln from N2(X) plane: 0.245(2) Å for 3-Sm, 0.3292(9) Å for 3-Tm and 0.312(2) Å for 3-Yb). As expected the Yb–F bond length of 3-Yb [1.983(2) Å] is shorter than the Ln–Cl bond lengths of 3-Sm (2.5813(7) Å) and 3-Tm (2.4832(5) Å) due to the smaller size of the fluoride anion; this also leads to differing N–Ln–N angles (3-Sm: 128.24(7)°; 3-Tm: 129.39(5)°; 3-Yb: 138.71(9)°). The mean Sm–N bond length of 3-Sm (2.306(3) Å) is significantly longer than the mean Ln–N bond lengths of 3-Tm (2.229(3) Å) and 3-Yb (2.231(4) Å), which corresponds with earlier Ln3+ ions being larger.1 The Ln–N bond lengths in 3-Ln are longer than those in 2-Ln, as expected from increasing the formal coordination number from two to three. Finally, as with 2-Ln the coordination spheres of the Ln3+ centres of 3-Ln are completed by multiple electrostatic contacts with methine and methyl groups. These are also likely to arise from Ln⋯Cγ–Siβ agostic-type interactions, though in 3-Ln there are fewer, and the Tm⋯C/H/Si distances are generally longer due to the presence of a halide [e.g. for 3-Tm: range three Tm⋯C: 2.874(2)–3.261(2) Å; range three Tm⋯H: 2.324–2.467 Å; range three Tm⋯Si: 3.195(2)–3.354(2) Å; mean three β-Si–C: 1.928(3) Å; range other Si–C: 1.899(2)–1.913(2) Å].
UV-vis-NIR spectroscopy
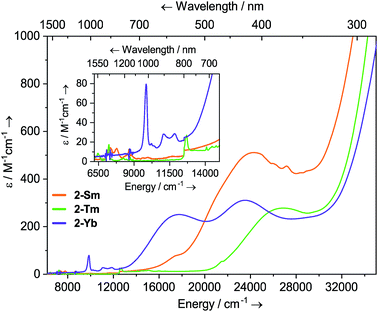
Dilute solutions of 2-Sm, 2-Tm and 2-Yb in DCM are pale red, green and purple, respectively, and their electronic absorption spectra are dominated by strong ligand to metal charge transfer bands tailing in from the UV region (Fig. 2 and ESI Fig. S19–S21†). Complex 2-Sm (4f5) exhibits the most intense absorption in the visible region [λmax = 411 nm (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1), ε = 511 M−1 cm−1], whilst 2-Tm and 2-Yb exhibit weaker visible absorptions [2-Tm; λmax = 373 nm (26
300 cm−1), ε = 511 M−1 cm−1], whilst 2-Tm and 2-Yb exhibit weaker visible absorptions [2-Tm; λmax = 373 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1), ε = 275 M−1 cm−1; 2-Yb: λmax = 425 nm (23
800 cm−1), ε = 275 M−1 cm−1; 2-Yb: λmax = 425 nm (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1), ε = 309 M−1 cm−1, λmax = 563 nm (17
500 cm−1), ε = 309 M−1 cm−1, λmax = 563 nm (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1), ε = 249 M−1 cm−1]. Weak absorptions (ε < 100 mol−1 dm3 cm−1) were seen for all 2-Ln in the near-IR region, corresponding to Laporte-forbidden f–f transitions:12-Sm shows absorptions at λmax = 1370 nm (7300 cm−1), ε = 14 M−1 cm−1 and 1285 nm (7782 cm−1), ε = 13 M−1 cm−1, which arise due to 6H5/2 → 6FJ transitions; 2-Tm shows absorptions at λmax = 1549 nm (6456 cm−1), ε = 6 M−1 cm−1 and λmax = 1383 nm (7230 cm−1), ε = 15 M−1 cm−1 which arise due to ligand field-split 3H6 → 3H4 transitions; 2-Yb has a broad feature at λmax = 1015 nm (9552 cm−1), ε = 77 M−1 cm−1 and two weaker absorptions at λmax = 904 nm (11
800 cm−1), ε = 249 M−1 cm−1]. Weak absorptions (ε < 100 mol−1 dm3 cm−1) were seen for all 2-Ln in the near-IR region, corresponding to Laporte-forbidden f–f transitions:12-Sm shows absorptions at λmax = 1370 nm (7300 cm−1), ε = 14 M−1 cm−1 and 1285 nm (7782 cm−1), ε = 13 M−1 cm−1, which arise due to 6H5/2 → 6FJ transitions; 2-Tm shows absorptions at λmax = 1549 nm (6456 cm−1), ε = 6 M−1 cm−1 and λmax = 1383 nm (7230 cm−1), ε = 15 M−1 cm−1 which arise due to ligand field-split 3H6 → 3H4 transitions; 2-Yb has a broad feature at λmax = 1015 nm (9552 cm−1), ε = 77 M−1 cm−1 and two weaker absorptions at λmax = 904 nm (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 cm−1), ε = 26 M−1 cm−1 and λmax = 844 nm (11
061 cm−1), ε = 26 M−1 cm−1 and λmax = 844 nm (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 cm−1), ε = 27 M−1 cm−1 which correspond to 2F7/2 → 2F5/2 transitions, showing the ligand field splitting in the excited 2F5/2 term. These absorptions are moderately strong for f–f transitions because they are all spin-allowed (ε < 200 M−1 cm−1).1 The spectral pattern of one intense absorption and two weaker absorptions of approximately equal intensity at higher energy for the 2F7/2 → 2F5/2 manifold is a common feature for Yb3+ complexes; Da Re et al.50 and Denning et al.51 have discussed these transitions in considerable detail previously.
840 cm−1), ε = 27 M−1 cm−1 which correspond to 2F7/2 → 2F5/2 transitions, showing the ligand field splitting in the excited 2F5/2 term. These absorptions are moderately strong for f–f transitions because they are all spin-allowed (ε < 200 M−1 cm−1).1 The spectral pattern of one intense absorption and two weaker absorptions of approximately equal intensity at higher energy for the 2F7/2 → 2F5/2 manifold is a common feature for Yb3+ complexes; Da Re et al.50 and Denning et al.51 have discussed these transitions in considerable detail previously.
Solutions of 3-Sm, 3-Tm and 3-Yb are pale yellow, green and red, respectively, and as with 2-Ln their absorption spectra, are dominated by ligand to metal charge transfer bands tailing in from the UV region (Fig. 3, ESI Fig. S22 and S23† and ref. 36) [3-Sm: λmax = 376 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595 cm−1), ε = 713 M−1 cm−1; 3-Tm: λmax = 327 nm (30
595 cm−1), ε = 713 M−1 cm−1; 3-Tm: λmax = 327 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 581 cm−1), ε = 378 M−1 cm−1; 3-Yb: λmax = 418 nm (23
581 cm−1), ε = 378 M−1 cm−1; 3-Yb: λmax = 418 nm (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 cm−1), ε = 250 M−1 cm−1, λmax = 326 nm (30
923 cm−1), ε = 250 M−1 cm−1, λmax = 326 nm (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 cm−1), ε = 99 M−1 cm−1]. In the near IR region f–f absorptions are observed for all complexes; 3-Sm exhibits three main peaks at
674 cm−1), ε = 99 M−1 cm−1]. In the near IR region f–f absorptions are observed for all complexes; 3-Sm exhibits three main peaks at ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 7246, 7710 and 8439 cm−1 due to 6H5/2 → 6FJ transitions, however there appear to be numerous weaker transitions. Complex 3-Tm shows two main absorptions at λmax = 1506 nm (6640 cm−1), ε = 47 M−1 cm−1 and λmax = 777 nm (12
7246, 7710 and 8439 cm−1 due to 6H5/2 → 6FJ transitions, however there appear to be numerous weaker transitions. Complex 3-Tm shows two main absorptions at λmax = 1506 nm (6640 cm−1), ε = 47 M−1 cm−1 and λmax = 777 nm (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 cm−1), ε = 86 M−1 cm−1, corresponding to 3H6 → 3H4 and 3H6 → 3F4 transitions, however again these are structured due to ligand field splitting. Complex 3-Yb displays two absorptions at λmax = 973 nm (10
870 cm−1), ε = 86 M−1 cm−1, corresponding to 3H6 → 3H4 and 3H6 → 3F4 transitions, however again these are structured due to ligand field splitting. Complex 3-Yb displays two absorptions at λmax = 973 nm (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 cm−1), ε = 22 M−1 cm−1 and λmax = 860 nm (11
277 cm−1), ε = 22 M−1 cm−1 and λmax = 860 nm (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 627 cm−1), ε = 17 M−1 cm−1 corresponding to ligand field-split 2F7/2 → 2F5/2 transitions. The f–f transitions are at higher energy for 3-Ln, presumably due to stronger ligand fields; this is most clear for the Yb pair, where for 2-Yb the lowest energy transition is at 9500 cm−1, whilst this is seen at 10
627 cm−1), ε = 17 M−1 cm−1 corresponding to ligand field-split 2F7/2 → 2F5/2 transitions. The f–f transitions are at higher energy for 3-Ln, presumably due to stronger ligand fields; this is most clear for the Yb pair, where for 2-Yb the lowest energy transition is at 9500 cm−1, whilst this is seen at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 for 3-Yb.
200 cm−1 for 3-Yb.
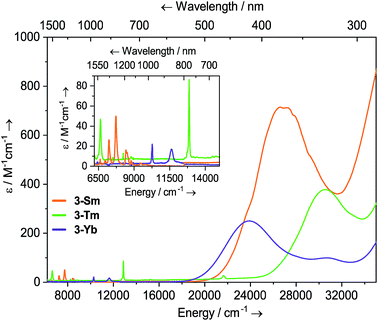 | ||
Fig. 3 Room temperature UV-vis-NIR spectra of 3-Ln (1 mM in THF) from 6200–35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. For 3-Sm, an empirical absorption correction of ε + 1.9 mol−1 dm3 cm−1 has been applied. 000 cm−1. For 3-Sm, an empirical absorption correction of ε + 1.9 mol−1 dm3 cm−1 has been applied. | ||
Magnetism and EPR spectroscopy
Linear and trigonal-planar environments should stabilize oblate- and prolate-spheroid electron density distributions, respectively, along the axis of quantization.2–5 This should then stabilize either the minimum or maximum |mJ| sublevels of the 2S+1LJ Russell Saunders ground term depending on the 4fn configuration.2–5 The ions studied here are 4f5 (Sm3+), 4f12 (Tm3+) and 4f13 (Tm2+, Yb3+) and in each case the electron density distribution in the maximum |mJ| states is prolate, hence an ideal linear geometry at Ln should give the minimum |mJ| = ±1/2 (Kramers) or 0 (non-Kramers) ground sublevels, along with easy-plane magnetic anisotropy. Correspondingly, ideal trigonal-planar geometry at Ln should give the maximum |mJ| = J ground levels and easy-axis magnetic anisotropy. These states can be probed by magnetometry and EPR spectroscopy. Room temperature solution phase magnetic moments (where χ is the molar magnetic susceptibility, T is the temperature) for 2-Ln and 3-Ln determined by the Evans method52 are in good agreement with those from solid-state SQUID magnetometry (Table 2 and ESI Fig. S24–S35†). We present the magnetic data for 2-Ln and 3-Ln pairs for each Ln3+ ion in turn.Complexes 2-Yb and 3-Yb have room temperature χT values of 1.98 and 1.93 cm3 mol−1 K, respectively (ESI Fig. S29 and S35†): these are lower than the free-ion 4f13 2F7/2 value due to substantial crystal field effects, as supported by CASSCF-SO calculations which gives the total spread of the J = 7/2 term approaching 2000 cm−1 (ESI Table S3†). The same is true for the isoelectronic 4f13 Tm2+ analogue 1-Tm.35 For 2-Yb and 3-YbχT decreases slowly on cooling, reaching 1.3 and 1.6 cm3 mol−1 K, respectively, at 2 K. At 2 K and 7 T, 2-Yb and 3-Yb reach saturation magnetizations of 1.80 and 1.84 μB, respectively, and the temperature dependence of the traces indicates isolated Kramers doublet ground states as expected (ESI Fig. S28 and S34†).35
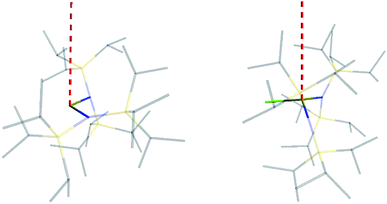
The similar properties of 2-Yb and 3-Yb were confirmed by low-temperature EPR spectroscopy (Fig. 4 and Table 3): solid 2-Yb has near-axial g-values of g1 = 6.80, g2 = 1.46 and g3 = 1.09, whilst solid 3-Yb gives g1 = 7.11 with g2,3 not observed but ≪1. Approximating g1 = g‖ and g2,3 = g⊥, this g‖ ≫ g⊥ pattern clearly demonstrates easy-axis magnetic anisotropy, consistent with a high |mJ| ground state doublet (the pure ±7/2 doublet would have g‖, g⊥ = 8.0, 0). This is expected for trigonal planar 3-Yb, but not for 2-Yb which has only two N-donors that we would expect to stabilize the low |mJ| doublet. Hence, for 2-Yb it appears that the N–Yb–N angle has sufficiently deviated from linearity such that the crystal field is still quantized along the axis normal to the YbN2 plane despite the loss of the in-plane fluoride from 3-Yb. Clearly this result is very different from the easy-plane isoelectronic near-linear Tm2+ compound 1-Tm (Fig. 4a). To further probe this finding, we examined the EPR spectra of the Yb3+ compounds in solution. EPR spectra of a frozen solution of 3-Yb is very similar to the solid state, with g1 = 7.51 (g2,3 not observed), however, a frozen solution of 2-Yb gives g1 = 4.38, g2 = 3.99 and g3 = 1.21 (Fig. 4), which unambiguously shows that there has been a switch to easy-plane anisotropy (now approximate g1,2 = g⊥ and g3 = g‖) as the g‖ ≪ g⊥ pattern indicates stabilization of a low |mJ| doublet (the pure ±1/2 doublet would have g‖, g⊥ = 1.14, 4.17).53 Thus, the structure of 2-Yb must relax in solution such that the N–Yb–N angle opens up and there is a flip of the orientation of the axis of quantization from being normal to the YbN2 plane to lying along the N⋯N direction. This is supported by CASSCF-SO results based on the crystal structures: these give ground Kramers doublet g1 = 7.12, g2 = 1.14 and g3 = 0.55 for 2-Yb, and g1 = 7.90, g2 = 0.10 and g3 = 0.07 for 3-Yb (Table 3), with g1 (g‖, defining the axis of quantization) oriented normal to the YbN2(F) plane (Fig. 5). The ground doublet is 99% |mJ| = 7/2 in character for 3-Yb, and slightly more mixed at 85% |mJ| = 7/2 for 2-Yb due to the competing components of the crystal field (ESI Table S3†).
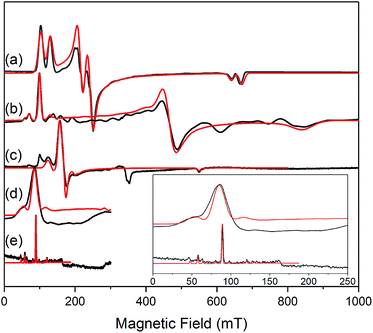 | ||
| Fig. 4 c.w. X-band EPR spectra. (a) 1-Tm as a powder at 10 K;35 (b) 2-Yb as a powder (in eicosane) at 10 K; (c) 2-Yb in 1 mM DCM solution at 10 K (the feature at 320 mT is a background signal); (d) 3-Yb as a powder (in eicosane) at 10 K; (e) 3-Yb in 1 mM DCM solution at 10 K. Insert shows an expansion of the low field region of (d) and (e); these spectra are truncated as there are no features arising from 3-Yb at higher fields. Experimental spectra are in black, simulations are in red. | ||
| Complex | N–Ln–N/° | Calculated g-values | Measured g-values | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Solid state | Frozen solution | |||||||||
| g 1 | g 2 | g 3 | g 1 | g 2 | g 3 | g 1 | g 2 | g 3 | ||
| 1-Tm 35 | 166.89(6) | 5.49 | 3.60 | 1.15 | 5.71 | 2.92 | 1.01 | 5.71 | 2.92 | 1.01 |
| 2-Yb | 127.7(2) | 7.12 | 1.14 | 0.55 | 6.80 | 1.46 | 1.09 | 4.38 | 3.99 | 1.21 |
| 3-Yb | 138.71(9) | 7.90 | 0.10 | 0.07 | 7.11 | — | — | 7.51 | — | — |
Complex 2-Tm has a χT value of 6.86 cm3 mol−1 K at 300 K, in good agreement with the free-ion 4f12 3H6 value. χT decreases rapidly with decreasing temperature due to depopulation effects within the multiplet, reaching ca. 0.8 cm3 K mol−1 at 2 K (ESI Fig. S27†). M(H) curves measured at 2 and 4 K are superimposable and fail to saturate (ESI Fig. S26†), suggesting a singlet non-magnetic ground state for this non-Kramers system. CASSCF-SO calculations, performed on the two crystallographically non-equivalent molecules in the unit cell of 2-Tm, confirm this, giving a singlet ground state which is separated from the first excited level by ca. 14.5 cm−1 (average for two independent molecules, ESI Table S3†). Magnetic data for 3-Tm are markedly different: χT (6.31 cm3 mol−1 K at 300 K) only decreases slowly on cooling, reaching 5.48 cm3 mol−1 K at 2 K (ESI Fig. S33†), and M(H) at 2 and 4 K saturate at 3.3 μB above ca. 4 T (ESI Fig. S32†); this is direct evidence of a pseudo-doublet magnetic ground state. Indeed, CASSCF-SO calculations give a ground state pseudo-doublet for 3-Tm with an intra-doublet gap of only 0.13 cm−1. The pseudo-doublet wave functions are mixtures of mJ = +6 and −6, which resolve into a pure mJ = +6 and mJ = −6 pair (98% purity) in a small applied magnetic field (ESI Table S5 and S6†). These results are supported by EPR spectroscopy of 2-Tm and 3-Tm in the solid state. We find that 2-Tm is EPR silent at 5 K (ESI Fig. S37†), consistent with the magnetic data and as predicted by CASSCF-SO, whilst 3-Tm has a near-zero-field EPR transition at X-band (ca. 9.39 GHz; ESI Fig. S38†) indicating a zero-field splitting between the pseudo-doublet states of ca. 0.3 cm−1, in excellent agreement with magnetometry and CASSCF-SO.
For 2-Sm and 3-Sm the room temperature χT products are 0.23 and 0.24 cm3 mol−1 K, respectively, higher than the free-ion value for the 4f5 6H5/2 multiplet (ESI Fig. S25 and S31).† This is indicative of low-lying, thermally accessible excited states as is commonly observed for Sm3+ (the 6H7/2 term lies at only ca. 1000 cm−1).54 On cooling, χT steadily decreases to 0.05 and 0.02 cm3 mol−1 K, respectively, at 2 K. For both 2-Sm and 3-Sm, the molar magnetization (M) at low temperatures fails to saturate as a function of applied magnetic field (H), reaching ca. 0.08 and 0.16 μB, respectively, at 2 K and 7 T (ESI Fig. S24 and S30†). In both cases, the traces for 2 and 4 K are distinct. These data are consistent with low magnetic moment Kramers doublet ground states. The 6H5/2 ground term has a low Landé factor of gJ = 2/7, hence the effective g-factors for all the Kramers doublets are low. The extreme cases of pure |mJ| = 1/2 and 5/2 doublets would have g‖, g⊥ = 0.29, 0.86 and 1.43, 0, respectively, and these would give rather similar and low magnetic moments for powders. Unfortunately, we were unable to obtain reliable EPR spectra for 2-Sm or 3-Sm. CASSCF-SO calculations give a reasonable agreement with the experimental χT(T) and M(H) curves for both 2-Sm and 3-Sm (ESI Fig. S24, S25 and S31†) and indicate that the ground state g-tensor for 2-Sm is strongly rhombic, whereas in the case of 3-Sm the main magnetic axis is perpendicular to the N2(Cl) plane with strongly easy-axis character.
Comparing 2-Yb with isoelectronic 1-Tm, the N–Ln–N angle in 1-Tm is much closer to linear at 166.89(6)° [cf. 127.7(2)° for 2-Yb] and it has easy-plane magnetic anisotropy as shown by EPR spectroscopy in both solid and frozen solution state with g1 = 5.6, g2 = 3.0 and g3 = 1.0.35 CASSCF-SO calculations for the crystal structure of 1-Tm give g1 = 5.49, g2 = 3.60 and g3 = 1.15, with g3 oriented along the N–Tm–N direction, resulting from a 99% pure |mJ| = 1/2 ground doublet.35 In order to test the importance of the identity of the metal ion vs. the N–Ln–N angle, we performed further CASSCF-SO calculations on the structure of 1-Tm [N–Ln–N 166.89(6)°] where we substitute Yb3+ in place of Tm2+, and on the structure of 2-Yb [N–Yb–N 127.7(2)°] where we substitute Tm2+ in place of Yb3+ (note the change in ion charge to maintain an f13 configuration in both cases). We find the former to have an |mJ| = 1/2 ground doublet (g1 = 5.34, g2 = 3.67, g3 = 1.16), and the latter to have an |mJ| = 7/2 ground doublet (g1 = 6.76, g2 = 1.97, g3 = 0.82): thus, it is the structure that dictates these differing properties for f13 configurations and it is not due to the identity of the metal ion. Nocton and co-workers have recently made similar observations for isoelectronic f13 Tm2+ and Yb3+ 18-crown-6 complexes.55 Whilst such reasoning is logical, it is not a phenomenon that has been observed frequently with real-world chemical systems.
Ab initio calculations
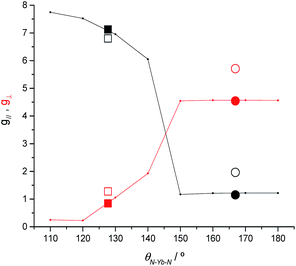
To clarify the dependence of the magnetic anisotropy on the N–Ln–N angle in 2-Yb we have carried out a systematic ab initio investigation. CASSCF-SO calculations have been performed on model structures based on the experimental structure of 2-Yb in which the N–Ln–N angle has been varied between 180° and 110°. The calculated g-values of the ground Kramers doublet of Yb3+ show a clear dependence of the type of magnetic anisotropy on the N–Ln–N angle, with the switching point located between 140° and 150° (Fig. 6): easy-axis-like (g1 > g2,3; g‖ > g⊥) for N–Ln–N angles <140° and easy-plane-like (g3 < g1,2; g‖ < g⊥) for angles> 150°. This implies that there must be a significant structural change in the N–Yb–N angle of 2-Yb in the solution phase, becoming at least 150°. Optimization of the structure of 2-Yb in the gas phase using density-functional theory (DFT) shows an increase in the N–Yb–N angle from 127 to 133° (ESI Table S13†). This indicates that the molecule tends to become more linear when removed from the solid state, suggesting that interactions with solvent molecules (absent in our gas phase calculations) stabilize larger N–Yb–N angles.We have conducted the same angular-dependent study of the electronic structure of 2-Tm as for 2-Yb. The N–Tm–N angle has been varied between 180° and 120° (ESI Fig. S36†). Our results show that there is also a characteristic change in electronic structure for f122-Tm: above 160° the singlet ground state is mainly a mixture of mJ = +1 and −1 functions, while below 150° the ground state is dominated by the mJ = 0 function (ESI Fig. S36†). The quantization axis in all cases is the direction that bisects the N–Tm–N angle; given the low symmetry of the complex and the fact that the molecule is neither linear nor trigonal this is not surprising. Therefore, the change in electronic structure from 2-Tm to 3-Tm appears to be in agreement with electron density arguments: the trigonal-planar coordination environment of 3-Tm stabilizes a prolate ground pseudo-doublet with maximum |mJ| where the quantization axis is normal to the trigonal plane, whilst the two-coordinate environment of 2-Tm stabilizes an oblate singlet state dominated by mJ = 0; however in the latter case, far from being linear with a N–Tm–N angle of 125.49(9)°, the axis of quantization bisects the N–Tm–N angle and thus does not follow simple electron density arguments.
To examine the impact of the Ln⋯Cγ–Siβ agostic-type interactions on the electronic structure of the Yb3+ ion in 2-Yb, we have performed a CASSCF-SO calculation on a model complex where the ligands have been trimmed to {N(SiH3)2}, thus removing the Ln⋯C and Ln⋯H electrostatic contacts; these calculations reveal changes of <10% to the SO energy levels (ESI Table S10†) and a slight increase in axiality of the ground Kramers doublet (ESI Table S11†) compared to 2-Yb. Although we cannot rule out changes to the N-donor strength for the trimmed ligand versus {N(SiiPr3)2}, these results suggest that the Ln⋯Cγ–Siβ agostic-type interactions have only a slight influence on the electronic structure at the Yb(III) site and that they are far weaker than the Ln–N coordination bonds that dominate the electronic structure.
Finally, as this study was driven by our attempts to isolate a near-linear two-coordinate Dy3+ complex, it is relevant to predict what the SMM properties of such a material could be now that we are far closer to a representative material with 2-Tm and 2-Yb, than in the previously reported near-linear 1-Sm.14 Hence, we have performed CASSCF-SO calculations using the molecular geometry of 2-Tm where Tm3+ has been replaced with Dy3+. As predicted based on simple model compounds,12 even this bent geometry with a N–Dy–N angle of 125.49(9)° and equatorial agostic interactions can produce a very high barrier to magnetic relaxation of ca. 1300–1400 cm−1 (ESI Fig. S39 and Table S12†), and thus bent two-coordinate Dy3+ complexes of the type presented here are still exciting synthetic targets.
Conclusions
The preference for bent geometries in [Ln{N(SiiPr3)3}2]+ cations can be accredited to the formation of multiple electrostatic contacts between the highly Lewis acidic Ln3+ ions and the electron density associated with the ligand σ-bonding network, together with dipole stabilization, crystal packing forces and dispersion force interactions. By a combination of magnetic studies, EPR spectroscopy and ab initio calculations we have deduced the electronic structures of the bent Ln3+ cations. Interestingly, in the solid state [Yb{N(SiiPr3)3}2]+ expresses a similar crystal field to its three-coordinate precursor, rather than the axial crystal field that would be predicted for a two-coordinate complex. EPR spectroscopy shows that [Yb{N(SiiPr3)3}2]+ switches to an axial crystal field in solution, indicating that the N–Ln–N angle is less bent in the solution phase. The electronic structures of these bent Ln3+ cations are therefore sensitive to changes in molecular geometry.Our synthetic results show that axial Dy3+ complexes such as [Dy{N(SiiPr3)2}2]+, proposed as SMMs with large energy magnetization reversal barriers,14 are feasible chemical targets, whilst our electronic structure results show that the physical properties of target complexes for the SMM community are not trivially predictable. As a bent [Dy{N(SiiPr3)2}2]+ cation is predicted to show a lower effective barrier to magnetic reversal than a linear analogue, it would be of benefit to be able to predict what ligand systems would provide two-coordinate Dy3+ complexes that are less bent. Although the [Ln{N(SiiPr3)2}2]+ framework is of sufficient steric bulk, a linear geometry is not enforced as the coordination sphere is flexible enough to be rearranged to increase the strength of ligand–metal electrostatic and ligand–ligand London dipole interactions. Given that recently isolated linear Dy2+ and Tb2+ metallocene systems have been proposed to exhibit significant s–d mixing,22 it can be inferenced that combining electronic stabilization with similarly bulky but more rigid ligand frameworks may be a useful strategy in the future pursuit of linear two-coordinate Ln3+ complexes.
Experimental
Materials and methods
All manipulations were conducted under argon with the strict exclusion of oxygen and water by using Schlenk line and glove box techniques. Toluene, benzene and hexane were dried by refluxing over potassium and were stored over potassium mirrors. Dichloromethane (DCM) was dried over CaH2 and was stored over 4 Å molecular sieves. All solvents were degassed before use. For NMR spectroscopy C6D6 was dried by refluxing over K and CD2Cl2 was dried by refluxing over CaH2. Both NMR solvents were vacuum transferred and degassed by three freeze–pump–thaw cycles before use. 1-Ln,14,35 [H(SiEt3)2][B(C6F5)4]21a and 3-Sm36 were prepared according to literature methods.1H (400 MHz), 13C{1H} (100 MHz and 125 MHz), 13C{19F} (126 MHz), 11B{1H} (128 MHz) and 19F{1H} (376 MHz) NMR spectra were obtained on an Avance III 400 MHz or 500 MHz spectrometer at 298 K. These were referenced to the solvent used, or to external TMS (1H, 13C), H3BO3/D2O (11B) or C7H5F3/CDCl3 (19F). UV-vis-NIR spectroscopy was performed on samples in Youngs tap-appended 10 mm path length quartz cuvettes on an Agilent Technologies Cary Series UV-vis-NIR Spectrophotometer from 175–3300 nm. FTIR spectra were variously recorded as Nujol mulls in KBr discs on a PerkinElmer Spectrum RX1 spectrometer or as microcrystalline powders using a Bruker Tensor 27 ATR-Fourier Transform Infrared (ATR-FTIR) spectrometer. EPR spectroscopic measurements were performed at X-band using a Bruker super-high-Q X-band resonator attached to a Bruker EMX bridge, on solid state and frozen solution samples contained in flame-sealed quartz EPR tubes. Elemental analysis was carried out by Mr Martin Jennings and Mrs Anne Davies at the Microanalytical service, School of Chemistry, the University of Manchester. Elemental analysis results for 2-Yb reproducibly gave low carbon values; this has consistently been seen for {N(SiiPr3)2} complexes and we have previously attributed this observation to the formation of carbides from incomplete combustion.14,35,36,56 However, all other analytical data obtained are consistent with the bulk purity of 2-Ln and 3-Ln.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the UK Engineering and Physical Sciences Research Council (EPSRC) (EP/N007034/1 for M. V., EP/K039547/1 for a single crystal X-ray diffractometer, EP/P002560/1 for consumables, a DTG studentship for H. M. N. and a Doctoral Prize Fellowship for C. A. P. G.), and the University of Manchester for funding this work. We acknowledge the EPSRC UK National Electron Paramagnetic Resonance Service for access to the EPR facility and the SQUID magnetometer, and the University of Manchester (Fellowship for N. F. C.) for access to the Computational Shared Facility. We thank the peer reviewers for constructive comments. We also thank Mr Adam Brookfield and Dr Amga Baldansuren for assistance with EPR spectroscopy and Dr Fabrizio Ortu for assistance with single crystal XRD. Research data files supporting this publication are available from Mendeley Data at doi: 10.17632/fh245wm5nj.1.Notes and references
- The Rare Earth Elements: Fundamentals and Applications, ed. D. A. Atwood, Wiley, Chichester, 2012 Search PubMed.
- D. Gatteschi and C. Benelli, Introduction to Molecular Magnetism, Wiley-VCH, Berlin, 2015 Search PubMed.
- Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-VCH, Berlin, 2015 Search PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC.
- Luminescence of Lanthanide Ions in Coordination Compounds and Nanomaterials, ed. A. de Bettencourt-Dias, John Wiley and Sons Ltd., London, 2014 Search PubMed.
- J.-C. G. Bünzli, J. Coord. Chem., 2014, 67, 3706 CrossRef.
- F. Ortu and D. P. Mills, Chapter 306 - Low Coordinate Rare Earth and Actinide Complexes, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier B. V., Amsterdam, 2019,55, p. 1 Search PubMed.
- J.-C. G. Bünzli and C. Piguet, Chem. Soc. Rev., 2005, 34, 1048 RSC.
- M. Shibasaki and N. Yoshikawa, Chem. Rev., 2002, 102, 2187 CrossRef CAS PubMed.
- Y.-S. Meng, L. Xu, J. Xiong, Q. Yuan, T. Liu, B.-W. Wang and S. Gao, Angew. Chem., Int. Ed., 2018, 57, 4673 CrossRef CAS PubMed.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086 RSC.
- N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101 RSC.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS.
- C. A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714 CrossRef CAS.
- C. A. P. Goodwin, D. Reta, F. Ortu, J. Liu, N. F. Chilton and D. P. Mills, Chem. Commun., 2018, 54, 9182 RSC.
- J. Liu, D. Reta, J. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem.–Eur. J., 2019, 25, 7749 CAS.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492 RSC.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400 CrossRef CAS PubMed.
- (a) J. B. Lambert, L. Lin and S. Keinan, Org. Biomol. Chem., 2003, 1, 2559 RSC; (b) E. S. Stoyanov, I. V. Stoyanova and C. A. Reed, Chem.–Eur. J., 2008, 14, 7880 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, J. Yu, T. J. Groshens, F. Furche, J. R. Long and B. G. Harvey, J. Am. Chem. Soc., 2019, 141, 12967 CrossRef CAS PubMed.
- D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Chem. Commun., 1972, 349 RSC.
- D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Dalton Trans., 1973, 1021 RSC.
- D. P. Mills and S. T. Liddle, Ligand Design in Modern Lanthanide Chemistry, in Ligand Design in Metal Chemistry: Reactivity and Catalysis, ed. M. Stradiotto and R. J. Lundgren, John Wiley & Sons Ltd., Hoboken, 2016, pp. 330–363 Search PubMed.
- C. A. P. Goodwin and D. P. Mills, Silylamides: towards a half-century of stabilising remarkable f-element chemistry, in Specialist Periodical Reports, Organometallic Chemistry: Volume 41, ed. I. Fairlamb, J. M. Lynam, N. J. Patmore and P. Elliott, Royal Society of Chemistry, Cambridge, 2017, pp. 123–156 Search PubMed.
- M. Niemeyer, Eur. J. Inorg. Chem., 2001, 1969 CrossRef CAS.
- A. Cofone and M. A. Niemeyer, Z. Anorg. Allg. Chem., 2006, 632, 1930 CrossRef CAS.
- I. V. Basalov, O. S. Yurova, A. V. Cherkasov, G. K. Fukin and A. A. Trifonov, Inorg. Chem., 2016, 55, 1236 CrossRef CAS PubMed.
- C. N. de Bruin-Dickason, A. J. Boutland, D. Dange, G. B. Deacon and C. Jones, Dalton Trans., 2018, 47, 9512 RSC.
- P. Zhao, Q. Zhu, J. C. Fettinger and P. P. Power, Inorg. Chem., 2018, 57, 14044 CrossRef CAS.
- C. Eaborn, P. B. Hitchcock, K. Izod and J. D. Smith, J. Am. Chem. Soc., 1994, 116, 12071 CrossRef CAS.
- C. Eaborn, P. B. Hitchcock, K. Izod, Z.-R. Lu and J. D. Smith, Organometallics, 1996, 15, 4783 CrossRef CAS.
- G. Qi, Y. Nitto, A. Saiki, T. Tomohiro, Y. Nakayama and H. Yasuda, Tetrahedron, 2003, 59, 10409 CrossRef CAS.
- C. A. P. Goodwin, N. F. Chilton, G. F. Vettese, E. Moreno Pineda, I. F. Crowe, J. W. Ziller, R. E. P. Winpenny, W. J. Evans and D. P. Mills, Inorg. Chem., 2016, 55, 10057 CrossRef CAS.
- C. A. P. Goodwin, B. L. L. Réant, J. G. C. Kragskow, I. M. DiMucci, K. M. Lancaster, D. P. Mills and S. Sproules, Dalton Trans., 2018, 47, 10613 RSC.
- J. Sievers, Z. Phys. B: Condens. Matter Quanta, 1982, 45, 289 CrossRef CAS.
- A. M. Bienfait, B. M. Wolf, K. W. Törnroos and R. Anwander, Inorg. Chem., 2018, 57, 5204 CrossRef CAS PubMed.
- L. J. Nugent, R. D. Baybarz, J. L. Burnett and J. L. Ryan, J. Phys. Chem., 1973, 77, 1528 CrossRef CAS.
- J. B. Lambert, S. Zhang and S. M. Ciro, Organometallics, 1994, 13, 2430 CrossRef CAS.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, NMR of Paramagnetic Molecules: Applications to Metallobiomolecules and Models, Elsevier B. V., Amsterdam, 2nd edn, 2015, pp. 255–276 Search PubMed.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1 CrossRef CAS.
- (a) J. L. Stewart and R. A. Andersen, Polyhedron, 1998, 17, 953 CrossRef CAS; (b) S. M. Mansell, B. F. Perandones and P. L. Arnold, J. Organomet. Chem., 2010, 695, 2814 CrossRef CAS.
- D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 0004 CrossRef.
- E. K. Brady, D. L. Clark, J. C. Gordon, P. J. Hay, D. W. Keogh, R. Poli, B. L. Scott and J. G. Watkin, Inorg. Chem., 2003, 42, 6682 CrossRef CAS PubMed.
- L. Perrin, L. Maron, O. Eisenstein and M. F. Lappert, New J. Chem., 2003, 27, 121 RSC.
- D. L. Clark, J. C. Gordon, P. J. Hay, R. L. Martin and R. Poli, Organometallics, 2002, 21, 5000 CrossRef CAS.
- L. Maron and O. Eisenstein, New J. Chem., 2001, 25, 255 RSC.
- IUPAC, Compendium of Chemical Terminology, ed. A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford, 2nd edn, (“the gold book”), 1997 Search PubMed.
- R. E. Da Re, C. J. Kuehl, M. G. Brown, R. C. Rocha, E. D. Bauer, K. D. John, D. E. Morris, A. P. Shreve and J. L. Sarrao, Inorg. Chem., 2003, 42, 5551 CrossRef CAS PubMed.
- R. G. Denning, J. Harmer, J. C. Green and M. Irwin, J. Am. Chem. Soc., 2011, 133, 20644 CrossRef CAS PubMed.
- S. K. Sur, J. Magn. Reson., 1989, 82, 169 CAS.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970 Search PubMed.
- J. H. Van Vleck, The Theory of Electric and Magnetic Susceptibility, Oxford University Press, Oxford, 1932 Search PubMed.
- M. Xémard, M. Cordier, F. Molton, C. Duboc, B. Le Guennic, O. Maury, O. Cador and G. Nocton, Inorg. Chem., 2019, 58, 2872 CrossRef PubMed.
- H. M. Nicholas, C. A. P. Goodwin, J. G. C. Kragskow, S. J. Lockyer and D. P. Mills, Molecules, 2018, 23, 1138 CrossRef PubMed , and references cited therein.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1880942–1880946. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc03431e |
| This journal is © The Royal Society of Chemistry 2019 |