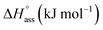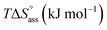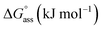Open Access Article
Open Access ArticleThermodynamic insights into the entropically driven self-assembly of amphiphilic dyes in water†
Pradeep P. N.
Syamala
 ab,
Bartolome
Soberats
ab,
Bartolome
Soberats
 b,
Daniel
Görl
b,
Daniel
Görl
 b,
Stephan
Gekle
b,
Stephan
Gekle
 *c and
Frank
Würthner
*c and
Frank
Würthner
 *ab
*ab
aUniversität Würzburg, Institut für Organische Chemie, Am Hubland, 97074 Würzburg, Germany. E-mail: wuerthner@uni-wuerzburg.de
bCenter for Nanosystems Chemistry & Bavarian Polymer Institute (BPI), Universität Würzburg, Theodor-Boveri-Weg, 97074 Würzburg, Germany
cUniversität Bayreuth, Biofluid Simulation and Modeling, Theoretische Physik VI & Bavarian Polymer Institute (BPI), 95440 Bayreuth, Germany. E-mail: stephan.gekle@uni-bayreuth.de
First published on 20th August 2019
Abstract
Self-assembly of amphiphilic dyes and π-systems are more difficult to understand and to control in water compared to organic solvents due to the hydrophobic effect. Herein, we elucidate in detail the self-assembly of a series of archetype bolaamphiphiles bearing a naphthalene bisimide (NBI) π-core with appended oligoethylene glycol (OEG) dendrons of different size. By utilizing temperature-dependent UV-vis spectroscopy and isothermal titration calorimetry (ITC), we have dissected the enthalpic and entropic parameters pertaining to the molecules' self-assembly. All investigated compounds show an enthalpically disfavored aggregation process leading to aggregate growth and eventually precipitation at elevated temperature, which is attributed to the dehydration of oligoethylene glycol units and their concomitant conformational changes. Back-folded conformation of the side chains plays a major role, as revealed by molecular dynamics (MD) and two dimensional NMR (2D NMR) studies, in directing the association. The sterical effect imparted by the jacketing of monomers and dimers also changes the aggregation mechanism from isodesmic to weakly anti-cooperative.
Introduction
Self-assembled nano- and mesoscale structures play a major role in nature and particularly in living organisms.1–4 The sophisticated functionalities of these structures is imputable to the interplay of hydrogen bonds (H-bonds)5 as well as solvophobic effects,6 derived to the unique role of water as a solvent.4,7 The desire to mimic and understand such naturally occurring self-assembled systems has prompted the investigation of various amphiphilic/bolaamphiphilic molecules consisting of non-polar hydrophobic cores attached with water solubilizing side chains.8 Through these investigations, a wide variety of nanometric supramolecular aggregates of different morphologies (tubular, fibrillar, micellar, vesicular) has been prepared via exploring solvophobic effects,9–11 H-bonding,12–15 electrostatic screening,16,17 metal-ion coordination,18–20 variation of hydrophilic/hydrophobic balance,21,22 and co-solvent modulation.23–25However, different from the very intensively conducted studies on the enthalpic and entropic contributions that govern supramolecular host-guest complex formation in water,26–28 studies devoted to an in-depth understanding of the thermodynamic profile of self-assembly processes of π-amphiphiles in water remain scarce.29 Nevertheless, such an understanding is warranted not only from a supramolecular design perspective, but also in therapeutic, and materials sciences.
In this direction, we have identified π-conjugated cores of perylene bisimide dyes appended with six oligoethylene glycol (OEG) chains as very useful amphiphilic molecules, whose self-assembly processes can be easily followed by various spectroscopic and microscopic techniques.30–33 But only very recently we unveiled our serendipitous discovery that the self-assembly of OEG substituted perylene bisimide (PBI) derivatives in water is not driven by enthalpic dispersion and electrostatic forces as in organic solvents,31 but by entropic factors, albeit the process can be shifted to an enthalpic route by the addition of only small amounts of an organic co-solvent.34 We attributed this intriguing behaviour to the exclusion of water molecules from the OEG side chains which leads to a dominant entropic contribution to the self-assembly in pure aqueous environment, which was also later demonstrated for other dye assemblies by Ghosh et al.35 Whilst these interesting results warrant further studies, our PBI systems aggregated too strongly in water, evading an in-depth thermodynamic characterization including isothermal titration calorimetry (ITC). Due to the smaller π-core, naphthalene bisimides (NBIs) appeared to be more promising because their self-assembly requires higher concentrations which is beneficial for methods like NMR and ITC.
Herein, we report our detailed studies on the self-assembly of a series of naphthalene bisimides functionalized with OEG chains of different glycol units (NBI 1: n = 2, NBI 2: n = 3, and NBI 3: n = 4) in water (Fig. 1a). By means of UV-vis spectroscopy and ITC studies, we have achieved the dissection of entropic and enthalpic contributions to their self-assembly. Remarkably, we found that enthalpy, entropy and free energy changes of NBIs 1–3 aggregation in water strongly depend on the interaction of water molecules with the ether oxygens and accordingly on the OEG chain length (Fig. 1b). Additional structural investigations by molecular dynamics (MD) and 2D-NMR techniques revealed back-folding of glycol chains with sequestration of the NBI π-cores from water, to be of importance as well.
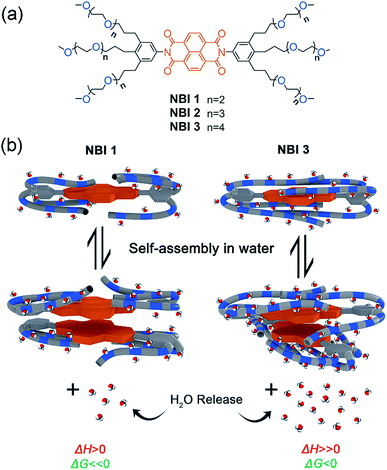 | ||
| Fig. 1 (a) Chemical structures of NBI 1–3. (b) Schematic illustration of self-assembly of NBI 1 and NBI 3 and corresponding changes in thermodynamic parameters. | ||
Results and discussion
Molecular design and synthesis
In our previous work, the larger π-core of PBI prevented the quantification of aggregation parameters in pure water due to its pronounced association tendency.34 Hence, for the current study, we have employed the smaller naphthalene homologue in lieu of perylene to assert moderate aggregation constants in water. Following the same design principles, bolaamphiphilic derivatives NBI 1–3 were prepared with OEG-substituted brushes at both ends of the π-core (Fig. 1a). The number of glycol units per chain was systematically increased from three to four and five for NBI 1, NBI 2 and NBI 3, respectively.The synthesis of amphiphilic brush substituents was carried out by a two-fold, one-pot Sonogashira reaction via coupling of 2-bromo-1,3-diiodo-5-nitrobenzene with respective glycol chain substituted with a propargyl unit.34 Subsequent reduction of the triple bonds and the nitro group in H2 atmosphere at high pressure in the presence of 10% Pd on carbon yielded the corresponding amino derivatives. Finally, these compounds were treated with naphthalene-1,4,5,8-tetracarboxylic dianhydride in acetic acid to obtain the bolaamphiphilic NBI derivatives. The synthetic details and characterization data for all new compounds are reported in the ESI.†
Temperature-dependent self-assembly and morphology of NBI aggregates
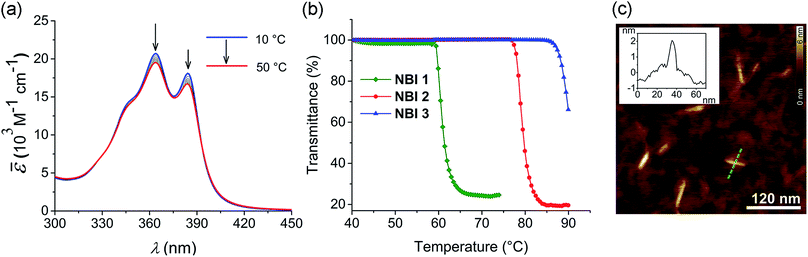
To investigate the aqueous self-assembly behaviour of NBIs 1–3, initially we performed temperature-dependent UV-vis experiments below the cloud point (vide infra). For comparison, first we measured the absorption spectra of the NBIs in CHCl3 (Fig. S1†). In an organic solvent of intermediate polarity like CHCl3, NBI 1 exists in monomeric form and shows an absorption maximum at 381 nm. In water, even at a dilute concentration of 9.7 × 10−5 M, this absorption maximum is shifted to 364 nm, suggesting an H-type aggregated state (Fig. 2a). While monitoring the temperature-dependent UV-vis spectra of NBI 1 in a range of 10 °C to 50 °C in water, we observed a decrease in the ratio of these two vibronic bands, with a concomitant hypochromic shift. This clearly indicates an increase in degree of aggregation with increasing temperature.13 Similarly, both NBI 2 and NBI 3 exhibit an inverse temperature response where the aggregation is favoured at elevated temperatures (Fig. S2†). Unlike the majority of supramolecular systems which disassemble upon heating, we have previously observed that bolaamphiphilic PBIs attached with OEG brushes show an inverse temperature response, where aggregation is favoured at higher temperatures.34 This unique thermodynamic signature is now also manifested in the current NBI series as corroborated by temperature-dependent UV-vis experiments. It is noteworthy that the spectral changes upon aggregation are by far less pronounced for NBIs compared to PBIs due to the much smaller transition dipole moment of their S0 → S1 transition.At higher temperatures, we observed the phase separation of the NBIs from the aqueous phase. This is attributed to the lower critical solution temperature (LCST) phenomenon which is typical for OEG appended systems.36 The specific temperature denoting the onset of this precipitation, called cloud point (CP), can be determined by monitoring the transmittance at a wavelength where the molecule does not absorb (here 800 nm). The phase separation from the binary solution is characterized by an abrupt drop in transmittance. The knowledge of CP is quintessential for our self-assembly studies since it sets the upper limit for the temperature window where aggregation can be monitored. Furthermore, it gives clue towards the amount of water molecules forming H-bonds to OEG chains, as the CP increases with extent of hydration. NBI 1, containing the shortest glycol chain, shows a CP of 59 °C at a concentration of 1 × 10−3 M in water, while NBI 2 and NBI 3 show phase separation at 78 and 88 °C, respectively, at the same concentration (Fig. 2b). Since the clouding is mainly associated with the dehydration of glycol units, an increase in the CPs suggests an increase in the extent of hydration with elongation of glycol chains.
In order to characterize the morphology of the aggregates formed below CP, stock solutions of NBIs in water at 22 °C were spin coated onto silicon wafer treated with argon plasma and visualized using atomic force microscopy (AFM). The microscopy images for NBI 1 obtained by tapping mode reveal short nanorods with a diameter of ∼2 nm and an average size distribution of 20–45 nm, suggesting a one dimensional (1D) self-assembly (Fig. 2c). The presence of anisotropic aggregates was further confirmed via DLS measurements which showed size dependence upon variation of the scattering angle (Fig. S3a†).37 Similarly, morphological investigations performed on NBI 2 as well as NBI 3 suggested nano-rod like self-assembled species with a diameter of ∼2 nm (Fig. S4†).
Thermodynamic profiling of NBI self-assembly
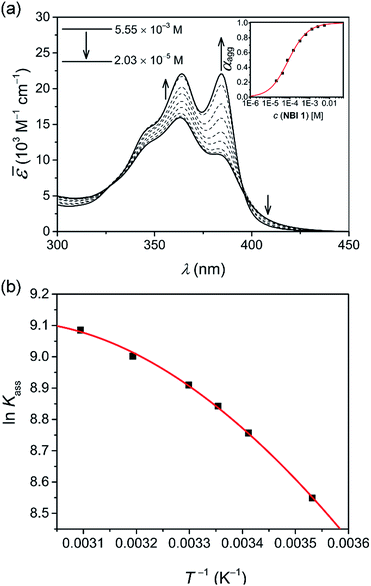
In an attempt to obtain a comprehensive thermodynamic profile for the self-assembly of NBIs 1–3 in water, we explored concentration-dependent UV-vis studies below CP to monitor their transformation from monomers to 1D – aggregates. Fig. 3a displays the spectral changes observed in our concentration-dependent experiment performed on NBI 1 at 25 °C.It was observed that with an increase in concentration, the absorption maximum shifts to 364 nm compared to the monomeric absorption maximum (381 nm), correlating to the spectral changes observed in temperature-dependent measurements. This suggests the formation of an H-type excitonically coupled stack.38 Moreover, the transition from the monomeric to aggregated state is characterized by the presence of two isosbestic points (324 nm and 394 nm), implying an equilibrium between monomeric and aggregated species.
Fig. 3a inset shows the corresponding plot of the degree of association (αagg) versus the logarithm of concentration. It was observed that the best fit for the data points was obtained with an isodesmic model, i.e. an equal association constant for each monomer addition.39 From this, the logarithm of the association constant, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kass = 3.8, and the standard Gibbs free energy of association
Kass = 3.8, and the standard Gibbs free energy of association 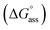 of −21.9 kJ mol−1 was estimated for NBI 1 (at 25 °C). From the concentration-dependent UV-vis studies, the critical aggregation concentration (CAC) of 0.33 mM was also determined for NBI 1 at 25 °C (Fig. S9a†).14 To delve deeper into the understanding of thermodynamic parameters associated with the self-assembly, we performed the same experiment at different temperatures, from 10 to 50 °C (Fig. S5†).
of −21.9 kJ mol−1 was estimated for NBI 1 (at 25 °C). From the concentration-dependent UV-vis studies, the critical aggregation concentration (CAC) of 0.33 mM was also determined for NBI 1 at 25 °C (Fig. S9a†).14 To delve deeper into the understanding of thermodynamic parameters associated with the self-assembly, we performed the same experiment at different temperatures, from 10 to 50 °C (Fig. S5†).
Previously, the van't Hoff equation has been successfully utilized to derive standard enthalpy 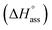 and standard entropy
and standard entropy 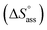 changes of self-assembly by assuming a linear relationship of the natural logarithm of aggregation constants with respect to temperature.40,41 However, this method is only valid when the enthalpy and entropy changes remain constant with changes in temperature.42 Processes in water, however, are usually associated with wide fluctuations in these parameters, thus impeding an accurate description of the self-assembly process.29,43,44 This limitation can be surpassed by taking the heat capacity changes into account. One such modification is Clarke–Glew method, where the isobaric temperature dependence of rate constants is described around a reference temperature, θ.45,46 This approach allows the calculation of the change in heat capacity at constant pressure, ΔCp, which is inaccessible by the van't Hoff equation due to its inherent assumptions. According to the simplified form of Clarke–Glew method (also referred as extended/integrated van't Hoff equation), the change in association constant with respect to temperature can be expressed by eqn (1).
changes of self-assembly by assuming a linear relationship of the natural logarithm of aggregation constants with respect to temperature.40,41 However, this method is only valid when the enthalpy and entropy changes remain constant with changes in temperature.42 Processes in water, however, are usually associated with wide fluctuations in these parameters, thus impeding an accurate description of the self-assembly process.29,43,44 This limitation can be surpassed by taking the heat capacity changes into account. One such modification is Clarke–Glew method, where the isobaric temperature dependence of rate constants is described around a reference temperature, θ.45,46 This approach allows the calculation of the change in heat capacity at constant pressure, ΔCp, which is inaccessible by the van't Hoff equation due to its inherent assumptions. According to the simplified form of Clarke–Glew method (also referred as extended/integrated van't Hoff equation), the change in association constant with respect to temperature can be expressed by eqn (1).
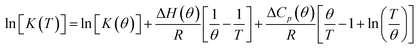 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [K(T)] is the natural logarithm of the equilibrium constant at temperature T, ln
[K(T)] is the natural logarithm of the equilibrium constant at temperature T, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [K(θ)] is the natural logarithm of the equilibrium constant at the reference temperature θ, ΔH(θ) is the enthalpy change at the reference temperature, and ΔCp is the change in heat capacity at constant pressure.
[K(θ)] is the natural logarithm of the equilibrium constant at the reference temperature θ, ΔH(θ) is the enthalpy change at the reference temperature, and ΔCp is the change in heat capacity at constant pressure.
While plotting the natural logarithm of the association constant versus the inverse of temperature, indeed a much better fit is obtained with the non-linear Clarke–Glew equation as compared to the van't Hoff equation (Fig. 3b). Accordingly, a standard enthalpy of 11.2 kJ mol−1 and a heat capacity change of −289 J mol−1 K−1 can be calculated for the self-assembly of NBI 1. With an elevation in temperature, an increase in aggregation strength is observed, quantitatively supporting our temperature-dependent UV-vis measurements. Furthermore, the negative slope of the curve suggests the endothermic nature of self-association over a broad temperature range, which is hence enthalpically disfavoured.
Similarly, concentration-dependent UV-vis experiments were conducted for NBI 2 and NBI 3 at different temperatures (Fig. S6 and S7†). In both cases, we observed that the mechanism of self-assembly differs from the isodesmic model and is better described by a weak anti-cooperative process with a cooperativity factor of σ = 2 and σ = 3 for NBI 2 and NBI 3, respectively. By fitting the data according to the Goldstein–Stryer model47 utilized for (anti)cooperative aggregation processes, a logarithm of the association constant, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kass = 3.3, and a standard Gibbs free energy,
Kass = 3.3, and a standard Gibbs free energy, 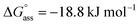 was determined for NBI 2 at 25 °C, suggesting a weaker aggregation tendency as compared to NBI 1. Using the Clarke–Glew plot, a standard enthalpy change of 18.1 kJ mol−1 is calculated, which shows that the self-assembly of NBI 2 is enthalpically more disfavoured than NBI 1 (Fig. S8a†). NBI 3 exhibited the weakest aggregation tendency of all three derivatives, with log
was determined for NBI 2 at 25 °C, suggesting a weaker aggregation tendency as compared to NBI 1. Using the Clarke–Glew plot, a standard enthalpy change of 18.1 kJ mol−1 is calculated, which shows that the self-assembly of NBI 2 is enthalpically more disfavoured than NBI 1 (Fig. S8a†). NBI 3 exhibited the weakest aggregation tendency of all three derivatives, with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kass = 2.8 and a standard Gibbs free energy,
Kass = 2.8 and a standard Gibbs free energy, 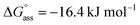 at 25 °C. The self-assembly, in this case, is disfavoured by a standard enthalpy
at 25 °C. The self-assembly, in this case, is disfavoured by a standard enthalpy 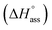 of 23.2 kJ mol−1 (Fig. S8b†). Furthermore, the CAC estimated for NBI 2 (1.6 mM) and NBI 3 (3.5 mM) at 25 °C confirms the decreasing tendency of aggregation while increasing the glycol chain length from NBI 1 to NBI 3 (Fig. S9b and c†).
of 23.2 kJ mol−1 (Fig. S8b†). Furthermore, the CAC estimated for NBI 2 (1.6 mM) and NBI 3 (3.5 mM) at 25 °C confirms the decreasing tendency of aggregation while increasing the glycol chain length from NBI 1 to NBI 3 (Fig. S9b and c†).
The thermodynamic signature at 25 °C obtained for the three derivatives is represented in Fig. 4, which depicts that the self-assembly for all the NBI derivatives in water is enthalpically disfavoured and entropically driven. Furthermore, this penalty in the standard enthalpy of association 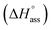 and the gain in standard entropy of association
and the gain in standard entropy of association 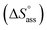 is augmented as the OEG chain length is increased from NBI 1 to NBI 3. Since our CP measurements suggest an increase in hydration with chain elongation, this trend can be attributed to the increased number of water molecules that are removed for well-hydrated monomer units upon aggregation. On the other hand, the aggregation tendency decreases with an increase of glycol units as reflected by increased
is augmented as the OEG chain length is increased from NBI 1 to NBI 3. Since our CP measurements suggest an increase in hydration with chain elongation, this trend can be attributed to the increased number of water molecules that are removed for well-hydrated monomer units upon aggregation. On the other hand, the aggregation tendency decreases with an increase of glycol units as reflected by increased 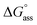 values.
values.
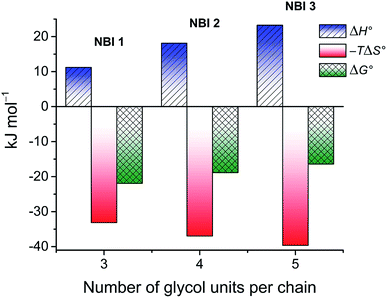 | ||
| Fig. 4 Thermodynamic profile for the self-assembly of NBI 1–3 in water obtained by concentration-dependent UV-vis experiments. | ||
In order to validate the thermodynamic parameters obtained by our UV-vis experiments, we resorted to an independent technique to derive the enthalpy, entropy and free energy of association. This technique is given with an ITC dilution experiment that allows direct determination of enthalpy and gathers insight into its temperature dependency, which is inaccessible via other methods. Even though ITC is well established for natural48,49 and synthetic host–guest interactions,28,50–52 the advent of this technique to probe self-assembly is quite recent.34,53–55
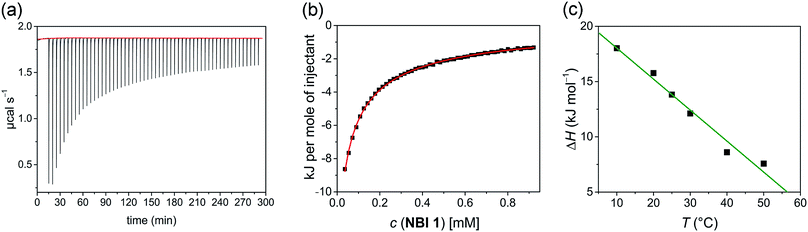
In a typical ITC dilution experiment, aliquots of a concentrated solution of the aggregated species is titrated into the pure solvent taken in the cell. The dissociation of the aggregate is then accompanied by non-constant heat signals along with constant heat of dilution.53 From this, enthalpy and other thermodynamic parameters can be determined. Fig. 5a shows the evolution of heat per injection of a concentrated aqueous NBI 1 solution (c = 5.2 × 10−3 M) into pure water at 25 °C leading to its disassembly, which depicts an exothermic heat flow, i.e., the dis-assembly process is enthalpically favoured. The corresponding enthalpogram could be well fitted to an isodesmic model (Fig. 5b).56,57 A standard enthalpy change of −13.8 kJ mol−1 for dis-assembly (or +13.8 kJ mol−1 for the corresponding self-assembly) and logarithm of the association constant, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kass = 3.8 at 25 °C was determined for NBI 1, which is indeed in good concordance with the previously obtained values from UV-vis experiments (vide supra). Also, a CAC value of 0.21 mM was deduced for NBI 1 from the aforementioned ITC dilution experiment (Fig. S10†).35 The accompanying heat of dilution estimated from the overall heat evolved during injection of NBI 1 is provided in Table S1.† Accordingly, different from our previous study of a strongly aggregating PBI,34 here we could for the first time quantify the entropically driven self-assembly thermodynamics in water and derive values for
Kass = 3.8 at 25 °C was determined for NBI 1, which is indeed in good concordance with the previously obtained values from UV-vis experiments (vide supra). Also, a CAC value of 0.21 mM was deduced for NBI 1 from the aforementioned ITC dilution experiment (Fig. S10†).35 The accompanying heat of dilution estimated from the overall heat evolved during injection of NBI 1 is provided in Table S1.† Accordingly, different from our previous study of a strongly aggregating PBI,34 here we could for the first time quantify the entropically driven self-assembly thermodynamics in water and derive values for 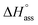 and Kass of high accuracy. The thermodynamic parameters obtained by both these methods are tabulated in Table 1.
and Kass of high accuracy. The thermodynamic parameters obtained by both these methods are tabulated in Table 1.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kass Kass |
CAC (mM) | ΔCp (J mol−1 K−1) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UV-visa | ITCb | UV-visc | ITCd | UV-vise | ITCb | UV-visf | ITCf | UV-visg | ITCg | UV-vise | ITCh | |
a Measured by concentration-dependent UV-vis experiment at 25 °C and calculated using the isodesmic model (NBI 1) or Goldstein–Stryer model (NBI 2 and NBI 3).
b Measured by ITC dilution experiment at 25 °C and calculated using the isodesmic model.
c Measured by concentration-dependent UV-vis experiment at 25 °C.
d Measured by ITC dilution experiment at 25 °C.
e Measured by concentration-dependent UV-vis experiment at different temperatures and calculated using Clarke–Glew eqn (1).
f Calculated according to the relation 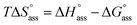 .
g Calculated according to the relation .
g Calculated according to the relation 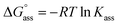 .
h Measured by ITC dilution experiment at different temperatures and calculated using a linear fit. .
h Measured by ITC dilution experiment at different temperatures and calculated using a linear fit.
|
||||||||||||
| NBI 1 | 3.8 | 3.8 | 0.33 | 0.21 | 11.2 | 13.8 | 33.1 | 35.8 | −21.9 | −22.0 | −289 | −280 |
| NBI 2 | 3.3 | — | 1.6 | — | 18.1 | — | 36.9 | — | −18.8 | — | −324 | — |
| NBI 3 | 2.8 | — | 3.5 | — | 23.2 | — | 39.6 | — | −16.4 | — | −411 | — |
Successively, to understand the influence of temperature on the enthalpy of self-assembly, we repeated the ITC dilution experiment at different temperatures, from 10 to 50 °C (Fig. S11†). It was observed that with increasing temperature, the enthalpy of association for NBI 1 is concomitantly decreased (Fig. 5c). It is expected that an elevation in temperature decreases the H-bond strength between the water molecules and OEG chains,58 thus reducing the enthalpic penalty associated with the dehydration of water molecules during self-assembly. The increased aggregation tendency of these systems at higher temperatures could be traced to this easiness in the release of H-bonded water molecules. The resulting heat capacity change for NBI 1 aggregation was quantified as −280 J mol−1 K−1 using eqn (2),
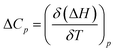 | (2) |
Similar dilution experiments in pure water were also performed for NBI 2 and NBI 3 at 25 °C (Fig. S12 and S13†). Here also the dilution experiments revealed exothermic signals for disassembly, accordingly the self-assembly is endothermic. Intriguingly, in both cases, we observed heat signals associated with two distinct processes (Fig. S12b and S13b†). Such two-step processes with similar heat signature have been previously reported for host-guest studies of ions with macrocycles which follow negative cooperative mechanism.59 We assume that since the aforementioned derivatives aggregate via a weak anti-cooperative mechanism, the first injections might represent the dissociation of fully aggregated aliquots into monomers whereas the latter injections show the dissociation into the dimeric species. Unfortunately, the currently available model was not able to describe these processes and hence hampers the accurate determination of aggregation parameters for NBI 2 and NBI 3. Furthermore, the lack of saturation at the end-point of dilution experiment due to lower aggregation tendency impedes the estimation of CAC for NBI 2 and NBI 3via ITC.
Thus, we could independently confirm by both UV-vis studies and ITC dilution experiments that the self-assembly of NBIs 1–3 in water is entropically driven and primarily attributable to the release of water molecules from the glycol units. Here the length of the OEG side chains plays a prominent role for both the enthalpic and entropic contributions to the aqueous self-assembly of our NBI series. In order to obtain deeper insights into the role of molecular structure in orchestrating this specific aggregation trend in water, structural attributes, especially the conformational nature of glycol units have to be investigated in detail.
Structural characterization via molecular dynamics (MD) and 2D NMR studies
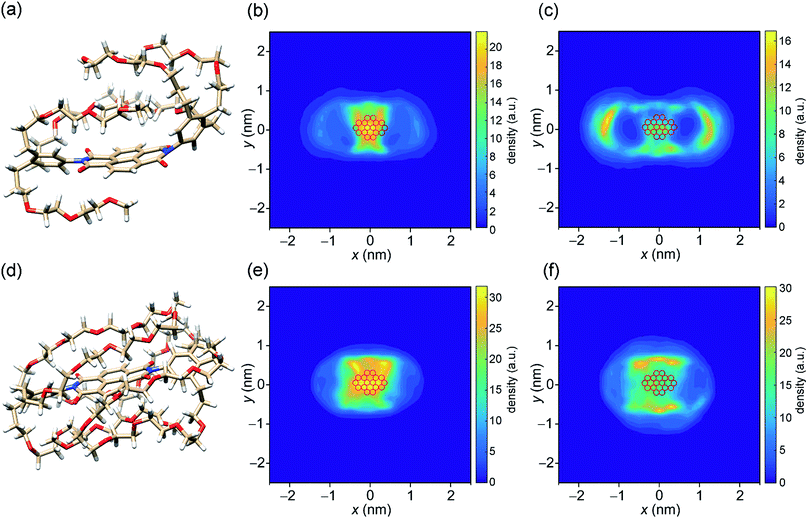
After procuring quantitative information about the thermodynamic signature associated with the self-assembly, we pondered upon the role of molecular structure in directing the association process. For this, we employed all atoms molecular dynamics (MD) simulations in pure water on NBI 1 and NBI 3 which have the shortest and the longest OEG chains, respectively, in the series. Interestingly, both NBIs show a back-folded conformation of glycol chains around the naphthalene core in the monomeric form (Fig. 6a and d). A similar observation was previously discussed by Meijer and Pavan et al. and has been attributed to the shielding of the hydrophobic surface from the surrounding bulk water.12,60Fig. 6b and e show the density profiles of C-atoms of OEG chain over the aromatic cores for NBI 1 and NBI 3. As seen clearly, the preferred orientation of side chains during the MD regime resides over the core instead of extending into the bulk water.Next, two such pre-equilibrated monomers were immersed into a periodic simulation box filled with explicit water molecules and allowed to equilibrate over MD regime. The distance between the two monomers (0.4 nm) suggests an explicit π–π stacking, with a rotational offset of 10° (Fig. S15a and S16a†). A snapshot from the trajectory of NBI 1 stacking depicts that the glycol chains still prefer a back-folded orientation in the aggregated state (Fig. S14a†). However, the tail density is now more distributed around the π-core, suggesting that some of the back-folding was replaced in order to accommodate the incoming monomer (Fig. 6c). This release of ordered chains might contribute to the conformational entropy of side chains, aiding overall entropy of the association, along with the removal of hydrated water molecules.
Similarly, for NBI 3, stacking interactions were studied via MD simulations (Fig. S14b†). Here we see again that the glycol chains are folded over the naphthalene core, in both monomeric and dimeric form. However, due to the increased length of OEG units, the density of back-folded conformation is concomitantly higher as compared to NBI 1 (Fig. 6f). The rotational offset for the NBI 3 stack (∼60°) is significantly larger compared to NBI 1, which could be rationalized by the steric hindrance of back-folded glycol chains (Fig. S16b†).
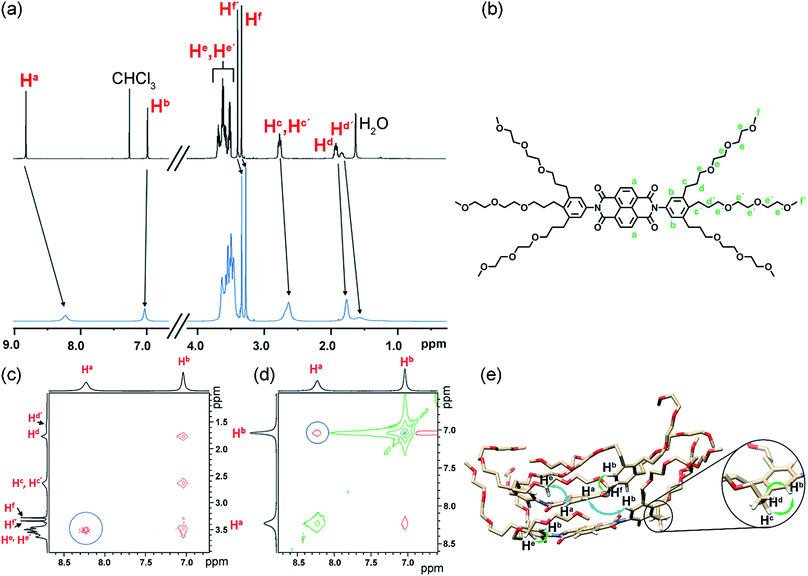
To experimentally verify the presence of back-folding as suggested by MD simulations and to unravel the aggregate structure, we conducted detailed one-dimensional (1D) and two dimensional (2D) NMR studies. The 1H NMR spectrum of NBI 1 in CDCl3 shows well resolved sharp signals corresponding to the monomeric state (Fig. 7a). In contrast, the naphthalene core protons are significantly broadened as well as up-field shifted in D2O, indicating an aggregated state aided by π–π stacking. Insights into the aggregate structure were probed subsequently via1H–1H Rotating Frame Overhauser Effect Spectroscopy (ROESY). Fig. 7c and d show selected regions of superimposed ROESY and COSY spectra of NBI 1 in D2O. Nuclear Overhauser Effect (NOE) correlations could be observed between the naphthalene core protons (Ha) and the glycol protons (He/He′) which is in compliance with the back-folded conformation of side chains. The coupling between the naphthalene core protons and phenyl protons suggests a slightly rotated offset between NBI 1 monomers in the stacked conformation as predicted by MD simulations. A tentative assignment of NOE correlations with a snapshot from MD regime of NBI 1 is given in Fig. 7e. Similarly, for both NBI 2 and NBI 3, through-space interactions could be traced between glycol chain protons (He/He′) and core protons (Ha), thus corroborating the presence of back-folded conformations in these systems (Fig. S17 and S18†) and validating the structural predictions from MD simulations.
In the thermodynamic analysis of the current system, we have observed that the elongation of glycol units from NBI 1 to NBI 3 is associated with a nearly ten-fold decrease in association constant and a concomitant drop in the magnitude of free energy. Combined results from MD simulations and NMR studies suggest that the back-folding of glycol chains is orchestrating this effect. Furthermore, the change of aggregation mechanism from isodesmic to weak anti-cooperative can also be attributed to the more pronounced jacketing of monomer and dimer species by the longer OEG chains.
In addition, our results also relate to the studies on biomolecules. Here, previously it was observed that the substitution of proteins with polyethylene glycol (PEG) results in a decrease in binding affinity due to the interactions between PEG chains and the active site of the protein.61,62 Meijer et al. predicted that this could be ascribed to the back-folding of the glycol chains operative in water.63 Our current studies prove that the back-folding indeed interferes with the association process by shielding the hydrophobic surface from the surrounding bulk water. Accordingly, we can conclude that OEG and PEG chains play a pivotal role in directing the thermodynamics of aggregation in water.
Conclusions
In this contribution, three archetype bolaamphiphilic naphthalene bisimides were studied to derive an understanding of the different factors that contribute to the entropically driven self-assembly of bolaamphiphilic moieties substituted with OEG units in water. By utilizing UV-vis and ITC dilution experiments, we have successfully dissected the thermodynamic parameters of the aggregation process. The entropically favoured nature of the self-assembly is attributed to the release of water molecules from the glycol units which is enthalpically penalized. Further, we were able to show that a thermodynamic tuning of π-core aggregation in water can be achieved by modulating the length of solubilizing OEG chains. With elongation of the side chains, the enthalpic as well as entropic parameters also increase, attributed to an increment in dehydrated water molecules upon aggregation. However, this augmentation in their length hinders the self-assembly via a back-folding process as revealed by MD simulations and 2D-NMR studies, resulting in a decrease of the magnitude of Gibbs free energy and deviation from the isodesmic mechanism. Our current study sheds light into the fundamental aspects of bolaamphiphilic aggregation in water and opens up a strategy for more predictable aqueous self-assembly processes of oligo- and polyethylene glycol functionalized amphiphilic molecules.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Niklaas J. Buurma for providing help to the thermodynamic analysis and Dr Mathias Grüne for 2D-NMR and Dr Vladimir Stepanenko for AFM measurements. Funding from the DFG (project Wu 317/15-1) and the State of Bavaria for the establishment of the Key Lab for Supramolecular Polymers of the Bavarian Polymer Institute (BPI) is gratefully acknowledged. S. G. thanks the SFB 840 (Project A12) for funding as well as the Jülich Supercomputing Center and the Keylab Theory and Simulation of the Bavarian Polymer Institute for computing power.Notes and references
- C. M. Dobson, Nature, 2003, 426, 884–890 CrossRef CAS PubMed.
- K. C. Holmes, D. Popp, W. Gebhard and W. Kabsch, Nature, 1990, 347, 44–49 CrossRef CAS PubMed.
- E. Nogales, Annu. Rev. Biochem., 2000, 69, 277–302 CrossRef CAS PubMed.
- E. Krieg, M. M. C. Bastings, P. Besenius and B. Rybtchinski, Chem. Rev., 2016, 116, 2414–2477 CrossRef CAS PubMed.
- T. P. Knowles, A. W. Fitzpatrick, S. Meehan, H. R. Mott, M. Vendruscolo, C. M. Dobson and M. E. Welland, Science, 2007, 318, 1900–1903 CrossRef CAS PubMed.
- T. F. A. de Greef, M. M. J. Smulders, M. Wolffs, A. P. H. J. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687–5754 CrossRef CAS PubMed.
- D. Görl, X. Zhang and F. Würthner, Angew. Chem., Int. Ed., 2012, 51, 6328–6348 CrossRef PubMed.
- B. N. S. Thota, L. H. Urner and R. Haag, Chem. Rev., 2016, 116, 2079–2102 CrossRef CAS PubMed.
- J. Baram, H. Weissman, Y. Tidhar, I. Pinkas and B. Rybtchinski, Angew. Chem., Int. Ed., 2014, 53, 4123–4126 CrossRef CAS PubMed.
- A. Ustinov, H. Weissman, E. Shirman, I. Pinkas, X. Zuo and B. Rybtchinski, J. Am. Chem. Soc., 2011, 133, 16201–16211 CrossRef CAS PubMed.
- M. Hariharan, Y. Zheng, H. Long, T. A. Zeidan, G. C. Schatz, J. Vura-Weis, M. R. Wasielewski, X. Zuo, D. M. Tiede and F. D. Lewis, J. Am. Chem. Soc., 2009, 131, 5920–5929 CrossRef CAS PubMed.
- M. B. Baker, L. Albertazzi, I. K. Voets, C. M. Leenders, A. R. A. Palmans, G. M. Pavan and E. W. Meijer, Nat. Commun., 2015, 6, 6234–6246 CrossRef PubMed.
- P. Rajdev, M. R. Molla and S. Ghosh, Langmuir, 2014, 30, 1969–1976 CrossRef CAS PubMed.
- P. Rajdev, S. Chakraborty, M. Schmutz, P. Mesini and S. Ghosh, Langmuir, 2017, 33, 4789–4795 CrossRef CAS PubMed.
- V. Grande, B. Soberats, S. Herbst, V. Stepanenko and F. Würthner, Chem. Sci., 2018, 9, 6904–6911 RSC.
- P. Besenius, G. Portale, P. H. H. Bomans, H. M. Janssen, A. R. A. Palmans and E. W. Meijer, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17888–17893 CrossRef CAS PubMed.
- C. Schaefer, I. K. Voets, A. R. A. Palmans, E. W. Meijer, P. van der Schoot and P. Besenius, ACS Macro Lett., 2012, 1, 830–833 CrossRef CAS.
- M. J. Mayoral, C. Rest, V. Stepanenko, J. Schellheimer, R. Q. Albuquerque and G. Fernández, J. Am. Chem. Soc., 2013, 135, 2148–2151 CrossRef CAS PubMed.
- G. Golubkov, H. Weissman, E. Shirman, S. G. Wolf, I. Pinkas and B. Rybtchinski, Angew. Chem., Int. Ed., 2009, 48, 926–930 CrossRef CAS PubMed.
- H. J. Kim, S. K. Kang, Y. K. Lee, C. Seok, J. K. Lee, W. C. Zin and M. Lee, Angew. Chem., Int. Ed., 2010, 49, 8471–8475 CrossRef CAS PubMed.
- X. Zhang, Z. Chen and F. Würthner, J. Am. Chem. Soc., 2007, 129, 4886–4887 CrossRef CAS PubMed.
- M. R. Molla and S. Ghosh, Phys. Chem. Chem. Phys., 2014, 16, 26672–26683 RSC.
- M. Ogasawara, X. Lin, H. Kurata, H. Ouchi, M. Yamauchi, T. Ohba, T. Kajitani, T. Fukushima, M. Numata, R. Nogami, B. Adhikari and S. Yagai, Mater. Chem. Front., 2018, 2, 171–179 RSC.
- X. Lin, H. Kurata, D. D. Prabhu, M. Yamauchi, T. Ohba and S. Yagai, Chem. Commun., 2017, 53, 168–171 RSC.
- M. Kumar and S. J. George, Chem.–Eur. J., 2011, 17, 11102–11106 CrossRef CAS PubMed.
- F. Biedermann, W. M. Nau and H.-J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171 CrossRef CAS PubMed.
- F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216–5300 CrossRef CAS PubMed.
- F. Biedermann, V. D. Uzunova, O. A. Scherman, W. M. Nau and A. De Simone, J. Am. Chem. Soc., 2012, 134, 15318–15323 CrossRef CAS PubMed.
- P. S. Cremer, A. H. Flood, B. C. Gibb and D. L. Mobley, Nat. Chem., 2017, 10, 8–16 CrossRef PubMed.
- X. Zhang, D. Görl, V. Stepanenko and F. Würthner, Angew. Chem., Int. Ed., 2014, 53, 1270–1274 CrossRef CAS PubMed.
- Z. Chen, B. Fimmel and F. Würthner, Org. Biomol. Chem., 2012, 10, 5845–5855 RSC.
- M. Sun, K. Müllen and M. Yin, Chem. Soc. Rev., 2016, 45, 1513–1528 RSC.
- D. Görl, X. Zhang, V. Stepanenko and F. Würthner, Nat. Commun., 2015, 6, 7009–7017 CrossRef.
- D. Görl and F. Würthner, Angew. Chem., Int. Ed., 2016, 55, 12094–12098 CrossRef.
- P. Dey, P. Rajdev, P. Pramanik and S. Ghosh, Macromolecules, 2018, 51, 5182–5190 CrossRef CAS.
- D. Görl, B. Soberats, S. Herbst, V. Stepanenko and F. Würthner, Chem. Sci., 2016, 7, 6786–6790 RSC.
- N. K. Allampally, A. Florian, M. J. Mayoral, C. Rest, V. Stepanenko and G. Fernández, Chem.–Eur. J., 2014, 20, 10669–10678 CrossRef CAS PubMed.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- Z. Chen, A. Lohr, C. R. Saha-Möller and F. Würthner, Chem. Soc. Rev., 2009, 38, 564–584 RSC.
- N. J. Van Zee, B. Adelizzi, M. F. J. Mabesoone, X. Meng, A. Aloi, R. H. Zha, M. Lutz, I. A. W. Filot, A. R. A. Palmans and E. W. Meijer, Nature, 2018, 558, 100–103 CrossRef CAS PubMed.
- K. Venkata Rao, D. Miyajima, A. Nihonyanagi and T. Aida, Nat. Chem., 2017, 9, 1133–1139 CrossRef CAS PubMed.
- H. Naghibi, A. Tamura and J. M. Sturtevant, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 5597–5599 CrossRef CAS PubMed.
- G. Weber, J. Phys. Chem., 1995, 99, 1052–1059 CrossRef CAS.
- J. R. Horn, D. Russell, E. A. Lewis and K. P. Murphy, Biochemistry, 2001, 40, 1774–1778 CrossRef CAS PubMed.
- E. C. W. Clarke and D. N. Glew, Trans. Faraday Soc., 1966, 62, 539–547 RSC.
- M. J. Blandamer, Chemical Equilibria in Solution, Ellis Horwood, Chichester, 1992 Search PubMed.
- R. F. Goldstein and L. Stryer, Biophys. J., 1986, 50, 583–599 CrossRef CAS.
- M. Kabiri and L. D. Unsworth, Biomacromolecules, 2014, 15, 3463–3473 CrossRef CAS PubMed.
- P. W. Snyder, J. Mecinović, D. T. Moustakas, S. W. Thomas, M. Harder, E. T. Mack, M. R. Lockett, A. Héroux, W. Sherman and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17889–17894 CrossRef CAS PubMed.
- M. V. Rekharsky, T. Mori, C. Yang, Y. H. Ko, N. Selvapalam, H. Kim, D. Sobransingh, A. E. Kaifer, S. Liu, L. Isaacs, W. Chen, S. Moghaddam, M. K. Gilson, K. Kim and Y. Inoue, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20737–20742 CrossRef CAS.
- M. Ciardi, A. Galán and P. Ballester, J. Am. Chem. Soc., 2015, 137, 2047–2055 CrossRef CAS PubMed.
- A. Camara-Campos, C. A. Hunter and S. Tomas, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3034–3038 CrossRef CAS PubMed.
- A. Arnaud and L. Bouteiller, Langmuir, 2004, 20, 6858–6863 CrossRef CAS PubMed.
- I. Turcu and M. Mic, J. Phys. Chem. B, 2013, 117, 9083–9093 CrossRef CAS PubMed.
- F. Aparicio, F. García and L. Sánchez, Chem.–Eur. J., 2013, 19, 3239–3248 CrossRef CAS PubMed.
- N. J. Buurma and I. Haq, J. Mol. Biol., 2008, 381, 607–621 CrossRef CAS PubMed.
- N. J. Buurma and I. Haq, Methods, 2007, 42, 162–172 CrossRef CAS.
- S. Sun and P. Wu, Macromolecules, 2013, 46, 236–246 CrossRef CAS.
- R. Molina-Muriel, G. Aragay, E. C. Escudero-Adán and P. Ballester, J. Org. Chem., 2018, 83, 13507–13514 CrossRef CAS PubMed.
- M. Garzoni, M. B. Baker, C. M. A. Leenders, I. K. Voets, L. Albertazzi, A. R. A. Palmans, E. W. Meijer and G. M. Pavan, J. Am. Chem. Soc., 2016, 138, 13985–13995 CrossRef CAS PubMed.
- S. Kubetzko, C. A. Sarkar and A. Plückthun, Mol. Pharmacol., 2005, 68, 1439–1454 CrossRef CAS.
- S. Kubetzko, E. Balic, R. Waibel, U. Zangemeister-Wittke and A. Plückthun, J. Biol. Chem., 2006, 281, 35186–35201 CrossRef CAS PubMed.
- T. F. A. de Greef, M. M. L. Nieuwenhuizen, R. P. Sijbesma and E. W. Meijer, J. Org. Chem., 2010, 75, 598–610 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed procedures and results for all reported experiments, along with synthetic details. See DOI: 10.1039/c9sc03103k |
| This journal is © The Royal Society of Chemistry 2019 |