Open Access Article
Open Access ArticleUnravelling the effects of oxidation state of interstitial iodine and oxygen passivation on charge trapping and recombination in CH3NH3PbI3 perovskite: a time-domain ab initio study†
Jinlu
He
,
Wei-Hai
Fang
and
Run
Long
 *
*
College of Chemistry, Key Laboratory of Theoretical & Computational Photochemistry of Ministry of Education, Beijing Normal University, Beijing, 100875, P. R. China. E-mail: runlong@bnu.edu.cn
First published on 9th September 2019
Abstract
Understanding nonradiative charge recombination mechanisms is a prerequisite for advancing perovskite solar cells. By performing time-domain density functional theory combined with nonadiabatic (NA) molecular dynamics simulations, we show that electron–hole recombination in perovskites strongly depends on the oxidation state of interstitial iodine and oxygen passivation. The simulations demonstrate that electron–hole recombination in CH3NH3PbI3 occurs within several nanoseconds, agreeing well with experiment. The negative interstitial iodine delays charge recombination by a factor of 1.3. The deceleration is attributed to the fact that interstitial iodine anion forms a chemical bond with its nearest lead atoms, eliminates the trap state, and decreases the NA electron–phonon coupling. The positive interstitial iodine attracts its neighbouring lattice iodine anions, resulting in the formation of an I-trimer and producing an electron trap. Electron trapping proceeds on a very fast timescale, tens of picoseconds, and captures the majority of free electrons available to directly recombine with free holes while inhibiting the recombination of free electrons and holes, delaying the recombination by a factor of 1.5. However, the positive interstitial iodine easily converts to a neutral iodine defect by capturing an electron, giving rise to a singly occupied state above the valence band maximum and acting as a hole trap. The photoexcitation valence band hole becomes trapped by the hole trap state very rapidly, followed by acceleration of recombination with the conduction band free electron by a factor of 1.6. Surprisingly, molecular oxygen interacting with interstitial iodine anion forms a stable IO3−1 species, which inhibits ion migration, stabilizes perovskites, and suppresses the electron–hole recombination by a factor of 2.7. Our simulations reveal the microscopic effects of the oxidation state of interstitial iodine defects and oxygen passivation in perovskites, suggesting an effective way to improve perovskite photovoltaic and optoelectronic devices.
1. Introduction
Lead halide perovskites (LHPs) APbX3 (A = CH3NH3, CH(NH2)2; X = Cl, Br, I) have received considerable attention in the past decades due to their outstanding electronic and optical properties,1 including excellent optical absorption,2 long minority carrier lifetimes and diffusion lengths,3–5 and appropriate optical band gaps.6 These fascinating properties give the LHPs great potential in a broad range of applications, such as solar cells,7–10 photodetectors,11 optically pumped lasers,12 light-emitting diodes13 and photocatalytic water-splitting assemblies.14 Its utilization in solar cells attracts particular concern due to the rapid growth in power conversion efficiencies (PCEs) from 3.8%15 to a certified 24.2% within ten years,16 showing a comparable value to the commercial silicon solar cells.17 However, the PCEs are still lower than the Shockley–Queisser limit18 for a single p–n junction solar cell due to the presence of channels for nonradiative charge and energy losses caused by various intrinsic and extrinsic defects.19–21Intrinsic defects are inevitable in low-temperature solution-processed LHPs due to the low stability against thermal and light radiation.22 Dozens of experimental and theoretical works have explored the roles played by a large number of native point defects in LHPs,20,23–30 which found those defects have significant impact on the performance of perovskite solar cells by controlling the quality of films and carrier dynamics.31–34 Sample quality can be directly detected by advanced experimental techniques, such as atomic force microscopy and scanning electron microscopy. However, photoinduced charge dynamics can be only measured via indirect spectroscopy methods, and their nature remains largely elusive.35,36
Interstitial iodine defects are common and active deep traps in MAPbI3,37 easily forming in the presence of excess iodine.37 The impacts of interstitial iodine defects on the electronic structure and charge dynamics of perovskites are under active research and debate. Petrozza and coauthors have shown, using photoluminescence spectroscopy, that a neutral interstitial iodine defect can trap a conduction band (CB) electron, subsequently recombining with a valence band (VB) hole on a surprisingly long timescale and leading to a significantly increased carrier lifetime and an enhanced open-circuit voltage of MAPbI3 perovskite solar cells.32 However, Yang et al. have demonstrated that excess iodine can suppress the formation of interstitial iodide defects and extend the carrier lifetimes.38 On the contrary, Wang et al. have demonstrated that interstitial iodine defects notably decrease carrier lifetimes and lower the photovoltaic performance of MAPbI3 perovskite solar cells.39 The positive and negative effects of interstitial iodine defects on the excited charge carrier lifetime of MAPbI3 perovskite may be related with their oxidation state. First-principles calculations have predicted that positive interstitial iodine (Ii+1) is unstable under light irradiation,37 which tends to trap an electron, resulting in the formation of an neutral interstitial iodine (Ii) that acts as a deep trap state,25 accelerating electron–hole recombination.28,38,40 In addition, the interstitial iodine defects have low migration activation energies (0.1 eV), and they easily diffuse in perovskites, which constitutes the main factor resulting in perovskite material degradation.41,42 In contrast, negative interstitial iodine (Ii−1) is relatively stable,37 while the ion migration, including both MA+ and I−, leads to notable current–voltage hysteresis of a perovskite solar cell.43 Interestingly, theoretical calculations have illustrated that oxygen preferentially interacts with the interstitial iodine anion rather than lattice iodine atom, forming thermodynamically stable IO3− species,44 which potentially stabilizes the MAPbI3 perovskite44 and rationalizes the improved perovskite solar cell performance as well as clarifies the enhanced reversible photoluminescence quantum yield upon material exposure to oxygen in experiments.45–49 Understanding the underlying mechanisms for the impact of oxidation state of interstitial iodine and oxygen passivation effect on the excited-state lifetime of MAPbI3 perovskite calls for a time-domain study of nonradiative electron–hole recombination in real time and at the atomistic level.
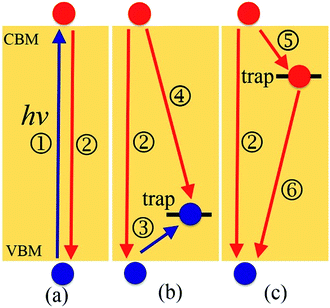
Motivated by both the experimental32,38,39,45–49 and theoretical works25,37,44 showing the positive and negative effects of interstitial iodine on the photoexcitation carrier lifetime of MAPbI3, as well as the role played by oxygen passivation, we have investigated the charge trapping and nonradiative electron–hole recombination processes (depicted in Fig. 1) of MAPbI3 in the presence of interstitial iodine defects with different oxidation states, Ii, Ii−1, and Ii+1, as well as oxygen passivation with the stable species IO3−1,44 using a combination of real-time time-dependent density functional theory (TD-DFT)50,51 and nonadiabatic molecular dynamics (NAMD).52–55 Our simulations show that the electron–hole recombination across the conduction band minimum (CBM) and valence band maximum (VBM) (Fig. 1a) in pristine MAPbI3 occurs over several nanoseconds, agreeing well with experimental data.56 The neutral Ii acts as an electron donor, creates a hole trap above the VBM (Fig. 1b), increases NA coupling, and accelerates the electron–hole recombination by a factor of 1.6. The negatively charged Ii−1 defect eliminates the trap state (Fig. 1a) and decreases the electron–hole recombination across the CBM–VBM energy gap by a factor of 1.3 compared to the pristine MAPbI3, arising due to reduced NA electron–phonon coupling. The Ii+1 defect introduces an electron trap below the CBM (Fig. 1c), which acts an electron acceptor. The CB free electrons are highly captured by the trap state, followed by recombining with the holes located in the VBM. The trap-assisted electron–hole recombination between the VBM and the trap state delays by a factor of 1.5 relative to the pristine MAPbI3. Meanwhile, positively charged interstitial iodine is easily converted to a neutral defect by capturing an electron, accelerating electron–hole recombination. Molecular oxygen interacting with Ii−1 defect forms a stable IO3−1 that inhibits ion migration and reduces current–voltage hysteresis. At the same time, oxygen passivation decreases the NA electron–phonon coupling further and suppresses electron–hole recombination across the band gap (Fig. 1a) by a factor of 2.7. This study reveals the impact of oxidation state of interstitial iodine defects on charge dynamics and rationalizes the phenomenon observed in the experiment that oxygen can be responsible for the enhanced perovskite solar cell performance and PLQY45–49 and reduced hysteresis,57 providing valuable guidelines for the design of high-performance perovskite photovoltaic devices.
2. Theoretical methodology
We have performed the NAMD with the decoherence induced surface hopping (DISH) technique58 implemented within TD-DFT in Kohn–Sham representation,50,59 to simulate the charge carrier trapping and recombination processes in MAPbI3, Ii, Ii−1, Ii+1, and IO3−1 systems. Since nuclei are heavier and slower than electrons, we describe the nuclei and electrons with (semi)classical and quantum mechanics, respectively. The DISH algorithm provides the physical mechanism for the trajectory branching, and surface hops occur at decoherence events. Because phonon-induced loss of quantum coherence time is much shorter than electron–hole recombination time, incorporating the effect of decoherence into the NAMD simulations is required.60–62 The decoherence time is analogous to the pure-dephasing time in the optical response theory that can be obtained by the second-order cumulant approximation.63 This approach has been used to study the photoexcitation charge dynamics in a broad range of systems,64–72 including perovskites,64–69,71 TiO2 contacting with graphene quantum dot interface,72 and black phosphorus.70 A detailed description of the approach can be found in the references.52,53A 192-atom 2 × 2 × 1 tetragonal73 supercell was used to represent the pristine MAPbI3. The neutral Ii structure is obtained by adding an iodine atom, colored green, into the pristine MAPbI3 system. The Ii−1 and Ii+1 systems are created via adding and removing an electron into/from the Ii structure. By introducing 3/2 O2 into the Ii−1 structure, we obtain the IO3−1 system. Geometry optimization, adiabatic MD, and NA coupling calculations are carried out with the Vienna Ab initio Simulation Package (VASP).74 The electron exchange–correlation effect is described with the Perdew–Burke–Ernzerhof (PBE) functional,75 and the electron–ion core interactions are treated with the projected-augmented wave (PAW) method.76 The energy cutoff of 400 eV is used to converge the total energy during geometry optimization with a Γ-centered 2 × 2 × 2 Monkhorst–Pack k-mesh.77 The adiabatic MD trajectory and NA couplings are obtained at Γ-point because the direct bandgaps for all five systems are at the Γ-point. In order to capture the weak van der Waals interactions within the perovskites, Grimme's DFT-D3 correction approach is used.78
After the geometry is optimized at 0 K, the five systems are heated to 300 K via velocity rescaling to 2 ps. Then, we obtained 6 ps adiabatic MD trajectories within the microcanonical ensemble simulations with a 1 fs atomic time step. In order to study the charge carrier trapping and recombination dynamics in the five systems, the first 4000 geometries of the 6 ps adiabatic MD trajectories were chosen as initial configurations for the NAMD simulations. During the NAMD simulations, the calculated energy gap of 1.65 eV for pristine MAPbI3 is scaled to the experimental value of 1.61 eV (ref. 79) by subtracting a constant. The energy gaps of Ii, Ii−1, Ii+1 and IO3−1 systems are subtracted the same constant. Because electron–hole recombination in perovskites occurs in a typical range from several nanoseconds to microseconds, it is a consuming task to solve the time-dependent Schrödinger equation on these timescales. Therefore, we run short-time NAMD simulations for each pair of states and obtain the rate constant for each process depicted in Fig. 1. Then, we construct the coupled equations, which are shown in ESI,† solve these equations using the obtained the rate constants, and obtain the long time-evolution populations of each state participating in the carrier relaxation. The details of the coupled kinetics equations and their solutions are presented in ESI.†
3. Results and discussion
We firstly focus on MAPbI3, and MAPbI3 containing interstitial iodine defects with all charged states (−1, 0, +1). The discussion starts with geometric structure and thermal fluctuations, followed by electronic structures, electron-vibrational interactions, and ends on charge trapping and recombination dynamics. Then, we investigate the effect of oxygen passivation on the geometry and charge dynamics of the IO3−1 system and find oxygen passivation can simultaneously inhibit ion migration and charge recombination.3.1 Geometric structure and thermal fluctuations
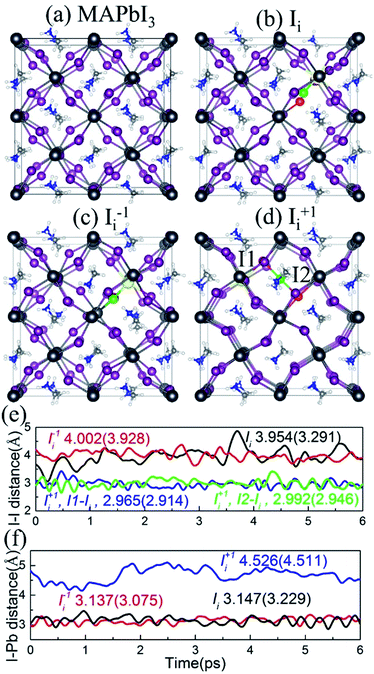
The optimized geometries of pristine MAPbI3 and MAPbI3 containing Ii, Ii−1 and Ii+1 are shown in Fig. 2a–d. The interstitial iodine atom and its nearest iodine and lead atoms are highlighted by green, red, and yellow spheres, and the corresponding I–I and I–Pb distances of the optimized geometry (numbers in parentheses) and their canonically averaged distances (numbers outside), as well as their time-evolution distances along the 6 ps trajectory, are shown in Fig. 2e and f. The inorganic I–Pb lattices are relatively rigid, while the MA cations are soft. In pristine MAPbI3, the MA cations are orderly arranged. Interstitial iodine atom gives rise to a small distortion of the I–Pb octahedrons around it, and most of the MA cations have rotated by different angles in the Ii, Ii−1 and Ii+1 systems. Neutral Ii forms an I–Pb chemical bond that pulls the interstitial iodine away from the lattice iodine, increasing the I–I distance to 3.291 Å at 0 K and 3.954 Å at 300 K (Fig. 2e). Negative Ii−1 repels the lattice iodine anion because they carry the same charge, with an increased I–I distance of 3.928 Å at 0 K and 4.002 Å at 300 K, while attracting the lattice lead cation, forming an I–Pb bond. On the contrary, positive Ii+1 repels the neighboring lead atom, while tending to attract lattice iodine anions, resulting in formation of an I-trimer. The bond lengths between the interstitial iodine and two adjacent iodides are close to each other at both 0 K and 300 K. As shown in Fig. 2f, the I–Pb distance is 3.229 Å in the Ii system, while it decreases slightly to 3.075 Å in the Ii−1 system and increases notably to 4.511 Å in the Ii+1 system at 0 K. The canonically averaged I–Pb distances become 3.147 Å, 3.137 Å and 4.526 Å in the Ii, Ii−1 and Ii+1 systems, respectively. The I–Pb distance of the Ii−1 system is shorter than that in the Ii system because the negatively charged interstitial iodine defect attracts the Pb cation. Alternatively, the I–Pb distance of the Ii+1 system is longer than that in the Ii system, arising due to the positively charged interstitial iodine defect pushing away the Pb cation in the presence of a repulsive force between them.In addition to the reported I–I and I–Pb distances, we computed the root-mean-square displacement velocity of atoms in the four systems to investigate the influence of oxidation state of the interstitial iodine defect on atomic fluctuations with thermal impact, by separating the atoms into organic (MA) and combined inorganic species (Pb and I). In order to further explore the effect of the defects, we differentiate the interstitial iodine atom from lattice Pb and I atoms in the defective systems (Table 1). The computed data show that interstitial iodine defects in all charged states accelerate the motion of all atoms in the order Ii+1 > Ii−1 > Ii compared to pristine MAPbI3. The sequence of the motions of both organic MA atoms and inorganic Pb/I atoms remains the same for all atoms, attributed to the correlated motions of organic and inorganic parts. The stronger motion in the defective systems than the pristine MAPbI3 indicates that the interstitial iodine defects lower the stability of perovskites; in particular, the instability primarily originates from the distortion of the inorganic I–Pb octahedrons due to their notably increased motions compared to the organic MA cations. The situation becomes stronger in the charged systems (Ii+1, Ii−1) compared to the neutral interstitial iodine system (Ii), rationalizing the larger migrations of iodine ions than iodine atoms.41,43,80–82 The analysis provides an excellent explanation that interstitial iodine defects significantly degrade perovskite films' exposure to light or thermal radiation.39
| Totala | MAb | Pb–Ic | Pb–Id | Ie | Of | |
|---|---|---|---|---|---|---|
| a Averaged on all atoms. b Averaged on atoms in MA. c Averaged on Pb and I atoms. d Averaged on Pb and I atoms except interstitial iodine atom. e Averaged on interstitial iodine atom. f Averaged on O atoms. | ||||||
| MAPbI3 | 0.0342 | 0.0469 | 0.0128 | — | — | — |
| Ii | 0.0352 | 0.0481 | 0.0141 | 0.0142 | 0.0059 | — |
| Ii−1 | 0.0356 | 0.0487 | 0.0140 | 0.0141 | 0.0066 | — |
| Ii+1 | 0.0374 | 0.0509 | 0.0152 | 0.0153 | 0.0060 | — |
| IO3−1 | 0.0300 | 0.0409 | 0.0130 | 0.0131 | 0.0055 | 0.0061 |
3.2 Electronic structure
Fig. 3a–d shows the projected density of states (PDOS) of the pristine MAPbI3, Ii, Ii−1 and Ii+1 systems, reflecting how the oxidation state of interstitial iodine affects the electronic structure. The charge densities of the key states involving charge trapping and recombination are displayed in the insets of Fig. 3. The PDOSs are split into MA, iodine and lead species. Apparently, VBM and CBM are mainly supported by iodine orbitals and lead orbitals, respectively. This situation favors weak NA coupling due to the small overlap between electron and hole wave functions according to the definition of NA electron–phonon coupling: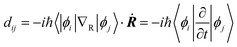 | (1) |
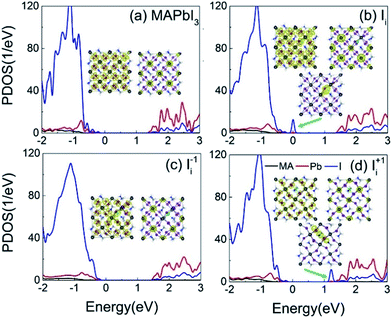 | ||
| Fig. 3 PDOSs of (a) pristine MAPbI3, (b) Ii, (c) Ii−1 and (d) Ii+1 systems. The insets show the charge densities of the key electronic states involved in the charge trapping and recombination. | ||
NA electron–phonon coupling arises due to the interaction between electronic and nuclear vibrational motions. The mixing of two wave functions of initial and final states directly determines the strength of NA coupling, dij. It is because inorganic iodine and lead atoms primarily create the electron–phonon coupling, leading to low electron–hole recombination rate. The organic MA species does not contribute to the band edges, while it simultaneously affects NA coupling in an indirect way and stabilizes the perovskite structure by filling the inorganic cages. The calculated bandgap of pristine MAPbI3 is 1.65 eV (Fig. 3a), agreeing well with the experimental data79 and DFT calculated values.83,84 Introduction of interstitial iodine for all charged states (0, −1, +1) into the pristine MAPbI3 has little influence on the bandgaps of the defective systems (Fig. 3b–d).
The neutral Ii defect creates a half-occupied trap state that is close to the VBM (Fig. 3b). Thus, it can trap holes or electrons, but the two processes cannot happen simultaneously due to the Pauli exclusion principle. Since the trap state is near the VBM that has strong NA coupling between the trap state and VBM due to a small energy gap, hole trapping becomes a major process. The trapped hole is populated, resulting in the Ii acting as a p-type dopant and introducing positive charge carriers near the VBM. As a result, photoexcited CB electrons can recombine with holes residing in both the VB and the trap state. The gap state is mainly localized on the interstitial iodine defect (inset of Fig. 3b). The increased charge density of VBM enhances the overlap between the VBM and CBM, strengthening the NA coupling between them compared to that in the pristine system.
The negatively charged iodine anion creates no gap state in the Ii−1 system (Fig. 3c). The interstitial iodine anion and lead cation form a strong I–Pb chemical bond, eliminating the unsaturated dangling bonds and moving the gap states into the VB. Iodine anion decreases the electron wave functions around itself while leaving the hole wave functions largely unchanged (inset of Fig. 3c) and, therefore, reducing their overlap, lowering NA electron–phonon coupling.
The positively charged iodine cation creates a trap state below the CBM in the Ii+1 system (Fig. 3d). The unoccupied trap state can serve as an electron acceptor, leading the Ii+1 to act as an n-type dopant, and produces negative charge carriers near the CBM. Because interstitial iodine cation and lattice iodine anions attract each other and form an I-trimer, the electron trap state is produced. Apparently, the I-trimer localizes the charge density on itself (inset of Fig. 3d), which also notably disturbs the I–Pb octahedrons and simultaneously decreases the charge densities of VBM and CBM (inset of Fig. 3d), and in particular for the CBM, further lowering the NA coupling between them with respect to the pristine and Ii−1 systems. Consequently, the photoexcited holes can recombine with the electrons located on both the CB and trap state. Because the energy gap between the trap state and the CBM is small, the electron trapping is expected to proceed very fast.
The analysis derived from Fig. 3 demonstrates that iodine chemistry has a significant influence on the electronic structure, and thus, on the charge trapping and recombination dynamics in perovskites.
3.3 Electron-vibrational interactions
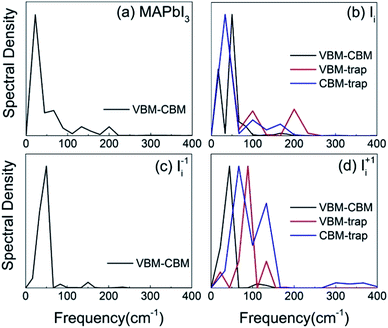
In order to identify the phonon modes that couple to the electronic subsystem and induce quantum transitions between the key pairs of states, we compute the influence spectrum by performing Fourier transforms (FTs) of the fluctuations of energy gaps. The intensity of each peak in the FTs marks the strength of electron–vibrational coupling at a given phonon frequency. Fig. 4 shows that low-frequency modes dominate spectral density because they come from the slow lead and iodine atoms that contribute to the CBM, trap state, and VBM. The major peaks around 100 cm−1 and below can be attributed to the I–Pb stretching and bending motions that create the majority of NA electron–phonon coupling.85,86 The phonon modes at 130–170 cm−1 can be interpreted as the librations of the organic cations. The peak around 200 cm−1 can be attributed to the torsional mode of the MA cations.86 It is reasonable that phonon modes originating from the MA cations are presented because they can indirectly influence the electron–phonon coupling though electrostatic interactions. Interstitial iodine defects break lattice symmetry, produce localized states, and create high-frequency modes.The pure-dephasing times, summarized in Table 2, are computed using the second-order cumulant approximation of the optical response theory.63 Quantum transition between a pair of states requires formation of coherent superposition states via NA electron–phonon coupling. Short-lived superpositions facilitate slow dynamics, which can be interpreted by quantum Zeno effect in the limit of infinitely fast loss of coherence.87 The ∼10 fs decoherence times are significantly shorter than the electron–hole recombination times that take place over several nanoseconds in the MAPbI3 perovskite.56 Thus, it is essential to consider the decoherence effect during the NAMD simulation.88 The short pure-dephasing times provide a reasonable explanation for the fact that perovskite materials have long excited state lifetimes, rationalizing the high performance of perovskite solar cells.
| Energy gap (eV) | NA coupling (meV) | Dephasing (fs) | Rate (×10−3 ps−1) | λ (eV) | ||
|---|---|---|---|---|---|---|
| Pristine | CBM → VBM | 1.61 | 1.02 | 10.8 | 0.64 | 0.071 |
| Ii | CBM → VBM | 1.70 | 2.09 | 8.7 | 1.85 | 0.063 |
| VBM → trap | 0.09 | 3.10 | 8.5 | 30.33 | 0.051 | |
| CBM → trap | 1.61 | 1.16 | 9.3 | 1.00 | 0.020 | |
| Hole trapping | — | — | — | — | 0.083 | |
| Electron trapping | — | — | — | — | 0.012 | |
| Ii−1 | CBM → VBM | 1.66 | 0.83 | 10.1 | 0.49 | 0.110 |
| CBM → VBM | 1.65 | 1.95 | 8.2 | 0.92 | 0.051 | |
| Ii+1 | Trap → VBM | 1.21 | 0.56 | 2.6 | 0.44 | 0.031 |
| CBM → trap | 0.44 | 2.12 | 3.4 | 23.81 | 0.020 | |
| IO3−1 | CBM → VBM | 1.69 | 0.73 | 7.0 | 0.24 | 0.011 |
3.4 Charge trapping and recombination
Next, we analyze the charge trapping and recombination processes depicted in Fig. 1 for the pristine MAPbI3 Ii, Ii−1 and Ii+1 systems. The time-evolution populations of key states are shown in Fig. 5. The time scales reported in Fig. 5 are obtained by fitting the data with an exponential function, The rise and decay components in the populations of trap states are fitted separately. The rate constants summarized in Table 2 are obtained by fitting the data shown in the ESI† with short-time NAMD simulations for each pair of states. The data presented in Fig. 5 are solutions of kinetics equations (ESI†) with the rate constants given in Table 2. The calculated timescales show that the oxidation state of interstitial iodine has strong influence on the charge trapping and recombination timescales in perovskites. In particular, charge carrier lifetime decreases in the sequence Ii+1 > Ii−1 > MAPbI3 > Ii.
The rise and decay components in the populations of trap states are fitted separately. The rate constants summarized in Table 2 are obtained by fitting the data shown in the ESI† with short-time NAMD simulations for each pair of states. The data presented in Fig. 5 are solutions of kinetics equations (ESI†) with the rate constants given in Table 2. The calculated timescales show that the oxidation state of interstitial iodine has strong influence on the charge trapping and recombination timescales in perovskites. In particular, charge carrier lifetime decreases in the sequence Ii+1 > Ii−1 > MAPbI3 > Ii.
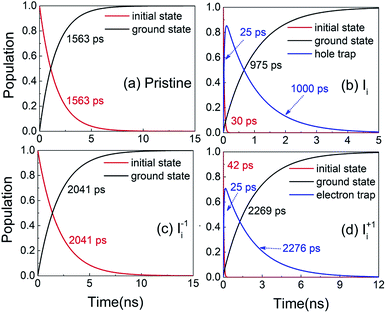 | ||
| Fig. 5 Evolution of populations of the key states for charge trapping and recombination in (a) pristine MAPbI3, (b) Ii, (c) Ii−1 and (d) Ii+1 systems. | ||
The electron–hole recombination in pristine MAPbI3 occurs in several nanoseconds (Fig. 5a), agreeing well with the experimental data.56 The long lifetime is attributed to the small NA coupling (1.02 meV) and short pure-dephasing time (10.8 fs). The electron–phonon coupling is small because the CBM and VBM are supported by lead and iodine atoms, Fig. 3a. The neutral Ii accelerates electron–hole recombination because the trap state provides new relaxation pathways (Fig. 5b). The trap state is across the Fermi level and above the VBM and is capable of trapping a photoexcited VB hole in tens of picoseconds due to a strong NA coupling of 3.10 meV. Once trapped, the hole can recombine with a CB electron in one nanosecond. Overall, the electron–hole recombination in the Ii system is accelerated by a factor of 1.6 compared with the pristine system. On the other hand, the occurrence of electron trapping is unlikely because the trap state is away from the CBM and the NA coupling between the states is small, 1.16 meV, making the direct recombination of CB electrons with the VB holes a highly impossible event because the process is 15 times slower than the hole trapping (Fig. S14 in ESI†). Therefore, neutral interstitial iodine accelerates the charge recombination via hole trap-assisted carrier relaxation pathways.
The negatively charged Ii−1 and positively charged Ii+1 defect suppress the electron–hole recombination by a factor of 1.3 (Fig. 5c) and 1.5 (Fig. 5d), respectively, operating by different mechanisms. The Ii−1 does not produce a mid-gap state (Fig. 3c) and possesses smaller NA electron–phonon coupling (0.83 meV) and comparable pure-dephasing time with respect to the pristine MAPbI3. A decrease in NA coupling occurs because the negatively charged interstitial iodine induces local geometry distortion and lowers electron wave functions, inset of Fig. 3c. The positively charged Ii+1 creates a trap state below the CBM, which can rapidly trap a CB electron in tens of picoseconds due to the large NA coupling of 2.12 meV. Once trapped, the VB hole can recombine with the trapped electron and a CB electron on a similar time scale of sub-3 nanoseconds. One should note that a direct electron–hole recombination between the CBM and VBM is negligible in the presence of Ii+1 defect because most electrons are trapped by the defect, followed by electron–hole recombination between the trap state and VBM. The deceleration in recombination is because the NA coupling (0.56 meV) reduces and pure-dephasing accelerates (Fig. 3 and Table 2). As a result, both negative and positive interstitial iodine can inhibit charge recombination and extend excited charge carriers' lifetimes. However, previous calculations show that Ii+1 easily captures an electron and converts to a neutral interstitial iodine,37 accelerating charge recombination and decreasing the excited-state lifetime.38,40 As a result, Ii−1 is the most possible interstitial iodine defect responsible for an extended excited-state lifetime and an enhanced solar cell performance.32 However, the mobile MA and I ions lead to unusual phenomena in LHP materials and optoelectronic/photovoltaic devices, such as current–voltage hysteresis and switchable photovoltaic effect, and degenerate the performance of devices.43
3.5 Oxygen passivation effect
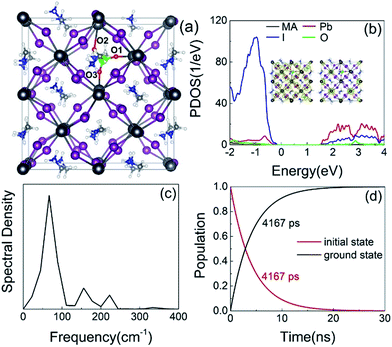
Finally, we consider the effect of oxygen-passivated negatively charged interstitial iodine that forms stable IO3−1 species.44 The optimized geometry (Fig. 6a) shows that the interstitial iodine atom forms three I–O chemical bonds with the three surrounding oxygen atoms, carrying almost identical bond length. The I–O(1)/(2)/(3) bond lengths are 1.843, 1.834, and 1.842 Å at 0 K, respectively. The averaged bond lengths of the 6 ps MD trajectory remain almost unchanged at 300 K, corresponding to 1.842, 1.828, and 1.847 Å. The change in bond length is smaller than that in the interstitial iodine defects for all charged states (0, −1, +1), which indicates the IO3−1 system becomes stable upon thermal fluctuations. The increased stability originates from the fact that the symmetric nature of the three I–O chemical bonds has little impact on the I–Pb octahedron. This observation is further supported by the calculated root-mean-square displacement velocity of atoms (Table 1). In addition to the grouped atoms discussed previously, we also present data for the oxygen atoms. First, the obtained data show that IO3−1 defect suppresses the motions of MA, Pb, and I and is responsible for a decreased NA coupling and reduced current–voltage hysteresis.57 Second, oxygen passivation also slows the motion of interstitial iodine atom compared to that in the defective perovskites. Third, the root-mean-square displacement velocity of oxygen atoms themselves is smallest. Overall, oxygen passivation can inhibit ion migration and stabilize the perovskite.44The PDOS shows that the IO3−1 defect creates no mid-gap state (Fig. 6b). Oxygen passivation does not change the components of the band edges, while it decreases the electron wave functions, and the hole wave functions remain unchanged (inset of Fig. 6b) compared to the Ii−1 system (inset of Fig. 3c), reducing the NA coupling further (0.73 meV). In Fig. 6c, FTs show that low-frequency modes dominate the spectral density, in agreement with Fig. 4. The dominant peak at 67 cm−1 can be assigned to the I–Pb bending.86 The peak at 155 cm−1 can be attributed to the librations of the organic cations.86 The frequencies in the 200–400 cm−1 range can be associated with the modes of oxygen/iodine product,44 agreeing with the fact that oxygen passivation stabilizes the perovskites, reflected by the almost unchanged I–O chemical bond lengths. Light and fast oxygen generates high-frequency modes and results in short dephasing time compared to the pristine and Ii−1 systems. Fig. 6d shows the time-evolution populations of the CBM and VBM, whose dynamics are depicted in Fig. 1a. The timescales are obtained by fitting the data to an exponent, 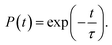 The recombination is delayed by a factor of 2.7 and 1.8 compared to the pristine and Ii−1 systems, respectively. The deceleration is attributed to the weak NA electron–phonon coupling and short pure-dephasing time. In particular, the NA coupling and pure-dephasing time are 0.73 meV and 7.0 fs in the present case, while they are 1.02 meV/10.8 fs and 0.83 meV/10.1 fs for the pristine and Ii−1 systems, respectively. Smaller electron–phonon coupling and shorter dephasing time favor a longer electron–hole recombination time.
The recombination is delayed by a factor of 2.7 and 1.8 compared to the pristine and Ii−1 systems, respectively. The deceleration is attributed to the weak NA electron–phonon coupling and short pure-dephasing time. In particular, the NA coupling and pure-dephasing time are 0.73 meV and 7.0 fs in the present case, while they are 1.02 meV/10.8 fs and 0.83 meV/10.1 fs for the pristine and Ii−1 systems, respectively. Smaller electron–phonon coupling and shorter dephasing time favor a longer electron–hole recombination time.
In addition to the above reported NA coupling, reorganization energy, λ, is another important parameter that reflects the charge transfer rate, which characterizes the energy cost due to geometry change experienced by a neutral to a charged system, and vice versa. In general, the lower the reorganization energy, the smaller the geometry relaxation and higher the charge transfer rate. Therefore, we calculated the reorganization energy using constrained DFT because this approach can well describe the unpaired electron, according to the equation:
| λ = E(M) − E(M*), | (2) |
The above discussions illustrate that the excited charge carriers' lifetimes can be significantly modulated by the oxidation state of interstitial iodine defects. Despite the ability of positive interstitial iodine to suppress electron–hole recombination, it tends to easily attract an electron to become a neutral defect that accelerates charge recombination. In turn, negative interstitial iodine favors the extension of charge carriers' lifetime, while the significant ion migrations in this case induce significant current–voltage hysteresis. The disadvantage is harmful to perovskite solar cells and even is a common problem in real applications because ion migration degrades perovskite films and devices. Oxygen can passivate negatively charged iodine defects and inhibit ion migration, as well as reduce hysteresis and nonradiative charge and energy losses, providing a mechanistic understanding for the prolonged excited charge carrier's lifetime in the presence of iodine defects and suggesting rational strategies to improve the photovoltaic performance of perovskite solar cells.
4. Conclusions
Using a combination of time-dependent density functional theory and nonadiabatic molecular dynamics, we have established the mechanisms responsible for charge trapping and recombination in MAPbI3 perovskites influenced by the oxidation state of interstitial iodine and oxygen doping. The calculated electron–hole recombination in pristine MAPbI3 occurs within several nanoseconds, in good agreement with the experiment. Negative interstitial iodine reduces charge recombination by a factor of 1.3 without creating trap states, due to the absence of unsaturated chemical bonds. Positive interstitial iodine produces an unoccupied trap below the CBM that can trap an electron. The trap state arises from the interstitial iodine cation forming an I-trimer with adjacent lattice iodine anions. Surprisingly, conduction band free electrons become trapped extremely fast, leading to a delayed recombination of the trapped electron with the valence band hole by a factor of 1.5. In turn, the direct band-to-band recombination of free electron and hole is highly excluded, although this process operates on a similar timescale. Unfortunately, a positive interstitial iodine defect easily tends to convert to a neutral iodine defect by capturing an electron, forming a singly occupied state above the VBM. Because of strong NA coupling between the trap state and VBM, the photoexcited hole proceeds to be rapidly trapped by the hole trap. Then, the recombination between the conduction band free electron and the trapped hole is accelerated by a factor of 1.6. Consequently, negative interstitial iodine is responsible for slowing charge recombination, while suffering from notable hysteresis due to ion migration. The instability of interstitial iodine defects under light and/or thermal radiation can be compensated by oxygen doping, because charged interstitial iodine defects with oxygen passivation forms stable IO3−1 species, which inhibits ion migration and stabilizes perovskites. At the same time, oxygen passivation reduces the NA electron–phonon coupling due to diminishing overlap of electron and hole wave functions, and it shortens the coherence time because light and fast oxygen atoms are active at higher frequencies, resulting in reduction of the band-to-band recombination of free electron and hole by a factor of 2.7. The nonradiative charge trapping is promoted by low-frequency Pb–I vibrations. Neutral and positive interstitial iodine defects produce higher frequencies due to the creation of localized states, and they generate stronger electron–phonon coupling between the band edges and the trap states.This study advances our understanding of the oxidation state of interstitial iodine and the role oxygen plays in the charge dynamics of perovskites, providing valuable insights for the development of high-performance perovskite photovoltaic and optoelectronic devices.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the National Natural Science Foundation of China, grant no. 21573022, 51861135101, 21688102, 21590801, and 21703222. R. L. acknowledges financial support from the Fundamental Research Funds for the Central Universities, the Recruitment Program of Global Youth Experts of China, and the Beijing Normal University Startup.References
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz and H. Tribukait, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Science, 2015, 348, 1234–1237 CrossRef CAS PubMed.
- D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger and K. Katsiev, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Chem. Sci., 2017, 8, 5628–5635 RSC.
- W.-W. Wang, J.-S. Dang, R. Jono, H. Segawa and M. Sugimoto, Chem. Sci., 2018, 9, 3341–3353 RSC.
- X. Lü, W. Yang, Q. Jia and H. Xu, Chem. Sci., 2017, 8, 6764–6776 RSC.
- D. Li, C. Sun, H. Li, H. Shi, X. Shai, Q. Sun, J. Han, Y. Shen, H.-L. Yip and F. Huang, Chem. Sci., 2017, 8, 4587–4594 RSC.
- E. T. Hoke, D. J. Slotcavage, E. R. Dohner, A. R. Bowring, H. I. Karunadasa and M. D. McGehee, Chem. Sci., 2015, 6, 613–617 RSC.
- B. Yang, O. Dyck, J. Poplawsky, J. Keum, S. Das, A. Puretzky, T. Aytug, P. C. Joshi, C. M. Rouleau and G. Duscher, Angew. Chem., Int. Ed., 2015, 54, 14862–14865 CrossRef CAS PubMed.
- H. Sun, K. Deng, Y. Zhu, M. Liao, J. Xiong, Y. Li and L. Li, Adv. Mater., 2018, 30, 1801935 CrossRef PubMed.
- H. Sun, W. Tian, F. Cao, J. Xiong and L. Li, Adv. Mater., 2018, 30, 1706986 CrossRef PubMed.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Y. Zhu, Nat. Mater., 2015, 14, 636–642 CrossRef CAS PubMed.
- S. Kumar, J. Jagielski, T. Tian, N. Kallikounis, W.-C. Lee and C.-J. Shih, ACS Energy Lett., 2018, 4, 118–125 CrossRef.
- Y.-S. Chen, J. S. Manser and P. V. Kamat, J. Am. Chem. Soc., 2015, 137, 974–981 CrossRef CAS PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- NREL, Efficiency chart, 2019, https://www.nrel.gov/pv/assets/pdfs/best-reserch-cell-efficiencies.20190411.pdf.
- K. Masuko, M. Shigematsu, T. Hashiguchi, D. Fujishima, M. Kai, N. Yoshimura, T. Yamaguchi, Y. Ichihashi, T. Mishima and N. Matsubara, Journal of Photovoltaics, 2014, 4, 1433–1435 Search PubMed.
- S. Rühle, Sol. Energy, 2016, 130, 139–147 CrossRef.
- J. Kim, S.-H. Lee, J. H. Lee and K.-H. Hong, J. Phys. Chem. Lett., 2014, 5, 1312–1317 CrossRef CAS PubMed.
- J. M. Ball and A. Petrozza, Nat. Energy, 2016, 1, 16149 CrossRef CAS.
- G. Gordillo, C. Otálora and A. Ramirez, Phys. Chem. Chem. Phys., 2016, 18, 32862–32867 RSC.
- A. B. Djurišić, F. Liu, A. M. C. Ng, Q. Dong, K. W. Man, A. Ng and C. Surya, Phys. Status Solidi RRL, 2016, 10, 281–299 CrossRef.
- W. J. Yin, T. Shi and Y. Yan, Appl. Phys. Lett., 2014, 104, 063903 CrossRef.
- R. Long, W. Fang and A. V. Akimov, J. Phys. Chem. Lett., 2016, 7, 653–659 CrossRef CAS PubMed.
- M. H. Du, J. Phys. Chem. Lett., 2015, 6, 1461–1466 CrossRef CAS PubMed.
- M. H. Du, J. Mater. Chem. A, 2014, 2, 9091–9098 RSC.
- A. Buin, P. Pietsch, J. Xu, O. Voznyy, A. H. Ip, R. Comin and E. H. Sargent, Nano Lett., 2014, 14, 6281–6286 CrossRef CAS PubMed.
- M. L. Agiorgousis, S. Yi-Yang, Z. Hao and Z. Shengbai, J. Am. Chem. Soc., 2014, 136, 14570–14575 CrossRef CAS PubMed.
- A. Buin, R. Comin, J. Xu, A. H. Ip and E. H. Sargent, Chem. Mater., 2015, 27, 4405–4412 CrossRef CAS.
- H. Uratani and K. Yamashita, J. Phys. Chem. Lett., 2017, 8, 742–746 CrossRef CAS PubMed.
- S. D. Stranks, V. M. Burlakov, T. Leijtens, J. M. Ball, A. Goriely and H. J. Snaith, Phys. Rev. Appl., 2014, 2, 034007 CrossRef.
- T. Leijtens, G. Eperon, A. Barker, G. Grancini, Z. Wei, J. Ball, A. R. S. Kandada, H. Snaith and A. Petrozza, Energy Environ. Sci., 2016, 9, 3472–3481 RSC.
- X. Wen, Y. Feng, S. Huang, F. Huang, Y.-B. Cheng, M. Green and A. Ho-Baillie, J. Mater. Chem. C, 2016, 4, 793–800 RSC.
- G. J. A. H. Wetzelaer, M. Scheepers, A. M. Sempere, C. Momblona and H. J. Bolink, Adv. Mater., 2015, 27, 1837–1841 CrossRef CAS PubMed.
- M. Z. Bellus, M. Mahjouri-Samani, S. D. Lane, A. D. Oyedele, X. Li, A. A. Puretzky, D. Geohegan, K. Xiao and H. Zhao, ACS Nano, 2018, 12, 7086–7092 CrossRef CAS PubMed.
- L. Wang, C. Xu, M.-Y. Li, L.-J. Li and Z.-H. Loh, Nano Lett., 2018, 18, 5172–5178 CrossRef CAS PubMed.
- D. Meggiolaro and F. De Angelis, ACS Energy Lett., 2018, 3, 2206–2222 CrossRef CAS.
- W. S. Yang, B.-W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim and J. H. Noh, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- S. Wang, Y. Jiang, E. J. Juarez-Perez, L. K. Ono and Y. Qi, Nat. Energy, 2017, 2, 16195 CrossRef CAS.
- R. J. Stewart, C. Grieco, A. V. Larsen, G. S. Doucette and J. B. Asbury, J. Phys. Chem. C, 2016, 120, 12392–12402 CrossRef CAS.
- J. M. Azpiroz, E. Mosconi, J. Bisquert and F. De Angelis, Energy Environ. Sci., 2015, 8, 2118–2127 RSC.
- A. M. A. Leguy, J. M. Frost, A. P. Mcmahon, V. G. Sakai, W. Kockelmann, C. H. Law, X. Li, F. Foglia, A. Walsh and B. C. O'Regan, Nat. Commun., 2015, 6, 7124 CrossRef PubMed.
- Y. Yuan and J. Huang, Acc. Chem. Res., 2016, 49, 286–293 CrossRef CAS PubMed.
- D. Meggiolaro, E. Mosconi and F. D. Angelis, ACS Energy Lett., 2017, 2, 2794–2798 CrossRef CAS.
- J. F. Galisteo-López, M. Anaya, M. E. Calvo and H. Míguez, J. Phys. Chem. Lett., 2015, 6, 2200–2205 CrossRef PubMed.
- Y. Tian, M. Peter, E. Unger, M. Abdellah, K. Zheng, T. Pullerits, A. Yartsev, V. Sundström and I. G. Scheblykin, Phys. Chem. Chem. Phys., 2015, 17, 24978–24987 RSC.
- S. G. Motti, M. Gandini, A. J. Barker, J. M. Ball, A. R. S. Kandada and A. Petrozza, ACS Energy Lett., 2016, 1, 726–730 CrossRef CAS.
- R. Brenes, C. Eames, V. Bulović, M. S. Islam and S. D. Stranks, Adv. Mater., 2018, 30, 1706208 CrossRef PubMed.
- H.-H. Fang, S. Adjokatse, H. Wei, J. Yang, G. R. Blake, J. Huang, J. Even and M. A. Loi, Sci. Adv., 2016, 2, e1600534 CrossRef PubMed.
- C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001 CrossRef PubMed.
- S. A. Fischer, B. F. Habenicht, A. B. Madrid, W. R. Duncan and O. V. Prezhdo, J. Chem. Phys., 2011, 134, 024102 CrossRef PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2014, 10, 789–804 CrossRef CAS PubMed.
- A. E. Sifain, J. A. Bjorgaard, T. R. Nelson, B. T. Nebgen, A. J. White, B. J. Gifford, D. W. Gao, O. V. Prezhdo, S. Fernandez-Alberti and A. E. Roitberg, J. Chem. Theory Comput., 2018, 14, 3955–3966 CrossRef CAS PubMed.
- S. Huang, T. M. Inerbaev and D. S. Kilin, J. Phys. Chem. Lett., 2014, 5, 2823–2829 CrossRef CAS PubMed.
- J. R. Klein, O. Flender, M. Scholz, K. Oum and T. Lenzer, Phys. Chem. Chem. Phys., 2016, 18, 10800–10808 RSC.
- L. Yang, M. Wu, F. Cai, P. Wang, R. S. Gurney, D. Liu, J. Xia and T. Wang, J. Mater. Chem. A, 2018, 6, 10379–10387 RSC.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- E. R. Bittner and P. J. Rossky, J. Chem. Phys., 1995, 103, 8130–8143 CrossRef CAS.
- B. J. Schwartz, E. R. Bittner, O. V. Prezhdo and P. J. Rossky, J. Chem. Phys., 1996, 104, 5942–5955 CrossRef CAS.
- Z. Chaoyuan, N. Shikha, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 121, 7658–7670 CrossRef PubMed.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford university press, New York, 1995 Search PubMed.
- Z. Zhang, W. H. Fang, M. V. Tokina, R. Long and O. V. Prezhdo, Nano Lett., 2018, 18, 2459–2466 CrossRef CAS PubMed.
- J. He, W. H. Fang and R. Long, J. Phys. Chem. Lett., 2018, 9, 4834–4840 CrossRef CAS PubMed.
- L. Liu, W. H. Fang, R. Long and O. V. Prezhdo, J. Phys. Chem. Lett., 2018, 9, 1164–1171 CrossRef CAS PubMed.
- R. Long, J. Liu and O. V. Prezhdo, J. Am. Chem. Soc., 2016, 138, 3884–3890 CrossRef CAS PubMed.
- Z. Zhang, R. Long, M. V. Tokina and O. V. Prezhdo, J. Am. Chem. Soc., 2017, 139, 17327–17333 CrossRef CAS PubMed.
- J. He, M. Guo and R. Long, J. Phys. Chem. Lett., 2018, 9, 3021–3028 CrossRef CAS PubMed.
- Y. Wei and R. Long, J. Phys. Chem. Lett., 2018, 9, 3856–3862 CrossRef CAS PubMed.
- W. Li, Y.-Y. Sun, L. Li, Z. Zhou, J. Tang and O. V. Prezhdo, J. Am. Chem. Soc., 2018, 140, 15753–15763 CrossRef CAS PubMed.
- R. Long, D. Casanova, W. H. Fang and O. V. Prezhdo, J. Am. Chem. Soc., 2017, 139, 2619–2629 CrossRef CAS PubMed.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- C. Quarti, E. Mosconi, J. M. Ball, V. D'Innocenzo, C. Tao, S. Pathak, H. J. Snaith, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2016, 9, 155–163 RSC.
- D. Meggiolaro, E. Mosconi and F. De Angelis, ACS Energy Lett., 2018, 3, 447–451 CrossRef CAS.
- J.-H. Yang, W.-J. Yin, J.-S. Park and S.-H. Wei, J. Mater. Chem. A, 2016, 4, 13105–13112 RSC.
- W. Ming, S. Chen and M.-H. Du, J. Mater. Chem. A, 2016, 4, 16975–16981 RSC.
- G. Giorgi, J.-I. Fujisawa, H. Segawa and K. Yamashita, J. Phys. Chem. C, 2014, 118, 12176–12183 CrossRef CAS.
- C.-J. Yu, U.-G. Jong, M.-H. Ri, G.-C. Ri and Y.-H. Pae, J. Mater. Sci., 2016, 51, 9849–9854 CrossRef CAS.
- A. M. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodríguezmartínez, O. J. Weber, A. Pallipurath, M. I. Alonso and M. Campoyquiles, Phys. Chem. Chem. Phys., 2016, 18, 27051 RSC.
- C. Quarti, G. Grancini, E. Mosconi, P. Bruno, J. M. Ball, M. M. Lee, H. J. Snaith, A. Petrozza and F. D. Angelis, J. Phys. Chem. Lett., 2014, 5, 279–284 CrossRef CAS PubMed.
- S. V. Kilina, A. J. Neukirch, B. F. Habenicht, D. S. Kilin and O. V. Prezhdo, Phys. Rev. Lett., 2013, 110, 180404 CrossRef PubMed.
- J. Liu, A. J. Neukirch and O. V. Prezhdo, J. Phys. Chem. C, 2014, 118, 20702–20709 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Coupled kinetics equations and their solutions; data fitting for the state-to-state transition rates; time-evolution populations of the electron trap-assisted electron–hole recombination in Ii system; the electronic configurations for reactant (initial) and product (final) states of each dynamics process. See DOI: 10.1039/c9sc02353d |
| This journal is © The Royal Society of Chemistry 2019 |