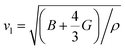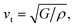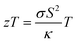Open Access Article
Open Access ArticleBonding heterogeneity and lone pair induced anharmonicity resulted in ultralow thermal conductivity and promising thermoelectric properties in n-type AgPbBiSe3†
Moinak
Dutta
a,
Koushik
Pal
b,
Umesh V.
Waghmare
b and
Kanishka
Biswas
 *a
*a
aNew Chemistry Unit, Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR), Jakkur P.O., Bangalore 560064, India. E-mail: kanishka@jncasr.ac.in
bTheoretical Sciences Unit, Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR), Jakkur P.O., Bangalore 560064, India
First published on 3rd April 2019
Abstract
Efficiency in generation and utilization of energy is highly dependent on materials that have the ability to amplify or hinder thermal conduction processes. A comprehensive understanding of the relationship between chemical bonding and structure impacting lattice waves (phonons) is essential to furnish compounds with ultralow lattice thermal conductivity (κlat) for important applications such as thermoelectrics. Here, we demonstrate that the n-type rock-salt AgPbBiSe3 exhibits an ultra-low κlat of 0.5–0.4 W m−1 K−1 in the 290–820 K temperature range. We present detailed analysis to uncover the fundamental origin of such a low κlat. First-principles calculations augmented with low temperature heat capacity measurements and the experimentally determined synchrotron X-ray pair distribution function (PDF) reveal bonding heterogeneity within the lattice and lone pair induced lattice anharmonicity. Both of these factors enhance the phonon–phonon scattering, and are thereby responsible for the suppressed κlat. Further optimization of the thermoelectric properties was performed by aliovalent halide doping, and a thermoelectric figure of merit (zT) of 0.8 at 814 K was achieved for AgPbBiSe2.97I0.03 which is remarkable among n-type Te free thermoelectrics.
1. Introduction
Almost all energy conversion processes liberate heat as their universal by-product with varying degrees. Minimizing this waste heat is thus of paramount importance, and a prime method for inhibiting such waste heat liberation is to have compounds that obstruct heat propagation. Hence compounds with innate low lattice thermal conductivity (κlat) are an intriguing prospect in this regard and can be utilized in the field of thermoelectrics.1–3 Typically, in crystalline solids, phonons and free charges are the primary carriers of heat. Since charge carriers are essential for efficient electrical conduction, inhibiting phonon propagation intrinsically is a primary method to reduce thermal conductivity, and is fostering significant attention towards developing materials with innately low κlat.4Investigations into the phonon-transport processes in solids with intrinsically low κlat led to unearthing of various avenues to enhance the phonon scattering processes. Skutterudites5 and clathrates6 accommodate rattling guest atoms in hollow structural cages, thereby decreasing the κlat. Similarly, Zintl chalcogenides are known to contain weakly bonded rattling cations within a rigid covalent anionic sublattice.7–9 Dynamic movement of cations in a crystalline matrix also causes lowering of κlatvia thermal damping effects.10–13 Site disorder and stereochemically active ns2 lone electron pairs cause lattice anharmonicity, thus lowering the κlat.14,15 Layered compounds are also known to have intrinsic ultralow κlat.3,16 Several extrinsic approaches were also demonstrated to lower κlat of compounds such as alloying, nano/meso structuring, etc.,17–19 but they come with a caveat of having to compromise on the electrical mobility. Thus, to develop compounds with intrinsically low κlat, a thorough investigation and fundamental understanding of their chemistry including bonding, lattice dynamics and thermal transport mechanisms is essential.
Herein, we observe an ultralow κlat of ca. 0.5 to 0.4 W m−1 K−1 for n-type AgPbBiSe3 in the temperature range of 290–823 K. AgPbBiSe3 adopts a rock-salt type structure where the Ag/Pb/Bi cations remain statistically disordered in the 4a Wyckoff position while the 4b Wyckoff site is occupied by the anion Se.20 The thermoelectric properties of a few compounds of AgPbBiQ3 (Q = S/Se/Te) were previously measured only at low temperatures (2–300 K), but the zT remains very low and the fundamental reasons behind the low κlat were not explored in detail.20,21 To investigate the origin of the low κlat of AgPbBiSe3, we have performed low temperature heat capacity measurements, which reveal Einstein modes and hence the presence of low lying optical phonons. Using first-principles (DFT) calculations, we show a remarkable crystallographic inhomogeneity associated with distinct bonding environments of the statistically disordered cations (Ag/Pb/Bi) coordinated with anions (Se). We also find high mode Gruneisen parameters (ϒqν ∼ 20), which are a measure of lattice anharmonicity, and trace their origin to the presence of 6s2 lone pairs on Pb and Bi. The pair distribution function (PDF) derived from the experimentally obtained synchrotron X-ray diffraction patterns enabled us to determine the bonding and lattice environment in terms of the nearest neighbour atoms in real space and obtain valuable microscopic insights into the mechanism behind the low κlat. Results of the PDF analysis corroborate our theoretical inferences of bonding heterogeneity and the presence of lone pairs, which are responsible for inhibition of the heat carrying acoustic phonons.
Demonstrating low thermal conductivity, which is a prerequisite to realization of high thermoelectric performance, we have optimised the thermoelectric figure of merit (zT) of this n-type AgPbBiSe3via aliovalent halogen doping. We have observed a further reduction in the κlat of AgPbBiSe3 to 0.23 W m−1 K−1 at 823 K, which is attributed to point defect scattering. As a result, we report a two-fold increase in the zT from 0.43 for pristine AgPbBiSe3 at 818 K to 0.8 for AgPbBiSe2.97I0.03 at 814 K.
2. Experimental section
Reagents
Elemental silver (Sigma Aldrich, 99.99%), lead (Alfa Aesar, 99.999%), bismuth (Sigma Aldrich, 99.999%), selenium (Alfa Aesar, 99.9999%) and BiX3 (X = Cl, Br, I; Sigma Aldrich, 99.99%) were used as starting materials for the synthesis, without further purification.Synthesis
A stoichiometric ratio of the reagents was used to prepare ∼10 g crystalline ingots of AgPbBiSe3 and AgPbBiSe3−yXy (X = Cl, Br, I and y = 0.03 for Cl and I, 0.02 for Br). The reagents were poured into 8 mm inner diameter quartz ampoules and subsequently flame-sealed under a high vacuum of 10−5 Torr. The vacuum-sealed ampoules were then heated gradually to 723 K in 12 h to minimize Se evaporation, followed by heating up to 1223 K in 5 h. They were then soaked at that temperature for 10 h with constant shaking to ensure homogeneity in the sample. The obtained melt compound was then cooled slowly to room temperature in 15 h. Upon cooling the ingots obtained were cut into disk (having dimensions of 8 mm diameter and 2 mm thickness) and parallelepiped (∼2 × 3 × 8 mm3) shapes. The disk-shaped samples were used for thermal diffusivity measurements and the parallelepiped shaped samples were used for electrical transport measurements.Powder X-ray diffraction (PXRD)
PXRD of the finely ground samples was performed using a Bruker D8 diffractometer with Cu Kα (λ = 1.5406 Å) as the radiation source, for all the as-synthesized samples.Thermal conductivity
Disk shaped samples were used for the measurement of thermal diffusivity (D) via the laser flash technique using a Netzsch LFA 457 instrument under a N2 atmosphere. The obtained diffusivity was then used to measure the thermal conductivity of the samples using the formula κ = DCpρ, where ρ is the density of the measured samples and Cp is the heat capacity using the Dulong–Petit limit. All the measured samples have a density greater than 94%. The error bars of the measured thermal conductivity data are within 10%.Electrical properties
Parallelepiped shaped samples were used for electrical transport measurements. All the samples were measured under a He atmosphere using an ULVAC-RIKO ZEM3 instrument. Both Seebeck coefficient and electrical conductivity were measured simultaneously within the temperature range 290–823 K.Hall measurement
Room temperature Hall measurement was performed using an in-house set up under a varying magnetic field of 0.0–0.57 T. The samples used were bar shaped and the current used was 75 mA.Band gap measurement
A finely ground sample was used to obtain the optical band gap of the synthesized samples. The optical band gap was estimated using a FT-IR Bruker IFS 66V/S spectrometer within the range of 6000–400 cm−1. Absorption (α/S) data were derived using the Kubelka–Munk equation, α/S = (1 − R)2/(2R), where R is the reflectance and α and S correspond to absorption and scattering coefficient, respectively. The energy band gaps were deduced from the α/S vs. Eg (eV) plot.X-ray Pair Distribution Function (PDF)
Finely ground AgPbBiSe3 was used for the temperature dependent PDF. The experiment was performed at beamline P02.1, PETRA III, DESY, Hamburg. The data were obtained as a 2D .tiff image file which was then converted to a 1D .chi file using the software fit2D.22 The obtained .chi file where the intensities of the peaks were plotted against Q-space (in nm) was converted into real space (as a .gr file) using the software PDFgetX2.23 The obtained .gr file was then refined using the software PDFgui.24Computational methods
Our first-principles calculations are based on density functional theory (DFT) using the Vienna Ab initio Simulation Package (VASP).25,26 The potential energy of the interaction between the ionic core of an atom and valence electrons was treated within the projected augmented wave (PAW)27 method. The exchange and correlation energy of electrons was included within a generalized gradient approximated (GGA)28 functional parametrized by Perdew, Burke and Ernzerhof.29 Expansions of electronic wave functions on a plane wave basis were truncated with a cut-off energy of 520 eV. Brillouin Zone (BZ) integrations were sampled on a uniform mesh of 8 × 8 × 8 k-points. The discontinuity in the occupation numbers of the electronic states near the gap was smeared with the Fermi–Dirac distribution functions with a broadening of kBT = 0.04 eV. To model AgPbBiSe3 (in which Ag, Pb and Bi are statistically disordered at the cation sites) in our DFT calculations, we constructed an isotropic supercell containing 6 atoms (3 cations and 3 anions). This supercell basically consists of three primitive unit cells of a face centered cubic lattice. As there are three cations (Ag, Pb, and Bi) in the crystal structure, and three cation sites in our supercell, there would be a total of six possible configurations. After fully optimizing all the structures, we found them to be iso-energetic (the energy difference between any two structures is less than 10−5 eV f.u.−1). We used one of the structures to perform further calculations. We provide the lattice vectors, atomic positions and all six configurations of AgPbBiSe3 in Fig. S2 of the ESI.† As phonon frequencies obtained using this supercell revealed imaginary phonon modes at several points (including the zone center, i.e., Γ) in the Brillouin zone, we distorted the crystal structure by displacing atoms along the eigen vectors of the unstable phonon mode at Γ and relaxed the atomic positions (the internal degrees of freedom of the supercell). We used this relaxed supercell (which stabilizes the Γ-point phonons) in further calculations to determine the electronic structure and lattice dynamic properties of AgPbBiSe3.Phonon dispersion of AgPbBiSe3 was determined using the finite-displacement method using Phonopy30 and VASP calculations on a (2 × 2 × 2) supercell containing 48 atoms. The Gruneisen parameter (γ) measures the degree of lattice anharmonicity in a material. We estimated the mode Gruneisen parameter (γqv) of AgPbBiSe3 using a central difference formula and phonon frequencies calculated at volumes (1.02V0 and 0.98V0) around the equilibrium volume (V0) of the supercell. While we included the effect of spin–orbit coupling (SOC) in the calculations of the electronic structure, phonon frequencies were obtained without including the SOC in our calculations. To check the convergence of the phonon frequencies with respect to the supercell size, we used a 3 × 3 × 3 supercell (with 162 atoms) and the same convergence criteria as above with a slightly reduced k-point grid (2 × 2 × 2). The changes in the phonon frequencies are not very significant particularly for the acoustic phonon branches (Fig. S3, ESI†) Hence, all further calculations were performed using the (2 × 2 × 2) supercell.
3. Results and discussion
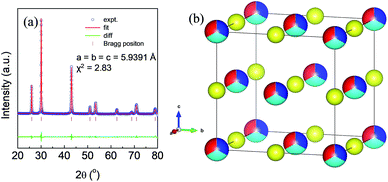
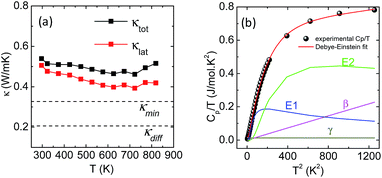
High quality pure crystalline ingots of AgPbBiSe3 were synthesized via a melting process under a high vacuum of 10−5 Torr. Fig. 1a shows Le Bail refinement of the powder-XRD data obtained using an in-house X-ray diffractometer (Cu Kα; λ = 1.5406 Å) with a cubic rock-salt model, which confirms that AgPbBiSe3 possesses a NaCl structure (space group, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The anion 4b Wyckoff site is occupied by the Se atoms whereas the cation 4a Wyckoff site is occupied by three cations in statistical disorder (i.e., Ag, Bi and Pb) as shown in Fig. 1b. The presence of 3 cations at the 4a Wyckoff site results in a greater degree of cation disorder in the crystal system. The global structure is apparently similar to rich LAST (AgPbmSbTe2+mi.e. PbTe rich),31 where 3 cations Ag/Pb/Sb at the same site provided enhanced scattering of phonons. Here too in Te free AgPbBiSe3, the positionally disordered cations at the same position were expected to result in lowering of thermal conductivity to a certain extent via a site scattering mechanism. Fig. 2a depicts the temperature dependent total thermal conductivity (κtot) and κlat of AgPbBiSe3. The κlat is found to be ultra-low and remains almost flat within the measured temperature range with values from 0.50 W m−1 K−1 at 296 K to 0.41 W m−1 K−1 at 818 K. Although the value is ultra-low it is found to be higher than the minimum κlat (0.206 W m−1 K−1) derived using the diffusion model32 as well as from Cahill's formulation (0.327 W m−1 K−1)33 which enhances the scope for further lowering of the κlat. The electronic contribution to the κtot is found to be very low and is given in Fig. S4, ESI.† For a better comprehension of this underlying ultralow lattice conductivity in AgPbBiSe3, we have measured the low temperature heat capacity Cp (∼2 K to ∼200 K; Fig. S5, ESI†). Fig. 2b shows the Cp/T vs. T2 plot with temperatures ranging from 2 K to 30 K. Modelling the plot using only Debye modes was insufficient; thus it was imperative to incorporate the Einstein oscillators for proper analysis of the data. The combined Debye–Einstein model8,10,34 (eqn (1)) is as follows.
m). The anion 4b Wyckoff site is occupied by the Se atoms whereas the cation 4a Wyckoff site is occupied by three cations in statistical disorder (i.e., Ag, Bi and Pb) as shown in Fig. 1b. The presence of 3 cations at the 4a Wyckoff site results in a greater degree of cation disorder in the crystal system. The global structure is apparently similar to rich LAST (AgPbmSbTe2+mi.e. PbTe rich),31 where 3 cations Ag/Pb/Sb at the same site provided enhanced scattering of phonons. Here too in Te free AgPbBiSe3, the positionally disordered cations at the same position were expected to result in lowering of thermal conductivity to a certain extent via a site scattering mechanism. Fig. 2a depicts the temperature dependent total thermal conductivity (κtot) and κlat of AgPbBiSe3. The κlat is found to be ultra-low and remains almost flat within the measured temperature range with values from 0.50 W m−1 K−1 at 296 K to 0.41 W m−1 K−1 at 818 K. Although the value is ultra-low it is found to be higher than the minimum κlat (0.206 W m−1 K−1) derived using the diffusion model32 as well as from Cahill's formulation (0.327 W m−1 K−1)33 which enhances the scope for further lowering of the κlat. The electronic contribution to the κtot is found to be very low and is given in Fig. S4, ESI.† For a better comprehension of this underlying ultralow lattice conductivity in AgPbBiSe3, we have measured the low temperature heat capacity Cp (∼2 K to ∼200 K; Fig. S5, ESI†). Fig. 2b shows the Cp/T vs. T2 plot with temperatures ranging from 2 K to 30 K. Modelling the plot using only Debye modes was insufficient; thus it was imperative to incorporate the Einstein oscillators for proper analysis of the data. The combined Debye–Einstein model8,10,34 (eqn (1)) is as follows.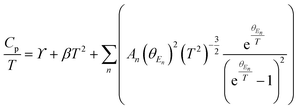 | (1) |
This combined Debye–Einstein model is composed of three terms. The temperature independent part of eqn (1), i.e., ϒ, signifies the electronic contribution. The second term, β, corresponds to contributions arising from Debye modes where,
| β = B(12π4NAκB/5)(θD)−3 | (2) |
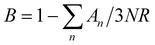 , where N and R represent the number of atoms per formula unit and the universal gas constant (8.314 J mol−1 K−1), respectively. The final term takes care of the Einstein oscillators, where An is the Einstein pre-factor to the nth Einstein mode (θEn). A minimum of 2 Einstein modes along with the Debye modes were mandatory for a better fitting of the low temperature Cp data (Fig. 2b). The individual contributions of each term are also plotted in Fig. 2b. The fitting parameters that are obtained are provided in Table S1, ESI.† The Debye temperature (θD) derived for AgPbBiSe3 is found to be 172 K. The characteristic temperature of the Einstein modes estimated from the fit are θE1 = 35.6017 K (∼24 cm−1) and θE2 = 74.47509 K (∼51 cm−1) which indicate the presence of low-lying optical modes. These low lying optical modes are pivotal for low κlat as they hinder the thermal flow via coupling with the heat-carrying acoustic phonons. We have determined the mean velocity of sound (vs) using the formula κBθD = ħ(6π2n)1/3vs,32 where n is the number density of atoms and ħ is the reduced Planck constant. The average or mean velocity of sound is derived to be ∼1710 m s−1.
, where N and R represent the number of atoms per formula unit and the universal gas constant (8.314 J mol−1 K−1), respectively. The final term takes care of the Einstein oscillators, where An is the Einstein pre-factor to the nth Einstein mode (θEn). A minimum of 2 Einstein modes along with the Debye modes were mandatory for a better fitting of the low temperature Cp data (Fig. 2b). The individual contributions of each term are also plotted in Fig. 2b. The fitting parameters that are obtained are provided in Table S1, ESI.† The Debye temperature (θD) derived for AgPbBiSe3 is found to be 172 K. The characteristic temperature of the Einstein modes estimated from the fit are θE1 = 35.6017 K (∼24 cm−1) and θE2 = 74.47509 K (∼51 cm−1) which indicate the presence of low-lying optical modes. These low lying optical modes are pivotal for low κlat as they hinder the thermal flow via coupling with the heat-carrying acoustic phonons. We have determined the mean velocity of sound (vs) using the formula κBθD = ħ(6π2n)1/3vs,32 where n is the number density of atoms and ħ is the reduced Planck constant. The average or mean velocity of sound is derived to be ∼1710 m s−1.
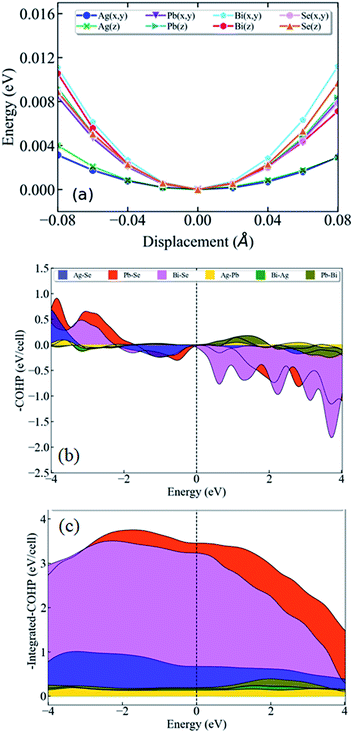
To learn further about the bonding environment and atomic dynamics within the crystal structure and their role in suppressing the κlat of AgPbBiSe3, we now present the results of first-principles density functional theory (DFT) calculations using the Vienna Ab initio Simulation Package (VASP).25,26 We analyse the chemical bonding environment in AgPbBiSe3 with the real space charge density and electron localization function (ELF). Charge density analysis (Fig. S6b, ESI†) reveals that electron clouds of more electropositive Bi atoms strongly overlap with Se, suggesting a strong covalent character of the bonding between them. On the other hand, the electron clouds around less electropositive Ag and Pb cations overlap relatively weakly with the anions, indicating weaker bonding. Co-existence of such strong and weak bonding and cationic disorder give rise to crystallographic heterogeneity, resulting in low lattice thermal conductivity in materials.7,8,16,35 To demonstrate the impact of bonding heterogeneity on the dynamics of the atoms, we calculated the potential energy (Fig. 3a) landscape of atomic displacements around their equilibrium positions in x- and z-directions. A shallow potential well of displacements of Ag atoms (see Fig. 3a) signifies the fact that Ag atoms are loosely bound to the lattice, and their vibrations result in greater dynamic structural disorder and entropy. Due to their relatively stronger bonding, Bi, Pb and Se atoms have deeper potential energy wells than Ag (Fig. 3a). Larger amplitudes of atomic vibrations of Ag atoms than of Pb, Bi and Se are also evident in the visualization of eigen vectors of the lowest energy optical phonons at the Γ point (Fig. S7, ESI†). The visualization of the eigen vectors at 30 cm−1 and 50 cm−1 (Fig. S7, ESI†) shows a greater vibration of Ag, which indicates that Ag is loosely bound to the lattice as compared to other cations which leads to the origin of these low lying optical phonons. These low energy Ag vibrations can be compared to the low lying optical modes derived from low temperature heat capacity (Cp) data.
We now present the crystal orbital Hamilton population (COHP) analysis, in which the energy of electronic states of a crystal is partitioned into pairwise orbital interactions, enabling quantification of the role of atomic orbitals in chemical bonding.36,37 Moreover, the integrated COHP (iCOHP) gives the contribution of a chemical bond to the band energy, indicating its strength.38,39 Here, we have used the LOBSTER code36 COHP analysis of different nearest neighbor pairs of atoms of AgPbBiSe3. We find that the nearest neighbor Ag–Se interaction results in the weakest peak (Fig. 3b) in COHP curves below the Fermi level, showing weaker interaction of Ag than of the other cations. As expected, the integrated COHP for Ag–Se interaction is the smallest (see area under the curves in Fig. 3c) confirming the weakest binding of Ag atoms to the lattice of AgPbBiSe3.
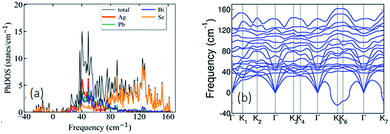
Visualization of the electron localization function (Fig. S6c, ESI†) shows the presence of lone pairs around Bi and Pb atoms. Lone pairs are known to play an important role in reducing the κlat in many well-known thermoelectric materials.14,15 To quantify this effect of the lone pairs in AgPbBiSe3, we calculated the mode Gruneisen parameters (ϒqν) which are a measure of the degree of anharmonicity in a lattice. They specifically give the third order interaction between phonons and acoustic waves (primary carriers of heat). Very high values of ϒqν (∼20) of the lowest energy optical phonons and of phonons in the acoustic branches (Fig. S8, ESI†) along several high symmetric directions (e.g., Γ-K1, Γ-K2 and Γ-K3) in the Brillouin zone indicate strong scattering of acoustic phonons by inhomogeneous strains associated with cationic disorder. Projected phonon density of states, DOS (Fig. 4a) reveals that low frequency optical modes (<50 cm−1) are dominated by vibrations of Ag atoms followed by the contributions from Pb and Bi atoms. This is also evident in the atom projected phonon dispersion curves (Fig. S9, ESI†). The role of the cations in the optical–acoustic phonon scattering processes is evident from the avoided crossing between the branches of acoustic and low frequency optical modes in the phonon dispersion (Fig. S10, ESI†). Thus, lone pairs of Bi and Pb atoms cause strengthening of their bonds with Se by off-centering, and consequent weakening of Ag–Se bonds. This results in a combination of chemical and structural heterogeneity at atomic scales, leading to suppression of relaxation times of acoustic phonon scattering and hence low κlat of AgPbBiSe3.
Calculated phonon dispersion (Fig. 4b) shows that the cut-off frequencies of the acoustic modes are quite low (<50 cm−1), suggesting low sound velocity which further contributes to lowering the thermal conductivity in AgPbBiSe3, through quadratic dependence (within the kinetic theory): κlat = 0.33Cvvs2τ. Here, Cv corresponds to the heat capacity at a constant volume, vs is the average sound velocity and τ denotes the phonon relaxation time. In Table S2, ESI† the cut-off frequencies for the longitudinal (LA) and two transverse (TA1 and TA2) acoustic modes for the in-plane and out-of-plane directions in the Brillouin zone are listed. The low cut-off frequency points are due to the presence of heavy atoms and the bonding inhomogeneity amongst them. The average sound velocity (vs) of AgPbBiSe3 is 1860 m s−1, calculated using 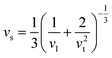 , which agrees well with the sound velocity (1710 m s−1) derived from the Cp measurements. We estimated the longitudinal (vl = 3310 m s−1) and transverse (vt = 1610 m s−1) sound velocities of this compound through the equations:
, which agrees well with the sound velocity (1710 m s−1) derived from the Cp measurements. We estimated the longitudinal (vl = 3310 m s−1) and transverse (vt = 1610 m s−1) sound velocities of this compound through the equations:
and
In mixed-valence systems, phonon scattering is enhanced by the electron charge transfer which contributes to a further reduction of κlat.20 To determine if there is any charge transfer occurring in AgPbBiSe3, we calculated the dynamical (born effective) charges (Z*), and found significant deviations from the nominal valence charges of each atom: (Ag: Z*xx(yy) = 2.3, Z*zz = 2.1; Pb: Z*xx(yy) = 4.3, Z*zz = 5.1; Bi: Z*xx(yy) = 6.4, Z*zz = 5.9; Se: Z*xx(yy) = −6, Z*zz = −1.6). Such anomalously large positive charges of the cations and negative charges of the anions indicate dynamic (hopping) transfer of electronic charge from cations to the anions during polar vibrations.
An in-depth experimental analysis of the structure for this ensuing low κlat is complicated due to the presence of disordered cations which might induce lattice strain. This implies that the local bonding environment might be different from the average/global structure. Hence it is paramount to augment the traditional crystallographic measurements with local structure measuring techniques. The atomic pair distribution function (PDF) specializes in providing both diffuse scattering (which gives information regarding the structure at an atomic level) and Bragg scattering (which provides information regarding the global atomic structure), thus providing us microscopic insights into the role that the structure plays in reducing the thermal conductivity. Fig. 5a depicts the temperature dependent synchrotron X-ray PDF data from 100–400 K at an equal interval of 50 K as a function of r (in Å). A decrease in intensity and broadening of the peaks were observed, which is normally due to the enhanced thermal vibrations along high symmetry directions in the Brillouin zone with increasing temperature. The temperature dependent PDF data were fitted using the cubic model of AgPbBiSe3 and the goodness of fit (Rw) is shown in Fig. S11a, ESI.†
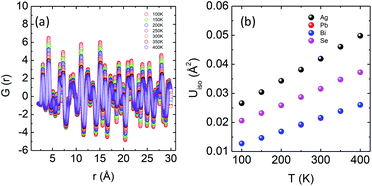 | ||
| Fig. 5 (a) Temperature dependent atomic PDF G(r) plots of AgPbBiSe3 plotted against real space. (b) Thermal ADPs of individual Ag, Pb, Bi and Se atoms plotted against temperature. | ||
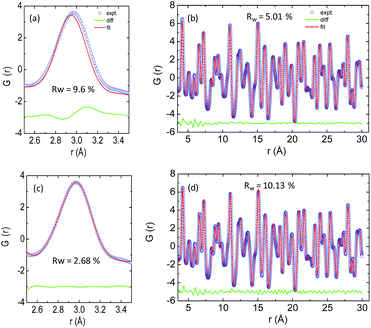
The temperature dependent lattice parameter, a is given in Fig. S11b, ESI† and is shown to linearly increase with temperature. The thermal parameter (Uiso) obtained from the refinement (please see the ESI† under the section “methods” for additional details regarding the refinement) clearly shows higher ADP values for Ag than for Se, with Bi and Pb having the lowest ADP values (Fig. 5b). ADPs of Pb are actually almost same as those of Bi and as a result ADPs of Bi overlap with those of Pb. The similar ADP values of both Pb and Bi are due to their similar size and the values are presented in Table S3, ESI.† The high ADP values of Ag compared to those of other atoms corroborate the theoretical prediction that the Ag atoms are loosely bonded in the crystal lattice and contribute to the anharmonicity, thereby suppressing κlat. Parts a and b of Fig. 6 represent the first peak (which provides information of the nearest atom–atom correlations) and total peak fitting using the cubic model, respectively. The blue circles correspond to the experimental data at a temperature of 100 K while the red line represents the fitted data. The difference between the fitted and experimental data is shown in green. It can be clearly seen that although the total average structure gives a good fit to the cubic model, the first peak which corresponds to the nearest anion to cation distance (i.e., at a distance of a/2) could not be properly fitted using the cubic model. To understand the local dynamics of the structure and subsequently their role in the low κlat of the compound, we tried to refine the first peak as it tells us about any local distortion in the system. We have observed that the best fit is possible when the cations are displaced from their original place in the 〈111〉 direction (see the ESI† for details).
Although the first peak gave a very good account of the local distortion, the overall fitting was worse compared to the cubic model as evident from the corresponding Rw values. Parts c and d of Fig. 6 show the fitting using the locally distorted cubic structure for the first atom–atom correlation and the total fit, respectively. It has been observed that by distorting Pb and Bi to a higher degree compared to Ag, the nature of the first peak fits better. Fig. S12, ESI† shows the first peak fitting at 400 K which can be compared with the first peak fitting at 100 K (Fig. 6c). The fitting of the first peak at these two temperatures (100 K and 400 K) was possible by off-centering Pb and Bi by 0.047 Å at 100 K and by 0.21 Å at 400 K. Ag gets off-centered to a lesser degree from 0.018 Å to 0.06 Å at 100 K and 400 K, respectively. The higher magnitude of off-centering in Pb and Bi might be due to the presence of 6s2 lone pair electrons, and is similar to that of PbTe and PbS, where it was argued that the stereochemical activity of 6s2 lone pairs of Pb2+ contributed to the off-centering of Pb and subsequent suppression of the κlat.40 Thus, lone pairs of Bi3+ and Pb2+ can be presumed to play a prominent role in suppressing κlatvia inducing strong lattice anharmonicity.
Hence, it can be argued that the low κlat in AgPbBiSe3 is a result of bonding heterogeneity whereby Ag, being loosely bonded, is effective in scattering heat carrying phonons as well as lone pairs of electrons on Pb and Bi which induce anharmonicity in the lattice.
Since materials with low κlat are useful in waste heat management, we have further improved the thermoelectric figure of merit in this n-type AgPbBiSe3via aliovalent halogen doping. The thermoelectric figure of merit (zT) of thermoelectric materials is determined using the formula
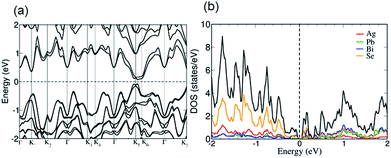
Band gap measurements reveal that n-type AgPbBiSe3 has a band gap (Eg) of 0.46 eV which is consistent with the earlier reported Eg of 0.48 eV.20 Halide doping in AgPbBiSe3 does not show any significant change in band gap as shown in Fig. S14, ESI† and the band gap values are given in Table S4, ESI.† The electronic structure (Fig. 7a) of AgPbBiSe3 determined from DFT calculations including spin–orbit coupling reveals that it possesses a small Eg of 0.14 eV. Theoretical calculations are known to underestimate band gaps of compounds and thus shows a lower value compared to the experimentally observed band gap. The projected electronic structure (Fig. S15, ESI†) and density of states (Fig. 7b) show that while valence bands just below the Fermi level are primarily constituted of orbital contributions of the Se atoms, the conduction bands above the Fermi level have contributions from all the atoms.
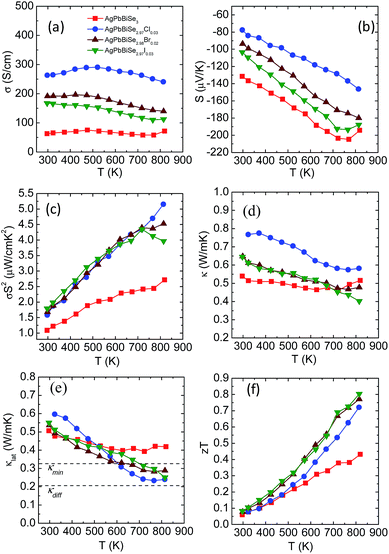
Electrical transport measurement has been performed for all the samples within the temperature range of 290–823 K. Electrical conductivity (σ), as expected, increases with halogen doping as it imparts an extra electron and can be understood via simple valence counting. For pristine AgPbBiSe3, the electrical conductivity at room temperature is 63 S cm−1 and rises slightly to 72 S cm−1 at 818 K (Fig. 8a). Cl doped AgPbBiSe2.97Cl0.03 contributes the most to enhancing the electrical properties. Doping with Cl increases the electrical conductivity to 263 S cm−1 at 297 K and 240 S cm−1 at 813 K compared to the pristine AgPbBiSe3 which has a considerably lower σ (Fig. 8a). Doping with Br and I increases the electrical conductivity too but the increase is considerably less compared to that with Cl (Fig. 8a). The difference in electrical conductivity with various doping is due to the respective size of the halogens. Cl, for which the size is close to that of Se as compared to Br and I, moves easily into the Se lattice and imparts the extra electron with better efficiency than Br or I. The carrier concentration and mobility of the doped AgPbBiSe3 are presented in Table S5, ESI† and resemble the electrical conductivity trend. The carrier concentration of pristine AgPbBiSe3 at room temperature is 1.44 × 1018 cm−3, which increases to 1.34 × 1019 cm−3 for AgPbBiSe2.97Cl0.03 (Table S5, ESI†). Similarly, the Seebeck coefficient (S) value measured for pristine AgPbBiSe3 is −131 μV K−1 at 296 K which increases to −204 μV K−1 at 770 K (Fig. 8b). The negative sign in the Seebeck coefficient value corresponds to n-type conduction which is also corroborated from the Hall measurement data. The S value decreases with the doping concentration which is in line with the electrical conductivity and carrier concentration (n) trend. The electrical conductivity and Seebeck co-efficient result in a power factor of 1.09 μW cm−1 K−2 at 296 K which increases to 2.71 μW cm−1 K−2 at 818 K for pristine AgPbBiSe3 (Fig. 8c). The power factor of the doped compounds is understandably higher compared to that of the pristine sample with a maximum power factor of ca. 5.15 μW cm−1 K−2 at 813 K for the Cl doped AgPbBiSe2.97Cl0.03 (Fig. 8c).
Fig. 8d and e depict the total thermal conductivity and lattice thermal conductivity of the doped compounds. It has been observed that the lattice thermal conductivity of the halogen doped AgPbBiSe3 decreases from 0.6 W m−1 K−1 at 290 K to around 0.23 W m−1 K−1 at 823 K. The decrease in the lattice thermal conductivity compared to that of the pristine counterpart is due to point defects arising from halogen doping which scatter the high frequency phonons. The carrier (n) vs. mobility (μH) plot (Fig. S16, ESI†) shows that the mobility decreases with the increase in carrier concentration. We noticed that μH ∼ n−1/3 dependency provides a correct description of their relationship, which indicates that the acoustic phonon scattering due to charge carriers is the major scattering process in these halogen doped samples.41
The thermoelectric figure of merit (zT) which takes into account the power factor and the thermal conductivity is found to be 0.43 for pristine AgPbBiSe3 at 818 K and it increases almost two-fold to 0.8 at 814 K in AgPbBiSe2.97I0.03, which is considerably high in n-type Te free compounds (Fig. 8f). In comparison, n-type AgBiSe2 has a peak zT of ∼0.9 at 810 K (ref. 42) and n-type (GeSe)0.50(AgBiSe2)0.50 exhibits a zT of 0.45 at 677 K.43 n-type BiSe achieved a zT of 0.8 at 425 K via Sb substitution.16 Polycrystalline n-type PbSe on the other hand achieved a peak zT of ∼1.8 at 723 K for PbSe0.998Br0.002-2%Cu2Se.44 Although PbSe based n-type thermoelectrics provide a much better zT, it is worth noting that it took almost a decade to achieve these types of zT values in PbSe. Our compound AgPbBiSe3 on the other hand is in its nascent stage and with further optimization of its electronic properties, a higher zT can also be achieved for AgPbBiSe3.
4. Conclusions
AgPbBiSe3 exhibits ultralow lattice thermal conductivity in the temperature range 290–823 K. Low temperature heat capacity experiments proved the presence of low lying optical phonon modes which are pivotal in scattering the heat-carrying acoustic phonons. Theoretical probing into the phonon mechanism using first principles DFT calculations revealed a high degree of anharmonicity arising from the chemical disorder of cations. The compound possesses bonding inhomogeneity wherein the Ag atoms are weakly bonded as compared to Pb and Bi in the lattice. Electron localization function analysis reveals the presence of 6s2 lone pairs in Pb and Bi which induce strong variation in the chemical bonding of cations, and hence the lattice anharmonicity. Thus, the synergistic presence of bonding heterogeneity and lattice anharmonicity arising from 6s2 lone pairs of Bi and Pb fosters low lattice thermal conductivity of 0.5 W m−1 K−1 at 296 K which further decreases to ca. 0.4 W m−1 K−1 at 818 K. Further reduction of this low thermal conductivity and enhancement in the power factor in the n-type AgPbBiSe3 compound have been performed by halogen substitution, and we achieved a high zT of 0.8 at 814 K in AgPbBiSe2.97I0.03. We hope that this fundamental understanding of the lattice thermal conductivity and its interplay with the structural aspects, chemical bonding and lattice dynamics will guide the designing and furnishing of new materials having low intrinsic thermal conductivity.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The work is supported by the Sheikh Saqr Laboratory and by the SERB (EMR/2016/651). M. D. acknowledges the University Grants Commission (UGC) for the research fellowship. UVW acknowledges support from a J C Bose National Fellowship of the Department of Science and Technology, Govt. of India and Sheikh Saqr Fellowship. Synchrotron X-ray measurements for this research were carried out at the light source PETRAIII at the DESY, a member of the Helmholtz Association (HGF). We would like to thank Dr J. C. Bednarcik for assistance at beamline P02.1, Petra III. Financial support from the Department of Science and Technology (Government of India) provided within the framework of the India@DESY collaboration is gratefully acknowledged.References
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- L.-D. Zhao, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2014, 7, 251–268 RSC.
- C. Chang, M. Wu, D. He, Y. Pei, C.-F. Wu, X. Wu, H. Yu, F. Zhu, K. Wang, Y. Chen, L. Huang, J.-F. Li, J. He and L.-D. Zhao, Science, 2018, 360, 778 CrossRef CAS PubMed.
- M. K. Jana and K. Biswas, ACS Energy Lett., 2018, 3, 1315–1324 CrossRef CAS.
- X. Shi, J. Yang, J. R. Salvador, M. Chi, J. Y. Cho, H. Wang, S. Bai, J. Yang, W. Zhang and L. Chen, J. Am. Chem. Soc., 2011, 133, 7837–7846 CrossRef CAS PubMed.
- T. Takabatake, K. Suekuni, T. Nakayama and E. Kaneshita, Rev. Mod. Phys., 2014, 86, 669–716 CrossRef CAS.
- M. K. Jana, K. Pal, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2016, 55, 7792–7796 CrossRef CAS PubMed.
- M. K. Jana, K. Pal, A. Warankar, P. Mandal, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2017, 139, 4350–4353 CrossRef CAS PubMed.
- S. Mukhopadhyay, D. S. Parker, B. C. Sales, A. A. Puretzky, M. A. McGuire and L. Lindsay, Science, 2018, 360, 1455 CrossRef CAS PubMed.
- H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422 CrossRef CAS PubMed.
- S. Roychowdhury, M. K. Jana, J. Pan, S. N. Guin, D. Sanyal, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2018, 57, 4043–4047 CrossRef CAS PubMed.
- S. N. Guin, J. Pan, A. Bhowmik, D. Sanyal, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2014, 136, 12712–12720 CrossRef CAS PubMed.
- B. Li, H. Wang, Y. Kawakita, Q. Zhang, M. Feygenson, H. L. Yu, D. Wu, K. Ohara, T. Kikuchi, K. Shibata, T. Yamada, X. K. Ning, Y. Chen, J. Q. He, D. Vaknin, R. Q. Wu, K. Nakajima and M. G. Kanatzidis, Nat. Mater., 2018, 17, 226–230 CrossRef CAS PubMed.
- S. N. Guin, A. Chatterjee, D. S. Negi, R. Datta and K. Biswas, Energy Environ. Sci., 2013, 6, 2603–2608 RSC.
- D. T. Morelli, V. Jovovic and J. P. Heremans, Phys. Rev. Lett., 2008, 101, 035901 CrossRef CAS PubMed.
- M. Samanta, K. Pal, P. Pal, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2018, 140, 5866–5872 CrossRef CAS PubMed.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414 CrossRef CAS PubMed.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634 CrossRef CAS PubMed.
- M. Samanta and K. Biswas, J. Am. Chem. Soc., 2017, 139, 9382–9391 CrossRef CAS PubMed.
- S. Sportouch, M. Basteat, P. Brazis, J. Ireland, C. R. Kannewurf, C. Uher and M. G. Kanatzidis, Mater. Res. Soc. Symp. Proc., 1999, 545, 123–130 CrossRef CAS.
- D. P. Spitzer, J. Phys. Chem. Solids, 1970, 31, 19–40 CrossRef CAS.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235–248 CrossRef.
- X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37, 678 CrossRef CAS.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- X. Hua, X. Chen and W. A. Goddard, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 16103–16109 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Hogan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2004, 303, 818 CrossRef CAS PubMed.
- M. T. Agne, R. Hanus and G. J. Snyder, Energy Environ. Sci., 2018, 11, 609–616 RSC.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131–6140 CrossRef CAS.
- H. Liu, J. Yang, X. Shi, S. A. Danilkin, D. Yu, C. Wang, W. Zhang and L. Chen, Journal of Materiomics, 2016, 2, 187–195 CrossRef.
- K. Pal, J. He and C. Wolverton, Chem. Mater., 2018, 30, 7760–7768 CrossRef CAS.
- R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- A. Lücke, U. Gerstmann, T. D. Kühne and W. G. Schmidt, J. Comput. Chem., 2017, 38, 2276–2282 CrossRef PubMed.
- E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis and S. J. L. Billinge, Science, 2010, 330, 1660 CrossRef PubMed.
- A. F. May, J.-P. Fleurial and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125205 CrossRef.
- S. N. Guin, V. Srihari and K. Biswas, J. Mater. Chem. A, 2015, 3, 648–655 RSC.
- S. Roychowdhury, T. Ghosh, R. Arora, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2018, 57, 15167–15171 CrossRef CAS PubMed.
- C. Zhou, Y. Yu, Y. K. Lee, O. Cojocaru-Mirédin, B. Yoo, S.-P. Cho, J. Im, M. Wuttig, T. Hyeon and I. Chung, J. Am. Chem. Soc., 2018, 140, 15535–15545 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Contains the method of refinement of PDF (Fig. S1), figures containing different unit cells (Fig. S2); phonon dispersion of different supercells (Fig. S3); low T Cp data (Fig. S4); κdiff values (Fig. S5); figures containing supercells, charge density and ELF of AgPbBiSe3 (Fig. S6); visualization of eigen vectors (Fig. S7); mode Gruneisen parameters (Fig. S8); phonon dispersion curves (Fig. S9); avoided acoustic–optical crossing (Fig. S10); temperature dependent Rw and lattice parameter, a (Fig. S11); local structure fit (Fig. S12), PXRD data (Fig. S13); band gaps (Fig. S14); atom projected electronic structure (Fig. S15); mobility vs. carrier plot (Fig. S16). Also contains tables of Cp/T vs. T2 refined parameters (Table S1); LA and TA frequencies (Table S2); Uiso values (Table S3); band-gap (Table S4); carrier conc. (n) vs. mobility (μH) (Table S5). See DOI: 10.1039/c9sc00485h |
| This journal is © The Royal Society of Chemistry 2019 |