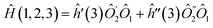Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revising the measurement process in the variational quantum eigensolver: is it possible to reduce the number of separately measured operators?†
Artur F.
Izmaylov
 *ab,
Tzu-Ching
Yen
ab and
Ilya G.
Ryabinkin
*ab,
Tzu-Ching
Yen
ab and
Ilya G.
Ryabinkin
 c
c
aDepartment of Physical and Environmental Sciences, University of Toronto Scarborough, Toronto, Ontario M1C 1A4, Canada
bChemical Physics Theory Group, Department of Chemistry, University of Toronto, Toronto, Ontario M5S 3H6, Canada. E-mail: artur.izmaylov@utoronto.ca
cOTI Lumionics Inc., 100 College Street 351, Toronto, Ontario M5G 1L5, Canada
First published on 12th February 2019
Abstract
Current implementations of the Variational Quantum Eigensolver (VQE) technique for solving the electronic structure problem involve splitting the system qubit Hamiltonian into parts whose elements commute within their single qubit subspaces. The number of such parts rapidly grows with the size of the molecule. This increases the computational cost and can increase uncertainty in the measurement of the energy expectation value because elements from different parts need to be measured independently. To address this problem we introduce a more efficient partitioning of the qubit Hamiltonian using fewer parts that need to be measured separately. The new partitioning scheme is based on two ideas: (1) grouping terms into parts whose eigenstates have a single-qubit product structure, and (2) devising multi-qubit unitary transformations for the Hamiltonian or its parts to produce less entangled operators. The first condition allows the new parts to be measured in the number of involved qubit consequential one-particle measurements. Advantages of the new partitioning scheme resulting in severalfold reduction of separately measured terms are illustrated with regard to the H2 and LiH problems.
1 Introduction
One of the most practical schemes for solving the electronic structure problem of current and near-future universal quantum computers is the variational quantum eigensolver (VQE) method.1–5 This approach involves the following steps: (1) reformulating the electronic Hamiltonian (Ĥe) in the second quantized form, (2) transforming Ĥe to the qubit form (Ĥq) by applying iso-spectral fermion-spin transformations such as Jordan–Wigner (JW)6,7 or more resource-efficient Bravyi–Kitaev (BK),8–12 (3) solving the eigenvalue problem for Ĥq by variational optimization of unitary transformations for a qubit wavefunction. The last step uses a hybrid quantum-classical technique where a classical computer suggests a trial unitary transformation U, and its quantum counterpart provides an energy expectation value of EU = 〈Ψ0|U†ĤqU|Ψ0〉, here |Ψ0〉 is an initial qubit wavefunction (it is frequently taken as an uncorrelated product of all spin-up states of individual qubits). The two steps, on classical and quantum computers, are iterated till convergence. The VQE was successfully implemented on several quantum computers and used for few small molecules up to BeH2.13One of the big problems of the VQE is that to calculate EU, the quantum computer measures parts of Hq rather than the whole Hq on the U|Ψ0〉 wavefunction. This stems from technological restrictions of what can be currently measured on available architectures. Dramatic consequences of this restriction can be easily understood with the following simple example. Let us assume that Ĥq =  + ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) , where  and
, where  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) are measurable components of Ĥq and [Â,
are measurable components of Ĥq and [Â, ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ] ≠ 0, otherwise they could be measured at the same time at least in principle. The actual hardware restrictions on measurable components are somewhat different and will be discussed later, for this illustration these differences are not important. Even if one has an exact eigenstate of Ĥq, U|Ψ0〉, measuring it on  or
] ≠ 0, otherwise they could be measured at the same time at least in principle. The actual hardware restrictions on measurable components are somewhat different and will be discussed later, for this illustration these differences are not important. Even if one has an exact eigenstate of Ĥq, U|Ψ0〉, measuring it on  or ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) would not give a certain result because  and
would not give a certain result because  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) do not commute with Ĥq. Thus, one would not be able to distinguish the exact eigenstate from other states by its zero variance. The origin of the discrepancy between quantum uncertainty given by the variance (Var) of Ĥq (true uncertainty) and by the sum of variances for  and
do not commute with Ĥq. Thus, one would not be able to distinguish the exact eigenstate from other states by its zero variance. The origin of the discrepancy between quantum uncertainty given by the variance (Var) of Ĥq (true uncertainty) and by the sum of variances for  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is neglect of covariances (Cov)
is neglect of covariances (Cov)
Var(Ĥq) = Var(Â) + Var(![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ) + Cov(Â, ) + Cov(Â, ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ) + Cov( ) + Cov(![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) , Â), , Â), | (1) |
| Var(Â) = 〈Â2〉 − 〈Â〉2, | (2) |
Cov(Â, ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ) = 〈Â ) = 〈Â![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) 〉 − 〈Â〉〈 〉 − 〈Â〉〈![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) 〉. 〉. | (3) |
Thus, even though the Ĥq average is equal to averages of  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) , the true quantum uncertainty of Ĥq is overestimated by a sum of variances for  and
, the true quantum uncertainty of Ĥq is overestimated by a sum of variances for  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) . Moreover, the number of measurements to sample  and
. Moreover, the number of measurements to sample  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is twice as many as that for Ĥq if the eigenstate nature of U|Ψ0〉 is not known a priori.
is twice as many as that for Ĥq if the eigenstate nature of U|Ψ0〉 is not known a priori.
The variance of any Hamiltonian depends only on the Hamiltonian and the wavefunction, but if one approximates the variance using only variances of Hamiltonian parts and neglects covariances between the parts, the result of such an approximation will depend on the partitioning. Importantly, the sum of variances for the Hamiltonian parts can either under- or overestimate the true Hamiltonian variance. To see how ignoring covariances can erroneously make estimates of the uncertainty arbitrarily small consider an artificial example, where the Hamiltonian variance is measured as n independent measurements of its Ĥq/n identical parts. Due to the linear scaling of the variance sum with n and the inverse quadratic scaling of variances of individual terms with n, the overall scaling of the variance is inversely proportional to n and can be made arbitrarily small by choosing large enough n. This follows from a wrong assumption that parts (Ĥq/n) are independent and covariances between them are zero.
Generally, the number of non-commuting terms in Ĥq grows with the size of the original molecular problem, and the total uncertainty from the measurement of individual terms will increase. This increase raises the standard deviation of the total measurement process and leads to a large number of measurements to reach convergence in the energy expectation value. The question we would like to address is whether it is possible to reduce the number of the Ĥq terms that needs to be measured separately.
In this paper we introduce a new systematic approach to decreasing uncertainty of the expectation energy measurement. We substitute the conventional measurement partitioning of the Hamiltonian with groups of qubit-wise commuting operators13,14 by partitioning to terms whose eigenstates can be found exactly using the mean-field procedure. Owing to a more general structure of such terms the Hamiltonian can be split into a fewer number of them. Interestingly, the general operator conditions on such mean-field terms have not been found in the literature and have been derived in this work for the first time. To decrease the number of these terms even further, we augment the mean-field treatment with few-qubit unitary transformations that allow us to measure few-qubit entangled terms. Measurement of newly introduced terms requires the scheme appearing in the cluster-state quantum computing,15,16 it is qubit-wise measurement with use of previous measurement results to define what single-qubit operators to measure next.
2 Theory
2.1 Qubit Hamiltonian
In order to formulate the electronic structure problem for a quantum computer that operates with qubits (two-level systems), the electronic Hamiltonian needs to be transformed iso-spectrally to its qubit form. This is done in two steps. First, the second quantized form of Ĥe is obtained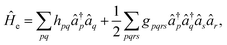 | (4) |
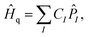 | (5) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) I are Pauli “words”, products of Pauli operators of different qubits
I are Pauli “words”, products of Pauli operators of different qubits![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) I = ⋯ I = ⋯![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) 2(I) 2(I)![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) 1(I), 1(I), | (6) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) i(I) is one of the
i(I) is one of the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , ŷ, ẑ Pauli operators for the ith qubit. The number of qubits N is equal to the number of spin-orbitals used in the second quantized form [eqn (4)]. Since every fermionic operator is substituted by a product of Pauli operators in both JW and BK transformations, the total number of Pauli words in Ĥq scales as N4.
, ŷ, ẑ Pauli operators for the ith qubit. The number of qubits N is equal to the number of spin-orbitals used in the second quantized form [eqn (4)]. Since every fermionic operator is substituted by a product of Pauli operators in both JW and BK transformations, the total number of Pauli words in Ĥq scales as N4.
2.2 Conventional measurement
In the conventional VQE scheme the Ĥq is separated into sums of qubit-wise commuting (QWC) terms,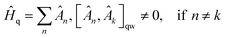 | (7) |
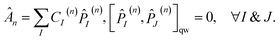 | (8) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) I(n),
I(n), ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) J(n)]qw denotes a qubit-wise commutator of two Pauli words, it is zero only if all one-qubit operators in
J(n)]qw denotes a qubit-wise commutator of two Pauli words, it is zero only if all one-qubit operators in ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) I(n) commute with their counterparts in
I(n) commute with their counterparts in ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) J(n). Clearly, if [
J(n). Clearly, if [![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) I(n),
I(n), ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) J(n)]qw then the normal commutator is [
J(n)]qw then the normal commutator is [![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) I(n),
I(n), ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) J(n)] = 0. The opposite is not true, a simple example is [
J(n)] = 0. The opposite is not true, a simple example is [![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2, ŷ1ŷ2] = 0 but [
2, ŷ1ŷ2] = 0 but [![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2, ŷ1ŷ2]qw ≠ 0. We will not be using non-zero results of the qubit-wise commutator and therefore their exact values are not important, but it is assumed that [.,.]qw is bi-linear for both operators.
2, ŷ1ŷ2]qw ≠ 0. We will not be using non-zero results of the qubit-wise commutator and therefore their exact values are not important, but it is assumed that [.,.]qw is bi-linear for both operators.
Partitioning of the Hq in eqn (7) allows one to measure all Pauli words within each Ân term in a single set of N one-qubit measurements. For every qubit, it is known from the form of Ân, what Pauli operator needs to be measured. The advantage of this scheme is that it requires only single-qubit measurements, which are technically easier than multi-qubit measurements. The disadvantage of this scheme is that the Hamiltonian may require measuring too many Ân terms separately.
A natural extension of partitioning in eqn (7) is to sum more general terms
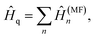 | (9) |
2.3 Mean-field Hamiltonians
What is the most general form of a qubit Hamiltonian whose eigenstates can be presented as single factorized products of one-qubit wavefunctions? Note that the well-known example of such Hamiltonians, separable operators,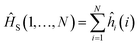 | (10) |
ĤMF(1,2) = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 + ẑ1ŷ2, 2 + ẑ1ŷ2, | (11) |
We formulate the general criterion for a Hamiltonian H(1,…N) to be in the MF class as follows. There should exist N one-particle operators {Ôk(k)}Nk = 1§ that commute [Ôk, ĤN−k+1] = 0 with the system of N Hamiltonians {ĤN−k+1}Nk = 1 constructed in the following way that we will refer as a reductive chain:
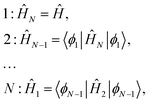 | (12) |
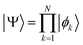 is an eigenfunction of Ĥ. Clearly, separable Hamiltonians are in the MF class because for them, Ôk's can be taken as ĥk(k) from eqn (10). However, note that because the system of Ôk operators is required to commute not with Ĥ but with the reduced set of Hamiltonians, the formulated criterion goes beyond separable Hamiltonians.
is an eigenfunction of Ĥ. Clearly, separable Hamiltonians are in the MF class because for them, Ôk's can be taken as ĥk(k) from eqn (10). However, note that because the system of Ôk operators is required to commute not with Ĥ but with the reduced set of Hamiltonians, the formulated criterion goes beyond separable Hamiltonians.
A general procedure to determine whether a particular qubit Hamiltonian Ĥ is in the MF class or not requires finding all N one-particle operators Ôk. The procedure starts with a check whether there is at least one qubit k for which
[Ĥ, (a![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k + bŷk + cẑk)] = 0 k + bŷk + cẑk)] = 0 | (13) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k + bŷk + cẑk is found its eigenstates can be integrated out to generate ĤN−1, and the procedure can be repeated to find Ô2 that commutes with ĤN−1.
k + bŷk + cẑk is found its eigenstates can be integrated out to generate ĤN−1, and the procedure can be repeated to find Ô2 that commutes with ĤN−1.
2.4 Measurement of mean-field Hamiltonians
Measuring an N-qubit mean-field Hamiltonian can be done by performing a single set of sequential N one-qubit measurements. Each qubit projective measurement in this set will collapse the measured wavefunction to an eigenstate of the corresponding single qubit operator. The single qubit operators that need to be measured are Ôk's operators. The definition of one particle operators may depend on the result of the previous measurement. Let us consider the mean-field Hamiltonian in eqn (11): Ô1(1) = ẑ1, and Ô2(2) =![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 ± ŷ2, where ± is determined by the eigenfunction chosen from the Ô1 spectrum to generate the Ĥ1 = 〈ϕ1±|ĤMF|ϕ1±〉 in the chain of eqn (12). This ambiguity does not allow one to present ĤMF as an operator with all qubit-wise commuting components. An attempt on this can be done by inserting the projectors on the eigenstates of ẑ1 instead of the operator:
2 ± ŷ2, where ± is determined by the eigenfunction chosen from the Ô1 spectrum to generate the Ĥ1 = 〈ϕ1±|ĤMF|ϕ1±〉 in the chain of eqn (12). This ambiguity does not allow one to present ĤMF as an operator with all qubit-wise commuting components. An attempt on this can be done by inserting the projectors on the eigenstates of ẑ1 instead of the operator:ĤMF = (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 + ŷ2)|ϕ1+〉〈ϕ1+| + ( 2 + ŷ2)|ϕ1+〉〈ϕ1+| + (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 − ŷ2)|ϕ1−〉〈ϕ1−| 2 − ŷ2)|ϕ1−〉〈ϕ1−| | (14) |
ĤMF = [(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 + ŷ2)(1 + ẑ1) + ( 2 + ŷ2)(1 + ẑ1) + (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 − ŷ2)(1 − ẑ1)]/2, 2 − ŷ2)(1 − ẑ1)]/2, | (15) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 ± ŷ2) parts do not.
2 ± ŷ2) parts do not.
Therefore, the scheme for measuring the ĤMF will be as shown in Fig. 1. Note that no matter how entangled the initial wavefunction is, measuring ĤMF does not require measuring ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 and ẑ1ŷ2 separately as was done in the regular VQE scheme.
2 and ẑ1ŷ2 separately as was done in the regular VQE scheme.
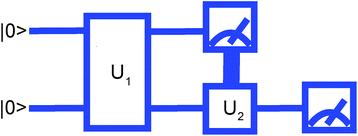 | ||
| Fig. 1 Measurement where the second qubit is rotated by U2 depending on the result of the first qubit measurement. | ||
In practice, qubit-wise measurements using previous measurement results to define what single-qubit operators to measure next, or feedforward measurements, have been implemented in quantum computers based on superconductor and photonic qubit architectures.18,19 The essential feasibility condition for the feedforward measurement is that the delay introduced by measurements is much shorter than the qubit coherence time. For superconducting (photonics) qubit architectures this condition has been achieved with typical timescales for a measurement and coherence as 2 μs (ref. 20) (150 ns (ref. 19)) and 40 μs (ref. 21) (100 ms (ref. 22)), respectively.
2.5 Mean-field partitioning
Even though regular molecular qubit Hamiltonians are not guaranteed to be in the MF class, it is always possible to split any N-qubit Hamiltonian into a sum of MF Hamiltonians. To see this, we will present a heuristic partitioning scheme that guarantees the MF partitioning.Our scheme uses ranking of all qubits k = 1,…,N based on a geometrical characteristic l(k), which is defined as follows. For an arbitrary qubit k, the total Hamiltonian can be written as
Ĥ = ĥx![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k + ĥyŷk + ĥzẑk + ĥe k + ĥyŷk + ĥzẑk + ĥe | (16) |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) x,y,z, we build matrix Ak = [
x,y,z, we build matrix Ak = [![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) x
x![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) y
y![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) z] with dimensions M by 3, where M is the number of different Pauli words in ĥx,y,z operators. To define l(k), we evaluate matrix Sk = A†kAk and assign l(k) = dim(ker(Sk)). Evaluating Sk is equivalent to obtaining the overlap between three vectors
z] with dimensions M by 3, where M is the number of different Pauli words in ĥx,y,z operators. To define l(k), we evaluate matrix Sk = A†kAk and assign l(k) = dim(ker(Sk)). Evaluating Sk is equivalent to obtaining the overlap between three vectors ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) x,y,z assuming the orthogonal basis, while the dimensionality of its kernel is the number of its zero eigenvalues.
x,y,z assuming the orthogonal basis, while the dimensionality of its kernel is the number of its zero eigenvalues.
l(k) allows one to answer a question on whether there is a transformation involving only the kth qubit that can present Ĥ in one of the two forms:
| Ĥ = ĥÔk + ĥe, | (17) |
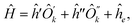 | (18) |
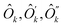 are operators containing only the kth qubit, and ĥ, ĥ′, ĥ′′ are the complementary operators that exclude the kth qubit. The positive answers in the forms of eqn (17) and (18) correspond to l(k) = 2 and l(k) = 1, respectively. l(k) = 2 is equivalent to the MF condition of eqn (13), with Ôk = a
are operators containing only the kth qubit, and ĥ, ĥ′, ĥ′′ are the complementary operators that exclude the kth qubit. The positive answers in the forms of eqn (17) and (18) correspond to l(k) = 2 and l(k) = 1, respectively. l(k) = 2 is equivalent to the MF condition of eqn (13), with Ôk = a![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k + bŷk + cẑk. For l(k) = 1, the MF treatment of the kth qubit is not possible but using eqn (18) the kth qubit dependence in the Hamiltonian can be somewhat compactified. Coefficients for
k + bŷk + cẑk. For l(k) = 1, the MF treatment of the kth qubit is not possible but using eqn (18) the kth qubit dependence in the Hamiltonian can be somewhat compactified. Coefficients for 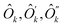 and ĥ, ĥ′, ĥ′′ operators can be found from non-zero eigenvectors of Sk (this process is detailed in Appendix B). The negative answer to the question leaves Ĥ in the original form of eqn (16) and is equivalent to l(k) = 0.
and ĥ, ĥ′, ĥ′′ operators can be found from non-zero eigenvectors of Sk (this process is detailed in Appendix B). The negative answer to the question leaves Ĥ in the original form of eqn (16) and is equivalent to l(k) = 0.
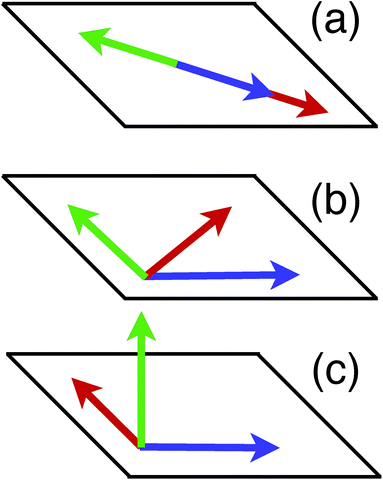
The question about possible compactification of the kth qubit dependence in the Hamiltonian has a simple geometric interpretation in terms of arrangement of the three vectors ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) x,y,z. These multi-dimensional vectors can be linearly independent (eqn (16)), located within some plane (eqn (18)), or collinear to each other (eqn (17)), Fig. 2 illustrates all three cases.
x,y,z. These multi-dimensional vectors can be linearly independent (eqn (16)), located within some plane (eqn (18)), or collinear to each other (eqn (17)), Fig. 2 illustrates all three cases.
Using a set of l(k)'s for a given Hamiltonian one can decide how many qubits can be treated using the MF procedure, these will be all qubits with l(k) = 2. Once all of such qubits have been considered, the MF partitioning of l(k) = 1 qubits begins. For l(k) = 1, the Hamiltonian can be split for any of such qubits into two parts: 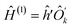 and
and 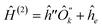 . In both parts the kth qubit can be treated using the MF treatment, which allows one to continue the consideration for ĥ′, ĥ′′ and ĥe. Finally, if only qubits with l(k) = 0 are left, then Ĥ needs to be partitioned to three Hamiltonians Ĥ(1) = ĥx
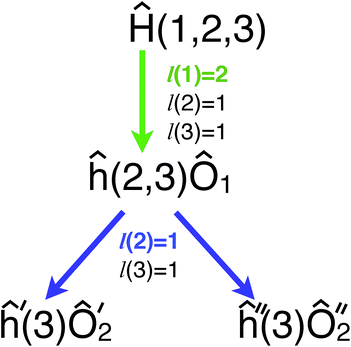
. In both parts the kth qubit can be treated using the MF treatment, which allows one to continue the consideration for ĥ′, ĥ′′ and ĥe. Finally, if only qubits with l(k) = 0 are left, then Ĥ needs to be partitioned to three Hamiltonians Ĥ(1) = ĥx![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k, Ĥ(2) = ĥyŷk, and Ĥ(3) = ĥzẑk + ĥe, where at least the kth qubit can be treated using MF. After this separation one can apply the reduction chain to each of the three operators. Fig. 3 illustrates the partitioning for a three qubit case detailed in Appendix B. In the case when reducing the kth qubit does not produce a Hamiltonian with reducible qubits the partitioning needs to be repeated, as in Fig. 3 when transforming qubit 1 led to h(2,3) where none of the qubits can be reduced.
k, Ĥ(2) = ĥyŷk, and Ĥ(3) = ĥzẑk + ĥe, where at least the kth qubit can be treated using MF. After this separation one can apply the reduction chain to each of the three operators. Fig. 3 illustrates the partitioning for a three qubit case detailed in Appendix B. In the case when reducing the kth qubit does not produce a Hamiltonian with reducible qubits the partitioning needs to be repeated, as in Fig. 3 when transforming qubit 1 led to h(2,3) where none of the qubits can be reduced.
Our scheme can be considered as an example of a greedy algorithm because at every step it tries to find locally the most optimal reduction, a qubit with the highest l(k). The reduction is only possible if there is linear dependency between complementary vectors 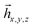 . The lower the dimensionality of the linear space, where these vectors are located, the more probable such linear dependence. Thus, treating qubits with the highest l(k) first is justified by the reduction of the space dimensionality along the reductive scheme. In the example of Fig. 3 treatment of qubits 2 and 3 in the beginning would require partitioning of the Hamiltonian to two branches for each of them, while leaving the 3rd qubit to the end did not generate any new terms for it.
. The lower the dimensionality of the linear space, where these vectors are located, the more probable such linear dependence. Thus, treating qubits with the highest l(k) first is justified by the reduction of the space dimensionality along the reductive scheme. In the example of Fig. 3 treatment of qubits 2 and 3 in the beginning would require partitioning of the Hamiltonian to two branches for each of them, while leaving the 3rd qubit to the end did not generate any new terms for it.
It is possible that more than one qubit will have the highest l(k). To do more optimal selection in this case, one would need to consider maxima of l(k) functions on qubits that enter complementary Hamiltonians ĥ for different reduction candidates. This consideration makes the partitioning computationally costly and was not performed in this work.
Applying the partitioning scheme guarantees to result in a sum of MF Hamiltonians that can be measured in N-qubit one-particle measurements. Since any linear combination of QWC terms form a MF Hamiltonian, this partitioning scheme cannot produce more terms than those used in the regular VQE measuring scheme.
2.6 Unitary transformations generating mean-fields
Partitioning the non-MF blocks in the Hamiltonian to obtain more MF terms leads to growth of the terms needed to be measured. An alternative treatment of non-MF groups is to search for multi-qubit operators that commute with them. Finding such operators may lead to unitary transformations that can transform non-MF Hamiltonians into Hamiltonians where qubits shared with the commuting operator can be treated using the mean-field procedure. Similar search for multi-qubit operators commuting with the system Hamiltonian was used recently by Bravyi and coworkers to reduce the qubit count in the conventional VQE scheme.23Let us consider an example where an N-qubit non-MF Hamiltonian Ĥ has a two-qubit operator Ô(2)(1,2) commuting with it (without loss of generality we can assume that Ô(2) acts on the first two qubits). Then, under certain conditions detailed in Appendix A, Ĥ allows for its eigenstates Ψ to be written as Ψ(1,…N) = Φ(1,2)ψ(3,…N), where Φ(1,2) is an eigenstate of Ô(2). One can always write Φ(1,2) = Û(1,2)ϕ1(1)ϕ2(2), where Û(1,2) is an operator entangling the product state ϕ1(1)ϕ2(2) into Φ(1,2). Using this unitary operator, one can obtain the Hamiltonian Ĥ12 = Û(1,2)†ĤÛ(1,2) that has an eigenstate Ψ12(1,…N) = ϕ1(1)ϕ2(2)ψ(3,…N) where qubits 1 and 2 are unentangled. Therefore, there should be one-particle operators of qubits 1 and 2 that commute with Ĥ12 and its MF-reduced counterpart. Finding these operators and their eigenfunctions ϕ1(1) and ϕ2(2) allows us to integrate out qubits 1 and 2
| ĤN−2 = 〈ϕ1ϕ2|H12|ϕ1ϕ2〉. | (19) |
Search for one- or multi-qubit operators commuting with ĤN−2 can be continued. The procedure to find commuting operators with increasing number of qubits requires exponentially increasing number of variables parametrizing such operators. Indeed, a k-qubit operator requires a 3k coefficient for all Pauli words in commutation equations similar to eqn (13), also the number of different k-qubit operators among N qubits is CNk ∼ Nk. Potentially, such operators always exist (e.g., projectors on eigenstates of the Hamiltonian) but the amount of resources needed for their search can exceed what is available. Thus we recommend interchanging this search with the partitioning described above if the multi-qubit search requires going beyond 2-qubit operators.
To illustrate the complete scheme involving multi-qubit transformations, let us assume that we can continue the reduction chain for Ĥ = ĤN by generating the set of Hamiltonians {ĤN, ĤN−2,…,Ĥk} using qubit unitary transformations {U(1,2), U(3,4,5),…,U(N − k,…N)} and integrating out variables from N to k. To take advantage of this reduction chain in measuring an expectation value of an arbitrary wavefunction χ(1,…N) on Ĥ, such a measurement should be substituted by the following set of conditional measurements:
Step 1: first two qubits are measured using Ĥ12 and the unitary transformed function |Û(1,2)†χ〉 because
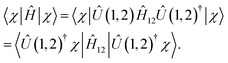 | (20) |
Depending on the results of these measurements the operator ĤN−2 is formulated and its unitary transformation U(3,4,5) is found. U(3,4,5) gives rise to the transformed Hamiltonian Ĥ35 = Û(3,4,5)†ĤN−2Û(3,4,5). The wavefunction after measuring qubits 1 and 2 is denoted as |χ12〉.
Step 2: qubits 3–5 are measured on Ĥ35 sequentially using the transformed wavefunction Û(3,4,5)†|χ12〉. Results of these measurements will define the next reduction step and the wavefunction that should be unitarily transformed for the next measurement.
These steps can be continued until all qubits have been measured. If resources allow for finding corresponding multi-qubit unitary transformations, the Ĥ Hamiltonian can be measured in N single-qubit measurements.
3 Numerical studies and discussion
To assess our developments we apply them to the Hamiltonians of the H2 and LiH molecules obtained within the STO-3G basis and used to illustrate the performance of quantum computing techniques previously.13,24,253.1 H2 molecule
The BK-transformed qubit Hamiltonian contains the following terms:ĤH2 = C0 + C1ẑ2 + C2ẑ3 + C3ẑ4 + C4ẑ1ẑ3 + C5ẑ2ẑ4 + C6ẑ3ẑ4 + C7ẑ1ẑ2ẑ3 + C8(1 + ẑ1)ẑ2ẑ3ẑ4 + C9ẑ1ẑ2ẑ4 + C10(1 + ẑ1)ŷ2ẑ3ŷ4 + C11(1 + ẑ1)![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 2ẑ3![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 4. 4. | (21) |
Ĥ24 = D0 + D1ẑ2 + D2ẑ4 + D3ẑ2ẑ4 + D4![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 4 + D5ŷ2ŷ4, 4 + D5ŷ2ŷ4, | (22) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 4], and the transformed MF Hamiltonian is
4], and the transformed MF Hamiltonian is| U(2,4)†Ĥ24U(2,4) = E0 + E1ẑ2 + E2ŷ2 + E3ŷ4 + E4ŷ2ŷ4 + E5ẑ2ŷ4, | (23) |
To illustrate the superiority of the scheme with the use of U(2,4) and measurements of the MF Hamiltonian over the regular approach with splitting ĤH2 to three groups of QWC operators, Table 1 presents variances for the Hamiltonian expectation value for two wavefunctions, the exact eigenfunction (ΨQCC) of and the mean-field approximation (ΨQMF) to the ground state of the H2 problem at R(H–H) = 1.5 Å.25 The exact solution measured in the new scheme (MF-partitioning 2p) gives only one value with zero variance, while the regular schemes give three distributions for each non-commuting term.
| Approach | Number of terms | Var (ΨQCC) | Var (ΨQMF) |
|---|---|---|---|
| a The number of terms corresponds to the number of separately measured N-qubit terms. For all partitionings, covariances have not been included in the Var estimates, which simulates practical estimation of the total variance. | |||
| H 2 | |||
| QWC-partitioning | 3 | 0.044 | 0.026 |
| MF-partitioning 2p | 1 | 0 | 0.053 |
| 〈ĤH22〉 − 〈ĤH2〉2 | 1 | 0 | 0.053 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| LiH | |||
| QWC-partitioning | 25 | 0.043 | 0.037 |
| MF-partitioning 1p | 13 | 0.029 | 0.036 |
| MF-partitioning 2p | 5 | 0.030 | 0.038 |
| 〈ĤLiH2〉 − 〈ĤLiH〉2 | 1 | 5.6 × 10−4 | 0.027 |
In the approximate wavefunction case, the true variance obtained from the Hamiltonian is larger than that of the conventional approach. This is a consequence of ignoring covariances in the conventional approach. The MF partitioning 2p variance is equal to the exact one, since it is obtained from measuring a single term (the MF Hamiltonian in eqn (23)) and thus does not neglect any covariances.
3.2 LiH molecule
We will consider the LiH molecule at R(Li–H) = 3.2 Å, it has a 6-qubit Hamiltonian containing 118 Pauli words (see Appendix C for details). This qubit Hamiltonian has 3rd and 6th stationary qubits, which allow one to replace the corresponding ẑ operators by their eigenvalues, ±1, thus defining the different “sectors” of the original Hamiltonian. Each of these sectors is characterized by its own 4-qubit effective Hamiltonian. The ground state lies in the z3 = −1, z6 = 1 sector; the corresponding 4-qubit effective Hamiltonian (ĤLiH) has 100 Pauli terms. Integrating out 3rd and 6th qubits can be done in the MF framework. The MF treatment of ĤLiH is not possible without its partitioning.Before discussing partitioning of ĤLiH it is worth noting that there are two 2-qubit operators commuting with Ĥ(4) (we re-enumerate qubits after the reduction from 6 to 4 qubits in the Hamiltonian)
| Ô1(2) = −ẑ1 + ẑ2 − ẑ1ẑ2 | (24) |
| Ô2(2) = −ẑ3 + ẑ4 + ẑ3ẑ4. | (25) |
Unfortunately, both operators have degenerate spectra with a single non-degenerate eigenstate and three degenerate states. Moreover, these degeneracies do not satisfy the factorability condition introduced in Appendix A thus proving it impossible to find 2-qubit unitary transformation that would factorize qubits 1 and 2 or 3 and 4.
Table 1 summarizes results of partitioning for ĤLiH and variances calculated for different wavefunctions and partitioning schemes. The partitioning involving only one-qubit transformations (MF-partitioning 1p) reduces the number of QWC terms by half. Involving the two-qubit transformations at the step before the last one in the MF partitioning reduces the number of terms to only 5 (MF-partitioning 2p), which is a fivefold reduction compared to the conventional QWC form. Alternative pathways in the MP partitioning scheme related to different choices of partitioned qubits with the same value of l(k) generated not more than 15 and 9 terms for MF partitioning 1p and 2p, respectively. As discussed previously, the qubit mean-field (ΨQMF) and qubit coupled cluster (ΨQCC) wavefunctions are considered, with the only difference that ΨQCC is a very accurate but not exact ground state wavefunction for LiH (thus there is a small but non-zero variance of the ĤLiH on ΨQCC). Details on the generation of these functions can be found in ref. 25. Variances across different partitionings do not differ appreciably and the main advantage of the MF-partitioning schemes is in the reduction of the number of terms that need to be measured.
4 Conclusions
We have introduced and studied a new method for partitioning of the qubit Hamiltonian in the VQE approach to the electronic structure problem. The main idea of our approach is to find Hamiltonian fragments that have eigenstates consisting of single products of one- and two-qubit wavefunctions. The most general criterion for identifying such Hamiltonian fragments was derived for the first time. Once such fragments are found the total wavefunction of the system can be measured on a fragment Hamiltonian in a single pass of N single-qubit measurements intertwined with one- and two-qubit rotations that are defined on-the-fly from results of previous qubit measurements. The main gain from such a reformulation is a decrease of separately measured Hamiltonian fragments. Indeed, illustrations on simple molecular systems (H2 and LiH) show three- and five-fold reductions of the number of terms that are needed to be measured with respect to the conventional scheme.In the process of deriving our partitioning procedure, we discovered criteria for eigenstate factorability for an arbitrary Hamiltonian acting on N distinguishable particles. Our criteria involve search for few-body operators commuting with the Hamiltonian of interest. Even though the criteria for factorability are exact, realistic molecular Hamiltonians do not satisfy them in general. Therefore, we needed to introduce a heuristic partitioning procedure (greedy algorithm) that splits the system Hamiltonian to fragments that have factorable eigenstates. Even though the procedure does not guarantee the absolutely optimal partitioning to the smallest number of terms, it does not produce more terms than the number of qubit-wise commuting sub-sets.
Interestingly, when one is restricted with single-qubit measurements, the commutation property of two multi-qubit operators  and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) has nothing to do with the ability to measure them together (see Table 2). This seeming contradiction with the laws of quantum mechanics arises purely from a hardware restriction that one can measure a single qubit at a time. On the other hand, qubit-wise commutativity is still a sufficient but not necessary condition for single-qubit measurability. Removing the single-qubit measurement restriction in the near future will not make our scheme obsolete but rather would allow us to skip the single-particle level. For example, if two-qubit measurements will be available, one can look for two-qubit operators commuting with the Hamiltonian and integrate out pairs of qubits to define next measurable two-qubit operators.
has nothing to do with the ability to measure them together (see Table 2). This seeming contradiction with the laws of quantum mechanics arises purely from a hardware restriction that one can measure a single qubit at a time. On the other hand, qubit-wise commutativity is still a sufficient but not necessary condition for single-qubit measurability. Removing the single-qubit measurement restriction in the near future will not make our scheme obsolete but rather would allow us to skip the single-particle level. For example, if two-qubit measurements will be available, one can look for two-qubit operators commuting with the Hamiltonian and integrate out pairs of qubits to define next measurable two-qubit operators.
| Â |
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif)
|
[Â, ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ] ] |
SQM of (Â + ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ) ) |
|---|---|---|---|
| ẑ 1 ẑ 2 | ẑ 2 ẑ 3 | 0 | Yes |
| ẑ 1 ẑ 2 |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
1
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2
2
|
0 | No |
| ẑ 1 ẑ 3 |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
ẑ
2
1
ẑ
2
|
≠0 | Yes |
| ẑ 1 ẑ 2 |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
ŷ
2
1
ŷ
2
|
≠0 | No |
The current approach can address difficulties arising in the exploration of the excited state via minimization of variance
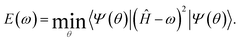 | (26) |
One of the largest practical difficulties is in an increasing number of terms that are required to be measured in eqn (26). Combining some of these terms using the current methodology can reduce the number of needed measurements.
A similar problem with a growing number of terms arises if one would like to obtain the true quantum uncertainty of the measurements for a partitioned Hamiltonian, it requires measuring all covariances between all parts. Ignoring covariances by assuming measurement independence can lead to incorrect estimation of the true uncertainty, both under- and over-estimation are possible.
From the hardware standpoint, the new scheme requires modification of the single-qubit measurement protocol, where measurement results for some qubits will define unitary rotations of other qubits before their measurement, so-called feedforward measurement. This type of measurement has already been implemented in quantum computers based on superconducting27 and photonic19,28,29 qubit architectures in the context of measurement-based quantum computing.15,16 Thus we hope that the new method will become the method of choice for quantum chemistry on a quantum computer in the near future.
Appendix A: factorization conditions for the Hamiltonian eigenstates
Here we prove that the condition given in the main text for a N-qubit Hamiltonian to be in the MF class is actually a necessary and sufficient condition, and hence is a criterion. We will split the proof into two parts: (1) If the Hamiltonian has N one-particle operators satisfying the reduction chain, its eigenfunctions can be written as products (sufficiency); (2) if all the Hamiltonian eigenfunctions are in a product form then it will have N commuting one-particle operators defined by the reduction scheme (necessity).(1) Proof of sufficiency: if there exist N one-particle operators commuting with a set of reduced Hamiltonians it is straightforward to check that a product of eigenstates of these operators is an eigenstate of the Hamiltonian. Note that any nontrivial one-qubit operator has a non-degenerate spectrum, therefore, there is no degree of freedom related to rotation within a degenerate subspace. The choice of the first eigenstate of the first operator (Ô1) can define the form of next one-particle operators and their eigenstates.
(2) Proof of necessity: for the N-particle eigenstate Ψ(1,…N) to have a product form it is necessary for the Hamiltonian to have eigenstates of the ϕ1(1)Φ(2,…N) form, where ϕ1(1) and Φ(2,…N) are some arbitrary functions from Hilbert spaces of qubit 1 and N − 1 qubits. The latter form is an eigenstate of an operator of the form Ô1 ⊗ IN−1, where IN−1 is an identity operator and Ô1 is an operator for which ϕ1(1) is an eigenfunction. Then, if the Hamiltonian and Ô1 ⊗ IN−1 share the eigenstates they must commute. This commutation is equivalent to [Ĥ, Ô1] = 0. The same logic can be applied to Φ(2,…N) because the next necessary condition for the total eigenfunction of the Hamiltonian to be in a product form is that Φ(2,…N) = ϕ2(2)![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (3,…N), this gives rise to another commuting operator Ô2 whose eigenfunction is ϕ2. It is important to note though that Ô2 does not need to commute with Ĥ but only with its reduced version HN−1 = 〈ϕ1|Ĥ|ϕ1〉. This chain can be continued until we reach the end of the variable list.
(3,…N), this gives rise to another commuting operator Ô2 whose eigenfunction is ϕ2. It is important to note though that Ô2 does not need to commute with Ĥ but only with its reduced version HN−1 = 〈ϕ1|Ĥ|ϕ1〉. This chain can be continued until we reach the end of the variable list.
Many-particle commuting operator extension
Similarly if we can find an M-particle operator Ô commuting with Ĥ then, because of the theorem on commuting operators, there is a common set of eigenfunctions. With multi-qubit operators one needs to be careful because they can have a degenerate spectrum. In the case of the non-degenerate spectrum of Ô the common eigenstates have the factorized form Ψ(1,…N) = Φ(1,…M)χ(M + 1,…N), which serves as a solid ground for the discussion in the main text. In the degenerate case, the most general form of a common eigenstate is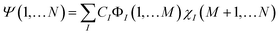 , where ÔΦI(1,…M) = λΦI(1,…M), I = 1,…k. In this case, the important question becomes whether the Hamiltonian allows for the eigenstates to be single product states,
, where ÔΦI(1,…M) = λΦI(1,…M), I = 1,…k. In this case, the important question becomes whether the Hamiltonian allows for the eigenstates to be single product states,or not? To answer this question one needs to construct a reduced matrix operator within the degenerate subspace {ΦI(1,…M)}
| ĤIJ(N−M) = 〈ΦI|Ĥ|ΦJ〉, | (27) |
| ĤIJ(N−M) = hIJĤ(N−M), | (28) |
Thus, in the degenerate case, having a product form is not guaranteed and therefore, one may be able to obtain the unitary transformation unentangling qubits only in the described two cases. Yet, finding the commuting operator Ô is a necessary condition for the existence of an unentangling unitary transformation.
Appendix B: illustration of the mean-field partitioning procedure
To illustrate the MF partitioning procedure with a nontrivial example let us consider the model Hamiltonian whose partitioning gives rise to the scheme in Fig. 3Ĥ = 3![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1 1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 3 + ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1 1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 5 2ŷ3 + 5![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1 1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 5 2ẑ3 + 5![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ŷ2 1ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 7 3 + 7![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ŷ2ẑ3 + 3 1ŷ2ẑ3 + 3![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ẑ2 1ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 3 + ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ẑ2ŷ3 + 5 1ẑ2ŷ3 + 5![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ẑ2ẑ3 + 6ŷ1 1ẑ2ẑ3 + 6ŷ1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2ŷ1 3 + 2ŷ1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 10ŷ1 2ŷ3 + 10ŷ1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 10ŷ1ŷ2 2ẑ3 + 10ŷ1ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 14ŷ1ŷ2ẑ3 + 6ŷ1ẑ2 3 + 14ŷ1ŷ2ẑ3 + 6ŷ1ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2ŷ1ẑ2ŷ3 + 10ŷ1ẑ2ẑ3 + 3ẑ1 3 + 2ŷ1ẑ2ŷ3 + 10ŷ1ẑ2ẑ3 + 3ẑ1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + ẑ1 3 + ẑ1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 5ẑ1 2ŷ3 + 5ẑ1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 5ẑ1ŷ2 2ẑ3 + 5ẑ1ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 7ẑ1ŷ2ẑ3 + 3ẑ1ẑ2 3 + 7ẑ1ŷ2ẑ3 + 3ẑ1ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + ẑ1ẑ2ŷ3 + 5ẑ1ẑ2ẑ3 3 + ẑ1ẑ2ŷ3 + 5ẑ1ẑ2ẑ3 | (29) |
To assess whether the partitioning of Ĥ is possible based on qubit k = 1 we rewrite the Hamiltonian as
Ĥ = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ĥx + ŷ1ĥy + ẑ1ĥz, 1ĥx + ŷ1ĥy + ẑ1ĥz, | (30) |
ĥx = 3![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 3 + ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 5 2ŷ3 + 5![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 5ŷ2 2ẑ3 + 5ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 7ŷ2ẑ3 + 3ẑ2 3 + 7ŷ2ẑ3 + 3ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + ẑ2ŷ3 + 5ẑ2ẑ3 3 + ẑ2ŷ3 + 5ẑ2ẑ3 | (31) |
ĥy = 6![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2 3 + 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 10 2ŷ3 + 10![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 10ŷ2 2ẑ3 + 10ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 14ŷ2ẑ3 + 6ẑ2 3 + 14ŷ2ẑ3 + 6ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2ẑ2ŷ3 + 10ẑ2ẑ3 3 + 2ẑ2ŷ3 + 10ẑ2ẑ3 | (32) |
ĥz = 3![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 3 + ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 5 2ŷ3 + 5![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 5ŷ2 2ẑ3 + 5ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 7ŷ2ẑ3 + 3ẑ2 3 + 7ŷ2ẑ3 + 3ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + ẑ2ŷ3 + 5ẑ2ẑ3 3 + ẑ2ŷ3 + 5ẑ2ẑ3 | (33) |
Each ĥx,y,z is transformed into a vector. For example
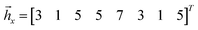 | (34) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2
2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3,
3, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3,
2ŷ3, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3, ŷ2
2ẑ3, ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3, ŷ2ẑ3, ẑ2
3, ŷ2ẑ3, ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3, ẑ2ŷ3, ẑ2ẑ3}. S1 is obtained as A†1A1, where
3, ẑ2ŷ3, ẑ2ẑ3}. S1 is obtained as A†1A1, where 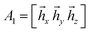 . Diagonalizing of S1 gives one non-zero eigenvalue d and a corresponding eigenvector
. Diagonalizing of S1 gives one non-zero eigenvalue d and a corresponding eigenvector 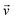 . The dimensionality of the S1 kernel is 2, l(1) = 2, and it implies collinearity of
. The dimensionality of the S1 kernel is 2, l(1) = 2, and it implies collinearity of 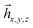 (Fig. 2a). Performing similar analysis for S2 and S3, one can find l(2) = l(3) = 1 (see Fig. 3). Therefore, we rewrite the Hamiltonian as Ĥ = ĥ(2,3)Ô1, where
(Fig. 2a). Performing similar analysis for S2 and S3, one can find l(2) = l(3) = 1 (see Fig. 3). Therefore, we rewrite the Hamiltonian as Ĥ = ĥ(2,3)Ô1, whereÔ1 = 0.408248![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1 + 0.816497ŷ1 + 0.408248ẑ1 1 + 0.816497ŷ1 + 0.408248ẑ1 | (35) |
ĥ(2,3) = 7.34847![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2.44949 3 + 2.44949![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ŷ3 + 12.2474 2ŷ3 + 12.2474![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2ẑ3 + 12.2474ŷ2 2ẑ3 + 12.2474ŷ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 17.1464ŷ2ẑ3 + 7.34847ẑ2 3 + 17.1464ŷ2ẑ3 + 7.34847ẑ2![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2.44949ẑ2ŷ3 + 12.2474ẑ2ẑ3 3 + 2.44949ẑ2ŷ3 + 12.2474ẑ2ẑ3 | (36) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1, ŷ1, ẑ1} and {ĥx, ĥy, ĥz} with coefficients from the eigenvector
1, ŷ1, ẑ1} and {ĥx, ĥy, ĥz} with coefficients from the eigenvector 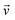 .
.
As the next step, we consider ĥ(2,3), it can be partitioned based on either qubit k = 2 or k = 3. Both qubits have the same values of l(k) = 1 and 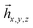 are in a single plane (Fig. 2b). Here, we choose arbitrarily k = 2, diagonalizing S2 leads to two non-zero eigenvalues (d1,d2) and corresponding eigenvectors
are in a single plane (Fig. 2b). Here, we choose arbitrarily k = 2, diagonalizing S2 leads to two non-zero eigenvalues (d1,d2) and corresponding eigenvectors 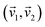 . Following the procedure, ĥ(2,3) decomposes to
. Following the procedure, ĥ(2,3) decomposes to
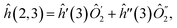 | (37) |
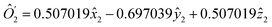 | (38) |
ĥ′(3)=−1.08532![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2.48388ŷ3 + 0.467647ẑ3 3 + 2.48388ŷ3 + 0.467647ẑ3 | (39) |
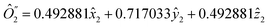 | (40) |
ĥ′′(3) = 16.0257![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 3 + 2.41461ŷ3 + 24.3676ẑ3. 3 + 2.41461ŷ3 + 24.3676ẑ3. | (41) |
The single-qubit operators 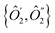 and their complements {ĥ′, ĥ′′} were obtained taking linear combinations of {
and their complements {ĥ′, ĥ′′} were obtained taking linear combinations of {![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2, ŷ2, ẑ2} and {ĥx, ĥy, ĥz} with coefficients from the eigenvectors
2, ŷ2, ẑ2} and {ĥx, ĥy, ĥz} with coefficients from the eigenvectors 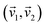 , respectively.
, respectively.
The complexity of a single step of the MF partitioning procedure is polynomial with the number of qubits. In each step we need to evaluate the l(k) function for each of the qubits present. Evaluation of the l(k) function requires building the corresponding overlap matrix Sk, which involves inner products between columns of Ak matrices. Since the length of Ak columns (![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) x,y,z) scales as N4 at most (this is the scaling of the total number of terms in the Hamiltonian), the construction of Sk scales as N4 as well. Thus funding l(k) functions for all qubits in general has O(N5) scaling.
x,y,z) scales as N4 at most (this is the scaling of the total number of terms in the Hamiltonian), the construction of Sk scales as N4 as well. Thus funding l(k) functions for all qubits in general has O(N5) scaling.
Appendix C: Hamiltonian details
H2 molecule
One- and two-electron integrals in the canonical restricted Hartree–Fock (RHF) molecular orbital basis for R(H–H) = 1.5 Å were used in the BK transformation to produce the corresponding qubit Hamiltonian. Spin-orbitals were alternating in the order α, β, α, …. The explicit expression for the BK qubit Hamiltonian is given in the ESI.†LiH molecule
A qubit Hamiltonian for R(Li–H) = 3.2 Å distance was generated using the parity fermion-to-qubit transformation.30 Spin-orbitals were arranged as “first all alpha then all beta” in the fermionic form; since there are 3 active molecular orbitals in the problem, this leads to a 6-qubit Hamiltonian. Further details on the Hamiltonian are given in the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
A.F.I. is grateful to D. Segal, P. Brumer, R. Kapral, J. Schofield, J. R. McClean, D. F. James, and I. Dhand for useful discussions. A.F.I. acknowledges financial support from the Natural Sciences and Engineering Research Council of Canada.References
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, Am. J. Phys., 2016, 18, 023023 Search PubMed.
- D. Wecker, M. B. Hastings and M. Troyer, Progress towards practical quantum variational algorithms, Phys. Rev. A, 2015, 92, 042303 CrossRef.
- J. Olson; Y. Cao; J. Romero; P. Johnson; P.-L. Dallaire-Demers; N. Sawaya; P. Narang; I. Kivlichan; M. Wasielewski and A. Aspuru-GuzikQuantum Information and Computation for Chemistry. arXiv.org 2017.
- S. McArdle; S. Endo; A. Aspuru-Guzik; S. Benjamin and X. YuanQuantum computational chemistry. arXiv.org 2018.
- P. Jordan and E. Wigner, Über das Paulische Äquivalenzverbot, Z. Phys., 1928, 47, 631–651 CrossRef CAS.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated Quantum Computation of Molecular Energies, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- S. B. Bravyi and A. Y. Kitaev, Fermionic Quantum Computation, Ann. Phys., 2002, 298, 210–226 CAS.
- J. T. Seeley, M. J. Richard and P. J. Love, The Bravyi-Kitaev transformation for quantum computation of electronic structure, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
- A. Tranter, S. Sofia, J. Seeley, M. Kaicher, J. McClean, R. Babbush, P. V. Coveney, F. Mintert, F. Wilhelm and P. J. Love, The Bravyi-Kitaev transformation: Properties and applications, Int. J. Quantum Chem., 2015, 115, 1431 CrossRef CAS.
- K. Setia and J. D. Whitfield, Bravyi-Kitaev Superfast simulation of fermions on a quantum computer, ArXiv e-prints, 2017.
- V. Havlíček, M. Troyer and J. D. Whitfield, Operator locality in the quantum simulation of fermionic models, Phys. Rev. A, 2017, 95, 032332 CrossRef.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature, 2017, 549, 242–246 CrossRef CAS PubMed.
- I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, Constrained Variational Quantum Eigensolver: Quantum Computer Search Engine in the Fock Space, J. Chem. Theory Comput., 2019, 15, 249–255 CrossRef CAS PubMed.
- M. A. Nielsen, Cluster-state quantum computation, Rep. Math. Phys., 2006, 57, 147–161 CrossRef.
- A. Mantri, T. F. Demarie and J. F. Fitzsimons, Universality of quantum computation with cluster states and (X, Y)-plane measurements, Sci. Rep., 2017, 7, 1–7 CrossRef PubMed.
- T. Helgaker; P. Jorgensen and J. OlsenMolecular Electronic-structure Theory, Wiley, 2000 Search PubMed.
- F. Albarrán-Arriagada, G. A. Barrios, M. Sanz, G. Romero, L. Lamata, J. C. Retamal and E. Solano, One-way quantum computing in superconducting circuits, Phys. Rev. A, 2018, 97, 032320 CrossRef.
- R. Prevedel, P. Walther, F. Tiefenbacher, P. Böhi, R. Kaltenbaek, T. Jennewein and A. Zeilinger, High-speed linear optics quantum computing using active feed-forward, Nature, 2007, 445, 65–69 CrossRef CAS PubMed.
- D. Ristè and L. DiCarloDigital feedback in superconducting quantum circuits. arXiv.org 2015 Search PubMed.
- R. Barends, J. Kelly, A. Megrant, D. Sank, E. Jeffrey, Y. Chen, Y. Yin, B. Chiaro, J. Mutus, C. Neill, P. O'Malley, P. Roushan, J. Wenner, T. C. White, A. N. Cleland and J. M. Martinis, Coherent Josephson Qubit Suitable for Scalable Quantum Integrated Circuits, Phys. Rev. Lett., 2013, 111, 080502 CrossRef CAS PubMed.
- M. Körber; O. Morin; S. Langenfeld; A. Neuzner; S. Ritter and G. Rempe, Decoherence-protected memory for a single-photon qubit. arXiv.org 2017.
- S. Bravyi; J. M. Gambetta; A. Mezzacapo and K. Temme, Tapering off qubits to simulate fermionic Hamiltonians. arXiv.org 2017.
- C. Hempel, C. Maier, J. Romero, J. McClean, T. Monz, H. Shen, P. Jurcevic, B. P. Lanyon, P. Love, R. Babbush, A. Aspuru-Guzik, R. Blatt and C. F. Roos, Quantum Chemistry Calculations on a Trapped-Ion Quantum Simulator, Phys. Rev. X, 2018, 8, 031022 Search PubMed.
- I. G. Ryabinkin, T.-C. Yen, S. N. Genin and A. F. Izmaylov, Qubit coupled cluster method: A systematic approach to quantum chemistry on a quantum computer, J. Chem. Theory Comput., 2018, 14, 6317–6326 CrossRef CAS PubMed.
- I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, Relation between fermionic and qubit mean fields in the electronic structure problem, J. Chem. Phys., 2018, 149, 214105 CrossRef PubMed.
- R. Vijay, C. Macklin, D. H. Slichter, S. J. Weber, K. W. Murch, R. Naik, A. N. Korotkov and I. Siddiqi, Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback, Nature, 2012, 490, 77–80 CrossRef CAS PubMed.
- L. M. Procopio, A. Moqanaki, M. Araújo, F. Costa, I. A. Calafell, E. G. Dowd, D. R. Hamel, L. A. Rozema, v. Brukner and P. Walther, Experimental superposition of orders of quantum gates, Nat. Commun., 2015, 6, 1–6 Search PubMed.
- C. Reimer, S. Sciara, P. Roztocki, M. Islam, L. R. Cortés, Y. Zhang, B. Fischer, S. Loranger, R. Kashyap, A. Cino, S. T. Chu, B. E. Little, D. J. Moss, L. Caspani, W. J. Munro, J. Azaña, M. Kues and R. Morandotti, High-dimensional one-way quantum processing implemented on d-level cluster states, Nat. Phys., 2019, 15, 148–153 Search PubMed.
- M. A. Nielsen The Fermionic canonical commutation relations and the Jordan-Wigner transform. School of Physical Sciences The University of Queensland 2005 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc05592k |
| ‡ Here, we use the notation |±σ〉n for the nth qubit eigenstates of a σ one-particle operator with ±1 eigenvalues. |
| § To simplify the notation we use freedom in qubit enumeration and assume that we work with the qubit enumeration that follows the described reductive sequence. |
| This journal is © The Royal Society of Chemistry 2019 |