Open Access Article
Open Access ArticleInsights into mechanochemical reactions at the molecular level: simulated indentations of aspirin and meloxicam crystals†
Michael
Ferguson
 ab,
M. Silvina
Moyano
ab,
M. Silvina
Moyano
 a,
Gareth A.
Tribello
c,
Deborah E.
Crawford
a,
Gareth A.
Tribello
c,
Deborah E.
Crawford
 b,
Eduardo M.
Bringa
d,
Stuart L.
James
*b,
Jorge
Kohanoff
b,
Eduardo M.
Bringa
d,
Stuart L.
James
*b,
Jorge
Kohanoff
 *c and
Mario G.
Del Pópolo
*c and
Mario G.
Del Pópolo
 *ac
*ac
aCONICET, Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Cuyo, Mendoza, Argentina. E-mail: mdelpopolo@fcen.uncu.edu.ar
bSchool of Chemistry and Chemical Engineering, Queen's University Belfast, Belfast, Northern Ireland, UK. E-mail: s.james@qub.ac.uk
cAtomistic Simulation Centre, School of Mathematics and Physics, Queen's University Belfast, Belfast, Northern Ireland, UK. E-mail: j.kohanoff@qub.ac.uk
dCONICET, Facultad de Ingenería, Universidad de Mendoza, Mendoza, Argentina
First published on 23rd January 2019
Abstract
Although solvent-free mechanochemical synthesis continues to gain ever greater importance, the molecular scale processes that occur during such reactions remain largely uncharacterised. Here, we apply computational modelling to indentations between particles of crystals of aspirin and meloxicam under a variety of conditions to mimic the early stages of their mechanochemical cocrystallisation reaction. The study also extends to the effects of the presence of small amounts of solvent. It is found that, despite the solid crystalline nature of the reactants and the presence of little or no solvent, mixing occurs readily at the molecular level even during relatively low-energy collisions. When indented crystals are subsequently drawn apart, a connective neck formed by a mixture of the reactant molecules is observed, suggesting plastic-like behaviour of the reacting materials. Overall the work reveals some striking new insights including (i) relatively facile mixing of crystals under solvent-free conditions, (ii) no appreciable local temperature increases, (iii) localised amorphisation at the contact region and neck of the reacting crystals, and (iv) small amounts of solvent have relatively little effect during this early stage of the reaction, suggesting that their accelerating effect on the reaction may be exerted at later stages.
Introduction
Mechanochemical synthesis involves inducing chemical reactions between solid reactants through the input of mechanical energy such as by grinding. It is gaining ever-increasing attention because it can provide solvent-free, economical, sustainable, chemical manufacturing as well as unique products.1 It is now being successfully scaled in continuous processes such as twin-screw extrusion and even commercialised.2 However, very little is known about the processes which occur at the molecular level during mechanochemical reactions. This reflects the general difficulty of imaging such processes at the molecular level. This knowledge gap is hampering the transition of the field from a largely empirical basis to a rational, predictive one.Here, we describe a combination of experiments on bulk materials with computational modelling at the molecular level. A test case reaction is used, specifically the cocrystallisation of aspirin and meloxicam (see Scheme 1), as first described by Cheney et al. under ball milling conditions.3 This system was chosen for three reasons. First, the reactants and product are relatively non-volatile and have melting points (aspirin 136 °C; meloxicam 255 °C; 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal 166 °C) significantly greater than the bulk temperatures reached under the milling conditions (ca. 60 °C,4), making it unlikely that the reaction proceeds significantly through gaseous or bulk melt phases.
1 co-crystal 166 °C) significantly greater than the bulk temperatures reached under the milling conditions (ca. 60 °C,4), making it unlikely that the reaction proceeds significantly through gaseous or bulk melt phases.
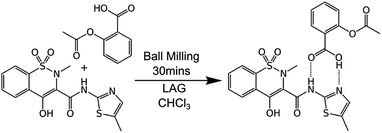 | ||
Scheme 1 The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystallisation of aspirin and meloxicam induced by grinding in the absence of solvent or in the presence of small amounts of chloroform (liquid assisted grinding, LAG). 1 cocrystallisation of aspirin and meloxicam induced by grinding in the absence of solvent or in the presence of small amounts of chloroform (liquid assisted grinding, LAG). | ||
Second, the reaction only involves the breaking and formation of hydrogen bonds, making computational modelling with classical force fields applicable and enabling larger systems to be studied than would be possible for covalent bond interchanges (which would require quantum mechanical methods). Third, as with many mechanochemical reactions, this cocrystallisation is accelerated by liquid assisted grinding (LAG), in particular by grinding in the presence of small amounts of CHCl3. This enables the effects of solvent at the molecular level to be studied.
Results and discussion
To provide experimental support for the modelling work, we began by reinvestigating the mechanochemical synthesis reported by Cheney et al.3 Using a Retsch MM400 shaker mill, milling of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of aspirin and meloxicam at 0.274 g (0.5 mmol) scale in a 25 mL steel jar containing a 13.6 g steel ball led to the expected 1
1 mixtures of aspirin and meloxicam at 0.274 g (0.5 mmol) scale in a 25 mL steel jar containing a 13.6 g steel ball led to the expected 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
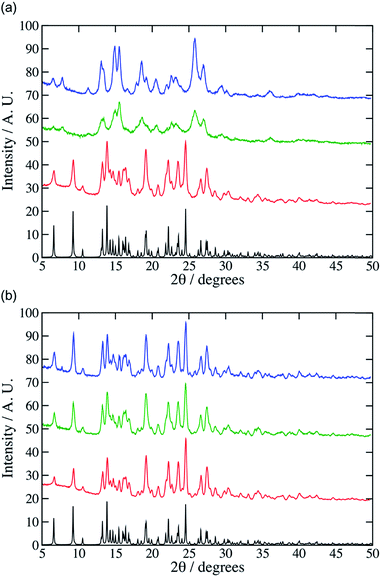
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal after 30 minutes at high vibration rates (e.g. 25 Hz). The PXRD pattern of the product was a close match with the pattern simulated from the single-crystal diffraction data for the 1
1 co-crystal after 30 minutes at high vibration rates (e.g. 25 Hz). The PXRD pattern of the product was a close match with the pattern simulated from the single-crystal diffraction data for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal (Fig. 1). At lower grinding frequencies (e.g. 10 or 15 Hz) after 30 minutes the experimental PXRD patterns did not match well to the simulated product pattern (Fig. 1, see for example additional peaks at 7 and 12°) which we ascribe to incomplete reactions. Adding small amounts of solvent (CHCl3, 0.05 mol equiv., 20 μL) accelerated the reaction, giving the cocrystal in 30 minutes even at 10 Hz. Cheney et al. found that CHCl3 was necessary for the formation of the cocrystal even at high vibrational frequencies. This difference may be ascribed to the use of different milling equipment in the two studies, which may supply different mechanical energy doses. To model this mechanochemical reaction at the molecular level we used the molecular dynamics code LAMMPS5 and the OPLS force field.6 In this model bonds and angles are simulated using harmonic potentials, while the specific OPLS Fourier series style is used for the dihedral angles.7 Non-bonded interactions were modelled using partial charges and Lennard-Jones potentials truncated at 12 Å. The charges on the various atoms were obtained from individual restrained electrostatic potential (RESP) fits8 that were performed with the CP2K code using the ab initio Quickstep module.9 These calculations were based on the PBE functional,10 and the wave-function was expanded using a TVZP-GTH basis set.11 Electrostatic interactions between point charges were calculated using a particle–particle mesh (PPPM) solver.12 The hydrogen bonds formed during co-crystallisation were incorporated by using a Dreiding overly13 of the Lennard-Jones parameters. Further details and a sample file containing the force field description along with an associated input file for LAMMPS can be found in the ESI† (data.co-crystal and in.co-crystal).
1 cocrystal (Fig. 1). At lower grinding frequencies (e.g. 10 or 15 Hz) after 30 minutes the experimental PXRD patterns did not match well to the simulated product pattern (Fig. 1, see for example additional peaks at 7 and 12°) which we ascribe to incomplete reactions. Adding small amounts of solvent (CHCl3, 0.05 mol equiv., 20 μL) accelerated the reaction, giving the cocrystal in 30 minutes even at 10 Hz. Cheney et al. found that CHCl3 was necessary for the formation of the cocrystal even at high vibrational frequencies. This difference may be ascribed to the use of different milling equipment in the two studies, which may supply different mechanical energy doses. To model this mechanochemical reaction at the molecular level we used the molecular dynamics code LAMMPS5 and the OPLS force field.6 In this model bonds and angles are simulated using harmonic potentials, while the specific OPLS Fourier series style is used for the dihedral angles.7 Non-bonded interactions were modelled using partial charges and Lennard-Jones potentials truncated at 12 Å. The charges on the various atoms were obtained from individual restrained electrostatic potential (RESP) fits8 that were performed with the CP2K code using the ab initio Quickstep module.9 These calculations were based on the PBE functional,10 and the wave-function was expanded using a TVZP-GTH basis set.11 Electrostatic interactions between point charges were calculated using a particle–particle mesh (PPPM) solver.12 The hydrogen bonds formed during co-crystallisation were incorporated by using a Dreiding overly13 of the Lennard-Jones parameters. Further details and a sample file containing the force field description along with an associated input file for LAMMPS can be found in the ESI† (data.co-crystal and in.co-crystal).
We generated model particles of each reactant by carving out spheres of diameter ∼6 nm from their respective crystal structures, followed by independently annealing each particle for 1 ns at a temperature of half of the melting point of the respective reactant, and finally allowing them to equilibrate at 300 K in preparation for modelling collisions. The number of molecules in each nanoparticle was 530 and 302 for aspirin and meloxicam, respectively. Taking 8 m s−1 as a reasonable impact velocity, based on estimated ball speed in a mixer mill,14 we then fired the reactant particles at each other.
In the initial configuration, the particles were separated by 5 Å along the x-axis, with their most reactive (010) surfaces oriented toward each other. The collisions were induced by augmenting the initial velocities of the atoms in the aspirin and meloxicam spheres with equal and opposite translational centre of mass (COM) velocities. This type of simulation is often used to study sticking and bouncing of nanoclusters, where melting and mixing of simple monoatomic substances have been observed.15 However, to some surprise, our particles simply bounced of each other with no apparent mixing and indeed little effect on the particles' structure. This occurred even at much faster (supersonic) impact velocities. It became clear that under these conditions only a small fraction of the translational kinetic energy of the grains was being transformed into rotational kinetic energy, with even smaller energy transfer to the clusters' internal degrees of freedom.
To resolve this issue we resorted to the approach used by Landman et al., in which simulations of indentations on intermetallic (Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni) and ionic (CaF2) systems were used to study adhesive contacts.16 This approach is based on the indentation and subsequent retraction of chunks of material. This meant in practise that the trajectory of some of the atoms in each of the two spheres were independently controlled. Specifically, we fixed the trajectory of some of the molecules in each of the two particles. The motion of the remaining, unfixed, molecules was then determined by solving Newton's equations of motion in the usual way. In our case, the position of 77 molecules of aspirin and 51 of meloxicam, which had the greatest mutual separation in the x-direction, were fixed. Furthermore, this allowed us to control the depth and rate of indentation. The maximum indentation depth, defined as the relative distance travelled by the fixed molecules of the clusters after their initial contact, was set at 25 Å. Once the particles reached this indentation depth, they were retracted from each other. During the indentation process the two spheres travelled with equal and opposite velocities. For the retraction the velocities of the spheres were simply reversed while maintaining the same magnitude. Simulations were performed at indentation rates of 4, 2, 1, and 0.5 m s−1.
Ni) and ionic (CaF2) systems were used to study adhesive contacts.16 This approach is based on the indentation and subsequent retraction of chunks of material. This meant in practise that the trajectory of some of the atoms in each of the two spheres were independently controlled. Specifically, we fixed the trajectory of some of the molecules in each of the two particles. The motion of the remaining, unfixed, molecules was then determined by solving Newton's equations of motion in the usual way. In our case, the position of 77 molecules of aspirin and 51 of meloxicam, which had the greatest mutual separation in the x-direction, were fixed. Furthermore, this allowed us to control the depth and rate of indentation. The maximum indentation depth, defined as the relative distance travelled by the fixed molecules of the clusters after their initial contact, was set at 25 Å. Once the particles reached this indentation depth, they were retracted from each other. During the indentation process the two spheres travelled with equal and opposite velocities. For the retraction the velocities of the spheres were simply reversed while maintaining the same magnitude. Simulations were performed at indentation rates of 4, 2, 1, and 0.5 m s−1.
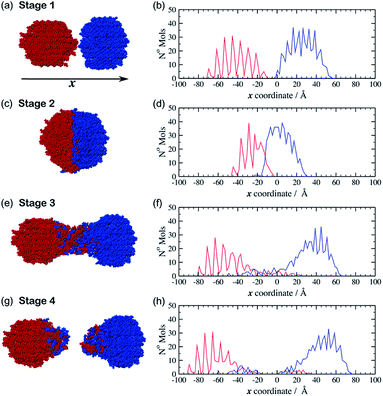
The movie provided as ESI† (indent_4ms.mp4), shows the trajectory from one of the simulations in which the spheres move at 4 m s−1. Fig. 2 shows a set of snapshots from this trajectory which illustrate some key stages during a typical indentation event. This particular simulation was started from a configuration (hereafter referred to as configuration I) in which the crystalline spheres of aspirin and meloxicam were aligned with their (010) crystal faces perpendicular to the indentation direction. The simulation begins at stage 1, in which the particles are set apart in preparation for the indentation (Fig. 2(a)). The two spheres are then driven together with equal and opposite velocities to an indentation depth of 25 Å. This point is referred to as stage 2 (Fig. 2(c)). The two particles are then retracted from each other. Interestingly, we observed that regardless of the indentation rate, a connective neck formed between the two spheres upon retraction. This feature kept the particles as a single contiguous object even when the COM separation surpassed the value pre-set at stage 1. Stage 3 (Fig. 2(e)), refers to the point at which a long connective neck exists between the two spheres and the COM separation is greater than that at stage 1. After sufficient elongation, the connective neck breaks leading to two separate entities (stage 4, Fig. 2(g)), which are no longer made of pure aspirin and pure meloxicam. Clearly some molecules have been transferred between the clusters during the indentation/retraction process, i.e. mixing has occurred.
Two further initial configurations (II and III), with different relative orientation between the particles, were also simulated. In configuration II the aspirin cluster was rotated by 90° around the x-axis, so that the (010) crystal planes were still perpendicular to the x-axis but the relative orientation of the aspirin molecules, with respect to those of meloxicam, was altered. In configuration III the original aspirin sphere was rotated by 90° about the y-axis. The (001) face of aspirin was thereby indented upon the (010) face of meloxicam. In all cases molecules at the distal end of the clusters, i.e. those farthest away from the colliding surfaces, were kept frozen during the simulation. As can be seen from ESI Fig. S2 and S3 (ESI†) the trends described for the configuration I trajectory described above (stages 1–4) were also observed for the simulations initiated from configurations II and III, and were similar at all the indentation rates investigated. To complement the visual inspection of the simulation trajectories, we performed a more quantitative analysis of the mixing process. This analysis was achieved by looking at the number density of aspirin and meloxicam molecules along the indentation direction, x. The position of each molecule, in x, was determined by its geometric COM. These positions were then collected into 120 bins each of width 2 Å in order to create a histogram. For the case of configuration I with indentation rate of 4 m s−1, the resulting histograms are shown alongside their respective snapshot (Fig. 2b, d, f and h). At stage 1 (Fig. 2(b)), when the clusters are unconnected, the density of aspirin (blue) and meloxicam (red) reveals the layering and crystal order of the material in the grains, and a small gap between the two particles. ESI Fig. S4† shows that there is a small attractive force between the two clusters at this stage due to dispersive and electrostatic interactions. As the grains approach each other the least coordinated molecules, i.e. those on the surfaces of the clusters, rearrange to form a small connective neck between the two spheres. Furthermore, Fig. S4† shows that as the indentation proceeds the average force on the fixed layers of the clusters becomes increasingly repulsive and that there is a series of elastic and plastic deformation events. The stress from the indentation event causes some amorphisation in the contact region as has been observed in a number of materials, including diamond.17 This amorphous material then goes on to make up the connective neck. A comparison of Fig. 2(b) with Fig. 2(d) demonstrates that, at the maximum indentation depth (stage 2), the spatial extents of the two grains are compressed by a considerable amount. Interestingly, the density profile of meloxicam is compressed to a greater extent than that of aspirin, which may seem surprising as the bulk modulus of meloxicam (18.5 GPa, Table S1, ESI†) is greater than that of aspirin (13.2 GPa, Table S1, ESI†). However, the bulk modulus is a measure of resistance to uniform compression, and not of anisotropic compression as it occurs during the indentation. The greater compression of meloxicam observed in the simulations is deemed to be connected to the relative compressibility of the (010) planes of meloxicam compared to the (010) and (001) planes of aspirin.
During retraction, the compressive force (Fig. S4, ESI†) is relieved and becomes zero at a distance at which the two clusters are still in close contact. From that point on starts the formation of an amorphous connective neck (stage 3) which is comprised of both aspirin and meloxicam, see Fig. 2(f). Furthermore, this figure shows that molecules of aspirin and meloxicam move in the opposite direction to their parent particle as the density profiles for each species are much more extended than those in Fig. 2(d). This indicates that most of the mixing occurs during the retraction stage and not during the indentation, which is initially counter-intuitive. This also contrasts with previous results on indentations of metal surfaces which showed the diffusion of nickel16 and palladium18 atoms from an indenter tip into the interstitial spaces of a gold surface during the indentation stage of the simulation. We attribute such difference to the greater size, the flexibility, and the more complex shapes of the aspirin and meloxicam molecules when compared to metal atoms, which lead to strongly anisotropic intermolecular forces in organic materials. These factors would likely hinder the diffusion of molecules when the interstitial space is continually reduced, i.e. during indentation, thus promoting the transfer of material during retraction when the interstitial space is continually expanded. Finally, at stage 4, when the connective neck has ruptured, the density profiles of Fig. 2(h) and the visual inspection of the final configurations show that the two resulting clusters have considerably lost crystalline order. Notice that indentation and retraction of the grains are energetically unfavourable processes. There is no conflict in this as in mechanochemistry energy is continuously supplied to the system. Ultimately, indentation and retraction of reacting grains is powered by random collisions and forced contacts between the grains. Retraction occurs due to subsequent collisions with other grains.
The general trends described for configuration I trajectories were also observed during the indentation of clusters with different relative orientations. While the visual inspection of these trajectories shows no discernible differences between the indentations performed at different velocities, the linear density profiles of aspirin and meloxicam do reveal some subtle differences in the quantity of molecules transferred from one cluster to another. However, in order to fully characterize the significance of these changes a much larger sample of indentation events should be considered, which is beyond the scope of the present investigation.
As described above, small amounts of CHCl3 have been shown to accelerate the reaction in the ball mill, i.e. CHCl3 provides a lower energy pathway for the process. We thus partially solvated the particles of configuration 1 with a total concentration of approximately 0.25 mol equiv., which is larger than the concentration used in the experiments. To set up this configuration we evenly distributed 112 and 82 CHCl3 molecules around the particles of aspirin and meloxicam respectively giving a total of 194 solvent molecules and an overall solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solid ratio of 23.5 mol%. A geometry optimization was performed and the partially solvated particles were subsequently heated from 0 to 300 K over 0.25 ns and allowed to equilibrate at that temperature for a further 1 ns. Due to its low vapour pressure, some CHCl3 evaporated from the clusters' surface. The two partially solvated particles were then carefully combined, ensuring that no two molecules of chloroform overlapped, to create configuration IV. Indentations were then performed and analysed using the same simulation protocol as before.
solid ratio of 23.5 mol%. A geometry optimization was performed and the partially solvated particles were subsequently heated from 0 to 300 K over 0.25 ns and allowed to equilibrate at that temperature for a further 1 ns. Due to its low vapour pressure, some CHCl3 evaporated from the clusters' surface. The two partially solvated particles were then carefully combined, ensuring that no two molecules of chloroform overlapped, to create configuration IV. Indentations were then performed and analysed using the same simulation protocol as before.
As illustrated by Fig. S3 (ESI†), the simulations performed with configuration IV follow the same sequence of events, and in general the same trends, as those of configuration I. In particular, the transfer of material between the two solids still occurs during stage 3. Interestingly, the presence of CHCl3 leads to greater elongations of the connective neck in comparison with the non-solvated systems (Table S3, ESI†), effect that becomes more evident at higher indentation rates. The elongation of the connective neck was also accompanied by a slight increase in the total percentage transfer of material (Table S2, ESI†), which further reinforces the idea that most of the transfer occurs during the retraction stage. However, given the limited scope of these simulations it is unclear whether the increased transfer we observe is statistically significant.
Apart from the enhanced ductility of the connective neck, the partial solvation with chloroform does not produce other significant effects on the outcome of the indentations. We thus believe that the role of chloroform is not relevant at this very early stage of the mechanochemical process, but may later provide a lower energy pathway to the nucleation of the co-crystal. For example, once a homogenised mixture has been achieved, a very high local concentration of chloroform may be sufficient to create a super-saturated localised fluid phase, from which the co-crystal nucleates and crystallises from. Due to the non-stationary nature of the ball milling process, this formation of a very localised super-saturated fluid followed by the immediate crystallisation of the product would be likely to occur continually, until the co-crystal is formed quantitatively.
The particles described in the previous paragraphs are relatively small and their high surface curvature could lead to highly labile molecules at their surfaces. We therefore also performed a trial simulation with crystals with surface curvatures approximately five times less than those described above. For that we created hemi-spherical particles with the desired surface curvature as shown in panel (a) of Fig. 3. Snapshots at stages 1–4 show that the process follows the same pattern of events as observed for the small clusters. It is clear that even with greatly reduced surface curvature, we still observe mechanochemical transfer of material between the two solids. Finally, we simulated impacts between a meloxicam sphere and a semi-infinite (100) surface of aspirin (Section 5, ESI†). The aim of these simulations was to test the occurrence of hot-spots that could lead to surface melting, extended defects, or amorphisation events. The theory of mechanochemical hot-spots has received much attention since its conception in the 1950s.19 Ma et al. have shown, for example, that high energy collisions between oxide-coated aluminium nanoparticles lead to transient hot-spots of almost 1000 K when the relative impact velocity is above 2000 m s−1.20 Research on the hot-spot theory, like that of Ma et al., is centred around inorganic materials rather than organic materials, and impacting at velocities greater than those considered here. It has already been suggested that such high temperatures in localised volumes could lead to the decomposition of organic material (albeit subject to how quickly the heat dissipates), something not generally observed in mechanochemical reactions.1 Thermal studies, such as those by Kulla et al. and Užarević et al., have found experimentally that bulk temperature increases are significantly smaller, e.g. 11.3 K after milling for 11 minutes at 30 Hz.4,21,22 In our work, we studied the local temperature increases during grain-slab collisions to investigate the potential for thermal causation of the mixing that we observed in our grain–grain indentations. The results showed minimal temperature increases (∼5 K) during collisions at experimentally feasible velocities (32, 8, 4 and 2 m s−1). Thus, we suggest that mixing of organic materials at the molecular level can occur at much lower temperatures than are suggested to exist in hot spot theory. This further implies that hot spots may not necessarily need to be invoked to explain solventless mechanochemical reactions of molecular organic materials.
Conclusions
In summary, we have made an important step in the process of achieving a molecular-level description of mechanochemical reactions between crystalline organic materials. Due to the inherent difficulties of imaging solid state reactions at the molecular level as they occur, especially under ball milling or extrusion conditions, the use of molecular simulation can be seen as a crucial tool in this area. This approach has given some striking new insights into the initial stages of mechanochemical reactions, including (i) relatively facile mixing of crystals under solvent-free conditions, (ii) no appreciable local temperature increases, (iii) localised amorphisation at the contact region and neck of the reacting crystals, and (iv) small amounts of solvent have relatively little effect during this early stage of the reaction, suggesting that their accelerating effect on the reaction may be exerted at later stages.Experimental
Aspirin and chloroform were obtained from Sigma Aldrich UK in 99% purity. Meloxicam was obtained from TCI Chemicals in 96% purity. All materials were used as obtained without further purification. Ball mill experiments were carried out using a Retsch MM400 mixer mill. PXRD measurements were carried out on a PANanalytical X'Pert Pro X-ray diffractometer. Copper was used as the X-ray source with a wavelength of 1.5405 Å. All experiments were carried out ex situ using a spinning stage. Diffractograms were typically carried out from 5–50 with a step size of 0.0167°.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the European Commission MSCA-RISE “ENACT” Programme (grant number 643998) for funding. M. G. D. P. and E. M. B. acknowledge financial support from CONICET, SECTyP-UNCUYO, and FONCyT (PICT-2015-1835 and PICT-2014-0696). We are also grateful for computational support from the UK national high-performance computing service, ARCHER, for which access was obtained via the UKCP consortium and funded by EPSRC grant ref. EP/K013564/1. G. A. T. also acknowledges funding from EPSRC (Grant EP/P005004/1). S. L. J. acknowledges funding from EPSRC (EP/L019655/1).Notes and references
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC; G. A. Bowmaker, Chem. Commun., 2013, 49, 334–348 RSC; G. W. Wang, Chem. Soc. Rev., 2013, 42, 7668–7700 RSC; A. Stolle, T. Szuppa, S. E. S. Leonhardt and B. Ondruschka, Chem. Soc. Rev., 2011, 40, 2317–2329 RSC; T. Friščić, J. Mater. Chem., 2010, 20, 7599–7605 RSC; A. Bruckmann, A. Krebs and C. Bolm, Green Chem., 2008, 10, 1131–1141 RSC.
- R. Dhumal, A. Kelly, P. Coates, P. York and A. Paradkar, Pharm. Res., 2010, 27, 2725 CrossRef CAS PubMed; C. Medina, D. Daurio, K. Nagapudi and F. Alvarez-Nunez, J. Pharm. Sci., 2010, 99, 1693 CrossRef PubMed; D. Daurio, K. Nagapudi, L. Li, P. Quan and F.-A. Nunez, Faraday Discuss., 2014, 170, 235 RSC; D. Crawford, J. Casaban, R. Haydon, N. Giri, T. McNally and S. L. James, Chem. Sci., 2015, 6, 1645 RSC; D. E. Crawford, L. A. Wright, S. L. James and A. P. Abbott, Chem. Commun., 2016, 45, 4215 RSC; D. E. Crawford, C. K. G. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Green Chem., 2017, 19, 1507 RSC; http://www.moftechnologies.com, accessed, 27th May 2017.
- M. L. Cheney, D. R. Weyna, N. Shan, M. Hanna, L. Wojtas and M. J. Zaworotko, J. Pharm. Sci., 2011, 100, 2172–2181 CrossRef CAS PubMed.
- X. Ma, W. Yuan, S. E. J. Bell and S. L. James, Chem. Commun., 2014, 50, 1585–1587 RSC; I. Halasz, T. Friščić, S. A. J. Kimber, K. Užarević, A. Puškarić, C. Mottillo, P. Julien, V. Štrukil, V. Honkimaki and R. E. Dinnebier, Faraday Discuss., 2014, 170, 203 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed; W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef.
- E. K. Watkins and W. L. Jorgensen, J. Phys. Chem. A, 2001, 105, 4118–4125 CrossRef CAS.
- C. C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- J. Vandevondele, M. Krack, F. Mohamed, M. Parinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 3856–3868 Search PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B, 1996, 54, 1703–1710 CrossRef CAS.
- R. Hockney and J. Eastwood, Computer Simulation Using Particles, Taylor & Francis, New York, 1988, p. 540 Search PubMed.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 101, 8897–8909 CrossRef.
- F. Delogu, M. Monagheddu, G. Mulas, L. Schiffini and G. Cocco, J. Non-Cryst. Solids, 1998, 232–234, 383–389 CrossRef CAS.
- M. L. Nietiadi, P. Umstätter, I. Alabd Alhafez, Y. Rosandi, E. M. Bringa and H. M. Urbassek, Geophys. Res. Lett., 2017, 44, 10822–10828 CrossRef; E. N. Millán, D. R. Tramontina, H. M. Urbassek and E. M. Bringa, Phys. Rev. E, 2016, 93, 063004 CrossRef PubMed.
- U. Landman, W. Luedtke and E. Ringer, Wear, 1992, 153, 3–30 CrossRef CAS.
- X. Ma, L. Shi, X. He, L. Li, G. Cao, C. Hou, J. Li, L. Chang, L. Yang and Y. Zhong, Carbon, 2018, 133, 69–76 CrossRef CAS.
- M. G. Del Pópolo, E. P. M. Leiva, M. Mariscal and W. Schmickler, Surf. Sci., 2005, 597, 133–155 CrossRef.
- P. Baláž, Mechanochemistry in Nanoscience and Minerals Engineering, Springer Berlin Heidelberg, Berlin, 2008 Search PubMed.
- B. Ma, F. Zhao, X. Cheng, F. Miao and J. Jidong Zhang, Phys. Rev. B, 2017, 121, 145108 Search PubMed.
- H. Kulla, M. Wilke, F. Fischer, M. Röllig, C. Maierhofer and F. Emmerling, Chem. Commun., 2017, 53, 1664–1667 RSC.
- K. Užarević, N. Ferdelji, T. Mrla, P. A. Julien, B. Halasz, T. Friščić and I. Halasz, Chem. Sci., 2018, 9, 2525–2532 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of force field validation, molecular transfer and connective neck analysis, and local heating simulations. Also provided are two movies of simulated indentations and the input files required to run a LAMMPS simulation of the co-crystal. See DOI: 10.1039/c8sc04971h |
| This journal is © The Royal Society of Chemistry 2019 |