Open Access Article
Open Access ArticleBimetallic nickel-lutetium complexes: tuning the properties and catalytic hydrogenation activity of the Ni site by varying the Lu coordination environment†
Bianca L.
Ramirez
 a,
Prachi
Sharma
a,
Prachi
Sharma
 ab,
Reed J.
Eisenhart
a,
Laura
Gagliardi
ab,
Reed J.
Eisenhart
a,
Laura
Gagliardi
 ab and
Connie C.
Lu
ab and
Connie C.
Lu
 *a
*a
aDepartment of Chemistry, University of Minnesota, Minneapolis, Minnesota 55455-0431, USA. E-mail: clu@umn.edu
bMinnesota Supercomputing Institute, Chemical Theory Center, University of Minnesota, Minneapolis, Minnesota 55455-0431, USA
First published on 4th February 2019
Abstract
We present three heterobimetallic complexes containing an isostructural nickel center and a lutetium ion in varying coordination environments. The bidentate iPr2PCH2NHPh and nonadentate (iPr2PCH2NHAr)3tacn ligands were used to prepare the Lu metalloligands, Lu(iPr2PCH2NPh)3 (1) and Lu{(iPr2PCH2NAr)3tacn} (2), respectively. Reaction of Ni(COD)2 (where COD is 1,5-cyclooctadiene) and 1 afforded NiLu(iPr2PCH2NPh)3 (3), with a Lu coordination number (CN) of 4 and a Ni–Lu distance, d(Ni–Lu), of 2.4644(2) Å. Complex 3 can further bind THF to form 3-THF, increasing both the Lu CN to 5 and d(Ni–Lu) to 2.5989(4) Å. On the other hand, incorporation of Ni(0) into 2 provides NiLu{(iPr2PCH2NAr)3tacn} (4), in which the Lu coordination environment is more saturated (CN = 6), and the d(Ni–Lu) is substantially elongated at 2.9771(5) Å. Cyclic voltammetry of the three Ni–Lu complexes shows an overall ∼410 mV shift in the Ni(0/I) redox couple, suggesting tunability of the Ni electronics across the series. Computational studies reveal polarized bonding interactions between the Ni 3dz2 (major) and the Lu 5dz2 (minor) orbitals, where the percentage of Lu character increases in the order: 4 (6.0% Lu 5dz2) < 3-THF (8.5%) < 3 (9.3%). All three Ni–Lu complexes bind H2 at low temperatures (−30 to −80 °C) and are competent catalysts for styrene hydrogenation. Complex 3 outperforms 4 with a four-fold faster rate. Additionally, adding increasing THF equivalents to 3, which would favor build-up of 3-THF, decreases the rate. We propose that altering the coordination sphere of the Lu support can influence the resulting properties and catalytic activity of the active Ni(0) metal center.
Introduction
Despite a growing understanding of the chemical bonding between transition metals and 4f elements, the application of d–4f metal interactions in homogeneous catalysis has rarely been studied.1–3 In contrast, utilization of 4f- and d-block metal cooperativity has proven beneficial in heterogeneous catalysis. For example, lanthanide-based oxide supports have been shown to modify the electronic properties of bulk transition metals in what has been termed as electronic metal-support interactions.4,5 These electronic perturbations have important ramifications in catalysis, where for example, Pt nanoparticles deposited on a ceria support showed a 20-fold rate enhancement in the water-gas shift reaction compared to Pt(111).6On a related note, 4f-block metal ions that have been incorporated into transition-metal oxide clusters can significantly alter the overall redox potentials and reactivity. For example, a study of {LnMn3O4} cubanes illustrates that the single Ln ion electronically modulates the Mn3O4 cores, where the {LnIIIMnIV3O4}/{LnMnIV2MnIIIO4} redox couple increases linearly with the pKa of the {LnIII(OH2)6} ion, a parameter of Lewis acidity.7 In a subsequent study on {LnIIICoII3(OAc)4} cubanes, the single Ln ion serves as an electronic modulator for the cluster and exerts a beneficial effect on the overall photocatalytic water oxidation. The Ln ion boosts the water oxidation activity of the cluster by: (1) increasing the electrochemical driving force, and (2) lowering the energy for acetate–water ligand exchange at the cluster. These effects result in a large increase in the initial rate by two orders of magnitude for {LnCo3(OAc)4} compared to the tetracobalt cubane, {CoII4(OAc)4}.8 Of note, in both of these systems, the d and 4f metal centers are separated by bridging oxygen atoms; and hence, these cubanes do not involve any direct d–4f metal interactions. Similarly, a heterobimetallic Ni–NdIII complex was recently reported where the metal centers are separated via bridging oxygen atoms at a long intermetal distance of 3.505(1) Å, which precludes a direct d–4f interaction.9
Expanding on previous work in using direct Ni-group 13 interactions for promoting Ni-mediated H2/CO2 catalysis,10–13 we hypothesized that a direct d–4f metal interaction would allow for a large electronic perturbation of the transition metal, and potentially offer a greater degree of tunability with respect to reactivity. Even so, structural examples of d–4f bonding interactions remain uncommon.14–23 Selected examples are shown in Fig. 1. To the best of our knowledge, no examples of catalytic reactivity have been reported for any coordination compounds containing a direct d–4f metal interaction. Considering the recent progress in using heterobimetallic metal–metal bonded complexes in catalysis,24–30 the pursuit of d–4f complexes seemed ripe for exploration. Furthermore, the ability of lanthanides to support a larger range of coordination numbers (CN = 3 to 12)31 may be advantageous as a new paradigm for tuning catalytic activity. In this case, controlling the supporting Ln ion's coordination environment affords another lever for catalyst tuning.
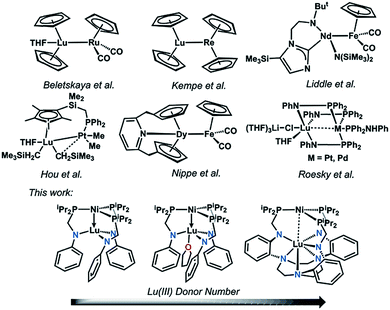 | ||
| Fig. 1 Selected examples of d–4f heterobimetallic complexes featuring the two metals in close proximity. | ||
Two new ligand frameworks were employed to make a triad of heterobimetallic nickel(0)–lutetium(III) complexes, allowing for the first study of nickel-lutetium bonding interactions. The choice of Lu was motivated by the fact that LuIII is a diamagnetic ion, which allows for facile characterization by NMR spectroscopy, and that LuIII is the most Lewis acidic of the Ln ions, with a pKa of the {LuIII(OH2)6} ion of 7.9 (cf. pKa of {LaIII(OH2)6} is 9.1).32 Additionally, we show that the electronic properties at Ni are strongly influenced by alteration of the coordination sphere at Lu. The lutetium ion, which acts as a σ-acceptor to Ni, is critical for initiating H2 binding at the nickel(0) center and its subsequent olefin hydrogenation catalysis. In general, this study probes the effect of tuning the active transition metal beyond its first coordination sphere by altering the coordination environment of the supporting metal.
Results and discussion
Preparation of monometallic Lu(III) and bimetallic Ni–Lu compounds
We introduce two ligands, bidentate iPr2PCH2NHPh33 and nonadentate (iPr2PCH2NHAr)3tacn, which are shown in Scheme 1. Both ligands comprise hard amido and soft phosphine donors. The key step in their syntheses is the condensation reaction of aniline or 1,4,7-tris(2-aminophenyl)-1,4,7-triazacyclononane34 (abbreviated as tacn) with either 1 or 3 equiv. of diisopropylphosphinomethanol, to afford iPr2PCH2NHPh or (iPr2PCH2NHAr)3tacn, respectively.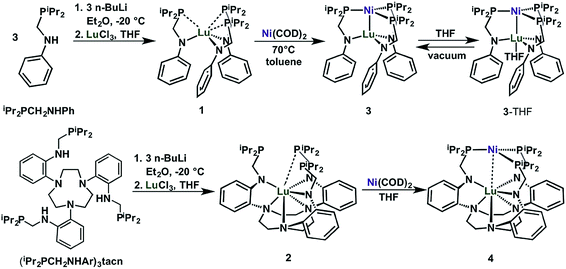 | ||
| Scheme 1 Synthesis of Lu(III) metalloligands (1 and 2) and the corresponding Ni–Lu heterobimetallic complexes (3, 3-THF, and 4). | ||
Deprotonation of iPr2PCH2NHPh (3 equiv.) or (iPr2PCH2NHAr)3tacn (1 equiv.) with 3 equiv. nBuLi and subsequent addition of LuCl3 afforded the Lu(III) metalloligands, Lu(iPr2PCH2NPh)3 (1) or Lu{(iPr2PCH2NAr)3tacn} (2), respectively, as white powders (Scheme 1). Complexes 1 and 2 display a single 31P NMR resonance at −9.4 and −7.1 ppm, respectively, in C6D6. These resonances are both shifted upfield from the free ligands, iPr2PCH2NHPh (4.2 ppm) and (iPr2PCH2NHAr)3tacn (3.3 ppm). The 1H-NMR spectrum of 1 shows a single sharp methylene resonance and two nearly coalesced methine resonances, which suggests a nearly ideal C3v solution-state geometry for 1 (Fig. S7†). On the other hand, the 1H-NMR spectrum of 2 has two distinct methine peaks and diastereotopic methylene protons in both the PCH2N and the tacn moieties, which is consistent with C3 solution-state geometry for 2 (Fig. S8†).
The heterobimetallic Ni–Lu compounds, NiLu(iPr2PCH2NPh)3 (3) and NiLu{(iPr2PCH2NAr)3tacn} (4), were isolated from the reaction of Ni(COD)2, where COD = 1,5-cyclooctadiene, with 1 and 2, respectively (Scheme 1). One interesting difference is that the metalation of 1 with Ni(COD)2 gave an immediate color change to dark red, whereas the color of the corresponding reaction with 2 deepened more gradually over several hours to a dark purple-red. Complexes 3 and 4 exhibit a single 31P-NMR resonance at −0.8 and 15.0 ppm, respectively, when dissolved in C6D6.
During the NMR studies, we uncovered a pronounced solvent effect on the speciation of 3. Upon changing the solvent to THF-d8, the 31P resonance shifts downfield by 11 ppm. We hypothesized that the THF solvent molecule can coordinate the unsaturated Lu center in 3 to form 3-THF. To interrogate this hypothesis, we sought to first understand the THF-binding equilibrium between 3 and 3-THF. Titrating THF into a toluene-d8 solution of 3 resulted in the broadening and shifting of a single 31P NMR resonance (Fig. S13,† Δδmax = 11.3). This behavior is consistent with a rapid equilibrium process, where the two species are rapidly interconverting such that only an average signal is observed.35 Plotting the change in the 31P chemical shift versus THF equivalents yields a hyperbolic binding isotherm that is consistent with a simple equilibrium of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding.36 At room temperature, saturation was observed at 80 equiv. of THF (Fig. S12–S14†), and the fitted binding equilibrium constant (Ka) of 59 ± 2 M−1,37,38 which corresponds to ΔG298K = −2.4 kcal mol−1, signifies weak binding of THF to 3.39,40
1 binding.36 At room temperature, saturation was observed at 80 equiv. of THF (Fig. S12–S14†), and the fitted binding equilibrium constant (Ka) of 59 ± 2 M−1,37,38 which corresponds to ΔG298K = −2.4 kcal mol−1, signifies weak binding of THF to 3.39,40
On the other hand, 4 showed no notable solvent-dependence of its 31P chemical shift, which is consistent with the Lu site being more fully coordinated and/or sterically protected within the triamido-tacn binding pocket. The 1H-NMR spectra of 3 and 3-THF are both consistent with an average C3v solution-state geometry, whereas the 1H-NMR spectrum of 4 is indicative of a locked C3 geometry (Fig. S9–S11†).
Molecular structures of monometallic Lu(III) and bimetallic Ni–Lu compounds
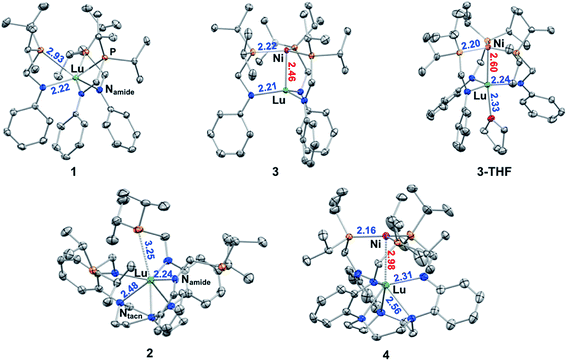
Single-crystal X-ray diffraction studies were performed on 1, 2, 3, 3-THF, and 4. The molecular structures are shown in Fig. 2 with average bond distances. Individual bond distances, bond angles, and other relevant geometrical parameters are provided in Table 1. As designed, the two ligand platforms provide different coordination environments for the Lu ion. The molecular structure of 1 reveals a six-coordinate Lu in an N3P3-donor environment. The average twist angle (θ) between the P3- and N3-triangular faces is 32.6 deg, which is close to the midpoint between an ideal octahedron (θ = 60 deg) and trigonal prism (θ = 0 deg).41,42| 1 | 2 | 3 | 3-THF | 4 | |
|---|---|---|---|---|---|
| a Estimated standard deviations (esd's) are provided in parentheses. | |||||
| Ni–Lu | — | — | 2.4644(2) | 2.5989(4) | 2.9771(5) |
| Ni–P | — | — | 2.2078(4), 2.2211(4) 2.2275(4) | 2.1834(8), 2.2046(9), 2.2121(8) | 2.1576(8), 2.1643(9), 2.1682(15) |
| Avg. Ni–P | — | — | 2.2188(2) | 2.2000(5) | 2.1634(6) |
| Lu–P | 2.8873(6), 2.9398(6), 2.9536(6) | 3.2451(9) | — | — | — |
| Avg. Lu–P | 2.9269(3) | — | — | — | — |
| Lu–Namide | 2.2207(17), 2.2233(19), 2.2251(17) | 2.210(3), 2.251(3), 2.252(3) | 2.2037(12) 2.2132(11) 2.2211(11) | 2.1834(8), 2.2046(9), 2.2121(8) | 2.298(2) 2.299(3) |
| 2.324(2) | |||||
| Avg. Lu–Namide | 2.223(1) | 2.238(1) | 2.213(1) | 2.200(1) | 2.307(1) |
| P–Ni–P | — | — | 121.133(15), 118.340(15) 119.928(15) | 121.99(3), 118.62(3), 118.58(3) | 120.26(3), 116.03(5), 122.35(5) |
| ∑(P–Ni–P) | — | — | 359.401(3) | 359.19(5) | 358.64(8) |
| Namide–Lu–Namide | 109.79(7), 108.75(6), 105.39(6) | 103.37(10) 106.64(10), 126.55(9) | 115.88(4), 118.47(4) 118.04(5) | 112.32(9), 114.48(9), 133.20(9) | 116.29(8), 119.31(9), 113.10(9) |
| ∑(Namide–Lu–Namide) | 323.93(11) | 336.56(17) | 352.39(8) | 360.00(16) | 348.69(15) |
| Lu–Ntacn | — | 2.445(3), 2.495(3), 2.502(3) | — | — | 2.559(2), 2.563(2), 2.563(2) |
| Avg. Lu–Ntacn | 2.481(2) | 2.562(1) | |||
| Lu to N3-plane | 0.7935(10) | −0.6281(16) | 0.3559(7) | 0.0090(13) | −0.4533(14) |
| Ni to P3-plane | — | — | 0.0995(3) | 0.1150(6) | 0.1464(8) |
In 2, the Lu center is coordinated by six N-donors: three relatively short Lu–Namide bonds of 2.238(5) Å and three slightly longer Lu–Ntacn bonds of 2.481(2) Å. The average twist angle of 34.0 deg is also indicative of an intermediate geometry between octahedral and trigonal prismatic. Further, owing to the favoring of high coordination numbers, an additional weak Lu–P interaction with a distance of 3.2451(9) Å was observed in the molecular structure of 2. The two Lu metalloligands also differ in the position of the Lu center relative to the triamido donor set, which will be referred to as forming the N3-plane. In 1, Lu resides in between the P3- and N3-planes at ∼0.8 Å “above” the N3-plane. On the other hand, Lu resides ∼0.6 Å “below” the N3-plane in 2.
The three Ni–Lu bimetallic complexes, 3, 3-THF, and 4, each have a common NiP3 site, but a different Lu geometry and coordination number (CN). In 3 and 3-THF, the Lu geometry is trigonal pyramidal (CN = 4) and trigonal bipyramidal (CN = 5, τ5 = 0.66), respectively.43 In 4, the Lu geometry is intermediate between octahedral and trigonal prismatic (CN = 6, θ = 35.6 deg). The Ni–Lu bond distance also varies significantly across the triad. Interestingly, the coordination environment of the Lu appears to dictate the proximity between Ni and Lu. For example, complex 3 possesses the lowest coordinate Lu in this series and has the shortest Ni–Lu bond distance of 2.4644(2) Å. In 3-THF, the addition of a single THF donor along the metal–metal axis increases the CN of Lu by 1 and elongates the Ni–Lu bond distance by 0.14 Å to 2.5989(4) Å. In 4, the 6-coordinate Lu center is either non- or only weakly bonding to Ni with a long Ni–Lu distance of 2.9771(5) Å, which is longer than that in 3 by over 0.5 Å.
Complexes 3, 3-THF, and 4 join a handful of crystallographically characterized compounds containing both Ni and Lu metals. Among these examples, the intermetal distances are too large to allow for any significant metal–metal interactions.44–50 Hence, without sufficient experimental comparisons to evaluate and/or interpret our Ni–Lu bond distances, we considered several different approaches for estimating a single bond length that is based on summing the two atoms' radii. Depending on the radii values, predictions of a single bond length can vary. Pyykkö and Atsumi derived a self-consistent system of single-bond covalent radii based on both experimental and theoretical data.51,52 Covalent radii have also been tabulated by Cordero and co-workers using a large data set obtained from the Cambridge Structural Database.53 Another complementary set of values are Pauling's single-bond metallic radii.54 Using the above approaches, the predicted distances of a single Ni–Lu covalent bond are: 2.72 Å (Pyykkö and Atsumi), 3.11 Å (Cordero et al.), and 2.706 Å (Pauling). Compared with these estimates, the Ni–Lu bond lengths in 3 (2.46 Å) and 3-THF (2.60 Å) are significantly shorter. Of note, the shortest Ni–Lu bond distances that were previously reported are in the range of 2.92 to 3.15 Å (Table S2†).44,48 Hence, we conclude that the Ni–Lu bond lengths in both 3 and 3-THF are consistent with direct Ni–Lu bonding interactions.
Notably, the intermetallic bond distance in 3 is significantly shorter than that of any other d–f bimetallic compound that has been crystallographically characterized (Table S2†). Prior to this work, the shortest d–f bond length of 2.520(1) Å was reported for NiUF(2-PPh2-4-Me-6-tBu(C6H2O))3.55 If one accounts for the single-bond covalent radius difference between Lu (1.62 Å) and U (1.70 Å), then 3 and NiUF(2-PPh2-4-Me-6-tBu(C6H2O))3 have similar r values of 0.91 and 0.90, respectively, where r is the ratio of their metal–metal bond distance to the corresponding sum of the metals' single-bond radii.51 Also, only a handful of Lu-group 10 compounds have been reported that have intermetal distances < 3 Å.15,44,56,57 These limited examples include (C5Me4SiMe2CH2PPh2)Lu(μ-CH2SiMe2CH2)(OC4H8)PtMe2 and [(Ph2PNHPh)M{μ-(Ph2PNPh)}3Lu(μ-Cl)Li(THF)3] (M = Pd or Pt), where the intermetallic distances are longer at 2.7668(5) Å, 2.9031(11), and 2.9523(9), respectively.
Comparing 3, 3-THF, and 4, the Lu–Namide bond length elongates with increasing CN. In both ligand systems, the Lu ion becomes increasingly co-planar with the triamido donors upon incorporating Ni into the metalloligand. The distance between Lu and the N3-plane also correlates well with the Ni–Lu distance. In 3, Lu is 0.4 Å above the N3-plane and closest to Ni. In 3-THF, Lu is nearly co-planar with a slightly longer Ni–Lu distance. In contrast, Lu is positioned below the N3-plane by 0.5 Å in 4, which is consistent with little or no interaction with Ni. On the other hand, the Ni site is relatively invariant across 3, 3-THF, and 4, where the distance between Ni and the P3-plane only changes slightly, from 0.10 to 0.15 Å. The only notable difference in the Ni coordination sphere is the contraction of the Ni–P bonds from 3 (avg. 2.22 Å) to 3-THF (2.20 Å) to 4 (2.16 Å). This trend is consistent with increased π-back-bonding from a more electron-rich Ni center in 4 (relative to 3 and 3-THF) to the phosphine ligands. The greater Ni electron density in 4 further suggests diminished Lewis acidity of Lu(III), which can be rationalized by the longer Ni–Lu distance and the increase in the Lu(III) coordination environment.
Electrochemistry
To probe the influence of the Lu(III) metalloligand on the electronics at the Ni center, cyclic voltammetry experiments were performed. Fig. 3 is an overlay of the cyclic voltammograms (CVs) of 3, 3-THF, and 4. The CVs were collected in 0.1 M [nPr4N][BArF4] electrolyte solutions (ArF = 3,5-bis(trifluoromethyl)phenyl) and internally referenced to the [FeCp2]+/0 potential. Because coordinating solvents can bind an unsaturated Lu(III) center, the electrochemical study of 3 was performed in 1,2-difluorobenzene (DFB).58 To minimize any shifts in the [FeCp2]+/0 reference potential due to solvent effects,59 the CV of 4 was also measured in DFB. For the CV study of 3-THF, the sample was prepared by adding 320 equiv. THF to 3 in DFB. For both 3-THF and 4, the CVs were also collected in THF.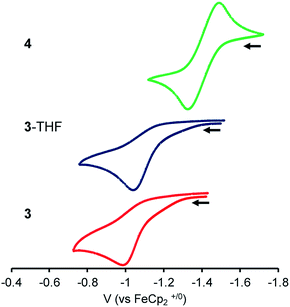 | ||
| Fig. 3 CVs of 3, 3-THF and 4 with 0.1 M [nPr4N][BArF4] electrolyte in DFB (scan rate of 100 mV s−1; collected under Ar). | ||
In DFB, 4 displayed a reversible Ni(0/I) oxidation at E1/2 = −1.41 V vs. [FeCp2]+/0 (Fig. 3).12 Complex 3 showed an irreversible oxidation at Epa = −1.00 V in DFB, which is ∼410 mV more positive than that of 4. In situ generation of 3-THF results in a ∼50 mV cathodic shift in the irreversible oxidation to Epa = −1.05 V (Fig. 3 and S42†). In THF, the Ni(0/I) oxidation for 3-THF becomes quasi-reversible at Epa = −0.97 V (ipc/ipa = 0.6 at 250 mV s−1, Fig. S43†). The Ni(0/I) redox couple for 4 remains reversible in THF, with E1/2 = −1.44 V (Fig. S45†). Of note, the Ni(0/I) redox potential for 3-THF is 470 mV more positive than that of 4 in THF, whereas the difference in their redox potentials decreases to ∼360 mV in DFB.
Overall, the Ni(0/I) oxidation potential becomes increasingly positive in moving from 4 to 3-THF to 3. This trend correlates with the increasing strength of the Ni–Lu interaction, as reflected by the intermetal distances. Hence, the Ni(0) center in 3 shows the greatest withdrawal of electron density, or alternatively, the Lu(III) support in 3 exhibits the greatest Lewis acidity in this series. This supports the hypothesis that the less coordinatively saturated Lu(III) supporting ion more greatly perturbs the Ni electronics, presumably via better bonding overlap with the soft Ni(0) Lewis base. Because the Ni–Lu interaction is greatly attenuated in 4, the Ni electronics may be expected to resemble that of the mononickel complex, Ni{N(o-(NCH2PiPr2)C6H4)3},60 which has an isostructural Ni(0) center within a tris(diisopropylphosphine) coordination environment. The mononickel complex displays a reversible Ni(0/I) redox couple at E1/2 = −1.26 V in 0.1 M [nPr4N][BArF4]/DFB (Fig. S46†), signifying that 4 is slightly more electron-rich than Ni{N(o-(NCH2PiPr2)C6H4)3}.
As an aside, an irreversible reduction at Epc ∼ −3 V was also observed for 3-THF in 0.1 M [nBu4N][PF6]/THF, whereas no reduction events are observed for 4 in the same electrolyte solution (Fig. S47†). So far, no reduction process has been observed for 3. However, this may be due to the more limited electrochemical window of DFB, for which we measured a lower limit of −2.8 V vs. [FeCp2]+/0 (Fig. S52†).
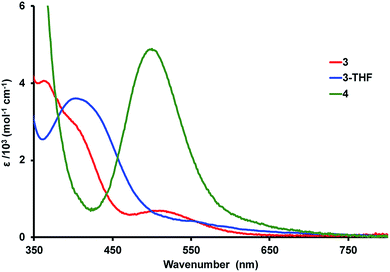
Electronic absorption spectroscopy
The colors of the Ni–Lu complexes are varying shades of red: bright red for 3, red orange for 3-THF, and purple red for 4. Fig. 4 shows an overlay of the UV-vis spectra for the Ni–Lu complexes. Compound 4 displays an intense band at 504 nm (ε = 4700 M−1 cm−1). A similar absorption was observed for the mononickel compound, Ni{N(o-(NCH2PiPr2)C6H4)3} (cf. 491 nm, ε = 4300 M−1 cm−1).60 The striking similarity between 4 and Ni{N(o-(NHCH2PiPr2)C6H4)3} also suggests that the Lu(III) ion minimally perturbs the Ni electronics in 4.Complexes 3 and 3-THF each display two overlapping bands in the region from 370 to 420 nm, and a third low-intensity absorption at higher wavelengths of 515 and 550 nm, respectively (Fig. 4, S50 and S51†). Both spectra qualitatively resemble that reported for NiAl{N(o-(NCH2PiPr2)C6H4)3}, which contains a dative Ni → Al bonding interaction.61 Hence, we propose that the stark change in the UV-vis spectrum of 4 and that of 3 or 3-THF is consistent with the presence of Ni → Lu bonding interactions in both 3 and 3-THF.
Computational investigation of 3, 3-THF, and 4
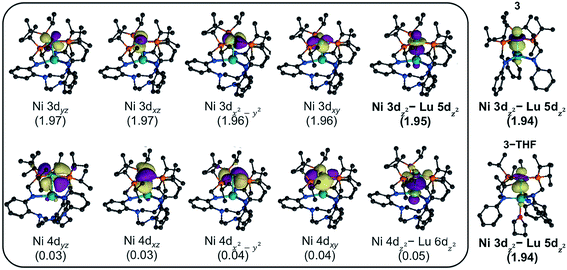
To investigate the electronic structures of 3, 3-THF, and 4 and to better understand the nature of their metal–metal interactions, we performed quantum-chemical calculations on the full structures. Geometry optimizations were conducted using density functional theory (DFT) at PBE-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62–64 level of theory, and the optimized ground-state geometries compare well to the experimental structures (Table S7†). For further studies, complete active-space self-consistent field (CASSCF)65 calculations were performed. For each Ni–Lu complex, the active natural orbitals included five Ni 3d orbitals that are each doubly occupied. Notably, one of the orbitals, though heavily Ni based (ca. 90% or greater), showed non-negligible contributions from Lu (Fig. 5, S52–S54†). This natural orbital revealed a polarized bonding interaction between the Ni 3dz2 and the Lu 5dz2, where the percentage of Lu character increases slightly in the order: 4 (6.0% Lu 5dz2) < 3-THF (8.5%) < 3 (9.3%) (Table S9†). The trend is consistent with the increasing proximity of the Ni and Lu centers and with a lower coordination number for Lu, both of which would result in better bonding overlap between these two metals. The large degree of polarization in this natural orbital further suggests that the Ni–Lu bonding is best described as a dative interaction of the Ni 3dz2 electrons into the empty Lu 5dz2 orbital.
62–64 level of theory, and the optimized ground-state geometries compare well to the experimental structures (Table S7†). For further studies, complete active-space self-consistent field (CASSCF)65 calculations were performed. For each Ni–Lu complex, the active natural orbitals included five Ni 3d orbitals that are each doubly occupied. Notably, one of the orbitals, though heavily Ni based (ca. 90% or greater), showed non-negligible contributions from Lu (Fig. 5, S52–S54†). This natural orbital revealed a polarized bonding interaction between the Ni 3dz2 and the Lu 5dz2, where the percentage of Lu character increases slightly in the order: 4 (6.0% Lu 5dz2) < 3-THF (8.5%) < 3 (9.3%) (Table S9†). The trend is consistent with the increasing proximity of the Ni and Lu centers and with a lower coordination number for Lu, both of which would result in better bonding overlap between these two metals. The large degree of polarization in this natural orbital further suggests that the Ni–Lu bonding is best described as a dative interaction of the Ni 3dz2 electrons into the empty Lu 5dz2 orbital.
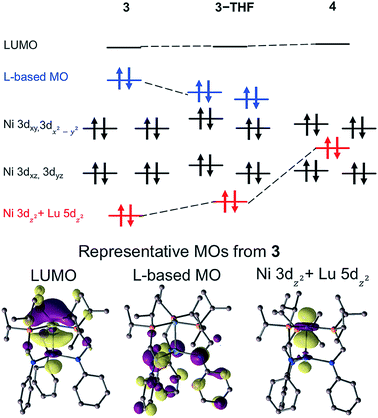
The molecular orbital (MO) diagrams for 3, 3-THF, and 4, which were obtained from DFT calculations, are shown in Fig. 6 (Fig. S55–S57†). In comparing 3 and 4, the different Lu supports have a profound effect on the relative energy of the Ni 3dz2 orbital. For 4, the Ni 3dz2 orbital is more destabilized than the Ni 3dxz/3dyz orbitals and is stabilized relative to the Ni 3dx2−y2/3dxy orbitals, as one would expect for a metal center with trigonal donors. For both 3 and 3-THF, the Ni 3dz2 orbital is the most energy-stabilized Ni d-orbital, presumably due to Ni 3dz2 → Lu 5dz2 interaction. Also of note, the LUMO for all the Ni–Lu bimetallic complexes is primarily comprised of the Ni 4pZ and Lu 6s/5dz2 orbitals, with additional contribution from the P 3pZ orbitals (Table S13†). The presence of an energetically accessible metal-based 4pZ LUMO has also been invoked in other transition metal-group 13 coordination complexes.28,66,67 Binding of weak sigma donors, ranging from solvent donors67 to H211,12,68,69 have been reported, which can be attributed to the energetically low-lying, metal-based 4pZ acceptor orbital.70 Hence, the prediction of similar LUMOs in each of the Ni–Lu bimetallic complexes may also indicate that their respective Ni sites are primed to bind H2.
H2 reactivity and catalysis
Compounds 3, 3-THF, and 4 showcase a range of H2 binding reactivity. At ambient temperature and 1 atm H2, none of these complexes showed any formation of the Ni(η2-H2) adducts.12 However, the 31P peak of the bimetallic compounds and the 1H signal for free H2 both shifted slightly, which could be a hint of weak binding (Fig. S16–S23†). Hence, to maximize H2 binding, samples of 3-THF and 4 in THF-d8 were subjected to 4 atm H2 (at room temperature) and characterized in situ by low-temperature NMR spectroscopy. To study H2 binding to 3, the same protocol was applied except that toluene-d8 was used as the solvent. The low-temperature NMR spectra for 3 have notably weaker signal intensities due to its poor solubility in non-coordinating solvents.At −80 °C and 4 atm H2, an equilibrium between 3 and a new species was observed in an approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 ratio based on the appearance of two 31P peaks at −1.7 and 9.6 ppm, respectively (Fig. S24 and S25†). The assignment of the new species as the η2-H2 adduct, 3–(H2), is based on the appearance of a broad 1H resonance at −1.4 ppm (Fig. S26†). T1 (min) relaxation time measurements, however, could not be obtained due to the broadness of the resonance. At −80 °C and 4 atm H2 in THF-d8, a similar equilibrium between 3-THF and a new species was observed in an approximate 1
0.4 ratio based on the appearance of two 31P peaks at −1.7 and 9.6 ppm, respectively (Fig. S24 and S25†). The assignment of the new species as the η2-H2 adduct, 3–(H2), is based on the appearance of a broad 1H resonance at −1.4 ppm (Fig. S26†). T1 (min) relaxation time measurements, however, could not be obtained due to the broadness of the resonance. At −80 °C and 4 atm H2 in THF-d8, a similar equilibrium between 3-THF and a new species was observed in an approximate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 ratio based on the appearance of two 31P peaks at 8.9 and 22.5 ppm, respectively (Fig. S29 and S30†). The assignment of the new species as the η2-H2 adduct, 3(H2)–THF, is based on the appearance of a broad 1H resonance at −1.3 ppm (Fig. S31†), whose short T1(min) relaxation time of 20(1) ms (400 MHz) is consistent with an intact H2 ligand (Fig. S33†).71 On the other hand, exposing 4 to 4 atm H2 at −80 °C (in either THF–d8 or toluene-d8) did not generate an observable H2 adduct, though broadening in the 31P resonance and the disappearance of the free H2 resonance both suggest that 4 does interact with H2, even if weakly (Fig. S34 and S35†). Hence, the strength of the H2 interaction with the Ni(0) center decreases in the order, 3-THF > 3 ≫ 4. Moreover, the in situ characterization of 3-(H2)THF adds to the few (η2-H2)Ni(0) examples in the literature.11,12 Since the Ni center is more electron-deficient in both 3-THF and 3 than in 4, the Ni–Lu compounds roughly follow the same trend that was observed previously for bimetallic Ni-group 13 complexes.12,28 Namely, the more Lewis acidic metalloligands lead to more stable Ni(η2-H2) adducts.
2.5 ratio based on the appearance of two 31P peaks at 8.9 and 22.5 ppm, respectively (Fig. S29 and S30†). The assignment of the new species as the η2-H2 adduct, 3(H2)–THF, is based on the appearance of a broad 1H resonance at −1.3 ppm (Fig. S31†), whose short T1(min) relaxation time of 20(1) ms (400 MHz) is consistent with an intact H2 ligand (Fig. S33†).71 On the other hand, exposing 4 to 4 atm H2 at −80 °C (in either THF–d8 or toluene-d8) did not generate an observable H2 adduct, though broadening in the 31P resonance and the disappearance of the free H2 resonance both suggest that 4 does interact with H2, even if weakly (Fig. S34 and S35†). Hence, the strength of the H2 interaction with the Ni(0) center decreases in the order, 3-THF > 3 ≫ 4. Moreover, the in situ characterization of 3-(H2)THF adds to the few (η2-H2)Ni(0) examples in the literature.11,12 Since the Ni center is more electron-deficient in both 3-THF and 3 than in 4, the Ni–Lu compounds roughly follow the same trend that was observed previously for bimetallic Ni-group 13 complexes.12,28 Namely, the more Lewis acidic metalloligands lead to more stable Ni(η2-H2) adducts.
Following the H2 binding studies, we investigated the propensity of 3 and 4 to mediate catalytic olefin hydrogenation, a process which is typically challenging for a single Ni center to perform.10,12,68,72–79 In general, the greater lack of molecular Ni hydrogenation catalysts compared to related first–row transitions metals such as Fe and Co may be attributed to the greater electronegativity of Ni, which would hinder π-backbonding and consequently, H2 activation.80 Using a loading of 2.5 mol%, 3 catalyzes the hydrogenation of styrene to ethyl benzene in high yield under 4 atm H2 and heating at 100 °C in toluene-d8 for 2 h (Table 2, entry 1). Under these standard conditions, 4 also performs the catalysis, albeit more sluggishly and in low yield (entry 2). The importance of the Lu supporting ion can be inferred from the monometallic Ni control reactions (entries 3–5), where neither the mononickel complex, Ni{N(o-(NCH2PiPr2)C6H4)3}, nor the catalyst mixtures of Ni(COD)2 with either of the current ligands gave any significant product. Further, the Lu metalloligands (1 and 2) by themselves do not mediate this catalysis (Table S4†). Finally, the presence of excess Hg during catalysis did not affect the turnovers achieved by either 3 or 4, which supports their homogeneous nature (see ESI†).
| Entry | Catalyst | T (°C) | % Conversion | Overall rate (h−1) |
|---|---|---|---|---|
| a Catalytic conditions: 2.5 mol% catalyst, 0.37 M olefin in ca. 600 μL of d8-toluene, 4 atm H2. Conversion are based on triplicate runs using 1H NMR integration. b In ca. 600 μL of d8-THF. c t = 2 h. d t = 10 h. | ||||
| 1 | 3 | 100 | 94(4)c | 18.8(9) |
| 2 | 4 | 100 | 24(3)c | 4.7(2) |
| 3 | Ni{N(o-(NCH2PiPr2)C6H4)3} | 100 | <1c | 0 |
| 4 | Ni(COD)2 + 3 equiv. iPr2PCH2NHPh | 100 | 8(1)c | 1.6(2) |
| 5 | Ni(COD)2 + (iPr2PCH2NHAr)3tacn | 100 | <1c | 0 |
| 6 | 3 | 63 | >99d | 4.1(1) |
| 7b | 3-THF | 63 | 35(2)d | 1.4(1) |
| 8 | 3 + 20 equiv. THF | 63 | 96(1)d | 3.9(1) |
| 9 | 3 + 40 equiv. THF | 63 | 86(2)d | 3.5(1) |
| 10 | 3 + 110 equiv. THF | 63 | 77(1)d | 3.1(1) |
| 11 | 3 + 660 equiv. THF | 63 | 68(3)d | 2.7(1) |
We also sought to investigate the effect of THF binding to the remote Lu site on the hydrogenation of styrene. If the reaction solvent is changed to THF (and consequently, a lower reaction temperature of 63 °C), then the overall rate of catalysis diminishes by nearly three-fold between 3 and 3-THF (entries 6 and 7). However, the addition of less than 40 equiv. THF has no observable effects on the rate. Above 40 equiv. THF, the rate perceptibly decreases with increasing THF equivalents. Presumably, the negligible changes in rate at lower concentrations of THF is due to its weak reversible binding at the LuIII center of 3 at 63 °C such that solvent effects are only manifested at higher concentrations. Indeed, the effect of THF on the rate of catalysis highlights the remote binding effect of THF on 3 and, in turn, the importance of the lanthanide coordination environment in the design of future d–f-bonded heterometallic catalysts.
Lastly, the substrate scope was further investigated for catalyst 3 (Table S5,† % conversion at 24 h). Under the standard catalytic conditions, 3 readily hydrogenated unhindered alkenes (>99%), including terminal and cyclic olefins: 1-octene, allylbenzene, and cis-cyclooctene. Linear internal olefins were either hydrogenated more sluggishly, e.g. trans-2-octene (68%), or were unreactive (<2%), e.g. trans-4-octene and trans-stilbene. For cis-stilbene, facile isomerization to the thermodynamically favored trans-stilbene was observed (93%) with some bibenzyl formation (7%). In the absence of H2, only a small amount of isomerization (7%) was observed even after 26 h, which demonstrates the importance of H2 for the isomerization reaction. Overall, the substrate scope for 3 is similar to that reported for a similar Ni–Ga complex.12 One surprising difference is the different outcomes with allylbenzene: 3 generated propylbenzene in nearly quantitative yield in 2 h, whereas reaction with the Ni–Ga catalyst only showed 3% yield at 24 h. Perhaps, the greater flexibility of the non-tethered ligand of 3 allows for its greater reactivity with this substrate.
Conclusions
This work studies the effect of tuning an active metal (Ni) beyond its primary coordination sphere, specifically by tuning the ligand environment of a supporting Lewis acidic ion (Lu). Through the employment of two new phosphinoamido ligand frameworks, 1 and 2, three new heterobimetallic Ni(0)-Lu(III) complexes were synthesized. The ligand [iPr2PCH2NPh]− stabilizes the Ni–Lu complex, 3, with a low-coordinate Lu ion (CN = 4), and the Ni–Lu interaction exists without any competing trans-ligand(s). The Ni–Lu interaction can be perturbed simply by the addition of THF, which binds reversibly to the Lu center in 3-THF (CN = 5). At the other extreme, the [(iPr2PCH2NAr)3tacn]3− ligand enforces a more saturated Lu environment (CN = 6), resulting in a diminished Ni–Lu interaction in 4. This work showcases the first two examples of coordination complexes with Ni–Lu bonding interactions, which also collectively add to the few examples of complexes with direct 3d–4f interactions.Varying the coordination environment of the distal Lu ion significantly impacts the ability of Lu to act as a Lewis acidic acceptor for the Ni metal, which consequently, impacts the Ni–Lu bonding interaction. Changes in the latter are reflected in the Ni–Lu distances differing by over 0.5 Å, as well as the variable mixing of the Lu and Ni dz2 orbitals in the σ-bonding MO. We propose that the different Ni–Lu bonding interactions are the underlying reason for the property and reactivity differences among these otherwise isostructural Ni sites. For example, tunability of the Ni electronics across the series is reflected in the ∼410 mV shift in the Ni(0/I) oxidation potential. Large variability in H2 binding is also evident: while barely detectable for 4, Ni(η2-H2) adducts are spectroscopically characterized at low T for both 3 and 3-THF. To our knowledge, the latter are the first reported non-classical H2 adducts for any d–f heterobimetallic compounds, and they represent the first demonstration of using Ln supports to induce H2 binding at a single Ni center.
The accumulation of these remote coordination effects on the Ni electronics further influences their catalytic activity. Complex 3 outperforms 4 in catalytic styrene hydrogenation by a factor of 4. Further, the presence of an open coordination site at Lu in 3 presents the unique opportunity to tune catalytic activity via external ligand binding at this remote site. Along these lines, adding increasing equivalents of THF to 3 does decrease the overall rate of hydrogenation, albeit more than 40 equiv. of THF are necessary to impede the rate.
In closing, d–f bonding interactions appear promising for promoting reactivity at a base transition metal center. From the perspective of catalyst design, lanthanide supporting ions may offer key advantages. The full Ln series is synthetically accessible for fine tuning of both the Lewis acidity and ionic size of the supporting 4f ion. Developing low-coordinate Ln metalloligands that allow for dynamic binding of external ligands may also be potentially useful for switchable catalysis applications, and as a general design strategy for tuning beyond the binding site. We are currently exploring these research avenues.
Conflicts of interest
There are no conflicts of interest.Acknowledgements
The authors thank Dr Laura J. Clouston and Dr Dale R. Pahls for preliminary results and helpful discussions. BLR is grateful to 3M for a research fellowship. The experimental work was supported by the American Chemical Society Petroleum Research Fund (57192-ND3). C. C. L. acknowledges the National Science Foundation (CHE-1665010) for support. The computational work was supported by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, of the U.S. Department of Energy under Grant USDOE/DESC002183. X-ray diffraction experiments were performed using a crystal diffractometer acquired through an NSF-MRI award (CHE-1229400) in the X-ray laboratory supervised by Dr Victor G. Young, Jr.References
- M. V. Butovskii and R. Kempe, New J. Chem., 2015, 39, 7544–7558 RSC.
- B. Oelkers and R. Kempe, in Molecular Metal-Metal Bonds, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 1st edn, 2015, pp. 47–71 Search PubMed.
- S. T. Liddle and D. P. Mills, Dalton Trans., 2009, 5592–5605 RSC.
- C. T. Campbell, Nat. Chem., 2012, 4, 597–598 CrossRef CAS PubMed.
- M. Ahmadi, H. Mistry and B. Roldan Cuenya, J. Phys. Chem. Lett., 2016, 7, 3519–3533 CrossRef CAS PubMed.
- A. Bruix, J. A. Rodriguez, P. J. Ramírez, S. D. Senanayake, J. Evans, J. B. Park, D. Stacchiola, P. Liu, J. Hrbek and F. Illas, J. Am. Chem. Soc., 2012, 134, 8968–8974 CrossRef CAS PubMed.
- P.-H. Lin, M. K. Takase and T. Agapie, Inorg. Chem., 2015, 54, 59–64 CrossRef CAS PubMed.
- F. Evangelisti, R. Moré, F. Hodel, S. Luber and G. R. Patzke, J. Am. Chem. Soc., 2015, 137, 11076–11084 CrossRef CAS PubMed.
- A. Kumar, D. Lionetti, V. W. Day and J. D. Blakemore, Chem.–Eur. J., 2018, 24, 141–149 CrossRef CAS PubMed.
- W. H. Harman and J. C. Peters, J. Am. Chem. Soc., 2012, 134, 5080–5082 CrossRef CAS PubMed.
- W. H. Harman, T.-P. Lin and J. C. Peters, Angew. Chem., Int. Ed., 2014, 53, 1081–1086 CrossRef CAS PubMed.
- R. C. Cammarota and C. C. Lu, J. Am. Chem. Soc., 2015, 137, 12486–12489 CrossRef CAS PubMed.
- R. C. Cammarota, M. V. Vollmer, J. Xie, J. Ye, J. C. Linehan, S. A. Burgess, A. M. Appel, L. Gagliardi and C. C. Lu, J. Am. Chem. Soc., 2017, 139, 14244–14250 CrossRef CAS PubMed.
- I. P. Beletskaya, A. Z. Voskoboynikov, E. B. Chuklanova, N. I. Kirillova, A. K. Shestakova, I. N. Parshina, A. I. Gusev and G. K. I. Magomedov, J. Am. Chem. Soc., 1993, 115, 3156–3166 CrossRef CAS.
- Y. Nakajima and Z. Hou, Organometallics, 2009, 28, 6861–6870 CrossRef CAS.
- M. V. Butovskii, C. Döring, V. Bezugly, F. R. Wagner, Y. Grin and R. Kempe, Nat. Chem., 2010, 2, 741–744 CrossRef CAS PubMed.
- M. V. Butovskii, O. L. Tok, V. Bezugly, F. R. Wagner and R. Kempe, Angew. Chem., Int. Ed., 2011, 50, 7695–7698 CrossRef CAS PubMed.
- M. V. Butovskii, O. L. Tok, F. R. Wagner and R. Kempe, Angew. Chem., Int. Ed., 2008, 47, 6469–6472 CrossRef CAS PubMed.
- C. Döring, A. M. Dietel, M. V. Butovskii, V. Bezugly, F. R. Wagner and R. Kempe, Chem.–Eur. J., 2010, 16, 10679–10683 CrossRef PubMed.
- A. Spannenberg, M. Oberthür, H. Noss, A. Tillack, P. Arndt and R. Kempe, Angew. Chem., Int. Ed., 1998, 37, 2079–2082 CrossRef CAS PubMed.
- P. L. Arnold, J. McMaster and S. T. Liddle, Chem. Commun., 2009, 818–820 RSC.
- C. P. Burns, X. Yang, J. D. Wofford, N. S. Bhuvanesh, M. B. Hall and M. Nippe, Angew. Chem., Int. Ed., 2018, 57, 8144–8148 CrossRef CAS PubMed.
- C. P. Burns, X. Yang, S. Sung, J. D. Wofford, N. S. Bhuvanesh, M. B. Hall and M. Nippe, Chem. Commun., 2018, 54, 10893–10896 RSC.
- B. G. Cooper, J. W. Napoline and C. M. Thomas, Catal. Rev., 2012, 54, 1–40 CrossRef CAS.
- P. Buchwalter, J. Rosé and P. Braunstein, Chem. Rev., 2015, 115, 28–126 CrossRef CAS PubMed.
- D. R. Pye and N. P. Mankad, Chem. Sci., 2017, 8, 1705–1718 RSC.
- I. G. Powers and C. Uyeda, ACS Catal., 2017, 7, 936–958 CrossRef CAS.
- R. C. Cammarota, L. J. Clouston and C. C. Lu, Coord. Chem. Rev., 2017, 334, 100–111 CrossRef CAS.
- N. P. Mankad, Chem.–Eur. J., 2016, 22, 5822–5829 CrossRef CAS PubMed.
- C. M. Thomas, Comments Inorg. Chem., 2011, 32, 14–38 CrossRef CAS.
- C. Huang and Z. Bian, in Rare Earth Coordination Chemistry, ed. C. Huang, John Wiley & Sons, Singapore, 1st edn, 2010, pp. 1–40 Search PubMed.
- D. D. Perrin, Ionisation Constants of Inorganic Acids and Bases in Aqueous Solution, ed. D. D. Perrin, Pergamon, Oxford, 2nd edn, 1982, pp. 1–138 Search PubMed.
- E. Payet, A. Auffrant, X. F. Le Goff and P. L. Floch, J. Organomet. Chem., 2010, 695, 1499–1506 CrossRef CAS.
- I. A. Fallis, R. D. Farley, K. M. A. Malik, D. M. Murphy and H. J. Smith, J. Chem. Soc., Dalton Trans., 2000, 3632–3639, 10.1039/b005402j.
- I. R. Kleckner and M. P. Foster, Biochim. Biophys. Acta, Proteins Proteomics, 2011, 1814, 942–968 CrossRef CAS PubMed.
- J. Kuriyan, B. Konforti and D. Wemmer, in The Molecules of Life: Physical and Chemical Properties, Garland Publishing, New York, 1st edn, 2013, pp. 531–580 Search PubMed.
- P. Thordarson, Supramolecular.org, http://supramolecular.org/, accessed July 13, 2018.
- D. Brynn Hibbert and P. Thordarson, Chem. Commun., 2016, 52, 12792–12805 RSC.
- L. Fielding, Tetrahedron, 2000, 56, 6151–6170 CrossRef CAS.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- K. R. Dymock and G. J. Palenik, Inorg. Chem., 1975, 14, 1220–1222 CrossRef CAS.
- E. L. Muetterties and L. J. Guggenberger, J. Am. Chem. Soc., 1974, 96, 1748–1756 CrossRef CAS.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356 RSC.
- P. Comba, M. Enders, M. Großhauser, M. Hiller, D. Müller and H. Wadepohl, Dalton Trans., 2017, 46, 138–149 RSC.
- S. R. Bayly, Z. Xu, B. O. Patrick, S. J. Rettig, M. Pink, R. C. Thompson and C. Orvig, Inorg. Chem., 2003, 42, 1576–1583 CrossRef CAS PubMed.
- N. Ahmed, C. Das, S. Vaidya, S. K. Langley, K. S. Murray and M. Shanmugam, Chem.–Eur. J., 2014, 20, 14235–14239 CrossRef CAS PubMed.
- V. Vieru, T. D. Pasatoiu, L. Ungur, E. Suturina, A. M. Madalan, C. Duhayon, J.-P. Sutter, M. Andruh and L. F. Chibotaru, Inorg. Chem., 2016, 55, 12158–12171 CrossRef CAS PubMed.
- N. Kondoh, Y. Shimizu, M. Kurihara, H. Sakiyama, M. Sakamato, Y. Nishida, Y. Sadaoka, M. Ohba and H. Okawa, Bull. Chem. Soc. Jpn., 2003, 76, 1007–1008 CrossRef CAS.
- T. Shiga, N. Ito, A. Hidaka, H. Ōkawa, S. Kitagawa and M. Ohba, Inorg. Chem., 2007, 46, 3492–3501 CrossRef CAS PubMed.
- S. Orita and T. Akitsu, Open Chem., 2014, 1, 1–14 CrossRef.
- P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337 CrossRef PubMed.
- P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197 CrossRef PubMed.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- L. Pauling, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- J. A. Hlina, J. R. Pankhurst, N. Kaltsoyannis and P. L. Arnold, J. Am. Chem. Soc., 2016, 138, 3333–3345 CrossRef CAS PubMed.
- F. Völcker, F. M. Muck, K. D. Vogiatzis, K. Fink and P. W. Roesky, Chem. Commun., 2015, 51, 11761–11764 RSC.
- F. Völcker and P. W. Roesky, Dalton Trans., 2016, 45, 9429–9435 RSC.
- T. R. O'Toole, J. N. Younathan, B. P. Sullivan and T. J. Meyer, Inorg. Chem., 1989, 28, 3923–3926 CrossRef.
- I. Noviandri, K. N. Brown, D. S. Fleming, P. T. Gulyas, P. A. Lay, A. F. Masters and L. Phillips, J. Phys. Chem. B, 1999, 103, 6713–6722 CrossRef CAS.
- (a) L. J. Clouston, R. B. Siedschlag, P. A. Rudd, N. Planas, S. Hu, A. D. Miller, L. Gagliardi and C. C. Lu, J. Am. Chem. Soc., 2013, 135, 13142–13148 CrossRef CAS PubMed; (b) R. Cammarota, PhD thesis, University of Minnesota, 2018.
- P. A. Rudd, S. Liu, L. Gagliardi, V. G. Young and C. C. Lu, J. Am. Chem. Soc., 2011, 133, 20724–20727 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- D. You, H. Yang, S. Sen and F. P. Gabbaï, J. Am. Chem. Soc., 2018, 140, 9644–9651 CrossRef CAS PubMed.
- B. R. Barnett, C. E. Moore, P. Chandrasekaran, S. Sproules, A. L. Rheingold, S. DeBeer and J. S. Figueroa, Chem. Sci., 2015, 6, 7169–7178 RSC.
- T.-P. Lin and J. C. Peters, J. Am. Chem. Soc., 2014, 136, 13672–13683 CrossRef CAS PubMed.
- M. V. Vollmer, J. Xie, R. C. Cammarota, V. G. Young, E. Bill, L. Gagliardi and C. C. Lu, Angew. Chem., Int. Ed., 2018, 57, 7815–7819 CrossRef CAS PubMed.
- G. Aullón and S. Alvarez, Inorg. Chem., 1996, 35, 3137–3144 CrossRef.
- P. J. Desrosiers, L. Cai, Z. Lin, R. Richards and J. Halpern, J. Am. Chem. Soc., 1991, 113, 4173–4184 CrossRef CAS.
- T. J. Mooibroek, E. C. M. Wenker, W. Smit, I. Mutikainen, M. Lutz and E. Bouwman, Inorg. Chem., 2013, 52, 8190–8201 CrossRef CAS PubMed.
- K. V. Vasudevan, B. L. Scott and S. K. Hanson, Eur. J. Inorg. Chem., 2012, 2012, 4898–4906 CrossRef CAS.
- I. M. Angulo and E. Bouwman, J. Mol. Catal. A: Chem., 2001, 175, 65–72 CrossRef CAS.
- J. Camacho-Bunquin, M. J. Ferguson and J. M. Stryker, J. Am. Chem. Soc., 2013, 135, 5537–5540 CrossRef CAS PubMed.
- I. M. Angulo, A. M. Kluwer and E. Bouwman, Chem. Commun., 1998, 2689–2690 RSC.
- Y. Wang, A. Kostenko, S. Yao and M. Driess, J. Am. Chem. Soc., 2017, 139, 13499–13506 CrossRef CAS PubMed.
- J. Wu, J. W. Faller, N. Hazari and T. J. Schmeier, Organometallics, 2012, 31, 806–809 CrossRef CAS.
- N. G. Léonard and P. J. Chirik, ACS Catal., 2018, 8, 342–348 CrossRef.
- P. L. Holland, Dalton Trans., 2010, 39, 5415–5425 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic and computational details, spectroscopic data, and detailed crystallographic information for 1–4. CCDC 1870303–1870307. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc04712j |
| This journal is © The Royal Society of Chemistry 2019 |