A hypervalent and cubically coordinated molecular phase of IF₈ predicted at high pressure

Abstract

Up to now, the maximum coordination number of iodine is seven in neutral iodine heptafluoride (IF₇) and eight in anionic octafluoride (IF₈⁻). Here, we explore pressure as a method for realizing new hypercoordinated iodine compounds. First-principles swarm structure calculations have been used to predict the high-pressure and T → 0 K phase diagram of binary iodine fluorides. The investigated compounds are predicted to undergo complex structural phase transitions under high pressure, accompanied by various semiconductor to metal transitions. The pressure induced formation of a neutral octafluoride compound, IF₈, consisting of eight-coordinated iodine is one of several unprecedented predicted structures. In sharp contrast to the square antiprismatic structure in IF₈⁻, IF₈, which is dynamically unstable under atmospheric conditions, is stable and adopts a quasi-cube molecular configuration with R3̄ symmetry at 300 GPa. The metallicity of IF₈ originates from a hole in the fluorine 2p-bands that dominate the Fermi surface. The highly unusual coordination sphere in IF₈ at 300 GPa is a consequence of the 5d levels of iodine coming down and becoming part of the valence, where they mix with iodine's 5s and 5p levels and engage in chemical bonding. The valence expansion of iodine under pressure effectively makes IF₈ not only hypercoordinated, but also hypervalent.

---

1. Introduction

It is well known that the coordination number of atoms in compounds can greatly affect chemical properties^1,2 and exploring new coordination motifs of elements is of importance to understand their chemical behavior and expand their applications.^3–5 Iodine has, with the exception of astatine, the lowest electronegativity, the largest polarizability, and the largest atom size of the halogens.^6–8 These properties and the ability to readily engage in hypercoordination, i.e. allowing for more atoms in its coordination sphere than what is predicted by the octet rule, combined with its low toxicity, make iodine distinct from the lighter p-block elements. The ability of iodine to engage in hypercoordination allows fabrication of compounds that are potential substitutes for transition metal-based catalysts.^9,10 Commercially available hypercoordinated iodine compounds have shown promise for mild and highly selective oxidizing ability and environmentally benign catalysis.^11–14

The highest known coordination number in a neutral iodine fluoride compound is seven, in IF₇.¹⁵ Isoelectronic XeF₇⁺ and TeF₇⁻ have been synthesized.¹⁶ With the exception of some caged ions,¹⁷ higher coordination numbers in neutral main group compounds are, to the best of our knowledge, non-existent. XeF₈ has been shown unstable even under pressures reaching 200 GPa.¹⁸ Chemically, the limit in the coordination number of iodine can be rationalized from the atom's seven valence electrons. Formally, the valence shell of iodine in IF₇ can either be seen allowing for seven polar covalent bonds or, alternatively, the formation of closed-shell I(VII) surrounded by seven fluoride ligands. Because d-orbitals typically do not partake in the chemical bonding of main group elements, the classification as hypervalent is controversial, and the term hypercoordination is preferred.¹⁹

By this logic, octacoordination should be allowed by the addition of one electron. Indeed, anionic octafluoride (IF₈⁻) has been synthesized as the [NO₂]⁺[IF₈]⁻ salt.²⁰ The coordination geometry of IF₈⁻ is square antiprismatic. This kind of arrangement is commonly observed in different transition metal octafluorides, for example in TaF₈³⁻, ReF₈⁻ and ZrF₈⁴⁻.²¹ Does this mean that the quest for higher coordination numbers in neutral iodine fluorides is over?

We do not believe so. Pressure is known to fundamentally change the chemistry and structure by, for example, overcoming reaction energy barriers, shortening interatomic distances, and modifying atomic orbital energy levels.^22,23 There are many examples of the utility of pressure in allowing remarkable new hypercoordinated compounds, for example H₅I,^24,25 XeF₆,¹⁸ HgF₄,²⁶ Li₅Cs,²⁷ CsF₅,²⁸ AuF₆,²⁹ Li₅Au,³⁰ AH₆ (A = Sr, Ba),^31,32 LaH₁₀,³³ and BaReH₉.³⁴

To explore the effects of pressure and search for higher coordination numbers in iodine fluorides, we have performed an extensive structure search of selected stoichiometries of IF_x (x = 1/3, 1/2, 2/3, and 1–12) from 100 to 300 GPa using swarm-intelligence-based structural prediction calculations. Dynamical stability is an important criterion when predicting structural stability. The calculated phonon spectra of the predicted phases are shown in the ESI† and show no phonon modes with imaginary frequencies (Fig. S1†). The most notable of our predictions is the stabilization of a molecular IF₈ phase of R3̄ symmetry at 300 GPa. The cubic coordination geometry of this molecular solid is distinct from the square antiprismatic structure in IF₈⁻. We will return to discuss this unprecedented iodine coordination sphere and its underlying electronic structure.

2. Results and discussion

2.1 Stability and crystal structures

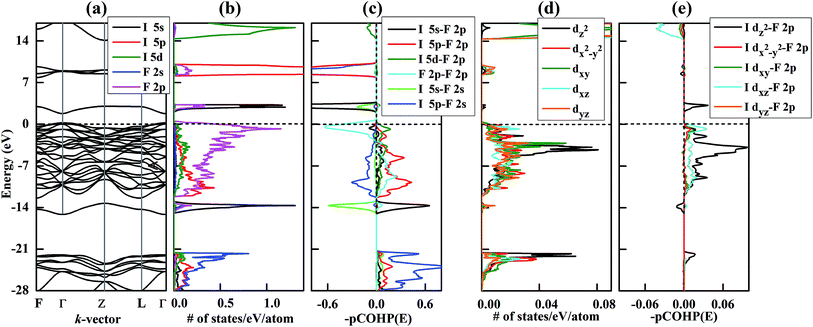
The relative stabilities of the different binary compositions were estimated by calculating the enthalpy of formation at T → 0 K and building the convex hull based on the most stable structures of the considered compositions (Fig. 1a). In Fig. 1a, the thermodynamically stable IF_x structures are depicted as filled symbols, which resist decomposing into elemental solids or other stable compounds. Besides reproducing the known structures of IF_x (x = 3, 5, 7) under ambient conditions,¹⁰ some unexpected compounds with stoichiometries of IF_x (x = 8, 10, 11, 12) are predicted to become thermodynamically stable under high pressure. Note that these stoichiometries do not mean the same coordination number of fluorine around iodine. The maximal coordination number found is 8. The crystal structures of iodine fluorides that show stability in some part of the investigated pressure range are shown in Fig. 2. The stable structures will be discussed separately. All other considered stoichiometries, not shown in Fig. 2, have enthalpies that sit slightly above the solid line in Fig. 1a and are either unstable or metastable. Decomposition enthalpies with respect to stable IF_x compounds and elemental solid I₂ or F₂ are shown in Table S1.†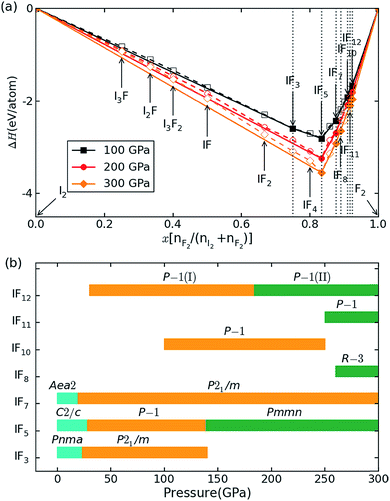

Fig. 1 Relative stability of iodine fluorides. (a) Convex hull diagram for iodine fluoride compositions at 100, 200 and 300 GPa. The elemental reference structures used are I₂ in the Fm3̄m phase and F₂ in the Cmca phase. These phases have previously been shown to be stable over the relevant pressure range.^35,36 Dotted lines connect the lowest energy data points, and solid lines denote the convex hull. Stable compositions are indicated by filled symbols. (b) Pressure-composition phase diagram of iodine fluorides.

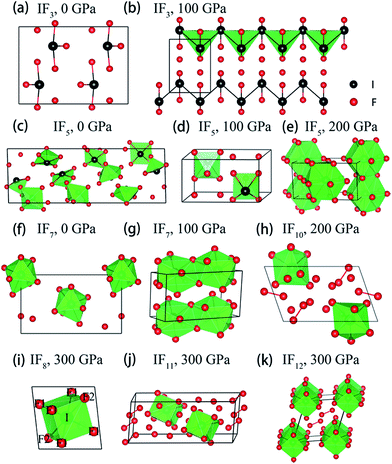Fig. 2 Stable crystal structures of the considered I–F compounds. (a) Pnma phase of IF₃ at 0 GPa. (b) P2₁/m phase of IF₃ at 100 GPa. (c) C2/c phase of IF₅ at 0 GPa (d) P1̄ phase of IF₅ at 100 GPa. (e) Pmmn phase of IF₅ at 200 GPa. (f) Aea2 phase of IF₇ at 0 GPa. (g) P2₁/m phase of IF₇ at 100 GPa. (h) P1̄ phase of IF₁₀ at 200 GPa. (i) R3̄ phase of IF₈ at 300 GPa. (j) P1̄ phase of IF₁₁ at 300 GPa. (k) P1̄ phase of IF₁₂ at 300 GPa. Black and red balls denote I and F atoms, respectively. The unit cell is drawn with black solid lines. Detail structural parameters of these I–F compounds are shown in Tables S2 and S3.†

A pressure-resolved phase diagram of iodine fluorides was built to facilitate experimental studies and is shown in Fig. 1b. At ambient pressure, the known molecular crystals of IF_x (x = 3, 5 and 7) are reproduced (Fig. 2a, c, and f). Under compression, these molecular structures are predicted to undergo phase transitions and eventually transform into aggregated phases. For IF₃, the ambient pressure orthorhombic Pnma structure transforms to a monoclinic phase (space group P2₁/m) at 23 GPa (Fig. 2b). The P2₁/m phase contains a zigzag iodine chain, in which an I–I distance of 2.7 Å is nearly the same as that in the I₂ molecule at 1 atm. The IF₃ molecular phase is predicted to become unstable with respect to IF₅ and I₂ above 140 GPa. Under compression, C2/c-structured IF₅ is predicted to first transform to another molecular phase with P1̄ symmetry at 28 GPa (Fig. 2d) and subsequently into a non-molecular P2₁/m phase above 139 GPa (Fig. 2e). In contrast to IF₅, IF₇ directly transforms into a non-molecular P2₁/m phase at 20 GPa (Fig. 2g). Compared with the structures under near ambient conditions (Fig. 2c and f), the IF₅ and IF₇ molecular phases become gradually more distorted with compression. IF₅ is predicted to transform into an orthorhombic structure with Pmmn symmetry, consisting of face-sharing 14-fold I–F polyhedra (Fig. 2e) at 200 GPa. P2₁/m-structured IF₇ is similarly predicted to be structured as an edge-sharing 12-fold polyhedron (Fig. 2g) at 100 GPa.

2.2 Unexpected IF₈

We arrive next to the IF₈ stoichiometry. Here a new stable compound with R3̄ symmetry is predicted to be stable above 260 GPa (Fig. 2i). Whereas a cubic coordination geometry is common in extended materials, such as in the bcc lattice, a cubic ligand field has, to the best of our knowledge, never been experimentally found in a molecule. We will therefore focus most of the remainder of this paper discussing IF₈. The unusual cubic coordination returns in the investigated IF_10, IF₁₁, and IF₁₂ compositions, which all consist of F₂ together with either IF₈ or IF₇ molecular structural units (Fig. 2h, j and k and S2†). Predicted IF₁₀, IF₁₁, and IF₁₂ phases are all compositions with P1̄ symmetry in their respective stable pressure ranges.

The primitive cell of the R3̄ phase of IF₈ contains one formula unit only, in which each I atom forms an eight-fold coordination with F atoms. That IF₈ shows a clear molecular character is evident from the analysis of bond distances: six shorter I–F1 (1.789 Å) and two slightly longer I–F2 (1.802 Å), followed by a set of third nearest neighbors at 2.333 Å (Fig. 2i and S3†). The nearest intermolecular F–F contacts between IF₈ units in the R3̄ crystal is 1.89 Å. In comparison, the nearest non-bonded contacts in a crystal of F₂ optimized at 300 GPa is 1.75 Å. The molecular character is also supported by chemical bonding analyses that we will return to.

After examining the results of our structural searches, we found another IF₈ phase with a square antiprismatic structure (space group Pn3̄n). However, the Pn3̄n-structured IF₈ (Fig. S4†) is unstable with respect to the quasi-cubical IF₈ (i.e. R3̄-structured IF₈) by 14.6 eV per formula unit. The large difference in enthalpy between the two structures can be attributed to a more favorable pV-term for the R3̄ structure and to the occupation of anti-bonding levels involving I 5d levels in the Pn3̄n structure (details are provided in the ESI†)

2.3 Chemical bonding and electronic properties of IF₈

Under normal ambient conditions molecular IF₇ takes a pentagonal bipyramidal coordination and ionic IF₈⁻ a square antiprismatic coordination. The coordination sphere of these closed-shell molecules can be straightforwardly rationalized with simple valence shell electron-pair-repulsion (VSEPR) arguments, in which ligands maximize distances to their neighbors to minimize exchange, or Pauli repulsion.³⁷ In contrast, molecular IF₈ is an electron deficient radical, with one hole in its valence p-shell. Under ambient conditions we are correct to expect such a structure to dissociate into IF₇ and an F atom. So how can IF₈ represent a stable composition under high compression, and why does it take its peculiar cubic structure?

We think that this can be explained in the following way: first, we know that the difference in electronegativity between F and I will not change meaningfully under high compression, and so we cannot expect a drastic change in the electronic structure for this reason.³⁸ In atomic iodine, the 5d levels lie 8.2 eV above the 5p levels.³⁹ Consequently, mixing, or hybridization, with 5d is not considered important for the chemical behavior of iodine under normal conditions.⁴⁰ As we shall see, this changes under compression. To understand why, we take a molecular orbital (MO) perspective.

We know that for a cubic ligand field, the expected splitting of non-bonding d-orbitals is three (T_2g) – over – two (E_g).^41,42 Work on 8-coordination by Burdett, Hoffmann and Fay (BHF) compared different coordination geometries using group theory arguments and extended Hückel calculations.⁴³ Among other things, it was demonstrated that the E_g levels (the d_z² and the d_x²−y² orbitals) should be non-bonding because they do not point along the bond axes of a cubic ligand field. However, the BHF work did not evaluate interactions that would occur with ligand p-levels in this specific coordination environment. The rarity of the cubic coordination sphere in nature is undoubtedly the reason for its near absence in the scientific literature.

To remedy the situation, we show in Fig. 3 the molecular orbital (MO) diagram for I 5s, 5p and 5d interacting with F 2p levels in a cubic (O_h symmetric) coordination geometry. This diagram is a sketch constructed from symmetry arguments applied to an isolated IF₈ molecule. The energy orderings have been predicted using DFT calculations on the different fragments in vacuum. Two orbital combinations, of A_1g and T_1u symmetry, predict the specific interactions of I 5s and 5p with the corresponding symmetry adapted MOs of the F₈ ligand cage. Assuming that the energy ordering shown in Fig. 3 is correct, five out of the six occupied MOs of these symmetries are I–F bonding. The T_2g and E_g levels are noteworthy, as they predict the exclusive bonding interaction between the formally unoccupied I 5d levels and the F 2p ligand orbitals of the same symmetry. The designations of the MOs as bonding and antibonding are based on symmetry arguments, and this will not change under pressure. What might change is the relative importance of the MOs, their energy relative each other, and the degree of mixing of what are, under ambient conditions, unoccupied I 5d-levels. How can occupation of I 5d orbitals be possible under compression?

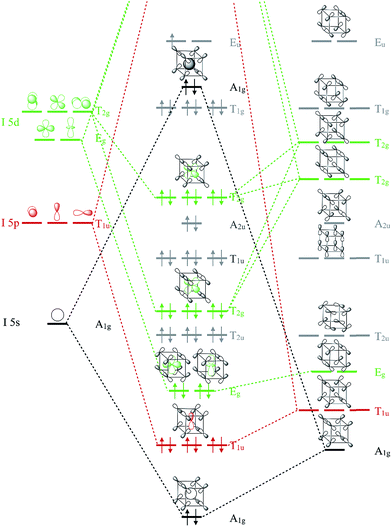Fig. 3 Molecular orbital diagram showing orbitals of iodine mixing with the symmetry adapted ligand orbitals of the F₈ cage. Energies are not to scale. Approximate energy orderings were predicted using DFT calculations on frozen fragments of IF₈ and F₈ in vacuum. The energy levels of atomic I are known from experiment.³⁷ Orbital symmetries responsible for I–F bonding are colored green for T_2g and E_g (I 5d), red for T_1u (I 5p) and black for A_1g (I 5s). One bonding combination of A_1g symmetry between I 5s and F 2s valence orbitals is omitted for clarity, as are the unoccupied orbitals.

That orbitals of different kind can cross due to compression is well known.^44,45 Mao-Sheng Miao and Roald Hoffmann have given a nice explanation as to why orbitals can cross in compressed atoms.⁴⁶ In brief, orbitals that are smaller, and have fewer radial nodes, are less affected by compression. For a given principal quantum number, compression tend to increase level energies as s > p > d. In complex systems such as IF₈, the purely physical effect of pressure is one factor affecting level ordering. A positive charge on iodine also helps to decrease the energy of I 5d levels relative to the ligand F orbitals, and we will return to address the oxidation state of iodine. As we shall see, chemical interactions with F atoms play a key role for bringing down I 5d levels in IF₈.

We can use the MO diagram in Fig. 3 to understand that as the volume of the F₈ cage decreases, as it will under compression, the overlap between I and F-based orbitals will naturally increase. Of course, iodine atoms and F₈ are just fictional references here – what matters are the IF₈ orbitals. Because the occupied T_2g and E_g MOs of IF₈ are all I–F bonding, these MOs will come down in energy relative to the other MOs as the pressure mounts and overlaps increase. The same goes for the I–F bonding A_1g and T_1u orbitals, which, together with the T_2g and E_g set, are predicted to drive the stabilization of the high symmetry cubic coordination under high pressure. Put differently, participation of I 5d, and the cubic coordination geometry, can be rationalized by symmetry facilitated bonding interactions with the ligand framework, which become increasingly pronounced as the volume of the system decreases (Fig. S5†). The ligand coordination is essential for bringing down the d-orbitals of iodine. There is, for example, no participation of I 5d levels in similarly compressed elemental iodine (Fig. S6†). There are, as the MO diagram shows, also simultaneous F–F interactions of both bonding and antibonding character in IF₈. However, as we shall see and quantify, I–F bonding interactions are significantly larger than F–F interactions, which largely cancel out under compression.

How does this analysis fit with the predicted R3̄ structure of IF₈ at 300 GPa? Remarkably well, as it turns out. First, our crystal orbital Hamilton populations (COHPs) confirm the predominately molecular character of the electronic structure, already inferred by the predicted bond lengths. The integrated COHP up to the Fermi level between iodine and its 8 nearest neighbors (F1 & F2) is −6.4/−6.2 eV, which is indicative of strong bonding interactions. In contrast, iodine's interactions with its third nearest neighbor (F3) is estimated as −0.7 eV, which clearly suggests that R3̄-structured IF₈ can be viewed predominately as a molecular crystal. The integrated COHPs between F1–F1, F1–F2 and F1–F3 are 0.06, 0.07 and −0.14 eV, respectively (F3 refers to an F atom in the nearest neighboring IF₈ unit). That F–F bonding and anti-bonding interactions within the IF₈ molecule largely cancel out, but are destabilizing overall, is in qualitative agreement with the MO diagram in Fig. 3. Bonding between IF₈ molecules (I–F3 and F1–F3) comes out as exclusively stabilizing in the COHP analysis (Fig. 4c and S4c†).

Fig. 4 Electronic structure of IF₈ in its R3̄-phase at 300 GPa. (a) Band structure. (b) Partial density of states (PDOS). (c) Crystal orbital Hamilton populations (COHP) for I–F2 (1.802 Å). Positive and negative denote bonding and antibonding orbital interactions, respectively. I 5d–F 2s is omitted because the corresponding integrated COHP is very small below the Fermi level (−0.17 eV). (d) Calculated PDOS of I d-levels. (e) Calculated COHP of I 5d–F2 2p. Note that the lines corresponding to I d_xy–F2 2p and I d_yz–F2 2p are overlaid by I d_x²−y²–F2 2p and I d_xz–F2 2p in this figure.

At 300 GPa, iodine's 5d band penetrates well into the valence region, where it undergoes a significant dispersion and mixes both with the 5s and 5p levels of iodine, and with the valence shell of fluorine (Fig. 4b). Our COHP analysis clearly shows significant bonding interactions involving d-levels below the Fermi level (Fig. 4c). The only anti-bonding interactions observed near the Fermi level are of I 5s–F 2p and F 2p–F 2p character, in good agreement with the schematic MO analysis of the IF₈ molecule in Fig. 3. The only other anti-bonding states identified in the COHP are due to overlap with F 2s, which we omitted from Fig. 3 for clarity.

What about the metallicity of the material? That the R3̄-structured IF₈ shows metallicity (Fig. 4) is expected from the fact that it's a molecular solid of an open-shell molecule. In contrast, the P2₁/m-structured IF₇, a molecular solid of a closed-shell molecule, is a semiconductor (Fig. S7†). We did perform an in silico experiment by artificially adding one electron to the IF₈ unit cell (the negative charge being compensated by a smeared out positive background charge in our program). The result of the extra electron is a material with semiconducting character that exhibits a similar Projected Density of States (PDOS) distribution (Fig. S8†). In IF₈, the Density of States (DOS) at the Fermi-level is dominated by the F 2p-bands. That the Fermi level should be dominated by F 2p is expected, and is also in good agreement with our MO analysis of the isolated IF₈ molecule (Fig. 3), which predicts the highest occupied level to be a pure F 2p–F 2p antibonding level of E_u symmetry. Spin-polarized calculations on the R3̄ phase of IF₈ shows that the material is not magnetic (Fig. S9†).

Because of significant mixing of s, p and d levels of iodine, we can conclude that a valence expansion of iodine has occurred. This implies that the IF₈ molecule, predicted to exist in the crystalline state at 300 GPa, is not only hypercoordinated but also hypervalent. Expansion of iodine's valence space is here a consequence of additional energy levels being available for bonding, not a classification based on the fact that the number of ligands around iodine exceeds seven. Our bonding and density of states analyses are based on orbital projection methods, which differ slightly depending on the program used. Even though these methods are not exact, in that they do not recover all of the electron density, all approaches that we tested (see the Fig. S10†) do support the general conclusion that there is a valence expansion and that the I 5d levels are essentially equally populated. The d_z² orbital does appear to be slightly more populated on average, which may explain the small structural deviation from a perfect cube (Table S4†).

What about the oxidation state of iodine? Because the predicted R3̄ phase of IF₈ is metallic, a formal ionic extrapolation is not possible.⁴⁷ If we nonetheless consider each F ligand as F⁻ and remove one electron from the ligands due to the radical character (the F 2p hole), the oxidation state of iodine in IF₈ becomes +VII. Our best estimate of the total iodine orbital occupation in IF₈ corresponds to an atomic charge of +3.8, when calculated using a Mulliken-type approach. The relative occupation of the I-based orbitals is s¹p^1.7d¹. We must stress that these values are approximate and sensitive to the internal basis set used in the projection scheme. Nevertheless, the orbital-based charge is in strikingly good agreement with a separately calculated QTAIM charge of +4.0 on iodine (see the ESI†). Combined, the orbital and charge density analyses, and the Electron localization Function (ELF, Fig. S11†) suggest a rather large degree of covalency in IF₈, and the presence of strong polar covalent and hypervalent bonds.

3. Conclusion

First-principles swarm structural search calculations have been employed to explore the phase stabilities and structures of I–F compounds under high pressure. Pressure favors the stabilization of fluoride-rich compounds (IF_x = 3, 5, 7, 8, 10, 11, and 12) rather than iodine-rich compounds. Several I–F compounds are predicted to undergo pressure-induced molecular to extended phase transformations, accompanied by semiconductor to metal transitions. We have focused our analyses on a predicted R3̄ phase of IF₈, where pressure stabilizes a unique cubical molecular structure. The predicted cubical coordination geometry is unique in main group chemistry, where square antiprismatic octa-coordination is common. The molecular crystal has an electron-deficient electronic structure that causes it to be metallic. Various molecular orbital and crystal orbital projection-based analyses support a conclusion that the electronic and geometric structure of IF₈ is a consequence of valence expansion of iodine.

4. Computational details

Searches for I–F binary compounds were performed with the CALYPSO structure prediction method,^48,49 while allowing for up to 4 formula units per unit cell. The predictive accuracy of this methodology has been repeatedly demonstrated on various systems, from elemental solids to binary and ternary compounds.^50–55 The Vienna Ab initio Simulation Package (VASP) code⁵⁶ and the Perdew–Burke–Ernzerhof⁵⁷ functional in the generalized gradient approximation⁵⁸ were adopted to perform structural relaxations within the framework of density-functional theory (DFT). The electron–ion interactions were represented by means of the all-electron projector augmented-wave method with 5s²5p⁵ and 2s²2p⁵ treated as the valence electrons of I and F atoms, respectively. A plane-wave basis set cutoff of 950 eV and the Monkhorst–Pack scheme⁵⁹ with a dense k-point grid spacing of 2π × 0.032 Å⁻¹ in the Brillouin zone were used to converge energies to less than 1 meV/atom. To ensure the validity of the pseudopotentials used, the equation of state of IF₈ was also calculated using the full-potential WIEN2k code,⁶⁰ with nearly identical results to the VASP calculations (Fig. S12†). Phonon calculations were performed using a supercell approach with the finite displacement method⁶¹ using Phonopy.⁶² The Electron Localization Function (ELF) was used to estimate the degree of electron localization.⁶³ Crystal Orbital Hamilton Population (COHP) analyses were performed using the LOBSTER program.^64,65 Van der Waals (vdW) interactions were included using the optB88-vdw approach.^66,67 DFT calculations on molecular fragments were made using Gaussian 16, revision B.01.⁶⁸

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research was supported by the National Key Research and Development Program of China (Grant No. 2016YFB0201200 and 2016YFB0201201), the National Natural Science Foundation of China (Grants No. 21573037, 21873017, 11534003, 11774127, and 11274136), the 2012 Changjiang Scholars Program of China, the Program for JLU Science and Technology Innovative Research Team, and the Science Challenge Project No. TZ2016001. Parts of the calculations were performed at the High-Performance Computing Center of Jilin University and Tianhe2-JK in the Beijing Computational Science Research Center. M. R. acknowledges financial support from Chalmers University of Technology and computational resources provided by the Swedish National Infrastructure for Computing (SNIC) at C3SE. Toby Zeng and Roald Hoffmann are acknowledged for valuable discussion and comments.

References

1. L. M. Yang, E. Ganz, Z. Chen, Z. X. WANG and P. V. R. Schleyer, Four Decades of the Chemistry of Planar Hypercoordinate Compounds, Angew. Chem., Int. Ed., 2015, 54, 9468–9501.
2. H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, FeB₆ Monolayers: the Graphene-like Material with Hypercoordinate Transition Metal, J. Am. Chem. Soc., 2016, 138, 5644–5651.
3. M. C. Lipke and T. D. Tilley, Hypercoordinate Ketone Adducts of Electrophilic η3-H₂SiRR' Ligands on Ruthenium as Key Intermediates for Efficient and Robust Catalytic Hydrosilation, J. Am. Chem. Soc., 2014, 136, 16387–16398.
4. Z. Wang and P. v. R. Schleyer, Planar Hypercoordinate Carbons Joined: Wheel-shaped Molecules with C–C axles, Angew. Chem., Int. Ed., 2002, 41, 4082–4085.
5. A. Khan and D. Foucher, Hypercoordinate Compounds of the Group 14 Elements Containing κn-C, N-, C, O-, C, S-and C, P-Ligands, Coord. Chem. Rev., 2016, 312, 41–66.
6. N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Elsevier, 2012.
7. T. Kaiho, Iodine Chemistry and Applications, John Wiley and Sons, 2014.
8. M. Rahm, R. Hoffmann and N. W. Ashcroft, Atomic and ionic radii of elements 1–96, Chem.–Eur. J., 2016, 22, 14625–14632.
9. V. V. Zhdankin and J. D. Protasiewicz, Development of new hypervalent iodine reagents with improved properties and reactivity by redirecting secondary bonds at iodine center, Coord. Chem. Rev., 2014, 275, 54–62.
10. S. Tang, Y. Wu, W. Liao, R. Bai, C. Liu and A. Lei, Revealing the Metal-like Behavior of Iodine: An Iodide-Catalysed Radical Oxidative Alkenylation, Chem. Commun., 2014, 50, 4496–4499.
11. R. D. Richardson and T. Wirth, Hypervalent Iodine Goes Catalytic, Angew. Chem., Int. Ed., 2006, 45, 4402–4404.
12. H. Liang and M. A. Ciufolini, Chiral Hypervalent Iodine Reagents in Asymmetric Reactions, Angew. Chem., Int. Ed., 2011, 50, 11849–11851.
13. A. Screenithya, C. Patel and C. Hadad, Hypercoordinate Iodine Catalysts in Enantioselective Transformation: The Role of Catalyst Folding in Stereoselectivity, ACS Catal., 2017, 7, 4189–4196.
14. A. Screenithya, K. Surya and R. B. Sunoj, Hypercoordinate Iodine (III) Promoted Reactions And Catalysis: An Update On Current Mechanistic Understanding, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1299.
15. V. V. Zhdankin, Hypervalent Iodine Chemistry: Preparation, Structure, and Synthetic Applications of Polyvalent Iodine Compounds, John Wiley and Sons, 2013.
16. K. O. Christe, D. A. Dixon, J. C. Sanders, G. J. Schrobilgen and W. W. Wilson, Heptacoordination: pentagonal bipyramidal heptafluoroxenon (1+) XeF₇⁺ and heptafluorotellurate (1−) TeF₇⁻ ions, J. Am. Chem. Soc., 1993, 115, 9461–9467.
17. M. G. Goesten, R. Hoffmann and F. M. Bickelhaupt, Eight-Coordinate Fluoride in A Sillicate Double-Four-Ring, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 828–833.
18. F. Peng, J. Botana, Y. Wang, Y. Ma and M. Miao, Unexpected Trend in Stability of Xe-F Compounds Under Pressure Driven by Xe-Xe Covalent Bonds, J. Phys. Chem. Lett., 2016, 7, 4562–4567.
19. E. Magnusson, Hypercoordinate molecules of second-row elements: d functions or d orbitals?, J. Am. Chem. Soc., 1990, 112, 7940–7951.
20. K. O. Christe, J. C. Sanders, G. J. Schrobilgen and W. W. Wilson, High-Coordination Number Fluoro-and-Oxofluoro-Anions. IF₆O⁻, TeF₆O²⁻, TeF₇⁻, IF₈⁻ and TeF₈²⁻, ChemInform, 1991, 13, 837–840.
21. S. Riedel and M. Kaupp, The Highest Oxidation States of the Transition Metal Elements, Coord. Chem. Rev., 2009, 253, 606–624.
22. L. Zhang, Y. Wang, J. Lv and Y. Ma, Materials Discovery at High Pressures, Nat. Rev. Mater., 2017, 2, 17005.
23. W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, The Chemical Imagination at Work in Very Tight Places, Angew. Chem., Int. Ed., 2007, 46, 3620–3642.
24. A. Shamp and E. Zurek, Superconducting High-pressure Phases Composed of Hydrogen and Iodine, J. Phys. Chem. Lett., 2015, 6, 4067–4072.
25. D. Duan, F. Tian, Y. Liu, X. Huang, D. Li, H. Yu, Y. Ma, B. Liu and T. Cui, Enhancement of Tc in the Atomic Phase of Iodine-doped Hydrogen at High Pressures, Phys. Chem. Chem. Phys., 2015, 17, 32335–32340.
26. J. Botana, X. Wang, C. Hou, D. Yan, H. Lin, Y. Ma and M. Miao, Mercury under Pressure Acts as a Transition Metal: Calculated from First Principles, Angew. Chem., Int. Ed., 2015, 127, 9412–9415.
27. J. Botana and M. S. Miao, Pressure-Stabilized Lithium Caesides with Caesium Anions beyond the −1 State, Nat. Commun., 2014, 5, 1–8.
28. M. Miao, Caesium in High Oxidation States and as a p-Block Element, Nat. Chem., 2013, 5, 846.
29. J. Liu, S. Zhang, W. Guan, G. Yang and Y. Ma, Gold with +4 and +6 Oxidation States in AuF₄ and AuF₆, J. Am. Chem. Soc., 2018, 140, 9545–9550.
30. G. Yang, Y. Wang, F. Peng, A. Bergara and Y. Ma, Gold as a 6p-Element in Dense Lithium Aurides, J. Am. Chem. Soc., 2016, 138, 4046–4052.
31. J. Hooper, T. Terpstra, A. Shamp and E. Zurek, Composition and constitution of compressed strontium polyhydrides, J. Phys. Chem. C, 2014, 118, 6433–6447.
32. J. Hooper, B. Altintas, A. Shamp and E. Zurek, Polyhydrides of the alkaline earth metals: a look at the extremes under pressure, J. Phys. Chem. C, 2013, 117, 2982–2992.
33. Z. M. Geballe, H. Liu, A. K. Mishra, M. Ahart, M. Somayazulu, Y. Meng and R. J. Hemley, Synthesis and stability of lanthanum superhydrides, Angew. Chem., Int. Ed., 2018, 57, 688–692.
34. T. Muramatsu, W. K. Wanene, M. Somayazulu, E. Vinitsky, D. Chandra, T. A. Strobel, V. V. Struzhkin and R. J. Hemley, Metallization and superconductivity in the hydrogen-rich ionic salt bareh9, J. Phys. Chem. C, 2015, 119, 18007–18013.
35. R. Reichlin, A. K. McMahan, M. Ross, S. Martin, J. Hu, R. J. Hemley, H.-K. Mao and Y. W. Wu, Optical, x-ray, and band-structure studies of iodine at pressures of several megabars, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 3725.
36. Q. Lv, X. Jin, T. Cui, Q. Zhuang, Y. Li, Y. Wang and X. Meng, Crystal structures and electronic properties of solid fluorine under high pressure, Chin. Phys. B, 2017, 26, 076103.
37. R. J. Gillespie and E. A. Robinson, Electron domains and the VSEPR model of molecular geometry, Angew. Chem., Int. Ed. Engl., 1996, 35, 495–514.
38. M. Rahm, R. Cammi, N. Ashcroft and R. Hoffmann, Electron Configuration and Electronegativity of the Atoms Under Compression, 256th ACS National Meeting & Exposition, Boston, MA, United States, 2018, PHYS-366.
39. A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database, version 5.1, 2013. See http://physics.nist.gov/asd.
40. W. Kutzelnigg, Chemical bonding in higher main group elements, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295.
41. M. Randić, Ligand field splitting of d orbitals in eight coordinated complexes of dodecahedral structure, J. Chem. Phys., 1962, 36, 2094–2097.
42. M. Randić, Ligand field splitting of d orbitals in eight coordinated complexes of square antiprism structure, Croat. Chem. Acta, 1960, 32, 189.
43. J. K. Burdett, R. Hoffmann and R. C. Fay, Eight-Coordination, Inorg. Chem., 1978, 17, 2553–2568.
44. J. P. Connerade, V. K. Dolmatov and P. A. Lakshmi, The filling of shells in compressed atoms, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 251.
45. L. J. Parker and J. V. Badding, Transition Element-Like Chemistry for Potassium under Pressure, Science, 1996, 273, 95–97.
46. M. S. Miao and R. Hoffmann, High Pressure Electrides: A Predictive Chemical and Physical Theory, Acc. Chem. Res., 2014, 47, 1311–1317.
47. P. Karen, Oxidation State, A Long-Standing Issue!, Angew. Chem., Int. Ed., 2015, 54, 4716–4726.
48. Y. Wang, J. Lv, L. Zhu and Y. Ma, Crystal Structure Prediction via Particle-Swarm Optimization, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 94116.
49. Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A Method for Crystal Structure Prediction, Comput. Phys. Commun., 2012, 183, 2063–2070.
50. H. Wang, S. T. John, K. Tanaka, T. Iitaka and Y. Ma, Superconductive Sodalite-like Clathrate Calcium Hydride at High Pressures, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6463–6466.
51. L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Reactions of Xenon with Iron and Nickel Are Predicted in the Earth's Inner Core, Nat. Chem., 2014, 6, 644.
52. J. Lv, Y. Wang, L. Zhu and Y. Ma, Predicted Novel High-Pressure Phases of Lithium, Phys. Rev. Lett., 2011, 106, 15503.
53. L. Zhu, H. Wang, Y. Wang, J. Lv, Y. Ma, Q. Cui, Y. Ma and G. S. Zou, Substitutional Alloy of Bi and Te at High Pressure, Phys. Rev. Lett., 2011, 106, 145501.
54. Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, The Metallization and Superconductivity of Dense Hydrogen Sulfide, J. Chem. Phys., 2014, 140, 174712.
55. S. Zhang, L. Zhu, H. Liu and G. Yang, Structure and Electronic Properties of Fe₂SH₃ Compound under High Pressure, Inorg. Chem., 2016, 55, 11434–11439.
56. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
57. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
58. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
59. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188.
60. P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Full-Potential, Linearized Augmented Plane Wave Programs for Crystalline Systems, Comput. Phys. Commun., 1990, 59, 399–415.
61. K. Parlinski, Z. Q. Li and Y. Kawazoe, First-Principles Determination of the Soft Mode in Cubic ZrO₂, Phys. Rev. Lett., 1997, 78, 4063.
62. A. Togo, F. Oba and I. Tanaka, First-Principles Calculations of the Ferroelastic Transition between Rutile-Type and CaCl₂-Type SiO₂ at High Pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
63. A. D. Becke and K. E. Edgecombe, A Simple Measure of Electron Localization in Atomic and Molecular Systems, J. Chem. Phys., 1990, 92, 5397–5403.
64. R. Dronskowski and P. E. Bloechl, Crystal Orbital Hamilton Populations (COHP): Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations, J. Phys. Chem., 1993, 97, 8617–8624.
65. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Analytic Projection from Plane-wave and PAW Wavefunctions and Application to Chemical-bonding Analysis in Solids, J. Comput. Chem., 2013, 34, 2557–2567.
66. K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Higher-Accuracy van Der Waals Density Functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 81101.
67. I. Hamada, Van Der Waals Density Functional Made Accurate, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103.
68. M. J. Frisch, et al., Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016See the ESI† for full list of authors.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed description of the calculation methods and structural predictions, main structural parameters, phonon band structures and density of states, various analyses of I₂ and IF_x (x = 7, 8, 12) structures, atomic charges on iodine in different structures, and equations of states. See DOI: 10.1039/c8sc04635b

‡ These authors contributed equally.

---