[La(η^x-B_x)La]⁻ (x = 7–9): a new class of inverse sandwich complexes

Abstract

Despite the importance of bulk lanthanide borides, nanoclusters of lanthanide and boron have rarely been investigated. Here we show that lanthanide–boron binary clusters, La₂B_x⁻, can form a new class of inverse-sandwich complexes, [Ln(η^x-B_x)Ln]⁻ (x = 7–9). Joint experimental and theoretical studies reveal that the monocyclic B_x rings in the inverse sandwiches display similar bonding, consisting of three delocalized σ and three delocalized π bonds. Such monocyclic boron rings do not exist for bare boron clusters, but they are stabilized by the sandwiching lanthanide atoms. An electron counting rule is proposed to predict the sizes of the B_x ring that can form stable inverse sandwiches. A unique (d-p)δ bond is found to play important roles in the stability of all three inverse-sandwich complexes.

---

1. Introduction

Over the past decade, joint experimental and quantum chemistry investigations have shown that small boron clusters form planar structures, consisting of localized two-center-two-electron (2c-2e) σ bonds on the periphery of the clusters and delocalized σ and π bonding in the interior of the cluster plane due to the electron deficiency of the boron atom.^1–6 The delocalized π bonding in the planar boron clusters has been shown to be analogous to aromatic hydrocarbons (arenes), giving rise to concepts of aromaticity and hydrocarbon analogues of boron clusters.^7–17 However, while arenes can form sandwich compounds with transition metals due to strong d–π interactions,^18–20 no similar sandwich complexes have been observed for the aromatic planar boron clusters. Because of the strong B–B bonds, such sandwich structures are energetically unfavourable, in comparison to the fusion of the two boron clusters. Instead, tubular-type or half-sandwich metal complexes of boron clusters have been observed.^21–26 A particularly interesting class of transition metal doped boron clusters is the metal-centered borometallic molecular wheels, M©B_x⁻ (x = 8–10), in which the monocyclic boron rings are stabilized by the central metal atoms,^27–33 even though such boron rings are not stable by themselves.^7,8 The largest ring size observed is B₁₀ with M = Nb and Ta,²⁹ while the smallest ring size is B₈ for M = 3d transition metals.^27,30 In fact, an even smaller B₇ ring exists in the planar B₈ cluster (D_7h),⁷ which can be viewed as B©B₇. The borometallic molecular wheels follow an electronic design principle, which requires double aromaticity in the σ and π frameworks.^27,31,33 However, no such borometallic molecular wheels have been observed for lanthanide-doped boron clusters, for which only half-sandwich type structures have been observed.^34,35 Recently, we have found that di-lanthanide B₈ clusters (Ln₂B₈⁻) form unprecedented inverse-sandwich structures, which feature a doubly aromatic B₈ monocyclic ring and strong (d-p)-π and -δ bonding between the B₈ ring and the two Ln atoms.³⁶ This recent study has shown that a variety of lanthanide elements can form the Ln(η⁸-B₈)Ln inverse sandwiches (Ln = La, Pr, Tb). Two interesting questions arise: can similar inverse sandwiches be formed with other monocyclic boron ring sizes? What is the trend and nature of the bonding in such complexes?

Here we report the discovery of a series of La₂B_x⁻ clusters and an electron counting rule for predicting stable boron–metal inverse sandwiches. We have found that both La₂B₇⁻ and La₂B₉⁻ can form highly symmetric inverse-sandwich clusters, similar to La₂B₈⁻, while no other B_x ring size is likely to form such exotic structures. The global minimum structure of La₂B₇⁻ is found to have a triplet ground state with D_7h symmetry (³A₂′), whereas that of La₂B₉⁻ is closed-shell with D_9h symmetry (¹A₁′). Chemical bonding analyses reveal that the La₂B_x⁻ clusters with x = 7–9 are highly stable with large HOMO–LUMO gaps and strong (d-p)-π and -δ interactions between the two La atoms and the boron rings. These highly symmetric and electronically stable clusters constitute a novel family of inverse-sandwich structures, [Ln(η^x-B_x)Ln]⁻ (x = 7–9), with tunable electronic and magnetic properties and may be viable for bulk syntheses with appropriate ligands. They also provide interesting motifs to design new lanthanide boride materials, such as one-dimensional nanowires.

2. Experimental method

The experiment was done using a magnetic-bottle type photoelectron spectroscopy (PES) apparatus coupled with a time-of-flight mass spectrometer and a laser vaporization cluster source, details of which has been published before.^5,37 The laser vaporization target was prepared by first mixing La powder (Alfa Aesar, 99.9% purity) with B powder (Alfa Aesar, 96% ¹¹B-enriched, 99.9% elemental purity) (5/2 La/B mass ratio) in a glove box and then pressing the mixture into a 12 mm diameter disc. The second harmonic of a Nd:YAG laser (532 nm) operated at a 10 Hz repetition rate was used for laser vaporization, synchronized with a high-pressure He carrier gas pulse seeded with 5% Ar. The ensuring nucleation led to the production of various La_mB_x⁻ clusters, which were entrained in the carrier gas and underwent a supersonic expansion. The size distribution and cooling of the clusters were controlled by the time delay between the vaporization laser pulse and the carrier gas pulse, as well as the resident time of the clusters inside the nozzle.⁵ The La₂B_x⁻ clusters of interest were mass-selected and decelerated before being photodetached by the 193 nm radiation from an ArF excimer laser. The photoelectron spectra were calibrated using the known spectrum of Bi⁻.³⁸ The energy resolution of the apparatus was about 2.5%, that is, ∼25 meV for 1 eV electrons.

3. Theoretical methods

The global-minimum structures of La₂B₇⁻ and La₂B₉⁻ were searched using the Tsinghua Global Minimum (TGMin) program,^39–41 which was based on a constraint Basin-Hopping algorithm.⁴² In total, more than 1700 minimal structures for La₂B₇⁻ and >2000 for La₂B₉⁻ with different spin multiplicities were evaluated using the ADF 2016 software.⁴³ Scalar relativistic effects were taken into account in the calculations via zero-order regular approximation (ZORA).⁴⁴ Density functional theory (DFT) with the PBE exchange–correlation functional⁴⁵ and the TZP Slater-type basis sets⁴⁶ were applied in the initial calculations. The frozen-core approximation was adopted for the [1s²] core of B and [1s²-4d¹⁰] core of La. All local minima were verified by calculations of the harmonic vibrational frequencies. Low-lying isomers within a PBE energy range of 100 kcal mol⁻¹ were subsequently re-optimized using the hybrid PBE0 functional⁴⁷ with the TZP basis set. To obtain even more accurate relative energies, we did further ab initio single-point CCSD(T) calculations for the three lowest-lying isomers using the Mopro 2012 package.⁴⁸ The calculated T1 diagnostic factors of the CCSD calculations were 0.023 and 0.019 for the global minima of La₂B₇⁻ and La₂B₉⁻, respectively, suggesting that multi-reference features were not significant for these two systems. In the CCSD calculations, the cc-pVTZ valence triple-ζ basis set⁴⁹ was used for B and the Stuttgart energy-consistent relativistic pseudopotential ECP28MWB(La) with the corresponding ECP28MWB_ANO basis set were used for La.^50,51

The first ADE and first VDE were calculated at the PBE, PBE0, and CCSD(T) levels. In order to compare with the experimental PES data, we computed the higher VDEs approximately using the ΔSCF-TDDFT approach⁵² with the SAOP exchange–correlation functional.⁵³ Chemical bonding was analysed using delocalized and localized MO approaches, as well as EDA-NOCV analyses.^54,55 We also performed bonding analyses using the local coordinate system (LCS) of the B₇ and B₉ moieties, where the z-axis of each atom is pointed to the center of the ring and the y-axis is along the tangential direction. The chemical bonding was also analyzed using the adaptive natural density partitioning (AdNDP) approach⁵⁶ at the PBE0/TZP level of theory. The charges of the atoms were calculated using various partition schemes, including Mulliken charge population,⁵⁷ Hirshfeld,^58,59 Voronoi⁶⁰ and multipole-derived charge (MDC) approaches.⁶¹ The bond order indexes were calculated using the Mayer,⁶² Gopinathan–Jug (G–J),⁶³ and Nalewajski–Mrozek⁶⁴ schemes.

4. Experimental results

The photoelectron spectra of La₂B₇⁻ and La₂B₉⁻ at 193 nm (6.424 eV) are shown in Fig. 1a and 2a, respectively. Major PES features are labeled with letters in Fig. 1a and 2a and the measured vertical detachment energies (VDEs) are given in Table 1, where they are compared with theoretical results to be presented below. The peak labeled X in each spectrum denotes the detachment transition from the ground electronic state of the respective anionic cluster to that of the corresponding neutral. The higher binding energy peaks (A, B, C…) represent detachment transitions from the ground state of the anion to excited electronic states of the neutral species.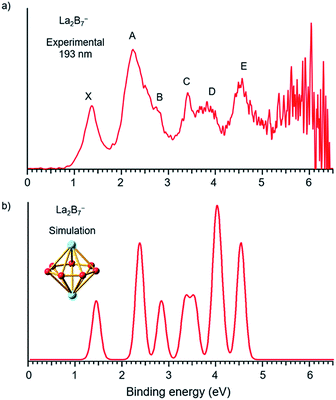

Fig. 1 (a) Photoelectron spectra of La₂B₇⁻ at 193 nm (6.424 eV) and (b) the simulated spectrum for the D_7h global minimum of La₂B₇⁻, obtained by fitting the computed VDEs from Table 1 with Gaussians of 0.1 eV width.

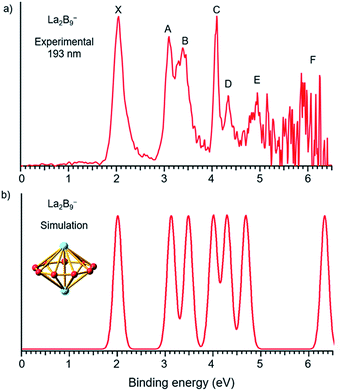Fig. 2 (a) Photoelectron spectra of La₂B₉⁻ at 193 nm (6.424 eV) and (b) the simulated spectrum for the D_9h global minimum of La₂B₉⁻, obtained by fitting the computed VDEs from Table 1 with Gaussians of 0.1 eV width.

Table 1 Experimental vertical detachment energies (VDE) from the photoelectron spectra of La₂B₇⁻ and La₂B₉⁻ in comparison with theoretical VDEs computed from the global minimum inverse sandwiches^a

Feature	VDE^b (exp)	Final state and electronic configuration	VDE (theo.)
a All energies are in eV. b The numbers in the parentheses represent the uncertainty in the last digit.
La 2 B 7 ^− (D 7h , ^3 A 2 ′)
X	1.35(3)	^2E2′′, {…1e2′^21e3′^43a2′′^24a1′^22e1′′^43e1′^41e2′′^1}	1.40
A	2.22(3)	^2E1′, {…1e2′^21e3′^43a2′′^24a1′^22e1′′^43e1′^31e2′′^2}	2.31
		^4E1′, {…1e2′^21e3′^43a2′′^24a1′^22e1′′^43e1′^31e2′′^2}	2.33
B	2.81(4)	^4E1′′, {…1e2′^21e3′^43a2′′^24a1′^22e1′′^33e1′^41e2′′^2}	2.77
C	3.42(3)	^2E1′′, {…1e2′^21e3′^43a2′′^24a1′^22e1′′^33e1′^41e2′′^2}	3.28
D	∼3.8	^4A1′′, {…1e2′^21e3′^43a2′′^14a1′^22e1′′^43e1′^41e2′′^2}	3.47
		^2A2′, {…1e2′^21e3′^43a2′′^24a1′^12e1′′^43e1′^41e2′′^2}	3.91
		^4A2′, {…1e2′^21e3′^43a2′′^24a1′^12e1′′^43e1′^41e2′′^2}	3.93
		^2A1′′, {…1e2′^21e3′^43a2′′^14a1′^22e1′′^43e1′^41e2′′^2}	4.01
E	4.47(4)	^2E3′, {…1e2′^21e3′^33a2′′^24a1′^22e1′′^43e1′^41e2′′^2}	4.44
		^4E3′, {…1e2′^21e3′^33a2′′^24a1′^22e1′′^43e1′^41e2′′^2}	4.46
		^4E2′, {…1e2′^11e3′^43a2′′^24a1′^22e1′′^43e1′^41e2′′^2}	7.22
		^2E2′, {…1e2′^11e3′^43a2′′^24a1′^22e1′′^43e1′^41e2′′^2}	7.36
La 2 B 9 ^− (D 9h , ^1 A 1 ′)
X	2.04(7)	^2E1′′, {…1a2′^24e1′^43a2′′^25a1′^25e1′^42e1′′^43e1′′^3}	1.98
A	3.09(9)	^2E1′′, {…1a2′^24e1′^43a2′′^25a1′^25e1′^42e1′′^33e1′′^4}	3.08
B	3.38(7)	^2E1′, {…1a2′^24e1′^43a2′′^25a1′^25e1′^32e1′′^43e1′′^4}	3.44
C	4.09(7)	^2A1′, {…1a2′^24e1′^43a2′′^25a1′^15e1′^42e1′′^43e1′′^4}	3.96
D	4.33(5)	^2A2′, {…1a2′^24e1′^43a2′′^15a1′^25e1′^42e1′′^43e1′′^4}	4.24
E	4.94(4)	^2E1′, {…1a2′^24e1′^33a2′′^25a1′^25e1′^42e1′′^43e1′′^4}	4.63
F	∼6.0	^2A2′, {…1a2′^14e1′^43a2′′^25a1′^25e1′^42e1′′^43e1′′^4}	6.43

---

The photoelectron spectrum of La₂B₇⁻

The photoelectron spectrum of La₂B₇⁻ displayed in Fig. 1a exhibits six well-resolved bands labeled as X, A, B, C, D, E. Beyond 5 eV, the signal-to-noise ratio is quite poor and no PES bands can be definitively identified. The maximum of peak X at 1.35 eV yields the first VDE for La₂B₇⁻. Its first adiabatic detachment energy (ADE) is estimated to be 1.2 eV from the onset of band X, which also represents the electron affinity (EA) of the corresponding neutral La₂B₇. Band A at a VDE of 2.22 eV is intense and broad with a shoulder peak B discernible at 2.81 eV. Peak C at 3.42 eV is relatively sharp, followed closely by a broad band D at about 3.8 eV, which may consist of multiple detachment channels. Another relatively broad peak E is observed at 4.47 eV. These resolved PES features serve as electronic fingerprints, which can be compared with theoretical calculations (Fig. 1b, vide infra) to provide insights into the structures and bonding of La₂B₇⁻ and its corresponding neutral species.

The photoelectron spectrum of La₂B₉⁻

Compared to the photoelectron spectrum of La₂B₇⁻, the spectrum of La₂B₉⁻ (Fig. 2a) is quite simple and all the PES features are much sharper, suggesting a stable and high symmetry structure. The strong ground state peak X yields the first VDE of 2.04 eV for La₂B₉⁻, and its leading edge gives an ADE of 1.94 eV, i.e., the EA of the corresponding neutral La₂B₉. Following a large energy gap, peak A is observed at a VDE of 3.09 eV, closely followed by peak B at a VDE of 3.38 eV. Peak C at 4.09 eV is very sharp and intense, followed by a weaker peak D at 4.33 eV. Although the signal-to-noise ratios become poor in the high binding energy side, peak E at 4.94 eV is clearly resolved, whereas a peak F at around 6.0 eV can also be tentatively identified. The simplicity of the spectral pattern and the sharpness of the PES features for La₂B₉⁻ are surprising, suggesting not only a high symmetry structure, but also high structural stability both for the anion and for the corresponding neutral.

5. Theoretical results

The global minimum of La₂B₇⁻

We performed an extensive global minimum search for La₂B₇⁻ using randomly-seeded structures with different spin multiplicities. In total, 1732 local minimum structures of La₂B₇⁻ were generated and the lowest 20 isomers are shown in Fig. S1.† Our calculations show that two inverse sandwich structures with different spin multiplicities are competing for the global minimum with all other isomers lying much higher in energy. The spin-triplet isomer I (³A₂′) with perfect D_7h symmetry is found to be the global minimum at all three levels of theory, whereas the spin-singlet isomer II (¹A₁) with C_2v symmetry is found to be 3.03 kcal mol⁻¹ higher in energy at the CCSD(T) level. In fact, these two isomers have very similar structures: the closed-shell isomer II (C_2v, ¹A₁) has pseudo-D_7h symmetry, where the two La atoms are slightly off the C₇ axis of the B₇ ring to break symmetry. The spin-singlet isomer II with exact D_7h geometry is subject to Jahn–Teller distortions and is a saddle point (barrier ∼ 2.3 kcal mol⁻¹) relative to the C_2v structure. The next isomer III lies much higher in energy, 25.98 kcal mol⁻¹ at the CCSD(T) level, above the global minimum D_7h structure (Fig. S1†). Isomer XIII represents another type of inverse sandwich structure with a B-centered D_6h-B₇ motif and longer La–B bond lengths. However, this isomer is 56.04 kcal mol⁻¹ higher in energy than the global minimum at the PBE0 level of theory. Two views of the global minimum of La₂B₇⁻ (D_7h, ³A₂′) with the relevant bond lengths are shown in Fig. 3.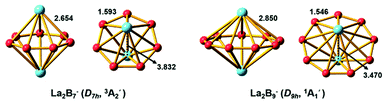

Fig. 3 The optimized global-minimum inverse-sandwich structures of La₂B₇⁻ and La₂B₉⁻ at the PBE0/TZP level.

The global minimum of La₂B₉⁻

Because the La₂B₉⁻ cluster has more degrees of freedom than La₂B₇⁻, a much larger number of structures (>2000) were generated in the search for its global minimum using both the inverse sandwich as a seed and random seeds with different spin multiplicities. The lowest 20 isomers are given in Fig. S2.† Remarkably, a D_9h inverse sandwich structure with a monocyclic B₉ ring and closed-shell electron configuration (¹A₁′) is found to be the global minimum for La₂B₉⁻. Two views of this structure with the relevant bond lengths are also given in Fig. 3. The closest isomer above the global minimum is found to have C_2v symmetry, being 10.43 kcal mol⁻¹ higher in energy at the CCSD(T)/VTZ level. All other isomers are much higher in energy (Fig. S2†), suggesting the overwhelmingly high stability of the inverse sandwich structure for La₂B₉⁻.

As can be seen in Fig. 3, the B–B bond distances in the B₇ and B₉ rings of La₂B₇⁻ and La₂B₉⁻ are similar, with the former being slightly longer (1.593 Å). The La–B bond lengths (2.654 Å) in La₂B₇⁻ are much shorter than those in La₂B₉⁻ (2.850 Å). With the increase of the B_x ring size, the La⋯La and B–B distances decrease, and the La–B distances increase.

6. Comparison between experiment and theory

The La₂B₇⁻ inverse sandwich

To validate the global minimum structure of La₂B₇⁻, we calculated its ADE and VDEs, as compared with the experimental data in Table 1 and Fig. 1b. The first ADE/VDE of the D_7h global minimum of La₂B₇⁻ were calculated at different levels of theory, as shown in Table 2. The computed first ADE/VDE of 1.35/1.40 eV at the CCSD(T) level are consistent with the experimental data of 1.2/1.35 eV. All the computed detachment channels and their comparison with the experimental data are given in Table 1. The simulated spectrum shown in Fig. 1b are obtained by fitting each detachment channel with a unit area Gaussian of 0.1 eV width.

Table 2 Experimental and theoretical first ADE and VDE, calculated from the PBE/TZP, PBE0/TZP, and CCSD(T)/VTZ methods for the global minimum inverse sandwich structures of La₂B₇⁻ and La₂B₉⁻

	ADE				VDE1
	Exp	PBE	PBE0	CCSD(T)	Exp	PBE	PBE0	CCSD(T)
La2B7^−	1.2	1.33	1.27	1.35	1.35	1.38	1.32	1.40
La2B9^−	1.94	1.88	1.78	1.93	2.04	1.92	1.90	1.98

---

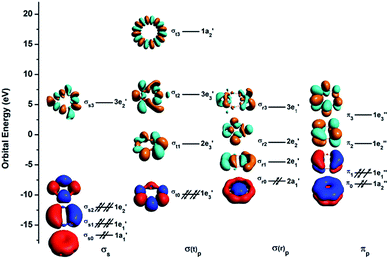
According to the MOs of La₂B₇⁻ shown in Fig. S3,† the ground state peak X is from electron detachment from the HOMO 1e₂′′ orbital, which is half-filled with two unpaired electrons. Detachment from the HOMO-1 3e₁′ orbital results in a low-spin and high-spin channel with similar VDEs, corresponding to the broad band A (Table 1). The calculated VDEs for the high-spin and low-spin channels for detachment from the HOMO-2 2e₁′′ orbital are separated by ∼0.5 eV, consistent with peaks B and C, respectively (Table 1). Detachment from the HOMO-4 3a₂′′ and HOMO-3 4a₁′ orbitals give rise to four channels with relatively close VDEs, in agreement with the broad band D. Finally, the two detachment channels from the HOMO-5 1e₃′ orbital have close VDEs of 4.44 and 4.46 eV, consistent with the broad band E at 4.47 eV. Overall, the simulated spectrum agrees well with the experimental data (Fig. 1), providing considerable credence to the D_7h inverse sandwich structure as the global minimum for La₂B₇⁻.

The La₂B₉⁻ inverse sandwich

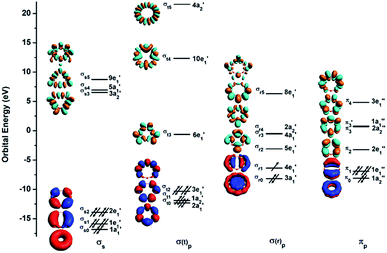
The first ADE/VDE for the La₂B₉⁻ inverse sandwich, calculated at different levels of theory, are also given in Table 2. The computed values of 1.93/1.98 eV at the CCSD(T) level are in excellent agreement with the experimental data of 1.94/2.04 eV. The computed VDEs for higher binding energy detachment channels are compared with the experimental values in Table 1. The simulated spectrum shown in Fig. 2b was obtained by fitting each computed detachment channel with a Gaussian of 0.1 eV width. Because the D_9h La₂B₉⁻ global minimum is closed shell, electron detachment from each MO (Fig. S4† and Table 1) yields a single detachment channel with a spin-doublet final state. Consequently, a very simple simulated spectral pattern is obtained, which is almost in quantitative agreement with the experimental spectrum, as revealed both in Fig. 2 and Table 1, unequivocally confirming the D_9h inverse sandwich global minimum for La₂B₉⁻. The sharpness of the La₂B₉⁻ PES features is quite surprising, which is evident of the extraordinary stability of the inverse sandwich structure for both the La₂B₉⁻ anion and the La₂B₉ neutral.

7. Discussions

Structures and chemical bonding analyses

Localized MO analyses in the B₇ and B₉ rings. To understand the exceptional stabilities of these inverse sandwich structures, we first investigate the local bonding in the B₇ and B₉ rings and see how they interact with the two La atoms. The LCS orbitals for the B₇ and B₉ rings are shown in Fig. 4 and 5, respectively. The B₇ ring has 28 2s-2p valence orbitals and the B₉ ring has 36 2s-2p valence orbitals. These orbitals can be divided into four categories using a tight-binding Hückel-type approach: σ_s, σ(t)_p, σ(r)_p and π_p, where the (t) and (r) refer to tangential and radial bonding and the subscript indicates B 2s or 2p orbitals. There are similarities between the B₇ and B₉ rings. In both systems, the occupied σ_s and σ(t)_p orbitals are mainly responsible for the B–B bonds in the B_x rings and can be transformed to x 2c-2e B–B bonds (vide infra). The other two sets of orbitals, σ(r)_p and π_p, are important in understanding the stability of the inverse sandwich structures; they are delocalized and mainly responsible for bonding with the two La atoms, as will be shown below. It should also be pointed out that the energy-level splitting for the σ(r)_p and π_p orbitals are smaller than that for the σ_s and σ(t)_p orbitals, mainly because the overlaps between the B atoms are smaller within the plane of the B_x rings, in comparison to the nearest neighbour B–B overlap around the ring periphery.

Fig. 4 The localized coordinate system (LCS) analysis for the B₇ ring at the PBE0/DZP level.

Fig. 5 The LCS analysis for the B₉ ring at the PBE0/DZP level.

Chemical bonding in La₂B_x⁻ (x = 7–9). It is clear now that we have a whole class of lanthanide inverse sandwiches with x = 7–9. Their bonding can be understood systematically on the basis of the interactions between the La⋯La atom pair and the LCS orbitals on the B_x ring moiety discussed above. Fig. 6 presents the schematic MO diagrams of La₂B_x⁻ (x = 7–9). The differences among La₂B₇⁻, La₂B₈⁻, and La₂B₉⁻ lie only in the occupation of the d_δ HOMO orbitals. The d_δ HOMO in La₂B₇⁻ is half-filled with two unpaired electrons, resulting in a triplet ground state, similar to the neutral La₂B₈ inverse sandwich. The additional electron in La₂B₈⁻ makes it a doublet ground state, leading to a Jahn–Teller distortion from D_8h in La₂B₈ to D_4h in La₂B₈⁻. In La₂B₉⁻, the d_δ HOMO is fully occupied, resulting in a closed-shell system and the exceptional stability for this large inverse sandwich. The stabilities of these inverse sandwich structures can be glimpsed from the large HOMO–LUMO gap revealed in the MO diagram of Fig. 6. The LUMO mainly originates from the La 6s orbitals, which only have weak interactions with the B_x rings. The 4f orbitals of the La atoms are also radially too contracted to contribute to chemical bonding with the B_x rings, so they form a nonbonding f-band just above the LUMO region. The 5d orbitals of the La atoms then play the most important role in bonding with the B_x ring in the inverse sandwich systems due to its large radial distribution and unique angular orientation. As can be seen in Fig. 6, the 5dδ orbitals of the La atoms are stabilized via bonding with the π₂ orbital of the B_x ring, forming a novel (d-p)δ bonding-type for the HOMO, which has also been found previously in inverse sandwiches of uranium with arenes.^65–68 The 5dπ orbitals overlap with the σ_r1 orbital of the B_x ring – this (d-p)π bonding accounts for most of the interactions between La⋯La and the B_x ring. The 5dσ orbitals of the La atoms overlap with the σ_r0 orbital of the B_x ring, and this (d-p)σ bonding-type also plays a tangible role in stabilizing the system.

Fig. 6 A schematic MO diagram for the La₂B_x⁻ (x = 7–9) inverse sandwiches, showing the major bonding interactions between the La 5d orbitals and the LCS orbitals of the B_x⁻ ring. Red and blue dots indicate the successive additional electrons for La₂B₈⁻ and La₂B₉⁻, respectively.

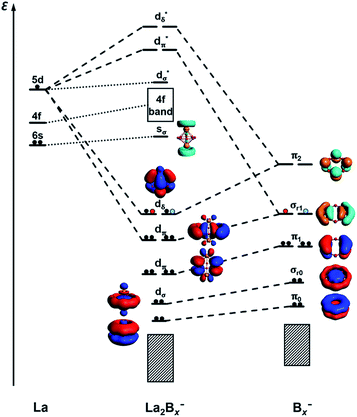
We have further analyzed the detailed contributions of each bonding interaction using the method of energy decomposition analysis with the natural orbital for chemical valence (EDA-NOCV)^54,55 for La₂B_x⁻ (x = 7−9), as summarized in Table S1.† The bonding between the La⋯La 5dπ orbitals and the B_x σ_r1 orbitals, i.e. E_orb(1), is the most important component of the total orbital interactions (La₂B₇⁻: 74.8%; La₂B₈⁻: 64.8%; La₂B₉⁻: 46.4%), with electrons flowing from La₂ to the B_x⁻ fragment. The La₂B₉⁻ complex has the most contribution (42.4%) from the unique (d-p)δ bonding orbitals, i.e. E_orb(2), relative to La₂B₇⁻ and La₂B₈⁻, because of its full occupation. In these two major bonding interactions, E_orb(1) and E_orb(2), electrons are principally accumulated on the boron rings. The calculated charges and Mulliken spin distributions on the La and B atoms are consistent with the EDA-NOCV analyses, as shown in Table S2.† It is also worthy to mention that E_orb(3) and E_orb(4) depicted in Table S1† correspond to weak back donations from B_x π₁ to La₂ 5dπ and B_x σ₀ to La₂ 5dσ, respectively. These two interactions account for a small percentage of the total bonding, about 8.7% for La₂B₇⁻ and only about 5.5% for La₂B₉⁻.

AdNDP bonding analyses. We further analyzed the bonding in La₂B₇⁻ and La₂B₉⁻ using the AdNDP method,⁵⁶ as shown in Fig. 7. Four types of bonds are found for the inverse sandwiches: (1) x 2c-2e σ bonds on the periphery of the B_x ring; (2) three delocalized nc-2e σ bonds from the interactions between the La 5d_π and 5d_σ orbitals and the in-plane delocalized σ bonds within the B_x ring; (3) three delocalized nc-2e π bonds from the interactions between the La 5d_π and 5d_σ orbitals and the out-of-plane delocalized π bonds of the B_x ring; (4) two (d-p)δ bonds due to the interactions of the La dδ orbitals and the π orbitals of the B_x ring. The three delocalized nc-2e σ and π bonds give rise to double aromaticity for the inverse sandwiches, each satisfying the 4n + 2 Hückel rule. The only difference between the bonding in La₂B₇⁻ and La₂B₉⁻ lies at the (d-p)δ bonds. In La₂B₇⁻, the (d-p)δ orbitals (Fig. 6) are half-filled, resulting in two 9c-1e (d-p)δ bonds. This situation is exactly the same as in the neutral La₂B₈ inverse sandwich, which features two 10c-1e (d-p)δ bonds, whereas the La₂B₈⁻ anion contains one 10c-2e (d-p)δ bond and one 10c-1e (d-p)δ bond. In La₂B₉⁻, the (d-p)δ orbitals (Fig. 6) are completely filled, resulting in two 11c-2e (d-p)δ bonds. Thus, the stability of the inverse sandwiches is derived from the double aromaticity and the unique (d-p)δ bonds between the La atoms and the boron rings. The extraordinary stability of the La₂B₉⁻ inverse sandwich can be understood from the two full (d-p)δ bonds, whereas the La₂B₇⁻ and La₂B₈⁻ inverse sandwiches only have partial (d-p)δ bonds.

Fig. 7 AdNDP analyses for the La₂B_x⁻ (x = 7, 9) inverse sandwiches at the PBE0/VTZ level. Occupation numbers (ON) are also given.

7.2. Stability of the inverse sandwich structures

To further quantify the stabilities of the La₂B_x⁻ (x = 7–9) inverse sandwiches, we examined the metal–metal interactions and the binding energies of the complexes, as shown in Table S3.† The binding energies were calculated as: La₂B_x⁻ → 2La + B_x⁻. All three complexes show strong binding energies between the La atoms and the boron ring, increasing from 340.4 kcal mol⁻¹ for x = 7 to 372.4 kcal mol⁻¹ for x = 9. This trend is also consistent with the increasing (d-p)δ bond order, as discussed above. As the size of the B_x ring increases, the metal–boron distances become larger, while the distances between the two La atoms become smaller, indicating gradually weaker metal–boron interactions and stronger metal–metal interactions. As shown in Fig. 7, even though the La⋯La distance ranging from 3.83 to 3.47 Å is within the La–La single-bond length (3.60 Å based on the self-consistent covalent radius of Pyykkö),⁶⁹ there is no clear La–La bond, which is reminiscent of the lack of metal–metal bonding in the Be₂O₂ rhombic structure.^70,71 Instead, the bonding between the two La atoms and between the La atoms and the boron rings is completely by delocalized multi-center bonds. The stabilities of the inverse sandwiches depend mainly on the optimal overlaps between the La 5d orbitals and the 2p orbitals on the B_x ring. If the B_x ring is too large, no effective overlap is possible between the La 5d and the 2p orbitals on the B_x ring. Hence, La₂B₉⁻ is likely the largest inverse sandwich between lanthanide and boron. The B₁₀ ring is probably too large to allow effective La–B interactions to form a stable La₂B₁₀⁻ inverse sandwich. Preliminary photoelectron data of La₂B₁₀⁻ showed a more complicated spectral pattern, incommensurate with a high symmetry structure. On the smaller side, it is more difficult to consider whether the B₆ ring can form lanthanide inverse sandwich structures solely on the basis of the geometrical argument. Our preliminary experimental and theoretical data both suggest that it does not have the inverse sandwich global minimum structure.

Further insights obtained from the electronic structure and bonding of the La₂B_x⁻ (x = 7–9) inverse sandwiches also indicate that it would not be favorable for La₂B₆⁻ and La₂B₁₀⁻ to form inverse sandwiches. Fig. 7 shows that the stabilities of the inverse sandwiches derive from both the double aromaticity and the unique (d-p)δ bonds. Thus, in the [La(η^x-B_x)La] inverse sandwiches, we need 2(x + 6 + y) electrons, where 2x electrons for the bonding in the periphery of the B_x ring, 12 electrons for the double aromaticity and 2y electrons for the (d-p)δ bonds (y = 1, half-filled; y = 2, fully filled). According to the 2(x + 6 + y) rule, we would need 28 electrons for a closed-shell La₂B₆ inverse sandwich complex (x = 6; y = 2), but La₂B₆ only has 24 valence electrons, which means that there would be no more electrons for the (d-p)δ bonds. For the La₂B₆⁻ anion, there would be only one electron for the (d-p)δ bonds, which explains the instability of a La₂B₆⁻ inverse sandwich structure. It is interesting to note that the Ta₂B₆ cluster with 28 valence electrons has been found previously to form a highly stable D_6h Ta(η⁶-B₆)Ta inverse sandwich.⁷² A similar electronic consideration suggests that a La₂B₁₀⁻ inverse sandwich would have one extra electron, which would occupy the high energy 6s-based LUMO (Fig. 6), making it energetically unfavorable. Hence, we conclude that La₂B_x⁻ (x = 7–9) would be the only likely inverse sandwich complexes in term of the size of the B_x ring. On the other hand, our previous work showed that the Ln₂B₈⁻ species can form inverse sandwiches for a range of lanthanide elements for Ln = La, Pr, and Tb.³⁶ Therefore, we expect that most lanthanides should also be able to form the inverse sandwiches in the same size range, [Ln(η^x-B_x)Ln]⁻ (x = 7–9). Given the diverse magnetic properties of the lanthanides, the Ln₂B_x⁻ (x = 7–9) clusters constitute a novel class of inverse sandwich complexes with tunable chemical and physical properties. They not only provide new motifs for bulk borides, but it is also conceivable that some of these inverse sandwiches may be able to be synthesized in solution with appropriate ligand coordination, similar to the actinide arene inverse sandwiches.^65–68

8. Conclusions

We report the discovery of a new class of di-lanthanide boron inverse sandwich complexes: [Ln(η^x-B_x)Ln]⁻ (x = 7–9). Photoelectron spectroscopy of La₂B₇⁻ and La₂B₉⁻ revealed relatively simple spectral patterns, suggesting highly symmetric structures for the two cluster anions. Global minimum searches found that these two clusters form highly stable inverse sandwich structures. Simulated photoelectron spectra are in excellent agreement with the experimental data, confirming the high symmetry and stability of the inverse sandwich structures. Strong delocalized chemical bonding is found in the inverse sandwiches, involving the La 5d orbitals and the 2p-based orbitals of the boron ring moiety via double (σ and π) aromaticity and strong (d-p)δ interactions. Geometrical, chemical bonding, and electronic structure analyses suggest that the size range of the di-lanthanide boron inverse sandwiches is likely to be limited to x = 7–9 for [Ln(η^x-B_x)Ln]⁻, which form a novel class of lanthanide–boron complexes with potentially tunable chemical and physical properties. These inverse sandwich structures provide opportunities to design new types of lanthanide–boride materials, such as 1D chain-like nanowires, and they may also be synthesized as new inorganic compounds with appropriate ligand protections.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The experiment done at Brown University was supported by the National Science Foundation (CHE-1763380). The theoretical work at Tsinghua University was supported by National Natural Science Foundation of China (Grant No. 21590792, 91426302, and 21433005). The calculations were done using supercomputers at the Southern University of Science and Technology, Tsinghua National Laboratory for Information Science and Technology, and the Computational Chemistry Laboratory of the Department of Chemistry under the Tsinghua Xuetang Talents Program.

References

1. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866.
2. D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 251–268.
3. E. Oger, N. R. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
4. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
5. L. S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69–142.
6. M. R. Fagiani, X. Song, P. Petkov, S. Debnath, S. Gewinner, W. Schöllkopf, T. Heine, A. Fielicke and K. R. Asmis, Angew. Chem., Int. Ed., 2017, 56, 501–504.
7. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
8. H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827.
9. A. P. Sergeeva, D. Y. Zubarev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246.
10. W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202.
11. A. P. Sergeeva, B. B. Averkiev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2011, 134, 224304.
12. W. L. Li, C. Romanescu, T. Jian and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 13228–13231.
13. A. P. Sergeeva, Z. A. Piazza, C. Romanescu, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 18065–18073.
14. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113.
15. W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 136, 12257–12260.
16. A. I. Boldyrev and L. S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 11589–11605.
17. Q. Chen, W. L. Li, X. Y. Zhao, H. R. Li, L. Y. Feng, H. J. Zhai, S. D. Li and L. S. Wang, Eur. J. Inorg. Chem., 2017, 2017, 4546–4551.
18. G. Wilkinson, M. Rosenblum, M. Whiting and R. Woodward, J. Am. Chem. Soc., 1952, 74, 2125–2126.
19. R. Woodward, M. Rosenblum and M. Whiting, J. Am. Chem. Soc., 1952, 74, 3458–3459.
20. E. Muetterties, J. Bleeke, E. Wucherer and T. Albright, Chem. Rev., 1982, 82, 499–525.
21. I. A. Popov, W. L. Li, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2014, 118, 8098–8105.
22. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654.
23. T. Jian, W. L. Li, I. A. Popov, G. V. Lopez, X. Chen, A. I. Boldyrev, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 154310.
24. T. Jian, W. L. Li, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Chem. Sci., 2016, 7, 7020–7027.
25. W. L. Li, T. Jian, X. Chen, H. R. Li, T. T. Chen, X. M. Luo, S. D. Li, J. Li and L. S. Wang, Chem. Commun., 2017, 53, 1587–1590.
26. W. L. Li, X. Chen, T. Jian, T. T. Chen, J. Li and L. S. Wang, Nat. Rev. Chem., 2017, 1, 0071.
27. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
28. W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2011, 134, 165–168.
29. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105.
30. C. Romanescu, T. R. Galeev, A. P. Sergeeva, W. L. Li, L. S. Wang and A. I. Boldyrev, J. Organomet. Chem., 2012, 721, 148–154.
31. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 138, 134315.
32. W. L. Li, A. S. Ivanov, J. Federič, C. Romanescu, I. Černušák, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 139, 104312.
33. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2012, 46, 350–358.
34. P. J. Robinson, X. Zhang, T. McQueen, K. H. Bowen and A. N. Alexandrova, J. Phys. Chem. A, 2017, 121, 1849–1854.
35. T. T. Chen, W. L. Li, T. Jian, X. Chen, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2017, 56, 6916–6920.
36. W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6972–E6977.
37. L. S. Wang, H. S. Cheng and J. Fan, J. Chem. Phys., 1995, 102, 9480–9493.
38. C. Feigerle, R. Corderman and W. Lineberger, J. Chem. Phys., 1981, 74, 1513–1515.
39. Y. F. Zhao, X. Chen and J. Li, Nano Res., 2017, 10, 3407–3420.
40. X. Chen, Y. F. Zhao, L. S. Wang and J. Li, Comput. Theor. Chem., 2017, 1107, 57–65.
41. X. Chen, Y. F. Zhao, Y. Y. Zhang and J. Li, J. Comput. Chem., 2018 , in press.
42. D. J. Wales and J. P. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116.
43. ADF, SCM, Theoretical Chemistry, Vrijie Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
44. E. v. Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
46. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
47. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
48. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
49. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
50. X. Cao and M. Dolg, J. Chem. Phys., 2001, 115, 7348–7355.
51. X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147.
52. J. Li, X. Li, H. J. Zhai and L. S. Wang, Science, 2003, 299, 864–867.
53. P. Schipper, O. Gritsenko, S. Van Gisbergen and E. Baerends, J. Chem. Phys., 2000, 112, 1344–1352.
54. A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939.
55. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
56. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
57. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
58. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
59. K. B. Wiberg and P. R. Rablen, J. Comput. Chem., 1993, 14, 1504–1518.
60. F. M. Bickelhaupt, N. J. van Eikema Hommes, C. Fonseca Guerra and E. J. Baerends, Organometallics, 1996, 15, 2923–2931.
61. M. Swart, P. T. van Duijnen and J. G. Snijders, J. Comput. Chem., 2001, 22, 79–88.
62. I. Mayer, Int. J. Quantum Chem., 1986, 29, 477–483.
63. M. Gopinathan and K. Jug, Theor. Chim. Acta, 1983, 63, 497–509.
64. A. Michalak, R. L. DeKock and T. Ziegler, J. Phys. Chem. A, 2008, 112, 7256–7263.
65. P. L. Diaconescu, P. L. Arnold, T. A. Baker, D. J. Mindiola and C. C. Cummins, J. Am. Chem. Soc., 2000, 122, 6108–6109.
66. P. L. Diaconescu and C. C. Cummins, J. Am. Chem. Soc., 2002, 124, 7660–7661.
67. B. M. Gardner, F. Tuna, E. J. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2015, 54, 7068–7072.
68. S. T. Liddle, Coord. Chem. Rev., 2015, 293, 211–227.
69. P. Pyykkö, J. Phys. Chem. A, 2014, 119, 2326–2337.
70. W. L. Li, J. B. Lu, L. Zhao, R. Ponec, D. L. Cooper, J. Li and G. Frenking, J. Phys. Chem. A, 2018, 122, 2816–2822.
71. Q. Zhang, W. L. Li, L. Zhao, M. Chen, M. Zhou, J. Li and G. Frenking, Chem.–Eur. J., 2017, 23, 2035–2039.
72. W. L. Li, L. Xie, T. Jian, C. Romanescu, X. Huang and L. S. Wang, Angew. Chem., Int. Ed., 2014, 53, 1288–1292.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc05443f

‡ These authors contribute equally.

---