Open Access Article
Open Access ArticleDensity matrix renormalization group pair-density functional theory (DMRG-PDFT): singlet–triplet gaps in polyacenes and polyacetylenes†
Prachi
Sharma‡
 a,
Varinia
Bernales‡
a,
Varinia
Bernales‡
 a,
Stefan
Knecht
a,
Stefan
Knecht
 *b,
Donald G.
Truhlar
*b,
Donald G.
Truhlar
 *a and
Laura
Gagliardi
*a and
Laura
Gagliardi
 *a
*a
aDepartment of Chemistry, Chemical Theory Center, Minnesota Supercomputing Institute, University of Minnesota, Minneapolis, Minnesota 55455, USA. E-mail: truhlar@umn.edu; gagliard@umn.edu
bLaboratory of Physical Chemistry, ETH Zürich, Vladimir-Prelog-Weg 2, CH-8093 Zürich, Switzerland. E-mail: stefan.knecht@phys.chem.ethz.ch
First published on 26th November 2018
Abstract
The density matrix renormalization group (DMRG) is a powerful method to treat static correlation. Here we present an inexpensive way to calculate correlation energy starting from a DMRG wave function using pair-density functional theory (PDFT). We applied this new approach, called DMRG-PDFT, to study singlet–triplet gaps in polyacenes and polyacetylenes that require active spaces larger than the feasibility limit of the conventional complete active-space self-consistent field (CASSCF) method. The results match reasonably well with the most reliable literature values and have only a moderate dependence on the compression of the initial DMRG wave function. Furthermore, DMRG-PDFT is significantly less expensive than other commonly applied ways of adding additional correlation to DMRG, such as DMRG followed by multireference perturbation theory or multireference configuration interaction.
1 Introduction
The accurate yet affordable treatment of large molecular systems with close-lying electronic states has long been a target for the development of new quantum chemical methods.1–7 Electron correlation is sometimes classified into two categories: static and dynamic correlation.4–6 Dynamic correlation arises mainly from minimizing short-range repulsion or maximizing long-range dispersion and middle-range dispersion-like interactions of electrons. Static correlation, on the other hand, arises when the state under consideration is inherently multiconfigurational, by which we mean that a single configuration state function does not provide a good reference wave function for perturbation theory, configuration interaction, or coupled cluster theory; this usually arises due to near degeneracy of two or more configurations that both contribute to the description of the state under consideration. Systems with high static correlation are called inherently multi-configurational or strongly correlated, and they are also called multireference systems because their electronic structure is best treated with methods – called multireference methods – involving a multi-configuration reference wave function. A realistic yet practical treatment of strongly correlated systems requires a better starting point than the usual independent-electron approach.8One example of strongly-correlated systems is the family of polyacenes (also called acenes), the ground states of which have polyradical character.9 The acenes are a series of compounds consisting of fused benzene rings; in the present article we only consider the case where they are arranged in a linear fashion as shown in Fig. 1. Polyacenes are especially interesting because their electronic properties make them useful for biodegradable and low-cost electronics.10–13 The smaller ones, such as naphthalene and anthracene, are used industrially to make various dyes, while larger acenes, like tetracene and pentacene along with their derivatives, are used as organic light-emitting diodes (OLEDs) and organic field-effect transistors (OFETs).14–25 Recently, tetracene and pentacene have been found to undergo singlet-fission where a high-energy singlet exciton converts to two low-energy triplet excitons, thereby increasing the efficiency of solar cells by up to 40%.26–33
Polyenes are another example of strongly correlated systems that contains alternating single and double bonds; in the present article we will consider polyacetylenes as examples of this class of compounds. They are often used as model systems to understand the electronic properties of more complicated biological systems such as carotenoids, retinal, and various antibiotics such as amphotericin B, nystatin, etc.34,35 Polyacetylenes also show high electrical conductivity, which further increases on doping with p-type dopants such as Br2, I2, Cl2, and AsF5.36–40
A theoretical method that plays a key role in many methods for treating multireference systems is CASSCF,41–43 which is a special case of the multiconfiguration self-consistent-field (MCSCF) method. In the CASSCF method, some orbitals are restricted to be doubly occupied in all configuration state functions; these are called inactive orbitals. An additional group of orbitals, called active orbitals, are allowed to have variable occupancy. The CASSCF wave function is then a configuration interaction wave function including all possible occupancies of the active orbitals; this is called full configuration interaction (FCI) in the active space. CASSCF is limited by the exponential increase in cost with size of the active space such that 20 electrons in 20 orbitals (20, 20) is the largest reported active space treated by the conventional CASSCF method.44 Although the CASSCF approach was originally designed as a way to recover the static correlation, inevitably it also includes some of the remaining electron correlation, which is called dynamic correlation, but usually only a small fraction of it. The dynamic correlation not included in a CASSCF calculation is called external correlation,45–47 and one of the main challenges in quantum chemistry is to design methods to include the external correlation energy efficiently.
The density matrix renormalization group (DMRG)48–51 algorithm is a replacement of the FCI solver in the CASSCF or CASCI methods.52,53 (CASCI is like CASSCF, but the orbitals are not self-consistently optimized for a given configuration list. In the present work we use self-consistently optimized orbitals.) The major advantage of DMRG comes from its polynomial scaling with respect to the size of the active space; this allows practical computation of numerically well-converged solutions for active spaces three to four times larger than standard CASSCF.54 Although multiconfigurational methods such as CASSCF or DMRG can be effectively applied to capture static correlation, and they in principle reduce the difficulty in choosing which orbitals to include in the active space (because they allow more orbitals to be included), they are not efficient at capturing all the correlation energy because of the slow convergence of external correlation with respect to the number of orbitals and configurations included.
A number of approaches have been advanced to make it more efficient to treat the dynamical correlation not included in an MCSCF-type calculation. For example, approaches that have been combined with DMRG include internally contracted multireference CI (MRCI),55,56 multireference perturbation theory (MRPT),57–68 and wave function theory-short range density functional theory (WFT-srDFT).69 In the present study we introduce the use of multiconfiguration pair-density functional theory (MC-PDFT)70,71 to include dynamic electron correlation beyond that captured within a DMRG wave function; this two-step procedure will be called DMRG-PDFT. The major advantage of DMRG-PDFT is that it treats both static and dynamic electron-correlation and gives accurate results at significantly lower memory and computational costs than multireference perturbation treatments and MRCI approaches. Therefore, it can attain high accuracy that would be too expensive to be practical with other methods.
We briefly review DMRG and MC-PDFT in Section 2, followed by a presentation of DMRG-PDFT. The computational methods are in Section 3. Results and discussion are in Section 4, and conclusions are in Section 5.
2 Theory
The matrix product state (MPS) is a key theoretical concept in the DMRG algorithm used here. In this section, we review the MPS and the DMRG algorithm, and we provide a brief discussion of MC-PDFT.2.1. Matrix product states (MPS) and density matrix renormalization group (DMRG)
Because DMRG (in a quantum-chemical context) is well described in the literature,50–53,59,72–80 we summarize only enough details as are necessary to specify the present applications.The non-relativistic electronic Hamiltonian may be written in second quantization as81
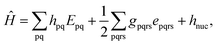 | (1) |
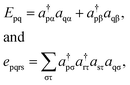 | (2) |
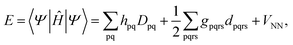 | (3) |
Each spatial orbital l (also referred to as a site in DMRG terminology) is associated with four possible occupations:
| nl = {|vac〉,|↑〉,|↓〉,|↑↓〉}. | (4) |
The eigenstate |Ψ〉 of the Hamiltonian (1) can be written in an occupation number basis as
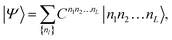 | (5) |
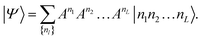 | (6) |
The size of the matrices Anl increases exponentially towards the middle of the product, then decreases again.53Eqn (6) is called a matrix product state (MPS). Note, that the first and the last matrices in eqn (6) are in practice 1 × 4-dimensional row and 4 × 1-dimensional column vectors, respectively, such that the final contraction of the matrices Anl yields a scalar CI coefficient Cn1n2…nL.
If no truncation is made in the matrix products, the MPS is equivalent to full configuration interaction (FCI). For practical work, one retains at most M terms in each of the matrix multiplication steps; this approximation is called compression, and M is called the bond dimension. Compression is the main approximation of DMRG as compared to FCI. The compressed MPS is then variationally optimized to give an upper bound to the ground-state energy. Thus, DMRG may be considered to be a way to calculate an approximate wave function that gives an upper bound to the FCI energy. We note though that we (and others) apply FCI only within the active space, so what we obtain is an upper bound to the CASSCF energy, which in turn is an upper bound to the FCI energy, which is an upper bound to the complete configuration interaction (CCI) energy, which is exact (CCI is FCI with a complete basis set).
As we have just explained, if one did not truncate the bond dimension in DMRG, the resulting wave function would correspond to FCI among the active orbitals, i.e., to CASSCF. In this context, DMRG may be considered to offer a possibility to calculate an approximate CASSCF wave function in a controlled manner such that it gives a variational upper bound to the CASSCF energy. However, its efficiency allows one to use many more active orbitals than in conventional CASSCF. The approximate solution to the large-active-space CASSCF problem will typically have a lower (and hence more accurate) energy than the uncompressed solution to the small-active-space CASSCF problem.
2.2. Multiconfiguration pair-density functional theory (MC-PDFT)
To correct the DMRG energy for dynamic correlation, we use pair-density functional theory.70,71 The MC-PDFT energy, for a generic multiconfiguration (MC) wave function is expressed as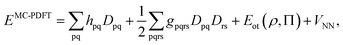 | (7) |
2.3 Implementation
The DMRG-PDFT implementation is based on an interface between the existing MC-PDFT code in the OpenMolcas 8.3 software package82,83 and the DMRG code in the QCMAQUIS program.72,75,84The MC-PDFT energy can be written in terms of inactive and active orbitals as
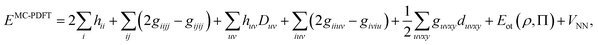 | (8) |
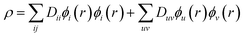 | (9) |
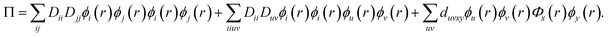 | (10) |
3. Computational methods
The vertical singlet–triplet gaps for polyacetylenes and polyacenes were computed using DMRG-PDFT. Geometries are very important for adiabatic S–T gaps. The geometries of the polyacenes for both the singlet (11Ag) and triplet (13B3u) states were taken from ref. 85. We optimized the geometry of polyacetylenes at the same level of theory as the polyacenes, using the Kohn–Sham density functional theory with the B3LYP exchange–correlation functional86,87 and the 6-31G(d,p) basis set. The optimized structures were then used to perform DMRG calculations followed by DMRG-PDFT calculations. All DMRG-PDFT calculations were performed with the tPBE on-top density functional.88 The 6-31+G(d,p) basis set was used for all DMRG-PDFT calculations.The active space is denoted as usual as (n, m) where n is the number of active electrons, and m is the number of active orbitals. The active spaces used here correspond to all the π electrons distributed in all the valence π orbitals; thus n = m. For all polyacene calculations, we constrained the wave functions to D2h symmetry, where the ground state has symmetry 1Ag, and the lowest triplet state has symmetry 3B3u. For the polyacetylene calculations, C2h symmetry was imposed. The ground state has symmetry 1Ag, and the lowest triplet state has symmetry 3Bu.
The convergence with respect to the bond dimension M was tested from 100 to 2000 for naphthalene and anthracene, and M was set to 500 for higher acenes. The convergence for polyacetylenes was studied from M = 4 to M = 1000. The DMRG calculations were performed with QCMAQUIS.72,75,84,89
4 Results and discussion
4.1. Singlet–triplet gap in polyacenes
The results for vertical and adiabatic singlet–triplet (S–T) gaps of naphthalene are reported in Table 1 as functions of bond dimension M. Convergence is reached at M = 200 with a value for the DMRG vertical excitation energy of 3.05 eV. The DMRG-PDFT vertical excitation energy is 3.35 eV, with a small deviation from other high-level calculations, in particular a deviation of 1.5% from CCSD(T)90 and a deviation of 2.3% from DMRG-ec-MRCISD+Q;91 in contrast plain DMRG has 7.4% and 11.1% deviations, respectively. The DMRG-PDFT adiabatic excitation energy is 2.91 eV, which is within the range of values (2.65–3.06 eV) calculated by various methods in ref. 13,34 and 93–96. These results are encouraging because DMRG-PDFT is applicable to much larger systems than other methods of comparable accuracy.| M | DMRG | DMRG-PDFT | GAS-PDFTa | Reference values | ||||
|---|---|---|---|---|---|---|---|---|
| Vert. | Ad. | Vert. | Ad. | Vert. | Ad. | Vert. | Ad.d | |
| a Generalized active-space pair-density functional theory with tPBE functional and 6-31G+(d,p) basis set from ref. 85. b DMRG-externally correlated multireference CI, DMRG-ec-MRCISD+Q at geometries optimized by UB3LYP/6-31G(d); see ref. 91 for details. c Restricted CCSD(T) with pV∞Z basis set at geometries optimized by B3LYP/cc-PVTZ; see ref. 90 for details. d Vibrationally corrected experimented values; see ref. 95 and 96 for experimental details. ΔZPE = −0.14 eV calculated by B3LYP/6-31G(d,p). | ||||||||
| 3.36 | 3.06 | 3.43,b 3.30c | 2.78, 2.79 | |||||
| 100 | 3.08 | 2.67 | 3.31 | 2.89 | ||||
| 200 | 3.05 | 2.66 | 3.35 | 2.91 | ||||
| 500 | 3.05 | 2.66 | 3.35 | 2.91 | ||||
| 1000 | 3.05 | 2.66 | 3.35 | 2.91 | ||||
In Table 2, vertical and adiabatic S–T gaps for different bond dimensions are reported for anthracene. We see convergence at M = 1000, and we observe a significant improvement in both vertical and adiabatic singlet–triplet gaps when the MC-PDFT method is used to calculate correlation energy starting from a DMRG wave function. The S–T gap predicted by DMRG decreases when the bond dimension is increased, but the DMRG-PDFT gap increases along the same sequence of M values. A key result is that the DMRG-PDFT results show less dependence on M than do the plain DMRG results; in fact DMRG-PDFT gives results close to the best previously available values90–93,95 even for an M value as small as M = 100.
| M | DMRG | DMRG-PDFT | GAS-PDFTa | Other literature values | ||||
|---|---|---|---|---|---|---|---|---|
| Vert. | Ad. | Vert. | Ad. | Vert. | Ad. | Vert. | Ad.d | |
| a Generalized active-space pair-density functional theory with tPBE functional and 6-31G+(d,p) basis set from ref. 85. b DMRG-externally correlated multireference CI, DMRG-ec-MRCISD+Q at geometries optimized by UB3LYP/6-31G(d); see ref. 91. c Restricted CCSD(T) (FPA-5Z3) at geometries optimized by B3LYP/cc-PVTZ. FPA − 5Z3 = (ECCSD(T)/cc-pVTZ − EMP4/cc-pVTZ) + SMP2 − 5Z + (SMP4 − 4Z − SMP2 − 4Z), where SMP2 − 5Z are obtained as the sum of the HF energy and MP2 electron correlation energy, both extrapolated to the CBS limit using Schwartz extrapolations employing HF and MP2 energies obtained using the cc-pVTZ, cc-pVQZ, and cc-pV5Z basis sets; ref. 90. d Vibrationally corrected experimented values; see ref. 95 and 97 for experimental details. ΔZPE = −0.10 eV calculated by B3LYP/6-31G(d,p). | ||||||||
| 2.22 | 1.97 | 2.47,b 2.46c | 1.95–1.97 | |||||
| 100 | 2.46 | 2.05 | 2.28 | 2.00 | ||||
| 200 | 2.42 | 2.03 | 2.26 | 1.97 | ||||
| 500 | 2.34 | 1.97 | 2.33 | 2.00 | ||||
| 1000 | 2.31 | 1.96 | 2.36 | 2.02 | ||||
| 2000 | 2.30 | 1.95 | 2.38 | 2.04 | ||||
The adiabatic S–T gaps for various systems, from naphthalene to heptacene, obtained with M = 500 are compared to literature values in Table 3. We observe that DMRG-PDFT gives very good agreement with the vibrationally corrected experimental S–T gaps for adiabatic singlet–triplet gaps with a mean unsigned deviation (MUD) of only 0.06 eV while DMRG without external correlation gives an MUD of 0.17 eV. While DMRG-CASPT2 and ACI-DSRG-MRPT2 underestimate the S–T gap with respect to the experiment, CCSD(T) tends to overestimate. The generalized active-space-pair density functional theory (GAS-PDFT) gives excellent agreement with the experimental results. In GAS101 based methods, the active space is further divided into smaller subspaces and only certain excitations are allowed within them, thereby making these methods more affordable. One difficulty with these approaches, though, is to choose the appropriate subspaces and appropriate restrictions on the kinds of included electron excitations because such choices are not systematic and often require subjective chemical intuition and specialized expertise.
| DMRGa | DMRG-PDFTa | GAS-PDFTb | pp-RPAc | DMRG-CASPT2d | DMRG-CASPT2e | CCSD(T)f | DMRG-ec-MRCISD+Qg | ACI-DSRG-MRPT2h | ΔZPEi | Exp. | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a M = 500. b Generalized active-space pair-density functional theory with the tPBE functional and the 6-31+G(d,p) basis set; for details see ref. 85. c Particle–particle random phase approximation (pp-RPA) with the B3LYP functional at geometries optimized by UB3LYP/6-31G*. See ref. 13 for details. d DMRG-CASPT2 at geometries optimized by CASPT2-D/cc-pVTZ(-f); see ref. 98 for details. e DMRG-CASPT2 at geometries optimized by CAM-B3LYP/6-31G*; see ref. 98 for details. f Restricted CCSD(T) (FPA-5Z3) at geometries optimized by B3LYP/cc-PVTZ with added ZPE correction. FPA − 5Z3 = (ECCSD(T)/cc-pVTZ − EMP4/cc-pVTZ) + SMP2 − 5Z + (SMP4 − 4Z − SMP2 − 4Z), where SMP2 − 5Z are obtained as the sum of the HF energy and MP2 electron correlation energy, both extrapolated to the CBS limit using Schwartz extrapolations employing HF and MP2 energies obtained using the cc-pVTZ, cc-pVQZ, and cc-pV5Z basis sets.; see ref. 90 for details. g DMRG-ec-MRCISD+Q on geometry optimized by UB3LYP/6-31G(d); see ref. 91 for details. h Adaptive CI with density a density-fitted implementation of second-order perturbative multiconfiguration driven similarity renormalization group (ACI-DSRG-MRPT2) calculations; see ref. 99. i Zero-point energy correction; calculated by B3LYP/6-31G(d,p). j See ref. 95. k Ref. 96. l Ref. 97. m Ref. 100. n Ref. 94. o Mean unsigned deviation with respect to vibrationally corrected experimental S–T gap. | |||||||||||
| Naphthalene (10, 10) | 2.66 | 2.91 | 3.06 | 2.87 | — | — | 2.85 | 2.71 | 2.70 | −0.14 | 2.64j, 2.65k |
| Anthracene (14, 14) | 1.97 | 2.00 | 1.97 | 1.98 | 1.73 | 1.69 | 2.09 | 1.81 | 1.87 | −0.10 | 1.85j, 1.87l |
| Tetracene (18, 18) | 1.54 | 1.37 | 1.46 | 1.39 | 1.29 | 1.18 | 1.45 | 1.23 | 1.23 | −0.08 | 1.28j |
| Pentacene (22, 22) | 1.24 | 0.98 | 1.10 | 0.98 | 0.86 | 0.82 | 1.10 | 0.92 | 0.78 | −0.06 | 0.86 ± 0.03m |
| Hexacene (26, 26) | 0.93 | 0.73 | 0.85 | 0.66 | 0.58 | 0.62 | 0.77 | 0.67 | 0.49 | −0.06 | 0.54 ± 0.05n |
| Heptacene (30, 30) | 0.67 | 0.62 | 0.72 | 0.39 | — | — | 0.58 | 0.48 | 0.33 | −0.05 | — |
| MUDo | 0.17 | 0.06 | 0.04 | 0.04 | 0.08 | 0.13 | 0.17 | 0.07 | 0.09 | ||
The vertical S–T gaps are reported in Table 4. Because it underestimates external correlation, DMRG overestimates the S–T gap for acenes larger than naphthalene. The adiabatic and vertical S–T gaps for DMRG and DMRG-PDFT are compared with experimental values for larger polyacenes in Fig. 2, showing reasonable agreement for both DMRG and DMRG-PDFT adiabatic S–T gaps.
| DMRG | DMRG-PDFTa | GAS-PDFTb | CCSD(T)c | DMRG-MRCISD+Qd | |
|---|---|---|---|---|---|
| a M = 500. b GAS-PDFT with 6-31+G(d,p) basis set; for details see ref. 85. c Restricted CCSD(T) with pV∞Z basis set at geometries optimized by B3LYP/cc-PVTZ; see ref. 90 for details. d DMRG-ec-MRCISD+Q on geometry optimized by UB3LYP/6-31G(d); see ref. 91 for details. | |||||
| Naphthalene (10, 10) | 3.05 | 3.35 | 3.36 | 3.30 | 3.43 |
| Anthracene (14, 14) | 2.34 | 2.33 | 2.22 | 2.46 | 2.47 |
| Tetracene (18, 18) | 1.88 | 1.58 | 1.69 | 1.75 | 1.81 |
| Pentacene (22, 22) | 1.56 | 1.13 | 1.29 | 1.36 | 1.36 |
| Hexacene (26, 26) | 1.19 | 0.79 | 0.99 | 0.99 | 0.98 |
| Heptacene (30, 30) | 0.81 | 0.61 | 0.75 | 0.78 | 0.67 |
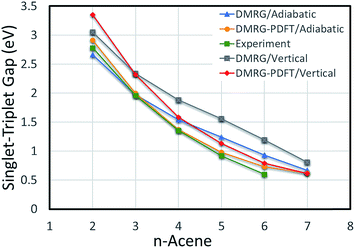 | ||
| Fig. 2 Adiabatic and vertical singlet–triplet gaps for polyacenes. Experimental values are vibrationally corrected. | ||
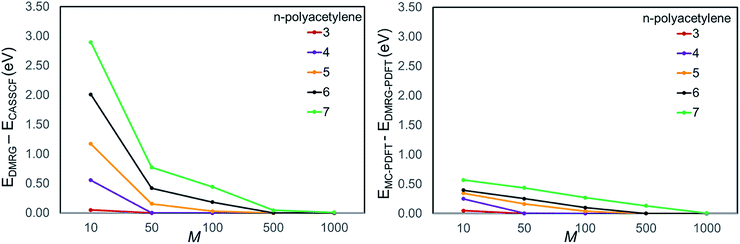
Before we conclude this session, we would like to briefly comment on the active space dependence of DMRG and DMRG-PDFT. It is well known that all multi-reference methods, both standard ones and new ones, have some dependence on active space. Table S5 in ESI† shows the effect of active-space expansion in the naphthalene system. DMRG-PDFT has an equal or smaller dependence on active space than does DMRG alone. In going from a (10, 10) active space to a (10, 20) active space both the vertical and adiabatic DMRG-PDFT excitation energies change by less than 0.1 eV for M = 500. The active space dependence of PDFT has been discussed in several papers (see for example ref. 70 and 71). The effect is not aggravated by using DMRG as a reference wave function.
4.2. Singlet–triplet gap in polyacetylenes
Singlet–triplet energies for polyacetylenes as calculated by DMRG and DMRG-PDFT are reported in Table 5. For smaller polyacetylenes (ethylene to octatetraene), DMRG-PDFT results agree well with the experimental values with an MUD of 0.18 eV. Our DMRG-PDFT results agree with CASPT2 results within 0.2 eV, which is encouraging because DMRG-PDFT is applicable to much larger systems than conventional CASPT2 or DMRG-PT2. Note that we used a small bond dimension of 50 for all the acetylene singlet–triplet gaps presented in Table 5. For acetylenes smaller than hexatriene, the DMRG results converge to the CASSCF values, which is not surprising because we found that ethylene and butadiene calculations need M values of only 4 and 16 to reproduce the CASSCF results. However, as could be expected, the deviation between the DMRG and CASSCF values increases for larger acetylenes when we use a fixed value of M.| Number of monomers | Active space | DMRG | DMRG-PDFT | CASSCF | CASPT2 | Literature values | Exp.a |
|---|---|---|---|---|---|---|---|
| a Experimental band maxima for ethylene,102–105 butadiene,106 and hexatriene.107 b CCSD(T)/cc-pVTZ result from ref. 108. c UCCSD result from ref. 109. d Multireference Møller–Plesset study corrected for basis-set and active-space effects, from ref. 110. e Mean unsigned deviation from experiment. | |||||||
| 1 | (2, 2) | 4.34 | 4.67 | 4.34 | 4.54 | 4.63b | 4.3–4.6 |
| 2 | (4, 4) | 3.37 | 3.46 | 3.37 | 3.38 | 3.45b, 3.20d | 3.22 |
| 3 | (6, 6) | 2.80 | 2.79 | 2.80 | 2.73 | 2.80b, 2.40d | 2.61 |
| 4 | (8, 8) | 2.43 | 2.37 | 2.43 | 2.33 | 2.42c, 2.10d | 2.10 |
| 5 | (10, 10) | 2.29 | 1.99 | 2.19 | 2.07 | 2.20c, 1.89d | |
| 6 | (12, 12) | 2.20 | 1.79 | 2.01 | 1.88 | 2.00c | |
| 7 | (14, 14) | 2.17 | 1.59 | 1.88 | 1.75 | 1.90c | |
| 8 | (16, 16) | 2.20 | 1.52 | ||||
| 9 | (18, 18) | 1.03 | 0.07 | ||||
| MUDe | 0.20 | 0.18 | 0.20 | 0.16 | |||
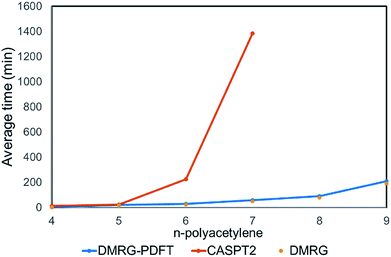
We plotted the convergence of singlet–triplet gaps in DMRG and DMRG-PDFT with respect to conventional CASSCF and MC-PDFT in Fig. 3. DMRG-PDFT converges faster with respect to M and shows less dependence on M than does DMRG. In Fig. 4, we show the average time required for DMRG and DMRG-PDFT with M = 50 as compared to the time for CASPT2 calculations for polyacetylenes (the times are averaged over singlet and triplet). All the calculations were performed on a single processor with a maximum memory of 62 gigabytes. The DMRG-PDFT calculations take considerably less time than the corresponding CASPT2 calculations for higher polyacetylenes (five or more monomers). For example, for seven monomers, CASPT2 takes fifteen times longer than DMRG-PDFT.
5 Conclusions
We have presented a new method, DMRG-PDFT, that combines the advantages of the DMRG and MC-PDFT approaches. We used the resulting new method to calculate singlet–triplet gaps in polyacenes and polyacetylenes. The energy gaps calculated using DMRG were found to be close to the reference data, and we found that the DMRG-PDFT calculations are in most of the cases more accurate than their bare DMRG counterparts. For polyacenes, singlet–triplet energies match reasonably well with the literature including experimental as well as various high-level calculations such as CCSD(T), DMRG-CASPT2, and DMRG-ec-MRCISD+Q values. For polyacetylene systems, we compared DMRG and DMRG-PDFT values with M = 50 to standard CASSCF and CAS-PDFT, and we found that DMRG-PDFT shows less dependence on the bond dimension than does DMRG. Using the on-top density functional to calculate correlation energy starting from a DMRG wave functions is shown to be a promising approach to study large systems at an affordable cost.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by Air Force Office of Scientific Research grant FA9550-16-1-0134. SK thanks Markus Reiher (ETH Zürich) for his continuous support.References
- J. A. Pople, J. S. Binkley and R. Seeger, Int. J. Quantum Chem., 1976, 10, 1–19 CrossRef CAS.
- C.W. Bauschlicher, S. R. Langhoff and P. R. Taylor, Adv. Chem. Rev., 1990, 160, 103–162 Search PubMed.
- K. Raghavachari and J. B. Anderson, J. Phys. Chem., 1996, 100, 12960–12973 CrossRef CAS.
- D. K. Mok, R. Neumann and N. C. Handy, J. Phys. Chem., 1996, 100, 6225–6230 CrossRef CAS.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- J. W. Hollett and P. M. Gill, J. Chem. Phys., 2011, 134, 114111 CrossRef.
- S. Wilson and G. H. Diercksen, Methods in computational molecular physics, Springer Science & Business Media, 2013 Search PubMed.
- P.-O. Löwdin, Phys. Rev., 1955, 97, 1509 CrossRef.
- J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309 CrossRef.
- M. Zander, Angew. Chem., 1965, 77, 875–876 CrossRef.
- M. Bendikov, F. Wudl and D. F. Perepichka, Chem. Rev., 2004, 104, 4891–4946 CrossRef CAS PubMed.
- J. E. Anthony, Chem. Rev., 2006, 106, 5028–5048 CrossRef CAS PubMed.
- Y. Yang, E. R. Davidson and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E5098–E5107 CrossRef CAS PubMed.
- Y.-Y. Lin, D. Gundlach, S. Nelson and T. Jackson, IEEE Electron Device Lett., 1997, 18, 606–608 CAS.
- D. Gundlach, J. Nichols, L. Zhou and T. Jackson, Appl. Phys. Lett., 2002, 80, 2925–2927 CrossRef CAS.
- C. D. Dimitrakopoulos and P. R. Malenfant, Adv. Mater., 2002, 14, 99–117 CrossRef CAS.
- G. Collin, H. Höke and H. Greim, Ullmann's encyclopedia of industrial chemistry, 2003 Search PubMed.
- J. Takeya, C. Goldmann, S. Haas, K. Pernstich, B. Ketterer and B. Batlogg, J. Appl. Phys., 2003, 94, 5800–5804 CrossRef CAS.
- V. Butko, X. Chi, D. Lang and A. Ramirez, Appl. Phys. Lett., 2003, 83, 4773–4775 CrossRef CAS.
- C. Goldmann, S. Haas, C. Krellner, K. Pernstich, D. Gundlach and B. Batlogg, J. Appl. Phys., 2004, 96, 2080–2086 CrossRef CAS.
- O. D. Jurchescu, J. Baas and T. T. Palstra, Appl. Phys. Lett., 2004, 84, 3061–3063 CrossRef CAS.
- P. S. Abthagir, Y.-G. Ha, E.-A. You, S.-H. Jeong, H.-S. Seo and J.-H. Choi, J. Phys. Chem. B, 2005, 109, 23918–23924 CrossRef CAS PubMed.
- F. Cicoira, C. Santato, F. Dinelli, M. Murgia, M. A. Loi, F. Biscarini, R. Zamboni, P. Heremans and M. Muccini, Adv. Funct. Mater., 2005, 15, 375–380 CrossRef CAS.
- G. Collin, H. Höke and J. Talbiersky, Ullmann's Encyclopedia of Industrial Chemistry, 2006 Search PubMed.
- Q. Meng, H. Dong, W. Hu and D. Zhu, J. Mater. Chem., 2011, 21, 11708–11721 RSC.
- S. Singh, W. Jones, W. Siebrand, B. Stoicheff and W. Schneider, J. Chem. Phys., 1965, 42, 330–342 CrossRef CAS.
- M. Hanna and A. Nozik, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- P. M. Zimmerman, Z. Zhang and C. B. Musgrave, Nat. Chem., 2010, 2, 648 CrossRef CAS PubMed.
- P. M. Zimmerman, F. Bell, D. Casanova and M. Head-Gordon, J. Am. Chem. Soc., 2011, 133, 19944–19952 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- W.-L. Chan, T. C. Berkelbach, M. R. Provorse, N. R. Monahan, J. R. Tritsch, M. S. Hybertsen, D. R. Reichman, J. Gao and X.-Y. Zhu, Acc. Chem. Res., 2013, 46, 1321–1329 CrossRef CAS PubMed.
- M. J. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378 CrossRef CAS PubMed.
- D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2008, 128, 144117 CrossRef.
- E. M. Woerly, J. Roy and M. D. Burke, Nat. Chem., 2014, 6, 484 CrossRef CAS.
- H. Shirakawa, E. J. Louis, A. G. MacDiarmid, C. K. Chiang and A. J. Heeger, J. Chem. Soc., Chem. Commun., 1977, 578–580 RSC.
- C. Chiang, S. Gau, C. Fincher Jr, Y. Park, A. MacDiarmid and A. Heeger, Appl. Phys. Lett., 1978, 33, 18–20 CrossRef CAS.
- A. G. MacDiarmid and A. J. Heeger, Synth. Met., 1980, 1, 101–118 CrossRef CAS.
- A. J. Heeger, Rev. Mod. Phys., 2001, 73, 681 CrossRef CAS.
- H. Shirakawa, A. McDiarmid and A. Heeger, Chem. Commun., 2003, 2003, 1–4 RSC.
- B. O. Roos, P. R. Taylor and P. E. Si, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- K. Ruedenberg, M. W. Schmidt, M. M. Gilbert and S. Elbert, Chem. Phys., 1982, 71, 41–49 CrossRef CAS.
- B. O. Roos, Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2, 2007, vol. 69, pp. 399–445 Search PubMed.
- K. D. Vogiatzis, D. Ma, J. Olsen, L. Gagliardi and W. A. de Jong, J. Chem. Phys., 2017, 147, 184111 CrossRef.
- H. J. Silverstone and O. Sinanoğlu, J. Chem. Phys., 1966, 44, 1899–1907 CrossRef CAS.
- G. Li, H.-J. Werner, F. Lique and M. H. Alexander, J. Chem. Phys., 2007, 127, 174302 CrossRef.
- J. Ivanic and M. W. Schmidt, J. Phys. Chem. A, 2018, 122, 5223–5237 CrossRef CAS PubMed.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863 CrossRef PubMed.
- S. R. White, Phys. Rev. B, 1993, 48, 10345 CrossRef CAS.
- U. Schollwöck, Rev. Mod. Phys., 2005, 77, 259 CrossRef.
- U. Schollwöck, Ann. Phys., 2011, 326, 96–192 Search PubMed.
- G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS PubMed.
- S. Wouters and D. Van Neck, Eur. Phys. J. D, 2014, 68, 272 CrossRef.
- G. K.-L. Chan and M. Head-Gordon, J. Chem. Phys., 2002, 116, 4462–4476 CrossRef CAS.
- M. Saitow, Y. Kurashige and T. Yanai, J. Chem. Phys., 2013, 139, 044118 CrossRef.
- M. Saitow, Y. Kurashige and T. Yanai, J. Chem. Theory Comput., 2015, 11, 5120–5131 CrossRef CAS PubMed.
- Y. Kurashige and T. Yanai, J. Chem. Phys., 2011, 135, 094104 CrossRef PubMed.
- Y. Kurashige, J. Chalupský, T. N. Lan and T. Yanai, J. Chem. Phys., 2014, 141, 174111 CrossRef PubMed.
- T. Yanai, Y. Kurashige, W. Mizukami, J. Chalupský, T. N. Lan and M. Saitow, Int. J. Quantum Chem., 2015, 115, 283–299 CrossRef CAS.
- E. Xu, D. Zhao and S. Li, J. Chem. Theory Comput., 2015, 11, 4634–4643 CrossRef CAS PubMed.
- Q. M. Phung, S. Wouters and K. Pierloot, J. Chem. Theory Comput., 2016, 12, 4352–4361 CrossRef CAS PubMed.
- S. Wouters, V. Van Speybroeck and D. Van Neck, J. Chem. Phys., 2016, 145, 054120 CrossRef.
- S. Guo, M. A. Watson, W. Hu, Q. Sun and G. K.-L. Chan, J. Chem. Theory Comput., 2016, 12, 1583–1591 CrossRef CAS.
- M. Roemelt, S. Guo and G. K.-L. Chan, J. Chem. Phys., 2016, 144, 204113 CrossRef.
- L. Freitag, S. Knecht, C. Angeli and M. Reiher, J. Chem. Theory Comput., 2017, 13, 451–459 CrossRef CAS PubMed.
- N. Nakatani and S. Guo, J. Chem. Phys., 2017, 146, 094102 CrossRef.
- S. Sharma, G. Knizia, S. Guo and A. Alavi, J. Chem. Theory Comput., 2017, 13, 488–498 CrossRef CAS PubMed.
- T. Yanai, M. Saitow, X.-G. Xiong, J. Chalupský, Y. Kurashige, S. Guo and S. Sharma, J. Chem. Theory Comput., 2017, 13, 4829–4840 CrossRef CAS PubMed.
- E. D. Hedegård, S. Knecht, J. S. Kielberg, H. J. A. Jensen and M. Reiher, J. Chem. Phys., 2015, 142, 224108 CrossRef PubMed.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS PubMed.
- L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Acc. Chem. Res., 2016, 50, 66–73 CrossRef PubMed.
- S. Keller, M. Dolfi, M. Troyer and M. Reiher, J. Chem. Phys., 2015, 143, 244118 CrossRef PubMed.
- G. K.-L. Chan, A. Keselman, N. Nakatani, Z. Li and S. R. White, J. Chem. Phys., 2016, 145, 014102 CrossRef PubMed.
- Ö. Legeza, R. Noack, J. Sólyom and L. Tincani, in Computational Many-Particle Physics, Springer, 2008, pp. 653–664 Search PubMed.
- S. Knecht, E. Hedegård, S. Keller, A. Kovyrshin, Y. Ma, A. Muolo, C. Stein and M. Reiher, Chimia, 2016, 70, 244 CrossRef CAS PubMed.
- G. K.-L. Chan and D. Zgid, Annu. Rep. Comput. Chem., 2009, 5, 149–162 CAS.
- K. H. Marti and M. Reiher, Z. Phys. Chem., 2010, 224, 583–599 CrossRef CAS.
- K. H. Marti and M. Reiher, Phys. Chem. Chem. Phys., 2011, 13, 6750–6759 RSC.
- R. Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang and G. K.-L. Chan, J. Chem. Phys., 2015, 142, 034102 CrossRef PubMed.
- S. Szalay, M. Pfeffer, V. Murg, G. Barcza, F. Verstraete, R. Schneider and Ö. Legeza, Int. J. Quantum Chem., 2015, 115, 1342–1391 CrossRef CAS.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, 2014 Search PubMed.
- S. Vancoillie, M. G. Delcey, R. Lindh, V. Vysotskiy, P. Å. Malmqvist and V. Veryazov, J. Comput. Chem., 2013, 34, 1937–1948 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos and L. Gagliardi, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- S. Keller and M. Reiher, J. Chem. Phys., 2016, 144, 134101 CrossRef PubMed.
- S. Ghosh, C. J. Cramer, D. G. Truhlar and L. Gagliardi, Chem. Sci., 2017, 8, 2741–2750 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- R. K. Carlson, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 4077–4085 CrossRef CAS PubMed.
- Y. Ma, S. Knecht, S. Keller and M. Reiher, J. Chem. Theory Comput., 2017, 13, 2533–2549 CrossRef CAS PubMed.
- B. Hajgató, M. Huzak and M. S. Deleuze, J. Phys. Chem. A, 2011, 115, 9282–9293 CrossRef PubMed.
- Y. Yao, K.-W. Sun, Z. Luo and H. Ma, J. Phys. Chem. Lett., 2018, 9, 413–419 CrossRef CAS PubMed.
- J. Fosso-Tande, T.-S. Nguyen, G. Gidofalvi and A. E. DePrince III, J. Chem. Theory Comput., 2016, 12, 2260–2271 CrossRef CAS PubMed.
- Y. Kawashima, T. Hashimoto, H. Nakano and K. Hirao, Theor. Chem. Acc., 1999, 102, 49–64 Search PubMed.
- H. Angliker, E. Rommel and J. Wirz, Chem. Phys. Lett., 1982, 87, 208–212 CrossRef CAS.
- W. Siebrand, J. Chem. Phys., 1967, 47, 2411–2422 CrossRef CAS.
- J. B. Birks, J. Luminescence, 1970, 1–2, 154–165 CrossRef.
- J. Schiedt and R. Weinkauf, Chem. Phys. Lett., 1997, 266, 201–205 CrossRef CAS.
- Y. Kurashige and T. Yanai, Bull. Chem. Soc. Jpn., 2014, 87, 1071–1073 CrossRef CAS.
- J. B. Schriber, K. P. Hannon and F. A. Evangelista, arXiv preprint arXiv:1808.09403, 2018.
- J. Burgos, M. Pope, C. E. Swenberg and R. Alfano, Phys. Status Solidi B, 1977, 83, 249–256 CrossRef CAS.
- D. Ma, G. Li Manni and L. Gagliardi, J. Chem. Phys., 2011, 135, 044128 CrossRef PubMed.
- W. Flicker, O. Mosher and A. Kuppermann, Chem. Phys. Lett., 1975, 36, 56–60 CrossRef CAS.
- E. Van Veen, Chem. Phys. Lett., 1976, 41, 540–543 CrossRef CAS.
- J. H. Moore Jr, J. Phys. Chem., 1972, 76, 1130–1133 CrossRef.
- A. Merer and R. S. Mulliken, Chem. Rev., 1969, 69, 639–656 CrossRef CAS.
- O. A. Mosher, W. M. Flicker and A. Kuppermann, Chem. Phys. Lett., 1973, 19, 332–333 CrossRef CAS.
- W. M. Flicker, O. A. Mosher and A. Kuppermann, Chem. Phys. Lett., 1977, 45, 492–497 CrossRef CAS.
- P. M. Zimmerman, J. Phys. Chem. A, 2017, 121, 4712–4720 CrossRef CAS PubMed.
- D. Zhang, Z. Qu, C. Liu and Y. Jiang, J. Chem. Phys., 2011, 134, 024114 CrossRef PubMed.
- K. Nakayama, H. Nakano and K. Hirao, Int. J. Quantum Chem., 1998, 66, 157–175 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Absolute energies in hartrees, timings, geometry comparison, and Cartesian coordinates. See DOI: 10.1039/c8sc03569e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |