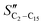The pivotal role of an interconnected cellular conductive structure to manage heat removal in compact Fischer–Tropsch fixed-bed reactors

Abstract

Fischer–Tropsch synthesis is a strongly exothermic process wherein T-management is crucial. In this work, we demonstrate that diluting the catalyst bed with fragments of a conductive material does not grant the same excellent T-control as when the catalyst is randomly packed into a connected cellular structure made of the same material.

---

1. Introduction

Although Fischer–Tropsch synthesis (FTS) was discovered in the early 20th century, the research activity on this process is still intense.¹ This is primarily because FTS allows the conversion of any carbon source (coal, natural gas, biomass or waste) into liquid hydrocarbons via synthesis gas as an intermediate. Consequently, it is a process of fundamental importance for energy systems based on liquid fuels. In particular, the interest in the so-called low temperature Fischer–Tropsch (LTFT) synthesis over Co-based catalysts in compact reactors has considerably grown in the last decades, in view of the possibility to monetize both associated and remote natural gas fields, currently untapped due to the bad economics.

LTFT is a highly exothermic reaction with a standard reaction enthalpy of −165 kJ mol_CO⁻¹. Heat removal is thus a key issue in technical reactors.^1,2

Fixed-bed and slurry reactors are used for FTS on the industrial scale. In slurry bubble column reactors (SBCRs), the well-mixed liquid phase results in nearly isothermal operation. However, SBCRs have a low specific productivity, which makes them convenient only on the large scale. On the other hand, packed-bed reactors (PBRs) are appreciated for their plug-flow behavior, which allows high conversions per pass. However, the scale down of these reactors is severely limited by their poor convective heat removal at low gas velocities. This leads, indeed, to non-isothermal operation of the reactors. In turn, the presence of relevant radial T-gradients negatively affects the catalyst selectivity, since the product distribution is shifted towards undesired light hydrocarbons, and, in the worst case, may lead to the onset of thermal runaway. Such an issue may be overcome by recycling a considerable fraction of unreacted gases and of the liquid reaction products at high flow rates. However, this increases pressure drops and makes the reactor less flexible for downscaling.³

In line with these premises, the design of a compact scale (<3000 BPD) reactor technology for FTS is a pivotal challenge. Recently, the adoption of highly conductive honeycomb structures, packed with micro-pelletized catalysts, within externally cooled multitubular fixed-bed reactors, was proposed.⁴ In this way, the heat transfer is strongly enhanced in compact reactors because the primary radial heat exchange mechanism is changed from convection to conduction within the thermally connected solid matrix of the honeycomb monolith.⁴

Besides packed honeycomb monoliths, other washcoated metallic structures with different geometries, such as micromonoliths⁵ and foams,^6,7 as well as micro-fibrous entrapped catalysts^8,9 were proposed for FTS. All these metallic structures exhibit an effective temperature control, but with the foremost limit of low catalyst inventory.^5–9

Closed-cross flow structures packed with catalyst pellets^10,11 were also proposed, claiming an increase of the C₅₊ productivity with respect to the aforementioned washcoated structures. However, these structures still exploit a flow-dependent heat transfer mechanism,^10,11 which implies a less flexible operation of the reactor.

As an alternative to packed honeycomb monoliths, we have recently demonstrated the possibility of enhancing the heat transport properties of FTS packed bed reactors through the adoption of highly conductive open-cell metal foams packed with catalyst pellets.¹² Open-cell foams are particularly attractive because they have high porosity, low density and high mechanical strength. They exploit the same conductive heat transfer mechanism of the monolithic substrates but, in addition, they have the advantage of enabling radial mixing within their structures, thus enhancing both heat transfer and flow uniformity.^13,14 As in the case of packed monoliths, a point of strength of the open-cell foams is the possibility of packing catalyst particles in the void cavities, which overcomes the inherently limited catalyst inventory of washcoated structured reactors.¹²

A question often raised on this reactor concept concerns the actual advantage of packing the catalyst within an interconnected conductive structure over simply diluting the catalyst bed with “particles” made of a conductive material.

To date, this aspect has only been investigated through numerical simulations of the thermal properties of SiC extrudates compared to those obtained with SiC foams.¹⁵ The authors reported that the use of a foam support enabled a better heat control than the extrudates, with a less pronounced effect on the yield of C₅₊ species. This was explained by the dilution of the heat generated in the bed volume due to the higher void fraction of the foam. In this regard, the authors attributed a strong effect to the contact between the foam and the reactor wall that governed the wall heat transfer coefficient.¹⁵

Based on this background, the present work aims at experimentally clarifying such an issue by comparing the performances of three lab-scale FTS reactors using different configurations: (i) a conventional packed-bed reactor diluted with low-conductivity particles, (ii) a packed Al-foam reactor, and (iii) a packed-bed reactor diluted with finely crushed fragments of the Al foam.

2. Experimental

The Co/Pt/Al₂O₃ catalyst used in this study is a Pt-promoted Co-based catalyst supported on γ-Al₂O₃ pellets (d_pellet = 300 μm) stabilized with Co-aluminate species. More details on the catalyst preparation method as well as on the chemical and physical properties of the Co/Pt/Al₂O₃ catalyst can be found in ref. 16.

The three reactor configurations investigated in this study are schematically shown in Fig. 1: (i) packed-bed reactor (PBr), (ii) packed-foam reactor (PFr) and (iii) crushed-foam reactor (CFr).

Fig. 1 Schematics of the (a) packed-foam, (b) packed-bed and (c) crushed-foam reactor configurations. The positions of the thermocouples (T_(r=0), T_(r=R/2) and T_ext) are also shown.

The open-cell foam used as the reactor internal in the PFr was purchased from ERG Aerospace. It is made of aluminum (Al6101) with a nominal pore density of 40 ppi (void fraction 0.908; average cell diameter 2 mm). The effective radial conductivity (k_er) of the foam estimated according to the Lemlich model¹⁷ is 6.68 W m⁻¹ K⁻¹: in comparison, the estimated k_er for the packed bed according to Specchia¹⁸ is 0.29 W m⁻¹ K⁻¹, i.e. over 20 times smaller. The shape of the foam is cylindrical with a length of 4 cm and a diameter of 2.78 cm, which matches the nominal internal diameter of the stainless-steel FT reactor used in the activity test, so as to limit the gap between the structure and the tube.

Two axial through-holes of 0.32 cm diameter located at the centerline of the structure (i.e. r = 0) and 6.95 mm away from the center in a radial position (i.e. r = R/2) are obtained by drilling the foam by the electrical discharge machining (EDM) technique. Both these channels are suitable for the insertion of the stainless steel thermowells (1/8′′ O.D.) protecting the sliding J-type thermocouples (0.5 mm O.D.) (Fig. 1).

Once the foam is loaded into the reactor tube and the thermowells are positioned in the foam, the system is packed as schematically shown in Fig. 1a. To this aim, ≈4.6 g of α-Al₂O₃ pellets (d_pellet = 300 μm) are poured into the structure, thus forming a ≈1.05 cm deep layer, then 7.2 g of Co/Pt/Al₂O₃ catalyst diluted with 1.1 g of α-Al₂O₃ are poured into the foam, thus covering ≈1.9 cm of the structure. Eventually, ≈4.6 g of α-Al₂O₃ pellets (d_pellet = 300 μm) are packed into the structure so as to fill the last ≈1.05 cm of the foam.

In the case of the PBr (Fig. 1b), the same amount of catalyst in the PFr (7.2 g) is loaded into the same reactor, but diluted with a large amount of α-Al₂O₃ (≈12.2 g), so as to compensate for the absence of the foam and to reach a catalyst bed length (4 cm) equal to the length of the packed foam (Fig. 1).

Finally, also in the case of the CFr system (Fig. 1c), we have used the same amount of catalyst (7.2 g), diluted with 10.3 g of α-Al₂O₃ and 0.3–0.4 cm-sized crushed fragments of the foam. The weight ratio of the catalyst mass to the Al fragment mass is 1.2 : 1, i.e. equal to the catalyst to foam weight ratio in the PFr. The catalyst bed length is 4 cm, as in the case of the PBr configuration.

Notably, the average catalyst volumetric density of the reactors, defined as the ratio between the catalyst mass and the volume occupied by the catalyst bed, is 0.64 g cm⁻³ for the PFr and 0.30 g cm⁻³ for both the PBr and CFr.

Temperature profiles are recorded longitudinally across the catalytic beds using the two J-type thermocouples sliding inside the two stainless steel thermowells located in the foam (Fig. 1). The temperature measured at the centerline and at the half radius is indicated as T_(r=0) and T_(r=R/2), respectively.

In the following, ΔT_cat is the difference between the maximum and the minimum axial bed catalyst temperature, whereas ΔT_rad is the radial temperature gradient, defined as the difference between T_(r=0) and T_(r=R/2).

A third thermocouple, anchored on the outer surface of the reactor tube (T_ext) in correspondence to the mid-point of the catalyst bed, is also present (Fig. 1). This allows the estimation of an effective temperature difference for heat exchange (ΔT_ext), calculated as the difference between the temperature reading at the center of the catalyst bed (T_(r=0)) and T_ext. Notably, ΔT_ext was systematically positive, indicating that the oven works as a heat sink and not as a heat source for all the three tested reactor configurations.

All the reactor configurations are tested in FTS in a fully automated lab-scale rig¹² equipped with a stainless-steel tubular fixed-bed reactor (2.78 cm I.D., 85 cm long) inserted in a three-zone split tube furnace (Carbolite TVS/600).

Catalytic tests are performed under FTS conditions relevant to industrial operation: T = 180–240 °C, P = 25 bar, H₂/CO inlet molar ratio = 2.0, GHSV = 6410 cm³ (STP) h⁻¹ g_cat⁻¹ and inert gasses (N₂ + Ar) in the feed = 24 vol%.

Prior to exposing the sample to syngas, the catalyst is reduced in situ at 400 °C (heating ramp = 2 °C min⁻¹) for 17 h using 5000 cm³ (STP) h⁻¹ g_cat⁻¹ of H₂ at atmospheric pressure.

The process conditions are never changed before reaching steady-state conditions for both the catalyst activity and selectivity. In order to verify the achievement of steady state conditions, multiple on-line GC analyses are carried out at different time-on-steam, so as to assess the reactant conversion and the C₁–C₄₉ product selectivity (C₁–C₄₉ paraffins, C₂–C₁₇ olefins, and CO₂). The data are considered steady when the CO conversion and the selectivity to the main FTS products vary within less than 3% in 24 h.

The volumetric heat duty (Q) is calculated according to eqn (1):

Q[kW m⁻³] = −ΔH⁰_r·Fⁱⁿ_CO·X_CO/V_cat (1)

where ΔH⁰_r is the standard reaction enthalpy set to −165 kJ mol_CO⁻¹, Fⁱⁿ_CO is the molar flow rate of CO fed into the reactor, X_CO is the CO conversion and V_cat is the volume occupied by the catalyst bed in the reactor. The latter is calculated from the reactor diameter (2.78 cm) and the catalyst bed height (1.9 cm for the PFr and 4 cm for both the PBr and CFr configurations, Fig. 1).

3. Results and discussion

Fig. 2 shows the CO conversion measured at different reaction temperatures in the PFr, PBr and CFr. The results obtained with both the PFr and PBr are similar to those obtained in ref. 12, in line with the fact that the same batch of catalyst is used.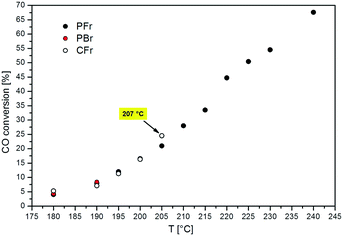

Fig. 2 CO conversion values obtained with the PFr (black circle), PBr (red circle) and CFr (white circle) as a function of the T.o.S. measured at different temperatures.

As clearly shown in Fig. 2, the adoption of the packed-foam allows the operation of the reaction in a wide temperature range spanning from 180 to 240 °C, measuring CO conversions up to 68%. In contrast, the catalyst performance with the conventional packed-bed reactor could be recorded only at 180 and 190 °C, since thermal runaway occurred during the slow temperature ramp from 190 to 195 °C.

This demonstrates the excellent ability of the “highly conductive packed-foam reactor” concept to manage the strong exothermicity of the Fischer–Tropsch reaction.¹² As a matter of fact, almost flat T-profiles are observed with the PFr configuration at all the temperatures investigated.¹²

With the PFr, limited axial and radial T-gradients (ΔT_cat (240 °C) = 6.4 °C and ΔT_rad (240 °C) = 1.0 °C) are obtained even in the presence of a large volumetric heat duty (Q (240 °C) = 1428 kW m⁻³). In contrast, in the case of the PBr, a ΔT_cat of around 9 °C and a ΔT_rad of 2.1 °C are obtained at the maximum temperature investigated of 190 °C (Q = 79 kW m⁻³).

As shown in Fig. 2, the addition of the crushed aluminum foam in the catalyst bed (CFr configuration) improves the thermal stability of the reactor with respect to the PBr. As a matter of fact, we were able to assess the performance of the CFr configuration up to a higher temperature (205 °C), corresponding to a CO conversion of 25% (volumetric power release of 251 kW m⁻³). However, the CFr does not reach the outstanding performance of the PFr, since a thermal runaway occurred during the T-ramp above 205 °C. Already at the temperature of 205 °C, the reactor is rather unstable, as indicated by the fact that the temperature of the catalyst bed is around 2 °C above the set point.

This can be explained by looking at the temperature profiles in the CFr, which reveal the presence of hot-spots along the catalyst bed at all the investigated temperatures (Fig. 3). In particular, the axial temperature gradient (ΔT_cat) increases on increasing the reaction temperature: ΔT_cat is found to be 3.8, 4.7, 6.8, 14.5 and 21.8 °C when the temperature is set to 180, 190, 195, 200 and 205 °C, respectively. Notably, the ΔT_cat values measured with the PBr at 180 and 190 °C (5 and 9 °C, respectively) are significantly higher than those obtained with the CFr at similar temperatures.

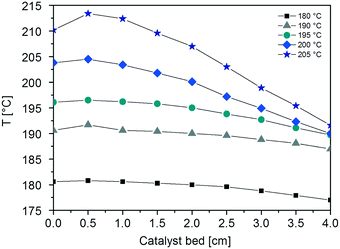Fig. 3 Axial temperatures profiles measured at different temperatures (T = 180, 190, 195, 200 and 205 °C) of the CFr by sliding the T_(r=0) thermocouple.

Also, the radial temperature gradients (ΔT_rad) measured with the CFr are lower than those obtained with the PBr (ΔT_rad = 0.8 °C at 180 °C and 2.1 °C at 190 °C). Indeed, ΔT_rad values of 0.1, 0.4, 0.8, 1.4 and 2.7 °C are obtained at 180, 190, 195, 200 and 205 °C, respectively.

This is in line with the fact that the onset of the thermal runaway in the CFr configuration occurs at higher temperatures than those in the PBr.

The volumetric heat duty (Q, eqn (1)) calculated during the FTS experiments carried out on the PFr, PBr and CFr configurations as a function of the external temperature difference (ΔT_ext) is shown in Fig. 4.

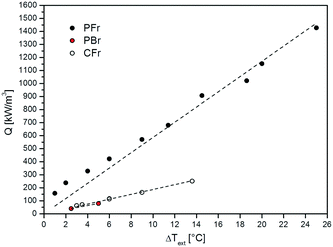Fig. 4 Volumetric heat duty (Q) calculated during FTS experiments at different temperatures as a function of the external (ΔT_ext) temperature difference.

A linear trend is observed, which proves that: i) the oven is acting as a heat sink and not as a heat source, since the heating elements are set to temperatures well below T_(r=0) and T_ext; ii) ill-defined heat exchange conditions from the reactor to the oven do not result in major anomalies of the heat transfer coefficient when using the temperature of the external skin of the reactor tube as the reference heat sink.

Notably, the PFr configuration strongly outperforms both the PBr and CFr configurations, indicating the dominant role of the highly conductive thermally connected solid matrix in managing the heat removal issue in FTS. In any case, the CFr shows a slightly better behavior than the PBr, with slightly lower external T-gradients (ΔT_ext) at a similar volumetric power heat release.

The results obtained with the CFr are clear evidence of the fact that diluting the catalyst bed with fragments of a conductive material leads only to a slight improvement of the heat transfer performance of the conventionally used packed-bed reactor configuration.

Such an enhancement is appreciable due to the very low flow velocity (v = 0.02 m s⁻¹) under the present test conditions, which results in a very low particle Reynolds number (Rep = 0.16 and 1.8 referred to the catalyst particles and to the aluminum fragments, respectively). Under such conditions, the static contribution to the effective radial conductivity of the packed bed is still important with respect to the normally dominant convective one.¹⁹ On the other hand, the high conductivity of the Al fragments cannot be fully exploited since the main resistance is associated with the multiple crossings of contact points between particles along the heat transfer pathways.²⁰ This is not the case of the PFr configuration where once the heat is transferred from the catalyst particles to the foam struts across a short distance path (dc = 2 mm), it is then dissipated through the low resistance network provided by the interconnected structure of the foam, thus allowing the FT reaction to run under more severe conditions (i.e. high CO conversion and large heat duty) with an outstanding T-control.

The FT product distribution obtained with the CFr configuration was measured at two distinct temperatures, 195 and 200 °C. The selectivity to CH₄ (S_CH4) is 12% and 14% at 195 °C and 200 °C, respectively. The selectivity to C₅₊ (S_C5+) at the same temperatures is 75% and 70%. Finally, the selectivities to olefins 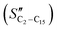and paraffins (S_C2–C15) in the C₂–C₁₅ range are 13% and 39% at 195 °C and 11% and 45% at 200 °C, respectively.

The chain growth probability estimated by considering the hydrocarbons with more than 15 carbon atoms (α_C15+) is 0.883 at 195 °C and 0.872 at 200 °C. These results are in line with the fact that the hydrogenation rate is promoted by increasing temperature, thus favoring the termination step over the growth step in the FTS chain growth mechanism.²¹

Table 1 compares the product distribution obtained with the CFr and that measured with the PFr reported in ref. 12 at similar temperatures (195 and 200 °C).

Table 1 Selectivity to the main FTS products calculated at different temperatures (at 195 and 200 °C) with the CFr and PFr¹²

	T [°C]	S CH4 [%]	[%]	S C2–C15 [%]	S C5+ [%]	α C15+
CFr	195	12	13	39	75	0.883
PFr	195	8	19	35	77	0.884
CFr	200	14	11	45	70	0.872
PFr	200	11	15	41	72	0.874

---

The selectivity to CH₄ is higher in the CFr than that in the PFr. Also, the selectivities to C₂–C₁₅ olefins and paraffins are influenced by the reactor design. In particular, the 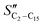(olefin selectivity) measured in the CFr is lower than that in the PFr, with the opposite trend for the S_C2–C15. The selectivity to C₅₊ is slightly lower in the CFr than that in the PFr configuration. In line with the small changes of the selectivity to long-chain hydrocarbons, the chain growth probability (α_C15+) estimated by considering the hydrocarbons with more than 15 carbon atoms is essentially unaffected (Table 1).

We believe that the differences noted in terms of product selectivity are mostly related to the presence of hot-spots along the catalyst bed in the case of the CFr (Fig. 3), which are known to negatively affect the FTS product distribution. In this regard, slightly higher temperatures favor the formation of lower molecular weight molecules as well as saturated products, with a less evident effect on the chain growth probability.

4. Conclusions

The present results are a direct indication that the heat exchange in packed-bed reactors can be enhanced to some extent by diluting the bed of catalyst particles with fragments of a conductive material. However, this is by far not sufficient to match the superior heat transfer performance of the packed-foam reactor configuration. Indeed, during our FTS runs, the onset of the thermal runaway in the CFr was only delayed to higher temperatures than that in the PBr, but could not be avoided.

This is also confirmed by looking at both the axial and the radial temperature gradients of the CFr, which were significantly higher than those observed in the PFr, at similar temperatures. Moreover, the presence of hot-spots along the catalyst bed in the CFr negatively affected the process selectivity, shifting the product distribution towards the undesired short-chain hydrocarbons.

As a whole, this communication evidences the necessity of an interconnected structure to fully exploit the conductive heat transfer mechanism, which is solely responsible for the enhancement of heat transfer observed in the case of the packed foam. Such an interconnected structure can be packed with catalyst pellets providing a technological solution which allows the FTS to run in compact reactors under severe conditions (i.e. high CO conversion and large heat duty), while keeping a remarkably effective temperature control.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research leading to these results has received funding from the European Research Council under the European Union's Horizon 2020 Research and Innovation Program (Grant Agreement no. 694910/INTENT). The authors would like to thank Dr. Mauro Bracconi for the schematics of the reactor technologies reported in Fig. 1.

References

1. R. Guttel and T. Turek, Energy Technol., 2016, 4, 44–54.
2. C. G. Visconti, E. Tronconi, G. Groppi, L. Lietti, M. Iovane, S. Rossini and R. Zennaro, Chem. Eng. J., 2011, 171, 1294–1307.
3. C. G. Visconti, E. Tronconi, L. Lietti, G. Groppi, P. Forzatti, C. Cristiani, R. Zennaro and S. Rossini, Appl. Catal., A, 2009, 370, 93–101.
4. M. Iovane, R. Zennaro, P. Forzatti, G. Groppi, L. Lietti, E. Tronconi, C. G. Visconti, S. Rossini and E. Mignone, WO Pat., 2010/130399, 2010.
5. D. Merino, O. Sanz and M. Montes, Chem. Eng. J., 2017, 327, 1033–1042.
6. L. C. Almeida, F. J. Echave, O. Sanz, M. A. Centeno, G. Arzamendi, L. M. Gandìa, E. F. Sousa-Aguiar, J. A. Odriozola and M. Montes, Chem. Eng. J., 2011, 167, 536–544.
7. M. Lacroix, L. Dreibine, B. de Tymowski, F. Vigneron, D. Edouard, D. Begin, P. Nguyen, C. Pham, S. Savin-Poncet, F. Luck, M. J. Ledoux and C. Pham-Huu, Appl. Catal., A, 2011, 397, 62–72.
8. M. Sheng, H. Yang, D. R. Cahela, W. R. Yantz Jr., C. F. Gonzales and B. J. Tatarchuck, Appl. Catal., A, 2012, 445–446, 143–152.
9. M. Sheng, H. Yang, D. R. Cahela and B. J. Tatarchuck, J. Catal., 2011, 281, 254–262.
10. N. Hooshyar, D. Vervloet, F. Kapteijn, P. J. Hamersma, R. F. Mudde and J. R. van Ommen, Chem. Eng. J., 2012, 207–208, 865–870.
11. B. Kaskes, D. Vervloet, F. Kapteijn and J. R. van Ommen, Chem. Eng. J., 2016, 283, 1465–1483.
12. L. Fratalocchi, C. G. Visconti, G. Groppi, L. Lietti and E. Tronconi, Chem. Eng. J., 2018, 349, 829–837.
13. C. G. Visconti, G. Groppi and E. Tronconi, Catal. Today, 2016, 273, 178–186.
14. G. Groppi, E. Tronconi, C. G. Visconti, A. Tasso and R. Zennaro, WO Pat., 2015/033266, 2015.
15. R. Philippe, M. Lacroix, L. Dreibine, C. Pham-Huu, D. Edourard, S. Savin, F. Luck and D. Schweich, Catal. Today, 2009, 147S, S305–S312.
16. L. Fratalocchi, L. Lietti, C. G. Visconti, N. Fischer and M. Claeys, Catal. Sci. Technol., 2019, 9, 3177–3192.
17. R. Lemlich, J. Colloid Interface Sci., 1978, 64, 107–110.
18. V. Specchia, G. Baldi and S. Sicardi, Chem. Eng. Commun., 1980, 4, 361–380.
19. A. G. Dixon, Can. J. Chem. Eng., 2012, 90, 507–527.
20. N. Wakao and K. Kato, J. Chem. Eng. Jpn., 1969, 2, 24–33.
21. V. R. R. Pendyala, W. D. Shafer, G. Jacobs and B. H. Davis, Catal. Lett., 2014, 144, 1088–1095.

---