Human bone probed by neutron diffraction: the burning process

Abstract

The first neutron diffraction study of human burned bone is reported, aiming at a comprehensive elucidation of the heat-induced bone diagenesis process. Chemical and crystallinity changes were probed in different types of bone (femur, humerus and tibia) upon heating to different maximum temperatures (from 400 to 1000 °C, under aerobic conditions). Fourier transform infrared spectroscopy has provided valuable complementary information. Noticeable crystallographic and domain size variations were detected, mainly between 700 and 900 °C, the high temperature interval (>700 °C) corresponding to an organized, highly symmetric inorganic bone matrix, virtually devoid of carbonates and organic constituents, while the lower range (<700 °C) revealed a considerably lower crystallinity associated with the presence of carbonates, lipids and collagen. This work contributes to a better understanding of heat-induced changes in bone and is therefore relevant for archaeology, biomaterials and forensic science.

---

Introduction

Although the (bio)chemistry of human bone has been extensively studied regarding archaeological, forensic and clinical scenarios, there is still a lot to be understood. Bone is a heterogeneous tissue composed mainly of type I collagen fibrils mineralized with small crystals of bioapatite (BioHAp), a carbonated substituted form of hydroxyapatite (HAp, Ca₁₀(PO₄)₆(OH)₂) in continuous lifetime renewal.^1–3 After death, the organic components of bone are gradually lost and the inorganic component becomes exposed to the environment, undergoing chemical changes that may give information on post mortem events. These taphonomic variations replicate some of the changes experienced by skeletal remains during heat exposure which are extremely important for their forensic and archaeological examination, to retrieve information on the circumstances of death, and on the biological profile of the deceased. Ultimately, this may contribute to achieve positive identifications in forensic settings and to outline funerary practices of past populations.

The analysis of bones affected by burning events causes serious problems, as heat induces considerable changes in the skeleton (e.g. variations in size), which interfere with the reliability of the available metric techniques that are based on references from unburned bones.^4–9 Heat-induced diagenetic variations in bone have been assessed by several methods, optical (Fourier transform infrared spectroscopy (FTIR) and Raman) and neutron vibrational spectroscopy (inelastic neutron scattering (INS)) having been established as powerful techniques for these types of study.^{4–7,10–20} FTIR spectroscopy in attenuated total reflectance mode (FTIR-ATR) is particularly suitable for a daily basis analysis of archaeological or forensic bones since it is easily accessible, inexpensive, fast and requires no specific sample preparation, yielding an accurate chemical and structural profile unique for each sample. Hence, extensive work has been performed by FTIR-ATR on heat-prompted changes in human bone.^{4–6,8,15,19,21–26} These analyses rely on the calculation of spectroscopic indices, based on specific biomarker bands, that should deliver the chemical composition of the bone as well as its crystallinity details.

Neutron diffraction techniques are particularly suitable for probing bone because neutrons are strongly scattered by hydrogen. This means that hydrogen is observable even in the presence of heavy metals. Hence, they are able to observe changes in the H-bonding pattern within bone's inorganic framework previously suggested by neutron spectroscopy.^2,27 However, neutron diffraction has been rarely applied to the investigation of human bone, only a few studies being found in the literature: on foot bones and subchondral trabecular bone,^28,29 on collagen within bone's hydroxyapatite matrix³⁰ and on osteoporosis in compact female bone.³¹ Moreover, of the reported work on animal bone,^{2,27–30,32,33} only two probed samples that were studied after heating, but only to one temperature (625 °C). This was done with a view to remove the bone's organic constituents,^28,33 but without any assessment of the impact of temperature on bone's crystallinity. X-ray diffraction studies are, however, frequently applied.^{13,22,34–38}

Following several successful studies in burned human bone (400 to 1000 °C) by combined FTIR, Raman and INS.^{4–6,8,21,26} The present study aimed to complement these spectroscopic results with diffraction data leading to a more detailed interpretation of the chemical and microcrystallinity variations already revealed spectroscopically, that will identify skeletal remains subject to unknown heating conditions. Bone's chemical and crystallinity changes were probed, upon an aerobic burning process at different maximum temperatures (from 400 to 1000 °C, chosen according to those reached in fire and explosion settings). To the best of the authors' knowledge, this was the first neutron diffraction study of human burned bone using a wide temperature range. The information thus gathered on the heat-induced changes in bone is expected to greatly contribute to a more accurate identification of archaeological and forensic human skeletal remains, as well to an improved design of biomaterials from bone (e.g. for regenerative medicine).

Experimental

Materials

The bone samples currently analysed belong to unidentified human skeletons housed at the Laboratory of Forensic Anthropology of the University of Coimbra. These correspond to unclaimed skeletons from the cemetery of Capuchos (Santarém, Portugal) which were donated for research, and therefore have the same origin and burial environment as the identified skeletons of the 21^st Century Identified Skeletal Collection.³⁹ Two femora (F), one humerus (H) and one tibia (T) bones from two different skeletons were analysed: CC_NI_41 and CC_NI_42, the naming convention is: cemetery of Capuchos (CC), unidentified (NI) skeletons 41 and 42 (hereafter denominated as Sk41 and Sk42). No replicates were performed due to limited sample resources. A skeleton human collection as rare as the one the authors had access to must be preserved (without compromising scientific advances).

The highly crystalline SRM 2910b calcium hydroxyapatite (Ca₁₀(PO₄)₆(OH)₂, Ca/P = 1.67, crystallinity index = 7.91) from NIST, Gaithersburg/MA (USA) (NIST) was used as a reference material.

Sample preparation and controlled bone burning

Bone sections from femora of Sk41 and Sk42 (F41 and F42), humerus and tibia of Sk42 (H42 and T42, respectively) were obtained with a Dremel mini-saw electric tool and contaminants from the outer layer were removed by gentle sanding. The fragments were then burned under controlled conditions, at 400, 500, 600, 700, 800, 900 and 1000 °C for 120 min burns, counting from the moment the maximum chosen temperature was reached, at a heating rate ranging from 3.33 to 8.33 °C min⁻¹ (aerobic burning/combustion). An electric muffle furnace was used (Barracha model K-3, manufactured by Barracha Lda., Leiria, Portugal), with an automatic programmer with digital temperature indicator, allowing programmed start-up and automatic heating speed variation. The temperature range chosen – 400 to 1000 °C – allowed us to probe different, important heat-degradation events such as water loss, pyrolysis of the organic component, changes in porosity and increase in crystal size.⁷ A two-hour period for all burning experiments allowed us to have two controlled variables: maximum temperature and burn duration. The temperature was measured with a type K probe (negative/nickel-aluminium, positive/nickel-chrome) following norm IEC 60584-2. The bones were not removed from the furnace after the burning process – they were left to cool overnight in the furnace, and removed only when at room temperature. After burning, the bones were ground followed by sieving (mesh size of 400 μm), yielding 6–10 g of each sample. (F41_500 °C, T42_400 °C, H42_400 °C, H42_500 °C, H42_600 °C and H42_700 °C were not measured due to lack of beam time).

Neutron diffraction

The time-of-flight (TOF) diffraction data were collected by the General Materials Diffractometer (GEM)⁴⁰ at the ISIS Pulsed Neutron and Muon Source of the Rutherford Appleton Laboratory (UK [GEM]), within the scattering angle range 8° to 170°.

The GEM powder diffractometer uses a polychromatic beam with neutron wavelengths ranging from 0.2 to 3.5 Å. For the present experiments, the powder samples (5–8 g) were loaded into vanadium containers of 11 mm diameter and 0.15 mm wall thickness. The containers were installed on a sample changer and measured under vacuum at room temperature. The beam size was 20 × 40 mm² (width × height). The counting time was about 1 h per sample.

Data sets were normalized and ‘focused’ using the MANTID software package⁴¹ with data from a solid V3% Nb rod collected under the same experimental conditions. This normalization procedure takes into account the spectral distribution of neutrons and provides a correction for efficiency variations of individual detector elements. The data focusing provides a grouping of the diffraction data into six histograms, i.e. diffraction patterns corresponding to average 2θ angles between 10° (Hist#1) and 155° (Hist#6), with normalized counts versus d-spacing.

FTIR-ATR

FTIR-ATR spectra were acquired for the powdered bone samples using a Bruker Optics Vertex 70 FTIR spectrometer purged by CO₂-free dry air and a Bruker Platinum ATR single reflection diamond accessory. A Ge on KBr substrate beamsplitter with a liquid nitrogen-cooled wide band mercury cadmium telluride (MCT) detector for the mid-IR interval (400–4000 cm⁻¹).

Each spectrum was the sum of 128 scans, at 2 cm⁻¹ resolution, and the 3-term Blackman–Harris apodization function was applied. Under these conditions, the wavenumber accuracy was better than 1 cm⁻¹. The spectra were corrected for the frequency dependence of the penetration depth of the electric field in ATR (considering a mean reflection index of 1.25) using the Opus 7.2 spectroscopy software.

Neutron diffraction data analysis

The Rietveld method of analysis of neutron diffraction data was performed with the software GSAS-EXPGUI,^42,43 using the reference structures of carbonated hydroxyapatite characterized by Fleet et al.⁴⁴ (BioHAp, obtained from the American Mineralogist Crystal Structure Database⁴⁵) and hexagonal hydroxyapatite (HAp) characterized by Kay et al.⁴⁶ obtained from the FIZ Karlsruhe – Leibniz Institute for Information Infrastructure (ICSD). LeBail refinements were carried out using GSAS-EXPGUI, using the space group P6₃/m and unit cell of hydroxyapatite. For the Rietveld or LeBail analysis all six GEM histograms were fitted. The GSAS time-of-flight profile function #2 (Ikeda Carpenter- Pseudo-Voigt) was used. The following parameters were refined: scale factors and background polynomials for six histograms; lattice parameters; zero shift parameters; profile parameters, with sig-1 being the linear term of the Gaussian peak width for the Rietveld fits, additionally one linear absorption parameter (function no. 1 in GSAS) and isotropic temperature parameters with constraint values for the same atom type were varied.

Results and discussion

The range of burning temperatures chosen for this work (and previous studies on burned human bones) is intended to span the range of temperatures likely to be encountered in forensic and archaeological scenarios (while conserving the scarce skeletal resources). Within this temperature interval most heat-induced osseous changes are likely to occur. Regarding the burning duration, 2 hours was chosen to be a suitable time lapse, in the light of the main events to be considered in future applications. These include: (i) terrorist attacks, that can actually involve fires even longer than two hours (e.g. those from the Twin Towers attacks went on for several weeks⁴⁷); (ii) house, forest or vehicle fires, which can also go on for this amount of time (e.g. the forest fires in Portugal/Pedrogão Grande (2017) which involved a large number of victims); (iii) funerary cremations, both from present and past populations, that may easily take two or more hours (e.g. Roman cremations often went on for the entire night);^48,49 (iv) archaeological hearths (often found with burnt human skeletal remains), that usually took place for about 2 hours; (v) foul-play destruction of bodies, carried out in actual furnaces (or even improvised ones), takes similar amounts of time.⁵⁰

Neutron diffraction data were measured for the human bone samples after ex situ heating of several sections of each type of bone from 400 °C up to a maximum of 1000 °C, with a view to establish the phases and composition at particular temperatures.

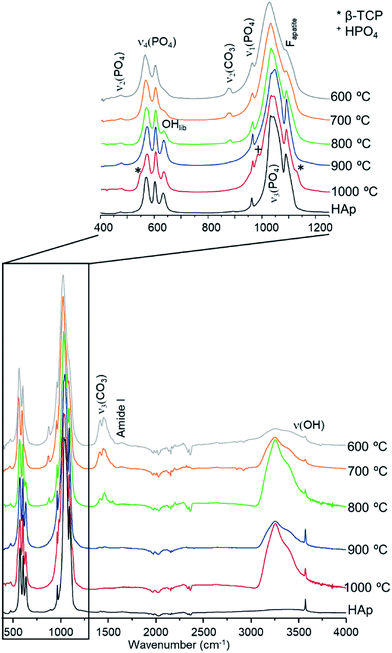
The diffraction patterns obtained for the human femur (F42) are shown in Fig. 1. It is evident that the more noticeable changes occurred within the 700–800 °C temperature range, the pattern of the samples burned at the highest temperatures (900 and 1000 °C) being identical to that of reference hydroxyapatite (HAp). There was a noticeable sharpening of the peaks for higher temperatures as well as the expected shift to larger d-spacing consistent with the thermal expansion of the samples. This behavior was observed for all samples under study, in accordance with previous results obtained from INS and FTIR spectroscopy.^5,6,21,51

Fig. 1 Neutron diffraction patterns (HIST#4) of human femoral sections (F42) burned at 400, 600, 700, 800, 900 and 1000 °C. (reference hydroxyapatite (HAp) is also shown for comparison).

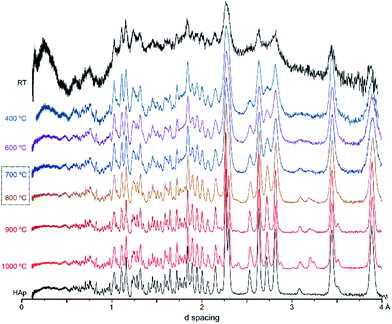
Fig. 2 represents the refinements of the neutron diffraction data measured for tibia sections (T42) burned at high temperatures (800, 900 and 1000 °C). For all samples subjected to 1000 °C, the highly crystalline hydroxyapatite (SRM 2910b from NIST) was used as a reference, and the HAp model by Kay et al.⁴⁶ was considered as a starting model for the least squares refinements. This initial structure (by Kay et al.⁴⁶) was refined against the experimental data to obtain fitting curves. The 800 and 900 °C samples were refined using the data from the highest previous temperature as a model (i.e. data from bone burned at 1000 °C was the reference for the sample burned at 900 °C, while this one was the reference for the sample burned at 800 °C). A good fit was obtained, and the phase model by Kay et al.⁴⁶ appeared to be suitable for these systems.

Fig. 2 Refined neutron diffraction data (Hist#5) for human tibia (T42) burned at 800, 900 and 1000 °C.

A progressive rise in peak intensity was observed as the temperature increased from 800 to 1000 °C. In addition, there was a noticeable decrease in the background as the burning temperature increased, which was due to the reduced incoherent scattering from the lipids, collagen and water that decrease and finally disappeared upon heating. The samples from T42 burned at 900 and 1000 °C displayed features at 2.033, 2.194, 2.375, 2.559 and 2.406 Å (identified with (o) in Fig. 2), which were also present for F41 (burned at 900 and 1000 °C), H42 (at 1000 °C) and F42 (at 900 and 1000 °C) (ESI Fig. S1.1(B)–S1.3†).

These additional features detected for the sections subjected to the highest temperatures may be assigned either to a second inorganic phase or to an impurity. The infrared measurements performed on exactly the same samples clarified this issue. Fig. 3 shows the FTIR data for the T42 sections burned at temperatures above 600 °C (FTIR data for the other samples are in the ESI, Fig. S2.1–S2.3†). The spectra showed some features apart from those ascribed to the standard (unburned) bone constituents, namely at 544 cm⁻¹ (shoulder) and 1125 cm⁻¹ assigned to β-tricalcium phosphate (β-TCP),^20,22 and at 982 cm⁻¹ due to hydrogenphosphate (ν₁(HPO₄²⁻)).⁵ Also, for F42 at 900 °C the ν₁ν₂(PO₄) domain (ca. 900–1100 cm⁻¹) was considerably broadened (ESI Fig. S2.1†) suggesting the existence of signals from additional components that overlapped with the characteristic HAp bands which would be the only ones expected at this high burning temperature. The infrared profiles also revealed the anticipated peak narrowing with increasing temperatures already evidenced in the diffraction measurements, thus allowing the detection of a splitting for the ν^as₃(PO₄) signal at 1031 and 1042 cm⁻¹ (this being a triply degenerate vibrational mode) for all the samples heated at 900 and 1000 °C. As expected, the bands assigned to carbonates B and (A + B), respectively at 1415 and 1450 cm⁻¹, progressively disappeared with incremental heating,^5,6 except for the F42 sample for which some traces of CO₃²⁻ were still detected above 800 °C (as previously found in a FTIR analysis of a large set of modern human bones).

Fig. 3 FTIR-ATR spectra for human tibia (T42) burned from 600 to 1000 °C. (reference hydroxyapatite, HAp, is also shown for comparison. F_apatite refers to fluorapatite. *Identifies the signals assigned to β-TCP and ⁺represents the signals assigned to HPO₄).

The samples burned at temperatures equal to or lower than 700 °C, were clearly shown to be structurally different from those heated at the highest temperatures: the calculated and observed neutron diffraction patterns diverging considerably as the burning temperature decreased (ESI Fig. S1.1 and S1.6†). In fact, the refinement of the data for these samples required a model of an inorganic phase that was different from HAp – an analogue of bioapatite (carbonated form of hydroxyapatite, BioHAp). The presence of A-type carbonates is reported to cause compression of the PO₄³⁻ tetrahedron along the c-axis and expansion of the a [Å] parameters within the lattice^2,52,53 while, B-type carbonates are reported to cause expansion of the c-parameter and compression of a [Å], as well as generation of Ca²⁺ and OH⁻ vacancies.^2,52,53 Consequently, the structure for carbonated hydroxyapatite (BioHAp) available from the American Mineralogist Crystal Structure Database⁴⁵ and characterised by Fleet et al.⁴⁴ was applied. This approach also did not provide a satisfactory fit, as the model and the observed structures did not match (ESI Fig. S1.4†). This is probably due to the high similarity between the two HAp and BioHAp models (ESI Fig. S1.5†), both failing to accurately represent the noticeable chemical and structural differences between the bone samples heated at low and high temperatures (<700 °C vs. >700 °C). Therefore, the final refinement of these samples was performed using the LeBail model, which is less restrictive, by delivering the unit cell and profile parameters but without constraint by the structure factors, i.e. Bragg peak intensities. This allowed us to use the unit cell and symmetry of the HAp model, without using the HAp atom positions and occupancies.

As verified for the higher temperatures, a progressive intensity increase was observed from 400 to 700 °C (Fig. 4), due to the loss of water and organic components within the bone coupled to a growing degree of crystallinity. This was particularly noteworthy between 700 and 800 °C (Fig. 1, 2 and 4), considerable chemical and structural changes having been formerly identified within this temperature interval by vibrational spectroscopic methods.^5,6,21 For d-spacing below 2 Å the diffraction patterns displayed a significant peak overlap due to the large density and widths of the detected features, especially at temperatures lower than 700 °C.

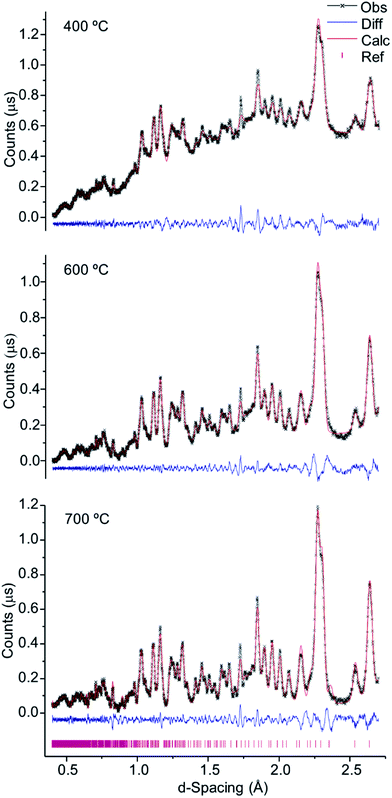Fig. 4 Refined neutron diffraction data (Hist#5) for human tibial sections (T42) burned at 400, 600 and 700 °C.

Table 1 comprises the unit cell parameters and respective estimated standard deviations (esd), χ² and weighted profile R-factors (wR_p) obtained from refinements (corresponding to Fig. 4, S1.1–S1.3 and S1.6†). For the samples displaying an additional inorganic phase or impurity, higher χ² and wR_p values were obtained reflecting an anticipated fit divergence at some point of the refinement.

Table 1 Unit cell parameters with respective standard deviations (esd), χ² and weighted profile R-factors (wR_p) obtained through the Rietveld and LeBail refinements for all bone samples burned from 400 to 1000 °C. (Values for hydroxyapatite were also calculated, for comparison purposes)

Sample	Unit cell parameters				χ^2	wRp
	a [Å]	esd	c [Å]	esd
HAp (NIST reference)	9.4235	9.6 × 10^−5	6.8882	9.20 × 10^−5	3.072	0.0229
F41_1000 °C	9.4193	8.20 × 10^−5	6.8813	8.60 × 10^−5	9.464	0.0363
F41_900 °C	9.4216	1.28 × 10^−4	6.8830	1.26 × 10^−4	11.690	0.0436
F41_800 °C	9.4184	7.40 × 10^−5	6.8846	7.30 × 10^−5	5.716	0.0283
F41_700 °C	9.4220	3.61 × 10^−4	6.8912	2.97 × 10^−4	2.889	0.0215
F41_600 °C	9.4147	5.93 × 10^−4	6.8882	5.02 × 10^−4	3.280	0.0206
F41_400 °C	9.4348	1.04 × 10^−3	6.8845	8.73 × 10^−4	1.813	0.0139
F42_1000 °C	9.4207	7.00 × 10^−4	6.8825	7.00 × 10^−5	6.875	0.0272
F42_900 °C	9.4191	7.00 × 10^−5	6.8840	7.00 × 10^−5	7.856	0.0286
F42_800 °C	9.4204	1.00 × 10^−4	6.8870	1.00 × 10^−4	5.744	0.0279
F42_700 °C	9.4196	3.40 × 10^−4	6.8928	2.80 × 10^−4	2.173	0.0160
F42_600 °C	9.4179	7.85 × 10^−4	6.8900	6.53 × 10^−4	3.929	0.0192
F42_500 °C	9.4108	7.88 × 10^−4	6.8941	6.37 × 10^−4	2.767	0.0152
F42_400 °C	9.4221	7.78 × 10^−4	6.8925	6.00 × 10^−4	9.633	0.0234
H42_1000 °C	9.4211	7.70 × 10^−5	6.8829	7.70 × 10^−5	8.177	0.0314
H42_900 °C	9.4210	7.40 × 10^−5	6.8832	7.30 × 10^−5	6.409	0.0287
H42_800 °C	9.4237	1.56 × 10^−4	6.8843	1.48 × 10^−4	6.812	0.0325
T42_1000 °C	9.4254	1.41 × 10^−4	6.8842	1.39 × 10^−4	13.880	0.0528
T42_900 °C	9.4254	8.50 × 10^−5	6.8829	8.30 × 10^−5	4.631	0.0303
T42_800 °C	9.4357	2.39 × 10^−4	6.8858	2.14 × 10^−4	6.210	0.0345
T42_700 °C	9.4329	3.55 × 10^−4	6.8896	2.86 × 10^−4	2.455	0.0227
T42_600 °C	9.4314	5.37 × 10^−4	6.8873	4.50 × 10^−4	3.822	0.0214
T42_400 °C	9.4271	8.23 × 10^−4	6.8942	6.98 × 10^−4	3.278	0.0144

---

From Table 1 and Fig. 5, it is possible to conclude that while the a lattice parameter (Fig. 5(A)) did not give useful information being relatively constant for all samples and temperatures, the c lattice parameter (Fig. 5(B)) clearly showed a tendency to decrease with increasing temperatures (F41 being an outlier for the lowest temperatures (400 to 600 °C)). This can be due to anisotropic thermal expansion or a consequence of the loss of the molecules going up in temperature, this trend is consistent with more symmetric crystallographic sites at higher burning temperatures.

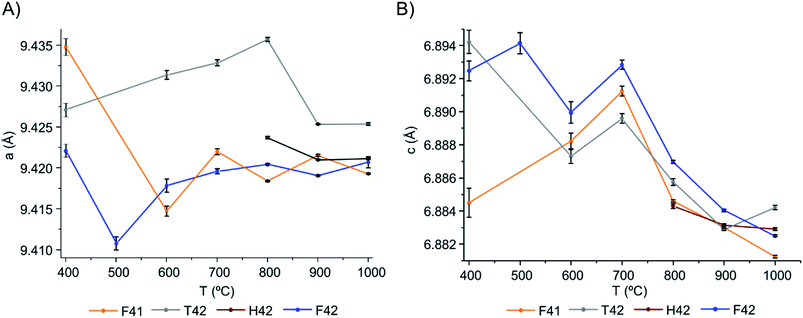Fig. 5 Graphical representation of the unit cell parameters obtained for the bone samples under study, as a function of temperature: (A) parameters a and (B) c, respectively.

Both lattice parameters showed greater fluctuations in the lower temperature range which is consistent with the low symmetry of the unit cells in the bone matrix. The progressive loss of bone's organic constituents and carbonates from 400 to 700 °C led to a reorganization of the atoms within the crystal framework. This behaviour is in agreement with the low intensity and broadened peaks observed in the diffraction profiles at these temperatures (Fig. 1, 4, S1.1(A) and S1.6†).

The particle size, in Ångström, was then calculated using eqn (1):

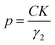where C represents the diffractometer parameter DIFC, K the Scherrer constant (here assumed as 1), and γ₂ the refined Gam-2 value. Table S1,† in ESI summarizes the obtained p values (in Ångström).

The Gam-2 parameter (γ₂) was refined and graphically represented, in Fig. 6(A) and (B) for Hist#5 and Hist#6, respectively (ESI Table S1† comprises the obtained values). This parameter is an empirical fitting parameter for TOF data which assumes that the instrument contribution to this parameter is zero and that any Lorentzian peak broadening visible as a non-zero value is related to a small domain size.

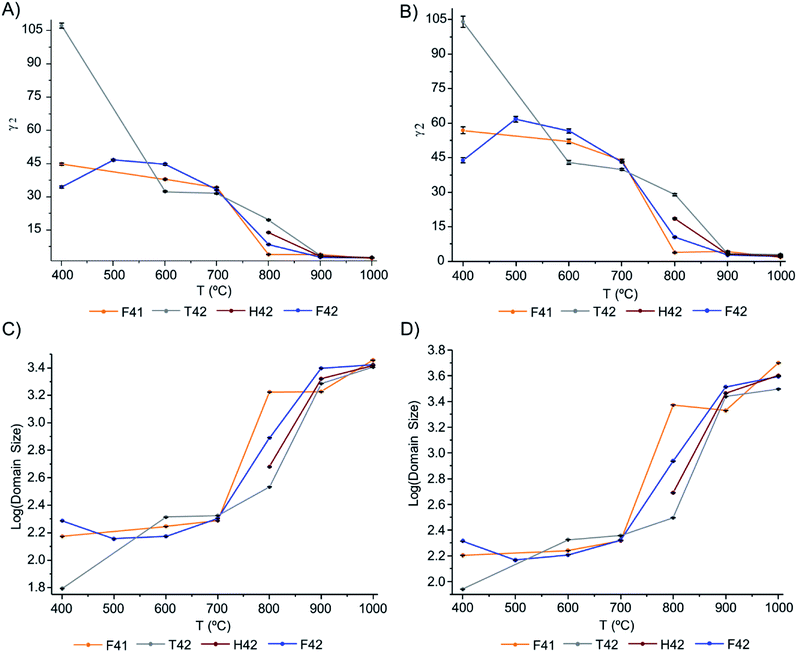Fig. 6 Graphical representation of: (A and B) Gam-2 values, as a function of temperature, for Hist#5 and Hist#6, respectively; (C and D) domain size variation, as a function of temperature, obtained through eqn (1), for Hist#5 and Hist#6, respectively, for the samples under study. Note that the y-axis is a log scale.

Hence, this was the parameter of choice to evaluate peak broadening and from it, the domain size at different temperatures.

The domain size of the crystals is presented in Fig. 6(C) and (D), respectively for Hist#5 and Hist#6. As previously reported^{5,17,19,24,54,55} the exposure to higher burning temperatures is reflected in an increased crystallinity which correlates with higher structural organization. According to Fig. 6, bioapatite crystals' domain size increased considerably when bones were exposed to temperatures higher than 700 °C, from an average particle size of 214.9 to 4010.7 Å for Hist#6 (ESI Table S1†). These values are in agreement with those reported by Piga et al.¹³ obtained for the human femora, through XRD. Hence, according to what was discussed above for the unit cell parameters a and c, a decrease in the size of the unit cell was accompanied by an increase in domain size.

The dominant term of the Gaussian widths of the TOF Bragg peaks, Sig-1, was also evaluated and is shown in Fig. S3† (in the ESI) for Hist#5 and Hist#6. Table S1† (in ESI) comprises the obtained Sig-1 values.

The data showed a general trend of decreasing Sig-1 values with increasing temperatures (Fig. S3(A) and (C)†), reflecting the peak sharpening with increasing temperature, in agreement with the observed diffraction profiles (Fig. 4, S1.1(A) and S1.6†).

Unexpectedly, from 800 to 900 °C Sig-1 increased for all samples except for sample F41 for which Sig-1 showed a very small variation with temperature (Fig. S3(B)†). Hence, data from Hist#6 was analysed (Fig. S3(C) and (D)†), since this corresponds to the most sensitive detector bank in the GEM diffractometer. While a very slight increase in Sig-1 was observed from 800 to 1000 °C (Fig. S3(D)†) for F42 and T42, H42 and F41 behaved very differently: for the former Sig-1 decreased considerably from 800 to 900 °C then remaining constant, and for F41 Sig-1 did not change from 800 to 900 °C but rose significantly from 900 to 1000 °C. At present, we do not have an explanation for this behaviour though, it is possible that the crystal changes at such temperatures are beyond the resolution of the GEM diffractometer.

From the results presented here, it is clear that in the 700–900 °C temperature range, interesting crystallographic and domain size events were observed. Regarding the unit cell parameters' alterations with heating, the c-axis is more affected than the a-axis, displaying a general trend to decrease with increasing temperatures. The domain size, in turn, shows increasing dimensions with increasing temperatures, with a considerable rise from 700 to 900 °C.

The bones subjected to temperatures below 700 °C are poorly crystalline with disorganized structures associated with the presence of carbonates, lipids and collagen. Below this temperature the bone's lattice appears to be in constant reorganization; the heat-induced changes in chemical composition prompting structural and crystalline rearrangements. In contrast, the samples burned at 800, 900 and 1000 °C display a single-phase hydroxyapatite lattice, virtually devoid of carbonates and organic constituents.

Despite differences previously identified by vibrational spectroscopic studies for distinct types of heated human bone,^5,21 the present neutron diffraction results clearly evidence structural changes triggered by the heating process, at various temperatures, which cannot be ascribed to a specific type of bone (femur, humerus or tibia). In addition, for some of the highly burned samples a second inorganic phase was detected in the diffraction patterns and identified by FTIR-ATR as β-tricalcium phosphate.

Conclusions

Neutron diffraction experiments, combined with FTIR-ATR measurements, were applied to human bone samples burned under aerobic conditions (from 400 to 1000 °C), as an innovative approach for the elucidation of heat-elicited crystallinity variations. Neutron diffraction is sensitive to hydrogen, so allows the organic content to be qualitatively (and perhaps quantitatively, this is still to be explored) tracked (Fig. 4), it also confirms that hydroxyls are present because they are required for successful Rietveld fits. A distinct advantage of neutron diffraction is that the sample size is several grams ensuring that the results are representative of the bulk.

Regarding the 700–900 °C interface, in particular, further investigations are needed in order to clarify the intricate ongoing phenomena that occur within the bone matrix within this temperature interval.

It is important to note that biochemical variations exist between the bones currently studied due to environmental differences, distinct mechanical and physical pressure as well as different bone remodelling rates according to the biological function of each bone, and to diagenetic events undergone by the different types of bones.^56,57 However, these are expected to be residual and not detectable upon high temperature exposure. Events such as dehydration, destruction of the collagen native conformation and consequently of the bioapatite crystals’ arrangement along the collagen fibrils are more significant than the inherent biochemical differences between types of bones, thus overruling this contribution.

Conflicts of interest

The authors have no conflicts of interests to declare.

Acknowledgements

The authors thank the Portuguese Foundation for Science and Technology for financial support under grants UID/MULTI/00070/2019, PEst-OE/SADG/UI0283/2013, PTDC/IVC-ANT/1201/2014, POCI-01-0145-FEDER-016766, SFRH/BPD/84268/2012. The STFC Rutherford Appleton Laboratory is thanked for access to neutron beam facilities.⁵⁸ The authors are grateful to Dr Giulia Festa (Centro Fermi, Rome) for helpful scientific discussions.

References

1. C. L. Lee and T. A. Einhorn, in Osteoporosis, ed. R. Marcus, D. Feldman and J. Kelsey, Academic Press, Stanford, California, 2nd edn, 2001, pp. 3–20.
2. D. Bazin, C. Chappard, C. Combes, X. Carpentier, S. Rouzière, G. André, G. Matzen, M. Allix, D. Thiaudière, S. Reguer, P. Jungers and M. Daudon, Osteoporosis Int., 2009, 20, 1065–1075.
3. J. A. Boskey, A. L. Gokhale and P. G. Robey, in Osteoporosis, ed. R. Marcus, D. Feldman and J. Kelsey, Academic Press, Stanford, California, 2nd edn, 2001, pp. 107–188.
4. D. Goncalves, A. R. Vassalo, A. P. Mamede, C. Makhoul, G. Piga, E. Cunha, M. P. M. Marques and L. A. E. Batista de Carvalho, Am. J. Phys. Anthropol., 2018, 166, 296–312.
5. M. P. M. Marques, A. P. Mamede, A. R. Vassalo, C. Makhoul, E. Cunha, D. Goncalves, S. F. Parker and L. A. E. Batista de Carvalho, Sci. Rep., 2018, 8, 15935.
6. A. P. Mamede, A. R. Vassalo, G. Piga, E. Cunha, S. F. Parker, M. P. M. Marques, L. A. E. Batista de Carvalho and D. Goncalves, Anal. Chem., 2018, 90, 11556–11563.
7. T. J. U. Thompson, Forensic Sci. Int., 2004, 146, S203–S205.
8. A. R. Vassalo, E. Cunha, L. A. E. B. de Carvalho and D. Gonçalves, Int. J. Leg. Med., 2016, 130, 1647–1656.
9. T. J. Thompson, J. Forensic Sci., 2005, 50, 1008–1015.
10. M. Stiner, S. Kuhn, S. Weiner and O. Bar-Yosef, J. Archaeol. Sci., 1995, 22, 223–237.
11. R. Shahack-Gross, O. Bar-Yosef and S. Weiner, J. Archaeol. Sci., 1997, 24, 439–446.
12. J. C. Hiller, T. J. U. Thompson, M. P. Evison, A. T. Chamberlain and T. J. Wess, Biomaterials, 2003, 24, 5091–5097.
13. G. Piga, T. J. U. Thompson, A. Malgosa and S. Enzo, J. Forensic Sci., 2009, 54, 534–539.
14. G. Piga, A. Malgosa, T. J. U. Thompson and S. Enzo, J. Archaeol. Sci., 2008, 35, 2171–2178.
15. T. J. U. Thompson, M. Gauthier and M. Islam, J. Archaeol. Sci., 2009, 36, 910–914.
16. M. Lebon, I. Reiche, J. J. Bahain, C. Chadefaux, A. M. Moigne, F. Fröhlich, F. Sémah, H. P. Schwarcz and C. Falguères, J. Archaeol. Sci., 2010, 37, 2265–2276.
17. C. Snoeck, J. A. Lee-Thorp and R. J. Schulting, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2014, 416, 55–68.
18. S. T. D. Ellingham, T. J. U. Thompson, M. Islam and G. Taylor, Sci. Justice, 2015, 55, 181–188.
19. S. T. D. Ellingham, T. J. U. Thompson and M. Islam, J. Forensic Sci., 2016, 61, 153–159.
20. G. Piga, A. Amarante, C. Makhoul, E. Cunha, A. Malgosa, S. Enzo and D. Goncalves, J. Spectrosc., 2018, 1–10.
21. M. P. M. Marques, D. Gonçalves, A. I. C. Amarante, C. I. Makhoul, S. F. Parker and L. A. E. Batista de Carvalho, RSC Adv., 2016, 6, 68638–68641.
22. G. Piga, D. Gonçalves, T. J. U. Thompson, A. Brunetti, A. Malgosa and S. Enzo, Int. J. Spectrosc., 2016, 2016, 1–9.
23. T. J. U. Thompson, M. Islam, K. Piduru and A. Marcel, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2011, 299, 168–174.
24. T. J. U. Thompson, M. Islam and M. Bonniere, J. Archaeol. Sci., 2013, 40, 416–422.
25. G. Dal Sasso, M. Lebon, I. Angelini, L. Maritan, D. Usai and G. Artioli, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2016, 463, 168–179.
26. G. Festa, C. Andreani, M. Baldoni, V. Cipollari, C. Martínez-Labarga, F. Martini, O. Rickards, M. F. Rolfo, L. Sarti, N. Volante, R. Senesi, F. R. Stasolla, S. F. Parker, A. R. Vassalo, A. P. Mamede, L. A. E. Batista de Carvalho and M. P. M. Marques, Sci. Adv., 2019, 5, eaaw1292.
27. F. Damay, D. Bazin, M. Daudon and G. André, C. R. Chim., 2016, 19, 1432–1438.
28. G. E. Bacon, P. J. Bacon and R. K. Griffiths, J. Anat., 1984, 139, 265–273.
29. C. Chappard, G. Andre, M. Daudon and D. Bazin, Eur. J. Clin. Invest., 2016, 46, 112.
30. J. M. S. Skakle and R. M. Aspden, J. Appl. Crystallogr., 2002, 35, 506–508.
31. Y. Choi, D. J. Paik, S. G. Bogdanov, E. Z. Valiev, P. A. Borisova, M. M. Murashev, V. T. Em and A. N. Pirogov, Phys. B, 2018, 551, 218–221.
32. G. E. Bacon, P. J. Bacon and R. K. Griffiths, J. Appl. Crystallogr., 1977, 10, 124–126.
33. A. Benmarouane, T. Hansen and A. Lodini, Phys. B, 2004, 350, 611–614.
34. K. D. Rogers and P. Daniels, Biomaterials, 2002, 23, 2577–2585.
35. E. T. Stathopoulou, V. Psycharis, G. D. Chryssikos, V. Gionis and G. Theodorou, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2008, 266, 168–174.
36. T. Sui, M. A. Sandholzer, A. J. G. Lunt, N. Baimpas, A. Smith, G. Landini and A. M. Korsunsky, J. R. Soc., Interface, 2014, 11, 20130928.
37. A. Person, H. Bocherens, J.-F. Saliège, F. Paris, V. Zeitoun and M. Gérard, J. Archaeol. Sci., 1995, 22, 211–221.
38. G. Piga, A. Santos-Cubedo, A. Brunetti, M. Piccinini, A. Malgosa, E. Napolitano and S. Enzo, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2011, 310, 92–107.
39. M. T. Ferreira, R. Vicente, D. Navega, D. Gonçalves, F. Curate and E. Cunha, Forensic Sci. Int., 2014, 245, 202.e201–202.e205.
40. A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88–107.
41. O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
42. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
43. A. C. Larson and R. B. Von Dreele, Los Alamos Laboratory Report, 1994, pp. 86–748.
44. M. E. Fleet, Biomaterials, 2009, 30, 1473–1481.
45. R. T. Downs and M. Hall-Wallace, Am. Mineral., 2003, 88, 247–250.
46. M. I. Kay, R. A. Young and A. S. Posner, Nature, 1964, 204, 1050–1052.
47. G. MacKinnon and A. Z. Mundorff, in Forensic Human Identification - An Introduction, ed. T. Thompson and S. Black, CRC Press, Boca Raton, 2006, ch. 28.
48. J. M. C. Toynbee, Death and Burial in the Roman World, John Hopkins University Press, Baltimore, 1971.
49. K. A. R. Kennedy, J. Forensic Sci., 1996, 41, 689–692.
50. S. Fairgrieve, Forensic Cremation: Recovery and Analysis, CRC Press, Boca Raton, Florida, 2007.
51. K. Rogers, S. Beckett, S. Kuhn, A. Chamberlain and J. Clement, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2010, 296, 125–129.
52. Y. Suetsugu, Y. Takahashi, F. P. Okamura and J. Tanaka, Solid State Chem., 2000, 155, 292–297.
53. E. A. P. Demaeyer, R. M. H. Verbeeck and D. E. Naessens, Inorg. Chem., 1993, 32, 5709–5714.
54. P. Shipman, G. Foster and M. Schoeninger, J. Archaeol. Sci., 1984, 11, 307–325.
55. L. E. Munro, F. J. Longstaffe and C. D. White, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2007, 249, 90–102.
56. E. P. Paschalis, E. DiCarlo, F. Betts, P. Sherman, R. Mendelsohn and A. L. Boskey, Calcif. Tissue Int., 1996, 59, 480–487.
57. M. P. Richards, R. J. Schulting and R. E. M. Hedges, Nature, 2003, 425, 366.
58. L. A. E. Batista de Carvalho, A. P. Mamede, W. Kockelmann, D. Gonçalves, S. Parker and M. P. M. Marques, ISIS Neutron and Muon Source Data Journal, 2018 DOI:10.5286/ISIS.E.RB1810025.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07728f

---