Open Access Article
Open Access ArticleComputational study on the mechanism and kinetics for the reaction between HO2 and n-propyl peroxy radical†
Zhenli Yangab,
Xiaoxiao Lin *a,
Jiacheng Zhouab,
Mingfeng Hua,
Yanbo Gai
*a,
Jiacheng Zhouab,
Mingfeng Hua,
Yanbo Gai a,
Weixiong Zhaoa,
Bo longc and
Weijun Zhang*ad
a,
Weixiong Zhaoa,
Bo longc and
Weijun Zhang*ad
aLaboratory of Atmospheric Physico-Chemistry, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei, 230031, Anhui, China. E-mail: wjzhang@aiofm.ac.cn; lxx1989@aiofm.ac.cn
bUniversity of Science and Technology of China, Hefei 230026, China
cCollege of Computer and Information Engineering, Guizhou Minzu University, Guiyang 550025, China
dSchool of Environmental Science and Optoelectronic Technology, University of Science and Technology of China, Hefei, 230026, Anhui, China
First published on 6th December 2019
Abstract
The n-propyl peroxy radical (n-C3H7O2) is the key intermediate during atmospheric oxidation of propane (C3H8) which plays an important role in the carbon and nitrogen cycles in the troposphere. In this paper, a comprehensive theoretical study on the reaction mechanism and kinetics of the reaction between HO2 and n-C3H7O2 was performed at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-311G(d,p) level of theory. Computational results show that the HO2 + n-C3H7O2 reaction proceeds on both singlet and triplet potential energy surfaces (PESs). From an energetic point of view, the formation of C3H7O2H and 3O2 via triplet hydrogen abstraction is the most favorable channel while other product channels are negligible. In addition, the calculated rate constants for the title reaction over the temperature range of 238–398 K were calculated by the multiconformer transition state theory (MC-TST), and the calculated rate constants show a negative temperature dependence. The contributions of the other four reaction channels to the total rate constant are negligible.
1. Introduction
Propane (C3H8) is one of the most important nonmethane hydrocarbons (NMHCs) with a lifetime of about 14 days and its global emissions are estimated to be 15–20 Tg per year.1,2 For decades, propane oxidation has been of great interest, and the n-propyl peroxy radical (n-C3H7O2) is one of the key intermediates during propane oxidation.3–6
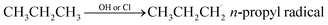 | (1) |
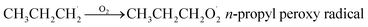 | (2) |
In clean environments where NOx concentrations are low, the reactions of HO2 with organic peroxy radicals (RO2) are generally considered as an important sink.7–11 The reaction mechanisms and kinetic data of HO2 + RO2 reactions have not yet been well-established mainly because of inherent problems in exploring radical–radical reactions.12 Besides, to the best of our knowledge, only a few studies for both kinetics and mechanism of the HO2 + n-C3H7O2 reaction have been reported. One of the difficulties is that the n-C3H7O2 radical is more complex than CH3O2 and C2H5O2 due to its rich conformational variety. It has been reported that the n-C3H7O2 radical has five different conformers: G1G2, G1T2, 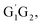 T1G2 and T1T2 (see Fig. S1 in the ESI†).13–15
T1G2 and T1T2 (see Fig. S1 in the ESI†).13–15
Hou and co-workers have developed a structure–activity relationships (SAR) model to study structure–activity relationships and the characteristics of the HO2 + RO2 reactions.10 They reported the calculated rate constant for HO2 + C3H7O2 reaction as 9.12 × 10−12 cm3 per molecule per s. However, the detailed reaction mechanism and kinetic data of HO2 + n-C3H7O2 reaction are still unclear. To better understanding of this issue, a systematic theoretical investigation on the HO2 + n-C3H7O2 reaction is required. In this work, quantum chemistry calculations have been performed to explore the detailed reaction mechanism of HO2 + n-C3H7O2 reaction both on the singlet and triplet potential energy surfaces. Then the rate constant of the title reaction was calculated using the multiconformer transition state theory (MC-TST) which considered that the n-C3H7O2 radical has multiple conformers.
2. Computational methods
The geometries of the reactants, intermediates, transitions states and products in the HO2 + n-C3H7O2 reaction were fully optimized by Density Functional Theory (DFT) method at the B3LYP/6-311G(d,p) level of theory.16,17 Harmonic vibrational frequencies were calculated at the same level to confirm that all minima are real frequencies, and transition states have only a single imaginary frequency. Vibrational frequencies and coordinates of all stationary points in the title reaction have been summarized Tables S1 and S2,† respectively (see ESI†). In addition, the intrinsic reaction coordinate (IRC) calculations were also carried out to verify that the transition states structures can be connected to the corresponding reactants and products.18–21 The zero-point energies (ZPEs) and the thermodynamic corrections at the temperature of 298.15 K and pressure of 1 atm were evaluated at the B3LYP/6-311G(d,p) level of theory and were incorporated in to the final energy barrier, enthalpy and Gibbs free energy. To get more reliable energy information, single point energy calculations were carried out at CCSD(T)/aug-cc-pVDZ level of theory.22 In CCSD (T) calculation, T1 diagnostic is thought to assess the reliability of the methods with respect to a possible multireference feature of the wave functions. For open-shell systems, if the T1 diagnostic value do not exceed 0.044, the wave functions of CCSD are considered to be reliable.23–26 The T1 diagnostic values of the stationary points are presented in Table S3 (ESI†). T1 diagnostic values of the stationary points except for G1G2-3TS1, G1T2-3TS1,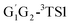 are less than 0.044 from Table S3,† revealing that the CCSD wave function could be reliable. All the computations were performed with Gaussian 09 program package.27 The CCSD(T) single point energy computations were carried out by Molpro package.28,29
are less than 0.044 from Table S3,† revealing that the CCSD wave function could be reliable. All the computations were performed with Gaussian 09 program package.27 The CCSD(T) single point energy computations were carried out by Molpro package.28,29
Since that the n-C3H7O2 has multiple conformers, such complexity should be taken account into the rate constant formula, multiconformer transition state theory (MC-TST) method were carried out for rate constant calculations.30–33 Within the framework of the conventional transition state theory (TST),34–36 the MC-TST expression for a rate constant k at temperature T can be written as
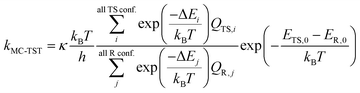 | (3) |
3. Results and discussion
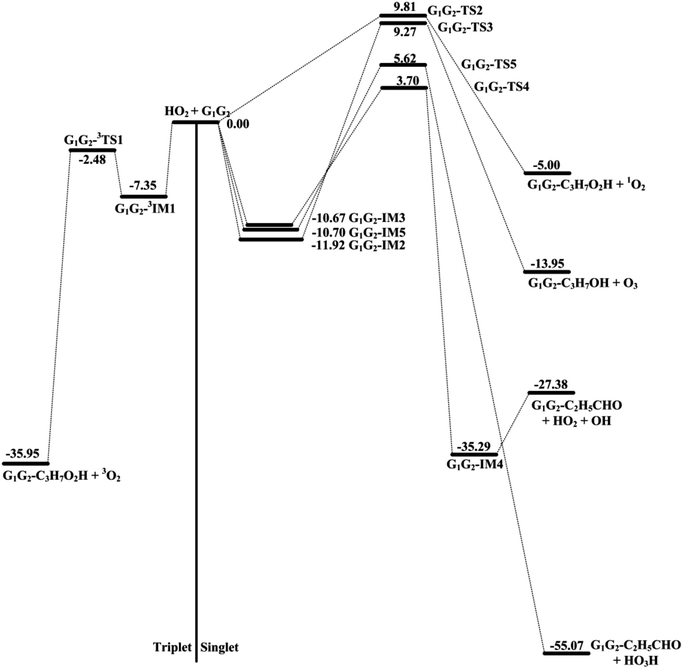
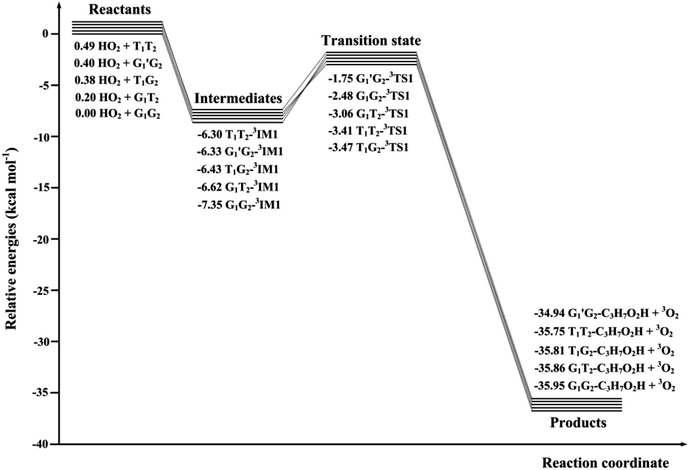
The scheme of the possible reaction routes for the HO2 + n-C3H7O2 reaction has been showed in Fig. 1. In this section, the reaction mechanism and kinetics of the HO2 + n-C3H7O2 reaction have been discussed. For simplicity, we first focus on the reaction mechanism of HO2 and the most stable G1G2 conformer reaction in the following parts. The HO2 + G1T2,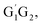 T1G2 and T1T2 reactions are compared with the HO2 + G1G2 reaction. The schematic energy diagram of the HO2 + G1G2 reaction is depicted in Fig. 2, whereas the corresponding profiles of the schematic energy diagram are shown schematically in Fig. S2–S5† for the HO2 + G1T2,
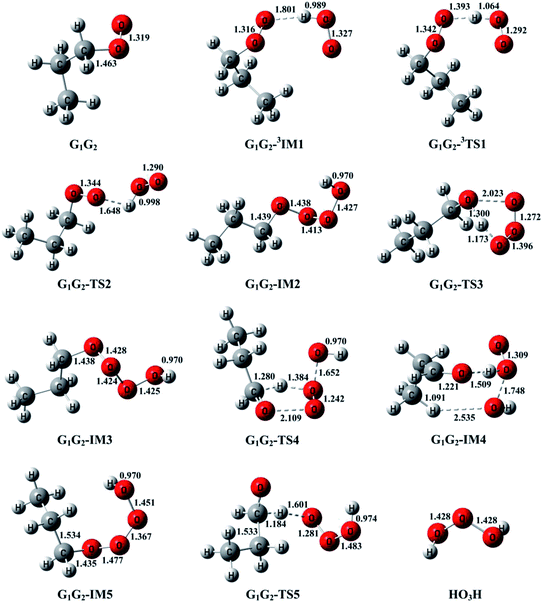
T1G2 and T1T2 reactions are compared with the HO2 + G1G2 reaction. The schematic energy diagram of the HO2 + G1G2 reaction is depicted in Fig. 2, whereas the corresponding profiles of the schematic energy diagram are shown schematically in Fig. S2–S5† for the HO2 + G1T2,  T1G2 and T1T2 reactions (ESI†), respectively. The selected geometric structures of the five reactions are displayed in Fig. 3 and S6–S9,† respectively. In what follows, energies of the HO2 + G1G2, G1T2,
T1G2 and T1T2 reactions (ESI†), respectively. The selected geometric structures of the five reactions are displayed in Fig. 3 and S6–S9,† respectively. In what follows, energies of the HO2 + G1G2, G1T2,  T1G2 and T1T2 reactions are shown in Tables 1 and S4–S7,† respectively. Besides, to study the relative importance of various products in the HO2 + n-C3H7O2, the rate constants of the most favorable channel for the five different reactions have been discussed. Finally, Arrhenius plot for the triplet channel of HO2 + n-C3H7O2 reaction is displayed in Fig. 4 and the calculated rate constants are fitted into Arrhenius three parameter equation.
T1G2 and T1T2 reactions are shown in Tables 1 and S4–S7,† respectively. Besides, to study the relative importance of various products in the HO2 + n-C3H7O2, the rate constants of the most favorable channel for the five different reactions have been discussed. Finally, Arrhenius plot for the triplet channel of HO2 + n-C3H7O2 reaction is displayed in Fig. 4 and the calculated rate constants are fitted into Arrhenius three parameter equation.
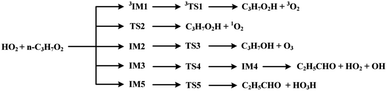 | ||
| Fig. 1 The scheme of possible reaction routes of HO2 + n-C3H7O2 reaction on both the singlet and triplet potential energy surfaces. | ||
| Compound | ZPE | ΔE298 K | ΔH298 K | ΔG298 K |
|---|---|---|---|---|
| G1G2 + HO2 | 71.62 | 0.00 | 0.00 | 0.00 |
| G1G2-3IM1 | 73.23 | −6.78 | −7.37 | 1.82 |
| G1G2-3TS1 | 70.85 | −2.47 | −3.06 | 7.59 |
| G1G2-C3H7O2H + 3O2 | 72.27 | −35.88 | −35.88 | −34.48 |
| G1G2-TS2 | 72.41 | 9.96 | 9.36 | 20.45 |
| G1G2-C3H7O2H + 1O2 | 72.25 | −4.93 | −4.93 | −2.88 |
| G1G2-IM2 | 74.18 | −12.02 | −12.61 | −0.41 |
| G1G2-TS3 | 71.22 | 8.76 | 8.17 | 21.28 |
| G1G2-C3H7OH + O3 | 72.58 | −14.26 | −14.26 | −13.41 |
| G1G2-IM3 | 73.98 | −10.77 | −11.36 | 0.85 |
| G1G2-TS4 | 69.91 | 3.58 | 2.99 | 15.51 |
| G1G2-IM4 | 72.52 | −34.70 | −35.29 | −24.64 |
| G1G2-C2H5CHO + HO2 + OH | 66.88 | −26.53 | −25.94 | −36.40 |
| G1G2-IM5 | 74.07 | −10.94 | −11.53 | 1.28 |
| G1G2-TS5 | 68.74 | 6.10 | 5.51 | 15.13 |
| G1G2-C2H5CHO + HO3H | 71.73 | −55.18 | −55.18 | −54.90 |
Throughout the discussions, the transition states and intermediates in each reaction are denoted by “TS’’ and “IM”, respectively, followed by a number. The optimized geometries involved in the five reactions are designated by the prefix G1G2, G1T2,  T1G2 and T1T2, respectively, followed by the “TS’’ or “IM”.
T1G2 and T1T2, respectively, followed by the “TS’’ or “IM”.
3.1 Mechanism of the HO2 + n-C3H7O2 reaction
For the triplet hydrogen abstraction process, the HO2 + G1T2, 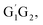 T1G2 and T1T2 four reactions are also identified to be kinetically favorable pathways via the same reaction mechanism as that of HO2 + G1G2 reaction (see Fig. S2–S5†). The selected geometric structures for the reactants, intermediates, transition states and products of the four reactions were shown in Fig. S6–S9,† respectively. As shown in Fig. S2–S5,† all the four reactions take place on the triplet surfaces from the reactants via intermediates (G1T2-3IM1,
T1G2 and T1T2 four reactions are also identified to be kinetically favorable pathways via the same reaction mechanism as that of HO2 + G1G2 reaction (see Fig. S2–S5†). The selected geometric structures for the reactants, intermediates, transition states and products of the four reactions were shown in Fig. S6–S9,† respectively. As shown in Fig. S2–S5,† all the four reactions take place on the triplet surfaces from the reactants via intermediates (G1T2-3IM1, 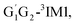 T1G2-3IM1 and T1T2-3IM1) and transition states (G1T2-3TS1,
T1G2-3IM1 and T1T2-3IM1) and transition states (G1T2-3TS1, 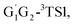 T1G2-3TS1 and T1T2-3TS1) to produce the C3H7O2H and triplet O2. The four intermediates are hydrogen bond complexes. The binding energies of four intermediates are −6.83 kcal mol−1 (G1T2-3IM1), −6.73 kcal mol−1
T1G2-3TS1 and T1T2-3TS1) to produce the C3H7O2H and triplet O2. The four intermediates are hydrogen bond complexes. The binding energies of four intermediates are −6.83 kcal mol−1 (G1T2-3IM1), −6.73 kcal mol−1 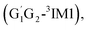 −6.81 kcal mol−1 (T1G2-3IM1) and −6.79 kcal mol−1 (T1T2-3IM1) kcal mol−1, respectively. In the structure of G1G2-3IM1, the binding energy is −7.35 kcal mol−1, which is close to that in the four intermediates above. The four corresponding transition states involve nearly linear O⋯H⋯O bond angles and are early barriers. The average distances of the breaking H–O bonds and forming O–H bonds are 1.041 and 1.466 Å, respectively. The barrier heights of the G1T2-3TS1,
−6.81 kcal mol−1 (T1G2-3IM1) and −6.79 kcal mol−1 (T1T2-3IM1) kcal mol−1, respectively. In the structure of G1G2-3IM1, the binding energy is −7.35 kcal mol−1, which is close to that in the four intermediates above. The four corresponding transition states involve nearly linear O⋯H⋯O bond angles and are early barriers. The average distances of the breaking H–O bonds and forming O–H bonds are 1.041 and 1.466 Å, respectively. The barrier heights of the G1T2-3TS1, 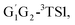 T1G2-3TS1 and T1T2-3TS1 are close to each other (−3.26, −2.15, −3.85 vs. −3.90 kcal mol−1). The average barrier height of the four transition states is −3.29 kcal mol−1, which is only 0.81 kcal mol−1 lower than G1G2-3TS1. Evidently, G1G2-3TS1, G1T2-3TS1,
T1G2-3TS1 and T1T2-3TS1 are close to each other (−3.26, −2.15, −3.85 vs. −3.90 kcal mol−1). The average barrier height of the four transition states is −3.29 kcal mol−1, which is only 0.81 kcal mol−1 lower than G1G2-3TS1. Evidently, G1G2-3TS1, G1T2-3TS1, 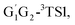 T1G2-3TS1 and T1T2-3TS1 are all early barriers. The reactions of HO2 with the five different conformers (G1G2, G1T2,
T1G2-3TS1 and T1T2-3TS1 are all early barriers. The reactions of HO2 with the five different conformers (G1G2, G1T2, 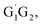 T1G2 and T1T2) have same reaction mechanism and have simpler triplet potential energy surfaces via hydrogen abstraction routes to form C3H7O2H + 3O2 molecule.
T1G2 and T1T2) have same reaction mechanism and have simpler triplet potential energy surfaces via hydrogen abstraction routes to form C3H7O2H + 3O2 molecule.
The formation of G1G2-C3H7O2H + 1O2 proceeds directly through one transition state G1G2-TS2 by abstracting the hydrogen atom of HO2 to the terminal O atom of G1G2, which has been shown in Fig. 2. The barrier height of G1G2-TS2 is calculated to be 9.81 kcal mol−1 higher than that of the initial HO2 + G1G2 reactants. This product channel is a hydrogen abstraction process, which is different from the hydrogen abstraction on the triplet surface. In summary, the singlet hydrogen abstraction process is distinct from the triplet one in three respects. Firstly, hydrogen abstraction process on the singlet potential energy surface may undergo directly through the transition state G1G2-TS2 producing G1G2-C3H7O2H and singlet O2 molecule, while the triplet one proceeds the intermediate G1G2-3IM1 prior to the transition state G1G2-3TS1 producing G1G2-C3H7O2H and triplet O2 molecule. Secondly, the O⋯H⋯O bond angle in G1G2-TS2 is much more bent (i.e., 107.77° in G1G2-TS2 vs. 171.93° in G1G2-3TS1). Thirdly, our calculation shows the barrier for G1G2-TS2 is much higher than that for G1G2-3TS1 by about 12.29 kcal mol−1. The G1G2-C3H7O2H + 1O2 formation channel is of minor importance due to the high barrier height.
On the singlet potential energy surface, except for direct hydrogen abstraction mechanism described above, addition–elimination mechanism is located as well. The remaining three reaction pathways precede via an addition–elimination mechanism. As shown in Fig. 2, HO2 + G1G2 → G1G2-IM2 → G1G2-TS3 → G1G2-C3H7OH + O3, this channel involves a rather high barrier and is exothermic. The structures of G1G2-IM2 and G1G2-TS3 are shown in Fig. 3. The lengths of three O–O bonds of G1G2-IM2 are about 1.4 Å. G1G2-IM2 is −11.92 kcal mol−1 with respect to the initial HO2 + G1G2 reactants. G1G2-TS3 is a five-membered ring structure. With respect to the HO2 + G1G2 reactants, the barrier of G1G2-TS3 is as high as 9.27 kcal mol−1. Compared with other pathways, the formations of G1G2-C3H7OH + O3 might be negligible because of the high barrier height.
The formation of G1G2-TS4 from the reactants HO2 + G1G2 radicals could also occur via G1G2-IM3. Similar to G1G2-IM2, G1G2-IM3 also has three OO bonds and the bond lengths are about 1.4 Å. The computed binding energy for G1G2-IM3 are −10.67 kcal mol−1. In G1G2-TS4, the hydrogen atom migrates from the C to O to form HO2, while the two O–O bonds cleavage to form post-reaction complex G1G2-IM4. The barrier for G1G2-TS4 is relatively higher than that for G1G2-3TS1 by about 6.18 kcal mol−1. After G1G2-TS4, this product channel proceeds through G1G2-IM4 complex to form G1G2-C2H5CHO + HO2 + OH products. It is found that the calculated relative energy of the G1G2-IM4 to the reactants HO2 + G1G2 is −35.29 kcal mol−1, which is lower than the products. It's worth noting that the reaction pathway of G1G2-C2H5CHO + HO2 + OH formation could be viewed as a HO2-mediated dissociation process of G1G2 because the HO2 radical is also reproduced in the final products.
The last channel examined on the singlet potential energy surface is the formation of G1G2-C2H5CHO and HO3H. As shown in Fig. 2, HO2 + G1G2→ G1G2-IM5 → G1G2-TS5 →G1G2-C2H5CHO + HO3H, this pathway involves a high barrier and is extremely exothermic. Analogous to the energies of G1G2-IM2 and G1G2-IM3, the binding energy for G1G2-IM5 is −10.70 kcal mol−1. G1G2-IM5 also has three OO bonds, all of which are about 1.4 Å in length. The barrier height for G1G2-TS5 is about 5.62 kcal mol−1 with respect to the reactants HO2 + G1G2. Clearly, the formation of G1G2-C2H5CHO and HO3H via G1G2-TS5 involves significant barrier and is the most exothermic pathway on the both triplet and singlet potential energy surfaces.
From the Fig. S2–S5 in the ESI,† we can see that the singlet potential energy surfaces for the HO2 + G1T2, 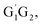 T1G2 and T1T2 four reactions, as well as the HO2 + G1G2 reaction proceed on the similar reaction mechanism which has been discussed above in detail in the present work. The formations of C3H7O2H + 1O2, C3H7OH + O3 and C2H5CHO + HO2 + OH in HO2 + G1T2,
T1G2 and T1T2 four reactions, as well as the HO2 + G1G2 reaction proceed on the similar reaction mechanism which has been discussed above in detail in the present work. The formations of C3H7O2H + 1O2, C3H7OH + O3 and C2H5CHO + HO2 + OH in HO2 + G1T2, 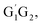 T1G2 and T1T2 four reactions have similar energetic data as that of the HO2 + G1G2 reaction. For example, in the C3H7O2H + 1O2 formation pathway, the barrier heights of the four transition states G1T2-TS2,
T1G2 and T1T2 four reactions have similar energetic data as that of the HO2 + G1G2 reaction. For example, in the C3H7O2H + 1O2 formation pathway, the barrier heights of the four transition states G1T2-TS2, 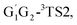 T1G2-TS2 and T1T2-TS2 are generally consistent with each other (9.82, 9.51, 9.53 vs. 9.52 kcal mol−1). The calculated barrier height for G1G2-TS2 is about 9.81 kcal mol−1. By comparison, we can conclude that the energy barriers of the above three channels in the five reactions of HO2 + G1G2, G1T2,
T1G2-TS2 and T1T2-TS2 are generally consistent with each other (9.82, 9.51, 9.53 vs. 9.52 kcal mol−1). The calculated barrier height for G1G2-TS2 is about 9.81 kcal mol−1. By comparison, we can conclude that the energy barriers of the above three channels in the five reactions of HO2 + G1G2, G1T2,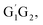 T1G2 and T1T2 have little difference. However, in the C2H5CHO and HO3H formation pathways, the average barrier height for the four transition states (G1T2-TS5,
T1G2 and T1T2 have little difference. However, in the C2H5CHO and HO3H formation pathways, the average barrier height for the four transition states (G1T2-TS5, 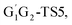 T1G2-TS5 and T1T2-TS5) is 14.80 kcal mol−1, which is 9.18 kcal mol−1 higher than G1G2-TS5. As a result, for HO2 + G1G2 reaction, the C3H7O2H + 1O2 formation pathway is the highest barrier height, while C2H5CHO and HO3H formation pathways are the highest barrier heights in the other four reactions. Compared with the energetically favorable triplet reactions, all the singlet reactions involve relatively high barriers.
T1G2-TS5 and T1T2-TS5) is 14.80 kcal mol−1, which is 9.18 kcal mol−1 higher than G1G2-TS5. As a result, for HO2 + G1G2 reaction, the C3H7O2H + 1O2 formation pathway is the highest barrier height, while C2H5CHO and HO3H formation pathways are the highest barrier heights in the other four reactions. Compared with the energetically favorable triplet reactions, all the singlet reactions involve relatively high barriers.
In summary, the reactions of HO2 with the five different conformers (G1G2, G1T2, 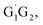 T1G2 and T1T2) have simpler triplet potential energy surfaces via hydrogen abstraction routes to form C3H7O2H + 3O2 molecule and more complicated singlet surfaces via direct hydrogen abstraction and addition–elimination mechanisms form various products. From the mechanism discussed above, we can conclude that the pathway of formation of C3H7O2H + 3O2 is the most important reaction channel and other channels can be negligible in the n-C3H7O2 + HO2 reaction.
T1G2 and T1T2) have simpler triplet potential energy surfaces via hydrogen abstraction routes to form C3H7O2H + 3O2 molecule and more complicated singlet surfaces via direct hydrogen abstraction and addition–elimination mechanisms form various products. From the mechanism discussed above, we can conclude that the pathway of formation of C3H7O2H + 3O2 is the most important reaction channel and other channels can be negligible in the n-C3H7O2 + HO2 reaction.
3.2 Kinetics of the HO2 + n-C3H7O2reaction
Based on the singlet and triplet potential energy surfaces, the rate constants of different reaction pathways for the individual conformer have been evaluated using the conventional transition-state theory (TST) over the temperature range of 238–398 K. For example, in the case of the lowest energy conformer HO2 + G1G2 reaction, the calculated rate constants for individual channel are listed in Table 2. As can be seen from Table 2, results show that the rate constants for the triplet hydrogen abstraction reaction contributes significantly to the overall rate constants. The rate constant of triplet channel is at least four orders of magnitude higher than that of singlet ones over the temperature range. This indicates that the triplet hydrogen abstraction channel for formation of G1G2-C3H7O2H + 3O2 products is the major channel, while the singlet channels can be negligible. The reactions of HO2 with the other conformers (G1T2,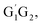 T1G2 and T1T2) have similar reaction mechanism and kinetic behavior as the HO2 + G1G2 reaction. Thus, only the rate constants of each individual triplet hydrogen abstraction channel are considered in the total rate constants calculations of the HO2 + n-C3H7O2 reaction. The triplet channels for each n-C3H7O2 conformer are displayed in Table 3. It is clear that rate constants for each triplet hydrogen abstraction channel give the total rate constants for the HO2 + n-C3H7O2 reaction. Considering that n-C3H7O2 has multiple conformers, the total rate constants for HO2 with n-C3H7O2 reaction are obtained by MC-TST method. Overview of triplet channels for the reactions of HO2 with the five conformers (G1G2, G1T2,
T1G2 and T1T2) have similar reaction mechanism and kinetic behavior as the HO2 + G1G2 reaction. Thus, only the rate constants of each individual triplet hydrogen abstraction channel are considered in the total rate constants calculations of the HO2 + n-C3H7O2 reaction. The triplet channels for each n-C3H7O2 conformer are displayed in Table 3. It is clear that rate constants for each triplet hydrogen abstraction channel give the total rate constants for the HO2 + n-C3H7O2 reaction. Considering that n-C3H7O2 has multiple conformers, the total rate constants for HO2 with n-C3H7O2 reaction are obtained by MC-TST method. Overview of triplet channels for the reactions of HO2 with the five conformers (G1G2, G1T2, 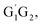 T1G2 and T1T2) showing the individual conformer of the reactants, intermediates, transition states, and products are shown in the Fig. 5. The MC-TST rate constant can be regarded as a sum of the individual TST reaction rate constants which weighted by the Boltzmann population of the corresponding n-C3H7O2 conformers. The overall calculated rate constant of the HO2 + n-C3H7O2 reaction over the temperature range of 238–398 K are listed in Table 4. Moreover, the calculated rate constants are fitted into Arrhenius three parameter equation as follows:
T1G2 and T1T2) showing the individual conformer of the reactants, intermediates, transition states, and products are shown in the Fig. 5. The MC-TST rate constant can be regarded as a sum of the individual TST reaction rate constants which weighted by the Boltzmann population of the corresponding n-C3H7O2 conformers. The overall calculated rate constant of the HO2 + n-C3H7O2 reaction over the temperature range of 238–398 K are listed in Table 4. Moreover, the calculated rate constants are fitted into Arrhenius three parameter equation as follows:
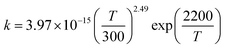 | (4) |
| T (K) | 3O2 | 1O2 | O3 | OH | HO3H |
|---|---|---|---|---|---|
| 238 | 3.44 × 10−12 | 4.70 × 10−24 | 9.71 × 10−22 | 6.18 × 10−19 | 2.57 × 10−19 |
| 258 | 2.22 × 10−12 | 2.43 × 10−23 | 8.96 × 10−22 | 9.85 × 10−19 | 6.70 × 10−19 |
| 278 | 1.56 × 10−12 | 1.01 × 10−22 | 1.08 × 10−21 | 1.52 × 10−18 | 1.56 × 10−18 |
| 298 | 1.16 × 10−12 | 3.49 × 10−22 | 1.52 × 10−21 | 2.27 × 10−18 | 3.30 × 10−18 |
| 318 | 9.13 × 10−13 | 1.05 × 10−21 | 2.35 × 10−21 | 3.28 × 10−18 | 6.47 × 10−18 |
| 338 | 7.45 × 10−13 | 2.79 × 10−21 | 3.78 × 10−21 | 4.62 × 10−18 | 1.19 × 10−17 |
| 358 | 6.27 × 10−13 | 6.73 × 10−21 | 6.14 × 10−21 | 6.35 × 10−18 | 2.07 × 10−17 |
| 378 | 5.42 × 10−13 | 1.49 × 10−20 | 9.91 × 10−21 | 8.53 × 10−18 | 3.43 × 10−17 |
| 398 | 4.80 × 10−13 | 3.06 × 10−20 | 1.57 × 10−20 | 1.12 × 10−17 | 5.47 × 10−17 |
| T (K) | HO2 + G1G2 | HO2 + G1T2 | HO2 + T1G2 | HO2 + T1T2 | |
|---|---|---|---|---|---|
| 238 | 3.44 × 10−12 | 1.05 × 10−11 | 1.12 × 10−12 | 2.83 × 10−11 | 4.61 × 10−11 |
| 258 | 2.22 × 10−12 | 6.30 × 10−12 | 8.27 × 10−13 | 1.57 × 10−11 | 2.53 × 10−11 |
| 278 | 1.56 × 10−12 | 4.11 × 10−12 | 6.45 × 10−13 | 9.57 × 10−12 | 1.53 × 10−11 |
| 298 | 1.16 × 10−12 | 2.87 × 10−12 | 5.27 × 10−13 | 6.31 × 10−12 | 1.00 × 10−11 |
| 318 | 9.13 × 10−13 | 2.12 × 10−12 | 4.45 × 10−13 | 4.42 × 10−12 | 7.00 × 10−12 |
| 338 | 7.44 × 10−13 | 1.64 × 10−12 | 3.87 × 10−13 | 3.26 × 10−12 | 5.14 × 10−12 |
| 358 | 6.27 × 10−13 | 1.31 × 10−12 | 3.44 × 10−13 | 2.50 × 10−12 | 3.93 × 10−12 |
| 378 | 5.42 × 10−13 | 1.08 × 10−12 | 3.12 × 10−13 | 1.99 × 10−12 | 3.11 × 10−12 |
| 398 | 4.80 × 10−13 | 9.19 × 10−13 | 2.88 × 10−13 | 1.63 × 10−12 | 2.54 × 10−12 |
| T (K) | ktotal |
|---|---|
| 238 | 2.30 × 10−11 |
| 258 | 1.38 × 10−11 |
| 278 | 8.98 × 10−12 |
| 298 | 6.27 × 10−12 |
| 318 | 4.64 × 10−12 |
| 338 | 3.58 × 10−12 |
| 358 | 2.88 × 10−12 |
| 378 | 2.38 × 10−12 |
| 398 | 2.02 × 10−12 |
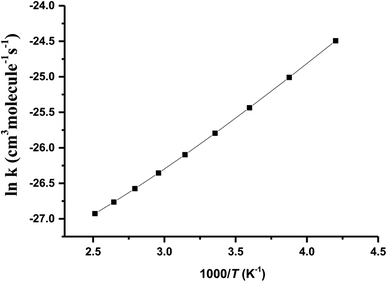
The Arrhenius plot for the reaction of HO2 and n-C3H7O2 is shown in Fig. 4. From the Arrhenius plot, it can be seen clearly that the negative temperature dependence for the title reaction in lower temperature regime (e.g. T < 400 K). This can be attributed to the formation of the pre-reaction complexes with negative barriers in the triplet channels of the title reaction. For example, in the triplet channel of HO2 + G1G2 reaction, the values of the rate coefficients of reverse process (G1G2-3IM1 to HO2 and G1G2) increases with the rising temperature, which reduces the value of the equilibrium constant. It can be said that when the reaction reaches equilibrium, the macroscopic rate coefficient decreases. This downward trend can be seen in the other four reactions of HO2 with the different conformers (G1T2, 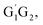 T1G2 and T1T2). Thus, the overall rate coefficient of the title reaction shows negative temperature dependence. The calculated rate constants for HO2 + n-C3H7O2 reaction is predicted to be 6.27 × 10−12 cm3 per molecule per s at 298 K. The kinetic results shown good agreement with the value 9.12 × 10−12 cm3 per molecule per s reported by Hou and his co-workers using structure–activity relationships (SAR) analysis.10 It shows that our CCSD(T)/aug-cc-pVDZ//B3LYP/6-311G(d,p) calculated rate constants are in good agreement with the available recent theoretical result in the related reference.
T1G2 and T1T2). Thus, the overall rate coefficient of the title reaction shows negative temperature dependence. The calculated rate constants for HO2 + n-C3H7O2 reaction is predicted to be 6.27 × 10−12 cm3 per molecule per s at 298 K. The kinetic results shown good agreement with the value 9.12 × 10−12 cm3 per molecule per s reported by Hou and his co-workers using structure–activity relationships (SAR) analysis.10 It shows that our CCSD(T)/aug-cc-pVDZ//B3LYP/6-311G(d,p) calculated rate constants are in good agreement with the available recent theoretical result in the related reference.
4. Summary and conclusions
In present study, the detailed mechanism and kinetics of the reaction of HO2 and n-C3H7O2 (including five conformers G1G2, G1T2,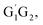 T1G2 and T1T2) have been investigated by quantum chemistry and MC-TST method. The mechanism for the reaction between HO2 and n-C3H7O2 radical on both singlet and triplet potential energy surfaces mainly includes hydrogen abstraction and addition–elimination mechanisms. The energy barriers show the main products are C3H7O2H and 3O2 on the triplet potential energy surface via the hydrogen abstraction mechanism. In addition, the rate constants of HO2 + n-C3H7O2 reaction were further studied over the temperature range of 238–398 K which show a negative temperature dependent. The kinetic calculations indicate that the formation of C3H7O2H + 3O2 channel is most kinetically favorable since that the rate constant of which is at least four orders of magnitude larger than that of the other channels at the studied temperature range. The calculated rate constant for HO2 + n-C3H7O2 reaction is predicted to be 6.27 × 10−12 cm3 per molecule per s at 298 K, which match good with the results from SAR analysis.10 The theoretical results can be helpful to deeply understand the chemical behaviors of HO2 + n-C3H7O2 reaction.
T1G2 and T1T2) have been investigated by quantum chemistry and MC-TST method. The mechanism for the reaction between HO2 and n-C3H7O2 radical on both singlet and triplet potential energy surfaces mainly includes hydrogen abstraction and addition–elimination mechanisms. The energy barriers show the main products are C3H7O2H and 3O2 on the triplet potential energy surface via the hydrogen abstraction mechanism. In addition, the rate constants of HO2 + n-C3H7O2 reaction were further studied over the temperature range of 238–398 K which show a negative temperature dependent. The kinetic calculations indicate that the formation of C3H7O2H + 3O2 channel is most kinetically favorable since that the rate constant of which is at least four orders of magnitude larger than that of the other channels at the studied temperature range. The calculated rate constant for HO2 + n-C3H7O2 reaction is predicted to be 6.27 × 10−12 cm3 per molecule per s at 298 K, which match good with the results from SAR analysis.10 The theoretical results can be helpful to deeply understand the chemical behaviors of HO2 + n-C3H7O2 reaction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank financial support from the National Natural Science Foundation of China (91544228, 41605102, 21876177, and 41575125), the National Key Research and Development Program of China (2016YFC0202205, 2017YFC0209401), the Youth Innovation Promotion Association CAS (2019439), and the Science and Technology Foundation of Guizhou Province, China ([2019]5648 and [2018]1080).References
- H. B. Singh, D. O'Hara, D. Herlth, W. Sachse, D. R. Blake, J. D. Bradshaw, M. Kanakidou and P. J. Crutzen, J. Geophys. Res., 1994, 99, 1805–1819 CrossRef CAS.
- R. Atkinson, J. Phys. Chem. Ref. Data, 1997, 26, 215–290 CrossRef CAS.
- C. M. Rosado-Reyes and J. S. Francisco, J. Geophys. Res., 2007, 112, D14310 CrossRef.
- L. K. Huynh, H.-H. Carstensen and A. M. Dean, J. Phys. Chem. A, 2010, 114, 6594–6607 CrossRef CAS PubMed.
- S. S. Merchant, C. F. Goldsmith, A. G. Vandeputte, M. P. Burke, S. J. Klippenstein and W. H. Green, Combust. Flame, 2015, 162, 3658–3673 CrossRef CAS.
- C. F. Goldsmith, W. H. Green and S. J. Klippenstein, J. Phys. Chem. A, 2012, 116, 3325–3346 CrossRef CAS PubMed.
- G. S. Tyndall, R. A. Cox, C. Granier, R. Lesclaux, G. K. Moortgat, M. J. Pilling, A. R. Ravishankara and T. J. Wallington, J. Geophys. Res.: Atmos., 2001, 106, 12157–12182 CrossRef CAS.
- J. J. Orlando and G. S. Tyndall, Chem. Rev., 2003, 103, 4657–4689 CrossRef CAS PubMed.
- A. A. Boyd, P.-M. Flaud, N. Daugey and R. Lesclaux, J. Phys. Chem. A, 2003, 107, 818–821 CrossRef CAS.
- H. Hou, J. Li, X. Song and B. Wang, J. Phys. Chem. A, 2005, 109, 11206–11212 CrossRef CAS PubMed.
- A. S. Hasson, G. S. Tyndall and J. J. Orlando, J. Phys. Chem. A, 2004, 108, 5979–5989 CrossRef CAS.
- Y. Shao, H. Hou and B. Wang, Phys. Chem. Chem. Phys., 2014, 16, 22805–22814 RSC.
- G. M. P. Just, P. Rupper, T. A. Miller and W. L. Meerts, Phys. Chem. Chem. Phys., 2010, 12, 4773–4782 RSC.
- S. J. Zalyubovsky, B. G. Glover, T. A. Miller, C. Hayes, J. K. Merle and C. M. Hadad, J. Phys. Chem. A, 2005, 109, 1308–1315 CrossRef CAS PubMed.
- G. Tarczay, S. J. Zalyubovsky and T. A. Miller, Chem. Phys. Lett., 2005, 406, 81–89 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- M. Page and J. W. McIver Jr, J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2000, 104, 9823–9840 CrossRef CAS.
- B. Long, X. Tan, Z. Long, Y. Wang, D.-s. Ren and W. Zhang, J. Phys. Chem. A, 2011, 115, 6559–6567 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2019, 141, 611–617 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles and G. Knizia, et al., MOLPRO, version 2010.1, a package of ab initio program, 2010 Search PubMed.
- K. H. Moller, R. V. Otkjaer, N. Hyttinen, T. Kurten and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 10072–10087 CrossRef PubMed.
- L. Vereecken and J. Peeters, J. Chem. Phys., 2003, 119, 5159–5170 CrossRef CAS.
- J. Peeters, J. F. Muller, T. Stavrakou and V. S. Nguyen, J. Phys. Chem. A, 2014, 118, 8625–8643 CrossRef CAS PubMed.
- H. Eyring, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07503h |
| This journal is © The Royal Society of Chemistry 2019 |