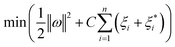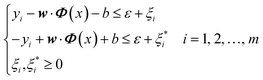Open Access Article
Open Access ArticleA novel method for total chlorine detection using machine learning with electrode arrays†
Zhe Li,
Shunhao Huang and
Juan Chen *
*
College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, PR China. E-mail: jchen@mail.buct.edu.cn
First published on 24th October 2019
Abstract
Chlorine is a common natural water disinfectant, but it reacts with ammonia's nitrogen to form chloramines, which affects the accuracy of free chlorine measurement. In this case, total chlorine can be used as an indicator to evaluate the content of the effective disinfectant. In this article, a novel method to detect total chlorine using an electrode array in water has been proposed. We made the total chlorine sensor and captured the cyclic voltammetry curve of the electrode at different concentrations of chlorine ammonia. Principal component analysis and a peak sampling method were used to extract cyclic voltammetry curves, and the total chlorine prediction model was established by support the vector machine and extreme learning machine. The results show that the best predicting power was achieved by support vector regression with principal component analysis (R2 = 0.9689). This study provides a simple method for determining total chlorine under certain conditions and likely can be adapted to monitor disinfection and water treatment processes as well.
1. Introduction
Chlorine has been using as the most common disinfectant for drinking water in many countries since the early 20th century.1,2 Natural water contains a large number of pathogenic bacteria and microorganisms, most of which can be continuously inactivated by free chlorine.3–5 By adding chlorine to natural water, water-borne diseases such as cholera and typhoid were effectively suppressed.6 As one of the widely used disinfectants, chlorine is also used for swimming pool disinfection,7 agricultural production8 and sewage treatment.9–12 The consumption of free chlorine depends on application scenarios and bacterial count. Therefore, it is necessary to measure the active chlorine to confirm whether the disinfectant was added appropriately.Free chlorine contains hypochlorite and hypochlorite ions. Hypochlorite is the main effective component in free chlorine, which reacts with various amino acids and nucleic acids in the virus.3,13 However, when natural water contained ammonia, hypochlorite will react with it and induce chloramine formation.14 Although chloramine also has antiseptic effects, it cannot be detected as free chlorine. One way to solve this problem is to measure total chlorine. At present, there are several methods to measure total chlorine, such as colorimetric method,15 gas chromatography,16 ion chromatography,17 inductively coupled plasma mass spectrometry,18,19 inductively coupled plasma emission spectrometry,20 electrode methods and etc. The traditional electrode methods of total chlorine are based on the iodine content method.21 Iodine and acid needed to add in the test process, which makes the measurement process not simple enough. Although some companies have developed other types of total chlorine electrodes, there are still few reports about the electrode method of total chlorine detection.
Total chlorine is the sum of free chlorine and combined chlorine. In other words, the total chlorine is composed of hypochlorite, hypochlorite ion, monochloramine, dichloramine and trichloramine. In previous studies, the researchers found that the concentration of monochloramine, dichloramine, trichloramine and hypochlorite ions has some relationship with the current value at a corresponding sweep potential.22,23 However, the relationship between these characteristics and total chlorine is not clearly given. Besides this, hypochlorite, hypochlorite ion, monochloramine, dichloramine and trichloramine are susceptible to pH changes, which makes it more complicated to calculate the total chlorine from the current values. The soft-sensing technique, which can predict hard-to-measure variables by measuring easy-to-measure variables, may suitable for solving the problem of measuring total chlorine by electrode method.
In this study, we made the total chlorine electrode arrays, designed the experiment and used the experimental data to establish the prediction model to predict the total chlorine concentration in the water. The cyclic voltammetry curves' features of the electrode were extracted by principal component analysis (PCA) and peak sampling (PS) method. Kernel extreme learning machine (KELM) and support vector regression (SVR) were used to establish total chlorine prediction models, and the prediction abilities of different models were compared. To the best of our knowledge, this measurement method of total chlorine has never reported before.
2. Materials, experimental and modeling procedure
2.1 Materials
The N,N-diethyl-p-phenylenediamine sulfate salt was obtained from Sigma-Aldrich. Sodium hypochlorite solution, monopotassium phosphate, dipotassium phosphate and other materials were obtained from Sinopharm Chemical Reagent and were analytical-reagent grade. Deionized water (resistivity = 18.2 MΩ cm) was obtained with Millipore (ADVANTAGE A10) ultrapure water system.2.2 Instrument and equipment
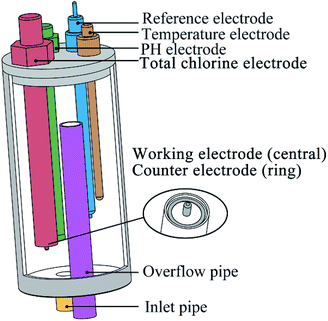
Cyclic voltammetry was performed using a CHI 660E electrochemical workstation (Shanghai Chenhua Apparatus Corporation, China) and measured in a conventional three-electrode cell and performed at a fixed potential range from −0.6 V to +1.2 V with a scan rate of 100 mV s−1.As shown in Fig. 1, the electrode arrays contain five electrodes. The working electrode was a platinum cylinder, 1 mm in diameter and 5 mm in height. The counter electrode was a platinum ring that concentric with the working electrode, 20 mm in diameter and 2 mm in width. Both of the working electrode and the counter electrode were integrated together on one end of a polytetrafluoroethylene rod. It is important to note that during cyclic voltammetry, the solution in the flow cell needs to stop flowing to ensure that the diffusion process on the electrode surface is stable. The reference electrode was an Ag/AgCl (3 M KCl) electrode. The other two electrodes are pH (Hach pHC101, connect to Hach HQ440D) and temperature (PT100, 4-wire, connect to Advantest TR2114 digital thermometer) compensated electrodes. An overflow pipe was designed in the flow cell to suppress the potential impact of the liquid level on the measurement.
2.3 Total chlorine calibration (DPD method)
The total chlorine was calibrated according to ISO 7393-2 standard24 and tested with Hach DR6000 spectrophotometer. The N,N-diethyl-p-phenylenediamine sulfate salt reacts with the free chlorine to form a red color complex. The concentration of free chlorine and total chlorine in the solution can be obtained by measuring the absorbance of the complex with the wavelength of 510 nm. Calibration curves were established using potassium iodate standard solution prior to the experiment. Any solution above the test range (0.03 mg l−1 to 0.5 mg l−1) was pre-diluted before the test to avoid the influence of high concentration of chlorine on color development.2.4 Experiment design
During water treatment, chlorine gas or hypochlorite hydrolyzes in water according to forming hypochlorite and hypochlorite ions.| Cl2 + H2O ⇌ HClO + Cl− + H+ | (1) |
| NaClO + H2O ⇌ HClO + Na+ + OH− | (2) |
| HClO ⇌ ClO− + H+ (pKHClO,25°C = 7.54) | (3) |
As shown by eqn (3), the concentration of hypochlorite ions affect by the pH value of the solution. When the pH is below 5.5, the main component of the solution is hypochlorite. When the pH is above 9.5, hypochlorite ions are the main component of the solution.
6ClO− + 3H2O ⇌ 2ClO−3 + 4Cl− + 6H+ + ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) O2 + 6e O2 + 6e
| (4) |
At a specific potential (about 1.1 V), the electrode reaction can be written as formula (4), and there is a fixed relationship between the reaction current and the concentration of hypochlorite ion.25,26 Therefore, it is feasible to estimate the free chlorine by measuring temperature, pH (above 5.5) and concentration of hypochlorite ion of the solution.
If ammonia is present in the solution, monochloramine, dichloramine and trichloramine are formed in sequence and their reactions are simplified described as follows.
| NH3 + ClO− → NH2Cl + OH− | (5) |
| NH4+ + 2HClO → NHCl2 + 2H2O + H+ | (6) |
| NH4+ + 3HClO → NCl3 + 3H2O + H+ | (7) |
When the pH of solution changes, monochloramine, dichloramine and trichloramine will convert to each other and the reaction equation can be written as follows.
| 2NH2Cl + H+ ⇌ NHCl2 + NH4+ | (8) |
| 3NHCl2 + H+ ⇌ 2NCl3 + NH4+ | (9) |
On the surface of the electrode, electrochemical reduction of chlorine occurs in sequence within a certain voltage range and the current of those reactions can be observed in the cyclic voltammetry curve. Those reactions are described as below.
| NCl3 + H+ + 2e− → NHCl2 + Cl− | (10) |
| NHCl2 + H+ + 2e− → NH2Cl + Cl− | (11) |
| NH2Cl + 2H+ + 2e− → NH4+ + Cl− | (12) |
Although the curve features are not obvious, this study still tries to estimate the total chlorine by processing and calculating the cyclic voltammetry curves. In addition, during the process of adding chlorine, excessive hypochlorite will react with monochloramine to form nitrogen, as shown in formula (13).
| 2NH2Cl + HClO → N2↑ + 3H+ + 3Cl− + H2O | (13) |
When chlorine/ammonia-nitrogen ratio (Cl2/N mass ratio) is higher than 7.6, breakpoint chlorination occurs.27 The combined chlorine decreases with the increase of free chlorine after the breakpoint, and finally the total chlorine is basically made up of free chlorine. Therefore, the chlorine/ammonia-nitrogen ratio is a necessary factor in the total chlorine measurement model.
It can be seen from eqn (5)–(9) and (11) that multiple reactions may occur simultaneously in the process of adding chlorine, and the reaction equilibrium is easily affected by changes in pH, even temperature and pressure. At the same time, the addition of a large amount of chlorine will produce the phenomenon of breaking point chlorination, resulting in the decomposition of chloramine. Therefore, pH, ammonium ion content and chlorine/ammonia-nitrogen ratio was selected as factors in this experiment. The experiment was carried out at a temperature of 20 °C without precise control, so the water temperature was recorded during the experiment and used as one of input of the prediction model. Due to the existence of the overflow pipe, the liquid level in the flow cell did not change dramatically, so the influence of pressure was not been considered in this paper.
The experiment divided into 65 groups, as shown in Table 1. For the first 50 experiments, every 10 groups had the same ammonium concentration and pH value. Firstly, a certain amount of sodium hypochlorite was added to the ammonium chloride solution to control the chlorine/ammonia-nitrogen ratio between 0 and 15. After that, the pH value was adjusted to the design value by adding hydrochloric acid or sodium hydroxide. When the pH value of the solution was stable, the cyclic voltammetry was performed, while the pH value and temperature value of the solution were recorded, and the total chlorine value of the solution was measured by DPD method. As a special case, ammonium chloride was not added in the last 15 groups. In this case, the total chlorine value of the solution is equal to the free chlorine value. In groups 50 to 55, the concentration of total chlorine increased gradually, while in groups 55 to 60 and 61 to 65, only the pH value of the solution adjusted. Similarly, cyclic voltammetry was performed in the last 15 experiments and total chlorine, pH, and temperature were recorded.
| Group | Factors | Result | ||||
|---|---|---|---|---|---|---|
| pH | Temperature (°C) | Ammonia-nitrogen (mg L−1) | Ratio (chlorine/ammonia-nitrogen) | Total chlorine (mg L−1) | ||
| 1 | 9.46 | 20.8 | 10 | 0.00 | 0.0 | Fig. S1(1) |
| 2 | 9.47 | 21.2 | 10 | 0.97 | 4.0 | Fig. S1(2) |
| 3 | 9.52 | 21.6 | 10 | 2.14 | 8.8 | Fig. S1(3) |
| 4 | 9.50 | 21.7 | 10 | 2.58 | 10.6 | Fig. S1(4) |
| 5 | 9.53 | 21.9 | 10 | 3.79 | 15.6 | Fig. S1(5) |
| 6 | 9.48 | 22.0 | 10 | 4.62 | 19 | Fig. S1(6) |
| 7 | 9.51 | 22.0 | 10 | 5.56 | 16.8 | Fig. S1(7) |
| 8 | 9.49 | 22.0 | 10 | 12.75 | 21.2 | Fig. S1(8) |
| 9 | 9.49 | 22.0 | 10 | 13.48 | 24.2 | Fig. S1(9) |
| 10 | 9.49 | 22.0 | 10 | 14.60 | 28.8 | Fig. S1(10) |
| 11 | 8.50 | 19.9 | 20 | 0.00 | 0.0 | Fig. S1(11) |
| 12 | 8.52 | 20.2 | 20 | 0.34 | 2.8 | Fig. S1(12) |
| 13 | 8.49 | 20.9 | 20 | 1.20 | 9.9 | Fig. S1(13) |
| 14 | 8.51 | 21.5 | 20 | 2.48 | 20.4 | Fig. S1(14) |
| 15 | 8.54 | 21.7 | 20 | 3.21 | 26.4 | Fig. S1(15) |
| 16 | 8.53 | 21.9 | 20 | 3.77 | 31 | Fig. S1(16) |
| 17 | 8.48 | 21.9 | 20 | 6.84 | 12.5 | Fig. S1(17) |
| 18 | 8.48 | 22.1 | 20 | 7.23 | 6.0 | Fig. S1(18) |
| 19 | 8.52 | 22.2 | 20 | 9.12 | 12.5 | Fig. S1(19) |
| 20 | 8.50 | 22.1 | 20 | 10.27 | 22 | Fig. S1(20) |
| 21 | 7.45 | 20.0 | 30 | 0.00 | 0.0 | Fig. S1(21) |
| 22 | 7.44 | 20.3 | 30 | 0.87 | 10.8 | Fig. S1(22) |
| 23 | 7.51 | 20.7 | 30 | 1.78 | 22 | Fig. S1(23) |
| 24 | 7.50 | 21.0 | 30 | 2.43 | 30 | Fig. S1(24) |
| 25 | 7.46 | 21.2 | 30 | 3.48 | 43 | Fig. S1(25) |
| 26 | 7.49 | 21.2 | 30 | 5.94 | 41 | Fig. S1(26) |
| 27 | 7.45 | 21.0 | 30 | 6.26 | 33 | Fig. S1(27) |
| 28 | 7.44 | 20.7 | 30 | 7.56 | 1.0 | Fig. S1(28) |
| 29 | 7.51 | 20.6 | 30 | 8.38 | 9.6 | Fig. S1(29) |
| 30 | 7.51 | 20.7 | 30 | 9.58 | 24.5 | Fig. S1(30) |
| 31 | 6.50 | 17.5 | 40 | 0.00 | 0.0 | Fig. S1(31) |
| 31 | 6.5 | 18.0 | 40 | 1.03 | 17 | Fig. S1(32) |
| 33 | 6.53 | 18.5 | 40 | 1.94 | 32 | Fig. S1(33) |
| 34 | 6.54 | 18.8 | 40 | 3.10 | 51 | Fig. S1(34) |
| 35 | 6.50 | 19.2 | 40 | 3.83 | 63 | Fig. S1(35) |
| 36 | 6.51 | 19.6 | 40 | 4.25 | 70 | Fig. S1(36) |
| 37 | 6.50 | 19.5 | 40 | 5.72 | 62 | Fig. S1(37) |
| 38 | 6.50 | 19.6 | 40 | 5.96 | 54 | Fig. S1(38) |
| 39 | 6.55 | 19.4 | 40 | 7.39 | 6.8 | Fig. S1(39) |
| 40 | 6.53 | 19.9 | 40 | 8.94 | 22 | Fig. S1(40) |
| 41 | 5.50 | 18.9 | 50 | 0.00 | 0.0 | Fig. S1(41) |
| 42 | 5.46 | 19.5 | 50 | 0.87 | 18 | Fig. S1(42) |
| 43 | 5.54 | 19.8 | 50 | 1.94 | 40 | Fig. S1(43) |
| 44 | 5.57 | 20.2 | 50 | 3.28 | 54 | Fig. S1(44) |
| 45 | 5.52 | 20.4 | 50 | 4.25 | 70 | Fig. S1(45) |
| 46 | 5.48 | 20.5 | 50 | 5.04 | 83 | Fig. S1(46) |
| 47 | 5.53 | 20.6 | 50 | 5.17 | 80 | Fig. S1(47) |
| 48 | 5.51 | 20.6 | 50 | 5.56 | 67 | Fig. S1(48) |
| 49 | 5.49 | 20.4 | 50 | 7.08 | 17 | Fig. S1(49) |
| 50 | 5.54 | 19.8 | 50 | 8.82 | 20 | Fig. S1(50) |
| 51 | 5.51 | 16.8 | 0 | — | 0.0 | Fig. S1(51) |
| 52 | 7.75 | 17.0 | 0 | — | 6.2 | Fig. S1(52) |
| 53 | 8.09 | 17.0 | 0 | — | 9.4 | Fig. S1(53) |
| 54 | 8.32 | 17.5 | 0 | — | 19.6 | Fig. S1(54) |
| 55 | 8.68 | 17.9 | 0 | — | 24.5 | Fig. S1(55) |
| 56 | 7.89 | 18.2 | 0 | — | 24.5 | Fig. S1(56) |
| 57 | 7.42 | 18.3 | 0 | — | 24.5 | Fig. S1(57) |
| 58 | 7.04 | 18.5 | 0 | — | 24.5 | Fig. S1(58) |
| 59 | 6.49 | 18.7 | 0 | — | 24.5 | Fig. S1(59) |
| 60 | 4.54 | 18.8 | 0 | — | 24.5 | Fig. S1(60) |
| 61 | 7.02 | 19.0 | 0 | — | 44 | Fig. S1(61) |
| 62 | 7.40 | 19.0 | 0 | — | 44 | Fig. S1(62) |
| 63 | 7.84 | 19.2 | 0 | — | 44 | Fig. S1(63) |
| 64 | 8.55 | 19.2 | 0 | — | 44 | Fig. S1(64) |
| 65 | 9.37 | 19.2 | 0 | — | 44 | Fig. S1(65) |
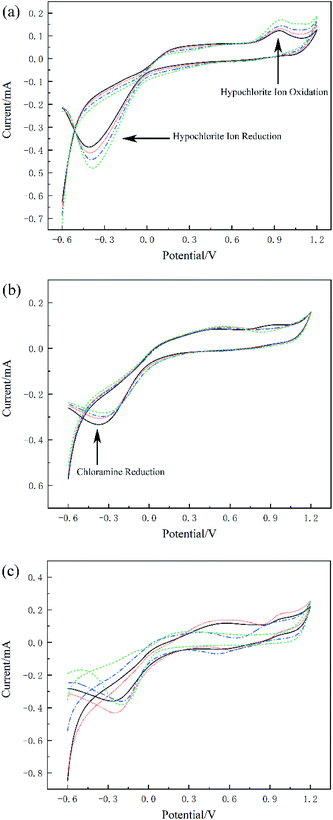
When ammonium ions absent in the solution, the cyclic voltammetry curve reflects the redox process of hypochlorite ions, as shown in Fig. 2(a). In this figure, black solid line is group 52 with total chlorine 6.2 mg L−1, red dot line is group 53 with total chlorine 9.4 mg L−1, blue dot dash line is group 54 with total chlorine 19.6 mg L−1, green dash line is group 55 with total chlorine 24.5 mg L−1. There was an obvious oxidation peak of hypochlorite ions around 1 V and an obvious reduction peak of hypochlorite ions around −0.3 V. The peak potential of these two peaks is proportional to the concentration of hypochlorite, which indicates that cyclic voltammetry can effectively detect the presence of hypochlorite ions. Fig. 2(b) shows another case, four groups with similar total chlorine values but completely different chloramines. In this figure, black solid line is group 6 with total chlorine 19 mg L−1, red dot line is group 14 with total chlorine 20.4 mg L−1, blue dot dash line is group 23 with total chlorine 22 mg L−1, green dash line is group 32 with total chlorine 17 mg L−1. The apparent non-coincidence of the cyclic voltammetry curve occurred in the region below −0.2 V, which reflected the difference in the reduction potential caused by the chloramine concentration changes. When the total chlorine and chloramine of the solution change at the same time, the characteristics of the cyclic voltammetry curve become difficult to distinguish directly, as shown in Fig. 2(c). In this figure, black solid line is group 44 with total chlorine 54 mg L−1, red dot line is group 46 with total chlorine 83 mg L−1 blue dot dash line is group 48 with total chlorine 67 mg L−1, green dash line is group 49 with total chlorine 17 mg L−1. As can be seen from the figure, there are great differences between different cyclic voltammetry curves, especially for the reduction curves, multiple reduction reactions occur simultaneously, which making it difficult to measure the concentration of a single substance. In this case, establishing a prediction model of total chlorine is a potential solution to total chlorine measurement.
2.5 Modeling procedure
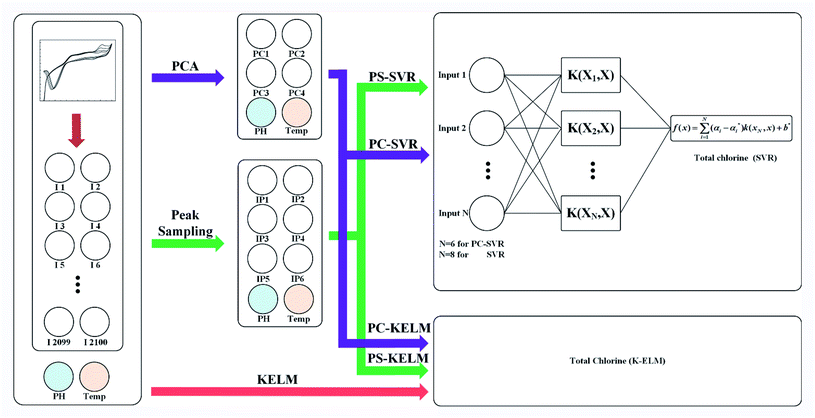
In order to reduce the oxygen interference and improve the accuracy of the model, only part of the curves near the oxidation peak that ranges from 0.9 V to 1.2 V were intercepted, while all reduction curves that range from 1.2 V to −0.6 V were preserved. The sampling rate of electrochemical workstation was 1000 points per volt, so each cyclic voltammetry curve contains 2100 dimensions.Fig. 3 represents the flow diagram of the modeling procedure. The prediction model consists of two stages. One is preprocessing of the original data, the other is the prediction model establishment and evaluation. Each original dataset contains pH, temperature and cyclic voltammetry curves with a total number of 2102 dimensions. During data preprocessing, only the 2100 dimensional data of the cyclic voltammetry curves were extracted by PCA or peak sampling method, and the pH value and temperature in the original dataset remained unchanged. Those two data and the extracted data constitute a new data set for the establishment of the prediction model.
On the first stage, the feature of the cyclic voltammetry curve was extracted by peak sampling and PCA method. For the former method, the peak voltage of the cyclic voltammetry curve needs to be determined first. As it is shown in K. A. S. Pathiratne's25 and F. Terzi's23 research, the oxidation peak of hypochlorite ion appeared at the position of 1030 mV, and the five reduction peaks were appeared at the position of −108 mV/−350 mV, 0 mV/380 mV and 200 mV respectively, representing electroreduction monochloramine, dichloramine and trichloramine. By looking up the file of the cyclic voltammetry curve, the current values of six peak voltages in each curve can be obtained. These six current values and the corresponding pH and temperature data will be used as new dataset in the subsequent modeling process. In this way, the original data is extracted to eight dimensions. Here, we call this method as peak sampling method.
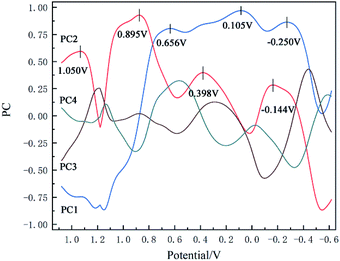
Another data processing method is the PCA method. In this method, the pH value and temperature in the original dataset remained unchanged, too. The 2100-dimensional original cyclic voltammetry curve dataset is represented as a linearly independent vector among various dimensions by linear transformation28 and replaced with fewer comprehensive variables under the principle of minimum original data loss.29 The original cyclic voltammetry curve data with dimension P can be expressed as X = (x1, x2, x3,…xp), in order to make all data have the same weight in the calculation process, it is necessary to standardize the data according to the following formula30,31 (14):
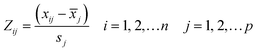 | (14) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) j and sj is the mean value and standard deviation of the original cyclic voltammetry curve data respectively.
j and sj is the mean value and standard deviation of the original cyclic voltammetry curve data respectively.
To verify whether the PCA method is valid on the data set, the Kaiser–Meyer–Olkin (KMO) test was carried out. The KMO index can be calculated by the following formula31,32 (15):
 | (15) |
By this method, each cyclic voltammetry curves was extracted into four principal components. These four principal components and the corresponding pH and temperature data will be used as new dataset in the subsequent modeling process. In this way, the original data is extracted to six dimensions. Here, we call this method as PCA method.
On the second stage, SVR and KELM were used to model those data samples obtained by the two feature extraction methods mentioned above, which are respectively called principal component analysis support vector regression (PC-SVR), peak sampling support vector regression (PS-SVR), principal component analysis kernel extreme learning machine (PC-KELM) and peak sampling kernel extreme learning machine (PS-KELM). Because of the speed of processing large data sets with KELM is extremely fast, this arithmetic was also used to model the original data directly.
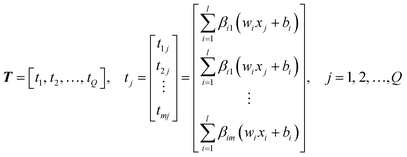 | (16) |
Defined here:
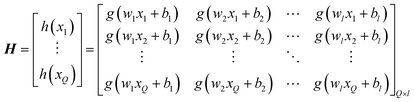 | (17) |
The output of SLFN can be expressed by the following formula:
| Hβ = T′ | (18) |
The output of ELM can be expressed by the following formula:
| f(x) = h(x)β = h(x)HT(HTH)−1T′ | (19) |
To avoid singularity of HTH, a variable I/C is introduced, where I is the identity matrix and C is the penalty factor.35 The following equation can be obtained:
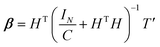 | (20) |
Substitute eqn (20) into eqn (19), the output of ELM can be written as:
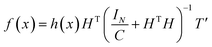 | (21) |
By introducing kernel function, the dot product of vector in high dimensional space is operationally mapped to low dimensional space. The kernel function is defined as k(x,y) = 〈ϕ(x),ϕ(y)〉 and the kernel matrix is constructed as Ω = HTH, Ωi,j = 〈h(xi),h(xj)〉. So the operations of HTH and h(x)HT in high dimensional space can be given by kernel matrix Ω in low dimensional space. KELM uses kernel function to replace the random value of the weight coefficient between the input layer and the hidden layer in ELM. Hence, there is no need to set the number of hidden layer nodes, which improves the generalization and accuracy of the model.36 The output function of KELM can be represented as:
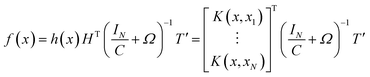 | (22) |
Let the spatial regression function be the following equation:
| f(x) = w·Φ(x) + b | (23) |
In order to improve the generalization ability of the model and prevent over-fit relaxation variables ξi and 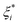 are introduced, and the objective function becomes:
are introduced, and the objective function becomes:
The constraint conditions can be written as:
After that, Lagrange functions and kernel functions are introduced and converted into dual forms, and the regression function can be expressed as:
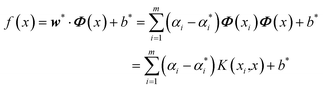 | (24) |
3. Result and discussion
3.1 Feature extraction
Before analyzing the cyclic voltammetry curve by using PCA, KMO test is applied to evaluate the strength of the relationship between the data sets. According to formula (15), the KMO index of the experimental data set is 0.769, which is higher than 0.5, indicating that there is sufficient correlation between the data and it is suitable to use PCA for dimension reduction.As can be seen from the Table 2, the cumulative variance of the first four principal components (PC1–PC4) reaches 95.39%. Therefore, the first four principal components are selected to replace the original cyclic voltammetry curve data set. These four principal components and the corresponding pH and temperature data will be used as new characteristics in the subsequent modeling process. With PCA, the final eigenvector is u = [pH,T,PC1,PC2,PC3,PC4].
| PC | Variance proportion/% | Cumulative variance proportion/% |
|---|---|---|
| PC1 | 55.7055 | 55.7055 |
| PC2 | 23.8902 | 79.5957 |
| PC3 | 8.6415 | 88.2372 |
| PC4 | 7.1534 | 95.3906 |
| PC5 | 1.7478 | 97.1384 |
| PC6 | 1.0480 | 98.1864 |
| PC7 | 0.7110 | 98.8974 |
The loading matrix curves of the first four principal components are obtained through calculation, as Fig. 4. It can be seen from the loading curve in the range from 0.9 V to 1.2 V that PC2 exhibits high overall loading, and its peak potential is 1.050 V. This peak potential is consistent with the oxidation voltage of hypochlorite ions on the electrode surface (formula (4)), which proves that the concentration change characteristics of hypochlorite ions were captured successfully by the method of PCA. In the voltage region corresponding to the reduction curve, PC2 exhibits high overall loading in the range of 1.2 V to 0.8 V, and its voltage peak value is 0.895 V, which may indicate that chlorine gas in solution was reduced here.40 The reaction equation is shown below:
| Cl2(aq) + 2e− → 2Cl− | (25) |
PC1 exhibits high loading over the whole range of 0.8 V to −0.6 V. Only three small peaks appear within this relatively flat curve. The first peak value at 0.656 V may represent the reduction of hypochlorite as following equation:40
| HClO(aq) + H+ + 2e− → Cl− + H2O | (26) |
The loading curve from 0.6 V to −0.6 V may represent the overall reduction process of chloramine. Just like Barbara Piela's research results,22 in the cyclic voltammetry curve, the position and gradient of chloramine reduction peak may change under different pH values and chloramine type, indicating that it is not sufficient to judge chloramine concentration only by peak value. This is the main difference between PCA and peak sampling method.
3.2 Model optimization
All data were(was) divided into two parts, the training set and the testing set. Among the 65 samples, 48 data used for the training set and 16 data used for the testing set. Meanwhile, in order to improve the generalization ability and prevent over-fitting of the model, k-folds cross-validation method was adapted in this paper. This method divides the data into K equal parts, in which K − 1 part used as the training set and the remaining part used as the validation set. Loop this process for K times, and each subset will used as the validation subset. Finally, the model generalization ability corresponding to each parameter is estimated by calculating the mean value of the validation sets' result. In this paper, 4 times of cross validation were used for modeling, and four statistical methods were introduced to evaluate the model performance.The grid method was used to find the optimal parameters for the data set processed by PCA. For PC-KELM, the number of the hidden layers can be automatically adjusted. In this paper, Radial Basis Function (RBF) K(x,y) = e−γ‖x−y‖2 were selected and the optimal result of the grid method is penalty coefficient C = 5 while super parameter γ = −3. For PC-SVR, the same RBF were selected and the optimal result of the grid method is penalty coefficient C = 3 while super parameter γ = 0.0221.
The similar optimization method was used for the peak sampling data. For PS-KELM, the optimal result of grid method is penalty coefficient C = 5 while super parameter γ = −0.5. For PS-SVR, the optimal result of grid method is penalty coefficient C = 3 while super parameter γ = 0.3536.
The KELM method with the direct raw data set as input was optimized in the same way and the result is penalty coefficient C = 5 while super parameter γ = 9.
3.3 Model evaluation
Four statistics were employed to evaluate the model.• Root mean square error (RMSE) is a very common error prediction method for general purpose. It can be written as follow:
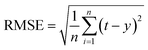 | (27) |
• Mean absolute error (MAE) reflects the size of the actual prediction error. It can be written as follow:
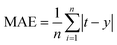 | (28) |
The smaller the MAE is, the better the model effect.
• Coefficient of determination (R2) represents the proportion of dependent variables that can be explained by controlled independent variables, which can be written as follow:
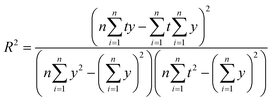 | (29) |
The larger the R-squared is, the better the model effect.
• Nash–Sutcliffe efficiency coefficient (NSE) represents the degree of coincidence between the plot of true value and predicted value and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line. It can be written as follow:
1 line. It can be written as follow:
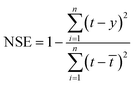 | (30) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) is the average of the true value of total chlorine. If the value of NSE is close to 1, the model is proved to be very accurate. When NSE value approaches 0, it means that the predicted value is close to the average value of the true value. When NSE value is much less than 0, the reliability of the model is poor and unacceptable.
is the average of the true value of total chlorine. If the value of NSE is close to 1, the model is proved to be very accurate. When NSE value approaches 0, it means that the predicted value is close to the average value of the true value. When NSE value is much less than 0, the reliability of the model is poor and unacceptable.
Table 3 shows the performance comparison of the algorithms used in this article. For the training data, all the models showed high R2 and NSE values, and the prediction of the total chlorine concentration was in good agreement with the experimental results. We mainly care about the generalization performance of the model on the unknown data set, that is, the performance on the testing set, as shown in Fig. 5. The SVR model of PCA dimensionality reduction data (Fig. 5(a) and (b)) shows a high prediction performance for the total chlorine concentration in the testing set. That is because of the core goal of SVR is to find support vectors, and the number of samples actually participating in model construction is far less than the given number of samples, which is suitable for small sample conditions. KELM model (Fig. 5(c) and (d)), which need to traverse samples, tend to show high fitting of training set and poor prediction performance of testing set because there are not enough samples to adjust each weight, resulting in over-fitting.
| Method | Data set | RMSE | MAE | R2 | NSE |
|---|---|---|---|---|---|
| a The optimal result of the training set.b The optimal result of the testing set. | |||||
| PC-SVR | Training data | 0.0549 | 0.0301 | 0.9883 | 0.9879 |
| Testing data | 0.0900a | 0.0619a | 0.9689a | 0.9639a | |
| PS-SVR | Training data | 0.0328 | 0.0204 | 0.9949 | 0.9949 |
| Testing data | 0.1071 | 0.0776 | 0.9587 | 0.9505 | |
| PC-KELM | Training data | 0.0893 | 0.0669 | 0.9701 | 0.9686 |
| Testing data | 0.1131 | 0.0825 | 0.9524 | 0.9434 | |
| PS-KELM | Training data | 0.1550 | 0.1168 | 0.9103 | 0.9072 |
| Testing data | 0.1972 | 0.1501 | 0.8705 | 0.8417 | |
| KELM | Training data | 0.0083b | 0.0069b | 0.9999b | 0.9998b |
| Testing data | 0.3516 | 0.2939 | 0.5666 | 0.3737 | |
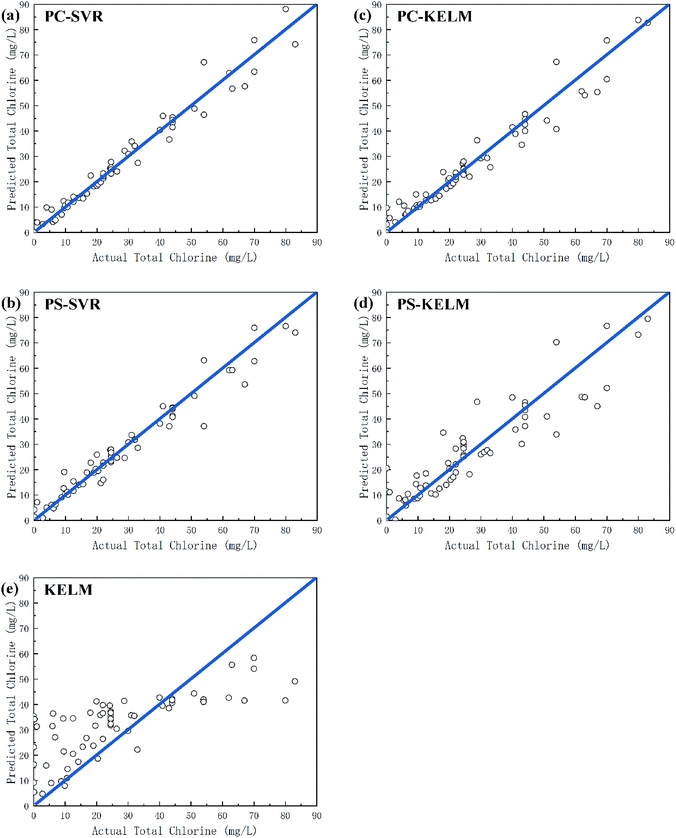 | ||
| Fig. 5 Relationship between actual values and predicted values of total chlorine for the testing set. (a) PC-SVR model. (b) PS-SVR model. (c) PC-KELM model. (d) PS-KELM model. (e) KELM model. | ||
In addition, the model performance of the PCA data sets is generally superior to peak sampling data set, this is because PCA computes and processes the entire cyclic voltammetry curve, preserving the original information to the maximum extent, while peak sampling is easier to ignore some useful information that cannot be observed by the naked eye, and richer feature information is undoubtedly better in model training.
The dimension of data is another factor that affects the model training. As shown in the Fig. 5(c)–(e), the training set results of KELM model are optimal on most indicators, but the test set results are the worst. The KELM model shows severe over-fitting when modeling the original data, and the modeling effect of PCA is obviously better than that of the original data. This indicates that the feature extraction of the cyclic voltammetry curve is a necessary and important part in the measurement model.
3.4 Detection range
According to IUPAC method,41 20 blank solutions (0.001 M sodium chloride was added as a supporting electrolyte) were prepared to determine the detection limit of each prediction model. The detection limit xL can be calculated by the following formula:
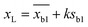 | (31) |
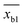 and sb1 represents the mean and standard deviation of the blank measures. A value of k = 3 was used in the calculation. According to the of training set of the prediction model, the detection range and the average quoted error can be calculated, as shown in Table 4. Similar to the conclusion in the previous section, PC-SVR model has the best prediction power, and its detection limit is 2.42 mg L−1. On the one hand, those errors caused by the insufficient precision of the model. On the other hand, they also affected by uncompensated interferences in the solution, like dissolved oxygen, which form background noise and affect the measurement in low concentration.
and sb1 represents the mean and standard deviation of the blank measures. A value of k = 3 was used in the calculation. According to the of training set of the prediction model, the detection range and the average quoted error can be calculated, as shown in Table 4. Similar to the conclusion in the previous section, PC-SVR model has the best prediction power, and its detection limit is 2.42 mg L−1. On the one hand, those errors caused by the insufficient precision of the model. On the other hand, they also affected by uncompensated interferences in the solution, like dissolved oxygen, which form background noise and affect the measurement in low concentration.
| Method | Detection limit (mg L−1) | Detection range (mg L−1) | Average quoted error (%) |
|---|---|---|---|
| PC-SVR | 2.42 | 2.42–83 | 3.8% |
| PS-SVR | 9.62 | 9.62–83 | 3.9% |
| PC-KELM | 15.45 | 15.45–83 | 4.6% |
| PS-KELM | 35.40 | 35.40–83 | 11.5% |
| KELM | 53.68 | 53.68–83 | 23.7% |
3.5 Real sample test
Two sources of water, namely tap water (Chaoyang District, Beijing, China) and waste water (Sun. River, Shunyi District, Beijing, China), were selected as the tested samples. After sedimentation, the wastewater was filtered with a 5 μm precision polypropylene filter to ensure its turbidity was low enough to meet the DPD test. Sodium hypochlorite solution was added to the two samples gradually, and the output value of PC-SVR model and the test value of DPD method were recorded, as shown in Table 5. For tap water, the PC-SVR model predicted the concentration of total chlorine accurately and the average prediction deviation is 1.98 mg L−1. However, when measuring wastewater samples, the prediction accuracy of PC-SVR model decreased, with an average prediction deviation of 3.52 mg L−1. This change may cause by a large number of impurities in wastewater. However, PC-SVR model still shows the correct trend of total chlorine.| No. | Tap water | Wastewater | ||||
|---|---|---|---|---|---|---|
| PC-SVR (mg L−1) | DPD method (mg L−1) | Deviation (mg L−1) | PC-SVR (mg L−1) | DPD method (mg L−1) | Deviation (mg L−1) | |
| 1 | 2.6 | 0.03 | 2.53 | 4.5 | 0 | 4.5 |
| 2 | 7.3 | 4.6 | 2.7 | 7.7 | 3.5 | 4.2 |
| 3 | 13.8 | 11.2 | 2.6 | 12.9 | 9.1 | 3.8 |
| 4 | 16.8 | 15.9 | 0.9 | 19.8 | 15.2 | 4.6 |
| 5 | 20.9 | 18.7 | 2.2 | 24.5 | 21.2 | 3.3 |
| 6 | 26.3 | 24.8 | 1.5 | 11.1 | 9.4 | 1.7 |
4. Conclusions
In this study, a simple electrode arrays were fabricated to detect total chlorine. By applying a fixed rate of scanning potential on the electrode, 1.67 times cycle voltammetry scans can be completed per minute. Two different algorithms are used to process the curves after dimension reduction. The results show that both PCA and peak sampling method can effectively reduce the dimension of cyclic voltammetry, but PCA retains more original information and thus has a better effect than peak sampling method. Compared with KELM, SVR model achieves the best predict power because of the limited experimental samples. The optimal combination is PC-SVR, and the model evaluation results of the testing set are as follows: RMSE = 0.0900, MAE = 0.0619, R2 = 0.9689 and NSE = 0.9639, which indicate this method can predict the total chlorine concentration effectively. Experimental results show that the detection limit of PC-SVR method is 2.42 mg L−1. When measuring tap water samples, the prediction accuracy of the PC-SVR method reached to the expected performance. However, the test of wastewater shows that some impurities disturbed this measurement method. Retraining the model according to the measurement scene will effectively improve the anti-interference ability of the model. This method is suitable for real-time and continuous monitoring of water treatment process. It can also be made into a small portable device for measuring total chlorine in field or ship.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61771034).References
- C. T. Butterfield, E. Wattie, S. Megregia and C. W. Chambers, Public Health Rep., 1943, 58, 1837–1866 CrossRef CAS.
- P. J. Vikesland and L. Raskin, Environ. Sci.: Water Res. Technol., 2016, 2, 561–564 RSC.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Marinas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS PubMed.
- N. J. Ashbolt, Curr. Environ. Health Rep., 2015, 2, 95–106 CrossRef CAS.
- B. F. Arnold and J. M. Colford Jr, Am. J. Trop. Med. Hyg., 2007, 76, 354–364 CrossRef.
- A. Omarova, K. Tussupova, R. Berndtsson, M. Kalishev and K. Sharapatova, Int. J. Environ. Res. Public Health, 2018, 15, 495 CrossRef.
- R. A. A. Carter and C. A. Joll, J. Environ. Sci., 2017, 58, 19–50 CrossRef.
- K. Scarlett, D. Collins, L. Tesoriero, L. Jewell, F. van Ogtrop and R. Daniel, Eur. J. Plant Pathol., 2015, 145, 27–38 CrossRef.
- A. Angelakis and S. Snyder, Water, 2015, 7, 4887–4895 CrossRef CAS.
- B. Petrie, R. Barden and B. Kasprzyk-Hordern, Water Res., 2015, 72, 3–27 CrossRef CAS PubMed.
- Y. H. Chuang, S. Chen, C. J. Chinn and W. A. Mitch, Environ. Sci. Technol., 2017, 51, 13859–13868 CrossRef CAS.
- W. Li, T. Jain, K. Ishida and H. Liu, Environ. Sci.: Water Res. Technol., 2017, 3, 128–138 RSC.
- S. Nuanualsuwan and D. O. Cliver, Appl. Environ. Microbiol., 2003, 69, 350–357 CrossRef CAS.
- M. Deborde and U. von Gunten, Water Res., 2008, 42, 13–51 CrossRef CAS.
- J. T. Wang, M. H. Chen, H. J. Lee, W. B. Chang, C. C. Chen, S. C. Pai and P. J. Meng, Int. J. Mol. Sci., 2008, 9, 542–553 CrossRef CAS.
- I. Sarudi and A. Szabó, Anal. Lett., 2003, 36, 853–859 CrossRef CAS.
- M. Huang and Y. Hang, Anal. Lett., 2012, 45, 1401–1411 CrossRef CAS.
- H. Osterlund, I. Rodushkin, K. Ylinenjarvi and D. C. Baxter, Waste Manage., 2009, 29, 1258–1264 CrossRef.
- A. Jakobik-Kolon, A. Milewski, P. Dydo, M. Witczak and J. Bok-Badura, Molecules, 2018, 23, 487 CrossRef PubMed.
- G. T. Druzian, M. S. Nascimento, R. F. Santos, M. F. Pedrotti, R. C. Bolzan, F. A. Duarte and E. M. M. Flores, Talanta, 2019, 199, 124–130 CrossRef CAS.
- J. C. Synnot and A. M. Smith, Chemistry for Protection of the Environment, 1986, pp. 777–791, DOI:10.1016/s0166-1116(08)70979-8.
- B. Piela and P. K. Wrona, J. Electrochem. Soc., 2003, 150, 255–265 CrossRef.
- F. Terzi, B. Zanfrognini, C. Zanardi, L. Pigani and R. Seeber, Electroanalysis, 2012, 24, 833–841 CrossRef CAS.
- ISO, Standard, 2017, ISO 7393-2:2017, 1–19.
- K. A. S. Pathiratne, S. S. Skandaraja and E. M. C. M. Jayasena, J. Natl. Sci. Found. Sri Lanka, 2008, 36, 25–31 CrossRef CAS.
- F. Kodera, M. Umeda and A. Yamada, Anal. Chim. Acta, 2005, 537, 293–298 CrossRef CAS.
- Z. Qiang and C. D. Adams, Environ. Sci. Technol., 2004, 38, 1435–1444 CrossRef CAS.
- E. N. Paula, K. Amine, P. Anne, P. Jean-Luc, O. Naim, D. Claude and E. A. Desiree, Ecol. Indic., 2019, 104, 13–23 CrossRef.
- S. Gu, J. Wang and Y. Wang, Food Chem., 2019, 292, 325–335 CrossRef CAS PubMed.
- S. Narasimhan and S. L. Shah, Contr. Eng. Pract., 2008, 16, 146–155 CrossRef.
- S. Shokri, M. T. Sadeghi, M. A. Marvast and S. Narasimhan, J. Cent. South Univ., 2015, 22, 511–521 CrossRef CAS.
- S. Shrestha and F. Kazama, Environ. Model. Softw, 2007, 22, 464–475 CrossRef.
- H. Guang Bin, Z. Qin Yu and S. Chee Kheong, presented in part at the 2004 IEEE International Joint Conference on Neural Networks, IEEE Cat. No. 04CH37541, 2004 Search PubMed.
- G. B. Huang, Q. Y. Zhu and C. K. Siew, Neurocomputing, 2006, 70, 489–501 CrossRef.
- G. B. Huang, H. Zhou, X. Ding and R. Zhang, IEEE Trans. Syst. Man Cybern. B Cybern., 2012, 42, 513–529 Search PubMed.
- W. Y. Deng, Y. S. Ong, P. S. Tan and Q. H. Zheng, Neurocomputing, 2016, 174, 72–84 CrossRef.
- C. Hangyang, D. Xiangwu, Z. Wuneng and D. Renqiang, Int. J. Electr. Power Energy Syst., 2019, 110, 653–666 CrossRef.
- L. Yang, H. Xu and Z. Jin, J. Cleaner Prod., 2019, 227, 472–482 CrossRef CAS.
- R. Ratolojanahary, R. H. Ngouna, K. Medjaher, J. Junca-Bourié, F. Dauriac and M. Sebilo, Expert Syst. Appl., 2019, 131, 299–307 CrossRef.
- K. Fumihiro, U. Minoru and Y. Akifumi, Bunseki Kagaku, 2009, 58, 583–594 CrossRef.
- IUPAC, Spectrochim. Acta, Part B, 1978, 33, 247–269 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06609h |
| This journal is © The Royal Society of Chemistry 2019 |