DOI:
10.1039/C9RA05916D
(Paper)
RSC Adv., 2019,
9, 41970-41976
Sheath-less high throughput inertial separation of small microparticles in spiral microchannels with trapezoidal cross-section†
Received
30th July 2019
, Accepted 28th November 2019
First published on 18th December 2019
Abstract
Various mechanisms of different designs have emerged for the purpose of microparticle separation and cell sorting. The main goals behind such designs are to create high throughput and high purity sample isolation. In this study, high efficiency, high throughput and precise separation of microparticles under inertial lift and drag forces induced by trapezoidal curvilinear channels are reported. This work is the first to focus and recover 2 from 5 μm and 2 from 10 μm particles in spiral channels in a sheath-less flow device, which reduces the overall complexity of the system and allows for higher throughput. The new microfluidic chip design is fabricated in glass using femtosecond laser ablation. In addition, mathematical force calculations were conducted during the design phase of the microfluidic channels and compared with experiments. The results show a close prediction of the equilibrium position of the tested microparticles.
Introduction
Size-based microparticle separation has drawn a lot of interest due to its applications in biomedical and biological research.1–6 Conventional separation techniques such as centrifugation, filtration, and sedimentation are associated with wearing and clogging, which affect their efficiency and reliability.7 Processing biological samples through microfluidic devices like focusing,8 on-chip labelling,9 separation,10,11 mixing12,13 and diagnostics10 is an area of high relevance to the life science community. Several methods have been developed to address this matter, which can be classified as active or passive.14 The active methods rely on external forces to manipulate the microparticle's position, such as dielectrophoretic (DEP)15 and magnetic forces.16 On the contrary, passive methods do not require any kind of external forces and separate microparticles based on physical properties such as channel geometry, particle size, and the characteristics of the fluid medium. Pinched flow fractionation,17 deterministic lateral displacement18 and inertial migration19 are well-known passive techniques, they depend on inertial forces inside the fluid that can typically be neglected in microfluidics when operating at low Reynolds numbers in the Stokes regime. In straight microfluidic channels, microparticles are driven away from the walls due to the asymmetric wake that forms when a particle is close to the wall,20 while the parabolic velocity profile in the Poiseuille flow induces an opposing shear gradient lift force by which the particles migrate towards the channel walls. To achieve high purity microparticle separation, the minimum number of force equilibrium positions for each particle size has to be obtained. In square microchannels (h/w = 1), four streamlines of particles form close to the channel's center where the wall and shear gradient lift forces are balanced, whereas in rectangular channels with (h/w < 1), two symmetric focusing positions result around the channel's center. Complex secondary flows are induced by using curved channel arrangements as in spiral microfluidics,21 or by forcing the fluid to follow a curved path as in contraction-expansion arrays (CEAs).22 In either method, two counter-rotating vortices (Dean vortices) develop at the upper and lower halves of the channel's cross-section due to the shift of the maximum velocity point towards the outer wall,23 which enhances particle focusing and adds an additional force that induces particle migration in a lateral direction across the channel's width.24 Spiral microchannels consist of a multi-turn loop; the side walls of the channels are referred to as the inner and outer walls, depending on which is closer to the spiral center. Given certain channel dimensions, larger particles experience higher lift forces and, therefore, have the tendency to migrate towards the inner wall. Moreover, drag forces are dominant on smaller particles, which re-circulate them to eventually settle in their equilibrium position25 where its location depends on the Reynolds number and the ratio of inertial lift forces to Dean drag force.26 Microparticle separation requires particles to focus in different positions to be selectively isolated through separate outlets; however, in a Dean flow fractionation device with a rectangular cross-section, the distance between the particles' focusing position is minimal because the centers of the Dean vortices are located at the center of the channel's cross-section. Therefore, spiral channels with trapezoidal cross-sections27,28 are used to shift the centers of vortices towards the deepest wall, creating a wider distance between focused particles of different sizes. Recently, multiple inertial mechanisms besides spiral microfluidics have been developed to separate smaller microparticles. Wang et al.29 demonstrated an asymmetric serpentine microfluidic channel of 20 μm × 10 μm (width × height) to focus 2 μm particles and 10 μm × 5 μm for 0.92 μm. Since the channels are small, a high-pressure syringe pump was needed to allow for high flow rates up to 1400 μL min−1 to increase the channel's throughput. Also, Cruz et al.30 presented a method to focus 0.5 and 0.7 μm particles and separate 1 and 2 μm particles with two curves connected with a small turn; the channel was 20 μm in width and 10 μm in depth to match FD and FL within the range of available flow rates provided by the pump. Cruz et al.30 turned to a high-performance liquid chromatography (HPLC) pump to achieve high pressure values, which is uncommon to the microfluidics community.
Several attempts have been made to focus and separate 2 μm in spiral channels, however, most designs used a sheath fluid and worked at low flow rates due to the high pressure induced in the small channel geometry as reported by Bhagat et al. and Lee et al.31,32 In a previous work,33 2 μm particles were focused by implementing microchambers along the last turn of a spiral channel; that design produced thin focusing streams but could not separate microparticles since all sizes focused near the inner wall. In this paper, we study the trapezoidal microfluidic channel's ability to separate small microparticles down to 2 μm in high throughput without utilizing a high-pressure pump and without adding a sheath fluid that complicates the testing setup and might limit its use in low setup areas, achieving a separation between 2 and 5 μm, and 2 and 10 μm fluorescent microparticles.
Implementing a sheath-less inertial focusing device reduces the setup complexity and most importantly, the number of expensive syringe pumps,34 because a pump would be needed for every buffer inlet. The total flow rate (sample flow rate + the buffer solution flow rate) that is often used to describe the focusing flow rate, can be higher than its sheath-less counterpart; however, unlike sheath-less focusing, the output fluid of a sheath-based device often has similar or lower concentration in comparison with the sample fluid, due to the addition of a buffer solution that dilutes the sample inside the focusing channels. Therefore, sheath-based focusing would not be the best choice for use in a particle concentration device.
Materials and methods
Microfluidic chip design and fabrication
Trapezoidal microfluidic chips with different dimensions were fabricated and tested for the purpose of high-efficiency separation. The microchannels consisted of an 8-turn spiral with radius increasing from 4.9 to 11.9 mm and an asymmetric branch at the end of the last turn to isolate the inner and outer wall fluids. The width of the channel cross-section was 220 μm and the heights were optimized after a few iterations to be 60 and 40 μm at the outer and inner wall, respectively.
Mechanism of operation
Microparticles experience inertial forces when flowing inside a microfluidic channel, which affect their lateral and axial positions. In a straight channel, only the wall-induced lift force (FLW) and shear-gradient lift force (FLS) are large enough to induce particle migration. The resultant of these forces is often referred to as the inertial lift force and can be represented as follows:35| |
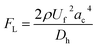 | (1) |
where ac is the particle diameter, Uf is the average fluid velocity, ρ is the fluid density and Dh is the channel's hydraulic diameter. Particle size is the dominant factor; therefore, aiming to focus on small particles is a challenge when counting only on inertial forces. On the contrary, the Dean drag force resulting from a high pressure gradient generated by the sharp velocity profile36,37 would be larger than the inertial force when calculated for smaller particles. The strength of the Dean vortices can be represented by the dimensionless Dean number De as follows:23,38| |
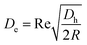 | (2) |
where R is the radius of curvature and Re is the Reynolds number. The velocity that the particles experience during lateral migration is called the Dean velocity and can be calculated as UDean = 1.8 × 10−4 De1.63.11 The resulting Dean force exerted on particles passing in a curved channel can be calculated using Stokes' Law:where μ is the dynamic viscosity of the fluid. The Dean drag force drives the particles in a direction opposite to the inertial lift forces and since it is less sensitive (linear dependence) to particle diameter, smaller particles are more affected and would be focused near the center of the Dean vortices (outer wall). Fig. 1(A) shows the used trapezoidal microfluidic chip with one inlet and two outlets, while Fig. 1(B) illustrates the direction of inertial and drag forces acting on particles inside the rectangular and trapezoidal microchannels as well as the skewed velocity profile due to the channel's curvature. The ratio of inertial lift and drag forces Rf = FL/FD. can be calculated with the help of eqn (1) and (3). Small values of Rf indicate the dominance of the Dean drag forces over inertial forces and particles would more likely be focused near the outer wall. On the other hand, as Rf increases, inertial forces become more dominant and particles would be focused closer to the inner wall.
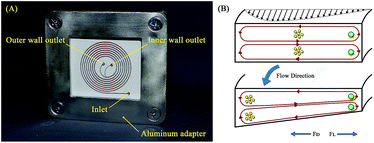 |
| | Fig. 1 Trapezoidal microfluidic chip representation. (A) Fabricated spiral microfluidic chip with one inlet and two outlets, the microchannels are filled with red dye for better contrast. (B) Illustration of the spiral channel principle of operation showing a comparison between Dean vortices in rectangular and trapezoidal channel cross-sections. | |
Chip fabrication
A laser workstation (microSTRUCT-C, 3D-Micromac, Chemnitz, Germany) equipped with a Yb:KGW solid-state femtosecond laser (Pharos, Light Conversion, Vilnius, Lithuania) was used to engrave the microchannels on a glass wafer. The machine's software offered two options for importing the drawings one method was to convert DXF files created on AutoCAD (AutoCAD 2018, Autodesk, San Rafael, CA, USA) into a machine-readable graphics file with certain filling strategies that define the lines through which the laser will pass when ablation is initiated. This method is versatile and simple but it produces large files leading to long ablation times. An alternative method is given by writing a Visual Basic for Applications (VBA) script that draws the required laser path (see Fig. 2(B)), where tighter lines produce a larger depth. Both methods were used to fabricate the spiral chip; the VBA script, described in previous work,21 to draw the spiral shape with multi-pitch strategy, and the filling strategy for the branch and holes. After laser ablation, the engraved glass wafer (BOROFLOAT®, Schott AG, Mainz, Germany) was dipped in glass etching solution (phosphoric acid, hydrofluoric acid and water, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9)39,40 for 90 s then rinsed with DI water to smoothen the ablated surface and remove any residual glass particles resulting from the engraving process. A wafer-cleaning machine (Fairchild Convac, Neuenstadt, Germany) was used to clean the wafer before it was bonded to a blank wafer by placing it in a muffle furnace at 620 °C for 6 hours. During the laser process development, a 3D microscope (Keyence VHX 5000, Japan-imported through Keyence Germany) was used to evaluate the ablated surface's shape as shown in Fig. 2(A), and to accurately measure the dimensions to finally produce a 220, 60 μm × 40 μm (w, h1 × h2) trapezoidal channel (see Fig. 2(C)).
9)39,40 for 90 s then rinsed with DI water to smoothen the ablated surface and remove any residual glass particles resulting from the engraving process. A wafer-cleaning machine (Fairchild Convac, Neuenstadt, Germany) was used to clean the wafer before it was bonded to a blank wafer by placing it in a muffle furnace at 620 °C for 6 hours. During the laser process development, a 3D microscope (Keyence VHX 5000, Japan-imported through Keyence Germany) was used to evaluate the ablated surface's shape as shown in Fig. 2(A), and to accurately measure the dimensions to finally produce a 220, 60 μm × 40 μm (w, h1 × h2) trapezoidal channel (see Fig. 2(C)).
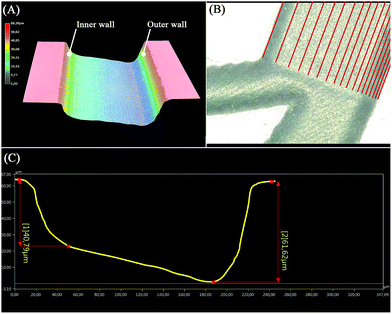 |
| | Fig. 2 The fabricated trapezoidal channel investigated by 3D microscopy. (A) Three-dimensional reconstruction of the trapezoidal microchannel showing the inner and outer walls. (B) Top view of the branch at the end of the spiral shape where the red lines indicate the paths generated by the VB script to produce trapezoidal channels. (C) Channel cross-section profile as referenced in (B), showing the depth at each wall. | |
Particle solution preparation
Fluorescent polystyrene microparticles of 2 μm and 10 μm (exc./emm.: 468/508 nm, 1% solids concentration, Fluoro-Max, Thermo Fisher Scientific, Massachusetts, USA) and 5 μm (exc./emm.: 502/518 nm, 2.5% solids concentration, microParticles GmbH, Berlin, Germany) were used in this work. For the 2 μm and 10 μm particles, 50 μL of particles solution were diluted in 10 mL DI water resulting in a 0.005% (w/v) suspension, while 10 μL of particles solution were diluted in 10 mL DI water for 5 μm particles, resulting in a 0.0025% (w/v) suspension concentration, which will be further discussed in a subsequent section.
Results and discussion
A set of experiments was designed to test the fabricated microfluidic chip with 2, 5, 10 μm fluorescent microparticles. The particle solution was filled in a glass syringe (SETonic GmbH, Ilmenau, Germany) and loaded into the syringe pump (NEMESYS low pressure module 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Cetoni GmbH, Korbussen, Germany). Live monitoring of the experiments was performed with a microscope 0065 camera (XC30) fixed on an inverted microscope (CKX53, both Olympus, Shinjuku, Tokyo, Japan) with blue light excitation (460–495 nm) from a mercury short-arc lamp (USH-103D, Ushio, Marunouchi, Chiyoda-ku, Tokyo) for particle fluorescence imaging. Force calculations on various chip designs were conducted during the design phase. The ratio Rf of inertial lift to drag forces has to be Rf ≪ 1 for the particles to focus near the outer wall, indicating the dominance of the drag forces. On the contrary, larger values of Rf ≫ 1 indicate the dominance of inertial forces. Table 1 shows detailed force calculations for 2, 5 and 10 μm particles for the final design at various flow rates. The lift forces exceeded the Dean forces for the 10 μm particles, which were, therefore, expected to focus near the inner wall. The Dean forces were greater than the lift forces for 2 μm particles, which were expected to focus near the outer wall. The magnitude of forces is also of great importance because even if the ratio between forces is significantly smaller or larger than 1, particles will not focus in a thin line unless the channel can provide enough force to migrate them. In the case of the 5 μm particles, it can be seen in Table 1 that the ratio Rf is very close to unity; this indicates that particles will experience two equilibrium positions on both ends of the channel, which will be further discussed in a subsequent section.
1, Cetoni GmbH, Korbussen, Germany). Live monitoring of the experiments was performed with a microscope 0065 camera (XC30) fixed on an inverted microscope (CKX53, both Olympus, Shinjuku, Tokyo, Japan) with blue light excitation (460–495 nm) from a mercury short-arc lamp (USH-103D, Ushio, Marunouchi, Chiyoda-ku, Tokyo) for particle fluorescence imaging. Force calculations on various chip designs were conducted during the design phase. The ratio Rf of inertial lift to drag forces has to be Rf ≪ 1 for the particles to focus near the outer wall, indicating the dominance of the drag forces. On the contrary, larger values of Rf ≫ 1 indicate the dominance of inertial forces. Table 1 shows detailed force calculations for 2, 5 and 10 μm particles for the final design at various flow rates. The lift forces exceeded the Dean forces for the 10 μm particles, which were, therefore, expected to focus near the inner wall. The Dean forces were greater than the lift forces for 2 μm particles, which were expected to focus near the outer wall. The magnitude of forces is also of great importance because even if the ratio between forces is significantly smaller or larger than 1, particles will not focus in a thin line unless the channel can provide enough force to migrate them. In the case of the 5 μm particles, it can be seen in Table 1 that the ratio Rf is very close to unity; this indicates that particles will experience two equilibrium positions on both ends of the channel, which will be further discussed in a subsequent section.
Table 1 Dean and lift forces calculations for different flow rates and particle sizes
| Particle diameter (μm) |
Flow rate (mL min−1) |
Dean number De |
FL (pN) |
FD (pN) |
Rf |
| 2 |
0.1 |
1.1094 |
0.11102 |
4.0265 |
0.0276 |
| 0.5 |
5.5469 |
2.7755 |
55.494 |
0.0500 |
| 1 |
11.0939 |
11.102 |
171.76 |
0.0646 |
| 5 |
0.1 |
1.1094 |
4.3367 |
10.066 |
0.4308 |
| 0.5 |
5.5469 |
108.42 |
138.74 |
0.7815 |
| 1 |
11.0939 |
433.67 |
429.40 |
1.0099 |
| 10 |
0.1 |
1.1094 |
69.388 |
20.132 |
3.4466 |
| 0.5 |
5.5469 |
1734.7 |
277.47 |
6.2518 |
| 1 |
11.0939 |
6938.8 |
858.81 |
8.0795 |
The effect of particle concentration
When designing a microfluidic chip for microparticle/cell separation, one of the aims is to maximize throughput, which directly relates to the suspension concentration. Some interactions and forces are typically neglected in mathematical models for particle focusing such as particle–particle interaction, which is often avoided in experiments by choosing a low particle fraction.41 Higher particle concentration affects the focusing efficiency and, in some cases, results in multiple focusing positions for the same particle size.42 Fig. 3 shows two fluorescence intensity plots for the 5 μm particle trajectory at 0.7 mL min−1. Once the flow rate has stabilized in the channel and reached a steady-state, another secondary focusing position appears at the outer wall, which limits the chip's operation.
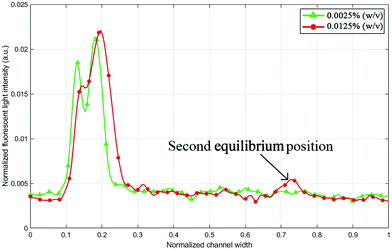 |
| | Fig. 3 Fluorescent green light intensity line profile (across the outlet channel) for 5 μm particles with 0.0125% (w/v) and 0.0025% (w/v) suspension concentration at 0.7 mL min−1. Higher concentration values may increase the number of equilibrium positions. | |
However, reducing the particle suspension concentration from 0.0125% to 0.0025% (w/v) was able to solve this problem within the tested range of operation. A critical flow rate at which the equilibrium positions of particles split into two (0.7 mL min−1 in the case of 0.0125% (w/v)) might just shift to higher flow rate values. It is noticeable in Fig. 3 that the concentration reduction also shifted the equilibrium position towards the inner wall. Normally, a small concentration variation does not notably affect the particle equilibrium position; however, in this case, the particles were not fully stable in the first place because the lift and Dean forces were almost identical at the tested flow rates. Flow rates below 0.7 mL min−1 returned one equilibrium position even for 0.0125% (w/v) concentration, but when the 2 μm particles were added to test the separation, a second equilibrium position started to emerge at lower flow rates.
Microparticle separation
Before injecting the chip with the particle solution, the chip was primed with DI water for a few minutes to remove air bubbles and any residual particles. Solutions with 2, 5 and 10 μm particles were pumped individually at flow rates varying from 0.1–1 mL min−1.
The 2 μm particles were recovered from the outer wall at all tested flow rates, while the 5 μm (0.0025% (w/v) suspension) particles were focused near the inner wall at flow rates 0.5–1.0 mL min−1. The 10 μm particles also focused on the inner wall for flow rates 1.0–1.5 mL min−1. Below 0.3 mL min−1, the focusing position was not stable for all tested particles due to the low magnitude of inertial forces. The experiments as shown in Fig. 4 agree with the calculations as summarized in Table 2, thereby confirming that the 2 μm particles experienced higher Dean forces at all flow rates and consequently focused at the outer wall, whereas the 5 μm (after suspension concentration optimization) and 10 μm particles experienced higher lift forces and focused at the inner wall. To verify the separation capability, mixtures of 2, 5 μm and 2, 10 μm particles were prepared at the same concentrations tested before with monodisperse suspension (as shown in Fig. 4). The acquired results confirmed that mixed particle populations allow the successful separation of 2, 5 and 10 μm particles at different flow rates. As shown in Fig. 5, the 2 μm and 5 μm particles were separated and recovered at 0.6 mL min−1, while the 2 μm and 10 μm particles were separated and recovered at 1.0 mL min−1. Furthermore, it is noticeable that the gap between focusing the streams of 81 μm for the 2 and 5 μm particle separation and 72 μm for the 2 and 10 μm particle separation is large enough to provide high purity separation. These results show the versatility of the fabricated chip to separate three particle sizes and possibly more if tested for 15 or 20 μm particles.
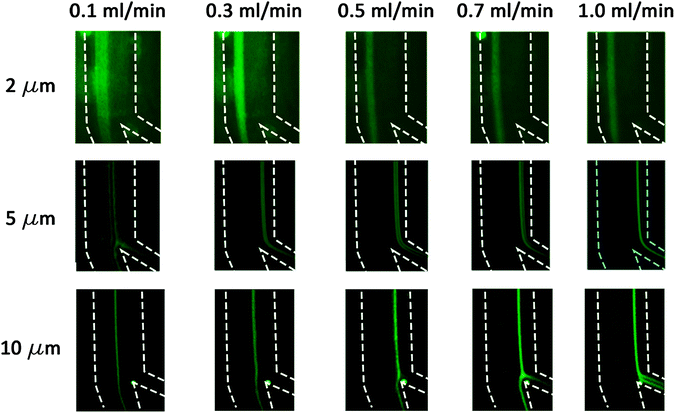 |
| | Fig. 4 The 2, 5 and 10 μm fluorescent microparticle trajectories at flow rates from 0.1–1.0 mL min−1. The dashed lines represent the channel's outline. | |
Table 2 A review of focusing/separation of 2 μm particles from the literature in spiral microchannels
| Group |
Turns |
Channel geometry |
Mechanism |
Width/height(μm) |
Particle sizes (μm) |
Total flow rate |
| Bhagat et al. 200831 |
5 |
Rectangular |
Spiral, sheath flow |
100/50 |
7.32, 1.9 |
20 μL min−1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample to sheath ratio 1 sample to sheath ratio |
| Lee et al. 201932 |
1.5 |
Rectangular |
Spiral, sheath flow |
50/20 |
0.81, 2.29, 4.7 |
78 μL min−1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 sample to sheath ratio 5 sample to sheath ratio |
| Al-Halhouli et al. 201933 |
8 |
Rectangular |
Spiral, sheath-less, microchambers |
200/50 |
2, 5, 10 focusing only |
350 μL min−1 |
| Current work |
8 |
Trapezoidal |
Spiral, sheath-less |
220/60, 40 |
2, 5, 10 |
600 μL min−1 (2, 5 μm), 1000 μL min−1 (2, 10 μm) |
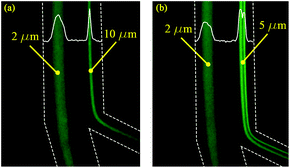 |
| | Fig. 5 The separation of 2 μm particles from 10 μm (a) at the flow rate of 1.0 mL min−1, and 2 μm particles from 5 μm (b) at the flow rate of 0.6 mL min−1. | |
Table 2 shows a comparison between earlier designs that could focus or separate 2 μm particles in spiral channels, with the results obtained in this work. Unlike the current results, it is evident that all previous designs reported in the literature separated particles at relatively low flow rates. Since smaller particles require higher lift force values, smaller channel dimensions are required to achieve focusing; however, the size reduction comes at a great cost of high pressure values, even at low flow rates. Therefore, in addition to the complex setup needed for sheath-based focusing, expensive syringe pumps with high linear force are required. Furthermore, particle separation in a sheath-less device is harder because the operator only has control over the sample flow rate and there is no way to actively change the particle position by varying another input parameter, but once the device is well optimized, it becomes easier to repeat and use.
Conclusion
It has been shown that trapezoidal spiral channels are able to focus particles as small as 2 μm due to a secondary flow without the implementation of a sheath flow. The fluorescent microparticle experiments confirmed predictions based on the calculations of inertial forces, where the expected focusing position depended on the ratio between the inertial lift and drag forces and the magnitude of the dominant force. Reducing the suspension concentration from 0.0125% (w/v) to 0.0025% (w/v) was essential for 5 μm particles since the ratio of lift to drag forces was close to unity; therefore, secondary focusing was expected at high flow rates. As a result, the successful separation of 2 and 5 μm particles, and 2, 10 μm particles was achieved with a spatial separation of 81 μm for 2 and 5 μm particles and 72 μm for 2 and 10 μm particles. Recently,30,32 spiral channels that were able to focus ∼2 μm particles exhibited small hydraulic diameters and a sheath flow; however, in our design, the sheath-less bigger channel reduced the complexity of the microsystem and the required syringe pumps and increased the throughput. Separation operated at a flow rate of 0.6–1.0 mL min−1, while in the literature,30–32 the flow rate was less than 200 μL min−1 even in other passive separation mechanisms besides spiral microfluidic channels.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research is funded by the German Academic Exchange Services (DAAD) under the project entitled “Inertial focusing for continuous nanoparticles separation in femtosecond laser 3D micromachined curved channels”. Special thanks to Zaid Doofesh for his notable contribution in chips fabrication and early experiments. The first author would like to thank GJU for the sabbatical year that allowed significant progress in finalizing the paper.
References
- T. Yang, P. Paiè, G. Nava, F. Bragheri, R. M. Vazquez, P. Minzioni, M. Veglione, M. Di Tano, C. Mondello, R. Osellame and I. Cristiani, Lab Chip, 2015, 15, 1262–1266 RSC.
- M. Terashima, E. S. Freeman, R. E. Jinkerson and M. C. Jonikas, Plant J., 2015, 81, 147–159 CrossRef CAS PubMed.
- D. T. Pederick, K. L. Richards, S. G. Piltz, R. Kumar, S. Mincheva-Tasheva, S. A. Mandelstam, R. C. Dale, I. E. Scheffer, J. Gecz, S. Petrou, J. N. Hughes and P. Q. Thomas, Neuron, 2018, 97, 59–66.e5 CrossRef CAS PubMed.
- P. Li, Z. S. Stratton, M. Dao, J. Ritz and T. J. Huang, Lab Chip, 2013, 13, 602–609 RSC.
- R. Moloudi, S. Oh, C. Yang, M. Ebrahimi Warkiani and M. W. Naing, Microfluid. Nanofluidics, 2018, 22, 1–14 CrossRef CAS.
- E. J. Lim, T. J. Ober, J. F. Edd, G. H. McKinley and M. Toner, Lab Chip, 2012, 12, 2199 RSC.
- M. E. Warkiani, C. P. Lou, H. B. Liu and H. Q. Gong, Biomed. Microdevices, 2012, 14, 669–677 CrossRef PubMed.
- P. Paiè, F. Bragheri, D. Di Carlo and R. Osellame, Microsyst. Nanoeng., 2017, 3, 17027 CrossRef PubMed.
- G. Velve-Casquillas, M. Le Berre, M. Piel and P. T. Tran, Nano Today, 2010, 5, 28–47 CrossRef CAS PubMed.
- M. E. Warkiani, A. K. P. Tay, B. L. Khoo, X. Xiaofeng, J. Han and C. T. Lim, Lab Chip, 2015, 15, 1101–1109 RSC.
- M. E. Warkiani, B. L. Khoo, L. Wu, A. K. P. Tay, A. A. sga, S. Bhagat, J. Han and C. T. Lim, Nat. Protoc., 2016, 11, 134–148 CrossRef CAS PubMed.
- C. Y. Lee, C. L. Chang, Y. N. Wang and L. M. Fu, Int. J. Mol. Sci., 2011, 12, 3263–3287 CrossRef CAS PubMed.
- A. Al-Halhouli, A. Alshare, M. Mohsen, M. Matar, A. Dietzel and S. Büttgenbach, Micromachines, 2015, 6, 953–968 CrossRef.
- W. Al-Faqheri, T. H. G. Thio, M. A. Qasaimeh, A. Dietzel, M. Madou and A. Al-Halhouli, Microfluid. Nanofluidics, 2017, 21, 1–23 CrossRef.
- P. R. C. Gascoyne, X.-B. Wang, Y. Huang and F. F. Becker, IEEE Trans. Ind. Appl., 1997, 33, 670–678 CrossRef PubMed.
- B. Verbruggen, T. Tóth, M. Cornaglia, R. Puers, M. A. M. Gijs and J. Lammertyn, Microfluid. Nanofluidics, 2014, 18, 91–102 CrossRef.
- A. V. Larsen, L. Poulsen, H. Birgens, M. Dufva and A. Kristensen, Lab Chip, 2008, 8, 818–821 RSC.
- L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CrossRef CAS PubMed.
- Z. Wu, Y. Chen, M. Wang and A. J. Chung, Lab Chip, 2016, 16, 532–542 RSC.
- L. Zeng, S. Balachandar and P. Fischer, J. Fluid Mech., 2005, 536, 1–25 CrossRef.
- A. Al-Halhouli, W. Al-Faqheri, B. Alhamarneh, L. Hecht and A. Dietzel, Micromachines, 2018, 9, 171 CrossRef PubMed.
- M. G. Lee, J. H. Shin, C. Y. Bae, S. Choi and J. K. Park, Anal. Chem., 2013, 85, 6213–6218 CrossRef CAS PubMed.
- N. Nivedita, P. Ligrani and I. Papautsky, Sci. Rep., 2017, 7, 1–10 CrossRef PubMed.
- J. M. Martel and M. Toner, Phys. Fluids, 2012, 24, 032001 CrossRef PubMed.
- P. Sajeesh and A. K. Sen, Microfluid. Nanofluidics, 2014, 17, 1–52 CrossRef.
- A. Russom, A. K. Gupta, S. Nagrath, D. Di Carlo, J. F. Edd and M. Toner, New J. Phys., 2009, 11, 075025 CrossRef PubMed.
- G. Guan, L. Wu, A. A. Bhagat, Z. Li, P. C. Y. Chen, S. Chao, C. J. Ong and J. Han, Sci. Rep., 2013, 3, 1–9 Search PubMed.
- M. E. Warkiani, G. Guan, K. B. Luan, W. C. Lee, A. A. S. Bhagat, P. Kant Chaudhuri, D. S. W. Tan, W. T. Lim, S. C. Lee, P. C. Y. Chen, C. T. Lim and J. Han, Lab Chip, 2014, 14, 128–137 RSC.
- L. Wang and D. S. Dandy, Adv. Sci., 2017, 4, 1700153 CrossRef PubMed.
- J. Cruz, T. Graells, M. Walldén and K. Hjort, Lab Chip, 2019, 19, 1257–1266 RSC.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Lab Chip, 2008, 8, 1906–1914 RSC.
- J. H. Lee, S. K. Lee, J. H. Kim and J. H. Park, Sens. Actuators A Phys., 2019, 286, 211–219 CrossRef CAS.
- A. Al-Halhouli, A. Albagdady, W. Al-Faqheri, J. Kottmeier, S. Meinen, L. J. Frey, R. Krull and A. Dietzel, RSC Adv., 2019, 9, 19197–19204 RSC.
- Y. Zhou, Z. Ma and Y. Ai, Microsyst. Nanoeng., 2018, 4, 5 CrossRef PubMed.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli, N. Kaval, C. J. Seliskar and I. Papautsky, Biomed. Microdevices, 2010, 12, 187–195 CrossRef PubMed.
- K. Cheng and M. Akiyama, Int. J. Heat Mass Transf., 1970, 13, 471–490 CrossRef.
- T. T. Chandratilleke and A. Nursubyakto, Int. J. Therm. Sci., 2003, 42, 187–198 CrossRef.
- W. R. Dean, Proc. R. Soc. A Math. Phys. Eng. Sci., 1928, 121, 402–420 CrossRef.
- P. Erfle, J. Riewe, H. Bunjes and A. Dietzel, Microfluid. Nanofluidics, 2017, 1–12 Search PubMed.
- P. Erfle, J. Riewe, H. Bunjes and A. Dietzel, Micromachines, 2019, 10, 220 CrossRef PubMed.
- A. Özbey, M. Karimzadehkhouei, S. Akgönül, D. Gozuacik and A. Koşar, Sci. Rep., 2016, 6, 1–11 CrossRef PubMed.
- X. Casadevall i Solvas and A. DeMello, Matters, 2016, 1–7 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05916d |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc,
Ahmed Albagdady
*abc,
Ahmed Albagdady a and
Andreas Dietzel
a and
Andreas Dietzel b
b
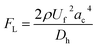
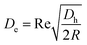
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9)39,40 for 90 s then rinsed with DI water to smoothen the ablated surface and remove any residual glass particles resulting from the engraving process. A wafer-cleaning machine (Fairchild Convac, Neuenstadt, Germany) was used to clean the wafer before it was bonded to a blank wafer by placing it in a muffle furnace at 620 °C for 6 hours. During the laser process development, a 3D microscope (Keyence VHX 5000, Japan-imported through Keyence Germany) was used to evaluate the ablated surface's shape as shown in Fig. 2(A), and to accurately measure the dimensions to finally produce a 220, 60 μm × 40 μm (w, h1 × h2) trapezoidal channel (see Fig. 2(C)).
9)39,40 for 90 s then rinsed with DI water to smoothen the ablated surface and remove any residual glass particles resulting from the engraving process. A wafer-cleaning machine (Fairchild Convac, Neuenstadt, Germany) was used to clean the wafer before it was bonded to a blank wafer by placing it in a muffle furnace at 620 °C for 6 hours. During the laser process development, a 3D microscope (Keyence VHX 5000, Japan-imported through Keyence Germany) was used to evaluate the ablated surface's shape as shown in Fig. 2(A), and to accurately measure the dimensions to finally produce a 220, 60 μm × 40 μm (w, h1 × h2) trapezoidal channel (see Fig. 2(C)).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Cetoni GmbH, Korbussen, Germany). Live monitoring of the experiments was performed with a microscope 0065 camera (XC30) fixed on an inverted microscope (CKX53, both Olympus, Shinjuku, Tokyo, Japan) with blue light excitation (460–495 nm) from a mercury short-arc lamp (USH-103D, Ushio, Marunouchi, Chiyoda-ku, Tokyo) for particle fluorescence imaging. Force calculations on various chip designs were conducted during the design phase. The ratio Rf of inertial lift to drag forces has to be Rf ≪ 1 for the particles to focus near the outer wall, indicating the dominance of the drag forces. On the contrary, larger values of Rf ≫ 1 indicate the dominance of inertial forces. Table 1 shows detailed force calculations for 2, 5 and 10 μm particles for the final design at various flow rates. The lift forces exceeded the Dean forces for the 10 μm particles, which were, therefore, expected to focus near the inner wall. The Dean forces were greater than the lift forces for 2 μm particles, which were expected to focus near the outer wall. The magnitude of forces is also of great importance because even if the ratio between forces is significantly smaller or larger than 1, particles will not focus in a thin line unless the channel can provide enough force to migrate them. In the case of the 5 μm particles, it can be seen in Table 1 that the ratio Rf is very close to unity; this indicates that particles will experience two equilibrium positions on both ends of the channel, which will be further discussed in a subsequent section.
1, Cetoni GmbH, Korbussen, Germany). Live monitoring of the experiments was performed with a microscope 0065 camera (XC30) fixed on an inverted microscope (CKX53, both Olympus, Shinjuku, Tokyo, Japan) with blue light excitation (460–495 nm) from a mercury short-arc lamp (USH-103D, Ushio, Marunouchi, Chiyoda-ku, Tokyo) for particle fluorescence imaging. Force calculations on various chip designs were conducted during the design phase. The ratio Rf of inertial lift to drag forces has to be Rf ≪ 1 for the particles to focus near the outer wall, indicating the dominance of the drag forces. On the contrary, larger values of Rf ≫ 1 indicate the dominance of inertial forces. Table 1 shows detailed force calculations for 2, 5 and 10 μm particles for the final design at various flow rates. The lift forces exceeded the Dean forces for the 10 μm particles, which were, therefore, expected to focus near the inner wall. The Dean forces were greater than the lift forces for 2 μm particles, which were expected to focus near the outer wall. The magnitude of forces is also of great importance because even if the ratio between forces is significantly smaller or larger than 1, particles will not focus in a thin line unless the channel can provide enough force to migrate them. In the case of the 5 μm particles, it can be seen in Table 1 that the ratio Rf is very close to unity; this indicates that particles will experience two equilibrium positions on both ends of the channel, which will be further discussed in a subsequent section.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample to sheath ratio
1 sample to sheath ratio![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 sample to sheath ratio
5 sample to sheath ratio



