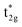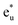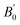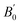Open Access Article
Open Access ArticleExploring half-metallic Co-based full Heusler alloys using a DFT+U method combined with linear response approach
Kenji
Nawa
 *a and
Yoshio
Miura
abc
*a and
Yoshio
Miura
abc
aResearch Center for Magnetic and Spintronic Materials (CMSM), National Institute for Materials Science (NIMS), 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan. E-mail: nawa.kenji@nims.go.jp
bCenter for Materials Research by Information Integration, National Institute for Materials Science (NIMS), 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
cCenter for Spintronics Research Network (CSRN), Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
First published on 25th September 2019
Abstract
A density functional theory (DFT)+U method based on linear response (LR) theory was applied to investigate the electronic structures of a Co-based ternary full Heusler alloy Co2YSi to explore half-metallic (HM) ferromagnets with a wide HM gap. The LR-based DFT+U calculations tend to obtain a reasonable correlation parameter for the Y site, while the correlation of the Co site misdirects to the unphysical ground state due to the overestimated parameter value that arises from the delocalized electronic structure of Co. Furthermore, we found that the HM gap of Co2MnSi originates from the Co 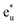 orbital in the conduction state and the Co–Mn hybridizing t2g orbital in the valence state around the Fermi energy. This means that the HM gap is a tunable property by selecting the Y element and/or mixing several elements into the Y site through t2g atomic-orbital coupling. Our LR-based DFT+U method was extended to other ternary Co2YSi and quaternary Co2(Y,Mn)Si. We found that Co2(Ti0.25,Mn0.75)Si and Co2(Fe0.25,Mn0.75)Si show HM nature, with the Fermi energy being at almost the center of the minority band gap, which leads to high thermal stability.
orbital in the conduction state and the Co–Mn hybridizing t2g orbital in the valence state around the Fermi energy. This means that the HM gap is a tunable property by selecting the Y element and/or mixing several elements into the Y site through t2g atomic-orbital coupling. Our LR-based DFT+U method was extended to other ternary Co2YSi and quaternary Co2(Y,Mn)Si. We found that Co2(Ti0.25,Mn0.75)Si and Co2(Fe0.25,Mn0.75)Si show HM nature, with the Fermi energy being at almost the center of the minority band gap, which leads to high thermal stability.
1 Introduction
A key property in the emerging field of spintronics is the so-called half-metallicity (HM); the majority and minority states are completely spin-polarized at the Fermi level, where a finite density of states (DOS) exists for majority spin and an energy band gap is opened for minority spin. The use of HM materials as ferromagnetic electrodes in magnetic tunnel junctions (MTJs) is a straightforward way to enhance the tunneling magnetoresistance (TMR) ratio,1 leading to high-performance spintronics applications such as non-volatile magnetic random access memories and the read-head of ultrahigh-density hard-disk drives. So far, many candidates have been proposed as HM materials, e.g., zinc-blende structural materials,2–4 colossal magnetoresistance materials,5,6 oxides such as rutile CrO2 (ref. 7–10) and spinel-type magnetite Fe3O4,11,12 and diluted magnetic semiconductors (SnO2, Y2O3).13–15 Among them, the family of Co-based full Heusler alloys has received considerable attention, as some of these have the potential to possess a high spin polarization (P) or ultimately HM (P = 100%) in addition to a high Curie temperature, e.g., 985 K for Co2MnSi16 and 1100 K for Co2FeSi.17,18The spin polarization of electrodes in an MTJ device can be evaluated using the Jullièr model1 with a simple formula 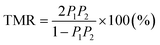 , where P1 and P2 are the tunneling spin polarizations of the two ferromagnetic electrodes in the MTJ. For a Co2MnSi MTJ with an aluminum oxide (Al–O) barrier, Sakuraba et al. observed the spin polarization to be over 80%.19,20 Then, a high value of 95.4%, which may be close to a fully spin-polarized electronic structure, was reported for the MgO barrier MTJ.21 However, P1(2) in the Jullièr formula is not the spin polarization in the bulk system but the polarization of the tunneling electrons in the MTJ. The electronic structure of the MTJ electrode differs from that of the bulk material because the band structure is drastically changed due to the interfacial effect arising from the insulating barrier. The tunneling electrons are also influenced by the spin-filtering effect.22 These facts imply that there is difficulty in an accurate estimation of purely bulk spin polarization from the TMR of MTJ.
, where P1 and P2 are the tunneling spin polarizations of the two ferromagnetic electrodes in the MTJ. For a Co2MnSi MTJ with an aluminum oxide (Al–O) barrier, Sakuraba et al. observed the spin polarization to be over 80%.19,20 Then, a high value of 95.4%, which may be close to a fully spin-polarized electronic structure, was reported for the MgO barrier MTJ.21 However, P1(2) in the Jullièr formula is not the spin polarization in the bulk system but the polarization of the tunneling electrons in the MTJ. The electronic structure of the MTJ electrode differs from that of the bulk material because the band structure is drastically changed due to the interfacial effect arising from the insulating barrier. The tunneling electrons are also influenced by the spin-filtering effect.22 These facts imply that there is difficulty in an accurate estimation of purely bulk spin polarization from the TMR of MTJ.
The point contact Andreev reflection (PCAR) technique has also been performed for spin polarization in several Heusler alloys. The conductance of metallic electrons is measured at a cryogenic temperature to evaluate the spin polarization in PCAR; hence, PPCAR, referred to as PCAR-measured spin polarization, is expressed as 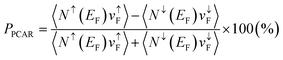 . Here, Nσ(EF) and vσF are the DOS at the Fermi energy and the Fermi velocity with spin index σ(=↑ or ↓) in a diffusive regime23,24 where the current electrons are not assumed to be ballistic because of the mean-free path being shorter than the point contact size in actual experiments. The vσF is the conductance of the electrons, but the d orbital localized around the Fermi energy is not dominant in the current electrons. This indicates that the spin polarization originating from the d electron is lost in the measured PPCAR. Previous work reported that the current spin polarization deduced by PCAR is only 59% for Co2MnSi25 and around 50% for Co2FeSi.26–28PPCAR = 64% is also observed in quaternary Co2(Fe,Mn)Si.29
. Here, Nσ(EF) and vσF are the DOS at the Fermi energy and the Fermi velocity with spin index σ(=↑ or ↓) in a diffusive regime23,24 where the current electrons are not assumed to be ballistic because of the mean-free path being shorter than the point contact size in actual experiments. The vσF is the conductance of the electrons, but the d orbital localized around the Fermi energy is not dominant in the current electrons. This indicates that the spin polarization originating from the d electron is lost in the measured PPCAR. Previous work reported that the current spin polarization deduced by PCAR is only 59% for Co2MnSi25 and around 50% for Co2FeSi.26–28PPCAR = 64% is also observed in quaternary Co2(Fe,Mn)Si.29
Another critical subject to overcome is the large temperature dependence of P.19–21,26,30–33 Experimental studies have reported that although an extremely high value of TMR ratio is demonstrated at low temperature in the MTJs consisting of Heusler electrodes and an MgO barrier, a significant reduction in TMR at room temperature is observed: for example, in the Co2MnSi/MgO/Co2MnSi MTJ21 the TMR at 4.2 K is 2010%, but it decreases to only 335% at 290 K and in Co2(Fe,Mn)Si/MgO/Co2(Fe,Mn)Si34 the TMR at 4.2 K is 2610%, but only 429% at 290 K. From the Jullièr model, the spin polarization P = 95% (98%) at low temperature and decreases to P = 79% (82%) at room temperature for MTJs with a Co2MnSi (Co2(Fe,Mn)Si) electrode. A similar situation occurred in a current-perpendicular-to-plane giant MR (CPP-GMR) device composed of Co2(Fe,Mn)Si electrodes and a nonmagnetic Ag spacer.30,32 To explain the strong thermal-dependence of TMR and GMR performances, it is known that the spin-flip inelastic tunneling process induced by magnon excitation lowers P in addition to spin-conserving elastic tunneling at increased temperatures.21,31 In this sense, the width of the energy band gap in the minority state is also important in the search for HM materials to improve the weak resistivity with respect to temperature.
Ab initio calculations based on density functional theory (DFT)35–37 are expected to play a leading role in the understanding of fundamental electronic and magnetic structures in material design using HM Heusler alloys. In the framework of DFT calculation within local spin density approximation (LSDA), Galanakis et al.38 presented an energy diagram of the atomic orbital hybridization of the Co2MnGe system to clarify the mechanism of the HM property; the minority energy band gap at the Fermi level originates from the t1u and eu orbitals, which are formed by the d orbital hybridizations between two Co atoms sitting in different sublattices in a unit cell. Numerous other studies have also been performed using DFT calculations.39–44
However, how to deal with correlation effects is a critical issue in the DFT study of a Heusler compound. The standard DFT calculations based on mean-field approximations, such as LSDA and generalized gradient approximation (GGA), often fail to predict the true ground-state electronic structures due to the presence of d orbital localization in the vicinity of transition metal atoms, making the many-body effect problematic. Various approaches introducing the many-body effect into the DFT scheme have been proposed to recover the correlation problem being missed in LSDA and GGA, e.g., dynamical mean field theory (DMFT),45,46 hybrid-type PBE0 functional,47 GW approximation,48,49 and the DFT+U method.50,51 However, the obtained electronic structures strongly depend on the employed method. For example, in Co2MnSi, the LDSA+DMFT calculations, where the dynamical correlation effect such as the spin-flip term is considered quantitatively, were performed on the basis of the linear muffin-tin orbital (LMTO) method52 and Korringa–Kohn–Rostoker (KKR) method.53 The former indicates that the Fermi energy is found at the conduction edge of the minority state, while the latter indicates that it is found at the valence edge. The calculation using the hybrid PBE0 functional also shows that the Fermi level locates at the valence top with a very big HM gap of ∼2 eV.54 The GW calculation,55 where the electronic self-energy correction is included by many-body perturbation theory, predicts that the Fermi energy lies between the valence and conduction bands of the minority state. For these approaches, the huge computational cost is also a serious problem; applying it to the MTJ model for properties including interfacial magnetocrystalline anisotropy and spin-dependent transport may be difficult. On the other hand, the DFT+U method,50,51 in which parametrized on-site coulomb (U) and exchange (J) interactions for d-orbitals are introduced in the manner of the Hubbard model,56,57 is a suitable approach on a practical level. Because of the efficient calculation cost, the DFT+U method can be applied to not only simple bulk materials but also large and realistic systems.
The suitable values of U and J for the DFT+U method are unknown; they depend on the atomic species and surroundings of the atom. A linear response (LR) approach58,59 is an advanced way to determine the correlation terms theoretically and to exclude the ad hoc selection of the parameter values. The +U values at respective localized atom sites can be evaluated with low computational costs using the response function of charge density obtained from the standard LSDA or GGA potential. This method has been applied to various correlated systems and succeeded in describing the ground state accurately.58–65 A recent study has also reported that the parameters are not transferable among different calculation methods due to non-negligible dependence on computational setups even in theoretically determined values.58 This implies that the optimal correlation parameters for the system of interest must be estimated by the method used for the calculation; however, the application of this LR-based DFT+U method to Heusler compounds has been limited to structural phase transitions.66
In the present work, electronic band calculations based on the DFT+U method are carried out for an L21 Co-based full Heusler alloy to address these issues. Focusing on the typical model Co2MnSi, we argue the importance of correlation correction in the alloy and the fundamental electronic structure for clarifying the origin of the minority HM gap. The LR calculations obtain a reasonable correlation parameter for the Y site (Y = Mn in Co2MnSi) and this correction plays an important role for correlated electrons. On the other hand, the correlation for the Co site is unexpectedly overestimated, and thus, the obtained results are misdirected to a rather unphysical ground state. The failure for this unreliable parameter of Co arises from the fact that the 3d electrons of the Co site behave in an itinerant fashion in the alloy, which means that the mean-field approximations such as LSDA and GGA are enough to describe the electronic structure of the Co site with high accuracy. We also revealed an important d-orbital hybridization between Co and Mn that mainly dominates the minority HM gap. The energy diagram proposed in this study suggests that the HM gap is tunable by a selected Y atom and/or mixing several elements into the Y site. The results obtained from the LR-based DFT+U method, where the determined correlation parameter is incorporated into only the strongly correlated Y site, are consistent with the experimental observations. Moreover, this methodology is superior to the standard GGA calculation, especially in terms of electronic and magnetic properties. This study is further extended to the other ternary Co2YSi and quaternary Co2(Yx,Mn1−x)Si, where some Mn atoms are substituted with 3d transition metal Y (Y = Ti, V, Cr, and Fe) to explore the potential for the HM ferromagnet with a wide band gap. The systematical calculations indicate that the ternary alloys are found to be ordinary ferromagnets, whose minority bands do not have a finite gap at the Fermi energy, but quaternary Co2(Ti,Mn)Si, Co2(V,Mn)Si, and Co2(Fe,Mn)Si alloys have the potential to be an HM material if the composition of Y is appropriately selected.
This paper is organized as follows. In Section 2, the model and computational details are described, and the LR calculation procedures for the correlation parameters are overviewed. Section 3 revisits Co2MnSi. The effective on-site coulomb interaction parameters for Co and Mn are first computed from the LR theory (Section 3.1). The structural parameters, including the equilibrium lattice constant and bulk modulus, are evaluated by standard GGA and GGA+U schemes with LR-determined parameters in Section 3.2. Using the obtained lattice constant, the electronic structures are investigated to clarify the HM origin within the GGA framework (Section 3.3). The understanding of a fundamental band structure in GGA is essential for discussing the effects of correlation correction on Mn and Co, which is given in Section 3.4. The LR-based DFT+U calculations for electronic and magnetic structures are presented and compared with previous theories and experiments in Section 3.5. Finally, in Section 4, systematical results for the other ternary and quaternary compounds are discussed and promising materials for HM ferromagnets are proposed.
2 Model and method
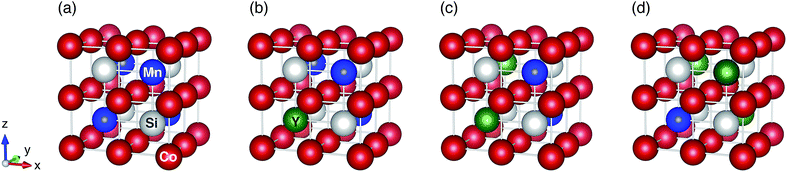
The full Heusler Co2MnSi compound with the L21 structure has Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Oh) symmetry (space group no. 225). For the modeling, a fcc-primitive cell that contains two Co atoms sitting at the Wyckoff position (1/4, 1/4, 1/4) (multiplicity with Wyckoff letter is 8c), one Mn atom at (1/2, 1/2, 1/2) (4b), and one sp-element Si at (0, 0, 0) (4a) was prepared (a conventional unit cell is shown in Fig. 1(a)). The detailed crystal structures for the ternary system Co2YSi, where Mn is replaced with Y of Ti, V, Cr, or Fe, and quaternary Co2(Y,Mn)Si, where some Mn atoms are substituted with Y, are described in Section 4.
m (Oh) symmetry (space group no. 225). For the modeling, a fcc-primitive cell that contains two Co atoms sitting at the Wyckoff position (1/4, 1/4, 1/4) (multiplicity with Wyckoff letter is 8c), one Mn atom at (1/2, 1/2, 1/2) (4b), and one sp-element Si at (0, 0, 0) (4a) was prepared (a conventional unit cell is shown in Fig. 1(a)). The detailed crystal structures for the ternary system Co2YSi, where Mn is replaced with Y of Ti, V, Cr, or Fe, and quaternary Co2(Y,Mn)Si, where some Mn atoms are substituted with Y, are described in Section 4.
The self-consistent DFT calculations were performed via the ab initio package of Quantum-ESPRESSO67 by implementing the ultra-soft pseudopotentials parametrized by the scheme of Rappe, Rabe, Kaxiras, and Joannopoulos68,69 that were taken from the PS Library. The plane wave basis sets for the wave function and charge density had cutoff energies of 40 and 400 Ry, respectively. The self-consistent procedures were achieved until the iterative total energy difference became less than the convergence criterion of 10−8 Ry, by using the Monkhorst–Pack special k-point mesh70 of 16 × 16 × 16 in the first Brillouin zone by the Methfessel–Paxton71 smearing method with a broadening parameter of 0.02 Ry. Previous works discussed the role of spin–orbit coupling (SOC) in the Heusler alloys and found that the orbital magnetic moment induced by the SOC is completely quenched.42,72 It is also reported that although a non-vanishing DOS appears in the minority gap by the effect of SOC, the reduction on P is very small.72–74 In present work, therefore, the SOC is not incorporated into all our calculations. Importantly, it is expected that the wide-gap half-metallic Heusler alloy is robust against the non-vanishing DOS arising from the SOC.
The GGA functional formulated by Perdew, Burke, and Ernzerhof75 was used for the exchange-correlation term. For the DFT+U method, the choice of “double-counting” correction term is also crucial to subtract the electron coulomb energy that is already included in the LSDA or GGA functional. This correction is conceptually desired to be the same energy contribution as that defined in LSDA or GGA. So far, however, an appropriate prescription for the double-counting term has not been established, but the so-called fully localized limit (FLL),76–79 which is also referred as the atomic limit (AL), and around mean-field (AMF)50,78 approaches are mostly used. The former functional favors integer electron occupation numbers at a localized site, and thus, might be useful for strongly correlated materials such as insulating oxide systems. The latter might be useful for an intermediate between strongly correlated and itinerant materials. It is still under debate which of the two functionals is a proper approach for Heusler compounds.80 In this study, the double-counting functional incorporated in the simplified rotationally invariant form,59,81,82 which is equivalent to the FLL approach but J = 0 (or approximately Ueff = U − J, where Ueff stands for the effective on-site coulomb interaction), was employed. We expect that this approach can easily address the underlying physics of correlated electronic structures, compared to AMF, because the electron-localization limit in FLL corresponds to the concept of the Hubbard model; thus, the scaling of Ueff can be simply understood as the strength of electron correlation. The Ueff is computed within the LR theory58,59 for all transition metal atoms, where we assume that the coulomb interaction is more dominant than the exchange at localized electron sites.
In the framework of LR theory,59 the on-site parameter for an atom α, ULR(α)eff, is evaluated from the second derivatives of the total energy functionals as
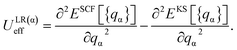 | (1) |
The total energies ESCF and EKS correspond to interacting (fully screened) and non-interacting systems. The second term in eqn (1) is necessary to subtract unphysical contributions in the total energy,83–85 which are caused by the conventional exchange-correlation functionals (LSDA and GGA), where the total energy has a curvature for non-integer occupation qα and often misdirects to incorrect energy minima. The total energy derivatives are calculated using the constrained DFT approach:
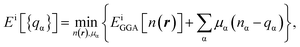 | (2) |
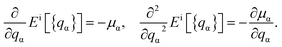 | (3) |
The Lagrange multiplier μα is a local perturbation potential that constrains the occupations nα (i = SCF, KS). In practice, eqn (2) is transformed into a tractable representation where the constraint fields are treated as independent variables by Legendre transformation and the variations of nα with respect to μα are evaluated.59 Using nonlocal linear response matrices
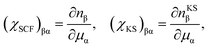 | (4) |
eqn (1) is rewritten to obtain ULR(α)eff as
| ULR(α)eff = (χKS−1 − χSCF−1)αα. | (5) |
The matrix elements of the response matrices are numerically computed; χSCF is obtained from the self-consistent (interacting) calculations under the applied local potential μα and χKS is obtained from the first iteration in a self-consistent cycle after the end of GGA ground-state calculations – the latter is occupation changes that arise from noninteracting hybridization due to μα. The LR approach, in principle, requires a response of the electron occupations to the perturbed potentials at a single site in an infinite crystal environment for an accurate Ueff evaluation, where all artifacts due to the periodic boundary conditions are excluded.58,59
3 Revisiting Co2MnSi
3.1 LR-calculation for effective on-site coulomb interaction parameter
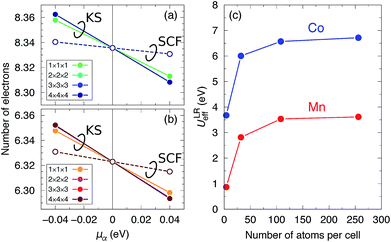
The LR calculations are performed to determine the correlation ULR(α)eff parameters. The response functions of eqn (4) are evaluated numerically from the gradient of the 3d electron occupation numbers with regard to the perturbed potential μα, which constrains the electrons of Co or Mn in the Co2MnSi alloy. For the LR calculations, the experimental lattice constant aExpt. = 5.645 Å (ref. 18) is employed. As presented in Fig. 2(a) and (b), the occupations’ variation of the KS term in the 1 × 1 × 1 primitive cell is slightly off the others (n × n × n cells where n = 2, 3, 4), although the SCF term does not change much (the plotted data are overlapping and the variations for different supercell sizes may not be visible from these figures). The calculated ULReff value is plotted as a function of the number of atoms per cell in Fig. 2(c). We find a 3 × 3 × 3 fcc supercell including 108 atoms is practically large enough to obtain well-converged parameters, meaning that the environment of the infinite crystal structure is well-reproduced. The obtained values result in ULR(Mn)eff = 3.535 and ULR(Co)eff = 6.570 eV for Mn and Co, respectively.The correlation parameter for Co is unexpectedly higher than the typically used empirical values, for instance, the Ueff(=U − J) of 2.5 eV in full-potential (FP)-LMTO86 and that of 2.1 eV in KKR53 calculations. The constrained random phase approximation (cRPA) approach87 determines a parameter value similar to that determined in our study for Mn (3.07 eV), but determines a value of almost half our LR result for Co (3.28 eV). Table 1 summarizes the numerical data of the d occupations (nα) and the changes (Δnα) induced by μα in the LR calculations for α atoms (α = Mn and Co). As defined in eqn (4) and (5), the ULReff is difference of the inversions of electron occupations’ responses with respect to the applied potential shift μα between the KS and SCF terms. For both the α = Mn and Co cases, the absolute values of Δnα in SCF are smaller than those in KS by one order of magnitude, so the inverted response function 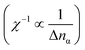 of SCF becomes a main factor in the computed correlation parameters. We also find that, for the SCF term, ΔnCo is small compared to ΔnMn. Therefore, the unreasonably overestimated parameter for Co originates from the difference in ΔnCo of the SCF term. Using the diagonal matrix elements of χKS−1 and χSCF−1 in eqn (5), the parameter for Co is calculated as ULR(Co)eff = −1.10114 − (−7.67152) = 6.570 eV. For Mn, ULR(Mn)eff = −0.98733 − (−4.52196) = 3.535 eV is obtained, where the inverted KS response function’s contribution (the first term) is almost the same as in the ULR(Co)eff case, while the SCF one (the second term) is significantly different.
of SCF becomes a main factor in the computed correlation parameters. We also find that, for the SCF term, ΔnCo is small compared to ΔnMn. Therefore, the unreasonably overestimated parameter for Co originates from the difference in ΔnCo of the SCF term. Using the diagonal matrix elements of χKS−1 and χSCF−1 in eqn (5), the parameter for Co is calculated as ULR(Co)eff = −1.10114 − (−7.67152) = 6.570 eV. For Mn, ULR(Mn)eff = −0.98733 − (−4.52196) = 3.535 eV is obtained, where the inverted KS response function’s contribution (the first term) is almost the same as in the ULR(Co)eff case, while the SCF one (the second term) is significantly different.
| μ α (eV) | KS | SCF | |||
|---|---|---|---|---|---|
| n α | Δnα | n α | Δnα | ||
| Mn | −0.04 | 6.35202 | 0.02908 | 6.33086 | 0.00792 |
| 0.00 | 6.32294 | 0.00000 | 6.32294 | 0.00000 | |
| 0.04 | 6.29357 | −0.02937 | 6.31500 | −0.00794 | |
| Co | −0.04 | 8.36249 | 0.02682 | 8.34047 | 0.00480 |
| 0.00 | 8.33567 | 0.00000 | 8.33567 | 0.00000 | |
| 0.04 | 8.30830 | −0.02737 | 8.33085 | −0.00482 | |
From the above discussion, we conclude that the overestimation of ULReff for the Co site arises from the fact that the charge density response of Co is insensitive compared to Mn or is still insufficient to evaluate the parameters through the SCF iteration cycles under the applied potential shift.88 This can be attributed to the delocalized electronic structures of Co compared to Mn, which originate from the fact that the Co d orbital distribution is spatially-spread due to the d orbital hybridization with first (Mn) and second (Co) neighboring atoms, whereas the Mn d orbital distribution is spatially-narrow due to the d hybridization with only first (Co) neighboring atoms, as discussed in Section 3.3. The localized characters of the Co electronic states compared to those of Mn are consistent with the fact that the spin magnetic moment of Co (1.05 μB) is much smaller than that of Mn (2.95 μB). Recently, an extended LR theory89 has been proposed to overcome the insufficiency of response of charge density; the second response of charge density is additionally included, which is required for complete cancelation of the electron–electron coulomb interaction (Hartree energy) term changed by the external potential (μα ≠ 0), which might be canceled incompletely in the current LR calculation. In the present study, the DFT+U method incorporated by the FLL formalism is used, but another approach for solving the failure in estimating ULReff for a weakly correlated Co site might be the use of the AMF approximation50,78 or a hybrid approach,90 where the AMF and FLL approximations are linearly interpolated.
3.2 Structural properties
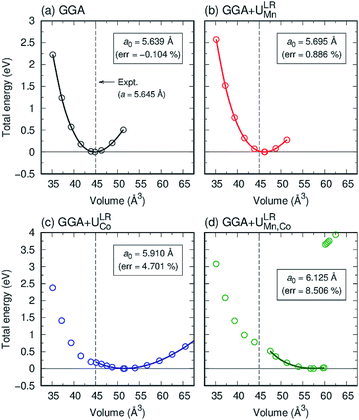
Here, we consider three schemes of LR-based DFT+U calculations, in addition to the standard GGA: the determined ULReff values are applied to only Mn (referred as GGA+ULRMn) or Co (GGA+ULRCo) and to both of them (GGA+ULRMn,Co). First, the GGA calculations are performed to evaluate the equilibrium lattice constant. The total energies at different volume sizes of primitive cell are obtained as shown in Fig. 3(a). The energy minimum is searched by energy fitting to the Murnaghan equation of states91 as a function of volume V,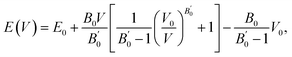 | (6) |
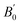 is the pressure derivative of the bulk modulus. The obtained lattice constant is 5.639 Å, which agrees with the experimental value.18 The error value between the calculated lattice constant a0 and experiment, defined as (a0 − aExpt.)/aExpt. × 100 (%), is only −0.104%. In the GGA+ULReff case, the obtained lattice constant of 5.695 Å is similar to the GGA result and the error from the experiment is less than 1% (0.866%), as shown in Fig. 3(b). On the other hand, a0 is significantly overestimated by the errors of 4.701 and 8.506% in the GGA+ULRCo and GGA+ULRMn,Co cases. Fig. 3(c) shows a local energy minimum around the experimental value but the global minimum is found at 51.62 Å3, corresponding to a0 = 5.910 Å. Note also that in the GGA+ULRMn,Co scheme (Fig. 3(d)), a jump of total energy change around the volume of ∼60 Å3 occurs due to a magnetic phase transition, but we confirm that an energy minimum, corresponding to a0 = 6.125 Å, exists at less than the volume where this magnetic transition is induced.
is the pressure derivative of the bulk modulus. The obtained lattice constant is 5.639 Å, which agrees with the experimental value.18 The error value between the calculated lattice constant a0 and experiment, defined as (a0 − aExpt.)/aExpt. × 100 (%), is only −0.104%. In the GGA+ULReff case, the obtained lattice constant of 5.695 Å is similar to the GGA result and the error from the experiment is less than 1% (0.866%), as shown in Fig. 3(b). On the other hand, a0 is significantly overestimated by the errors of 4.701 and 8.506% in the GGA+ULRCo and GGA+ULRMn,Co cases. Fig. 3(c) shows a local energy minimum around the experimental value but the global minimum is found at 51.62 Å3, corresponding to a0 = 5.910 Å. Note also that in the GGA+ULRMn,Co scheme (Fig. 3(d)), a jump of total energy change around the volume of ∼60 Å3 occurs due to a magnetic phase transition, but we confirm that an energy minimum, corresponding to a0 = 6.125 Å, exists at less than the volume where this magnetic transition is induced.
We present bulk modulus B0 and its pressure derivative 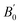 in Table 2, through comparisons of theoretical literature.42,92–95 Among the previous reports, the B0 of LSDA is greater than that of GGA. Our GGA result is almost similar to the reported values in B0 and
in Table 2, through comparisons of theoretical literature.42,92–95 Among the previous reports, the B0 of LSDA is greater than that of GGA. Our GGA result is almost similar to the reported values in B0 and 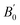 , while the GGA+ULRMn result is slightly smaller in B0. On the other hand, the B0 calculated by the GGA+ULRCo and GGA+ULRMn,Co methods is one order of magnitude smaller than the other calculations. Because the experimental data of the bulk modulus and its derivative are not available for Co2MnSi at this moment, we cannot conclude the validity of our method. However, at least focusing on the lattice constant, these results indicate that the introduction of ULReff to the Mn atom tends to obtain a reasonable result, as well as GGA, from the comparison with experiments, while the inclusion of ULReff to Co fails to evaluate the a0 of Co2MnSi.
, while the GGA+ULRMn result is slightly smaller in B0. On the other hand, the B0 calculated by the GGA+ULRCo and GGA+ULRMn,Co methods is one order of magnitude smaller than the other calculations. Because the experimental data of the bulk modulus and its derivative are not available for Co2MnSi at this moment, we cannot conclude the validity of our method. However, at least focusing on the lattice constant, these results indicate that the introduction of ULReff to the Mn atom tends to obtain a reasonable result, as well as GGA, from the comparison with experiments, while the inclusion of ULReff to Co fails to evaluate the a0 of Co2MnSi.
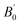 for Co2MnSi. The ULReff values determined by the LR approach are employed in the present study: ULR(Mn)eff = 3.535 eV for GGA+ULRMn, ULR(Co)eff = 6.570 eV for GGA+ULRCo, and both for GGA+ULRMn,Co
for Co2MnSi. The ULReff values determined by the LR approach are employed in the present study: ULR(Mn)eff = 3.535 eV for GGA+ULRMn, ULR(Co)eff = 6.570 eV for GGA+ULRCo, and both for GGA+ULRMn,Co
| a 0 (Å) | B 0 (GPa) | |||
|---|---|---|---|---|
| a Ref. 92. b Ref. 42. c Ref. 93. d Ref. 94. e Ref. 95. f Ref. 18. | ||||
| Present work | GGA | 5.639 | 217.63 | 4.30 |
| GGA+ULRMn | 5.659 | 186.29 | 4.41 | |
| GGA+ULRCo | 5.910 | 65.40 | 1.25 | |
| GGA+ULRMn,Co | 6.125 | 60.70 | 5.74 | |
| Theory | LSDA | 5.54a | 258.0a | |
| GGA | 5.643b, 5.633c, 5.639d, 5.642e | 226b, 212.8c, 214d, 240.89e | 4.680c, 4.674d, 4.983e | |
| Experiment | 5.645f | |||
3.3 Origin of half-metallicity
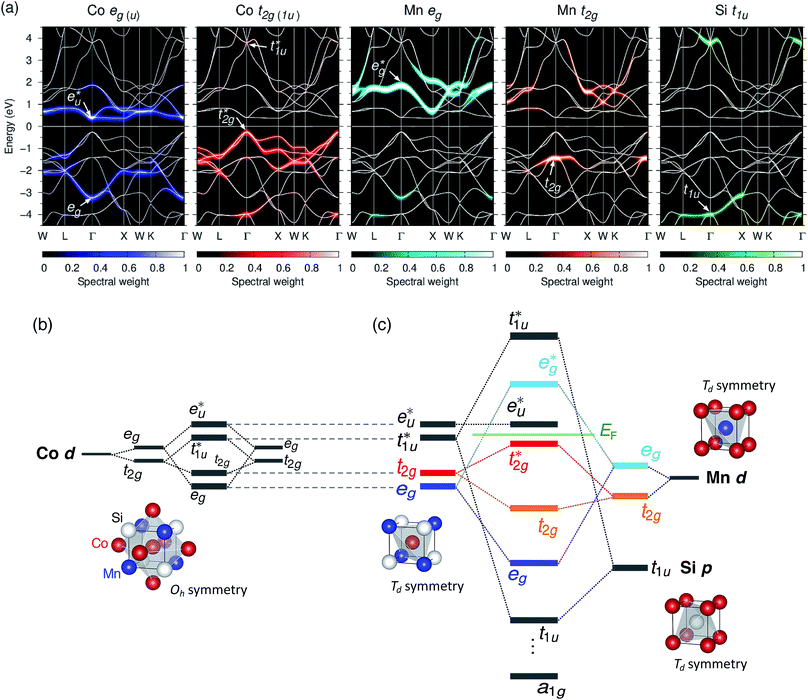
As mentioned in Section 2, the full Heusler alloy of L21 structure belongs to the octahedral (Oh) space group symmetry. In this whole-crystal symmetry, we first focus on the Co lattice by ignoring the first-neighboring Mn and Si atoms. The lattice is assumed to be a simple cubic composed by the second-neighboring Co at different sublattices in the primitive cell, which leads to the Co sitting at Oh site symmetry. Secondly, our focus turns to the tetrahedral (Td) site symmetry. Neglecting the chemical atomic species, every atom forms a bcc lattice structure and is surrounded by a tetrahedral environment. The hybridization diagram of atomic orbital energy is discussed by following these two steps. Note that, to avoid confusion regarding the notations, the symmetric characters of the atomic orbitals are unified using only representations for the Oh site symmetry, which corresponds to the space group of the L21 full Heusler compound, as done in previous research.38We again start with the results of the standard GGA calculations to discuss the underlying electronic structure of Co2MnSi. Fig. 4(a) shows the band structures for the minority spin states projected into the Co eg(u) (dz2, dx2−y2) and t2g(1u) (dxz, dyz, dxy), Mn eg (dz2, dx2−y2) and t2g (dxz, dyz, dxy), and Si t1u (px, py, pz) orbitals. The lattice constant is set to the theoretically obtained value of 5.639 Å. The d states of Co and Mn are visible around the Fermi energy, while the Si t1u state can be seen only very far from the Fermi energy. To discuss the orbital hybridization mechanism, the eigenstates at the Γ point in the Brillouin zone are focused on. At 0.4 eV above the Fermi energy, the Co 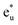 state (this state is an anti-bonding state as discussed in the next paragraph) appears but the other orbital components are not included in these eigenstates, which means that Co
state (this state is an anti-bonding state as discussed in the next paragraph) appears but the other orbital components are not included in these eigenstates, which means that Co 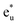 does not hybridize with the other atomic orbitals. We can find t2g hybridization between Co and Mn that forms a bonding Mn t2g state at −1.4 eV and an anti-bonding Co
does not hybridize with the other atomic orbitals. We can find t2g hybridization between Co and Mn that forms a bonding Mn t2g state at −1.4 eV and an anti-bonding Co 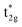 at 0.3 eV. As a result, a minority band gap originates from the anti-bonding
at 0.3 eV. As a result, a minority band gap originates from the anti-bonding 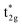 and non-bonding
and non-bonding 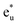 states of the Co atom. Another essential orbital hybridization is found in the t1u symmetry character between Co and Si. The eigenstate components of Co and Si exist at energy levels of 3.8 and 3.9 eV, respectively, so that the Co and Si atoms contribute to the anti-bonding state
states of the Co atom. Another essential orbital hybridization is found in the t1u symmetry character between Co and Si. The eigenstate components of Co and Si exist at energy levels of 3.8 and 3.9 eV, respectively, so that the Co and Si atoms contribute to the anti-bonding state 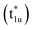 and to the bonding state (t1u), respectively. We do not mention the eg hybridization between Co and Mn as it has already been discussed previously.38
and to the bonding state (t1u), respectively. We do not mention the eg hybridization between Co and Mn as it has already been discussed previously.38
Fig. 4(b) presents an energy diagram of Co atoms with Oh site symmetry. Due to the crystal field, the eg and t2g orbitals are formed and hybridize with the same character orbitals of Co at the other site. These hybridizations arise from the bonding states of eg and t2g orbitals and anti-bonding states of 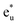 and
and 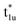 orbitals. The t2g orbital hybridization, including dxz − dxz, dyz − dyz, and dxy − dxy, is expected to form a π-like bonding in the Oh atomic positions, and the eg hybridization, including dz2 − dz2 and dx2–y2 − dx2–y2, is expected to form a σ-like bonding, whose orbital coupling is stronger than that of π-like bonding. Accordingly, the energy gap between bonding eg and anti-bonding
orbitals. The t2g orbital hybridization, including dxz − dxz, dyz − dyz, and dxy − dxy, is expected to form a π-like bonding in the Oh atomic positions, and the eg hybridization, including dz2 − dz2 and dx2–y2 − dx2–y2, is expected to form a σ-like bonding, whose orbital coupling is stronger than that of π-like bonding. Accordingly, the energy gap between bonding eg and anti-bonding 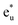 states arising from eg hybridization becomes wide compared to that from the bonding t2g and anti-bonding
states arising from eg hybridization becomes wide compared to that from the bonding t2g and anti-bonding 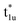 states from t2g hybridization.
states from t2g hybridization.
Next, the orbital interactions between the first-neighboring atoms are discussed by focusing on Td site symmetry. Before that, we mention here the correlation between the Oh and Td site symmetries and the possibility of atomic orbitals hybridizing. The Td site symmetry, which is a subgroup of the Oh site symmetry, has the same irreducible representations as the Oh site symmetry except for an absence (presence) of inversion symmetry in Td (Oh) site symmetry. The Co–Co d orbital’s character in the Oh site symmetry can be transformed into the Td notation; the doublet eg and 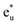 orbitals in Oh are represented as the e character in Td, and the triplet t2g and
orbitals in Oh are represented as the e character in Td, and the triplet t2g and 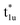 orbitals as t2 character. The Td site symmetry also gives the e (dz2, dx2–y2) and t2 (dxz, dyz, dxy) characters for Mn and t2 (px, py, pz) for Si. These augments allow Co–Mn and Co–Si to interact in the atomic orbitals in Td site symmetry, i.e., t2g orbital hybridization of Co–Mn and t1u orbital hybridization of Co–Si in Oh site symmetry.
orbitals as t2 character. The Td site symmetry also gives the e (dz2, dx2–y2) and t2 (dxz, dyz, dxy) characters for Mn and t2 (px, py, pz) for Si. These augments allow Co–Mn and Co–Si to interact in the atomic orbitals in Td site symmetry, i.e., t2g orbital hybridization of Co–Mn and t1u orbital hybridization of Co–Si in Oh site symmetry.
Fig. 4(c) illustrates the possible energy diagram between Co–Co and Mn or Si. The a1g orbital corresponds to the Si s orbital, which does not appear in the band structure of Fig. 4(a) because the energy level is very low. The anti-bonding Co 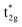 state dominates the highest orbital state in the valence band, which hybridizes with the bonding Mn t2g. The Co
state dominates the highest orbital state in the valence band, which hybridizes with the bonding Mn t2g. The Co 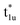 is pushed up to quite a higher energy through hybridization with the Si t1u (p) orbital and the non-bonding Co
is pushed up to quite a higher energy through hybridization with the Si t1u (p) orbital and the non-bonding Co 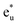 is left at above the Fermi level. This energy diagram, thus, suggests that the main contributions to constructing the minority band gap arise from the t2g coupling of Co and Mn atoms and the t1u orbital of Co no longer contributes to the gap; this conclusion is different from that of a previous study,38 where the band gap in the minority state is mostly dominated by Co eu and t1u orbitals (these orbital characters are used in previous work). Instead, more importantly, our diagram proposes that the HM property and electronic structure near the Fermi level can be tuned by selection of the Y atom and/or a mix of several atoms in the Y site through t2g coupling in L21 Heusler alloys.
is left at above the Fermi level. This energy diagram, thus, suggests that the main contributions to constructing the minority band gap arise from the t2g coupling of Co and Mn atoms and the t1u orbital of Co no longer contributes to the gap; this conclusion is different from that of a previous study,38 where the band gap in the minority state is mostly dominated by Co eu and t1u orbitals (these orbital characters are used in previous work). Instead, more importantly, our diagram proposes that the HM property and electronic structure near the Fermi level can be tuned by selection of the Y atom and/or a mix of several atoms in the Y site through t2g coupling in L21 Heusler alloys.
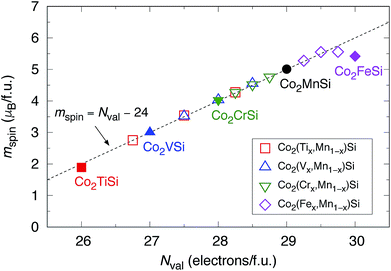
Even though our diagram differs from the previously reported one,38 the 12 valence electrons for Co2MnSi are confirmed to occupy three Co 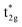 , three Mn t2g, two Co eg, three Si t1u, and one Si a1g orbitals in the down-spin state. This means our diagram satisfies the well-known Slater–Pauling relation:38 the magnetic moment of the system, mspin, obeys mspin = Nval − 24, where Nval is the total number of valence electrons. The calculations obtain a total magnetic moment of 5.01 μB, which is very close to the integer value expected by the Slater–Pauling rule and in agreement with a previous theory within LSDA38 and GGA,42,44 as well as experiments,96–99 as summarized in Table 3.
, three Mn t2g, two Co eg, three Si t1u, and one Si a1g orbitals in the down-spin state. This means our diagram satisfies the well-known Slater–Pauling relation:38 the magnetic moment of the system, mspin, obeys mspin = Nval − 24, where Nval is the total number of valence electrons. The calculations obtain a total magnetic moment of 5.01 μB, which is very close to the integer value expected by the Slater–Pauling rule and in agreement with a previous theory within LSDA38 and GGA,42,44 as well as experiments,96–99 as summarized in Table 3.
| Total | Co | Mn | Si | |
|---|---|---|---|---|
| a FS-KKR: full-potential screened Korringa–Kohn–Rostoker Green’s function method; ASA: atomic sphere approximation; ASW: augmented spherical waves method; FLAPW: full-potential linearized augmented plane wave method; FP-LMTO: full-potential liner muffin-tin orbital method; MLWF: maximally localized Wannier functions; GW: GW approximation. b The U and J values of 3.5 (5.0) and 1.0 (0.9) eV for Co (Mn), respectively, are chosen to reproduce the total spin magnetic moment observed experimentally. c The respective Ueff values of 3.28 and 3.07 eV for Co and Mn are determined by cRPA. d The U and J values of 3.0 and 0.9 eV, which have been reported as average values of the determined parameters by theory for pure bulk 3d transition metals, are used. e Sucksmith: Sucksmith ring-balance measurement by Faraday method; SQUID: superconducting quantum interface device magnetometry. | ||||
| Present work | ||||
| GGA | 5.01 | 1.05 | 2.95 | −0.05 |
| GGA+ULRMn | 5.01 | 0.72 | 3.63 | −0.08 |
| GGA+ULRCo | 6.95 | 1.88 | 3.19 | −0.09 |
| GGA+ULRMn,Co | 8.08 | 1.94 | 4.05 | −0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Theory a | ||||
| FS-KKR38 (LSDA) | 4.94 | 1.02 | 2.97 | −0.07 |
| ASA-ASW44 (GGA) | 5.00 | 0.93 | 3.21 | −0.06 |
| FLAPW42 (GGA) | 5.00 | 1.06 | 2.92 | −0.04 |
| FP-LMTO86 (GGA+Ub) | 5.00 | 1.08 | 2.97 | −0.08 |
| MLWF-FLAPW87 (GGA+Uc) | 5.00 | 1.05 | 3.01 | −0.06 |
| KKR53 (LSDA+DMFTd) | 4.97 | |||
| FLAPW-GW55 (GGA) | 5.00 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Experiment e | ||||
| Sucksmith96 | 5.07 | 0.75 | 3.57 | |
| Ref. 97 | 5.01 | |||
| SQUID98 | 4.97 | |||
| SQUID99 | 5.00 | 0.72 | 3.34 | |
Note that the previous study38 was carried out for Co2MnGe, where the number of valence electrons is equivalent to that of Co2MnSi. Thus, Co2MnGe is confirmed to be similar to Co2MnSi. The energy diagram obtained from the band structure calculations corresponds to Fig. 4(c) and the integer value of the total spin magnetic moment is calculated (mspin = 5.00 μB).
3.4 Correlation effects on Mn and Co
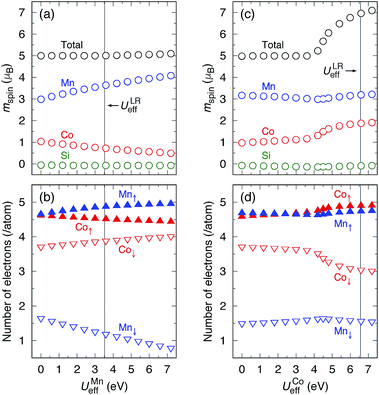
As mentioned in the introduction, the behaviors of electron localizations are supposed to be different at Co and Mn sites. This fact motivates us to investigate the effects of the correlations for each site. To discuss the influence of +U on the atomic energy diagram, modifications of magnetic moment and band structure are studied by performing DFT+U calculations with varying Ueff parameters for Co and Mn atoms independently. Here, we refer to the case where the varying Ueff is applied to only the Mn (Co) site for the GGA+UMn (GGA+UCo) representation, where the lattice constant is set to the theoretical value of 5.695 Å (5.910 Å) obtained in Section 3.2.We first mention the GGA+UMn case. The total mspin is constant but the Mn (Co) mspin monotonically increases (decreases) when the correlation parameter for Mn, UMneff, increases (see Fig. 5(a)). Note that two of the Co atoms exist in the primitive cell, so the variation of the Co mspin is estimated to be twice as great. The increased mspin of Mn arises from a significant reduction in minority spin electron occupations, as shown in Fig. 5(b). This reflects the following behavior: a large +U value intensifies the coulomb interaction contributions and allows electrons to occupy not the same but different orbitals with parallel spins from Pauli exclusion principles and Hund’s rule, leading to a gain in kinetic energy.
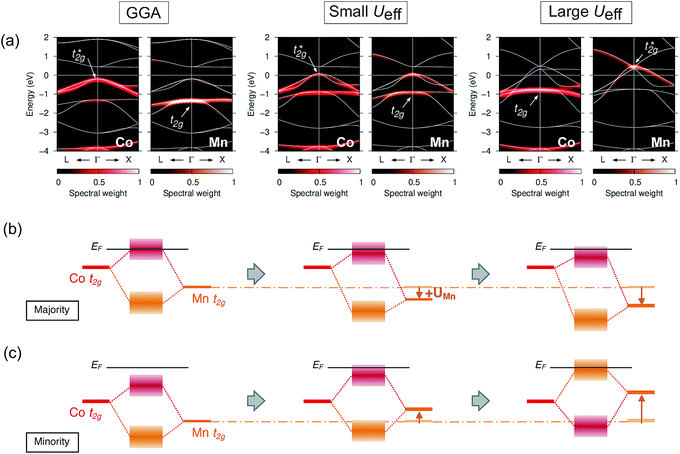
As the t2g orbitals of Co and Mn change the most noticeably depending on the UMneff value, we trace modifications in the band structures of these orbitals. Fig. 6(a) presents the minority spin band structures around the Γ point calculated by standard GGA and the GGA+UMn with small (UMneff = 3 eV) and large (6 eV) parameter values. The GGA results indicate that the anti-bonding Co 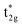 is dominant just below the Fermi energy and the bonding Mn t2g is visible at 1.5 eV in a minority state. Interestingly, increasing the UMneff value modifies the spectral weights of the minority components; the Mn and Co orbital weights in bonding and anti-bonding states are almost identical at small UMneff, but the anti-bonding
is dominant just below the Fermi energy and the bonding Mn t2g is visible at 1.5 eV in a minority state. Interestingly, increasing the UMneff value modifies the spectral weights of the minority components; the Mn and Co orbital weights in bonding and anti-bonding states are almost identical at small UMneff, but the anti-bonding 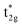 becomes dominated by Mn compared to Co and
becomes dominated by Mn compared to Co and 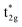 shifts above the Fermi energy at a large UMneff. Schematic diagrams are illustrated in Fig. 6(b) and (c). In the majority spin, the valence Mn t2g atomic orbital is shifted to a lower energy by the UMneff effect and the anti-bonding state Co
shifts above the Fermi energy at a large UMneff. Schematic diagrams are illustrated in Fig. 6(b) and (c). In the majority spin, the valence Mn t2g atomic orbital is shifted to a lower energy by the UMneff effect and the anti-bonding state Co 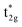 is drawn to a lower energy by the hybridization with Mn t2g. On the other hand, in the minority state, the energy level of the Mn valence state becomes higher as UMneff increases, and the anti-bonding Co
is drawn to a lower energy by the hybridization with Mn t2g. On the other hand, in the minority state, the energy level of the Mn valence state becomes higher as UMneff increases, and the anti-bonding Co 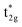 orbital gradually touches the Fermi energy. When the Mn t2g state becomes energetically higher than that of Co at a large UMneff, the major component of the anti-bonding
orbital gradually touches the Fermi energy. When the Mn t2g state becomes energetically higher than that of Co at a large UMneff, the major component of the anti-bonding 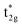 is switched from Co to Mn in minority spin.
is switched from Co to Mn in minority spin.
Surprisingly, UMneff shifts the minority occupied state of Mn upward energetically; this shifting is an opposite tendency to the well-known fact of DFT+U study. In general, the +U term opens the band gap with the valence (conduction) state being lower (higher) energy in the insulating and semi-conducting materials regardless of the spin channels. However, ferromagnetic materials, including the Heusler alloy, are different from insulators and semi-conductors because a finite DOS lies at the Fermi energy in ferromagnets. In principle, the total number of valence electrons at each atom site must be preserved even though the +U effect is introduced. Accordingly, the upward shifting in the valence state of the minority Mn d orbital can be understood as follows: the occupations in a spin channel (majority state) increase due to the applied +U effect, but simultaneously, the occupations in the opposite spin (minority state) are reduced to keep the total occupations constant at each atom. This argument is based on the energy diagrams in Fig. 6(b) and (c), and is consistent with the behaviors of the spin magnetic moment and electron occupations at each atomic site [Fig. 5(a) and (b)]; thus, this scenario can be concluded to be behind the effects of +U on the Mn d orbitals.
Secondly, the GGA+UCo result is considered. In the range of UCoeff less than around 4 eV, the increase in the spin magnetic moment at the Co site is not significant, but it suddenly increases afterward [Fig. 5(c)]. In Fig. 7, the UCoeff-dependent electronic band structures and hybridization behaviors of Co and Mn are summarized. In the valence states, it can be seen that the contribution to the anti-bonding 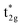 is switched from Co to Mn [Fig. 7(a)]. In contrast, the anti-bonding
is switched from Co to Mn [Fig. 7(a)]. In contrast, the anti-bonding 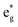 state is switched from Mn to Co [Fig. 7(b)] with increasing UCoeff. The
state is switched from Mn to Co [Fig. 7(b)] with increasing UCoeff. The 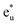 state in Fig. 7(b) moves to a higher energy on increasing UCoeff, but does not hybridize with Mn.
state in Fig. 7(b) moves to a higher energy on increasing UCoeff, but does not hybridize with Mn.
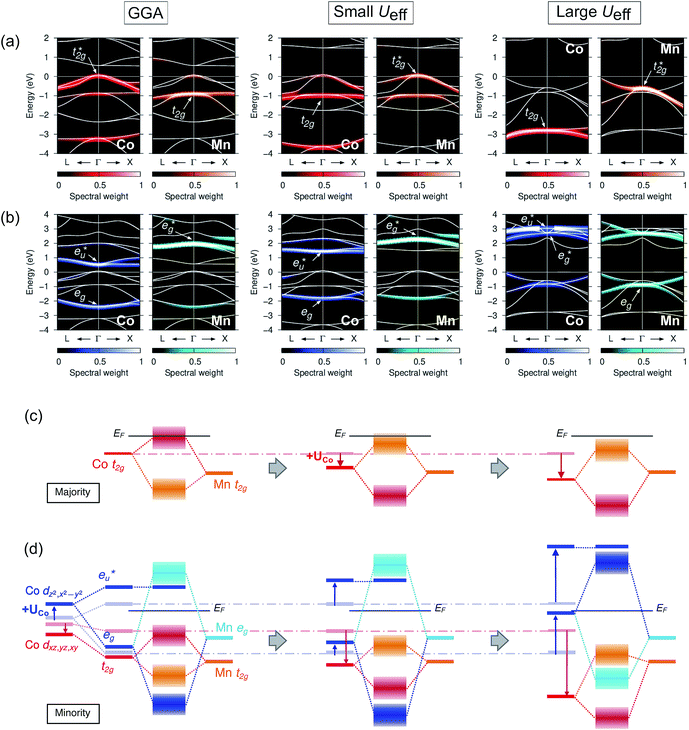 | ||
| Fig. 7 Dependence of the minority band structures on the varying +UCo parameter values, i.e., GGA (Ueff = 0 eV for the Co site), small (3 eV), and large (6 eV), where the projected spectral weights for the (a) Co and Mn t2g states are shown in the left (red) and right (orange) panels, and for the (b) Co and Mn eg states are shown in the left (blue) and right (sky-blue), respectively. Note that the energy ranges in (a and b) are different. Schematic summary of the changes in atomic orbital hybridizations for (c) majority and (d) minority states. Notation is the same in Fig. 6. | ||
To understand the behavior of the changing mspin and electron numbers in GGA+UCo in Fig. 5(c) and (d), the possible energy diagrams for the majority and minority states are illustrated in Fig. 7(c) and (d). The majority Co 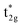 simply goes to a lower energy on the introduction of UCoeff, so that the Co d spin-up occupation increases and is saturated at larger UCoeff values (∼7 eV). For the minority state, the d bands’ behaviors of Co and Mn are intricate, but can be understood by going back to the principle view that first attention is paid to the hybridization between Co atoms in different sublattices and then that between the Mn and Co–Co states afterward, as discussed in Section 3.3 and a previous report.38 The Co dz2 and dx2–y2 (dxz, dyz, and dxy) orbitals are pushed up (down) due to UCoeff, and hybridize with the Mn eg (t2g) state [Fig. 7(d)]. Increasing UCoeff affects the energy gap, and most notably, the Co eg orbital becomes an un-occupied anti-bonding state at a large UCoeff value, while it is an occupied bonding state at a small UCoeff (see the blue band of the energy diagram in Fig. 7(d)). This event induces a significant reduction in the minority Co occupations [red down-pointing triangle in Fig. 5(d)], resulting in an increase in the total mspin in the range of UCoeff over ∼4 eV, as shown by black plots in Fig. 5(c).
simply goes to a lower energy on the introduction of UCoeff, so that the Co d spin-up occupation increases and is saturated at larger UCoeff values (∼7 eV). For the minority state, the d bands’ behaviors of Co and Mn are intricate, but can be understood by going back to the principle view that first attention is paid to the hybridization between Co atoms in different sublattices and then that between the Mn and Co–Co states afterward, as discussed in Section 3.3 and a previous report.38 The Co dz2 and dx2–y2 (dxz, dyz, and dxy) orbitals are pushed up (down) due to UCoeff, and hybridize with the Mn eg (t2g) state [Fig. 7(d)]. Increasing UCoeff affects the energy gap, and most notably, the Co eg orbital becomes an un-occupied anti-bonding state at a large UCoeff value, while it is an occupied bonding state at a small UCoeff (see the blue band of the energy diagram in Fig. 7(d)). This event induces a significant reduction in the minority Co occupations [red down-pointing triangle in Fig. 5(d)], resulting in an increase in the total mspin in the range of UCoeff over ∼4 eV, as shown by black plots in Fig. 5(c).
From the above discussions, the underlying physics of the correlation effects on the magnetic moment can be addressed from the viewpoint of electronic structure for both the GGA+UMn and GGA+UCo cases. Thus, the consistency of our energy diagram proposed in Fig. 4(c) is demonstrated successfully.
3.5 Electronic and magnetic properties
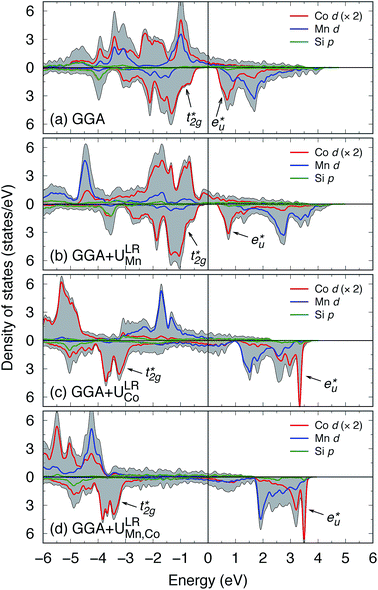
We now discuss the electronic and magnetic properties obtained from the band calculations that incorporate the LR-determined correlation parameters (3.535 eV for Mn and 6.570 eV for Co). First, the mspin obtained from the GGA+ULRMn method is compared with that from the GGA method in Table 3. The value of the total mspin is the same as that of GGA and agrees with previous reports.53,55,86,87,96–99 On the other hand, regarding the atom-resolved contributions, the results for mspin of Co (0.72 μB) and Mn (3.63 μB) are not in agreement with GGA and previous calculations, but in good agreement with experiments.96,99 Thus, the GGA+ULRMn calculation results are superior to the standard GGA results.In the GGA-calculated DOS in Fig. 8(a), we can clearly see that the Co d orbital is broad over a wide energy region (from the Fermi energy to 5 eV for the majority state and from 0.5 eV to 4.5 eV for the minority state). Contrarily, the Mn d orbital is relatively localized compared to the Co one and splits into two peaks located around 3 and 1 eV (1.5 and 1.8 eV) in the majority (minority) state, respectively. As expected from Fig. 4(b) and (c), we also confirm the 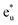 and
and 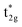 orbital characters of the Co d states above and below the Fermi energy, as shown by arrows in Fig. 8(a). The value of spin polarization referred to as PDOS is estimated by
orbital characters of the Co d states above and below the Fermi energy, as shown by arrows in Fig. 8(a). The value of spin polarization referred to as PDOS is estimated by 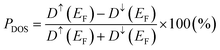 , where Dσ(EF) is the DOS of the majority (σ = ↑) or minority (σ = ↓) spin state at the Fermi energy. A 100% PDOS value is obtained, and the energy band gap in the minority spin state E↓gap is around 0.8 eV. The GGA+ULRMn calculation modifies the DOS from GGA. The energy level of the Mn occupied (unoccupied) states is shifted to a lower (higher) level due to the exchange splitting induced by the ULR(Mn)eff effect. As a result, the valence and conduction edges are dominated mainly by Co d components and only a few Mn d states appear around the Fermi energy. Due to the presence of a few Co d DOSs at the Fermi energy, the half-metallicity is broken but high spin polarization PDOS = 90.5% is obtained.
, where Dσ(EF) is the DOS of the majority (σ = ↑) or minority (σ = ↓) spin state at the Fermi energy. A 100% PDOS value is obtained, and the energy band gap in the minority spin state E↓gap is around 0.8 eV. The GGA+ULRMn calculation modifies the DOS from GGA. The energy level of the Mn occupied (unoccupied) states is shifted to a lower (higher) level due to the exchange splitting induced by the ULR(Mn)eff effect. As a result, the valence and conduction edges are dominated mainly by Co d components and only a few Mn d states appear around the Fermi energy. Due to the presence of a few Co d DOSs at the Fermi energy, the half-metallicity is broken but high spin polarization PDOS = 90.5% is obtained.
By contrast, GGA+ULRCo and GGA+ULRMn,Co seem to fail to obtain the total magnetic moment reasonably consistently with the experimental observations96,99 because of the overestimated ULR(Co)eff parameters (see Table 3). Fig. 8(c) indicates the fact that the exchange splitting arising from the large ULR(Co)eff induces a fully-occupied Co d state in majority spin states, which leads to a Co mspin of 1.88 μB and total mspin of 6.95 μB. The energy gap does not appear in the minority channel and the top of the valence states around 2 eV from the Fermi energy is composed of the Mn d orbital of the majority states. Similarly, in the GGA+ULRMn,Co case, the overestimated value of the total mspin of 8.08 μB arises from the fact that the majority electrons of Co and Mn are fully occupied at low energy (4 eV and below) through both ULR(Mn)eff and ULR(Co)eff, as shown in Fig. 8(d). In this scheme, the half-metallic electronic structure is broken by a few DOS that are widely broad around the Fermi energy. The spin polarizations are found to be negative and small absolute values: PDOS = −26.97 and 33.82% for the respective GGA+ULRCo and GGA+ULRMn,Co methods.
From the experimental point of view, hard X-ray photoelectron spectroscopy measurements reported that the valence band structure in the binding energy region from the Fermi energy to ∼1.2 eV (corresponding to −1.2 eV in calculated DOS) is mostly contributed to by Co 3d electrons100 as while the Mn d state does exist in this binding-energy region, the number of electrons is very few compared to Co.101 Based on the above comparative discussions between our calculations and experiments on the electronic structure and magnetic moment (as well as the equilibrium lattice constant in Section 3.2), we can conclude that the static many-body correlation +U at the Y site (Y = Mn for Co2MnSi) plays an important role in obtaining ground-state properties that are in good agreement with the experiments. On the other hand, the Co d electrons are rather itinerant in the alloy; thus, the LR approach tends to overestimate the correlation parameter for the Co site, which is not reliable for accurate band calculations. In other words, for the Co site, correlation correction may not be necessary and mean-field approximation (GGA or LSDA) is enough to treat the itinerant Co d electrons. Thus, hereafter, all LR-based DFT+U calculations are performed with ULReff only for the Y site; i.e., correlation correction is excluded for Co. We here explicitly mention that the energy diagram obtained from the GGA+ULRMn calculation corresponds to Fig. 4(b) and (c), which are obtained from the GGA results.
4 Searching for HM materials of other ternary and quaternary alloys
To consider the ternary Co2Y Si alloys, where Y is changed from Mn to Ti, V, Cr, or Fe atoms, the LR calculations for ULR(Y)eff are first carried out using the lattice constants assumed in experiments,16,18,102 as in the case of Co2MnSi. To the best of our knowledge, there are no experimental data for Co2CrSi, so the lattice constant obtained from Murnaghan fitting91 by the GGA potential is employed for the ULR(Cr)eff calculation. In this study the initial magnetization for the SCF calculation is assumed to be the ferromagnetic state in all ternary models. The determined parameters are around 3–4 eV depending on the materials: ULR(Y)eff = 2.942, 3.979, 3.169, and 3.922 eV for Co2TiSi, Co2VSi, Co2CrSi, and Co2FeSi, respectively.103Calculated total DOSs are shown in Fig. 9(a)–(d), and the results for the spin magnetic moments are summarized in Table 4. Co2TiSi is not HM (PDOS = 25.8%), where the Fermi energy is located at the minority conduction edge state. For Co2VSi and Co2CrSi, a few broad minority DOSs are found around the Fermi energy; thus, the electronic structure is not HM, but the highly spin-polarized values are estimated as PDOS = 98.2 and 89.3%, respectively. On the other hand, negative spin polarization, PDOS = −62.3%, is obtained in Co2FeSi, where the minority DOS is much greater compared to the majority state at Fermi energy. Note that, as the Y atom is changed from a large atomic number (ZFe = 26) to small (ZV = 23), the Fermi energy position seems to move away from the conduction state of minority spin, but this is not the case for Y = Ti. This exception is attributable to the fact that the Ti spins in Co2TiSi couple with those of Co with anti-parallel direction and the ferrimagnetic structure is obtained in our calculations, while the other systems favor the ferromagnetic structure (see Table 4). Total spin magnetic moments are calculated as 1.89, 3.00, 4.03, and 5.42 μB for Co2TiSi, Co2VSi, Co2CrSi, and Co2FeSi, respectively.
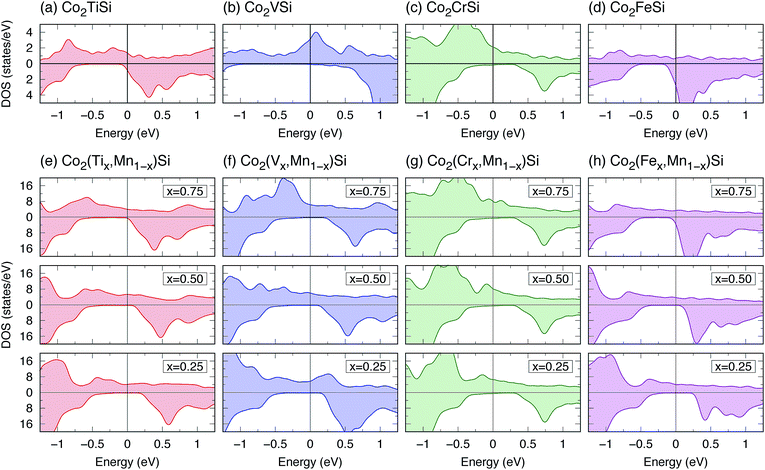 | ||
| Fig. 9 (a–d) Total DOS for ternary Co2YSi (Y = Ti, V, Cr, or Fe), and (e–h) total DOS dependence on composition x for quaternary Co2(Yx,Mn1−x)Si (x = 0.25, 0.5, or 0.75) calculated by the LR-based DFT+U method. In each panel, the upper (bottom) region shows the DOS for up- (down-) spin states, and the Fermi energy is set to zero. Note that the vertical axis range of DOS in (a–d) is different from that in (e–h) as the number of atoms per primitive cell of the ternary system is a quarter of the quaternary one (see Fig. 1). | ||
| N val | Spin magnetic moment | ||||
|---|---|---|---|---|---|
| Total | Co | Y | Mn | ||
| Co2TiSi | 26 | 1.89 | 0.97 | −0.02 | |
| Co2(Ti0.75Mn0.25)Si | 26.75 | 2.76 | 0.94 | −0.09 | 3.85 |
| Co2(Ti0.50Mn0.50)Si | 27.5 | 3.54 | 0.90 | −0.21 | 3.75 |
| Co2(Ti0.25Mn0.75)Si | 28.25 | 4.28 | 0.83 | −0.37 | 3.69 |
| Co2VSi | 27 | 3.00 | 1.26 | 0.59 | |
| Co2(V0.75Mn0.25)Si | 27.5 | 3.51 | 0.84 | 1.19 | 3.75 |
| Co2(V0.50Mn0.50)Si | 28 | 4.03 | 0.38 | 1.06 | 3.70 |
| Co2(V0.25Mn0.75)Si | 28.5 | 4.56 | 1.10 | 0.15 | 3.13 |
| Co2CrSi | 28 | 4.03 | 0.52 | 2.90 | |
| Co2(Cr0.75Mn0.25)Si | 28.25 | 4.28 | 0.58 | 2.90 | 3.63 |
| Co2(Cr0.50Mn0.50)Si | 28.5 | 4.52 | 0.62 | 2.88 | 3.61 |
| Co2(Cr0.25Mn0.75)Si | 28.75 | 4.77 | 0.67 | 2.94 | 3.63 |
| Co2(Fe0.25Mn0.75)Si | 29.25 | 5.27 | 0.94 | 2.91 | 3.65 |
| Co2(Fe0.50Mn0.50)Si | 29.5 | 5.55 | 1.15 | 2.94 | 3.69 |
| Co2(Fe0.75Mn0.25)Si | 29.75 | 5.58 | 1.25 | 2.95 | 3.75 |
| Co2FeSi | 30 | 5.42 | 1.29 | 2.92 | |
The structural properties are also investigated as summarized in Table 5. The estimated lattice constants are in good agreement with the experiments16,18,102,104 and their error values from the experiments are less than 1% for Co2TiSi, Co2VSi, and Co2FeSi. In Co2CrSi, the lattice constant of 5.694 Å is close to the previous calculation.105 The bulk moduli in all models estimated from the LR-based DFT+U method are slightly smaller than those in the previous calculations. This trend is similar to the Co2MnSi case, and might come from the fact that the previous studies were conducted by standard LSDA105–109 and GGA.92 The experimentally measured B0 is available only for Y = Fe (B0 = 240 GPa).104 From our calculations, the B0 and 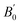 in Co2FeSi are found to be 183.263 GPa and 4.679, respectively. The LSDA calculation92 shows a reasonably consistent value of B0 = 241.9 GPa with the experiment, although the GGA calculation105,107,109 underestimates B0 (B0 = 203.5–207.1 GPa). Zhu et al.109 also performed GGA+U calculations, where the empirical parameters of U = 3.5 and J = 0.9 eV for Co and those of U = 3.4 and J = 0.9 eV for Fe were employed, and obtained B0 = 209.3 GPa and
in Co2FeSi are found to be 183.263 GPa and 4.679, respectively. The LSDA calculation92 shows a reasonably consistent value of B0 = 241.9 GPa with the experiment, although the GGA calculation105,107,109 underestimates B0 (B0 = 203.5–207.1 GPa). Zhu et al.109 also performed GGA+U calculations, where the empirical parameters of U = 3.5 and J = 0.9 eV for Co and those of U = 3.4 and J = 0.9 eV for Fe were employed, and obtained B0 = 209.3 GPa and 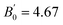 (the GGA+U results are not shown in Table 5). Therefore, the LSDA calculations might be suitable for the bulk modulus compared to the GGA+U approaches, while it seems to underestimate the lattice constant from the experiments, for example, a0 = 5.52 Å in Co2FeSi.92 However, the LR-based DFT+U method provides reasonable results at least for a0 values.
(the GGA+U results are not shown in Table 5). Therefore, the LSDA calculations might be suitable for the bulk modulus compared to the GGA+U approaches, while it seems to underestimate the lattice constant from the experiments, for example, a0 = 5.52 Å in Co2FeSi.92 However, the LR-based DFT+U method provides reasonable results at least for a0 values.
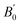 for Co2YSi comparing the present study, previous calculations, and experiments. The results of the present study are obtained from the LR-based DFT+U method with parameters of ULR(Y)eff = 2.942, 3.979, 3.169, and 3.922 eV for Y = Ti, V, Cr, and Fe, respectively. Previous calculation results are from GGA, except for the bottom row for Co2FeSi that are from LSDA
for Co2YSi comparing the present study, previous calculations, and experiments. The results of the present study are obtained from the LR-based DFT+U method with parameters of ULR(Y)eff = 2.942, 3.979, 3.169, and 3.922 eV for Y = Ti, V, Cr, and Fe, respectively. Previous calculation results are from GGA, except for the bottom row for Co2FeSi that are from LSDA
| Present work | Theory | Experiment | ||||||
|---|---|---|---|---|---|---|---|---|
| a 0 (A) | B 0 (GPa) | a 0 (A) | B 0 (GPa) | a Expt (A) | B 0 (GPa) | |||
| a Ref. 106. b Ref. 105. c Ref. 107. d Ref. 92. e Ref. 108. f Ref. 109. g Ref. 16. h Ref. 18. i Ref. 102. j Ref. 104. | ||||||||
| Co2TiSi | 5.774 | 189.494 | 4.191 | 5.764a | 204–244.8304a,b,c,e | 4.5151e | 5.743g | |
| Co2VSi | 5.667 | 192.408 | 7.485 | 5.7609b, 5.679c | 216b, 221.5c | 5.647h | ||
| Co2CrSi | 5.694 | 174.169 | 5.106 | 5.6295b, 5.638c | 227b, 225.3c | |||
| Co2FeSi | 5.685 | 183.263 | 4.679 | 5.6431b | 203.5–207.1b,c,f | 4.62f | 5.644i, 5.650j | 240j |
| 5.52d | 241.9d | |||||||
We finally investigate the quaternary Heusler compounds of chemical formula Co2(Yx,Mn1−x)Si (Y = Ti, V, Cr, or Fe) with a composition x (x = 0.25, 0.50, or 0.75). To model these systems in L21 structure, as illustrated in Fig. 1(b)–(d), cubic primitive cells consisting of 16 atoms are considered. The lattice constant is given by Vegard’s law110,111 using the obtained equilibrium lattice constants for Co2YSi (aCYS) and Co2MnSi (aCMS) as a(x) = xaCYS + (1 − x)aCMS. The correlation parameters of the Mn and Y atoms for quaternary systems at all compositions are assumed to be the values of ULR(Mn)eff and ULR(Y)eff, which are determined by the LR theory for ternary Co2MnSi and Co2YSi. For the quaternary compounds, in which the atomic position of the different elements is not symmetric as in the ternary system, the structures are geometrically relaxed under the equilibrium lattice constants by force calculations using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm112–115 until the forces acting on each atom are minimized below the criterion of 10−3 Ry per bohr.
The calculated mspin values for the quaternary alloys are also available in Table 4. In the case of only Y = Ti, the Ti spins are ferrimagnetically coupled with Co and Mn similar to that in the ternary model. The Mn mspin is a large value over 3 μB in all systems. Fig. 10 plots the total mspin for ternary and quaternary Co-based full Heusler compounds under study as a function of Nval in the system. The Slater–Pauling relation is satisfied in the range of less than 29.5 in Nval while being slightly underestimated for the range over Nval = 29.5, which corresponds to Co2(Fe0.75,Mn0.25)Si, and Co2FeSi.
The results for DOS for quaternary alloys are shown in Fig. 9(e)–(h). A perfectly HM electronic structure (PDOS is equal to 100%) is found in Co2(Ti0.25,Mn0.75)Si, Co2(V0.25,Mn0.75)Si, Co2(V0.50,Mn0.50)Si, and Co2(Fe0.25,Mn0.75)Si. Among them, Co2(V0.75,Mn0.25)Si has the largest minority band gap E↓gap = 0.5 eV, and thus, this material can be a good candidate for a wide-gap HM ferromagnet. Co2(Ti0.25,Mn0.75)Si and Co2(Fe0.25,Mn0.75)Si are also HM candidates because of the advantage in Fermi energy position, as it locates at almost the center of the valence and conduction states in minority states. These HM characters lead to the robustness of spin polarization due to the broadening of valence and conduction states at finite temperature. Nearly HM (PDOS is almost 100%) is found in Co2(Ti0.50,Mn0.50)Si (PDOS = 99.9%) and Co2(Fe0.50,Mn0.50)Si (99.4%). Fig. 11 presents the composition dependence of PDOS. Although the Y = Cr system does not show the HM property at each composition, an interesting trend we observed is that a high PDOS is independent of the composition, and Y = V is also the same, whereas a large reduction of PDOS occurs with an increase in x in the other systems, especially for Co(Fex,Mn1−x)Si.
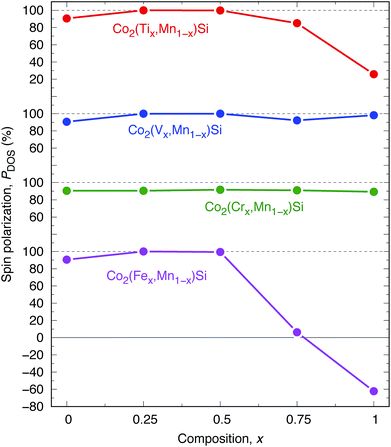 | ||
| Fig. 11 Spin polarization PDOS dependence on composition x in Co2(Yx,Mn1−x)Si. Red, blue, green, and pink plots are Y of Ti, V, Cr, and Fe, respectively. | ||
Finally, we state the results of systems including Fe by comparing with previous studies. Whether the electronic structure of the Co2FeSi compound shows HM is still under debate and has been for the past few decades, considering theories both with and without correlation effects.17,116 Our LR-based DFT+U calculations indicate that it is not a HM ferromagnet. However, we emphasize that tuning the composition in quaternary Co2(Fe,Mn)Si demonstrates that the electronic structure can be HM. This conclusion is supported by a consistency in anisotropic magnetoresistance (AMR) measurement.117 According to an extended model for AMR formulated by Kokado et al., the negative sign of the AMR effect arising from the empty DOS, either spin-up or -down states, at the Fermi level is a signature of HM.118–120 Based on this model analysis, positive AMR behavior is found in Co2FeSi117, which indicates a ferromagnetic without the minority band gap, but the negative sign is confirmed in Co2(Fe,Mn)Si,121 leading to HM. Note that the composition range of Fe and Mn for Co2(Fe,Mn)Si, showing HM, is different between our study and the AMR experiment, which may be because the present quaternary models [Fig. 1(b)–(d)] are assumed to be a periodic structure not including the disordered properties of Fe and Mn, and/or the ordering parameter of the L21 structure in the experiment117 is rather low at all compositions. Nonetheless, we suggest that the quaternary Co2(Fe0.25,Mn0.75)Si is one of the most promising candidates as an HM Heusler ferromagnet because of the sizable E↓gap(=0.4 eV) and the Fermi energy position being at almost the center of the gap. We believe our present results encourage experiments to improve the degree of crystallinity of bulk Heusler alloys and/or to fabricate a clean interface without any atomic inter-diffusion in MTJ and CPP-GMR devices for the enhancement of MR performances in the future.
5 Summary
In summary, we revisited the fundamental electronic structure and effects of the correlation parameters for 3d electrons in a Co-based full Heusler Co2YSi alloy via the LR-based DFT+U method, where the correlation correction Ueff parameters were determined from the LR approach and the +U formalism was incorporated as the FLL form. Focusing on Co2MnSi (Y = Mn), we considered the origin of the minority HM gap from the projected band structures calculated by the standard GGA, and found that the t2g hybridization between Co and Mn is important for the gap. The energy diagram of atomic-orbital hybridizations revealed that the HM gap originates from the Co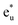 of the conduction state and the Co–Mn hybridizing t2g orbitals of the valence state at the Fermi energy. Thus, the gap is tunable by selecting a Y element and/or mixing different elements into the Y site through t2g atomic orbital coupling. The LR calculations tend to obtain a reasonable value as a correlation parameter for the Y site (Y = Mn in Co2MnSi) but an unexpectedly large value for the Co site, which misleads to an unphysical ground state. The failure in determining ULReff for the Co site arises from the fact that the d electrons of the Co site behave in a rather itinerant fashion in the alloy. This means that the mean-field approximations such as LSDA and GGA are enough to describe the ground-state properties with high accuracy; thus, we propose the LR-based DFT+U method, where the determined ULReff parameters are incorporated into only strongly-correlated Y sites, as a suitable methodology on a practical level for L21 Co-based full Heusler alloys. For Co2MnSi, our results are consistent with the experimental observations and superior to the standard GGA calculation, particularly in terms of electronic and magnetic properties. It is also indicated that Co2MnSi is not HM but a highly spin-polarized ferromagnet. Further investigations were carried out for the other ternary and quaternary Co2(Y,Mn)Si to explore the potential for HM ferromagnets. The results showed that the Co2(Ti,Mn)Si, Co2(V,Mn)Si, and Co2(Fe,Mn)Si compounds are expected to be HM materials when the composition of the Y element is appropriately selected. Co2(Cr,Mn)Si does not show the HM property at every composition, but a notable tendency is that the high spin polarization is independent of the composition. However, for using in spintronics applications, Co2(Fe0.25,Mn0.75)Si, in which the HM nature is consistent with the experimental AMR study, is one of the most promising candidates because of the sizable HM gap in the minority state and as the Fermi energy position is at almost the center of the gap.
of the conduction state and the Co–Mn hybridizing t2g orbitals of the valence state at the Fermi energy. Thus, the gap is tunable by selecting a Y element and/or mixing different elements into the Y site through t2g atomic orbital coupling. The LR calculations tend to obtain a reasonable value as a correlation parameter for the Y site (Y = Mn in Co2MnSi) but an unexpectedly large value for the Co site, which misleads to an unphysical ground state. The failure in determining ULReff for the Co site arises from the fact that the d electrons of the Co site behave in a rather itinerant fashion in the alloy. This means that the mean-field approximations such as LSDA and GGA are enough to describe the ground-state properties with high accuracy; thus, we propose the LR-based DFT+U method, where the determined ULReff parameters are incorporated into only strongly-correlated Y sites, as a suitable methodology on a practical level for L21 Co-based full Heusler alloys. For Co2MnSi, our results are consistent with the experimental observations and superior to the standard GGA calculation, particularly in terms of electronic and magnetic properties. It is also indicated that Co2MnSi is not HM but a highly spin-polarized ferromagnet. Further investigations were carried out for the other ternary and quaternary Co2(Y,Mn)Si to explore the potential for HM ferromagnets. The results showed that the Co2(Ti,Mn)Si, Co2(V,Mn)Si, and Co2(Fe,Mn)Si compounds are expected to be HM materials when the composition of the Y element is appropriately selected. Co2(Cr,Mn)Si does not show the HM property at every composition, but a notable tendency is that the high spin polarization is independent of the composition. However, for using in spintronics applications, Co2(Fe0.25,Mn0.75)Si, in which the HM nature is consistent with the experimental AMR study, is one of the most promising candidates because of the sizable HM gap in the minority state and as the Fermi energy position is at almost the center of the gap.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to K. Masuda, H. Sukegawa, and S. Mitani for critical comments and suggestions. K. N. also thanks K. Nakamura, T. Oguchi, and M. Weinert for fruitful discussions. This work was supported in part by Grants-in-Aid for Scientific Research (S) (Grant Numbers JP16H06332 and JP17H06152) from the Japan Society for the Promotion of Science, the ImPACT Program of Council for Science, Technology and Innovation, ‘Materials Research by Information Integration Initiative (Mi2i)’ Project of the Support Program for Starting Up Innovation Hub from Japan Science and Technology Agency (JST), and Center for Spintronics Research Network (CSRN), Osaka University. The computations in this study were performed on a Numerical Materials Simulator at NIMS.References
- M. Jullière, Phys. Lett. A, 1975, 54, 225 CrossRef.
- I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 012406 CrossRef.
- W.-H. Xie, Y.-Q. Xu, B.-G. Lie and D. G. Pettifor, Phys. Rev. Lett., 2003, 91, 037204 CrossRef.
- B.-G. Lie, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 172411 CrossRef.
- W. E. Pickett and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1146 CrossRef CAS.
- D. J. Singh and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 88 CrossRef CAS.
- K. Schwarz, J. Phys. F: Met. Phys., 1986, 16, L211 CrossRef CAS.
- H. van Leuken and R. A. de Groot, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 51, 7176 CrossRef.
- S. P. Lewis, P. B. Allen and T. Sasaki, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10253 CrossRef CAS.
- M. A. Korotin, V. I. Anisimov, D. I. Khomskii and G. A. Sawatzky, Phys. Rev. Lett., 1998, 80, 4305 CrossRef CAS.
- R. A. de Groot and K. H. J. Buschow, J. Magn. Magn. Mater., 1986, 54–57, 1377 CrossRef CAS.
- M. Pénicaud, B. Siberchicot, C. B. Sommers and J. Kübler, J. Magn. Magn. Mater., 1992, 103, 212 CrossRef.
- B. Chakraborty and L. M. Ramaniah, J. Magn. Magn. Mater., 2015, 1385, 207 CrossRef.
- B. Chakraborty and L. M. Ramaniah, J. Phys.: Condens. Matter, 2016, 28, 336001 CrossRef.
- B. Chakraborty, P. K. Nandi, Y. Kawazoe and L. M. Ramaniah, Phys. Rev. B, 2018, 97, 184411 CrossRef CAS.
- K. H. J. Bushow, P. G. v. Engen and R. Jogebreur, J. Magn. Magn. Mater., 1983, 38, 1 CrossRef.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser, H.-J. Lin and J. Morais, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184434 CrossRef.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H.-J. Lin, Appl. Phys. Lett., 2006, 88, 032503 CrossRef.
- Y. Sakuraba, J. Nakata, M. Oogane, H. Kubota, Y. Ando, A. Sakuma and Y. Miyazaki, Jpn. J. Appl. Phys., 2005, 44, L1100 CrossRef CAS.
- Y. Sakuraba, M. Hattori, M. Oogane, Y. Ando, H. Kato, A. Sakuma and T. Miyazaki, Appl. Phys. Lett., 2006, 88, 192508 CrossRef.
- B. Hu, K. Moges, Y. Honda, H. X. Liu, T. Uemura, M. Yamamoto, J. I. Inoue and M. Shirai, Phys. Rev. B, 2016, 94, 094428 CrossRef.
- W. H. Butler, X.-G. Zhang, T. C. Schulthess and J. M. MacLaren, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 054416 CrossRef.
- R. J. Soulen, J. M. Byers, M. S. Osofsky, B. Nadgorny, T. Ambrose, S. F. Cheng, P. R. Broussard, C. T. Tanaka, J. Nowak, K. S. Moodera, A. Barry and J. M. D. Coey, Science, 1998, 282, 85 CrossRef CAS PubMed.
- M. S. Bahramy, P. Murugan, G. P. Das and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 054404 CrossRef.
- A. Rajanikanth, Y. K. Takahashi and K. Hono, J. Appl. Phys., 2009, 105, 063916 CrossRef.
- Z. Gercsi, A. Rajanikanth, Y. K. Takahashi and K. Hono, Appl. Phys. Lett., 2007, 89, 082512 CrossRef.
- S. V. Karthik, A. Rakanikanth and T. M. Nakatani, J. Appl. Phys., 2007, 102, 043903 CrossRef.
- L. Makinistian, M. M. Faiz, R. P. Panguluri, B. Balke, S. Wurmehl, C. Felser, E. A. Albanesi, A. G. Petukhov and B. Nadgorny, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 220402 CrossRef.
- L. Bainsla, A. I. Mallick, M. M. Raja, A. K. Nigam, B. S. D. Ch. S. Varaprasad, Y. K. Takahashi, A. Alam, K. G. Suresh and K. Hono, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104408 CrossRef.
- Y. Sakuraba, M. Ueda, S. Bosu, K. Saito and K. Takanashi, J. Magn. Soc. Jpn., 2014, 38, 45 CrossRef CAS.
- S. Tsunegi, Y. Sakuraba, M. Oogane, K. Takanashi and Y. Ando, Appl. Phys. Lett., 2008, 93, 112506 CrossRef.
- Y. Sakuraba, M. Ueda, Y. Miura, K. Sato, S. Bosu, K. Saito, M. Shirai, T. J. Konno and K. Takanashi, Appl. Phys. Lett., 2012, 101, 252408 CrossRef.
- K. Moges, Y. Honda, H. X. Liu, T. Uemura, M. Yamamoto, Y. Miura and M. Shirai, Phys. Rev. B, 2016, 93, 134403 CrossRef.
- H. Liu, T. Kawami, K. Moges, T. Uemura, M. Yamamoto, F. Shi and P. M. Voyles, J. Phys. D: Appl. Phys., 2015, 48, 164001 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- W. Kohn, Rev. Mod. Phys., 1999, 71, 1253 CrossRef CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429 CrossRef.
- R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024 CrossRef CAS.
- K. Schwarz, J. Phys. F: Met. Phys., 1986, 16, L211 CrossRef CAS.
- S. Ishida, S. Fujii, S. Kashiwagi and S. Asano, J. Phys. Soc. Jpn., 1995, 64, 2152 CrossRef CAS.
- S. Picozzi, A. Continenza and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 094421 CrossRef.
- M. Shirai, J. Appl. Phys., 2003, 93, 6844 CrossRef CAS.
- E. Şaşioğlu, L. M. Sandratskii, P. Bruno and I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184415 CrossRef.
- V. I. Anisimov, A. I. Poteryaev, M. A. Korotin, A. O. Anokhin and G. Kotliar, J. Phys.: Condens. Matter, 1997, 9, 7359 CrossRef CAS.
- A. I. Lichtenstein and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6884 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- S. Kobayashi, Y. Nohara, S. Yamamoto and T. Fujiwara, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155112 CrossRef.
- H. Jiang, R. I. Gomez-Abal, P. Rinke and M. Scheffler, Phys. Rev. Lett., 2009, 102, 126403 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Liechtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- M. I. Katsnelson, V. Yu. Irkhin, L. Chioncel, A. I. Lichtenstein and R. A. de Groot, Rev. Mod. Phys., 2008, 80, 315 CrossRef CAS.
- S. Chadov, G. H. Fecher, C. Felser, J. Minar, J. Braun and H. Ebert, J. Phys. D: Appl. Phys., 2009, 42, 084002 CrossRef.
- A. Nourmohammadi and M. R. Abolhasani, Solid State Commun., 2010, 150, 1501 CrossRef CAS.
- M. Meinert, C. Friedrich, G. Reiss and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245115 CrossRef.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1965, 285, 542 CrossRef CAS.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1967, 296, 82 CrossRef CAS.
- K. Nawa, T. Akiyama, T. Ito, K. Nakamura, T. Oguchi and M. Weinert, Phys. Rev. B, 2018, 97, 035117 CrossRef CAS.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121 CrossRef.
- B. Himmetoglu, R. M. Wentzcovitch and M. Cococcioni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115108 CrossRef.
- K. Tao, J. Zhou, Q. Sun, Q. Wang, V. S. Stepanyuk and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 085103 CrossRef.
- A. G. Marinopoulos, P. Santos and J. Coutinho, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075124 CrossRef.
- X. Huang, S. K. Ramadugu and S. E. Mason, J. Phys. Chem. C, 2016, 120, 4919 CrossRef CAS.
- K. Nawa, Y. Kitaoka, K. Nakamura, H. Imamura, T. Akiyama, T. Ito and M. Weinert, Phys. Rev. B, 2016, 94, 035136 CrossRef.
- B. Himmetoglu, V. M. Katukuri and M. Cococcioni, J. Phys.: Condens. Matter, 2012, 24, 185501 CrossRef.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef; S. Baroni, A. Dal Corso, S. de Gironcoli and P. Giannozzi, http://www.pwscf.org.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227 CrossRef.
- Because even the theoretically derived Ueff value depends on the computational details, as discussed in ref. 58, we explicitly specify which pseudopotential is employed in the present study: Si.pbe-n-rrkjus_psl.0.1.UPF; Ti.pbe-spn-rrkjus_psl.0.3.1.UPF; V.pbe-spn-rrkjus_psl.0.2.3.UPF; Cr.pbe-spn-rrkjus_psl.0.2.3.UPF; Mn.pbe-spn-rrkjus_psl.0.3.1.UPF; Fe.pbe-spn-rrkjus_psl.0.2.1.UPF; and Co.pbe-n-rrkjus_psl.0.2.3.UPF. The used pseudopotential scheme given in ref. 68 is known to beappropriate for 3d transition metal and non-magnetic sp atoms.
- A. Baldereschi, Phys. Rev. B: Solid State, 1973, 7, 5212 CrossRef CAS; D. J. Chadi and M. L. Cohen, Phys. Rev. B: Solid State, 1973, 8, 5747 CrossRef; H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef; J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS.
- I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 012413 CrossRef.
- Ph. Mavropoulos, K. Sato, R. Zeller, P. H. Dederichs, V. Popescu and H. Ebert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 012413 CrossRef.
- Ph. Mavropoulos, I. Galanakis, V. Popescu and P. H. Dederichs, J. Phys.: Condens. Matter, 2004, 16, S5759 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467 CrossRef CAS.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyźyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929 CrossRef CAS.
- M. T. Czyźyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14211 CrossRef PubMed.
- I. V. Solovyev, P. H. Dederichs and V. I. Anisimov, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 16861 CrossRef CAS.
- C. Tsirogiannis and I. Galanakis, J. Magn. Magn. Mater., 2015, 393, 297 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884 CrossRef CAS.
- L. J. Sham and M. Schlüter, Phys. Rev. Lett., 1983, 51, 1888 CrossRef.
- A. Akriche, H. Bouafia, S. Hiadsi, B. Abidri, B. Sahli, M. Elchikh, M. A. Timaoui and B. Djebour, J. Magn. Magn. Mater., 2017, 422, 13 CrossRef CAS.
- E. Şaşioğlu, I. Galanakis, C. Friedrich and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 134402 CrossRef.
- In order to consider the effect of size of applied potential shift, various values of μCo were tested to compute the ULR(Co)eff, for example, μCo = ±0.06, ±0.1, ±0.5, ±1.0, and ±2.0 eV. The obtained parameters are almost same with differences less than 0.05 eV with an exception of the μCo = ±2.0 eV case, where the stationary self-consistent solution was not obtained because of the too large potential shift.
- B. Huang, Phys. Chem. Chem. Phys., 2017, 19, 8008 RSC.
- A. G. Petukhov, I. I. Mazin, L. Chioncel and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 153106 CrossRef.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244 CrossRef CAS.
- J. N. Gonçalves, J. S. Amaral and V. S. Amaral, IEEE Trans. Magn., 2014, 50, 1301104 Search PubMed.
- A. Candan, G. Uğur, Z. Charifi, H. Baaziz and M. R. Ellialtioğlu, J. Alloys Compd., 2013, 560, 25 CrossRef.
- G. Gökŏglu and O. Gülseren, Eur. Phys. J. B, 2010, 76, 321 CrossRef.
- S. Amuri, R. Mebsout, S. Méçabih, B. Abbar and B. Bouhafs, Intermetallics, 2014, 44, 26 CrossRef.
- P. J. Webster, J. Phys. Chem. Solids, 1971, 32, 1221 CrossRef CAS.
- H. Ido, J. Magn. Magn. Mater., 1986, 54, 937 CrossRef.
- B. Balke, G. H. Fecher, H. C. Kandpal, C. Felser, K. Kobayashi, E. Ikenaga, J.-J. Kim and S. Ueda, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 104405 CrossRef.
- P. Klaer, M. Kallmayer, C. G. F. Blum, T. Graf, J. Barth, B. Balke, G. H. Fecher, C. Felser and H. J. Elmers, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 144405 CrossRef.
- K. Miyamoto, A. Kimura, Y. Miura, M. Shirai, M. Ye, Y. Cui, K. Shimada, H. Namatame, M. Taniguchi, Y. Takeda, Y. Saitoh, E. Ikenaga, S. Ueda, K. Kobayashi and T. Kanomata, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 100405 CrossRef.
- T. Kanomata, et al., Heusler alloy as a functional material, Uchida Rokakuho, Tokyo, 2011 Search PubMed.
- E. I. Gladyshevskii, Powder Metall. Met. Ceram., 1983, 1, 262 CrossRef.
- The LR calculations were also done for the ULR(Co)eff in Co2YSi. Similar to Co2MnSi, large values of 6.536, 6.563, 6.674, and 5.782 eV are obtained for Co of Co2YSi, where Y is Ti, V, Cr, and Fe, respectively. Based on the discussion in Section 3, the ULReff values for Co are not used for the calculations in the present work.
- A. B. Garg and V. Vijayakumar, J. Appl. Phys., 2011, 100, 083523 CrossRef.
- X.-Q. Chen, R. Podloucky and P. Rogl, J. Appl. Phys., 2006, 100, 113901 CrossRef.
- S. M. Mareii, H. Arabi and R. Sarhaddi, Physica B, 2012, 407, 3339 CrossRef.
- S. C. Wu, G. H. Fecher, S. S. Naghari and C. Felser, J. Appl. Phys., 2019, 125, 082523 CrossRef.
- I. Asfour, D. Rached, A. Girard soraya and S. Didier, Universal Journal of Mechanical Engineering, 2019, 7, 16 Search PubMed.
- X. Zhu, Y. Wang, L. Wang, Y. Dai and C. Luo, J. Phys. Chem. Solids, 2014, 75, 391 CrossRef CAS.
- L. Vegard, Z. Phys., 1920, 5, 17 CrossRef.
- A. R. Denton and N. W. Ashcroft, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 3161 CrossRef CAS.
- C. G. Broyden, SIAM J. Appl. Math., 1970, 6, 76 Search PubMed.
- R. Fletcher, Comput. J., 1970, 13, 317 CrossRef.
- D. Goldfarb, Math. Comput. Model., 1970, 24, 24 Search PubMed.
- D. F. Shanno, Math. Comput. Model., 1970, 24, 647 Search PubMed.
- H. C. Kandpal, G. H. Fecher, C. Felser and G. Schönhense, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094422 CrossRef.
- Y. Sakuraba, S. Kokado, Y. Hirayama, T. Furubayashi, H. Sukegawa, S. Li, Y. K. Takahashi and K. Hono, Appl. Phys. Lett., 2014, 104, 172407 CrossRef.
- S. Kokado, M. Tsunoda, K. Harigaya and A. Sakumra, J. Phys. Soc. Jpn., 2012, 81, 024705 CrossRef.
- S. Kokado and M. Tsunoda, Adv. Mater. Res., 2013, 750, 978 Search PubMed.
- S. Kokado and M. Tsunoda, Phys. Status Solidi C, 2014, 11, 1026 CrossRef CAS.
- F. J. Yang, Y. Sakuraba, S. Kokado, Y. Kota, A. Sakuma and K. Takanashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 020409 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |