Open Access Article
Open Access ArticleDevelopment of a robust tool to extract Mulliken and Löwdin charges from plane waves and its application to solid-state materials†
Christina Erturala,
Simon Steinberg a and
Richard Dronskowski
a and
Richard Dronskowski *abc
*abc
aInstitute of Inorganic Chemistry, RWTH Aachen University, Landoltweg 1, D-52056 Aachen, Germany. E-mail: drons@HAL9000.ac.rwth-aachen.de
bJülich-Aachen Research Alliance (JARA-FIT and -HPC), RWTH Aachen University, D-52056 Aachen, Germany
cHoffmann Institute of Advanced Materials, Shenzhen Polytechnic, 7098 Liuxian Blvd, Nanshan District, Shenzhen, China
First published on 20th September 2019
Abstract
Chemically understanding the electronic structure of a given material provides valuable information about its chemical as well as physical nature and, hence, is the key to designing materials with desired properties. For example, to rationalize the structures of solid-state materials in terms of the valence-electron distribution, highly schematic, essentially non-quantum-mechanical electron-partitioning models such as the Zintl–Klemm concept have been introduced by assuming idealized ionic charges. To go beyond the limits of the aforementioned concept, a Mulliken and Löwdin population analytical tool has been developed to accurately calculate the charges in solid-state materials solely from first-principles plane-wave-based computations. This population analysis tool, which has been implemented into the LOBSTER code, has been applied to diverse solid-state materials including polar intermetallics to prove its capability, including quick access to Madelung energies. In addition, a former weakness of the population analysis (namely, the basis-set dependency) no longer exists for the present approach which therefore represents a comparatively fast and accurate wave-function-based alternative for plane-wave calculations for which density-based charge approaches (e.g., Bader like) have been very popular.
Introduction
Chemically envisioning intermetallic compounds with desired electrical, magnetic, and optical properties has stimulated an enormous impetus among chemists, physicists, and materials scientists.1 While designing such new materials requires a proper knowledge and, equally important, understanding of the electronic structures of such materials in terms of atoms and bonds,2,3 intermetallic compounds still lack “universal” counting rules for the valence electrons, which would clearly facilitate recognition of the relationship between a given crystal structure and the underlying electronic structure.4–6 And yet, certain concepts including those of Hume-Rothery7–9 and Zintl10–12 have been demonstrated as beneficial means in rationalizing the crystal-structure−electronic-structure relationships for several intermetallics. In the cases of the Hume-Rothery phases,7,8 electronically favorable situations, i.e., positioning the Fermi levels in pseudogaps, are accomplished for specific values of the valence-electron concentration, e/a, in which e and a represent the amounts of the valence electrons and the atoms, respectively. In the framework of the Zintl–Klemm concept,10–12 the valence electrons are assumed of having been transferred from the “electropositive” to the electronegative elements, thereby assembling clusters or fragments (“Zintl anions”) which are also encountered in the crystal structures of elements being isoelectronic to the anions. Such anions are typically assembled by elements from main groups IV to VI, while the cations are metals from main group I, II, III, as well as the transition metals. And yet, previous research has shown that this classic delineation is not strict, as, for instance, the late transition metals may also act as p-metals.13–15Among the different classes of intermetallic compounds, Zintl phases have received an increased attention because of their potential use for clean-energy technologies, particularly, if used in devices for thermoelectric energy conversion.16–20 In the quest for previously unknown thermoelectric materials, Zintl phases have also attracted greater interest because of their transport features being influenced by the complexity of a given crystal structure and the presence of a band gap at the Fermi level; several intermetallic compounds, however, which are charge-balanced following to the Zintl–Klemm rule, exhibit attributes of metallic conductors (in contrast to the strict semiconductor definition).16 Indeed, several thermoelectric materials, which are structurally related to Zintl phases, do not fulfill the aforementioned strict definition.16 Also, applying the Zintl–Klemm concept to certain intermetallic compounds comprising low-dimensional fragments leads to electron-imprecise charges, thereby demonstrating the concept's limits even in the light of hypervalency.21 More precise pictures of the actual electronic structures and nature of bonding for such polar intermetallic compounds are obviously needed, and they should be gained from first-principles computations.12,22,23
Because previous research on polar intermetallics demonstrated that certain hurdles exist in recognizing Zintl–Klemm charge distributions, we aim at identifying the actual valence-electron distribution and, furthermore, the effective atomic charges in such materials. For the exemplary case of polar intermetallic compounds, we now present a robust and fast tool allowing for accurately projecting both Mulliken and Löwdin charges from first-principles computations. We first provide the mathematical apparatus of this tool, then validate its performance for simple molecular examples, and finally apply it to ionic as well as polar intermetallic compounds.
Methodological approach and computational details
Full structural optimizations (lattice parameters and atomic positions) and electronic-structure computations of the materials inspected herein were carried out with the projector-augmented-wave (PAW) method, as implemented in the Vienna Ab initio Simulation Package (VASP).24–28 Correlation and exchange were described by the generalized gradient approximation (GGA) by Perdew, Burke, and Ernzerhof (PBE)29 with an energy cutoff of 500 eV. The k-points sets employed to generate the meshes according to the Monkhorst–Pack method30 may be found in the ESI (cf. Table S6†). For partial band occupancies, the tetrahedron method with Blöchl's correction was used. In addition to the structural optimizations, real-space density-based charges according to Bader31–36 were calculated for the compounds to facilitate a comparison to the here obtained wave-function-based Mulliken and Löwdin charges. Furthermore, (static) single-point calculations were carried out prior to the projection of the PAW functions to local orbitals37 with the Local Orbital Basis Suite Towards Electronic-Structure Reconstruction program (LOBSTER).38,39 It has been traditionally impossible to directly calculate charges from plane waves because of severe technical difficulties, so indirectly deriving Bader charges from the real-space plane-wave density was the time-consuming way to go. More precisely, the plane-wave-based computations required for obtaining the Bader charge densities are quite consuming with respect to computational resources as we will show below. This problem no longer persists in the LOBSTER framework as accurately projecting from a delocalized description of the electronic structure to a local one is now analytically possible, and this enables to regain formerly lost chemical information, such as bonding characteristics (e.g., via COHP analysis40) or charges as well.41 To do so, the crystal wave function ψj(k) is constructed as a linear combination of Bloch sums42 of atomic orbitals χμ(k) at certain values of k38 using the normalized, non-orthogonal basis set χ in the LCAO-CO approximation43,44
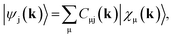 | (1) |
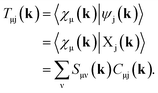 | (2) |
By using eqn (9) in ref. 38, the coefficient matrix elements Cμj(k) can be obtained from the transfer matrix elements Tμj(k). A fully detailed description of the LOBSTER algorithms for both coefficients and wave functions has been reported elsewhere.38,39 The mathematical apparatus of Mulliken and Löwdin population analysis,41,46–48 which has been briefly mentioned recently,49 is also implemented within LOBSTER, as described below and in the appendix.
Both Mulliken and Löwdin population analyses are computationally straightforward. The Mulliken or Löwdin charges qA, given in units of the elementary charge e, of an atom A are obtained from the difference of the number of the atom's valence electrons N (when using pseudopotentials) and the so-called gross population (GP),
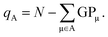 | (3) |
In the molecular quantum-chemical literature, both Mulliken and Löwdin population analyses are well known but sometimes described as suffering from what is dubbed “basis-set dependency” because the atomic charges derived from those population analyses scatter as a function of the local basis set. Indeed, the charges as calculated for hydrogen in a 10-electron series of simple molecules (methane, ammonia, water, hydrogen fluoride) taken from a superb textbook50 show exactly that, and we simply reproduce these numbers (obtained from self-consistent Hartree–Fock calculations) to plot the trend in Fig. 1a and b. Clearly, the charges on H increase as the electronegativity of the bonding partners increase (C → N → O → F) for both Mulliken and Löwdin, making perfect chemical sense, but in each series the charges increase upon going from STO-3G → 4-31G → 6-31G* but then decrease when reaching 6-31G**. As we will show in a moment, neither the Mulliken nor the Löwdin scheme can be blamed for that effect; on the contrary, both schemes correctly reproduce the fact that the local basis sets significantly change their character upon going from 6-31G* (by adding d functions to C, N, O, and F) to 6-31G** (by adding p functions to H).
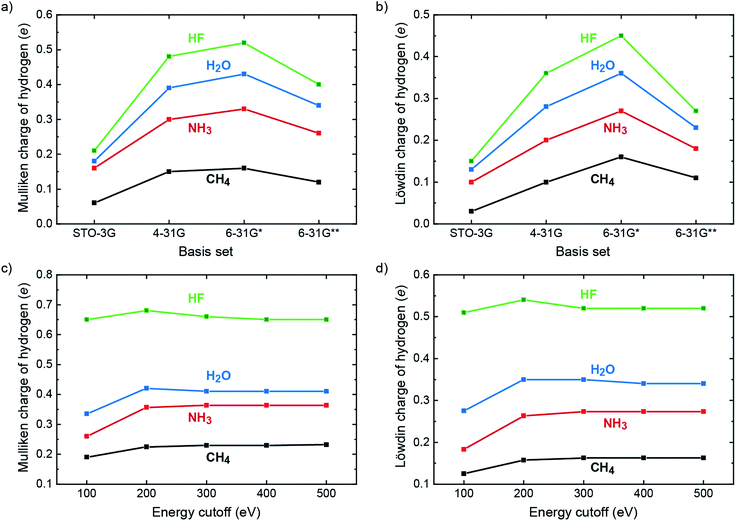 | ||
| Fig. 1 Population analyses for the ten-electron series of CH4, NH3, H2O and HF. (a) Mulliken and (b) Löwdin charges of the hydrogen atom based on Hartree–Fock calculations for basis sets STO-3G, 4-31G, 6-31G* and 6-31G**. Values taken from ref. 50. (c) Mulliken and (d) Löwdin charges of the hydrogen atom based on PAW plane-wave LDA calculations with varying energy cutoffs (= size of the plane-wave basis set). | ||
Aforementioned qualitatively changing basis-set characteristics of a local basis set do not exist, in principle, for a completely delocalized plane-wave basis which does not “know” about atoms. Instead, Hilbert space is continuously filled with plane waves with an ever increasing kinetic energy (up to about 500 eV and more) until energetic convergence is reached in terms of typically 10−9 eV, thereby continuously and steadily improving the quality of the calculation. How do the Mulliken and Löwdin schemes perform in such a scenario? For testing, we repeated the aforementioned molecular calculations with combinations of plane waves using a box with one k-point while correlation and exchange were described by the simplest functional, the local-density approximation51 (LDA), with energy cutoffs from 100 to 500 eV. The auxiliary local basis set for projection consisted of LOBSTER's standard contracted multiple-ζ STO as derived by Bunge, Barrientos, and Bunge37 which is known for its supreme accuracy of only a few μHartrees above the numerical Hartree–Fock limit and ca. 0.002% concerning the average error of the electron density of the free atoms in the first and second period.52 Alternatively expressed, these local functions represent the numerical optimum and are practically complete. As shown in Fig. 1c and d, the Mulliken and Löwdin charges as projected from plane waves resemble the molecular ones as regards the electronegativity trend. With respect to the completeness of the plane-wave basis set, however, the values of the Mulliken and Löwdin charges easily converge to a certain value for each computation. For all four cases, an energy cutoff somewhere between 200 and 300 eV already marks the beginning convergence. Since these energy cutoffs are way below typical plane-wave DFT calculations, we regard the Mulliken and Löwdin charges as effectively basis-set independent in the new plane-wave setting, a very assuring sign for all what follows. For reasons of completeness, aforementioned Mulliken charges taken from the literature50 and computed by VASP (LDA) were recalculated by using state-of-the-art Hartree–Fock techniques (i.e., Gaussian,53 cf. Table S5 and Fig. S2†). Only the 6-31G** calculations yield improved results as compared to the literature but still face the problem of basis-set dependency due to being local. Reiterating the effective basis-set independence of Mulliken and Löwdin charges as derived from plane waves, it results from a fortunate synergy of (i) the nonlocality of the plane-wave basis set for DFT calculation and (ii) the superb quality (completeness) of the local basis set for analysis by LOBSTER.
Results and discussion
Both orbital-based Mulliken and Löwdin population analyses as implemented in LOBSTER automatically and accurately derive atomic charges in solid-state materials, and we will demonstrate their performance as regards ionic compounds, polar intermetallics, including commonly known archetypal Zintl phases, as well as another polar intermetallic compound, i.e., stützite.54 The latter mineral was chosen for the prototypical application of the tool, as more recent research54 revealed that applying the Zintl–Klemm concept to it should be taken with a pinch of salt.For comparison, density-based Bader charges were also calculated for the present compounds. Ahead of chemical comparisons, a word as regards technical performance (i.e., time and resource consumption) seems appropriate. On average, Bader charge analyses (cf. Tables S7 and S8, Fig. S3 and S4†) consume significantly more time (5.1×) and slightly more resources (1.1×) than the respective LOBSTER calculations, the latter of which include the entire projection ahead of Mulliken and Löwdin population analyses, and also COHP and COOP analyses. In comparison to LOBSTER, the best Bader performance is achieved for LiAl and, in general, for high-symmetry compounds adopting the [NaCl] and [CsCl] type structures. In contrast, LOBSTER's population analyses excel in examining complex structures with low symmetry or disordered fragments. For instance, just 1/3 of Bader's resource requirements and 1/20 of its time consumption was required by LOBSTER for the case of S8(AsF6)2.
Nonetheless, we note that Bader's density-based (and extremely quick) algorithm for charge calculation can not be blamed for that. On the contrary, VASP needs to perform resource-hungry all-electron calculations for the core charge densities as a prerequisite for Bader, and this is the numerical price paid for working with the density. Because LOBSTER operates directly with the wave function, its prior VASP calculations are significantly faster (see again Tables S7 and S8, Fig. S3 and S4†), a natural advantage of the non-density-based Mulliken and Löwdin approaches.
Ionic compounds
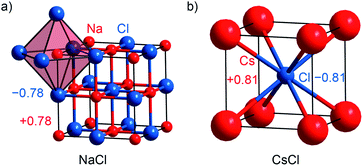
Alkaline halides MX with M = Na, K, Cs and X = F, Cl, Br, I are prototypical examples of salt-like materials. NaX, KX and CsF crystallize with the [NaCl] type (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; no. 225; Fig. 2a), while the remaining Cs-containing compounds adopt the [CsCl] type (Pm
m; no. 225; Fig. 2a), while the remaining Cs-containing compounds adopt the [CsCl] type (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; no. 221; Fig. 2b).55–64 The Mulliken charges (given in Table S1†) evidence that the new method implemented in LOBSTER reproduces the expected ionicity trend of the series, which is even clearer based on the Löwdin charges. The Mulliken charge is around ±0.8e for every alkali halide compound with the exception of CsF (with ±0.87e). The alkaline fluorides show the largest Löwdin charges with ±0.8 to 0.9e, whereas the alkaline iodides exhibit the lowest charges with ±0.6 to 0.7e. Bader charges are closer to Mulliken charges (cf. Table S1†) but do not reproduce the electronegativity trend as nicely as Mulliken's approach does.
m; no. 221; Fig. 2b).55–64 The Mulliken charges (given in Table S1†) evidence that the new method implemented in LOBSTER reproduces the expected ionicity trend of the series, which is even clearer based on the Löwdin charges. The Mulliken charge is around ±0.8e for every alkali halide compound with the exception of CsF (with ±0.87e). The alkaline fluorides show the largest Löwdin charges with ±0.8 to 0.9e, whereas the alkaline iodides exhibit the lowest charges with ±0.6 to 0.7e. Bader charges are closer to Mulliken charges (cf. Table S1†) but do not reproduce the electronegativity trend as nicely as Mulliken's approach does.
Zintl phases and polar intermetallics
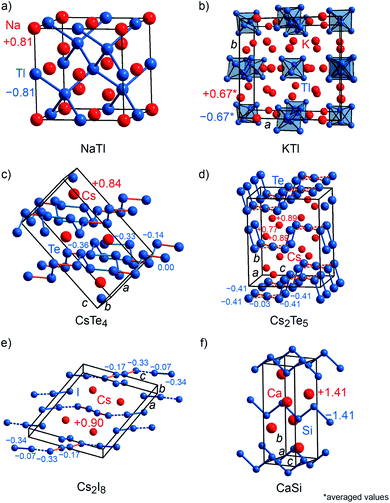
To probe the validity of formal valence-electron distributions following the Zintl–Klemm idea, archetypal Zintl phases, i.e., LiAl, LiTl, NaTl, KTl, CaSi, and several polyanionic (CsTe4, Cs2Te5, Cs2I8) as well as polycationic (S8(AsF6)2, Te6(AsF6)4) compounds were chosen as prototypical examples for Mulliken and Löwdin population analyses.22,65–73 Furthermore, the computed charges were compared to freshly computed Bader charges and those which had been previously reported in the literature. NaTl (Fig. 3a) crystallizes with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 227) and its crystal structure is composed of a diamond-like network formed by the Tl anions enclosing the Na cations. LiAl is isostructural to NaCl (Fig. 2a), whereas LiTl crystallizes with the [CsCl] type of structure (Fig. 2b). KTl (Fig. 3b) crystallizes within Cmce (no. 64), a subgroup of Fmmm (a subgroup of I4/mmm, which is a subgroup of Fm
m (no. 227) and its crystal structure is composed of a diamond-like network formed by the Tl anions enclosing the Na cations. LiAl is isostructural to NaCl (Fig. 2a), whereas LiTl crystallizes with the [CsCl] type of structure (Fig. 2b). KTl (Fig. 3b) crystallizes within Cmce (no. 64), a subgroup of Fmmm (a subgroup of I4/mmm, which is a subgroup of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) because of the presence of distorted Tl66− octahedra.22 Although NaTl, LiAl, LiTl and KTl are isoelectric compounds, they exhibit different charge tendencies (cf. Table S2†). With a Mulliken charge of +0.81e for the sodium cation and −0.81e for the thallium anion, the NaTl result almost coincides with the idealized Zintl–Klemm charges this is seemingly enough to allow for four Tl–Tl bonds per Tl anion, typical for a main-group IV pseudo element. Nonetheless, LiAl (±0.5e) and LiTl (±0.4e) show much lower charges. Because the charge transfer is lower, neither Al nor Tl become sufficiently main-group IV-like, so LiAl and LiTl do not adopt the [NaTl] type with Al–Al or Tl–Tl bonds but the [NaCl] and [CsCl] types, respectively.22 Since the structure of KTl is disordered, the Mulliken charges for the potassium cations range from +0.56e to +0.74e and for Tl− from −0.55e to −0.73e, resulting in an average charge of ±0.67e. Astonishingly enough, the computed Bader charges for NaTl (±0.7e), LiAl (±0.8e) and LiTl (±0.9e) do not fit in the aforementioned picture (cf. Table S2†) and, thus, are chemically less meaningful. The average Bader charge of KTl (±0.66e), however, coincides with that obtained from Mulliken charge analysis since the Bader charges for K+ range from +0.64e to +0.68e and for Tl− from −0.57e to −0.72e.
m) because of the presence of distorted Tl66− octahedra.22 Although NaTl, LiAl, LiTl and KTl are isoelectric compounds, they exhibit different charge tendencies (cf. Table S2†). With a Mulliken charge of +0.81e for the sodium cation and −0.81e for the thallium anion, the NaTl result almost coincides with the idealized Zintl–Klemm charges this is seemingly enough to allow for four Tl–Tl bonds per Tl anion, typical for a main-group IV pseudo element. Nonetheless, LiAl (±0.5e) and LiTl (±0.4e) show much lower charges. Because the charge transfer is lower, neither Al nor Tl become sufficiently main-group IV-like, so LiAl and LiTl do not adopt the [NaTl] type with Al–Al or Tl–Tl bonds but the [NaCl] and [CsCl] types, respectively.22 Since the structure of KTl is disordered, the Mulliken charges for the potassium cations range from +0.56e to +0.74e and for Tl− from −0.55e to −0.73e, resulting in an average charge of ±0.67e. Astonishingly enough, the computed Bader charges for NaTl (±0.7e), LiAl (±0.8e) and LiTl (±0.9e) do not fit in the aforementioned picture (cf. Table S2†) and, thus, are chemically less meaningful. The average Bader charge of KTl (±0.66e), however, coincides with that obtained from Mulliken charge analysis since the Bader charges for K+ range from +0.64e to +0.68e and for Tl− from −0.57e to −0.72e.
CsTe4 (Fig. 3c) and Cs2I8 (Fig. 3e) crystallize with space group no. 14 (P21/c and P21/a), while Cs2Te5 (Fig. 3d) and CaSi (Fig. 3f) follow Cmcm (no. 63), S8(AsF6)2 (Fig. 4a) adopts P21/c (no. 14) but C2/c (no. 15) for Te6(As(V)F6)4·As(III)F3 (Fig. 4b). The crystal structures of the tellurium-, iodine-, and sulfur-containing compounds comprise both anionic (Te4−, Te52−, I82−) and cationic (S82+, Te64+) units (Fig. 3c–e and 4a–b), while the respective counter ions are located between them. The charges for the cesium polytellurides and Cs2I8 perfectly match with those expected from applying the Zintl–Klemm concept (Table S2†). The Te4− anionic unit in CsTe4 exhibits a total charge of −0.83e, the Te52− unit in Cs2Te5 a total charge of −1.67e and the I82− unit in Cs2I8 a total charge of −1.82e. The individual atomic charges in those units can be taken from Fig. 3c–e. The Bader charges of the compounds (cf. Table S2†) show similar values. CaSi, a typical example of a Zintl phase, arrives at Mulliken and Löwdin charges of ±1.4e (Table S2†) and, therefore, indicates a less ionic character than expected if considering the Zintl–Klemm concept (±2e). And yet, this finding agrees well with previous research,71 which revealed, by means of experimental and theoretical techniques (e.g., Bader charges ±1.28e, which also coincides with Bader charges of ±1.26e calculated in this work, cf. Table S2†), that the Ca–Si bond in CaSi must have a somewhat covalent character, too. In the cases of the compounds incorporating polycationic units, S8(AsF6)2 and Te6(AsF6)4, the total Mulliken and Löwdin charges of +1.9e and +3.5e for the S82+ cation unit and Te64+ unit, respectively, (Table S2,† individual charges of the atoms in Fig. 4a–b) agree well with the expectations. Here, Bader charges also coincide with Mulliken charges (cf. Table S2†).
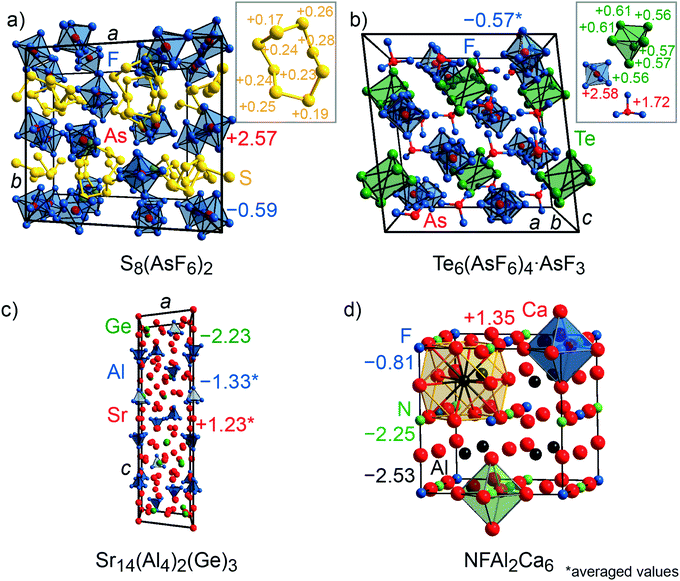 | ||
| Fig. 4 (a) Representations of the crystal structures of S8(AsF6)2, (b) Te6(As(V)F6)4As(III)F3, (c) Sr14(Al4)2(Ge)3, and (d) NFAl2Ca6 (elpasolite structure). Mulliken charges are shown. | ||
The quaternary phase NFAl2Ca6, which adopts the elpasolite type of structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, no. 225; Fig. 4d), was also investigated in this work because this compound exhibits a rather exotic oxidation state for Al, that is, Al(−II), with a Bader charge of around −2e, otherwise found in significantly larger Zintl phases like Sr14(Al4)2(Ge)3 (R
m, no. 225; Fig. 4d), was also investigated in this work because this compound exhibits a rather exotic oxidation state for Al, that is, Al(−II), with a Bader charge of around −2e, otherwise found in significantly larger Zintl phases like Sr14(Al4)2(Ge)3 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , no. 148; Fig. 4c).74,75 The density-based Bader charges of the strontium cations in Sr14(Al4)2(Ge)3 were previously reported75 to range from +1.13 to +1.20e, while that of aluminum is −1.7e, indicating an oxidation state of –II, as written before, and that of germanium is −2.2e. These charges are confirmed by the present orbital-based Mulliken and Löwdin population analyses (Table S3†) which reveal the Mulliken charges for Sr to range from +1.17 to +1.29e (Löwdin charges +1.28 to +1.36e), for Al from −1.18 to −1.41e (Löwdin charges −1.28 to −1.45e), and for Ge, the Mulliken charge is −2.23e (Löwdin charge −2.40e). Note that the Mulliken and Löwdin charges are lower than the Bader charge for aluminum. It is striking that all three charge analyses only yield half of the charge that is expected based on the Zintl–Klemm recipe. In the case of NFAl2Ca6, the Bader,74 Mulliken and Löwdin charges depict the same picture of the electronic situation (Table S3†). While the computed Bader charge and the one from the literature for nitrogen is −2e and the Mulliken/Löwdin charge is around −2.3e, the charge for fluoride is around −1e in all three cases. Aluminum exhibits a rather unexpected Bader charge of −2.27e (computed) and −2.13e (literature), respectively, and a Mulliken/Löwdin charge of −2.5e. The calcium cation has a similar Bader and Mulliken/Löwdin charge with +1.2e and +1.4e, respectively.
, no. 148; Fig. 4c).74,75 The density-based Bader charges of the strontium cations in Sr14(Al4)2(Ge)3 were previously reported75 to range from +1.13 to +1.20e, while that of aluminum is −1.7e, indicating an oxidation state of –II, as written before, and that of germanium is −2.2e. These charges are confirmed by the present orbital-based Mulliken and Löwdin population analyses (Table S3†) which reveal the Mulliken charges for Sr to range from +1.17 to +1.29e (Löwdin charges +1.28 to +1.36e), for Al from −1.18 to −1.41e (Löwdin charges −1.28 to −1.45e), and for Ge, the Mulliken charge is −2.23e (Löwdin charge −2.40e). Note that the Mulliken and Löwdin charges are lower than the Bader charge for aluminum. It is striking that all three charge analyses only yield half of the charge that is expected based on the Zintl–Klemm recipe. In the case of NFAl2Ca6, the Bader,74 Mulliken and Löwdin charges depict the same picture of the electronic situation (Table S3†). While the computed Bader charge and the one from the literature for nitrogen is −2e and the Mulliken/Löwdin charge is around −2.3e, the charge for fluoride is around −1e in all three cases. Aluminum exhibits a rather unexpected Bader charge of −2.27e (computed) and −2.13e (literature), respectively, and a Mulliken/Löwdin charge of −2.5e. The calcium cation has a similar Bader and Mulliken/Löwdin charge with +1.2e and +1.4e, respectively.
In summary, the implemented Mulliken and Löwdin population analysis method has been successfully applied to a series of salt-like compounds as well as polar intermetallics in order to accurately calculate the valence-electron distributions, directly using the electronic structure in reciprocal space. And yet, certain deviations between the Mulliken and Löwdin charges and the charges expected from Zintl–Klemm concept have been identified.
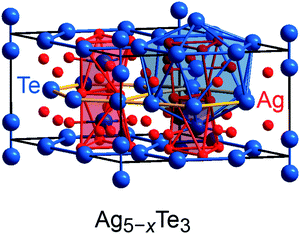
Previous research on polar intermetallics revealed the existence of certain compounds which are also composed of polyanionic units but are poorer in valence electrons relative to the Zintl phases.5,6,76 In particular, the mineral stützite Ag5−xTe3, for which a homogeneity range from x = −0.25 to x = 1.44 has been identified,77–79 was chosen as a prototypical example for the application of the population analysis tool, as its crystal structure comprises building units similar to those observed for Zintl phases, but its electronic structure can scarcely be recognized by the Zintl–Klemm idea.54 The crystal structure of stützite (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 2m, no. 189; Fig. 5) is composed of tellurium dumbbells [Te−]2 and, furthermore, honeycomb (h)- and Kagome (K)-fashioned tellurium nets, which are not Te–Te bonded (because of interatomic distances larger than 4.7 Å) but stacked in a sequence of –h–K–h–K–. The silver atoms are distributed between the tellurium nets and surround the tellurium atoms, thereby forming different types of polyhedra. A detailed structural analysis of stützite also revealed the presence of positional disorder for diverse silver as well as tellurium sites; details regarding the structure determinations have been reported elsewhere.54,80
2m, no. 189; Fig. 5) is composed of tellurium dumbbells [Te−]2 and, furthermore, honeycomb (h)- and Kagome (K)-fashioned tellurium nets, which are not Te–Te bonded (because of interatomic distances larger than 4.7 Å) but stacked in a sequence of –h–K–h–K–. The silver atoms are distributed between the tellurium nets and surround the tellurium atoms, thereby forming different types of polyhedra. A detailed structural analysis of stützite also revealed the presence of positional disorder for diverse silver as well as tellurium sites; details regarding the structure determinations have been reported elsewhere.54,80
When attempting to describe this material by means of the Zintl–Klemm concept, formal electron distributions such as (Ag+)34(Te2−)13([Te−]2)4 and (Ag+)36(Te2−)13([Te−]2)4(e−)2 come to mind for a “Ag34Te21” composition and a “Ag36Te21” composition, respectively. Because previous research on the phase widths of stützite (see above) identified the existence of compositions being poorer in silver content relative to the electron-precise Ag34Te21 (=Ag4.86Te3), one may raise the question how the valence-electron distributions in such electron-poorer intermetallics can be understood. In this connection, it should also be noted that the difference between absolute electronegativities81 of silver (4.44 eV) and tellurium (5.49 eV) is rather small. Hence, as the application of the Zintl concept is a clear oversimplification and probably reaches its limits in the present case, we employed the Mulliken and Löwdin population analysis tool to extract the charge distributions in this telluride from first-principles.
An application of Mulliken's approach yields an average charge distribution – note that the crystal structure is disordered – of (Ag+0.37)32(Te−0.66)13([Te−0.40]2)4 for “Ag32Te21”, of (Ag+0.36)34(Te−0.68)13([Te−0.36]2)4 for “Ag34Te21”, and of (Ag+0.33)36(Te−0.64)13([Te−0.42]2)4 for “Ag36Te21”; the lesser charged Te atoms play the role of X halogen atoms (forming X2 dumbbells) whereas the higher charged Te atoms stay isolated and, hence, resemble noble-gas atoms with a filled octet. The corresponding Löwdin charges are similar, cf. Table S4.† Clearly, the electron transfer from Ag to Te is mirrored by the computed (and significant) charges, and the charge distributions resemble the tendencies proposed from a Zintl–Klemm treatment in a certain way; however, as also pointed out by more recent research,54 the (electronic) structure and, so, the electron (or charge) distribution are apparently not strongly influenced by the silver content of the compound. And yet, is it possible to extract further information about the tendency to adopt a certain composition based on the computed charges?
In fact, the knowledge of the charges allows computing the Madelung energies, εM, for all three stützite models. There is a plethora of (historical) publications demonstrating that Madelung energies can serve as a reliable method for quickly examining the electronic structures and stabilities of solid-state compounds,82–85 including a very recent study.86 In the present case, the Madelung energies were achieved using the Fourier method as implemented in VESTA87,88 by taking the Mulliken charges as obtained by LOBSTER's population analysis. For the Madelung calculations, the radii of anionic spheres were set to 1.3 Å (less than half of the smallest interatomic distance), and the reciprocal-space ranges were set to 3.2 Å−1. The convergence of the Madelung energies with variations of the parameters was also ensured. In addition to the Madelung energies, the formation enthalpies of all stützite models were evaluated as independent theoretical data. The formation enthalpies were derived from the total energies E of the respective stützite models and elemental silver and tellurium – a procedure that is valid for a pressure close to zero, as the pV term in H = E + pV vanishes, so that the total energy is equivalent to the enthalpy E = H.41
A look at the formation enthalpies (Table 1) yields that all inspected stützite models are exothermic compounds. In addition, a comparison with the Madelung energies (also Table 1) not only reveals that the lowest energy corresponds to the “Ag34Te21” model, which is also related to the lowest formation energy, but the courses of formation enthalpies and Madelung energies run parallel. In other words, the Madelung energies mirror the total energies which is surprising for a phase in which the absolute electronegativities are quite close. We also note that recent research54 on the vibrational properties of the three stützite compositions, i.e., “Ag36Te21”, “Ag34Te21”, and “Ag32Te21”, showed all three of them to be dynamically stable, although “Ag34Te21” is energetically most favorable. Thus, how can the trends seen from both the formation enthalpies as well as Madelung energies be understood at the atomic scale? An additional inspection of the densities-of-states (DOS) curves (Fig. S1†) and crystal-orbital-Hamilton-populations for the aforementioned stützite models reveals a rather subtle interplay between the location of the Fermi level at a maximum of the DOS in the silver-poorest telluride and the occupations of antibonding Ag–Te states for the silver-richer compositions. Furthermore, the Fermi level in “Ag34Te21” falls into a band gap – an electronically favorable situation (cf. DOS (εF) in Table 1). Accordingly, “Ag34Te21” is related to the most negative Madelung energy as the electronically most favorable situation – a gap at the Fermi level is achieved for that model. The composition “Ag36Te21” corresponds to the least exothermic formation enthalpy and least negative Madelung energy and, hence, is the least favorable model due to the occupations of additional antibonding states. ΔHf and εM of “Ag32Te21” are located in-between those of “Ag34Te21” and “Ag36Te21”, since the Fermi level is located at a maximum of the DOS, but fewer antibonding states are occupied for this composition (cf. ref. 54 and ESI of ref. 54). In summary, it can be inferred that the wave-function-based computations of the atomic charges (and Madelung energies) for the three models provide a straightforward way to identify the stability trends for the (structurally) complex intermetallic, irrespective of the size of the charge transfer. For reasons of completeness, we also mention alternative density-based approaches (e.g., DDEC) which have been specially proposed to reproduce the electrostatic potential and energy of systems based on DFT calculations.89
| Compound | ΔHf (kJ mol−1) | εM (kJ mol−1) | DOS (εF) |
|---|---|---|---|
| “Ag32Te21” | −275.78 | −4138.2 | 19.96 |
| “Ag34Te21” | −301.00 | −4302.8 | 0.00 |
| “Ag36Te21” | −221.41 | −3873.3 | 12.63 |
Conclusions
Implementing both Mulliken and Löwdin population analyses into the LOBSTER package has been demonstrated as a way to effectively and accurately calculate basis-set independent charges from plane-wave calculations. By doing so, one arrives at straightforward and inexpensive means to recognize the charge distributions in ionic as well as polar intermetallics directly using the wave function without the costlier need to partition electron densities in real space. In the cases of the Zintl compounds, the charges calculated with the new tool correlate well to those charges expected from applying the Zintl–Klemm concept. Additionally, more light was shed on the electronic situation in the mineral stützite, where an application of the Zintl–Klemm concept could not clarify the actual electron distributions. Although the Mulliken and Löwdin charges somehow resemble the ones assumed by a Zintl–Klemm treatment and there is indeed charge transfer from silver to tellurium, the charges vary slightly relative to the silver content in the model structures of stützite, and they are only around one third of the charges expected from the Zintl concept. In addition, it was demonstrated that Madelung energies can be easily computed from the wave-function-based Mulliken charges, thereby providing a straightforward approach to evaluate the stability trends for that (structurally) complex intermetallic.Conflicts of interest
There are no conflicts of interest to declare.Appendix
In order to determine GPμ from eqn (3) using Mulliken's approach, the electron-density distribution in a molecule or solid is divided into a net population (NP) and an overlap population (OP) by using the normalization condition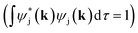 of a square-integrable wave function in k-space
of a square-integrable wave function in k-space
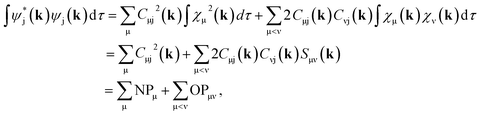 | (4) |
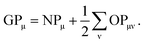 | (5) |
In the density-matrix formalism, GPμ is defined as
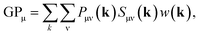 | (6) |
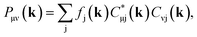 | (7) |
| Sμν(k) = 〈χμ(k)|χν(k)〉, | (8) |
To proceed with Löwdin population analysis, the basis set χ must be orthogonalized, accomplished via application of Löwdin's symmetric orthogonalization (LSO).47,48 A new basis set χ′ and a new coefficient matrix C′ are then constructed from the old ones by linear transformation
| χ′(k) = S−1/2(k)χ(k), | (9) |
| C′(k) = S1/2(k)C(k). | (10) |
The positive and negative square root of the overlap matrix S can be obtained from diagonalization of S.48 The LSO ensures that the orthogonalized basis functions lie as closely as possible (in Hilbert space) to the original functions. After applying the LSO, a new density matrix P′ = S1/2PS1/2 is obtained and the Löwdin gross orbital population GPμ can be calculated as follows
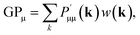 | (11) |
Acknowledgements
The authors wish to thank the IT Center of RWTH Aachen University and Deutsche Forschungsgemeinschaft for providing the computational time as well as the resources, and Dr Ryky Nelson and Philipp M. Konze for technical assistance regarding the generation of the code and the pictures. S. T. is grateful for a Liebig stipend of the Verband der Chemischen Industrie e.V. (FCI), Frankfurt, Germany. We would also like to thank two perceptive reviewers who made us explicitly highlight the principal difference between wave-function-based and density-based charge approaches.References
- D. C. Schmitt, B. L. Drake, G. T. McCandless and J. Y. Chan, Acc. Chem. Res., 2015, 48, 612–618 CrossRef CAS PubMed.
- G. J. Miller, Eur. J. Inorg. Chem., 1998, 1998, 523–536 CrossRef.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- R. Nesper, Angew. Chem., Int. Ed. Engl., 1991, 30, 789–817 CrossRef.
- J. D. Corbett, Inorg. Chem., 2010, 49, 13–28 CrossRef CAS PubMed.
- F. C. Gladisch and S. Steinberg, Crystals, 2018, 8, 80 CrossRef.
- T. B. Massalski and U. Mizutani, Prog. Mater. Sci., 1978, 22, 151–262 CrossRef CAS.
- U. Mizutani and H. Sato, Crystals, 2017, 7, 9 CrossRef.
- H. Jones, Proc. Phys. Soc., 1937, 49, 250–257 CrossRef CAS.
- E. Zintl, Angew. Chem., 1939, 52, 1–6 CrossRef CAS.
- H. Schäfer, B. Eisenmann and W. Müller, Angew. Chem., Int. Ed. Engl., 1973, 12, 694–712 CrossRef.
- G. J. Miller, M. W. Schmidt, F. Wang and T.-S. You, Struct. Bonding, 2011, 139, 1–55 CrossRef CAS.
- J. D. Corbett, Angew. Chem., Int. Ed., 2000, 39, 670–690 CrossRef CAS PubMed.
- M.-H. Whangbo, C. Lee and J. Köhler, Angew. Chem., Int. Ed., 2006, 45, 7465–7469 CrossRef CAS PubMed.
- J. Köhler and M.-H. Whangbo, Solid State Sci., 2008, 10, 444–449 CrossRef.
- E. S. Toberer, A. F. May and G. J. Snyder, Chem. Mater., 2010, 22, 624–634 CrossRef CAS.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8639 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- S. M. Kauzlarich, S. R. Brown and G. J. Snyder, Dalton Trans., 2007, 2099–2107 RSC.
- X. Sun, X. Li, J. Yang, J. Xi, R. Nelson, C. Ertural, R. Dronskowski, W. Liu, G. J. Snyder, D. Singh and W. Zhang, J. Comput. Chem., 2019, 40, 1693–1700 CrossRef CAS PubMed.
- G. A. Papoian and R. Hoffmann, Angew. Chem., Int. Ed., 2000, 39, 2408–2448 CrossRef.
- F. Wang and G. J. Miller, Inorg. Chem., 2011, 50, 7625–7636 CrossRef CAS PubMed.
- F. C. Gladisch and S. Steinberg, Eur. J. Inorg. Chem., 2017, 3395–3400 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse, M. Marsman and J. Furthmüller, Vienna Ab initio Simulation Package (VASP), The Guide, Computational Materials Physics, Faculty of Physics, Universität Wien, Vienna, Austria, 2014 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1994 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- C. Bunge, J. Barrientos and A. Bunge, At. Data Nucl. Data Tables, 1993, 53, 113–162 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- R. Dronskowski, Computational Chemistry of Solid State Materials - A Guide for Material Scientists, Chemists, Physicists and others, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2005 Search PubMed.
- F. Bloch, Z. Phys., 1929, 50, 555–600 CrossRef.
- C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89 CrossRef CAS.
- S. Steinberg and R. Dronskowski, Crystals, 2018, 8, 225 CrossRef.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- P. O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- L. Piela, Ideas of Quantum Chemistry (Appendix J), Elsevier B.V., Amsterdam, 1st edn, 2007 Search PubMed.
- W.-L. Li, C. Ertural, D. Bogdanovski, J. Li and R. Dronskowski, Inorg. Chem., 2018, 57, 12999–13008 CrossRef CAS PubMed.
- A. Szabo and N. S. Ostlund, Modern Quantum Chemistry - Introduction to Advanced Electronic Structure Theory, Dover Publications, Inc., Mineola, New York, 1996 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- T. Koga, K. Kanayama, S. Watanabe and A. J. Thakkar, Int. J. Quantum Chem., 1999, 71, 491–497 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. C. Göbgen, F. C. Gladisch and S. Steinberg, Inorg. Chem., 2018, 57, 412–421 CrossRef PubMed.
- Y. Shirako, Y. G. Shi, A. Aimi, D. Mori, H. Kojitani, K. Yamaura, Y. Inaguma and M. Akaogi, J. Solid State Chem., 2012, 191, 167–174 CrossRef CAS.
- V. L. Cherginets, V. N. Baumer, S. S. Galkin, L. V. Glushkova, T. P. Rebrova and Z. V. Shtitelman, Inorg. Chem., 2006, 45, 7367–7371 CrossRef CAS PubMed.
- J. E. Nickels, M. A. Fineman and W. E. Wallace, J. Phys. Chem., 1949, 53, 625–628 CrossRef CAS.
- H. E. Swanson, E. Posnjak and R. W. G. Wyckoff, Natl. Bur. Stand. Circ., 1955, 539, 31–32 Search PubMed.
- G. J. Finch and S. Fordham, Proc. Phys. Soc., 1936, 48, 85–94 CrossRef CAS.
- M. Ahtee, Ann. Acad. Sci. Fenn., Ser. A6, 1969, 313, 1–11 Search PubMed.
- E. Posnjak and R. W. G. Wyckoff, J. Wash. Acad. Sci., 1922, 12, 248–251 CAS.
- V. Ganesan, Pramana–J. Phys., 1986, 27, 469–474 CrossRef CAS.
- A. Demont, C. Prestipino, O. Hernandez, E. Elkaim, S. Paofai, N. Naumov, B. Fontaine, R. Gautier and S. Cordier, Chem.–Eur. J., 2013, 19, 12711–12719 CrossRef CAS PubMed.
- A. Smakula and J. Kalnajs, Phys. Rev., 1955, 99, 1737–1743 CrossRef CAS.
- E. Zintl and W. Dullenkopf, Z. Phys. Chem., 1932, 16, 195–205 Search PubMed.
- K. Kishio and J. O. Brittain, J. Phys. Chem. Solids, 1979, 40, 933–940 CrossRef CAS.
- W. Baden, P. C. Schmidt and A. Weiss, Phys. Status Solidi A, 1979, 51, 183–190 CrossRef CAS.
- P. Böttcher and U. Kretschmann, Z. Anorg. Allg. Chem., 1985, 523, 145–152 CrossRef.
- P. Böttcher and U. Kretschmann, Z. Anorg. Allg. Chem., 1982, 491, 39–46 CrossRef.
- E. E. Havinga, Dissertation, Univ. Groningen, Holland, 1957.
- I. M. Kurylyshyn, T. F. Fässler, A. Fischer, C. Hauf, G. Eickerling, M. Presnitz and W. Scherer, Angew. Chem., Int. Ed., 2014, 53, 3029–3032 CrossRef CAS PubMed.
- C. G. Davies, R. J. Gillespie, J. J. Park and J. Passmore, Inorg. Chem., 1971, 10, 2781–2784 CrossRef CAS.
- R. C. Burns, D. R. Slim, R. J. Gillespie and W. C. Luk, Inorg. Chem., 1979, 18, 3086–3094 CrossRef CAS.
- F. A. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Phys. Rev. Lett., 2016, 117, 135502 CrossRef PubMed.
- M. Wendorff and C. Röhr, Z. Naturforsch., 2007, 62b, 1227–1234 Search PubMed.
- Q. Lin and G. J. Miller, Acc. Chem. Res., 2018, 51, 49–58 CrossRef CAS PubMed.
- W. Kälin and J. R. Günter, J. Solid State Chem., 1996, 123, 391–397 CrossRef.
- J. Peters, O. Conrad, B. Bremer and B. Krebs, Z. Anorg. Allg. Chem., 1996, 622, 1823–1832 CrossRef CAS.
- R. M. Imamov and Z. G. Pinsker, Kristallografiya, 1966, 11, 182–190 Search PubMed.
- F. Baumer and T. Nilges, Inorg. Chem., 2017, 56, 13930–13937 CrossRef CAS.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- M. F. C. Ladd and W. H. Lee, Prog. Solid State Chem., 1964, 1, 37–82 CrossRef CAS.
- M. F. C. Ladd and W. H. Lee, Prog. Solid State Chem., 1965, 2, 378–413 CrossRef CAS.
- T. C. Waddington, Adv. Inorg. Chem. Radiochem., 1959, 1, 157–221 CrossRef CAS.
- H. D. B. Jenkins, Rev. Chim. Miner., 1979, 16, 134–150 CAS.
- D. Kato, K. Hongo, R. Maezono, M. Higashi, H. Kunioku, M. Yabuuchi, H. Suzuki, H. Okajima, C. Zhong, K. Nakano, R. Abe and H. Kageyama, J. Am. Chem. Soc., 2017, 139, 18725–18731 CrossRef CAS PubMed.
- M. P. Tosi, Solid State Phys., 1964, 16, 1–120 CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2001, 44, 1272–1276 CrossRef.
- T. A. Manz and N. Gabaldon Limas, RSC Adv., 2016, 6, 47771–47801 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05190b |
| This journal is © The Royal Society of Chemistry 2019 |