Open Access Article
Open Access ArticleRelationship between dynamic fatigue crack propagation properties and viscoelasticity of natural rubber/silicone rubber composites†
Qingyuan Hana,
Liqun Zhang ab and
Youping Wu
ab and
Youping Wu *ab
*ab
aState Key Laboratory of Organic–Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029, China. E-mail: wuyp@mail.buct.edu.cn; Fax: +86-10-64456158; Tel: +86-10-64442621
bBeijing Engineering Research Centre of Advanced Elastomers, Beijing University of Chemical Technology, Beijing 100029, China
First published on 20th September 2019
Abstract
In this paper, dynamic fatigue crack propagation properties of natural rubber/silicone rubber (NR/VMQ) composites are studied under constant tearing energy (G) input. Through dynamic fatigue crack growth testing, it is found that with the increase of VMQ fraction, NR/VMQ exhibits a lower crack growth rate (dc/dN). The viscoelastic parameters have been recorded in real-time during crack propagation, including the storage modulus E′, loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, and loss compliance modulus J′′, and their relationships with crack propagation behaviour have been established. The improved crack propagation resistance is attributed to the reduced J′′, resulting from the synergistic effect of increased E′ and decreased tan
δ, and loss compliance modulus J′′, and their relationships with crack propagation behaviour have been established. The improved crack propagation resistance is attributed to the reduced J′′, resulting from the synergistic effect of increased E′ and decreased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, and thus more energy dissipation occurred in the linear viscoelastic region in front of the crack tip, which consumed part of the energy for crack growth. Finally, good correlation between dc/dN and J′′ could be successfully established.
δ, and thus more energy dissipation occurred in the linear viscoelastic region in front of the crack tip, which consumed part of the energy for crack growth. Finally, good correlation between dc/dN and J′′ could be successfully established.
Introduction
The fatigue phenomenon widely exists in rubber products, such as tires, seals, dampers and conveyor belts, which are usually exposed to dynamic stress. Therefore, exploring the fatigue damage mechanism of rubber composites has great significance in improving the service life of their products.According to the rubber fracture mechanics theory established by Rivlin and Thomas,1 when a pre-notched rubber strip is torn, the strain energy consumed to produce a unit area of new crack surface is called tearing energy (G):
 | (1) |
With the increase of G, crack growth rate (dc/dN) would increase in four different manners.2 When G exceeds critical tearing energy Gc, in the power-law region, dc/dN − G exhibits an exponential relationship:
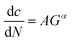 | (2) |
Furthermore, Persson and Brener have pointed out that the energy dissipation around the crack G(v) consists of two parts:4
 | (3) |
As shown in Fig. 1, G0 occurs in the innermost area of the crack tip, and it is a highly non-linear process, which includes forming of cavities, breaking of chemical bonds, pulling out of molecular chains and stringing; G0 f(v, T) is the bulk dissipation of linear viscoelastic region in front of the crack tip, which makes the major contribution to G(v), where f(v, T) is a function of crack growth rate v and temperature T. And according to the time–temperature equivalence principle, T could be replaced by the Williams–Landel–Ferry (WLF) coefficient αT,5 so that G(v) could be presented as the function of time (frequency) without temperature:
 | (4) |
 | (5) |
[E′′/|E*|] is loss compliance modulus J′′, which is also the function of storage modulus E′ and loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. Therefore, eqn (4) could also be written as the form of G(v) − J′′ as shown in eqn (6).6,7
δ. Therefore, eqn (4) could also be written as the form of G(v) − J′′ as shown in eqn (6).6,7
 | (6) |
Because of the characteristic of strain induced crystallization (SIC), natural rubber (NR) exhibits outstanding mechanical strength and fatigue crack propagation resistance, but its anti-ageing properties is poor. As for the highly saturated and inorganic backbone structure (–Si–O–) of silicone rubber (VMQ), it possesses excellent high-temperature and ageing resistance. So in this study, NR/VMQ composites8,9 were prepared to improve anti-ageing and anti-fatigue properties of tire materials at the same time.10–12
Constant strain/stress loading conditions are generally used in fatigue testing,13 but different modulus of rubber would lead to different G input, further to influence their fatigue properties. Therefore, here we have kept G input constant, and storage modulus E′, loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and loss compliance modulus J′′ were recorded real-time as function of fatigue cycles during crack propagation testing. The purpose of our study is to establish a connection between fatigue crack propagation properties and bulk viscoelastic properties of NR/VMQ composites.14,15
δ and loss compliance modulus J′′ were recorded real-time as function of fatigue cycles during crack propagation testing. The purpose of our study is to establish a connection between fatigue crack propagation properties and bulk viscoelastic properties of NR/VMQ composites.14,15
Experimental
Materials
NR smoke sheet 1# was purchased from Indonesia. VMQ 110-9 (Mn = 4.5 × 105, vinyl content = 5%) was provided by Hesheng Silicon Industry Co., Ltd. (Zhejiang, China). Precipitated silica (Ultrasil VN3) was purchased from Evonik Degussa Co., Ltd. (Qingdao, China). Silane coupling agent TESPT (bis-[3-(triethoxysilyl)-propyl]-tetrasulfide) was provided by Shuguang chemical Co., Ltd. (Nanjing, China). Silane coupling agent VTES (CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHSi(OC2H5)3) was purchased from Chenguang Chemical Industry Co., Ltd. (Shandong, China). Curing agent DBPMH (2,5-dimethyl-2,5-di(tert-butylperoxy)-hexane) was provided by AkzoNobel Co., Ltd (Jiangsu, China). Other ingredients are all commercially available products.
CHSi(OC2H5)3) was purchased from Chenguang Chemical Industry Co., Ltd. (Shandong, China). Curing agent DBPMH (2,5-dimethyl-2,5-di(tert-butylperoxy)-hexane) was provided by AkzoNobel Co., Ltd (Jiangsu, China). Other ingredients are all commercially available products.
Sample preparation
In order to overcome the mixing difficulties caused by the large viscosity difference between NR and VMQ, VMQ/silica masterbatch was firstly prepared by a two-roll mill (X(S)K-160, Shanghai rubber machinery Co., Ltd., China) with feeding ratio of VMQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) silica
silica![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VTES
VTES![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hydroxyl terminated polysiloxane = 100
hydroxyl terminated polysiloxane = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.16 Then a two-stage procedure was adopted for the preparation of NR/VMQ compounds according to formula shown in Table 1. The first stage was conducted in a Haake torque rheometer (RM-200C, Hapro electric technology Co., Ltd, Harbin, China) with rotor speed of 60 rpm and filling fraction of 0.7. When temperature of the mixing chamber rose to 100 °C, rubber, silica, silane coupling agent TESPT, antioxidants TMQ and MB were mixed in sequence. When temperature reached 145 °C, maintained 5 min for complete silanization, then dumped. The second stage was conducted on two-roll mill, and curing agent DBPMH was mixed into the first- stage compounds.
1.16 Then a two-stage procedure was adopted for the preparation of NR/VMQ compounds according to formula shown in Table 1. The first stage was conducted in a Haake torque rheometer (RM-200C, Hapro electric technology Co., Ltd, Harbin, China) with rotor speed of 60 rpm and filling fraction of 0.7. When temperature of the mixing chamber rose to 100 °C, rubber, silica, silane coupling agent TESPT, antioxidants TMQ and MB were mixed in sequence. When temperature reached 145 °C, maintained 5 min for complete silanization, then dumped. The second stage was conducted on two-roll mill, and curing agent DBPMH was mixed into the first- stage compounds.
| a Parts per 100 parts of rubber.b Poly(1,2-dihydro-2,2,4-trimethylquinoline), (C12H15N)n, n = 6–8.c 2-Mercaptobenzimidazole, C7H6N2S. | ||||
|---|---|---|---|---|
| NR/VMQ | 100/0 | 90/10 | 80/20 | 70/30 |
| NR | 100 | 90 | 80 | 70 |
| VMQ | 0 | 10 | 20 | 30 |
| Silica | 50 | 50 | 50 | 50 |
| Silane coupling agent | 4 | 4 | 4 | 4 |
| Curing agent DBPMH | 2 | 2 | 2 | 2 |
| Antioxidant TMQb | 1 | 1 | 1 | 1 |
| Antioxidant MBc | 1 | 1 | 1 | 1 |
| Hydroxyl terminated polysiloxane | 0 | 0.1 | 0.2 | 0.3 |
| Total | 158 | 158.1 | 158.2 | 158.3 |
Rotorless moving die rheometer (MR-C3, RADE instrument Co., Ltd., Beijing, China) was applied to determine optimum vulcanization time (t90). Then a platen press vulcanizer (LB-D350 × 350, Dongfang machinery Co., Ltd., Huzhou, China) was conducted to prepare vulcanized specimens under pressure of 15 MPa at 170 °C for t90.
Physical mechanical properties testing
An electronic tensile machine (SANS Test Machine Corporation, Shenzhen, China) was conducted to test tensile properties, which according to standard ISO 37: 2011, with cross-head speed of 500 mm min−1.Rubber processing analysis (RPA)
Strain amplitude dependence of viscoelastic parameters in NR/VMQ compounds were measured by rubber processing analyzer RPA (RPA 2000, Alpha technology Co., Ltd., America) with strain range of 0.28–400% and frequency of 1 Hz at 100 °C. After the first strain-sweeping, all compounds were vulcanized at 170 °C for t90. Then the vulcanizates were conducted by strain-sweeping with range of 0.28–40% and frequency of 10 Hz at 60 °C.Transmission electron microscopy (TEM)
Phase morphology of NR/VMQ masterbatch and silica dispersion morphology of its filled composites were investigated by TEM (H-9500, Hitachi Co., Ltd., Japan) with accelerating voltage of 200 kV. Samples for TEM were cut by an ultra-microtome (EM FC7, Leica Co., Ltd., Germany) under cooling of liquid nitrogen at −100 °C.Atomic force microscopy (AFM)
Phase morphology of NR/VMQ masterbatch was also studied by AFM (Nanoscope IV Controller, Bruker Co., Ltd., Germany) in Peak Force Quantitative Nano-Mechanical mode. Samples for AFM were cut and polished by the ultra-microtome under liquid nitrogen atmosphere. Then the scanning was operated by a Si3N4 cantilever (Bruker SNL-10, radius of curvature = 2 nm, nominal spring constant = 0.35 N m−1) at 1.0 nN peak tapping force. All tests were conducted with 1.0 kHz Z-piezo oscillation frequency and 150 nm peak force amplitude under room temperature.Measurements of contact angle and surface energy
The surface energy of NR and VMQ was determined according to Owens–Wendt–Rabel–Kaelble (OWRK) method17 via measuring contact angle of water (polar liquid) and diiodomethane (non-polar liquid) via video optical contact angle tester (Dataphysics Co., Ltd, America).Dynamic fatigue crack growth testing and dynamic mechanical thermal analysis (DMTA)
Dynamic fatigue crack growth test was conducted on the DMA + 1000 tester (Metravib Co., Ltd, France) using pure shear (PS) specimen (40 mm long, 15 mm high and 2 mm thick, with double edge pre-notch of 2 mm by razor blade) as shown in Fig. 2(a). According to eqn (7), G for PS specimen only depends on strain energy density (W), marked by dashed lines as shown in Fig. 2(b) and initial specimen height (h0), so its dc/dN would not be affected by the crack length.18–20| GPS = Wh0 | (7) |
First, a 2000 stretch-retract cycles were applied to the specimen with frequency of 20 Hz under room temperature to eliminate the Mullins effect in rubber.21 Then, a dynamic strain, corresponding to constant G input of 1000 J m−2, was conducted for the fatigue crack propagation.22 Through locating coordinates of the crack tip by microscope assembled front (Fig. 2(c)), crack growth rate dc/dN can be characterized.23 Meanwhile, the viscoelastic parameters, including storage modulus E′, loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and loss compliance modulus J′′, were recorded as function of fatigue cycles in the real-time of crack propagation.
δ and loss compliance modulus J′′, were recorded as function of fatigue cycles in the real-time of crack propagation.
Besides, temperature dependence of these three viscoelastic parameters in NR/VMQ vulcanizates were also tested by dynamic mechanical thermal analyzer DMTA (VA-3000, 01dB-Metravib Co., Ltd., France). The measurement was conducted in tension mode with temperature range of −80 to 80 °C and heating rate of 3 °C min−1, strain of 0.1% and frequency of 10 Hz.
Results and discussion
Vulcanization characteristic
According to torque curves of NR/VMQ compounds during vulcanization process in Fig. 3, it is figured out that except for 80/20 blend, with the increase of VMQ content, the maximum torque values increase, indicating higher cross-linking density. This is attributed to the stronger reactivity between VMQ and curing agent DBPMH in the peroxide vulcanization system, for the methyl and vinyl groups are easier to be attacked by the peroxyl radicals than double bonds and methylene groups in NR.24,25Filler network and dispersion morphology
The RPA storage modulus G′–strain sweeping curves of NR/VMQ vulcanizates are shown in Fig. 4(a). The high G′ level at lower strains and its rapid decline at higher strains is called Payne effect,26–28 which is mainly caused by the existence of filler network under lower strains and its progressive collapse and destruction under higher strains.29–31 As can be seen, with more addition of VMQ, G′ of NR/VMQ increases, which indicates stronger structure of filler network. | ||
| Fig. 4 (a) Strain dependency of storage modulus G′ of NR/VMQ vulcanizates by RPA (b) photographs of silica dispersion morphology by TEM. | ||
For figuring out the silica dispersion morphology in NR/VMQ, TEM photographs were taken as shown in Fig. 4(b). With higher VMQ fractions in NR/VMQ, more inhomogeneous dispersion and bigger silica aggregates could be seen, especially for 70/30 blend, which could be correlated with its highest G′ level.
Phase morphology of NR/VMQ silica masterbatch
In order to investigate the cause of the uneven filler dispersion in NR/VMQ, phase morphology of NR/VMQ silica masterbatch blends via TEM and AFM are further characterized. Firstly, in 80/20 and 70/30 blends, the pre-mixed silica particles in VMQ masterbatch, marked with red circles in Fig. 5(a), have migrated into NR phase after blending, which proves the different affinity between silica and NR or VMQ phase. This is consistent with the higher silica agglomeration degree in NR/VMQ with higher VMQ content in Fig. 4(a) and (b) mentioned above.Moreover, the darker area marked by red arrows in Fig. 5(a) and (b) refers to VMQ phase, and the brighter area refers to NR matrix. With increasing VMQ content, the domain size of VMQ phase becomes larger, and exhibits irregular shape and inhomogeneous distribution in NR matrix. As for 70/30 blend, the largest VMQ domains can be seen among the three. The poor compatibility between NR and VMQ could be attributed to their large surface characteristic difference, for the surface energy of pure NR we measured is 25.2 mN m−1, and 17.6 mN m−1 for pure VMQ.
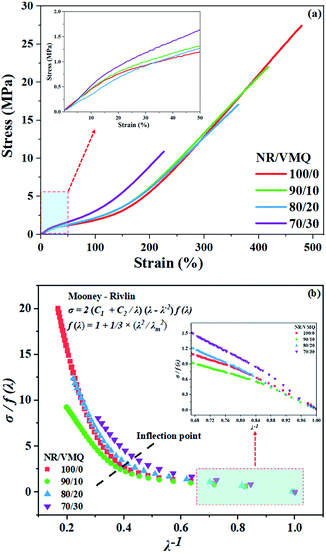
Stress–strain behaviour
Fig. 6(a) shows the stress–strain curves of NR/VMQ composites including enlarged details at strain range of 0–50%, it can be seen that although the addition of VMQ decreases ultimate tensile strength of NR/VMQ, it increases modulus at strains below 50%, which exhibits more evident in 70/30 blend.As for rubber with strain-induced crystallization (SIC) characteristic, with the increase of strain, the sharp rise of stress is mainly contributed by SIC and the finite extensibility of molecular chains. Furukawa et al.32 introduced correction parameter f(λ) into Mooney–Rivlin model to exclude effects of the latter, and the inflection point of [σ/f(λ) − λ−1] plot could represent the extension ratio λ when SIC happens.7,33,34 So according to the Mooney–Rivlin curves in Fig. 6(b), with increasing VMQ content, the inflection point emerges at lower strain, especially for 70/30 blend, which indicates easier occurrence of SIC. In addition, as for 0.67 < λ−1 < 1, that is, below 50% strains, 70/30 blend also exhibits the highest [σ/f(λ)] value among the four composites, which is consistent with the result of the highest modulus in Fig. 6(a).
The relationship between dynamic crack propagation behaviour and viscoelasticity of NR/VMQ composites
Average values and standard deviations of dynamic fatigue crack growth rate dc/dN at constant G input of 1000 J m−2 are shown in Fig. 7. It is pointed out that the addition of VMQ could improve the crack propagation resistance of NR/VMQ, for 80/20 and 70/30 blends exhibit the lowest dc/dN, and pure NR shows the highest dc/dN among the four composites.According to Persson and Brener's theory introduced above,4,5 storage modulus E′, loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and loss compliance factor J′′ were selected for recording as function of fatigue cycles in the real-time of crack propagation as shown in Fig. 8(a)–(c), respectively, which in order to build up connections between crack propagation properties and viscoelasticity of NR/VMQ composites.
δ and loss compliance factor J′′ were selected for recording as function of fatigue cycles in the real-time of crack propagation as shown in Fig. 8(a)–(c), respectively, which in order to build up connections between crack propagation properties and viscoelasticity of NR/VMQ composites.
With addition of VMQ, E′ of NR/VMQ increases compared with that of NR as shown in Fig. 8(a), especially for 70/30 blend. As for tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, it appears decline in NR/VMQ with higher VMQ fraction in Fig. 8(b). Evident decrease of J′′ with more addition of VMQ has been found in Fig. 8(c), this is consistent with eqn (5), for the combined effects of the increased E′ and decreased tan
δ, it appears decline in NR/VMQ with higher VMQ fraction in Fig. 8(b). Evident decrease of J′′ with more addition of VMQ has been found in Fig. 8(c), this is consistent with eqn (5), for the combined effects of the increased E′ and decreased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ would finally cause the decline of J′′.
δ would finally cause the decline of J′′.
Besides, for further evidence, temperature dependency of E′, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and J′′ were also characterized by DMTA as shown in Fig. S1(a)–(c),† respectively, including enlarged details at 20–70 °C. Similar results have been acquired as mentioned above in Fig. 8(a)–(c), with increasing VMQ fraction, E′ increases, tan
δ and J′′ were also characterized by DMTA as shown in Fig. S1(a)–(c),† respectively, including enlarged details at 20–70 °C. Similar results have been acquired as mentioned above in Fig. 8(a)–(c), with increasing VMQ fraction, E′ increases, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and J′′ decrease in the three NR/VMQ composites.
δ and J′′ decrease in the three NR/VMQ composites.
On the basis of the above results, we proposed the mechanism sketch of improved crack propagation resistance of NR/VMQ in Fig. 9. On the one hand, incorporation of VMQ into NR caused stronger silica filler network, higher cross-linking density, and easier occurrence of SIC compared with NR, and correspondingly NR/VMQ exhibited higher stress level at smaller strains, that is, the increased E′.35 On the other hand, due to the flexible chain structure and quite low glass-transition temperature of VMQ, NR/VMQ showed lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ relative to NR. The synergistic effect of the increased E′ and decreased tan
δ relative to NR. The synergistic effect of the increased E′ and decreased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ would lead to the decrease of J′′. Lower J′′ resulted in higher G0 f(v, T), which demonstrated more energy dissipation in the bulk linear viscoelastic region.4 As for constant G(v) input in our study, higher G0 f(v, T) means lower G0, and so the energy used as crack propagation would decrease.5,36 As a result, the crack propagation resistance of NR/VMQ was improved.
δ would lead to the decrease of J′′. Lower J′′ resulted in higher G0 f(v, T), which demonstrated more energy dissipation in the bulk linear viscoelastic region.4 As for constant G(v) input in our study, higher G0 f(v, T) means lower G0, and so the energy used as crack propagation would decrease.5,36 As a result, the crack propagation resistance of NR/VMQ was improved.
 | ||
| Fig. 9 Mechanism sketch of the improved crack propagation resistance of NR/VMQ with addition of VMQ. | ||
Further, polynomial fitting of dc/dN–E′, dc/dN–tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and dc/dN–J′′ have been done for revealing the underlined linkages between them, as shown in Fig. 10(a)–(c), respectively, for the viscoelastic parameters were chosen as the average values of different fatigue cycles in Fig. 8. It is worth noting that dc/dN–J′′ exhibits the best relevance (R2 = 0.99) among the three fitting curves, which proves the combined effects of E′ and tan
δ and dc/dN–J′′ have been done for revealing the underlined linkages between them, as shown in Fig. 10(a)–(c), respectively, for the viscoelastic parameters were chosen as the average values of different fatigue cycles in Fig. 8. It is worth noting that dc/dN–J′′ exhibits the best relevance (R2 = 0.99) among the three fitting curves, which proves the combined effects of E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ on J′′ again. Therefore, loss compliance modulus J′′ is a reliable viscoelastic parameter to correlate with the crack propagation behaviour of NR/VMQ composites.
δ on J′′ again. Therefore, loss compliance modulus J′′ is a reliable viscoelastic parameter to correlate with the crack propagation behaviour of NR/VMQ composites.
 | ||
Fig. 10 Polynomial fit between crack growth rate dc/dN and viscoelastic parameters of NR/VMQ: (a) dc/dN–E′, (b) dc/dN–tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and (c) dc/dN–J′′. δ and (c) dc/dN–J′′. | ||
Conclusions
In this study, dynamic fatigue crack propagation properties of NR/VMQ composites at constant G input of 1000 J m−2 are emphatically discussed. Results showed that more addition of VMQ could improve crack propagation resistance of NR/VMQ. The mechanism of this phenomenon has been put forward by characterizing the viscoelastic parameters in the real-time of fatigue process, and good correlation has been established between loss compliance modulus J′′ and crack growth rate dc/dN. The synergistic effect of the increased E′ and decreased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ cause the decline of J′′. Then the corresponding bulk energy dissipation G0 f(v, T) in the linear viscoelastic region in front of the crack tip has been strengthened, as for constant G(v) input, energy used as crack propagation G0 would decrease, which contributed to the declined crack propagation rate. Therefore, J′′ is a reliable viscoelastic parameter to correlate with the crack growth behaviour of NR/VMQ composites.
δ cause the decline of J′′. Then the corresponding bulk energy dissipation G0 f(v, T) in the linear viscoelastic region in front of the crack tip has been strengthened, as for constant G(v) input, energy used as crack propagation G0 would decrease, which contributed to the declined crack propagation rate. Therefore, J′′ is a reliable viscoelastic parameter to correlate with the crack growth behaviour of NR/VMQ composites.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial supports from the National Key Research and Development Program of China (No. 2017YFB0307002).References
- R. S. Rivlin and A. G. Thomas, J. Polym. Sci., 1953, 10, 291–318 CrossRef CAS.
- G. J. Lake, Rubber Chem. Technol., 1995, 68, 435–460 CrossRef CAS.
- M. E. Yaagoubi, D. Juhre, J. Meier, N. Kröger, T. Alshuth and U. Giese, Int. J. Fatigue, 2018, 112, 341–354 CrossRef.
- B. N. J. Persson and E. A. Brener, Phys. Rev. E, 2005, 71, 036123 CrossRef CAS PubMed.
- B. N. J. Persson, O. Albohr, G. Heinrich and H. Ueba, J. Phys.: Condens. Matter, 2005, 17, 1071–1142 CrossRef.
- S. Rooj, A. Das, I. A. Morozov, K. W. Stöckelhuber, R. Stocek and G. Heinrich, Compos. Sci. Technol., 2013, 76, 61–68 CrossRef CAS.
- Y. J. Nie, B. Y. Wang, G. S. Huang, L. L. Qu, P. Zhang, G. S. Weng and J. R. Wu, J. Appl. Polym. Sci., 2010, 117, 3441–3447 CrossRef CAS.
- M. J. Li, Y. Li, J. Zhang and S. Feng, Polym. Eng. Sci., 2014, 54, 355–363 CrossRef CAS.
- T. T. N. Dang, J. K. Kim and K. J. Kim, J. Vinyl Addit. Technol., 2010, 16, 254–260 CrossRef.
- H. J. Kim and G. R. Hamed, Rubber Chem. Technol., 2000, 73, 743–752 CrossRef CAS.
- K. Sahakaro, N. Naskar, R. N. Datta and J. W. M. Noordermeer, J. Appl. Polym. Sci., 2007, 103, 2538–2546 CrossRef CAS.
- W. H. Waddell, Rubber Chem. Technol., 1998, 71, 590–618 CrossRef CAS.
- J. R. Beatty, Rubber Chem. Technol., 1964, 37, 1341–1364 CrossRef CAS.
- Y. Morishita, K. Tsunoda and K. Urayama, Polymer, 2019, 179, 121651 CrossRef CAS.
- Y. Morishita, K. Tsunoda and K. Urayama, Phys. Rev. E, 2016, 93, 043001 CrossRef.
- Z. Sun, Q. Huang, Y. Z. Wang, L. Q. Zhang and Y. P. Wu, Ind. Eng. Chem. Res., 2017, 56, 1471–1477 CrossRef CAS.
- D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- B. Dong, C. Liu and Y. P. Wu, Polym. Test., 2014, 38, 40–45 CrossRef CAS.
- G. Andreini, P. Straffi, S. Cotugno, G. Gallone and G. Polacco, Rubber Chem. Technol., 2013, 86, 132–145 CrossRef.
- R. Stoček, G. Heinrich, M. Gehde and R. Kipscholl, Fracture Mechanics & Statistical Mech, LNACM, vol. 70, pp. 269–301 Search PubMed.
- Y. X. Ding, X. J. Cao, G. S. Weng, Q. Y. Yin, L. T. Wang and Z. R. Chen, J. Appl. Polym. Sci., 2017, 134, 44527 Search PubMed.
- A. J. Chang, G. S. Weng, K. Fu, Y. X. Ding and D. R. Gong, J. Appl. Polym. Sci., 2016, 133, 42972 Search PubMed.
- H. Yao, G. S. Weng, Y. P. Liu, K. Fu, A. J. Chang and Z. R. Chen, J. Appl. Polym. Sci., 2015, 132, 41980 CrossRef.
- J. Kruželák, R. Sýkora and I. Hudec, Rubber Chem. Technol., 2017, 90, 60–88 CrossRef.
- R. Rajan, S. Varghese and K. E. George, Rubber Chem. Technol., 2016, 86, 488–502 CrossRef.
- R. Q. Yang, Y. H. Song and Q. Zheng, Polymer, 2017, 116, 304–313 CrossRef CAS.
- Z. Sun, Q. Huang, L. Q. Zhang, Y. Z. Wang and Y. P. Wu, RSC Adv., 2017, 7, 38915–38922 RSC.
- L. L. Qu, L. J. Wang, X. M. Xie, G. Z. Yu and S. H. Bu, RSC Adv., 2014, 4, 64354–64363 RSC.
- H. M. Zhou, L. X. Song, A. Lu, T. Jiang, F. M. Yu and X. C. Wang, RSC Adv., 2016, 6, 15155–15166 RSC.
- A. Das, K. W. Stöckelhuber, R. Jurk, M. Saphiannikova, J. Fritzsche, H. Lorenz, M. Klüppel and G. Heinrich, Polymer, 2008, 49, 5276–5283 CrossRef CAS.
- S. K. Srivastava and Y. K. Mishra, Nanomaterials, 2018, 8, 945 CrossRef PubMed.
- J. Furukawa, Y. Onouchi, S. Inagaki and H. Okamoto, Polym. Bull., 1981, 6, 381–387 CrossRef.
- B. Dong, C. Liu, Y. L. Lu and Y. P. Wu, J. Appl. Polym. Sci., 2015, 132, 42075 Search PubMed.
- B. Dong, C. Liu, L. Q. Zhang and Y. P. Wu, RSC Adv., 2015, 5, 17140–17148 RSC.
- S. B. Zhang, L. Zheng, D. H. Liu, Z. C. Xu, L. Q. Zhang, L. Liu and S. P. Wen, RSC Adv., 2017, 7, 40813–40818 RSC.
- P. Ghosh, R. Stoček, M. Gehde, R. Mukhopadhyay and R. Krishnakumar, Int. J. Fract., 2014, 188, 9–21 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05833h |
| This journal is © The Royal Society of Chemistry 2019 |