Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Raman spectroscopic study of ZnO/NiO nanocomposites based on spatial correlation model†
Sarang Dev G.a,
Vikas Sharma*a,
Ashish Singhb,
Vidushi Singh Baghela,
Masatoshi Yanagida c,
Atsuko Nagatakic and
Neeti Tripathi‡
c,
Atsuko Nagatakic and
Neeti Tripathi‡
 *a
*a
aDepartment of Physics, School of Physical Sciences (SoPS), Doon University, Dehradun – 248001, Uttarakhand, India. E-mail: vsharma.ph@doonuniversity.ac.in; neetidtripathi@gmail.com
bSchool of Materials Science and Technology, Indian Institute of Technology (IIT) BHU, Varanasi – 221005, India
cGlobal Research Center for Environment and Energy based on Nanomaterials Science (GREEN), National Institute of Materials Science (NIMS), Tsukuba, Ibaraki 305-0044, Japan
First published on 28th August 2019
Abstract
The effect of nickel concentration has been investigated in ZnO/NiO nanocomposites synthesized using the co-precipitation method. The X-ray diffraction and TEM measurements confirm the distinct phase of NiO in the ZnO/NiO samples. Furthermore, the Raman study shows the sharp modes at 99 cm−1 and 438 cm−1 corresponding to E(low)2, E(high)2 of hexagonal wurtzite ZnO structure and, 1080 cm−1 associated to the two-phonon (2P) mode of NiO, respectively. We also compared the effect of Ni concentration on the formation of ZnO/NiO by analyzing Ehigh2 Raman mode of ZnO with the help of spatial correlation model. The correlation lengths, broadening and asymmetry ratio obtained from the fitting showed good agreement with the experimental results.
Introduction
Over the years, zinc oxide (ZnO) has attracted tremendous interest in the field of photovoltaics, photocatalysis, supercapacitor and spintronics applications.1,2 It is now well established that the structural, optical, and electrical properties can be modified by intentional doping of the metal ions into the ZnO host matrix. While extensive studies have been devoted to the partial substitution of Zn2+ with the transition metal ions into the ZnO host matrix,2 the nanocomposite materials showed better chemical and mechanical stability, higher electrical conductivity and new interface properties in comparison with the separate phases.3 Therefore nanocomposites with unique properties physical and chemical properties can be applied in diverse fields, including medicine, energy, and ecology. Particularly, ZnO–NiO nanocomposites showed interesting properties due to the fact that n-type ZnO and p-type NiO build-up an inner electric field at the p–n junction interface, which possesses superior functional performances in comparison to the properties of individual phases. For example, Li et al.,4 observed much higher photocatalytic activity of ZnO/NiO heterojunction nanofibers than that of pure ZnO and NiO nanofibers due to highly efficient separation of photogenerated electron–hole pairs. Similarly, Zhou et al.,5 demonstrated a higher value of short-circuit current density (JSC) of 22.34 mA cm−2 and a PCE of 7.01%, compared to that of isolated ZnO/NiO photoanodes. Recent study showed, that the ZnO/NiO nanocomposites exhibit resistive switching properties which are exploited in the fabrication of Resistive Random-Access Memories (ReRAMs).6 Though, significant attention has been paid to the morphological evolution of the ZnO/NiO composites,7–9 a detail understanding about the structural disorder and defects is particularly of interest from both, theoretical and experimental point of view. Since Raman scattering study is based on the inelastic scattering due to lattice phonons, the nature of the material structure and structural disorder and, can be investigated using the Raman spectroscopic techniques.In this paper, we investigated the structural evolution of ZnO/NiO nanocomposite at varying Ni concentrations. Samples were synthesized via co-precipitation method10 with varying Ni concentrations i.e., 0.10 M, 0.20 M and 0.30 M. Samples were characterized using X-ray diffraction (XRD), transmission electron microscopy (TEM) and Raman spectroscopy. We further employed the spatial correlation (SC) model11 on the experimentally observed Raman scattering data, to attain the important information regarding the nature of the solid on a scale of the order of a few lattice constants. Therefore, an insight towards the material properties in terms of correlation lengths and asymmetry constants has been presented.
Experimental details
Zinc acetate [(CH3COO)2Zn·2H2O] (Fisher Scientific) and nickel acetate tetrahydrate [C4H6NiO4·4H2O] (SRL Chemicals) were used as the starting materials. The precursor solutions were prepared by dissolving the zinc acetate and nickel acetate in 100 ml deionized water. Solutions were then placed on a magnetic stirrer and the temperature was maintained at 80 °C. The pH of the solution was maintained around 10, by adding the NaOH solution dropwise to the precursor solution. The stirring was continued for further 1 hour and then the samples were allowed to cool down. The cooled samples were washed with deionized water several times to remove the free ions and then filtered out by the filtration apparatus. The filtered samples were then dried in the hot air oven at 80 °C for 4 hours and annealed at 450 °C for 2 hours in muffle furnace under air ambience. Similar procedure was repeated for three nickel acetate molar concentrations i.e.; 0.10 M, 0.20 M and 0.30 M.The structure of the ZnO/NiO nanocomposites was investigated using an X-ray diffractometer [Bruker D8 Advanced] with Cu Kα radiation (λ = 1.534 Å). A detailed information about the crystalline quality were gathered by using a high resolution Transmission Electron Microscope (TEM) equipped with a FEG source using FEI Tecnai TF20 TEM operated at 200 keV. The Raman spectra of the samples were recorded (model: Raman Touch-VIS-NIR, Nanophoton) at room temperature in XY-mapping mode using 488 nm laser wavelength at excitation power 1.02 mW and exposure time 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ms. During the measurement the laser current was maintained 100% and the signals were recorded by a TE cooled back-thinned CCD camera.
000 ms. During the measurement the laser current was maintained 100% and the signals were recorded by a TE cooled back-thinned CCD camera.
Hereafter, the samples will be designated as ZnO, ZnO-1, ZnO-2 and ZnO-3 corresponding to the pure ZnO, Zn0.9Ni0.1O, Zn0.8Ni0.2O, and Zn0.7Ni0.3O respectively as shown in the Table 1.
| Sample code | Description | Crystallite size (nm) | Dislocation density | Strain (×10−3) |
|---|---|---|---|---|
| ZnO | ZnO | 28.15 | 0.0355 | 7.885 |
| ZnO-1 | Zn0.9Ni0.1O | 39.39 | 0.0253 | 5.636 |
| ZnO-2 | Zn0.8Ni0.2O | 38.73 | 0.0258 | 5.732 |
| ZnO-3 | Zn0.7Ni0.3O | 34.24 | 0.0292 | 6.482 |
Results and discussion
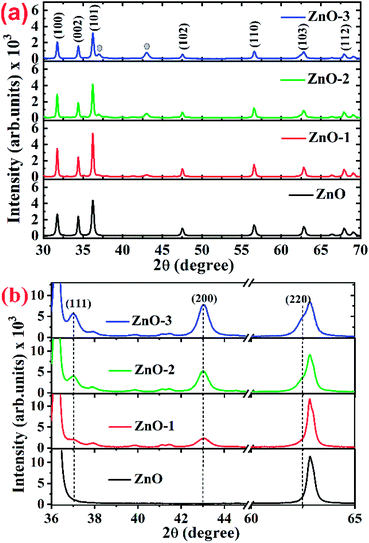
Fig. 1(a) shows the XRD patterns of the pure ZnO and ZnO/NiO samples. The sharp peaks in the patterns indicate the highly crystalline nature of the samples. The diffraction peaks at various 2θ positions, can be indexed to (100), (002), (101), (102), (110), (103) and (112) hexagonal wurtzite structure of ZnO crystal.3 In all the samples other than pure ZnO, the traces of NiO were observed at 2θ positions 37.03 and 43.02 corresponding to the (111) and (200) planes of NiO fcc-cubic structure.12 Fig. 1(b) showed the enlarged graph for the NiO peaks emerged after the addition of NiO in to the ZnO matrix. The de-convolution of XRD peak at 2θ position 62.87, shows the two contributions, one from ZnO (103) and another from NiO (220) plane for the samples ZnO-2 and ZnO-3, respectively, as shown in the Fig. 2(a). It is also observed that the intensity of NiO peaks increases linearly with increasing nickel concentration (Fig. 2(b)). The distinct features of NiO phase formation in all three Ni-doped ZnO samples indicated the ZnO/NiO nanocomposite formation. Further, the crystallite size (D) has been calculated using Debye–Scherrer formula (D = kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ),10 where λ is the wavelength of X-rays (1.534 Å), θ is the diffraction angle, D is the crystallite size, k (=0.9) is the shape factor and β is the full width at half maximum (FWHM) of the peak. The calculated crystallite size for each sample is as shown in the Table 1. There is a significant increase in the crystallite size, when the NiO is introduced into the ZnO sample. This can be due to the distortion produced because of the mismatch between the ionic radii of Zn2+ and Ni2+. But on further increase in the Ni concentration beyond ZnO-1, the nucleation is suppressed and the crystallite size is reduced subsequently. The strain in the samples is obtained by the equation ε = β/2
θ),10 where λ is the wavelength of X-rays (1.534 Å), θ is the diffraction angle, D is the crystallite size, k (=0.9) is the shape factor and β is the full width at half maximum (FWHM) of the peak. The calculated crystallite size for each sample is as shown in the Table 1. There is a significant increase in the crystallite size, when the NiO is introduced into the ZnO sample. This can be due to the distortion produced because of the mismatch between the ionic radii of Zn2+ and Ni2+. But on further increase in the Ni concentration beyond ZnO-1, the nucleation is suppressed and the crystallite size is reduced subsequently. The strain in the samples is obtained by the equation ε = β/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where β is the FWHM of the peak and θ is the Bragg angle.10,13 The strain in the pure ZnO sample is calculated (given in the Table 1) to be 7.88 × 10−3 and reduced to a minimum of 5.63 × 10−3 for ZnO-1. On further increasing the Ni concentration, the strain increased up to 6.48 × 10−3 for ZnO-3. It is evident from, that the increased strain in the ZnO lattice due to Ni doping, causes the reduction in particle size. However, the strain of ZnO-1 is decreased from that of pure ZnO which may be due to the fact that the incorporated impurity has been trapped in non-equilibrium positions. As the concentration of Ni increases, the Ni2+ and the strain increases. The value of dislocation density (δ) is calculated using the relation δ = 1/D2,10 where D is the crystallite size (“D” values taken from the Table 1). It is observed that the dislocation density is decreased to a minimum for the sample ZnO-1 and then increased with the increase in the Ni concentration which is obvious from the strain calculations.
θ, where β is the FWHM of the peak and θ is the Bragg angle.10,13 The strain in the pure ZnO sample is calculated (given in the Table 1) to be 7.88 × 10−3 and reduced to a minimum of 5.63 × 10−3 for ZnO-1. On further increasing the Ni concentration, the strain increased up to 6.48 × 10−3 for ZnO-3. It is evident from, that the increased strain in the ZnO lattice due to Ni doping, causes the reduction in particle size. However, the strain of ZnO-1 is decreased from that of pure ZnO which may be due to the fact that the incorporated impurity has been trapped in non-equilibrium positions. As the concentration of Ni increases, the Ni2+ and the strain increases. The value of dislocation density (δ) is calculated using the relation δ = 1/D2,10 where D is the crystallite size (“D” values taken from the Table 1). It is observed that the dislocation density is decreased to a minimum for the sample ZnO-1 and then increased with the increase in the Ni concentration which is obvious from the strain calculations.
 | ||
| Fig. 1 (a) Full 2θ range of XRD patterns for ZnO and ZnO/NiO samples, (b) extended 2θ range of XRD patterns for highlighting the NiO peaks in ZnO and ZnO/NiO samples. | ||
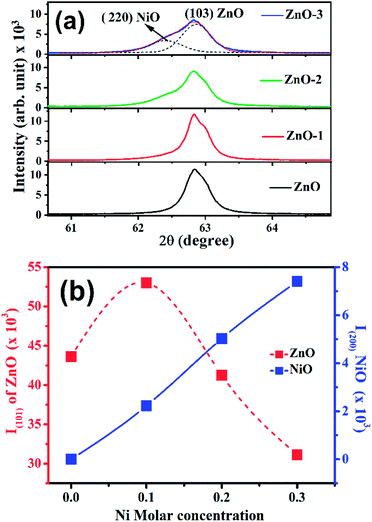 | ||
| Fig. 2 (a) Deconvolution of X-ray diffraction peak at 62.87° into two peaks i.e., (220) NiO and (103) ZnO, (b) intensity dependence of ZnO (101) and NiO (200) peaks on the Ni molar concentrations. | ||
More detailed information about the structure of the samples was further obtained from the TEM analysis. As seen in the Fig. 3(a), the selected area electron diffraction (SAED) patterns of the ZnO sample verifies polycrystalline feature of ZnO nanoparticles. The SAED ring patterns representing the planes (100), (101), (102), (110), (103), and (201) correspond to the hexagonal wurtzite ZnO structure and confirm the high crystallinity of the sample. In addition, the high resolution TEM image (HRTEM) shown in the Fig. 3(b) detects the lattice fringes of spacing 0.156 nm which corresponds to the (110) plane of wurtzite ZnO. It is also noticed from the Fig. 3(c) and other low magnification TEM images that the nanoparticles were formed mostly with hexagonal shape. Further, the size distribution of the particles was analysed with the help of a histogram of 100 particles given in the Fig. 3(d). The particle sizes determined from the TEM images range from 11 nm to 66 nm and from the Gaussian fit, the estimated average particle size is 27.4 nm for pure ZnO sample. For the sample ZnO-3 containing 0.30 M Ni, the SAED pattern is shown in the Fig. 4(a). Interestingly, along with the ZnO planes the diffraction rings corresponding to the (111), (200), (220), and (311) planes of the fcc-cubic phase of NiO were also detected here. This observation confirms the presence of separate NiO phase and the evidence of the ZnO/NiO nanocomposite formation. Fig. 4(b) shows a high resolution TEM micrograph depicting the fringes of spacing 0.147 nm corresponding to the (220) NiO plane. In comparison with the pure ZnO sample, the particle size distribution is narrow, in the case of ZnO-3 and the greater number of particles seem to possess similar shapes as shown in the low magnification micrograph in the Fig. 4(c). The histogram provided in the Fig. 4(d) explains the size distribution of particles ranging from 4 nm to 27 nm. The average particle size of the ZnO-3 sample is found to be around 10.4 nm using a Gaussian fit on the particle size histogram. The sizes calculated from TEM micrographs are quite smaller than the crystallite sizes from XRD. This can be understood as the breaking of agglomerates during the ultrasonic treatment while preparing the samples for TEM measurement on carbon coated grids. Nevertheless, SAED patterns and fringe patterns revealed the high quality ZnO/NiO nanocomposite samples, obtained via co-precipitation method.
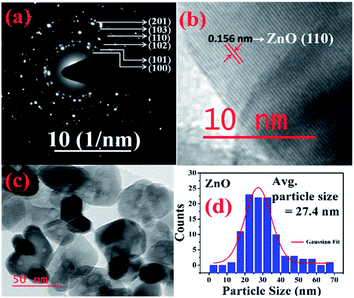 | ||
| Fig. 3 (a) SAED pattern, (b) HR-TEM, d-spacing (c) particle size (d) particle size distribution, of pure ZnO sample. | ||
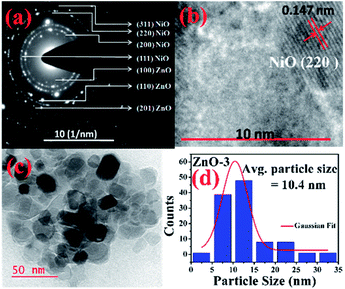 | ||
| Fig. 4 (a) SAED pattern, (b) HR-TEM, d-spacing (c) particle size (d) particle size distribution, of ZnO-3 sample. | ||
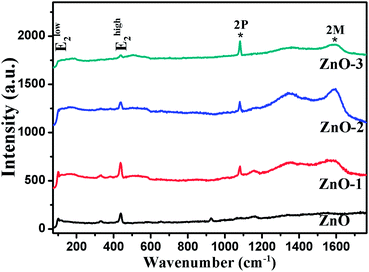
Raman spectroscopy was performed to confirm the crystallinity and structure of the samples. ZnO has a hexagonal wurtzite structure with one Zn ion surrounded tetrahedrally by four oxygen ions and vice versa.14 With four atoms per unit cell, it has three acoustic and nine optic phonon branches. The zone-center optical phonons can be classified according to the following irreducible representation: Γopt = A1 + E1 + 2E2 + 2B1, where B1 modes are silent, A1 and E1 are polar modes, both Raman and IR active, while E2 modes (Elow2 and Ehigh2) are nonpolar and Raman active only.15,16 Fig. 5 shows the Raman spectra of all the four samples. The Raman modes at 99 cm−1 and 438 cm−1 corresponding to Elow2 and Ehigh2 respectively are representatives of wurtzite structure of good crystalline quality.16,17 The modes present at 1080 cm−1 and 1593 cm−1 show the two-phonon (2P) and two-magnon (2M) modes respectively corresponding to the NiO phase.18 Hereafter, the Raman study is concentrated on the analysis of Ehigh2 mode, which is a characteristic of wurtzite ZnO crystal. The effects of disorder and Alloy Potential Fluctuations (APF) in the ZnO/NiO can be investigated using the Spatial Correlation (SC) Model or Phonon Confinement Model (PCM).15,16,19,20 In an ideal crystal, the spatial correlation function is infinite because of the momentum conservation (q = 0) of Raman scattering. Then the Raman lineshape would be symmetric and purely Lorentzian. However, any structural disorder in the crystal may destroy the symmetry in the Raman lineshape and can break the momentum selection rule leading to a finite phonon correlation length (L). Using the SC model, we can calculate the correlation length, which is physically interpreted as average grain size of the localized region. According to this model, Raman intensity (I(ω)) at a frequency ω can be written as:16,19,20
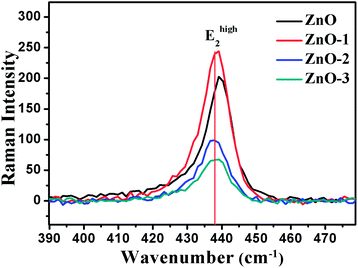
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(πq), where A (=425.5 cm−1) is zone-center phonon frequency and B (=12.5 cm−1) is the difference between the zone-center and the zone-boundary frequencies of the phonon dispersion curve.16,19 Using the correlation length L as an adjustable parameter, we can get the value of L by fitting the Raman line-shape of Ehigh2 mode. Fig. 6 shows the SC model fitted of Ehigh2 mode for ZnO and ZnO-3 samples. The value of L is calculated as a fitting parameter in the SC model for all the samples, which is found to be in good agreement with the crystallite size observed from the XRD data as shown in the Table 2. The value of L increased with the molar concentration of Ni. This indicated that the phonon extended region became large in ZnO/NiO composite.
cos(πq), where A (=425.5 cm−1) is zone-center phonon frequency and B (=12.5 cm−1) is the difference between the zone-center and the zone-boundary frequencies of the phonon dispersion curve.16,19 Using the correlation length L as an adjustable parameter, we can get the value of L by fitting the Raman line-shape of Ehigh2 mode. Fig. 6 shows the SC model fitted of Ehigh2 mode for ZnO and ZnO-3 samples. The value of L is calculated as a fitting parameter in the SC model for all the samples, which is found to be in good agreement with the crystallite size observed from the XRD data as shown in the Table 2. The value of L increased with the molar concentration of Ni. This indicated that the phonon extended region became large in ZnO/NiO composite.
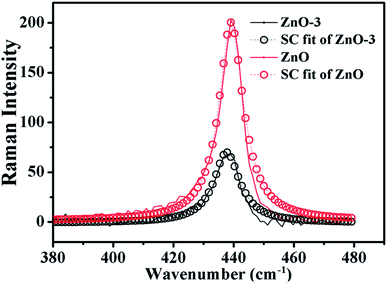 | ||
| Fig. 6 SC model fitting of the experimentally observed Raman data (Ehigh2 Raman mode) for ZnO and ZnO-3 samples. | ||
| Sample | Correlation length (L) | Γa/Γb | Γ | Δω |
|---|---|---|---|---|
| ZnO | 28.4 | 0.657 | 10.01 | 0.90 |
| ZnO-1 | 39.4 | 0.888 | 10.20 | 0.20 |
| ZnO-2 | 38.6 | 1.092 | 9.79 | 0.60 |
| ZnO-3 | 34.5 | 1.293 | 9.88 | 0.46 |
Fig. 7 illustrates the Raman shift at the Ehigh2 mode. A red shift in the Ehigh2 Raman mode in ZnO/NiO samples indicates the tensile strain along the c-axis of the hexagonal wurtzite ZnO phase.15 Further, to analyse the disorder in more detail, we have calculated the broadening (Γ), the broadening asymmetry (Γa/Γb), and the shift (Δω) in the peak position of the Raman line shape at Ehigh2 mode. The calculated parameters are tabulated in the Table 2 and the Fig. 8 shows the change in asymmetry ratio (Γa/Γb) as a function of Ni concentration in the ZnO/NiO samples. It is evident that the sample ZnO-1 is having the lowest asymmetry in the lineshape.
Conclusions
ZnO and ZnO/NiO nanoparticles were synthesized using co-precipitation method. Distinguishable NiO phase was observed in the XRD, TEM and Raman spectroscopy, which suggested the formation of ZnO/NiO nanocomposites. XRD revealed, that the defects are created due to the incorporation of Ni in the ZnO lattice. A detailed insight of Ehigh2 Raman mode showed that 0.10 M Ni concentration is optimal to obtain the maximum phonon correlation lengths with minimum asymmetry. The increased value of correlation length and lower asymmetry at 0.10 M Ni concentration inferred that, the phonon extended region became large with small amount of Ni addition in to ZnO matrix.Conflicts of interest
There are no conflicts to declare.Acknowledgements
One of the author N. Tripathi acknowledge the research funding under the DST-Inspire Faculty Scheme (Ref: DST/INSPIRE/04/2015/001190) of Department of Science & Technology (DST), India.Notes and references
- A. B. Djurišić, X. Chen, Y. H. Leung and A. M. C. Ng, J. Mater. Chem., 2012, 22, 6526–6535 RSC.
- X. G. Zhao and Z. Tang, J. Appl. Phys., 2012, 111, 084321 CrossRef.
- P. P. Dorneanu, A. Airinei, N. Olaru, M. Homocianu, V. Nica and F. Doroftei, Mater. Chem. Phys., 2014, 148, 1029–1035 CrossRef CAS.
- J. Li, F. Zhao, L. Zhang, M. Zhang, H. Jiang, S. Li and J. Li, RSC Adv., 2015, 5, 67610 RSC.
- X. Zhou, J. Yang, J. Cheng, Y. Qiang, H. Shi and Y. Xie, J. Alloys Compd., 2018, 765, 287–298 CrossRef CAS.
- H. L. Yuan and J. C. Li, J. Alloys Compd., 2017, 709, 752–759 CrossRef CAS.
- K. H. Kim, Y. Yoshihara, Y. Abe, M. Kawamura and T. Kiba, Mater. Lett., 2017, 186, 364–367 CrossRef CAS.
- X. Zheng, X. Yan, Y. Sun, Z. Bai, G. Zhang, Y. Shen, Q. Liang and Y. Zhang, ACS Appl. Mater. Interfaces, 2015, 7, 2480–2485 CrossRef CAS PubMed.
- J. Moon, J.-A. Park, S.-J. Lee, S. C. Lim and T. Zyung, Curr. Appl. Phys., 2009, 9, S213–S216 CrossRef.
- K. Raja, P. S. Ramesh and D. Geetha, Spectrochim. Acta, Part A, 2014, 120, 19–24 CrossRef CAS PubMed.
- P. Parayanthal and F. H. Pollak, Phys. Rev. Lett., 1984, 52, 1822 CrossRef CAS.
- M. El-Kemary, N. Nagy and I. El-Mehasseb, Mater. Sci. Semicond. Process., 2013, 16, 1747–1752 CrossRef CAS.
- A. Samanta, M. N. Goswami and P. K. Mahapatra, J. Alloys Compd., 2018, 730, 399–407 CrossRef CAS.
- S. Das, K. Dutta and A. Pramanik, CrystEngComm, 2013, 15, 6349 RSC.
- M. Scepanovic, M. Grujic-Brojcin, K. Vojisavljevic, S. Bernik and T. Sreckovik, J. Raman Spectrosc., 2010, 41, 914–921 CrossRef CAS.
- N. Tripathi, K. Vijayarangamuthu and S. Rath, Mater. Chem. Phys., 2011, 126, 568–572 CrossRef CAS.
- N. Tripathi and S. Rath, Mater. Charact., 2013, 86, 263–269 CrossRef CAS.
- G. George and S. Anandhan, RSC Adv., 2014, 4, 62009 RSC.
- J. B. Wang, H. M. Zhong, Z. F. Li and W. Lu, J. Appl. Phys., 2005, 97, 086105 CrossRef.
- K. Samanta, P. Bhattacharya, R. S. Katiyar, W. Iwamoto, P. G. Pagliuso and C. Rettori, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245213 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: XPS and UV-visible. See DOI: 10.1039/c9ra04555d |
| ‡ Current affiliation: National Institute of Advanced Industrial Science and Technology (AIST), 1-8-31 Midorigaoka, Ikeda, Osaka 563-8577, Japan. |
| This journal is © The Royal Society of Chemistry 2019 |