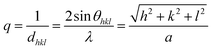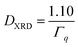Nanostructured spinel cobalt ferrites: Fe and Co chemical state, cation distribution and size effects by X-ray photoelectron spectroscopy

Abstract

Nanostructured spinel cobalt ferrite samples having crystallite size ranging between 5.6 and 14.1 nm were characterized by X-ray photoelectron spectroscopy and X-ray induced Auger electron spectroscopy in order to determine the chemical state of the elements, the iron/cobalt ratio and the cation distribution within tetrahedral and octahedral sites. The presence of size-dependent trends in the binding energy of the main photoelectron peaks and in the kinetic energy of the X-ray induced O KLL signal was also investigated. The results showed that iron is present as Fe^III and cobalt is present as Co^II. The iron/cobalt ratio determined by XPS ranges between 1.8 and 1.9 and it is in very good agreement, within experimental uncertainty, with the expected 2 : 1 ratio. The percentage of Fe in octahedral sites ranges between 62% and 64% for all samples. The kinetic energy of the O KLL signals increases with crystallite size. These results are explained in terms of changes in the ionicity of the metal–oxygen bonds. The results of this investigation highlight how the XPS technique represents a powerful tool to investigate the composition, the chemical state and inversion degree of cobalt spinel ferrites, contributing to the comprehension of their properties.

---

Introduction

Nanostructured spinel cobalt ferrite (CoFe₂O₄), because of its unique properties, has received great attention in a wide range of applications,^1,2 which include magnetic recording,^3,4 catalysis,^5,6 biomedicine^7–11 and sensors.^12,13 Among the cubic ferrites, CoFe₂O₄ is the material with the highest magnetocrystalline anisotropy and reasonably high magnetization¹⁴ and it shows excellent chemical and thermal stabilities, good mechanical properties and is also easily synthesized by different approaches.^15–18 In the spinel structure, oxygen ions are close-packed in a cubic arrangement in which metallic cations fill one out of the eight tetrahedral interstices (commonly identified as T_d or with round brackets) and half of the octahedral ones (O_h or square brackets). Tetrahedral sites are occupied by divalent cations in a direct or normal spinel (M^II)[M^III]₂O₄, whereas trivalent cations replace them in an inverse spinel (M^III)[M^II;M^III]₂O₄.¹⁹

The chemical and physical properties are directly correlated to the composition and to the structure. Bulk cobalt ferrite shows an inverse spinel structure: all Co^II cations occupy the octahedral sites, and the Fe^III cations are equally distributed in T_d and O_h sites (γ = 1, γ is the inversion degree or the fraction of divalent cations in octahedral sites). The coupling of the magnetic moments associated with the ions in T_d and O_h sites justifies the ferrimagnetic behavior of the cobalt ferrite below 860 K.¹⁹ Conversely, when prepared in form of nanostructured material Co^II and Fe^III are randomly distributed (γ = 0.66). In the literature, different techniques (⁵⁷Fe-Mössbauer spectroscopy, EXAFS, neutron diffraction) have been applied in order to determine the inversion degree of nanostructured CoFe₂O₄ synthesized with various approaches and the values fall in the 0.68–0.76 range.^10,20–22

It is clear that among all the factors that mainly influence the properties of the ferrites, besides the size and the shape of the particles, the stoichiometry and the cation distribution play a crucial role. Therefore, the knowledge of the chemical composition, of the structure and of the properties is the key to design a material for a specific application.

In this context, X-ray photoelectron spectroscopy is acknowledged to be a state-of-art tool for providing elemental, chemical state and quantitative information also when investigating nanostructured materials.²³ Due to the above mentioned features it is often used as a complementary technique in papers dealing with nanostructured ferrites.^24–26

The chemical state analysis of XPS data usually starts with the curve fitting of the most intense photoelectron signal. For the transition metals this procedure is not straightforward being the line shapes of the 2p peaks complicated by peak asymmetry, multiplet splitting, by the presence of shake-up satellites and plasmon loss structures. Furthermore, if iron and cobalt are simultaneously present in a sample, as in CoFe₂O₄, the photoelectron Fe 2p and Co 2p peaks overlap the Auger Co L₃M₄₅M₄₅ and Fe L₃M₄₅M₄₅ respectively, when the Al Kα X-ray source is used.

Among the scientific literature on ferrites, only few papers provide details on the curve fitting procedure.^27,28 Some of the papers report XPS spectra, tables listing the binding energy values and the quantitative composition without details on the spectra processing.^29–31 The present work focuses on the use of XPS for the characterization of nanostructured cobalt ferrites samples with crystallite size ranging between 5.6 and 14.1 nm.

In order to determine the iron and cobalt chemical states, their most intense photoelectron signals were resolved in components following two different approaches. The first one is based on the results of the calculation of the multiplet structure expected for 2p core levels of iron and cobalt free ions, proposed by Gupta and Sen³² and the strategy developed in ref. 25 for first row transition metals oxides and hydroxides. This model was successfully applied for curve fitting the iron signals in various applications ranging from the environmental³³ to the biological ones.³⁴ According to the curve fitting strategy proposed in literature²⁷ the iron of a nickel ferrite is composed of four components that were chosen as starting point for curve fitting the spectra in this paper.

The magnetic properties of the ferrites are influenced by disorder in the cation distribution between octahedral and tetrahedral sites, which can influence saturation magnetization, exchange couplings, and ferrimagnetic ordering temperatures;³⁵ in order to determine the spinel inversion degree of the cobalt ferrite, a second curve fitting strategy, based on that proposed by Aghavniana and co-workers,³⁶ has been adopted in this paper.

Since it is known that the binding energy of photoelectron lines is a size dependent parameter,^37–40 in this paper it is also evaluated if a systematic chemical shift of the binding energy of iron Fe 2p_3/2, cobalt Co 2p_3/2, oxygen O 1s and of the kinetic energy of the X-ray induced O KLL signal is observable, changing the cobalt ferrite crystallite size. Since initial and final state effects influence the chemical shift of both photoelectron and Auger lines, an explanation of the observed trends is provided.

Experimental

Cobalt ferrite samples (labelled as Co1-5 in Table S1†) with different crystallite size have been synthesized following a solvothermal procedure similar to the one described elsewhere.^41,42 In order to tune the crystallite size, the amount of the mixed Co^II–Fe^III oleate precursor, the solvents as well as the temperature were properly modified. In details: the amount of precursor for the 5.6 nm nanoparticles (NPs) was 3 mmol in 20 cm³ of 1-pentanol and 10 cm³ of distilled water. The synthesis was conducted at 180 °C for 10 h. The same temperature and reaction time were used for the synthesis of the 6.7 nm NPs: in this case 6 mmol of precursor were added to 10 cm³ of 1-pentanol, 10 cm³ of octanol, and 5 cm³ of distilled water. With the same amount of precursor and solvents, but at 220 °C for 10 h, 8.8 nm NPs were obtained. 11.2 nm NPs were synthetized starting with 2.5 mmol of precursor, 10 cm³ of 1-pentanol, 10 cm³ of toluene and 5 cm³ of distilled water at 230 °C for 10 h. The largest nanoparticles (14.1 nm) were obtained by a seed-mediated approach using a solvothermal procedure set up for core–shell nanoparticles having a CoFe₂O₄ core and MnFe₂O₄ or Fe₃O₄/γ-Fe₂O₃ shell.⁴²

Table S1† summarises the synthesis conditions adopted in this work. The first column reports the sample notation.

X-ray diffraction, using a PANalytical X'Pert PRO with Cu Kα radiation (1.5418 Å), secondary monochromator, and a PIXcel position-sensitive detector was used for characterizing the crystalline phases. Calibration of the peak position and instrumental width was carried out using powder LaB₆ from NIST. The hexane dispersions were dried on a glass plate and measured in the angular range of 10–90° with a step of 0.039°. The XRD patterns aiming to the identification of the crystalline phase, after background subtraction, were processed using PANalytical X'Pert HighScore software. The most intense X-ray peaks [(220), (311), (400), (422), (511), (440)] were fitted with Origin Software by PseudoVoigt function, using a 1 : 1 Gaussian/Lorentzian ratio. In reciprocal space for the cubic system, the reciprocal of the interplanar distance q is defined as

where d_hkl is the interplanar distance of the (hkl) planes, λ is the wavelength of the X-ray beam, θ_hkl is the angle of diffraction for the (hkl) planes, h, k, l are the Miller's indexes and a is the lattice parameter. The crystallite size (diameter) was obtained from full width at half maximum of q (denoted as Γ_q) by Repko et al.⁴¹
where

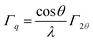
In this equation, the value 1.10 takes into account the information on size distribution and shape of the particles and the model derived from Repko et al.⁴¹ based on the fitting of the peak of Fourier-transformed solid spheres with volume-weighted log-normal size distribution with σ = 0.18, which are almost Gaussian. For each sample, the crystallite size is given as average of the values calculated on the most intense peak and the associated error is the standard deviation.

AFM analysis was performed on spin-coated silicon wafer-samples to observe the changes occurring on their surfaces when varying the spin-coating conditions.

To obtain a uniform layer, the ideal suspension concentration was 4 mg cm⁻³. 100 μL of each solution were deposited on each silicon wafer and the spin-coating conditions were 4000 rpm for one minute.

AFM images were acquired using an Icon Dimension (Bruker, Camarillo, California, USA) with a silicon cantilever (BudgetSensors, Bulgaria) with a spring constant of about 26 N m⁻¹ (manufacturer's value).

XPS measurements were carried out using a Sigma2 XPS and a Thetaprobe manufactured by ThermoFisher Scientific Inc., East Grinstead, UK. Sigma 2 is equipped with an Al/Mg Kα twin source. A non-monochromatic Mg Kα source (1253.6 eV) operated at 200 W was used in order to eliminate the overlap between Fe 2p and Co LMM peaks and between Co 2p and Fe LMM peaks, which is observed if an Al Kα source is used. The residual pressure during the analysis was always lower than 10⁻⁶ to 10⁻⁷ Pa. The emitted electrons are collected by an Alpha 110 hemispherical analyzer, and a multichannel detector consisting of seven channeltrons is used. The analyzer was operated in fixed-analyzer transmission mode setting the pass energy at 25 eV for collecting the high-resolution spectra and at 50 eV for the survey spectra; a step size of 0.05 eV and 1 eV was respectively used. The instrument was used in large-area mode (diameter of the analyzed area: 8 mm). The energy resolution in large-area XPS mode, expressed as the full width at half maximum (FWHM) of the Ag 3d_5/2 signal was 1.1 eV; the intensity was 3.7 Mcps using an Al window less than 1 μm thick to limit the contribution of backscattered electrons and to reduce the contribution of Bremsstrahlung radiation.

The Thetaprobe spectrometer is equipped with a monochromatic Al Kα X-ray source; the residual pressure during the analysis was always lower than 10⁻⁷ Pa. Spectra were collected using a monochromatic beam (Al Kα_1,2E = 1486.6 eV) operated at 4.7 mA and 15 kV (70 W), with a nominal spot size of 300 μm. The analyzer was operated in fixed analyzer transmission mode at 100 eV pass energy for collecting narrow scan spectra and at 200 eV for the survey spectra with a step size of 0.05 eV and 1 eV, respectively. The linearity of the binding energy scale of both spectrometers was monthly checked according to the literature⁴³ and to ISO 15472:2010, using Cu, Au and Ag reference samples. Data were acquired under computer control. Binding energy values were corrected by referencing to the aliphatic carbon at 285.0 eV. Thetaprobe was used to acquire the O 1s and O KLL spectra since the lower FWHM allowed obtaining a better-resolved O KLL signal.

Magnetic nanoparticles dispersed and dried on silicon wafer can be characterized by XPS taking care of checking the shape of the survey spectrum at the low kinetic energy side i.e. below 200 eV. This part of the spectrum is reported to be affected in the presence of stray magnetic fields.⁴⁴ No changes at the low kinetic energy values were observed during this investigation. Fe/Co ratios were calculated correcting the experimental areas for the relative sensitivity factors. The details are reported in the ESI.†

Results

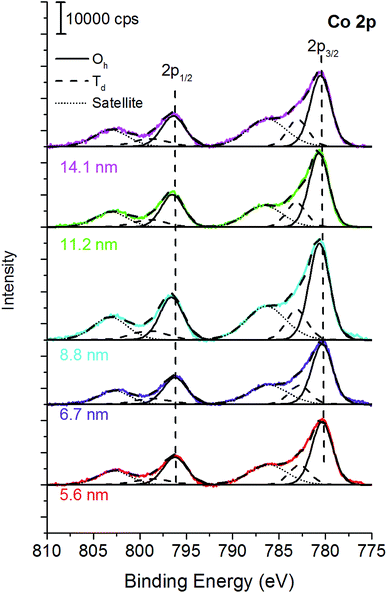
For all the samples XRD results indicated the presence of a spinel cobalt ferrite nanophase, as confirmed by the comparison with the CoFe₂O₄ PDF-Card 0221086 (Fig. S1†).⁴² The absence of other XRD peaks is a clear indication of the presence of a unique spinel phase, within the detection limit of the technique. The crystallites size determined by XRD is shown in Table S1.† Cobalt ferrite samples were dispersed in hexane and deposited on silicon wafer by spin coating, dried, and analyzed by XPS. To check the homogeneity of the covering of the silicon wafer substrate, atomic force microscopy was used. The optimum concentration for achieving the best coverage of the silicon wafer was found to be 4 mg of ferrites in 1 cm³ of hexane. At lower concentration of the dispersion (1–2 mg cm⁻³) disordered and not homogeneous depositions were obtained (Fig. S2†). Together with the signals due to the presence of iron and cobalt, the survey spectra (Fig. S3†) showed the signals due to oxygen from both the ferrite and the capping agent, and the peaks due to carbon deriving from both the capping agent and a possible organic contamination due to the exposure of the samples to the laboratory environment. The absence of signals at about 100 eV and 150 eV allowed excluding the presence of the silicon contribution from the wafer, confirming a proper coverage.

Fe 2p peaks (Fig. 1a) exhibit a doublet separated by 13.5 eV due to spin–orbit coupling. For the curve-fitting purpose only the Fe 2p_3/2 peak was taken into account.

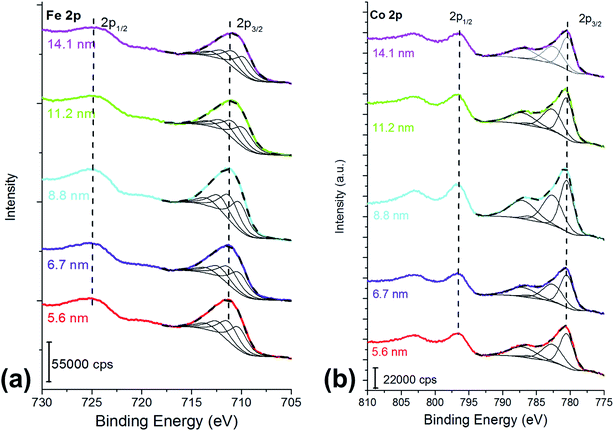Fig. 1 (a) Fe 2p and (b) Co 2p peaks of the cobalt ferrite samples following the curve-fitting procedure based on the multiplet splitting approach.²⁷ The crystallite size is reported in the graph. X-ray source: Mg Kα.

Fe 2p_3/2 peaks were resolved in four components due to multiplet splitting phenomena, following what is reported in literature²⁷ for NiFe₂O₄. The binding energy of the four components are listed in Table 1.

Table 1 Fe/Co ratios determined by XPS and binding energies (eV) of the components of Fe 2p_3/2 and Co 2p_3/2 peaks after multiplet splitting curve-fitting.²⁷ X-ray source: Mg Kα. Standard deviations on three independent measurements are reported in brackets

Crystallite size (nm)	Fe/Co ratio	Fe 2p I	Fe 2p II	Fe 2p III	Fe 2p IV	Co 2p I	Co 2p II	Co 2p III	Co 2p IV
5.6 (2)	1.8	710.3 (1)	711.3 (1)	712.5 (1)	713.9 (1)	780.5 (1)	782.6 (1)	786.0 (1)	787.0 (1)
6.7 (1)	1.9	710.2 (1)	711.2 (1)	712.4 (1)	713.8 (1)	780.5 (1)	782.6 (1)	786.0 (1)	787.0 (1)
8.8 (2)	1.9	710.1 (1)	711.1 (1)	712.4 (1)	713.8 (1)	780.5 (1)	782.6 (1)	786.0 (1)	787.0 (1)
11.2 (6)	1.9	710.1 (1)	711.1 (1)	712.4 (1)	713.8 (1)	780.5 (1)	782.6 (1)	786.0 (1)	787.0 (1)
14.1 (8)	1.9	710.0 (1)	711.0 (1)	712.2 (1)	713.6 (1)	780.4 (1)	782.5 (1)	785.9 (1)	786.9 (1)

---

The curve-fitting parameters are shown in the ESI (Table S2†): the full width at half-maximum of the peak height and the area ratios were kept constant during curve synthesis, while the position of the components was let free to change. Despite this degree of freedom, the binding energy difference between the first peak (Fe 2p I) and the other peaks was reproducible, and it is reported in Table S2.† The binding energy of the signals (Table 1) is typical for Fe^III 27 and no evidence of Fe^II is observed. Fig. 1a and Table 1 show a small binding energy shift of the Fe 2p_3/2 components with the crystallite size: the smaller the cobalt ferrites particles size, the higher the binding energy of the peak.

Co 2p peak is a doublet due to spin–orbit coupling (Fig. 1b); the binding energy separation between Co 2p_3/2 and Co 2p_1/2 was 16 eV and it allowed us to exclude the presence of Co^III, thus the experimental lines were curve-fitted starting from the fitting parameters of CoO reported in Biesinger et al.²⁷ Also in this case, for curve-fitting purposes, only the Co 2p_3/2 was taken into account (Fig. 1b). The shape of the Co 2p_3/2 signal, which shows an intense satellite separated by 6.5 eV from the main most intense peak, is typical of Co^II.²⁷ No significant shifts were observed for the different samples (Table 1). The curve-fitting parameters are listed in Table S3† of the ESI.†

O 1s is a multicomponent peak (Fig. 2a): the most intense component is found at about 530 eV (Table 2) and it is ascribed to oxygen in the oxide lattice.²⁷ The component at about 531.5 eV can be ascribed to both hydroxides and defective oxygen.²⁷ The peak at the highest binding energy value might be due to water and/or to the oleic acid used as capping agent.²⁷

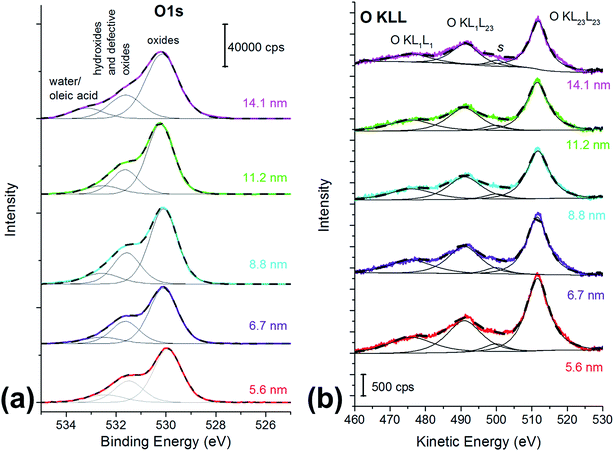Fig. 2 (a) O 1s spectra and (b) O KLL spectra of the cobalt ferrite nanoparticles samples. The particle size is reported in the graph. X-ray source: monochromatic Al Kα.

Table 2 Binding energy (eV) of the O1s signals, kinetic energy (eV) of the O KL₂₃L₂₃ component and Auger parameter values (eV) for the various ferrites. Standard deviations on three independent measurements are reported in brackets

Crystallite size (nm)	O1s oxide	O1s hydroxide or defective oxygen	O1s water	O KL23L23	O KL1L23	ΔKEOKLL	I KL23L23/IKL1L23	α′^a	Δα′^b	ΔR^ea^c
a α′ = (BEO 1s + KEO KL23L23). b Δα′= (α′CoFe2O4 NPs − α′Fe2O3 taken at 1042 eV). c ΔR^ea = Δα′.
5.6 (2)	530.0 (1)	531.5 (1)	532.4 (1)	511.2 (1)	490.5 (1)	20.7 (1)	1.75	1041.2 (2)	−0.8	−0.4
6.7 (1)	530.0 (1)	531.6 (1)	532.6 (1)	511.4 (1)	490.8 (1)	20.6 (1)	1.78	1041.4 (2)	−0.6	−0.3
8.8 (2)	530.1 (1)	531.5 (1)	532.4 (1)	511.5 (1)	491.0 (1)	20.5 (1)	1.80	1041.6 (2)	−0.4	−0.2
11.2 (6)	530.1 (1)	531.6 (1)	532.3 (1)	511.7 (1)	491.3 (1)	20.4 (1)	1.89	1041.8 (2)	−0.2	−0.1
14.1 (8)	530.1 (1)	531.5 (1)	532.5 (1)	511.9 (1)	491.3 (1)	20.4 (1)	2.04	1042.0 (2)	0	0

---

O KLL spectrum showed the presence of two prominent peaks, assigned to O KL₂₃L₂₃ and O KL₁L₂₃ (Fig. 2b),⁴⁵ together with a component at about 477 eV assigned to the KL₁L₁ Auger transition⁴⁵ and a small peak at 501 eV (peak s in Fig. 2b) that may be due to shake-up and shake-off contribution to the Auger peak.⁴⁵

The kinetic energy values of the O KL₂₃L₂₃ components are reported in Table 2, together with KE_{O KL23L23} − KE_{O KL1L23} difference, which is related to the ionicity of the oxides, in agreement with literature.⁴⁶ The identification of the three different oxygen species (oxide, hydroxides or defective oxygen, and water or oleic acid) by curve-fitting of the O KLL signals was not attempted since it was beyond the scope of this work. The O KLL signals were resolved in their main components in order to calculate the modified Auger parameter (α′) and to evaluate any possible size effect in the kinetic energy values of the peak maxima. The values of the modified Auger parameter⁴⁷α′ = BE_O1s + KE_OKL23L23 are also reported in Table 2.

Iron/cobalt ratios of the CoFe₂O₄ samples are found to be close to 2 : 1 (Table 1) for all the samples, in agreement with the ICP-OES (inductively coupled plasma–optical emission spectrometry) results obtained on CoFe₂O₄ samples synthesized by an identical synthesis route.⁴² To evaluate the ratio by XPS data, the Tougaard's background-subtracted Fe 2p and Co 2p peaks (both 2p_3/2 and 2p_1/2 components) were considered. Tougaard's background was chosen since it is less sensitive to the choice of the minimum and maximum of the selected energy range than the Shirley background, especially if large energy ranges are taken into account.⁴⁸ In the present case the energy range was 35 eV for Co 2p and 25 eV for Fe 2p.

Discussion

The curve-fitting approach adopted for Fe 2p_3/2 and for Co 2p_3/2 (Fig. 1), following the calculated components and their intensity ratio presented by Gupta and Sen³² and in agreement with the curve-fitting reported in literature²⁷ provided the evidence of the presence of Fe^III and of Co^II. Gupta and Sen³² calculated the multiplet structure of core p vacancy levels for the 3d-transition metal ions. McIntyre and coworkers,⁴⁹ since 1977, adopted Gupta and Sen³² prediction for resolving Fe 2p and, later, Co 2p spectra of bulk powder.²⁷ The curve-fitting showed in this work is in agreement not only with Gupta and Sen³² but also with successive publications by McIntyre and co-workers.⁴⁹ Thus in this paper it is demonstrated that the fit predicted for the isolated ions,³² tested on bulk powders,^27,49,50 can be successfully used also for nanostructured cobalt ferrites. The multiplet splitting of Fe 2p_3/2 signals from different iron oxides was investigated by Grosvenor and coworkers⁵⁰ and it was shown that the Fe^III octahedrally-coordinated (α-Fe₂O₃) can be distinguished from the same signal in γ-Fe₂O₃, in which 75% of Fe^III cations are octahedrally-coordinated and 25% of the cations are tetrahedrally coordinated. The main differences between the two Fe 2p_3/2 signals are the different area ratios between the multiplet splitting components for α-Fe₂O₃ and γ-Fe₂O₃ and their binding energy (BE) separation. However, the proposed curve-fitting did not allow distinguishing, in the case of γ-Fe₂O₃, between octahedral and tetrahedral iron.⁵⁰ The results obtained in this work for Fe 2p are comparable with those obtained for NiFe₂O₄:²⁷ the presence of Fe^II can be ruled out since no peaks at about 708 eV and 709 eV ^27,50 are observed but nothing can be said about cation distribution.

The curve-fitting strategy of Co 2p peaks proposed by other authors³⁶ was thus followed in order to estimate the spinel inversion parameter from XPS data. The estimation strategy starts with distinguishing between Co^II in octahedral sites (O_h) and Co^II in tetrahedral (T_d) sites on Co 2p peaks (Fig. 3). Both Co 2p_3/2 and Co 2p_1/2 are taken into account after Shirley background subtraction, in agreement with literature.³⁶ Co 2p_3/2 was curve-fitted with a peak located at 780.5 eV, which is ascribed to cobalt in O_h sites, with a peak at 782.9 eV due to Co^II in T_d sites, and with a satellite at 786.3 eV for all the samples (Table 3 and Fig. 3).

Fig. 3 Octahedral and tetrahedral Co^II from XPS.

Table 3 Binding energy (BE, eV), full width at half maximum (FWHM, eV), energy separation between Co 2p_3/2 and Co 2p_1/2, fraction of cobalt in octahedral sites (γ) and percentage of iron in octahedral sites determined following literature³⁶

Crystallite size (nm)	Co 2p3/2 (Oh)		Co 2p3/2 (Td)		Co 2p3/2 SAT		ΔBE 2p3/2 − 2p1/2 (eV)	γ	% Fe (Oh)
	BE (eV)	FWHM (eV)	BE (eV)	FWHM (eV)	BE (eV)	FWHM (eV)
5.6 (2)	780.4 (1)	2.6 (1)	782.8 (1)	2.6 (1)	786.2 (1)	4.9 (1)	16.0 (1)	0.76	62
6.7 (1)	780.4 (1)	2.6 (1)	782.8 (1)	2.6 (1)	786.2 (1)	4.9 (1)	15.9 (1)	0.75	62
8.8 (2)	780.5 (1)	2.6 (1)	782.9 (1)	2.6 (1)	786.4 (1)	5.0 (1)	15.9 (1)	0.76	62
11.2 (6)	780.5 (1)	2.5(1)	783.0 (1)	2.5(1)	786.6 (1)	4.7 (1)	15.8 (1)	0.75	63
14.1 (8)	780.5(1)	2.6 (1)	782.9(1)	2.6 (1)	786.3 (1)	5.0 (1)	16.0 (1)	0.72	64

---

Despite the larger number of oxygen atoms near the Co^II in octahedral sites, its BE is lower than the BE of Co^II in tetrahedral sites. This is explained in terms of effective charge on the cobalt atoms and of oxygen polarizability.⁵¹ The BE separation between Co^II in O_h and T_d sites is fixed.³⁶ The area ratio between Co^II in O_h and T_d in Co 2p_1/2 was constrained to be equal to their ratio in Co 2p_3/2. Assuming a general formula: (Fe_yCo_1−y)_Td[Fe_2−yCo_y]_OhO₄ the percentages of area of the Co^II components in O_h and T_d sites allow the estimation of y, thus the fraction of cobalt in O_h sites. The percentage of iron in octahedral sites is thus calculated with the formula %Fe (O_h) = (y × 0.5 + (1 − y) × 1) × 100.³⁶ The percentage of Fe in octahedral sites calculated following this approach for all the samples ranges between 62 and 64% (Table 3) and it is in very good agreement with the cation distribution formula obtained by ⁵⁷Fe Mössbauer spectroscopy and for nanostructured CoFe₂O₄:^10,20,21(Fe^III_0.7Co^II_0.3)[Fe^III_1.3Co^II_0.7]O₄.

On the basis of these results it seems that this curve synthesis based on two symmetric peaks for distinguishing between differently coordinated iron and cobalt is effective to estimate the cation distribution.

Due to the presence of the oleic acid shell, which is estimated to be about 1 nm thick in agreement with Shard,⁵² the signals from cobalt ferrite are attenuated. The sampling depth of an electron travelling in a ferrite nanoparticle can be estimated by the formula 3λ_ferritecos θ where λ_ferrite is the inelastic mean free path determined for inorganic compounds, according to Seah and Dench,⁵³ and θ is the emission angle. For iron Fe 2p, for example, the sampling depth was found to be 4.6 nm for electrons travelling in pure cobalt ferrite. Due to the presence of the 1 nm-thick oleic acid layer, the sampling depth is reduced and it can be estimated by the formula 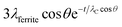, where t = 1 nm is the thickness of the organic layer and λ_C is the inelastic mean free path of an electron from Fe 2p travelling in an organic layer, determined according to Seah and Dench.⁵³

The sampling depth for an Fe 2p electron starting from the cobalt ferrite nanoparticle and attenuated by the oleic acid layer is estimated to be 4.0 nm.

The agreement between the results obtained by XPS (cation distribution and the Fe/Co ratios) on the surface and those extracted by bulk techniques (⁵⁷Fe Mössbauer spectroscopy and ICP-OES)⁴² supports a compositional and structural homogeneity throughout the nanoparticle, also for the larger NPs, for which only 1/3 of their volume is sampled by XPS.

It is known that the binding energy of photoelectron peaks can be strongly influenced by the particle size. In many papers dealing with metal nanoparticles a positive shift of the binding energy values is observed with decreasing particle size.^38,54 In other papers a negative shift is observed for metal supported nanoparticles and it might be attributed to the interaction between the metal nanoparticles and the support rather than to an intrinsic particle size effect.^37,38 The observed chemical shift, due to both size effects and to metal/support interactions, has been explained taking into account both initial- and final-state effects. The reduced coordination number of surface atoms, which is more significant for small NPs, is an initial-state effect; the electron exchange between the support and the NPs and the screening of the core hole on the photo-emitting atom (relaxation energy) are final-state effects and are influenced by particle size as well.³⁸

Concerning the oxides, a positive shift of Cu 2p_3/2 from CuO with decreasing nanoparticles size was observed and it was explained on the basis of the quantum-size effect.³⁹ The shift toward higher BE for smaller NPs was interpreted with the increase of Cu–O bond ionicity. A study on the effect of particle size of ZnO showed an opposite trend in the binding energy of the Zn 2p signal: the smaller the particle the lower the binding energy.⁴⁰ The authors explained this shift with a decrease of the number of oxygen atoms in nanocrystalline ZnO that reduces the charge transfer from Zn to oxygen and increases the shielding effect of the valence electrons in Zn ions, resulting in the decrease of the Zn 2p binding energy. In this paper only a small positive shift (0.3 eV) of the binding energy of the Fe 2p_3/2 peak was observed, when decreasing the particle size from 14.1 to 5.6 nm (Table 1): these results seem to be in agreement with the results obtained on CuO.

If there is a size-dependent effect on the ionicity of the iron-involving bonds (Fe–O) the same effect should be observed on oxygen. For this reason, the effect of the particle size on O 1s and the O KLL signals was also evaluated (Table 2). The binding energy of the photoelectron O 1s signal does not show significant differences with the ferrite particle size, being the chemical shift between the smallest and the largest particles within the experimental uncertainty (0.1 eV). On the contrary, a trend in the kinetic energy of the most intense Auger peak, O KL₂₃L₂₃, is observed. Auger O KLL lines provide information not only on the chemical state of oxygen, but also on the ionicity of the oxygen-involving bonds and on their polarizabilities.^46,55 The ΔKE_OKLL difference between the kinetic energies of O KL₂₃L₂₃ and O KL₁L₂₃ and the ratio between their intensity were calculated (Table 2). Both these parameters are influenced by the ionicity of the M–O bond.^46,56 A correlation was found between the ΔKE_OKLL value and the charge on the oxygen atom (q) calculated after Pauling's electronegativity scale, following a previous study.⁵⁵ The lower was q (lower ionicity) the higher was ΔKE_OKLL. Similarly, a correlation between the I_OKL23L23/I_OKL1L23 intensity ratio and the ΔKE_OKLL value was found, and it was observed that highly ionic oxides (MgO) showed higher values of the intensity ratios and lower values of ΔKE_OKLL.⁴⁶ They proposed a phenomenological model for oxygen Auger spectra that allows justifying this finding. The authors considered an oxygen ion having a charge q immersed in a dielectric oxide and proposed an equation that relates the ΔKE_OKLL shift to the charge on the oxygen atom.⁴⁶ In this paper ΔKE_OKLL decreases with increasing crystallite size (Table 2), thus we can deduce that the charge on oxygen atom is higher and thus the ionicity of the M–O bond. Furthermore, the smallest particles (5.6 ± 0.2 nm) showed the lowest I_OKL23L23/I_OKL1L23 intensity ratio and the highest ΔKE_OKLL value. This result suggests that the ionicity of the metal–oxygen bond decreases with the particle size. Further information can be obtained from the oxygen Auger parameter shifts. It is known that differences in the Auger parameter values (Δα′) reflect differences in the extra-atomic relaxation energies:⁵⁷

Δα′ = ΔR^ea

In this work Δα′ was calculated referring it to bulk Fe₂O₃. The values are reported in Table 2. Δα′ increases with the decrease of the particle size (Fig. 4) and it reaches the maximum value for the smallest particles (5.6 nm). This results in lower relaxation energies than those of bulk Fe₂O₃ (similar results are obtained if Co₃O₄ is taken into account). Lower values of relaxation energy indicate lower polarizabilities of the chemical environment: for the smallest particles, the polarizability of the electronic cloud towards the hole is less effective than in bulk oxides.

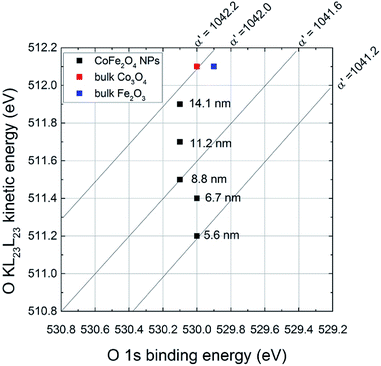Fig. 4 Oxygen chemical state plot. Data from this work are reported (black dots) together with data from literature⁵⁵ (colored squares).

Conclusions

In this work a surface chemical characterization by X-ray photoelectron spectroscopy and X-ray induced Auger electron spectroscopy of nanostructured cobalt ferrite CoFe₂O₄ synthesized by solvothermal route is presented. The results show that XPS can provide very useful information about the composition of nanostructured ferrite samples, highlighting the possibility not only to univocally determine the cation chemical states and their ratio but also correlate the peak position with the crystallite size. Furthermore, the cation distribution between the tetrahedral and octahedral sites was determined by fitting the Co 2p_3/2 signals: the results are in very good agreement with those obtained by ⁵⁷Fe Mössbauer spectroscopy. It is proposed that the crystallite size, which likely affects the ionicity of the metal–oxygen bond, influences the kinetic energy of the X-ray induced Auger O KLL signal.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Prof. N. D. Spencer for providing access to the X-ray photoelectron spectrometers and the AFM facilities during the ERASMUS stage of Mr Fausto Secci. The authors wish to express their gratitude to Mr Giovanni Cossu for the technical support in the XPS measurements. The financial support of Fondazione di Sardegna and Regione Autonoma della Sardegna Progetti Biennali di Ateneo Annualità 2016, Fondazione Sardegna CUP F72F16003070002 is gratefully acknowledged.

References

1. L. Wu, A. Mendoza-Garzia, Q. Li and S. Sun, Chem. Rev., 2016, 116, 10473–10512.
2. S. Jauhar, J. Kaur, A. Goyal and S. Singhal, RSC Adv., 2016, 6, 97694–97719.
3. E. Manova, B. Kunev, D. Paneva, I. Mitov and L. Petrov, Chem. Mater., 2004, 16, 5689–5696.
4. A. Hutlova, D. Niznansky and M. Kurmoo, Adv. Mater., 2003, 15, 1622–1625.
5. M. Nasrollahzadeh, M. Bagherzadeh and H. Karimi, J. Colloid Interface Sci., 2016, 465, 271–278.
6. J. Deng, Y. Shao, C. Tan, S. Zhou and X. Hu, J. Hazard. Mater., 2013, 15, 836–844.
7. N. V. Long, Y. Yang, T. Teranishi, C. M. Thi, Y. Cao and M. Nogami, J. Nanosci. Nanotechnol., 2015, 15, 10091–10107.
8. C. Tudisco, M. T. Cambria, and G. G. Condorelli, in Biomedical Applications of functionalized nanomaterials. Concepts, development and clinical translation, ed. B. Sarmento and J. das Neves, Elsevier, Amsterdam, Netherlands, 2018, ch. 12, pp. 335–361.
9. S. Zhang, and S. Sun, in Nanotechnology for biomedical imaging and Diagnostics. From nanoparticles design to clinical applications, ed. M. Y. Berezin, John Wiley and Sons, Inc., Hoboken (NJ), 2015, ch. 2, pp. 27–48.
10. V. Mameli, A. Musinu, A. Ardu, G. Ennas, D. Peddis, D. Nižňanský, C. Sangregorio, C. Innocenti, N. T. K Thanh and C. Cannas, Nanoscale, 2016, 8, 10124–10137.
11. L. T. T. M. Karoline, T. N. E. Taveira, H. A. A. Winkler, F. Hatem and P. E. A. Gòmez, J. Colloid Sci. Biotechnol., 2016, 5, 45–54.
12. M. A. Mohamed, F. M. El-Badawy, H. S. El-Desoky and M. M. Ghoneim, New J. Chem., 2017, 41, 11138–11147.
13. Y. Yuan, B. Wang, C. Wang, X. Li, J. Huang, H. Zhang, F. Xia and J. Xiao, Sens. Actuators, B, 2017, 239, 462–466.
14. B. D. Cullity and C. D. Graham, Introduction to magnetic materials, John Wiley and Sons, Inc., Hoboken (NJ), 2009.
15. C. Cannas, A. Ardu, A. Musinu, L. Suber, G. Ciasca, H. Amenitsch and G. Campi, ACS Nano, 2015, 28, 7277–7286.
16. C. Cannas, A. Musinu, D. Peddis and G. Piccaluga, Chem. Mater., 2006, 18, 3835–3842.
17. C. Cannas, A. Musinu, A. Ardu, F. Orrù, D. Peddis, M. Casu, R. Sanna, F. Angius, G. Diaz and G. Piccaluga, Chem. Mater., 2010, 22, 3353–3361.
18. V. Mameli, M. S. Angotzi, C. Cara and C. Cannas, Liquid Phase Synthesis of Nanostructured Spinel Ferrites—A Review, J. Nanosci. Nanotechnol., 2019, 19, 4857–4887.
19. A. R. West, Solid State Chemistry and its applications, John Wiley and Sons, Inc., Hoboken (NJ), 2nd edn, 2014.
20. D. Peddis, N. Yaacoub, M. Ferretti, A. Martinelli, G. Piccaluga, A. Musinu, C. Cannas, G. Navarra, J. M. Greneche and D. Fiorani, J. Phys.: Condens. Matter, 2011, 23, 426004–426011.
21. G. Concas, G. Spano, C. Cannas, A. Musinu, D. Peddis and G. Piccaluga, J. Magn. Magn. Mater., 2009, 321, 1893–1897.
22. D. Carta, M. F. Casula, A. Falqui, D. Loche, G. Mountjoy, C. Sanregorio and A. Corrias, J. Phys. Chem. C., 2009, 113, 8606–8611.
23. D. R. Baer and M. H. Engelhard, J. Electron Spectrosc. Relat. Phenom., 2010, 178–179, 415–432.
24. S. Diodati, L. Pandolfo, A. Caneschi, S. Gialanella and S. Gross, Nano Res., 2014, 7, 1027–1042.
25. J. Bennet, R. Tholkappiyan, K. Vishista, N. V. Jaya and F. Hamed, Appl. Surf. Sci., 2016, 383, 113–125.
26. A. S. Albuquerque, M. V. C. Tolentino, J. D. Ardisson, F. C. C. Moura, R. de Mendonca and W. A. A. Macedo, Ceram. Int., 2012, 38, 2225–2231.
27. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson, R. St and C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
28. E. Kester and B. Gillot, J. Phys. Chem. Solids, 1998, 59, 1259–1269.
29. D. Zhao, X. Wu, H. Guan and E. Han, J. Supercrit. Fluids, 2007, 42, 226–233.
30. N. V. Long, Y. Yang, T. Teranishi, C. M. Thi, Y. Cao and M. Nogami, RSC Adv., 2015, 5, 56560–56569.
31. Y. Sun, G. Ji, M. Zheng, X. Chang, S. Li and Y. Zhang, J. Mater. Chem., 2010, 20, 945–952.
32. R. P. Gupta and S. K. Sen, Phys. Rev., 1975, 12, 15–19.
33. M. Fantauzzi, A. Pacella, D. Atzei, A. Gianfagna, G. B. Andreozzi and A. Rossi, Anal. Bioanal. Chem., 2010, 396, 2889–2898.
34. Y. Shen, L. Posavec, S. Bolisetty, F. M. Hilty, G. Nyström, J. Kohlbrecher, M. Hilbe, A. Rossi, J. Baumgartner, M. B. Zimmermann and R. Mezzenga, Nat. Nanotechnol., 2017, 12, 642–647.
35. M. A. Willard, Y. Nakamura, D. E. Laughlin and M. E. McHenry, J. Am. Ceram. Soc., 1999, 82, 3342–3346.
36. T. Aghavniana, J.-B. Moussy, D. Stanescu, R. Belkhou, N. Jedrecy, H. Magnan, P. Ohresser, M. A. Arrio, P. Sainctavit and A. Barbier, J. Electron Spectrosc. Relat. Phenom., 2015, 202, 16–21.
37. A. M. Venezia, A. Rossi, D. Duca, A. Martorana and G. Deganello, Appl. Catal., A, 1995, 125, 113–128.
38. J. Radnik, C. Mohr and P. Claus, Phys. Chem. Chem. Phys., 2003, 5, 172–177.
39. K. Borgohain, J. B. Singh, M. V. Rama Rao, T. Shripathi and S. Mahamuni, Phys. Rev. B, 2000, 61, 11093–11096.
40. Y. Y. Tay, S. Li, C. Q. Sun and P. Chen, Appl. Phys. Lett., 2006, 88, 173118–173120.
41. A. Repko, J. Vejpravová, T. Vacková, D. Zákutná and D. Nižňanský, J. Magn. Magn. Mater., 2015, 390, 142–151.
42. M. Sanna Angotzi, A. Musinu, V. Mameli, A. Ardu, C. Cara, D. Nižňanský, H. L. Xin and C. Cannas, ACS Nano, 2017, 11, 7889–7900.
43. M. P. Seah, Surf. Interface Anal., 2001, 31, 721–723.
44. M. P. Seah, Surf. Interface Anal., 1993, 20, 243–266.
45. D. E. Ramaker, J. S. Murday, G. Moore, M. G. Lagally and J. Houston, Phys. Rev. B, 1979, 19, 5375–5387.
46. P. Ascarelli and G. Moretti, Surf. Interface Anal., 1985, 7, 8–12.
47. C. D. Wagner, L. H. Gale and R. H. Raymond, Anal. Chem., 1979, 51, 466–482.
48. G. C. Smith, in Handbook of Surface and Interface Analysis: Methods for Problem-Solving, ed. J. C. Riviere and S. Myhra, CRC Press, Taylor and Francis Group, Boca Raton, FL, 2nd edn, 2009, ch. 5, pp. 159–208.
49. N. S. McIntyre and D. G. Zetaruk, Anal. Chem., 1977, 49, 1521–1529.
50. A. P. Grosvenor, B. A. Kobe, M. C. Biesinger and N. S. McIntyre, Surf. Interface Anal., 2004, 36, 1564–1574.
51. J. P. Bonnelle, J. Grimbolt and A. D. Huysser, J. Electron Spectrosc. Relat. Phenom., 1975, 7, 151–162.
52. A. G. Shard, J. Phys. Chem. C, 2012, 116, 16806–16813.
53. M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2–11.
54. M. Carrus, M. Fantauzzi, F. Riboni, M. Makosch, A. Rossi, E. Selli and J. van Bokhoven, Appl. Catal., A, 2616, 519, 130–138.
55. C. D. Wagner, D. A. Zatko and R. H. Raymond, Anal. Chem., 1980, 52, 1445–1451.
56. R. Weiβmann, Solid State Commun., 1979, 31, 347–349.
57. C. D. Wagner, Faraday Discuss. Chem. Soc., 1975, 60, 291–300.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03488a

---