Open Access Article
Open Access ArticleMechanism and kinetic study of the reaction of benzoic acid with OH, NO3 and SO4− radicals in the atmosphere†
Xianghe Zhanga,
Chenxi Zhang *b,
Xiaomin Suna,
Jiaoxue Yanga and
Chen Zhu*c
*b,
Xiaomin Suna,
Jiaoxue Yanga and
Chen Zhu*c
aEnvironment Research Institute, Shandong University, Jinan 250100, P. R. China
bDepartment of Biological and Environment, Binzhou University, Binzhou 256600, P. R. China. E-mail: sdzhangcx@163.com
cShandong Province Environmental Monitoring Center, Jinan 250013, P. R. China
First published on 18th June 2019
Abstract
Benzoic acid (BA) is one of the most common organic acids in the Earth’s atmosphere and an important component of atmospheric aerosol particles. The reaction mechanism of OH, NO3 and SO4− radicals with BA in atmospheric water droplets and that of OH radicals with BA in the atmosphere were studied in this paper. The results show that in atmospheric water droplets the potential barriers of the elementary addition reactions of BA with OH radicals are lower than those of elementary abstraction reactions, and the potential barriers of OH-initiated reactions are less than for NO3 and SO4− reactions. The initiation reactions of OH radicals and BA are exothermic, but the abstraction reactions of NO3 and SO4− are endothermic processes. Among the products, 6-hydroxybenzoic acid (6-HBA) and 4,6-dihydroxybenzoic acid (4,6-DHBA) are the most stable, while 3-hydroxybenzoic acid (3-HBA) and 3,5-dihydroxybenzoic acid (3,5-DHBA) are much less stable and, thus, much less abundant compared to 6-HBA and 4,6-DHBA. The initiation and subsequent degradation of BA with OH radicals in the gas phase were calculated. The products of addition and abstraction reactions of BA with OH radicals can be further oxidized and degraded by O2/NO. According to the results of kinetic calculations, the total reaction rate constant of OH radicals with BA at 298.15 K in atmospheric water droplets is 2.35 × 10−11 cm3 per molecule per s. The relationship between reaction rate constants, temperature and altitude were also investigated and discussed in the present study.
Introduction
Benzoic acid (BA) is a simple aromatic acid which has the smell of benzene or formaldehyde, and its steam is a strong irritant. In the natural environment, BA often exists in plants in the form of free acid, ester and carboxylic acid derivatives.1 BA has also been found in automobiles, diesel truck exhausts,2 roofing tar pot heating asphalt and coal tar,3 industrial boilers burning distillate fuel,4 and biomass combustion.5 It is a degradation intermediate of many aromatic compounds, thus it may release into the environment during the process of BA preparation and organic biodegradation.6,7 In the atmosphere, the concentration of BA is 0.3 ± 0.1 ng m−3 in the Indo-Gangetic-Plain outflow, and 0.3 ± 0.2 ng m−3 in the Southeast-Asia outflow.8The steam of BA may irritate the skin, eye and upper respiratory tract, and it has a toxic effect upon long term exposure to the human body. Studies have shown that the stabilizing efficiency of some organic acids appears to be close to or higher than NH3, which can contribute to the aerosol nucleation process by binding to H2SO4.9,10 BA can work as a catalyst to enhance the nucleation of H2SO4, which has been verified by experimental and theoretical research.11,12 Thus, the study of the chemical behavior of BA can help to analyze similar atmospheric processes.
Electrosorptive removal of BA was used in experimental research. With the development of the photo-Fenton oxidation and catalyst process, photocatalytic degradation of BA has been widely used. Aerobic and anaerobic microorganisms, like Burkholderia xenovorans and Thauera aromatica, were used to degrade BA through different methods.13,14 Moreover, the use of the OH radical is an effective method to remove organic contaminants. BA existing in atmospheric water droplets is mainly derived from the photodegradation process of various organic compounds in the atmosphere or by volatilisation with water vapor into the atmosphere. In the atmosphere, a variety of free radicals can be used for the removal of organic compounds.15,16 OH radical, an important atmospheric oxidant,17 plays a significant role in the conversion and removal of air pollutants.18,19 Besides, in a water droplet, the concentration of O2 is smaller than in the atmosphere, therefore, we only consider the participation of O2 in the gas phase.
Several studies have reported on the degradation of BA by OH radicals.20,21 As a strong oxidant, OH radicals are useful, common and fast when compared with other radicals.22 These research results are generally carried out through experiments to study the reaction process between OH radicals and BA.23 Determination of the products and intermediates is used to speculate upon the reaction process. A kinetic model is built to simulate the system behavior. The changing variables in the reaction are controlled to account for their effects on the degradation rate of the reaction, such as the difference between the photoelectrocatalytic degradation and photocatalytic degradation of BA, the pH or wavelength, the concentration of BA and the properties of the catalyst. As a result, a first order reaction kinetic equation is established to obtain the reaction rate constant.21,24 Studies have used heat-activated persulfate to produce SO4− radicals, and through their oxidative properties, BA undergoes decarboxylation and hydroxylation reactions to achieve degradation.25 In previous studies there were also degradation reactions using SO4− radicals and BA derivatives such as benzoate, and their reaction products were detected.26 At night, NO3 radicals can be used as an important oxidant to degrade atmospheric organic pollutants.27 Therefore, we can study the reaction of NO3 in the degradation of BA.
Using quantum chemistry methods, the specific processes and mechanism of the reaction can be explored and the rate constant of the reaction can be calculated. In this paper, the mechanism of the production of hydroxybenzoic acids and the initiated reactions of BA with NO3 and SO4− radicals in atmospheric water droplets, as well as the reaction of BA with OH radicals in the atmosphere, were studied by MPWB1K density functional theory. Then, the rate constants of the elementary reactions were calculated using transition state theory, which can provide useful data for further study.
Computational methods
Mechanism study
Quantum chemistry calculations were performed using the Gaussian 09 program.28 As an accurate model for calculating thermochemical kinetics, the MPWB1K method of density functional theory has been applied to the degradation reaction.29 The geometry configuration of reactants, transition states, intermediates, products and the vibrational frequencies of all the reactions were calculated and optimized at the 6-31+G(d,p) level. Meanwhile intrinsic reaction coordinate (IRC) calculations are used to verify whether the reaction channels are correct. The single point energy of the stationary points is calculated at the MPWB1K/6-311+G(3df,2p) level. As for the reactions occurring in the atmospheric water droplets, the polarizable continuum model (PCM) is used to amend the solvent effect.30 In order to verify the reliability of the computational results, the vibrational wavenumber, IR intensities and Raman activities were calculated using density functional theory methods, and they were found to be in good agreement with the experimental values.31Kinetic analysis
By means of the POLYRATE 9.7 program,32 the canonical variational transition state theory (CVT) with small-curvature tunneling (SCT) correction is used to calculate the reaction rate constants of OH radicals with BA. The results are used to fit the Arrhenius formula of rate constants with temperature as follows:
k(T) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/RT), exp(−Ea/RT),
| (1) |
Results and discussion
The reaction of BA with OH radicals in atmospheric water droplets
By means of the Gaussian 09 programs, high-accuracy quantum chemical calculations were carried out. The geometrical parameters of the reactants, transition states, and products were optimized at the MPWB1K level with a standard 6-31+G(d,p) basis set. The reactions of BA and OH radicals in atmospheric water droplets have two possible reaction pathways which are divided by the elementary reactions of BA and OH radicals. The first pathway is the abstraction and addition reaction of BA with OH radicals, while the second pathway is the addition and abstraction reaction of BA with OH radicals. Wu et al. have studied the elementary reactions of BA, benzoate and OH radicals at the M06-2X/6-311+G(d,p) level, but this paper is mainly about the initiation reactions of the different sites; the reaction in water droplets to produce monohydroxybenzoic acid and the subsequent reactions in gas phase are not involved.34 Besides, the OH radical is an important oxidant in atmospheric aqueous phases such as cloud and fog droplets and water-containing aerosol particles,35 and we concentrate on the reactions of OH radicals with monohydroxybenzoic acid (MHBA) and dihydroxybenzoic acid (DHBA).Production of MHBA
Reactions of BA and OH radicals may occur in the benzene ring on the ortho-position, meta-position and para-position. Because the molecular configuration of BA is not symmetrical, there are five different carbon sites in the benzene ring that can react with OH radicals. After structural optimization, the final products are selected with a stable structure and reaction energy calculation.The reactions pathways of BA and OH radicals are shown in Fig. 1 and 2, and the atom labels of carbon sites are also indicated. In addition, transition states (TS), intermediates (IM), the reaction potential barriers (ΔEb) and reaction energy (ΔEr) are labeled for convenience. Meanwhile a & b show the two pathways; the unit of energy is kcal mol−1.
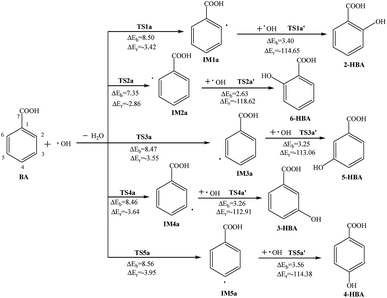 | ||
| Fig. 1 Reaction pathways for the abstraction and addition reaction of BA with OH radicals in atmospheric water droplets. | ||
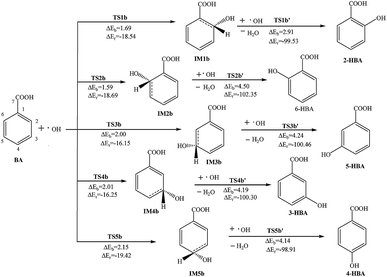 | ||
| Fig. 2 Reaction pathways for the addition and abstraction reaction of BA with OH radicals in atmospheric water droplets. | ||
In other carbon sites of the benzene ring, the reaction processes are similar. The OH radical is close to the hydrogen atom in the benzene ring and forms the transition state TS; meanwhile, the hydrogen atom vibrates between the OH radical and the original carbon atom. After the hydrogen atom is abstracted, the formation of intermediate IM and the loss of a molecule of H2O has a potential barrier of 7.35–8.56 kcal mol−1 and releases 2.86–3.95 kcal mol−1 of heat. Then, another OH radical is close to the carbon atom which has lost the hydrogen atom and through the transition state TS, monohydroxybenzoic acid (MHBA) is formed. These processes have potential barriers of 2.63–3.56 kcal mol−1 and release reaction heats from 112.91 to 118.62 kcal mol−1. As shown in Fig. 1, the potential barriers in the process of intermediate generation at the ortho-position reaction, 6-hydroxybenzoic acid (6-HBA), and the meta-position, 3-hydroxybenzoic acid (3-HBA), are smaller, while those of the para-position reaction, 4-hydroxybenzoic acid (4-HBA), is relatively larger.
Production of DHBA
After the structures of the monohydroxybenzoic acids are optimized, the ortho-, meta- and para-addition products are obtained according to the different positions that OH radicals added to the benzene ring. By comparing the energy of the products, five kinds of reaction products with the lowest energy are selected, and then the OH radicals are added to obtain DHBA, resulting in four types of DHBAs. The reaction processes of the DHBA generation are similar to those in the production of MHBA.The meaning of each symbol in the following Figures is similar to those of Fig. 1, as well as the atom labels of carbon sites. After optimization of the products and energy comparison, the products with the lowest energy in two pathways were consistent. There are 10 kinds of dihydroxy addition reaction products, and these are shown in Fig. 3. For these reactions, the two pathways to form the product DHBA are described in the ESI.†
The potential barriers of elementary addition reactions are smaller than the elementary abstraction reactions, and the released heat of the addition-initiated reactions is also less than that of the abstraction-initiated reactions. Besides, in the abstraction-initiated reactions, the potential barrier to finally get 4,6-DHBA is the smallest, 7.30 kcal mol−1; while that to finally produce 3,4-DHBA is the biggest, 9.08 kcal mol−1. In the addition initiated reactions, the potential barrier to finally get 3,4-DHBA is the smallest, 0.06 kcal mol−1; while that to finally produce 4,5-DHBA is the biggest, 4.68 kcal mol−1.
The reaction of BA with NO3 radicals in atmospheric water droplets
In the troposphere and stratosphere of the Earth’s atmosphere, there is a certain amount of NO3, and it is an important oxidant during the night. NO3 can extract hydrogen from the benzene ring or undergo an addition reaction. The abstraction reactions of NO3 with BA are studied, and the reaction potential barriers and reaction energy are marked in Fig. 4, along with the reactants and products. These reactions can take place at the ortho, meta and para-positions; the NO3 radicals can abstract the hydrogen atom and generate the intermediates and HNO3.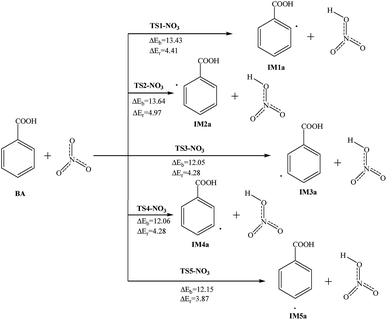 | ||
| Fig. 4 Reaction pathways for the abstraction reaction of BA with NO3 radicals in atmospheric water droplets. | ||
Taking the reaction at the C2 site as an example, the O atom with a single electron on the NO3 radicals is close to the H atom, the C–H bond is broken and then the H–O bond is formed. The reaction is endothermic and requires 4.41 kcal mol−1 of energy, and this reaction needs a slightly higher barrier of 13.43 kcal mol−1. The reactions at the C3, C4, C5 and C6 sites are similar to the C2 sites; the reaction potential barriers are 12.05 to 13.64 kcal mol−1. All the reactions are endothermic and the reaction energies are 3.87 to 4.97 kcal mol−1. In these reaction pathways, the reaction potential barriers in the meta-position are lowest and the reactions in the ortho-position are the highest.
The reaction of BA with SO4− radicals in atmospheric water droplets
In the liquid phase and in droplets of aerosol particles, SO2 will produce HSO3− after dissolution and then the HSO3− can be oxidized by O3, H2O2, NH3 and metal ion catalysts.36 Gaseous SO2 can also be oxidized on the surface of acidic droplets to obtain SO3− and SO4− radicals.37 Besides, SO4− radicals can be produced by heating or catalysis of persulfate. These reactions are important sources of SO4− radicals. We also talk about the abstraction reactions of SO4− radicals with BA in this paper. The reaction potential barriers and reaction energy are marked in Fig. 5, and the reactants and products are also shown.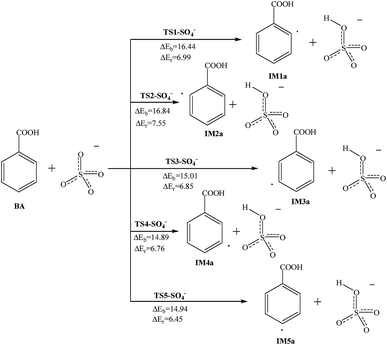 | ||
| Fig. 5 Reaction pathways for the abstraction reaction of BA with SO4− radicals in atmospheric water droplets. | ||
The reaction at the C2 site has a reaction potential barrier of 16.44 kcal mol−1, and the reaction needs to absorb 6.99 kcal mol−1 of energy. The reactions at the remaining carbon sites are all similar and endothermic. The reaction potential barriers are 14.89–16.84 kcal mol−1. Comparing the energy changes of the reaction process, the reaction potential barriers of the para-position and meta-position reactions are lower, and in the ortho-position reactions they are relatively higher.
The reaction of BA with OH radicals in the atmosphere
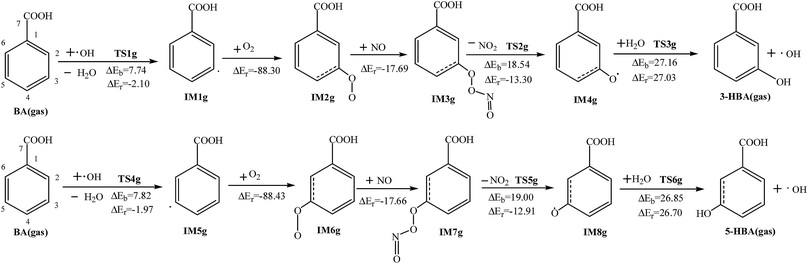
For the possible reaction of BA in the gas phase, the abstraction and addition reactions of BA and the subsequent reactions with oxidants including O2 and NO have been studied in this section. The meta-analysis of only BA, including the extraction of the OH groups at C3 and C5, and the addition of OH at the C5, is used as an example. The reaction process is shown in Fig. 6 and 7. The meanings of the symbols are similar to the previous ones. The unit of energy in the reactions is kcal mol−1.Fig. 6 is about the abstraction reactions and the subsequent reactions of BA and OH radicals in the atmosphere. The two reactions can generate the intermediates IM1g and IM5g with a single electron, and release 2.10 and 1.97 kcal mol−1, respectively. Meanwhile, the reaction potential barriers are slightly smaller than those in the liquid phase (7.34 and 7.82 kcal mol−1). Then, the intermediates can further react with O2 and NO, and this process will release energy. After these reactions, a molecule of NO2 is removed. The reactions need to cross 18.54 and 19.00 kcal mol−1 of energy, and release 13.30 and 12.91 kcal mol−1 of energy, respectively. These products respectively have an oxygen atom with a single electron and thus can combine with water in the atmosphere to generate MHBA and OH radical. This reaction is an endothermic reaction, and the reaction potential barriers are slightly higher (27.16 and 26.85 kcal mol−1, respectively).
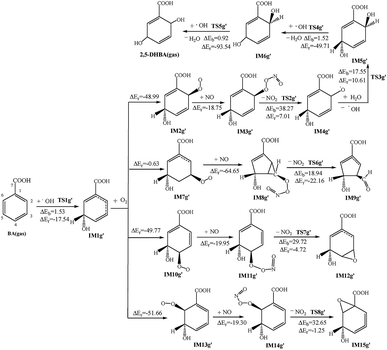
As for the addition reaction of OH radicals with BA in the atmosphere, the reaction potential barrier to get IM1g′ is also lower than that in the liquid phase, only 1.53 kcal mol−1, and this reaction will release 17.54 kcal mol−1 of energy. After the addition reaction in the benzene ring, due to the substituent positioning effect, the density of the electron cloud changes and affects the conjugation effect, which makes the further ortho and para-position addition reactions of the OH group on the benzene ring easier. In addition, the reaction energy of different carbon sites are significantly different. The reaction heat and reaction potential barriers of C2, C3, C4 and C6 sites are given in Fig. 7.
In the corresponding subsequent meta-reactions, the reaction of IM1g′ with O2 is an exothermic reaction with no reaction potential barrier and releases 0.63 kcal mol−1. The addition reaction of NO and IM7g′ results in an intramolecular cyclization reaction, with the C2 and C4 bonds on the benzene ring, then obtains a five-membered ring; this reaction generates more heat than other sites (64.65 kcal mol−1). When a molecule of NO2 is removed, the C–C bond between C2 and C3 is broken, and the O–O bond is also disconnected. In product IM9g′, there is an aldehyde group at the C3 site, and the energy that must be crossed is slightly lower than other reactions (18.94 kcal mol−1), while the energy released is slightly higher, 22.16 kcal mol−1.
In the relative ortho-position reaction of OH radicals, the reaction products IM2g′, IM10g′ and IM13g′ are exothermic (releasing energies of 49.77, 48.99, and 51.66 kcal mol−1, respectively), and then the reactions of the peroxide group with NO and H2O take place. The following reaction processes involve the nitrogen atom in NO attacking the terminal oxygen atom and then removing one molecule of NO2. The NO addition reaction is an exothermic reaction. The energy generated by these three intermediate products is less than those of the O2 addition reaction, which are 18.75, 19.95 and 19.30 kcal mol−1, respectively. The NO2 removal reactions are slightly different. The corresponding ortho-position reactions are exothermic, with reaction potential barriers of 29.72 and 32.65 kcal mol−1, respectively. An epoxy group is formed on the benzene ring of the final reaction products. Meanwhile the reaction of the corresponding para-position reaction is endothermic, and the reaction potential barrier is slightly higher than that of the ortho-reactions, which is 38.27 kcal mol−1. The oxygen with a single electron in the product can react with H2O in the atmosphere and extract the hydrogen in the H2O to give the products IM5g′ and an OH. This reaction is endothermic (10.61 kcal mol−1). After that, it will extract two hydrogen atoms from the C5 and C2 sites on the benzene ring by OH radicals to give the final product DHBA. These two reactions both release a large amount of heat (49.17 and 93.54 kcal mol−1), but the reaction potential barriers are not high (1.52 and 0.92 kcal mol−1, respectively).
The kinetic calculation
The kinetic calculations of the elementary reactions for BA with OH radicals in the atmosphere are carried out by using the CVT/SCT method within a temperature range of 200 to 400 K. In order to calculate the rate constants, 40 points near the transition state along the minimum energy path have been selected, 20 points on the reactant side and 20 points on the product side. For each point, the frequency is calculated to obtain the Cartesian coordinates, gradient and Hessian matrix at the MPWB1K/6-31+G(d,p) level. The reaction rate constants can be obtained at different temperatures and most of the calculated rate constants can fit the Arrhenius formula with a correlation coefficient R2 above 0.99. The reaction rate constants at 298.15 K are depicted for the kinetic study.The kinetic data for the elementary reactions of BA and OH radicals are shown in Table 1. The rate constants for the abstraction reactions of the ortho-position, meta-position and para-position shown in Fig. 1 are 4.44 × 10−15, 1.23 × 10−13, 3.63 × 10−15, 4.80 × 10−14 and 1.77 × 10−13 cm3 per molecule per s, respectively. The rate constants for the addition reactions of the ortho-position, meta-position and para-position shown in Fig. 2 are 1.15 × 10−12, 1.3 × 10−11, 6.65 × 10−13, 3.53 × 10−12 and 4.79 × 10−12 cm3 per molecule per s, respectively. The total rate constant is 2.35 × 10−11 cm3 per molecule per s at 298.15 K, which corresponds well with the value of 4.22 × 10−11 cm3 per molecule per s.34
| Reactions | k298.15 K | Arrhenius formulas | R2 |
|---|---|---|---|
| R + OH → IM1a + H2O | 4.44 × 10−15 | 3.31 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−3330.7/T) exp(−3330.7/T) |
0.9991 |
| R + OH → IM2a + H2O | 1.23 × 10−13 | 1.10 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2697/T) exp(−2697/T) |
0.9970 |
| R + OH → IM3a + H2O | 3.63 × 10−15 | 2.36 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−3298.2/T) exp(−3298.2/T) |
0.9992 |
| R + OH → IM4a + H2O | 4.8 × 10−14 | 1.71 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−3114.2/T) exp(−3114.2/T) |
0.9993 |
| R + OH → IM5a + H2O | 1.77 × 10−13 | 9.54 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−3233.7/T) exp(−3233.7/T) |
0.9993 |
| R + OH → IM1b | 1.15 × 10−12 | 3.24 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1672/T) exp(−1672/T) |
0.9996 |
| R + OH → IM2b | 1.3 × 10−11 | 2.89 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−914.34/T) exp(−914.34/T) |
0.9995 |
| R + OH → IM3b | 6.65 × 10−13 | 2.73 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1783.3/T) exp(−1783.3/T) |
0.9998 |
| R + OH → IM4b | 3.53 × 10−12 | 1.74 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1837.6/T) exp(−1837.6/T) |
0.9996 |
| R + OH → IM5b | 4.79 × 10−12 | 2.45 × 10−9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1849.1/T) exp(−1849.1/T) |
0.9996 |
| Total | 2.35 × 10−11 |
The atmospheric lifetimes of the reactants can be calculated and analyzed according to the rate constants of the elementary reactions. For the average OH radical concentration of 9.7 × 105 molecule cm3, the atmospheric lifetimes (τ) can be calculated by τ = 1/(kOH[OH]), from which the lifetime of BA in the atmosphere is determined to be 0.51 days.38
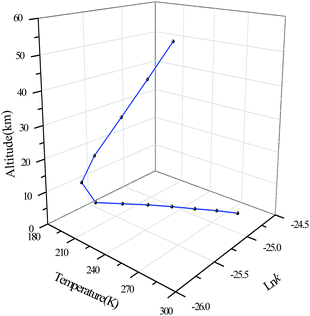
The relationship between reaction rate constants, temperature and altitude
Due to the vertical structure of the atmosphere, the relationship between the altitude, temperature and the reaction rate constant is shown in Fig. 8. The rate constants in the Figure are the total reaction rate constants of BA with OH radicals, and they are calculated in the form of natural logarithms and the unit of the reaction rate constants is cm3 per molecule per s.In the troposphere, the temperature decreases as the altitude increases, as well as the reaction rate constant. At the bottom of the stratosphere, the temperature varies little with the altitude, and the rate constant also increases slowly. At the upper side of the stratosphere, the temperature increases with altitude, as does the rate constant.
Conclusions
The reaction of BA initiated by OH, NO3 and SO4− radicals in atmospheric water droplets, the abstraction and addition reaction of BA with OH radicals and the subsequent reactions with oxidants including O2 and NO are investigated in this paper. The rate constants of elementary reactions of BA with OH radicals are calculated using the CVT/SCT method. Some valuable conclusions can be drawn as follows:(1) Among the products of MHBA and DHBA, 6-HBA and 4,6-DHBA have the lowest energy. By comparing reaction potential barriers and reaction heat, it was found that the reaction of OH radicals with BA is easier than that of NO3 and SO4− radicals. In the gas phase, the intermediate which initiates the reaction can be further reacted with O2/NO, and hydroxybenzoic acid can be obtained.
(2) The total reaction rate constant of OH radicals and BA is 2.35 × 10−11 cm3 per molecule per s, and the elementary reaction rate constants of the hydrogen atom abstraction reactions are smaller than those of addition reactions. The lifetime of BA in the atmosphere is determined to be 0.51 days.
(3) The reaction rate constants increase with the increasing temperature. At the bottom of the troposphere and the top of the stratosphere, the temperature is relatively higher, and the reaction constants of the BA with OH radicals are also higher.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (21607011, 21337001, 21577021, 21377028) and the Fundamental Research Funds of Shandong University (2015JC020), Ministry of Science and Technology of China (2016YFE0112200).Notes and references
- M. C. Wildermuth, Curr. Opin. Plant Biol., 2006, 9, 288–296 CrossRef CAS PubMed
.
- W. F. Rogge, L. M. Hildemann, M. A. Mazurek, G. R. Cass and B. R. Simoneit, Environ. Sci. Technol., 1993, 27, 636–651 CrossRef CAS
.
- W. F. Rogge, L. M. Hildemann, M. A. Mazurek, G. R. Cass and B. R. Simoneit, Environ. Sci. Technol., 1997, 31, 2726–2730 CrossRef CAS
.
- W. F. Rogge, L. M. Hildemann, M. A. Mazurek, G. R. Cass and B. R. Simoneit, Environ. Sci. Technol., 1997, 31, 2731–2737 CrossRef CAS
.
- Y. Iinuma and H. Herrmann, J. Chromatogr. A, 2003, 1018, 105–115 CrossRef CAS PubMed
.
- J. R. Payne and C. R. Phillips, Environ. Sci. Technol., 1985, 19, 569–579 CrossRef CAS PubMed
.
- N. Zhao, Q. Zhang and W. Wang, Sci. Total Environ., 2016, 563–564, 1008–1015 CrossRef CAS PubMed
.
- S. K. R. Boreddy, T. Mochizuki, K. Kawamura, S. Bikkina and M. M. Sarin, Atmos. Environ., 2017, 167, 170–180 CrossRef CAS
.
- A. B. Nadykto and F. Q. Yu, Chem. Phys. Lett., 2007, 435(1–3), 14–18 CrossRef CAS
.
- W. Xu and R. Y. Zhang, J. Phys. Chem. A, 2012, 116(18), 4539–4550 CrossRef CAS PubMed
.
- Y. S. Xu, A. B. Nadykto, F. Q. Yu, J. Herb and W. Wang, J. Phys. Chem. A, 2010, 114, 387–396 CrossRef CAS PubMed
.
- R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Science, 2004, 304, 1487–1490 CrossRef CAS PubMed
.
- K. Breese, M. Boll, J. Alt-Mörbe, H. Schägger and G. Fuchs, Eur. J. Biochem., 1998, 256, 148–154 CrossRef CAS PubMed
.
- V. J. Denef, J. A. Klappenbach, M. A. Patrauchan, C. Florizone, J. L. Rodrigues, T. V. Tsoi, W. Verstraete, L. D. Eltis and J. M. Tiedje, Appl. Environ. Microbiol., 2006, 72, 585 CrossRef CAS PubMed
.
- R. Atkinson, Atmos. Environ., 2007, 41, 200–240 CrossRef
.
- C. Zhang and X. Sun, Sci. Total Environ., 2014, 468–469, 104–110 CrossRef CAS PubMed
.
- A. Hofzumahaus, F. Rohrer, K. Lu, B. Bohn, T. Brauers, C.-C. Chang, H. Fuchs, F. Holland, K. Kita and Y. Kondo, Science, 2009, 324, 1702–1704 CrossRef CAS PubMed
.
- R. Gutbrod, R. N. Schindler, E. Kraka and D. Cremer, Chem. Phys. Lett., 1996, 252, 221–229 CrossRef CAS
.
- X. Zhao, W. Liu, J. Fu, Z. Cai, S. O’Reilly and D. Zhao, Mar. Pollut. Bull., 2016, 109, 526–538 CrossRef CAS PubMed
.
- M. A. Oturan and J. Pinson, J. Phys. Chem., 1995, 99, 13948–13954 CrossRef CAS
.
- Y. Deng, K. Zhang, H. Chen, T. Wu, M. Krzyaniak, A. Wellons, D. Bolla, K. Douglas and Y. Zuo, Atmos. Environ., 2006, 40, 3665–3676 CrossRef CAS
.
- L. Kang, C. Zhang and X. Sun, RSC Adv., 2015, 5, 96518–96524 RSC
.
- D. Vione, C. Minero, V. Maurino, M. E. Carlotti, T. Picatonotto and E. Pelizzetti, Appl. Catal., B, 2005, 58, 79–88 CrossRef CAS
.
- R. Andreozzi and R. Marotta, Water Res., 2004, 38, 1225–1236 CrossRef CAS PubMed
.
- N. Zrinyi and A. L. Pham, Water Res., 2017, 120, 43–51 CrossRef CAS PubMed
.
- H. Zemel and R. W. Fessenden, J. Phys. Chem., 1978, 82, 2670–2676 CrossRef CAS
.
- A. M. Winer, R. Atkinson and J. N. Pitts, Science, 1984, 224, 156–159 CrossRef CAS PubMed
.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision A, Gaussian. Inc., Wallingford CT, 2009 Search PubMed
.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918 CrossRef CAS
.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS
.
- V. Krishnakumar and R. Mathammal, J. Raman Spectrosc., 2009, 40, 264–271 CrossRef CAS
.
- J. C. Corchado, Y. Y. Chuang, P. L. Fast, J. Villa, W. P. Hu, Y. P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels,V. S. Melissas, B. J. Lynch, I. Rossi, E. L. Coitino, A. F. Ramos, J. Pu, T. V. Albu, R. B. C. Garrett and D. G. Truhlar, POLYRATE Version 9.7, University of Minnesota, Minneapolis, 2007 Search PubMed
.
- K. J. Laidler, J. Chem. Educ., 1984, 61, 494 CrossRef CAS
.
- C. Wu, A. D. Visscher and I. D. Gates, RSC Adv., 2017, 7, 35776–35785 RSC
.
- D. E. Heard and M. J. Pilling, Chem. Rev., 2003, 103, 5163–5198 CrossRef CAS PubMed
.
- W. L. Chameides and D. D. Davis, J. Geophys. Res.: Oceans, 1982, 87, 4863–4877 CrossRef CAS
.
- H. M. Hung and M. R. Hoffmann, Environ. Sci. Technol., 2015, 49, 13768–13776 CrossRef CAS PubMed
.
- R. G. Prinn, R. F. Weiss, B. R. Miller, J. Huang, F. N. Alyea, D. M. Cunnold, P. J. Fraser, D. E. Hartley and P. G. Simmonds, Science, 1995, 269, 187–192 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Mechanism and kinetic study on the reaction of benzoic acid with OH, NO3 and SO4− radicals in the atmosphere. See DOI: 10.1039/c9ra02457c |
| This journal is © The Royal Society of Chemistry 2019 |