Comprehensive study on the degradation of ochratoxin A in water by spectroscopic techniques and DFT calculations

Abstract

Ochratoxin A (OTA) is one of the most important dietary risk factors and is classified as a possible carcinogen to humans. Assessing the conditions to remove it from foodstuffs in a simple and effective way is of the utmost importance. OTA behaviour in water in the pH range 1.0–12.5 was elucidated to investigate the conditions for irreversible toxicity inactivation of OTA. The results indicate that four forms, from neutral to trianionic, intervene depending on the pH. pK_a1,2 were rigorously established by independent spectroscopic techniques to overcome the scarcity of literature. Then, Density Functional Theory (DFT) calculations were used to determine the most probable degradation mechanism and this was confirmed by fluorescence spectroscopy. At pH 12.5, hydrolyzation of the lactone ring starts in less than one hour, but only after two hours does the degradation process lead to fragmentation. After one week this process is not yet completed. The reaction products occurring upon re-acidification were also investigated. OTA degradation is still reversible if acidic conditions are promptly restored, yielding again a hazardous molecule. However, degradation becomes irreversible after fragmentation. This finding suggests proceeding with due caution if a base is exploited to remove the toxin.

---

1. Introduction

Ochratoxin A (OTA) is a potent mycotoxin that severely affects animal and human health. It is produced by the secondary metabolisms of Aspergillus and Penicillium species contaminating a large variety of alimentary commodities.^1–5 Since it is considered one of the most important chronic dietary risk factors, the International Agency for Research on Cancer has classified OTA as a possible carcinogen to humans.⁶ The European Food Safety Authority set a tolerable weekly intake of 120 ng kg⁻¹ body weight^7–10 and maximum levels of OTA in foodstuffs were established by the Commission Regulation (EC) no. 1881/2006.¹¹ Immunochemical methods,^12–15 liquid chromatography coupled to fluorescence spectroscopy^14,16–20 and mass spectrometry^15,20,21 are commonly used for OTA determination. OTA, i.e. N-[[(3R)-5-chloro-8-hydroxy-3-methyl-1-oxo-7-isochromanyl]carbonyl]-3-phenyl-L-alanine,²² consists of a dihydroisocumaric ring amide-linked to L-phenylalanine.²³

In this work comprehensive description of OTA behaviour in aqueous solutions in the pH range 1.0–12.5 was carried out to provide useful information for further toxicological studies of one of the most dangerous and diffused natural foodstuff toxins.

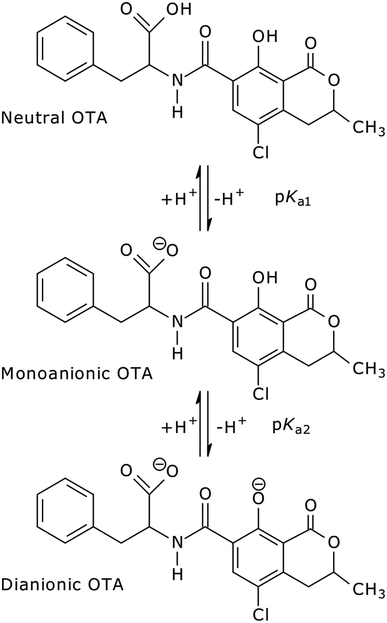
In aqueous solution, OTA shows three levels of proton dissociation in the pH range 1.0–8.0 (Fig. 1) ruled by the characteristic acid dissociation constants (pK_a1,2). The neutral form is present under acidic conditions, increasing the pH the phenylalanine carboxylic group loses a proton (monoanionic form), and the phenolic group loses a second proton at neutral pH (dianionic form).

Fig. 1 OTA structures in aqueous solution in acidic to neutral pH range.

Table 1 shows the pK_a1,2 of OTA reported in articles where the authors determined them experimentally. The literature on this topic is scarce and generally old. The variability of the reported values is not negligible and the experimental description is often careless.

Table 1 pK_a values of OTA from literature

Reference	Value
a In 0.1 mol L^−1 phosphate buffer.b In 0.16 mol L^−1 KCl.c In 0.16 mol L^−1 KCl; at 25 °C.
pKa1
Uchiyama et al. (1985)^24	4.4
pKa2
Gillman et al. (1999)^25	7.0
Xiao et al. (1996)^26	7.0 ± 0.02^a
Marquardt (1992)^27	7.05–7.1
Uchiyama et al. (1985)^24	7.3
Chu et al. (1972)^28	7.05–7.10^b
Chu et al. (1971)^29	7.04^c
Pitout (1968)^30	7.1

---

The scope of this work is to investigate the protonation equilibria of OTA and the conditions of irreversible toxicity deletion of the toxin due to pH and time effects only.

The pK_a1,2 were estimated by UV-Vis absorption spectrophotometry and fluorescence spectroscopy with stoichiometric and chemometric approach, respectively. In this study, the collection and the analysis of data were carefully detailed, compared to older works. Thanks to the high molar absorptivity and the high intensity of the fluorescence emission of OTA, these techniques allow working at low concentration levels, which is desirable because of its high toxicity. Moreover, the reaction products under alkaline conditions were identified and the transformation products occurring when the solution is brought back to acidic conditions were studied. Under alkaline conditions, OTA displays degradation processes whose reaction products were revealed at pH above 12, such as OTA with hydrolyzed lactone ring and ochratoxin alpha (OTα) with hydrolyzed ring, obtained by hydrolysis of the amide bond of OTA. The product of lactone ring opening and OTα are less toxic than OTA.²⁹ The reaction reversibility upon reacidification was ascertained by fluorescence spectroscopy.

The experimental findings were flanked by a Density Functional Theory (DFT) calculations, which were carried out for the first time to reveal the most probable reaction products of the degradation mechanism of OTA. The scope of this work was to provide detailed information about the protonation equilibria of OTA and to determine the conditions of irreversible toxicity deletion of the toxin due to pH and time effects. The analysis of UV-Vis and fluorescence spectra and the determination of pK_a values were meant to augment and improve the related literature. Moreover, DFT was needed to identify the thermodynamically stable reaction products responsible of the experimental bands obtained in the fluorescence maps. Novel results required for further OTA investigations were provided by theoretical degradation path calculation. The conditions upon which the different forms of OTA are stably present in aqueous solution would allow to obtain aqueous solutions containing mainly one specific form of OTA. This paves the way towards specific toxicological studies of OTA in different protonation and hydrolyzation conditions.

The full identification of the reaction products of OTA throughout a wide pH range was needed to elucidate the chemical behaviour, which influences the toxicological profile of each OTA form and has strong biological implications.^27,29–32 A comprehensive description of OTA behaviour in aqueous solutions in the pH range 1.0–12.5 was carried out to provide useful information for further toxicological studies of one of the most dangerous and diffused natural foodstuff toxins.

2. Experimental section

2.1 Chemicals

A reference material composed of a solution of OTA (1 g L⁻¹ in dimethyl sulfoxide, Sigma-Aldrich) was used to prepare the solutions for the spectrophotometric measurements. Diluted stock solutions at 0.001 g L⁻¹ were used for the fluorescence spectroscopy. All OTA solutions were prepared in ultra-pure water (Milli-Q quality).

The ionic strength was fixed at 0.4 mol L⁻¹ with phosphate buffer, for OTA solutions under neutral conditions, and at 0.1 mol L⁻¹ with KCl for OTA solutions under acidic and alkaline conditions. Aliquots of HCl (0.1 mol L⁻¹) and NaOH (0.01 mol L⁻¹ or 0.5 mol L⁻¹, concentration standardised against potassium hydrogen phthalate) were used to adjust the pH.

The UV-vis spectrophotometric measurements were conducted on OTA solutions 2 × 10⁻⁵ mol L⁻¹. For fluorescence spectroscopy, the concentration of OTA was 1.24 × 10⁻⁷ mol L⁻¹. Under neutral conditions, a phosphate buffer composed of NaH₂PO₄ (0.1 mol L⁻¹)/Na₂HPO₄ (0.1 mol L⁻¹), was added to OTA solutions for their stabilization. HCl 37% was added to study the reversibility of OTA degradation from alkaline to acidic conditions. A standard OTα solution (10.2 ± 0.1 mg L⁻¹ in acetonitrile, LGC Standards) was used for fluorescence spectroscopy analysis.

Reagents were at high purity level. NaClO (5% active chlorine) was used to clean the glassware. OTA solutions were stored at 4 °C in the dark.

2.2 Methods

2.2.1 Spectrophotometric measurements and stoichiometric analysis. The absorption spectra of OTA solutions were acquired in the range 250–450 nm with a Jasco V-550 UV-Vis double-beam spectrophotometer, provided with Hellma quartz cuvettes for flow-through measurement (10.00 mm optical path length). The pH of the solutions was evaluated by a Metrohm potentiometer (model 713, resolution of 0.001 pH units) equipped with a Metrohm combined glass electrode (mod. 6.0259.100). The combined electrode was daily calibrated in terms of H⁺ concentration. The slope and the formal potential E⁰ of the Nernst equation were elaborated by the ESAB2M program.³³ The experiments were conducted in oxygen-free atmosphere by flowing nitrogen in the solution, in continuous stirring, at 25 °C (thermocryostat mod. D1-G Haake). Initially, the OTA solution (20 mL) was adjusted to pH 3 with HCl. Subsequent aliquots of NaOH solution (10 μL) were added by a Metrohm 765 Dosimat burette (resolution 1 μL) until the OTA solution reached a pH value of about 7.5. Each addition corresponded to an increase of 0.1/0.2 pH units.

A total of 45 UV-Vis spectra were elaborated with HypSpec® software³⁴ that operates with stoichiometric principles by applying mass and charge balance equations and Lambert–Beer's law.

2.2.2 Fluorescence spectroscopy and chemometric analysis. Excitation–emission maps (EEMs) of OTA solutions at different pH were collected. A Horiba Scientific Fluorolog-3 spectrofluorometer (model FL3-21) provided with a Hellma quartz cuvette (10.00 mm optical pathlength) was used. OTA solutions were measured in right angle geometry.³⁵ The excitation and emission range of 310–395 nm and 400–475 nm, respectively (wavelength resolution 1 nm). 2 nm slits and integration time of 1 s were used for the EEMs related both to the determination of pK_a values and for the degradation steps investigation. For the determination of the pK_a1 EEMs were elaborate by Parallel Factor Analysis (PARAFAC)^36–39 using PLS Toolbox from Eigenvector Research, Inc. for Matlab R2015a (Mathworks). The size of the EEMs array was 12 × 86 × 76, where 12 are the samples, 86 the number of emission wavelengths and 76 the number of excitation wavelengths in the scanned ranges. Multiway center was applied as data preprocessing and non negativity and unimodality constraints were use. The scores of the two involved components (neutral and monoanionic) were plotted as a function of pH and fitted with a linear and a 2nd order polynomial function. Then, the intersection of the two curves was calculated. The fits' uncertainty was calculated and propagated by Monte Carlo method.⁴⁰ For the determination of pK_a2, PARAFAC modeling was not adopted since the excitation bands were sufficiently distincted in the EEM. The bands' intensity of the two species (monoanionic and dianionic) was evaluated at fixed λ_Em 446 nm. The intensity ratio I₃₃₂ over I₃₇₂ was used to estimate the pK_a2. The experimental ratio points plotted against the pH were fitted using an exponential decay function and the uncertainty related to the fit was evaluated. pK_a2 corresponds to I₃₃₂/I₃₇₂ = 1, with its associated uncertainty deriving from the fit.

To elucidate the degradation process, the EEMs with the bands related to the significant reaction products were identified. Moreover, the EEM of the final reaction products in the degradation process was compared with the EEM obtained by the analysis of the standard OTα solution as a confirmation.

2.3 Theoretical method

All stationary points on the energy hypersurface were determined by gradient procedures^41–45 within DFT.⁴⁶ The ωB97XD functional was chosen.⁴⁷ Pople's 6–311++G(d,p) basis set^48,49 was used in the DFT optimizations and in the vibrational analysis (both including solvent effects), by which the nature of the critical points was checked. The reacting molecules were considered as a solute in a polarized continuum (water), within the Solvation Model based on Density (SMD)^50,51 and Integral Equation Formalism-Polarizable Continuum Model (IEF-PCM) schemes.⁵² One explicit water molecule was considered only for the steps TI1–4 and TI2–5 (TI = tetrahedral intermediate), because literature data^53–55 show that water helps the bond cleavage by cooperating in a hydrogen transfer. These two barriers, without the cooperative effect of explicit water, are significantly overestimated.

Throughout the paper, the relative Gibbs free energies in solution (ΔG) are reported, estimated at T = 298 K, and expressed in kcal mol⁻¹.

Excitation energies were calculated by single point time dependent-DFT calculations,^56–59 using the O3LYP functional⁶⁰ and the same basis set of the optimizations. Other functionals were also tested and O3LYP was found to better reproduce the experimental spectrum of the OTA. It was also satisfactorily used in some recent works.^61,62 The first 6 excited states were calculated for each structure. Simulated UV absorption spectra were obtained by using Gaussian convolution with half width value σ = 0.4, as described in http://gaussian.com/uvvisplot/.

Geometry optimizations and thermochemistry calculations were carried out by using the Gaussian 09 system of programs.⁶³ The MOLDEN program⁶⁴ was exploited to display the optimized transition structures reported in the ESI (Fig. S7 and S8†)

3. Results and discussion

3.1 Proton dissociation

The UV-Vis spectra recorded as a function of pH are reported in Fig. 2.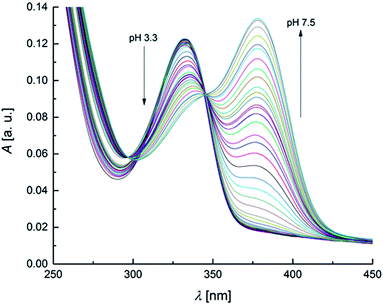

Fig. 2 UV-Vis spectra of OTA solution (2 × 10⁻⁵ mol L⁻¹) within the pH range 3.3–7.5 (increment of 0.1–0.2 pH units for each spectrum).

The spectra show defined isosbestic points at 346 and 297 nm, suggesting the presence of two OTA forms, without intermediates in between. The absorption band at about 332 nm could be attributed to both neutral and monoanionic forms (1 in Scheme 1) because they absorb at the same wavelength. The absorption band at 378 nm was associated to the dianionic form (3 in Scheme 1). These results are in accordance with the absorption spectra reported in literature.^32,65 The values of the molar absorptivity (ε) for the three OTA forms, pK_a1 and pK_a2 were deduced by the HypSpec® software. Fig. S1 in the ESI† shows the variation of ε as a function of λ for each OTA form.

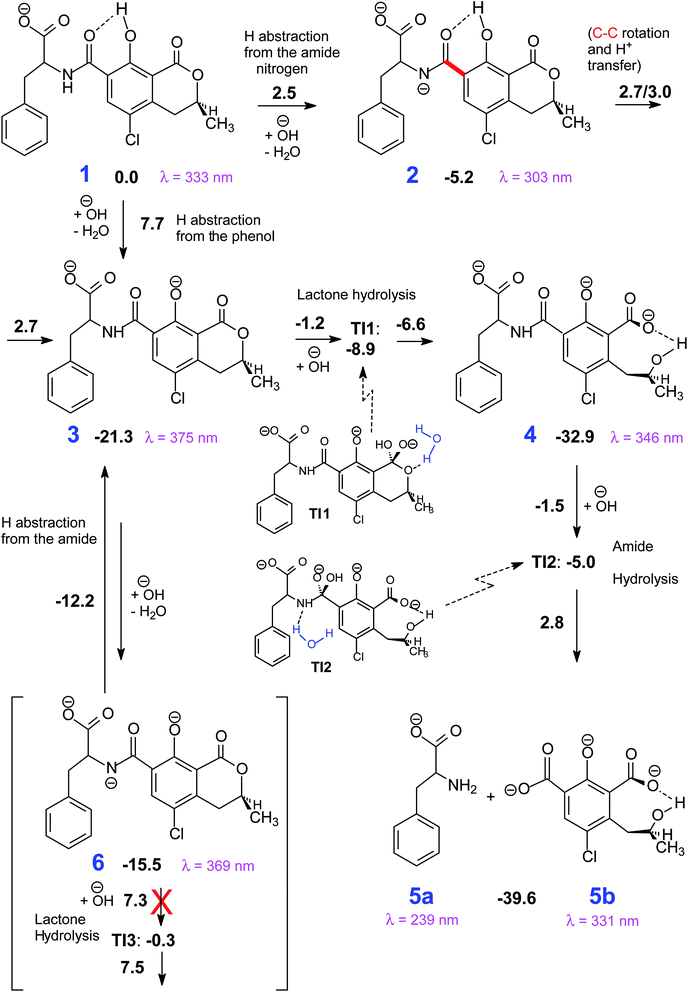Scheme 1 The most viable reaction pathways that connect 1 to the degradation products (5). Gibbs free energy differences with respect to 1 in kcal mol⁻¹.

In Table 2, the experimental and calculated values of maximum absorptivity, ε_max, and maximum absorption wavelength, λ_max, obtained by the theoretical method and spectrophotometric measurements are compared with literature data (the simulated UV spectra are reported in Fig. S2†). A good agreement between experimental, calculated and literature values was found. No data concerning the ε_max of the monoanionic form of OTA were found in literature.

Table 2 λ_max and ε_max (experimental and calculated) values for the different OTA forms

Source	Neutral form		Monoanionic form		Dianionic form
	λmax [nm]	εmax [cm^−1 mol^−1 L]	λmax [nm]	εmax [cm^−1 mol^−1 L]	λmax [nm]	εmax [cm^−1 mol^−1 L]
This study, exp./calc	332/329	5990/8258	332/333	6544/6920	378/375	9682/10 378
Il'ichev et al. (2001)^32	332	6650	332	—	380	10 970
Verrone et al. (2007)^65	330	6600	330	—	379	9115

---

Even though the absorption bands related to the neutral and monoanionic forms are strongly overlaid, the elaboration of UV-Vis data with HypSpec® not only allows to define a value for pK_a2 but also an estimate of pK_a1. The details of the calculation procedure are reported in the ESI file.† The values of the protonation constants, and the corresponding standard deviations, were evaluated: pK_a1 = 4.4 ± 0.1 and pK_a2 = 7.09 ± 0.01. These results are in quite good agreement with the literature data.^24–30

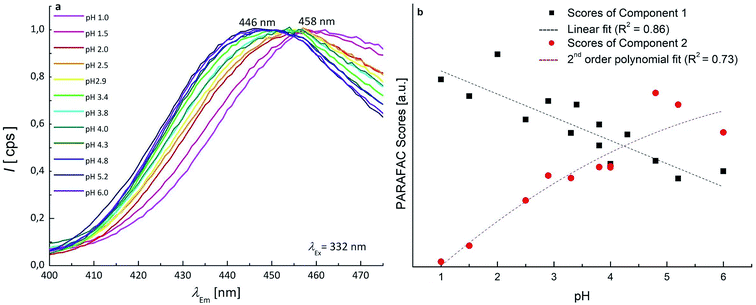
Concerning the fluorescence spectroscopy measurements, a set of 12 EEMs of OTA solutions under acidic and neutral conditions was acquired in the pH range 1.0–6.0, where two known fluorophores (neutral and monoanionic OTA) are present in different ratios. The total fluorescence spectra obtained between pH 1.0–4.8 show a single band at excitation/emission wavelengths (λ_Ex/Em) of 332/458 nm (Fig. 3a), which gradually shifts to λ_Ex/Em = 328/446 nm increasing the pH (Fig. 3b). This shift is due to the transition from the neutral form of OTA to the monoanionic form (1). The dianionic form (3) is still absent in this pH range.

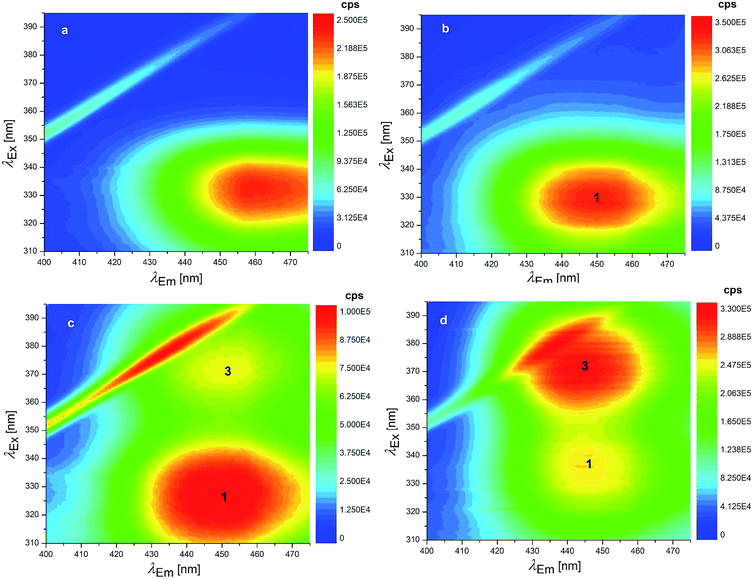Fig. 3 EEMs of 1.24 × 10⁻⁷ mol L⁻¹ OTA solutions: (a) pH 1.0 (HCl solution), (b) 4.8 (HCl solution), (c) 6.6 (phosphate buffer) and (d) 7.1 (phosphate buffer). The numbers superimposed on the bands of these EEMs make reference to the molecular structures reported in Scheme 1.

Since the neutral form and 1 exhibit two overlapping bands, PARAFAC was used to mathematically separate the contributions and obtain a concentration profile of the two forms along the pH scale. The two components PARAFAC model explains 61.1% of variance and shows 100% of core consistency. The PARAFAC emission and excitation loadings can be considered as the best approximations of the fluorescence spectra of pure analytes. The obtained emission profiles of neutral form and 1 were in agreement with raw emission spectra obtained at fixed λ_Ex of 332 nm, that show emission maxima at 458 nm and 446 nm (Fig. 4a). Fig. S3† shows the loadings profile corresponding to the emission mode. The intensity maxima of the modeled emission spectra (i.e. the loadings) are positioned at λ_Em of 459 nm and 436 nm. The first component is associated to neutral OTA, present at pH < 4, whereas the second component is associated to 1, that appears at pH ≃ 3 and becomes predominant at pH > 4. The modeled excitation profiles of the two forms are superimposed with λ_Ex = 332 nm, in agreement with the absorption spectra of Fig. S1.† However, the slight differences in the λ_Em were sufficient to estimate them separately. The scores of the model represent the amount of each form at each pH value (Fig. 4b). The point where the concentration curve of 1 intersects that of the neutral form corresponds to the pK_a1. The pK_a1 value obtained with this model was estimated 4.2 with a fit uncertainty of 0.9.

Fig. 4 (a) Experimental emission spectra of OTA 1.24 × 10⁻⁷ mol L⁻¹ in the pH range 1.0–6.0 (normalised intensity scale); (b) scatter scores plot as a function of pH, the scores of the two components of PARAFAC model are shown.

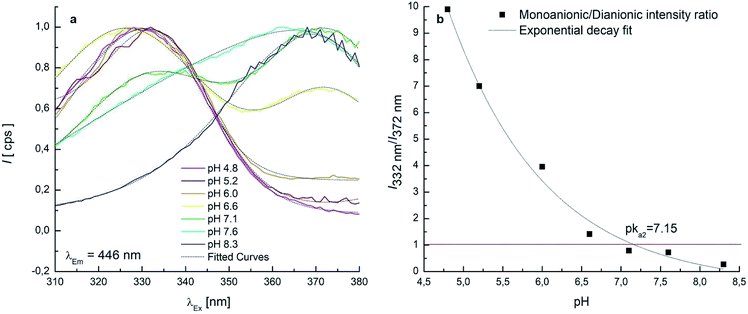
7 EEMs between pH 4.8–8.3 were acquired to investigate the pK_a2 range where monoanionic form (1) and dianionic form (3) intervene. As long as the pH increases, a decrease of 1 is evidenced in Fig. 3c and d and a new peak rises at λ_Ex/Em = 372/443 nm, due to 3. 1 and 3 showed two separated maxima in correspondence of λ_Em = 446 nm. The normalised and fitted excitation spectra are reported in Fig. 5a. The excitation spectrum at λ_Em = 446 nm was isolated to evaluate the excitation maxima of the two forms of OTA at λ_Ex = 332 nm (1) and λ_Ex = 372 nm (3) (Fig. 5a). The intensity I₃₃₂ to I₃₇₂ ratio between 1 and 3 was used to estimate the value of pK_a2, which is the pH value corresponding to the inversion of the intensity ratio (Fig. 5b). The pK_a2 = 7.15 was estimated. However, this value was obtained at an ionic strength 0.4 mol L⁻¹. In order to make this pK_a2 value comparable with the value obtained by UV-Vis spectrophotometry and with literature data, it was adjusted considering the ionic strength 0.1 mol L⁻¹. Upon application of an extended Debye–Hückel equation,⁶⁶ the pK_a2 was evaluated 7.0 with a fit uncertainty of 0.4.

Fig. 5 (a) Excitation spectra collected at fixed λ_Em = 446 nm in the pH range 4.8–8.3 (normalised intensity scale and Gaussian fitted curves); (b) monoanionic/dianionic intensity I₃₃₂ to I₃₇₂ ratio as a function of the solution pH.

It can be noticed that the maximum attributed to 1 undergoes a shift toward higher λ_Ex going from pH 6.6 (Fig. 3c) to pH 7.1 (Fig. 3d). This effect can be ascribed to the swelling of the band attributed to 3, while a significant overlap of the two bands is present. Deconvolution of the profile along λ_Ex clearly shows the origin of the maximum shift (Fig. S4†).

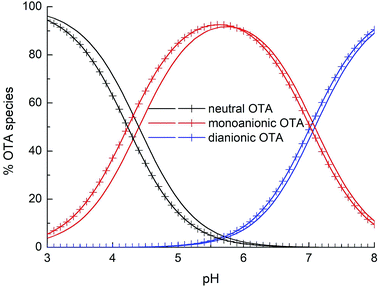
Fig. 6 shows the distribution diagram of the differently protonated forms of OTA, as a function of pH, starting by the pK_a1,2 values obtained by both spectrophotometric and fluorescence data. The spectrophotometric and fluorescence pK_a1 (namely 4.4 and 4.2) and pK_a2 (namely 7.09 and 7.0) represent consistent results.

Fig. 6 Percentage distribution of the OTA forms as a function of pH for a solution 2 × 10⁻⁵ mol L⁻¹. Solid lines: species distribution obtained from UV-Vis spectra elaboration; lines with crosses: species distribution obtained from fluorescence data elaboration.

The mechanism proposed theoretically is sketched in Scheme 1. The related Gibbs free energy profiles are shown in Fig. 7. The reaction pathway, starting from the monoanionic form of OTA (1), branches right from the beginning upon HO attack onto 1. If HO⁻ abstracts a proton from N–H (ΔG^‡ = 2.5 kcal mol⁻¹) the resonant amide anion 2 is generated. On the other hand, upon hydrogen abstraction from the phenolic O–H (ΔG^‡ = 7.7 kcal mol⁻¹) the phenate 3 forms. Whilst the 1–2 step is kinetically favoured over 1–3, 2 is thermodynamically less stable than 3, and the backwards step 2–1 requires overcoming a barrier of 7.7 kcal mol⁻¹. Alternatively, the anion 2 can undergo a clockwise or anti-clockwise rotation around the C–C bond highlighted in red in Scheme 1. This movement defines two rotation transition structures and opens the way to two non-equivalent hydrogen migrations from the phenolic O to the partially anionic N. Two series of constrained optimizations were carried out, in correspondence of frozen values of the dihedral angle that expresses the said rotation in opposite directions. In the highly asynchronous concerted 2–3 processes, C–C rotation entails barriers with ΔG^‡ = 7.9 or 8.2 kcal mol⁻¹ height. Following either all-downhill pathway from each rotation transition structure shows that the subsequent H transfer takes place in both cases without any barrier. The result is in both cases the phenate (dianionic form of OTA) 3, which is consequently formed from 1 in two ways: directly (1–3), as expected, and also indirectly (1–2–3). The latter process is preferred because the second step is unimolecular. The excitation energy of 2 (computed peak at 303 nm) may not be observed experimentally because 1 transforms to 3 rather easily. The calculated excitation energy of 3 (375 nm) is consistent with the 372 nm maximum in the spectrum displayed in Fig. 3c and d.

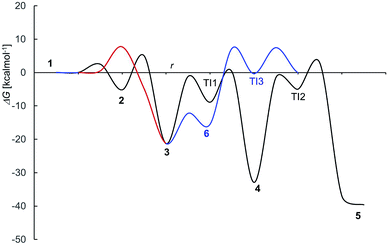Fig. 7 Free energy profile for OTA alkaline deprotonation and degradation (compare Scheme 1); r stays for a generic “reaction coordinate”.

3.2 Degradation processes

Several degradation pathways are conceivable from 3 (Scheme S1†). The two most probable are reported in Scheme 1. In both of them an acyl group is hydrolyzed. The 3–4 lactone hydrolysis is a two-step reaction, which passes through the tetrahedral intermediate TI1 (12.4 kcal mol⁻¹ higher in energy than 3). The slowest step is 3–TI1 (ΔG^‡ = 20.1 kcal mol⁻¹), in good agreement with the barrier of 19.2 kcal mol⁻¹ estimated by Gómez-Bombarelli et al.⁵³ for the valerolactone (however their calculations including six explicit water molecules). Then, a fast ring opening leads to the trianion 4. The inclusion of one explicit molecule of water was necessary to obtain a more reliable estimate of its barrier (ΔG^‡ = 2.3 kcal mol⁻¹). Otherwise, the barrier would have been 9.1 kcal mol⁻¹ high. Water promotes hydrogen migration by taking one H and leaving another. Despite only one water molecule was added, the barrier is closer to that calculated by Gómez-Bombarelli et al. who found ΔG^‡ = 3.9 kcal mol⁻¹. The overall energy barrier 3–4 is rather high, and consequently the reaction is supposed to be quite slow: this is the likely reason why the experimental signal at 346 nm (Fig. 8b) appears only after several days at pH 11.5, or after about one hour at pH 12.5 (the computed absorption is at 346 nm as well). Subsequently, 4 can undergo an alkaline hydrolysis of the amide group. It is again a two-step reaction through a tetrahedral intermediate TI2. The first step presents an energy barrier of 31.4 kcal mol⁻¹.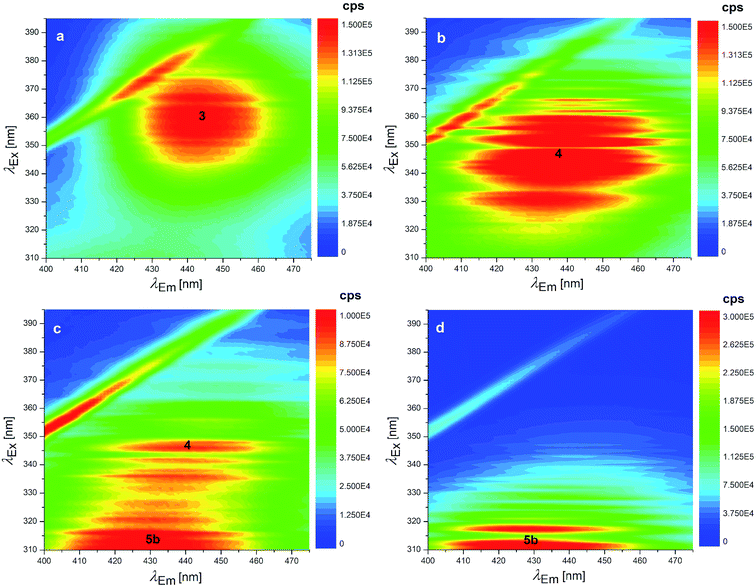

Fig. 8 EEMs of 1.24 × 10⁻⁷ mol L⁻¹ OTA solutions at pH: (a) 11.6 (fresh solution), (b) 12.5 (fresh solution), (c) 12.5 (as in b after 7 days stored at 4 °C in the dark) and EEM of 1.24 × 10⁻⁷ mol L⁻¹ OTα solution at pH: (d) 12.5. The numbers superimposed on the bands of these EEMs make reference to the molecular structures reported in Scheme 1.

In order to assess the importance of introducing explicit water molecules, two tests the first hydrolysis step of N-methylacetamide were carried out. For this molecule experimental data are available.⁵⁵ For the test, the ωB97XD/6-31+G(d) method was used, first without explicit water molecules and then including 8 explicit H₂O molecules. In both cases the surrounding solvent was introduced as a polarizable continuum. Without explicit water, the free energy barrier for the OH addition, the first step of the hydrolysis, is ΔG^‡ = 25.4 kcal mol⁻¹ (ΔH^‡ = 13.9 kcal mol⁻¹), with 8 water molecules drops to ΔG^‡ = 19.2 kcal mol⁻¹ (ΔH^‡ = 16.7 kcal mol⁻¹). The experimental value is ΔG^‡ = 22.9 kcal mol⁻¹ (ΔH^‡ = 17.1 kcal mol⁻¹).⁵⁵ The addition of explicit solvent molecules clearly has lowered the barrier, but still with unsatisfactory agreement when free energy differences are considered. In any case, inclusion of a large number of explicit solvent molecules would be unfeasible on the OTA molecule. The initial and transition structures are displayed in Fig. S8 of the ESI.†

The barrier for the cleavage of TI2, is overestimated if no explicit water molecules are introduced (see Tang et al.;⁵⁴ Galabov et al.⁵⁵). One H₂O molecule added in the calculation lowered the barrier to 7.8 kcal mol⁻¹,‡ from 17.6 kcal mol⁻¹ estimated without the said cooperative effect. Regarding the amide hydrolysis 4–5, the overall§ barrier is huge: 35.7 kcal mol⁻¹. It can be surmised that the present estimate of the barrier is too high, due to the approximate description of water solvation. Anyhow, it indicates an extremely slow reaction, consistently with the fluorescence results (detailed below) where one excitation peak around 313 nm (likely due to the OTα derivative 5b) appears only after several days at pH 12.5 (Fig. 8c). The computed value for the absorption peak of 5b is 331 nm.¶

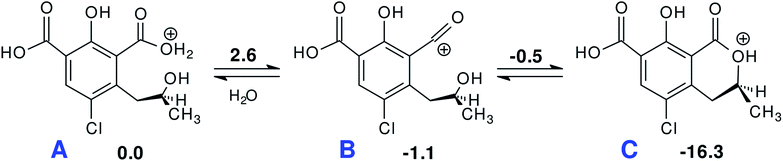
An alternative step from 3 begins with hydrogen abstraction from nitrogen to form the trianionic intermediate 6 (blue line in Fig. 7). This 3–6 step (ΔG^‡ = 9.1 kcal mol⁻¹) is actually easier than 3–4. However, 6 is thermodynamically less stable than 3: between 3 and 6 an equilibrium is established but strongly shifted towards 3. Moreover, the only reaction that might generate 6 is the lactone hydrolysis, whose first step leads to TI3 (−0.3 kcal mol⁻¹ with respect to 1); but an overall barrier of 23.0 kcal mol⁻¹ hampers this hydrolysis. Lactone hydrolysis from 3 has a lower barrier (21.5 kcal mol⁻¹) and leads to the trianionic amide 4, which is more stable than 3. Consequently, the well corresponding to 4 (Fig. 7) gets more easily populated than the well corresponding to 6. Then the reaction can proceed from 4. Scheme 1 shows the intrinsic inclination of the OTA system to evolve towards OTα, but the rate of the processes and the possible equilibria depends on OH⁻ concentration.

The EEM of a fresh solution at pH 11.6, in Fig. 8a, shows a band positioned at 365/443 nm related to 3. Fig. 8b shows that at pH of 12.5 the fresh OTA solution degraded faster than the time of measurement. The new band at λ_Ex/Em 346/440 nm was associated to OTA with the hydrolyzed lactone (4 in Scheme 1) because the excitation wavelength agrees with the theoretical λ_max = 346 nm and with λ_max at 345 nm reported by Xiao et al.²⁶ Conversely, it does not agree with λ_max at 385 nm at pH ≥ 11 reported by Bazin et al.⁶⁷ Fig. 8c reports the EEM of the OTA solution at pH of 12.5 after 7 days. 4 is still present, but another peak arises at λ_Ex/Em of 313/430 nm, probably related to OTα with the hydrolyzed ring (5b in Scheme 1). However, if the solution is maintained at pH 11.5, 4 is still present after 9 days, and 5b probably does not form. The EEM of Fig. 8d shows the band of the standard solution of OTα adjusted at pH of 12.5, and confirms the assignment of the band (see also Fig. S5†). 5b derives from the amide hydrolysis under alkaline condition of 4 and is less toxic than OTA. The other reaction product is phenylalanine (5a in Scheme 1), whose band is at 258/284 nm, outside the scanned range.⁶⁸

In this work, studies of reversibility of the reaction products of OTA were also conducted. The OTA solution at pH 7.1, containing mainly 3 (Fig. 3d) was acidified down to pH 1.0 using HCl solution. The correspondent EEM, measured as soon as the solution was acidified, shows a single band positioned at λ_Ex/Em of 332/458 nm due to neutral form of OTA.

Regarding the reaction of OTA degradation under alkaline conditions, instead, the reversibility depends on what form is present in the solution. Indeed, while 4 is easily brought back to the neutral form of OTA by acidifying the solution, 5b does not return to the neutral form but returns to OTα (see Fig. S6†), as expected (5b does not reasonably react with 5a to form OTA again). Otherwise, at pH 12.5 after more than one month 5b does not return to OTα.

In the computations, OTα was chosen as a proxy model for 4 to examine a possible backwards evolution of this intermediate. Re-acidification of a solution where 4 is predominant leads to the neutral form of OTA. In order to understand whether lactone regeneration is possible in acid environment, the acid-catalyzed backwards mechanism was considered, starting from the monoprotonated 5b. The reaction seems to proceed very fast with low energy barriers toward a supposedly protonated OTα (Scheme 2). The free energy barrier for H₂O loss from the protonated carboxylate group A is only 2.6 kcal mol⁻¹. The acyl cation group in B can undergo intramolecular nucleophilic attack by the alcoholic hydroxyl (ΔG^‡ = 0.6 kcal mol⁻¹) to form the very stable protonated lactone C.

Scheme 2 Acid-catalysed lactone formation.

4. Conclusions

The proton dissociations and the degradation processes of OTA in aqueous solution were investigated in a wide range of pH to provide useful information for further toxicological studies of one of the most dangerous and diffused natural toxins. The pK_a1,2 values were determined by two independent techniques. Even though the neutral and the monoanionic OTA absorb at the same wavelength, pK_a1 was estimated by UV-Vis spectrophotometry, on the basis of the molar absorptivity, and by fluorescence spectroscopy using a 3-way chemometric approach. Thanks to the different absorption wavelengths of the monoanionic and dianionic forms of OTA, pK_a2 was obtained with higher accuracy. pK_a1 and pK_a2 were estimated 4.4 and 7.09 (fit uncertainty 0.1 and 0.01, respectively) by UV-Vis spectrophotometry and 4.2 and 7.0 (fit uncertainty 0.9 and 0.4, respectively) by fluorescence spectroscopy, showing consistency between the results.

For the first time, OTA degradation was thoroughly studied by fluorescence spectroscopy assisted by DFT calculations for the identification of the most stable reaction products. In alkaline environment, the excitation–emission matrices highlighted that over time, the dianionic OTA undergoes some degradation reactions that lead to (i) the OTA derivative with the hydrolyzed lactone ring and then (ii) to the OTα derivative with the hydrolyzed lactone ring. Both these forms are less toxic than OTA.²⁸ In order to verify the conclusion of the degradation process, the OTA reaction product, OTα, was compared with a standard OTα solution, as no EEM reference was found in the literature for this molecule. However, the reversibility studies showed that the species obtained upon re-acidification depend on those initially present under alkaline conditions, that can differ depending on pH and storage time. Dianionic and trianionic forms of OTA at pH 12.5 in fresh solution return to the neutral form of OTA when the acidic conditions are quickly restored, representing again a hazard to humans. Conversely, OTα with the hydrolyzed ring does not return to the neutral OTA, but only to the neutral OTα. Irreversible fragmentation can be completed only after a very long time (more than one week) in strongly basic solutions. These conditions are necessary to achieve an effective OTA inactivation.

The theoretical modelistic study suggests a reaction pathway that matches experimental data and facilitates their interpretation. Also, the computed absorption maxima of the intermediates along the suggested pathway resulted consistent with experiments. The possibility to prepare stable aqueous solutions containing specific forms of OTA is useful in view of further toxicological studies specific for each OTA form.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by Progetto Premiale d4l 2014, “Cibo e Salute” by INRIM and by local funding of the University of Torino. The authors thank Danilo Serazio (INRIM) for the necessary modifications of the devices for the fluorescence measurements.

References

1. H. J. Lee and D. Ryu, J. Agric. Food Chem., 2017, 65, 7034–7051.
2. L. Covarelli, G. Beccari, A. Marini and L. Tosi, Food Control, 2012, 26, 347–356.
3. A. Dalcero, C. Magnoli, C. Hallak, S. M. Chiacchiera, G. Palacio and C. A. R. Rosa, Food Addit. Contam., 2002, 19, 1065–1072.
4. A. Prelle, D. Spadaro, A. Garibaldi and M. L. Gullino, Food Control, 2014, 39, 192–197.
5. S. Z. Iqbal, Z. Mehmood, M. R. Asi, M. Shahid, M. Sehar and N. Malik, J. Food Saf., 2018, 38, e12462.
6. World Health Organization, Some naturally occurring substances: food items and constituents, heterocyclic aromatic amines and mycotoxins, Ochratoxin A, IARC Monographs on the evaluation of carcinogenc risks to human, International Agency for Research on Cancer, 1993, vol. 56, pp. 489–521.
7. Eur. Food Saf. Agency, EFSA J., 2006, 4, 1–56,  DOI:10.2903/j.efsa.2006.365.
8. Eur. Food Saf. Agency, EFSA J., 2010, 8, 1627–1665,  DOI:10.2903/j.efsa.2010.1627.
9. N. J. Mitchell, C. Chen, J. D. Palumbo, A. Bianchini, J. Cappozzo, J. Stratton, D. Ryu and F. Wu, Food Chem. Toxicol., 2017, 100, 265–273.
10. S. C. Duarte, C. M. Lino and A. Pena, Food Addit. Contam., Part A, 2010, 27, 1440–1450.
11. Commission Regulation (EC) no 1881/2006 setting maximum levels for certain contaminants in foodstuffs,http://ec.europa.eu/food/food/chemicalsafety/contaminants/legisl_en.htm.
12. N. W. Turner, S. Subrahmanyam and S. A. Piletsky, Anal. Chim. Acta, 2009, 632, 168–180.
13. A. Kaushik, S. K. Arya, A. Vasudev and S. Bhansali, Open J. Appl. Biosens., 2013, 02, 1–11.
14. L. Anfossi, C. Giovannoli and C. Baggiani, Curr. Opin. Biotechnol., 2016, 37, 120–126.
15. Á. Molinero-Fernández, A. Jodra, M. Moreno-Guzmán, M. Á. López and A. Escarpa, Chem.–Eur. J., 2018, 24, 7172–7176.
16. M. L. Savastano, I. Losito and S. Pati, Food Control, 2016, 68, 391–398.
17. F. Chen, C. Luan, L. Wang, S. Wang and L. Shao, J. Sci. Food Agric., 2016, 97, 1805–1810.
18. C. Giovannoli, C. Passini, F. Di Nardo, L. Anfossi and C. Baggiani, J. Agric. Food Chem., 2014, 62, 5220–5225.
19. L. González-Osnaya, J. M. Soriano, J. C. Moltó and J. Mañes, Food Chem., 2008, 108, 272–276.
20. L. Monaci and F. Palmisano, Anal. Bioanal. Chem., 2004, 378, 96–103.
21. F. Berthiller, C. Brera, M. H. Iha, R. Krska, V. M. T. Lattanzio, S. MacDonald, R. J. Malone, C. Maragos, M. Solfrizzo, M. Stranska-Zachariasova, J. Stroka and S. A. Tittlemier, World Mycotoxin J., 2017, 10, 5–29.
22. F. Malir, V. Ostry, A. Pfohl-Leszkowicz, J. Malir and J. Toman, Toxins, 2016, 8, 191.
23. A. E. el Khoury and A. Atoui, Toxins, 2010, 2, 461–493.
24. S. Uchiyama, Y. Saito and M. Uchiyama, Food Hyg. Saf. Sci., 1985, 26, 651–657.
25. I. G. Gillman, T. N. Clark and R. A. Manderville, Chem. Res. Toxicol., 1999, 12, 1066–1076.
26. H. Xiao, S. Madhyastha, R. R. Marquardt, S. Li, J. K. Vodela, A. A. Frohlich and B. W. Kemppainen, Toxicol. Appl. Pharmacol., 1996, 137, 182–192.
27. R. R. Marquardt and A. A. Frohlich, J. Anim. Sci., 1992, 70, 3968–3988.
28. F. Sun Chu, I. Noh and C. C. Chang, Life Sci., 1972, 11, 503–508.
29. F. S. Chu, Arch. Biochem. Biophys., 1971, 147, 359–366.
30. M. J. Pitout, Toxicol. Appl. Pharmacol., 1968, 13, 299–306.
31. F. S. Chu and B. J. Wilson, CRC Crit. Rev. Toxicol., 1973, 2, 499–524.
32. Y. V. Il’ichev, J. L. Perry, R. A. Manderville, C. F. Chignell and J. D. Simon, J. Phys. Chem. B, 2001, 105, 11369–11376.
33. C. De Stefano, P. Princi, C. Rigano, C. Van de Wiele and S. Sammartano, Ann. Chim., 1987, 77, 643–675.
34. P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753.
35. R. Karoui and C. Blecker, Food Bioprocess Technol., 2011, 4, 364–386.
36. R. A. Harshman, UCLA Working Papers in Phonetics, 1970, 16, 1–84.
37. C. M. Andersen and R. Bro, J. Chemom., 2003, 17, 200–215.
38. S. Leurgans and R. T. Ross, Stat. Sci., 1992, 7, 289–310.
39. R. T. Ross and S. Leurgans, Component resolution using multilinear models, in Methods in Enzymology, Academic Press, 1995, pp. 679–700,  DOI:10.1016/0076-6879(95)46029-2.
40. Joint Committee for Guides in Metrology, JCGM 101: Evaluation of Measurement Data - Supplement 1 to the ‘Guide to the Expression of Uncertainty in Measurement’ - Propagation of Distributions Using a Monte Carlo Method, 2008.
41. J. A. Pople, P. M. W. Gill and B. G. Johnson, Chem. Phys. Lett., 1992, 199, 557–560.
42. H. B. Schlegel, in Computational Theoretical Organic Chemistry, ed. I. G. Csizmadia and R. Daudel, Springer, Netherlands, Dordrecht, 1981, pp. 129–159.
43. H. B. Schlegel, J. Chem. Phys., 1982, 77, 3676–3681.
44. H. B. Schlegel, J. S. Binkley and J. A. Pople, J. Chem. Phys., 1984, 80, 1976–1981.
45. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
46. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989.
47. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
48. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
49. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
50. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
51. R. E. Skyner, J. L. McDonagh, C. R. Groom, T. Van Mourik and J. B. O. Mitchell, Phys. Chem. Chem. Phys., 2015, 17, 6174–6191.
52. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
53. R. Gómez-Bombarelli, E. Calle and J. Casado, J. Org. Chem., 2013, 78, 6880–6889.
54. Y. Jin, Y. Zhu and M. Tang, Comput. Theor. Chem., 2011, 963, 268–272.
55. D. Cheshmedzhieva, S. Ilieva, B. Hadjieva and B. Galabov, J. Phys. Org. Chem., 2009, 22, 619–631.
56. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
57. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
58. G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107.
59. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
60. A. J. Cohen and N. C. Handy, Mol. Phys., 2001, 99, 607–615.
61. P. Krawczyk, J. Mol. Model., 2015, 21, 118.
62. M. H. Khalilian, S. Mirzaei and A. A. Taherpour, J. Mol. Model., 2016, 22, 270.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016.
64. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
65. R. Verrone, L. Catucci, P. Cosma, P. Fini, A. Agostiano, V. Lippolis and M. Pascale, J. Inclusion Phenom. Macrocyclic Chem., 2007, 57, 475–479.
66. A. Casale, P. G. Daniele, A. De Robertis and S. Sammartano, Ann. Chim., 1988, 78, 249–260.
67. I. Bazin, V. Faucet-Marquis, M. C. Monje, M. El Khoury, J. L. Marty and A. Pfohl-Leszkowicz, Toxins, 2013, 5, 2324–2340.
68. J. Christensen, L. Nørgaard, R. Bro and S. B. Engelsen, Chem. Rev., 2006, 106, 1979–1994.

---

Footnotes

† Electronic supplementary information (ESI) available: Spectra, emission–excitation matrices, DFT energetics, figures of the transition structures, optimized geometries and all examined reactions. See DOI: 10.1039/c9ra02086a

‡ The TS TI2-5 actually leads to a somewhat stable intermediate, in which a water proton has moved to nitrogen, leaving an OH⁻ interacting with a quaternary cation, shown in Fig. S9. Its potential energy is below the TS, but its free energy lies 0.2 kcal mol⁻¹ above it. This intermediate easily dissociates to 5a + 5b (ΔG^‡ = 1.0 kcal mol⁻¹).

§ For these two-step hydrolyses, we intend by ‘overall barrier’ the free energy difference between the highest-G transition structure TI1–4 or TI2–5 and the intermediates 3 or 4, respectively. In the first case −1.2 + 21.3, in the second 2.8 + 32 (see Fig. 7).

¶ The computed value is significantly dependent of the dihedral angle related to the almost free rotation of the leftmost (in 5b) carboxylate group, not engaged in a hydrogen bond. The values span the rather large range 300–331 nm, and the dihedral angle itself may be influenced by the interaction with explicit water molecules.

---