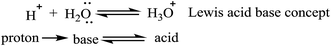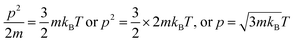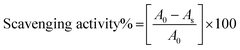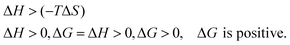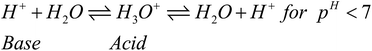DOI:
10.1039/C9RA00851A
(Paper)
RSC Adv., 2019,
9, 15805-15835
Hydrophobics of CnTAB in an aqueous DMSO–BSA nanoemulsion for the monodispersion of flavonoids†
Received
31st January 2019
, Accepted 17th April 2019
First published on 21st May 2019
Abstract
Herein, philicphobic interactions between flavonoids (quercetin, apigenin, and naringenin) and bovine serum albumin (BSA) were analyzed using physicochemical properties obtained at T = 298.15, 303.15, 308.15 K and 0.1 MPa, from 0.01 to 0.10 mol kg−1 of alkyl trimethyl ammonium bromide (CnTAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DTAB, Cn = 12; TDTAB, Cn = 14; HDTAB, Cn = 16). The flavonoids with cationic surfactants strongly interacted with BSA, as illustrated by the physicochemical parameters (PCPs), refractive index (nD), Walden product, pH, electrostatic potential and molar conductance (Λm). Viscosity (η), density (ρ), ηD, sound velocity (u) and specific conductance (k) data were used to calculate the relative viscosity (ηr), viscous relaxation time (τ), Walden product, entropy (ΔS), enthalpy (ΔH), Gibbs free energy (ΔG), heat capacity (Δq) limiting dielectric constant (ε∞), speed of light (C), acoustic impedance (Z) and molar refraction (R). These PCPs have quantitatively predicted the hydrophilic and hydrophobic (philicphobic) interactions developed are on increasing the alkyl chain (AC) of CnTAB. These interactions assist a monodispersion of the flavonoids, and a similar mechanism could equally be applicable to monodisperse the antioxidants in the aqueous nanoemulsions. Their philicphobic stoichiometry weakened the cohesive forces (CF) when the shear stress was increased, and enhanced surface activities were achieved that facilitated the flavonoids to interact with BSA due to intermolecular forces (IMF) to develop a stable nanoemulsion; Upon increasing the CnTAB concentrations, the nD value increases since the polarizability increases with stronger shear stress due to van der Waal forces and electrostatic interactions to achieve better flavonoid–BSA linkages.
DTAB, Cn = 12; TDTAB, Cn = 14; HDTAB, Cn = 16). The flavonoids with cationic surfactants strongly interacted with BSA, as illustrated by the physicochemical parameters (PCPs), refractive index (nD), Walden product, pH, electrostatic potential and molar conductance (Λm). Viscosity (η), density (ρ), ηD, sound velocity (u) and specific conductance (k) data were used to calculate the relative viscosity (ηr), viscous relaxation time (τ), Walden product, entropy (ΔS), enthalpy (ΔH), Gibbs free energy (ΔG), heat capacity (Δq) limiting dielectric constant (ε∞), speed of light (C), acoustic impedance (Z) and molar refraction (R). These PCPs have quantitatively predicted the hydrophilic and hydrophobic (philicphobic) interactions developed are on increasing the alkyl chain (AC) of CnTAB. These interactions assist a monodispersion of the flavonoids, and a similar mechanism could equally be applicable to monodisperse the antioxidants in the aqueous nanoemulsions. Their philicphobic stoichiometry weakened the cohesive forces (CF) when the shear stress was increased, and enhanced surface activities were achieved that facilitated the flavonoids to interact with BSA due to intermolecular forces (IMF) to develop a stable nanoemulsion; Upon increasing the CnTAB concentrations, the nD value increases since the polarizability increases with stronger shear stress due to van der Waal forces and electrostatic interactions to achieve better flavonoid–BSA linkages.
1. Introduction
Research on the interaction of flavonoids with globular proteins using surfactants and ionic liquids is of significant interest for numerous biological, medicinal, pharmaceutical and pharmacological properties to enhance the interaction abilities, especially in the case of the flavonoid and protein interactions. Flavonoids are polyphenols and secondary metabolites that have significant potential due to their numerous health benefits.1 Flavonoids are abundantly found in foods and beverages of plant origin, fruits, vegetables, tea, cocoa and wine and are termed as dietary flavonoids. Thus, the molecular structure of flavonoids can be characterized by a biphenyl propane (C6–C3–C6) skeleton (Fig. S1†) due to the similarity in structures. The flavonoids have two phenolic rings (A and B) that are attached by a heterocyclic C-ring (Fig. S1†)2 and are classified by the number and position of the phenolic (–OH) groups and the presence/absence of a double bond in the molecular structures of flavone, flavanone, anthocyanins, flavonol, chalcone, and isoflavonoids.3,4 Flavonoids are an excellent free-radical scavenger and have been broadly studied for their antioxidant, anticancer, antiviral, and anti-inflammatory properties as well as their ability to prevent activities that cause heart disease.1,5,6 Flavonoids regulate several enzymes7,8 by scavenging the free radicals and have the ability to chelate transition and noble metal ions; this enhances their anti-inflammatory and antioxidant activities.9 Thus, flavonoids initiate a secondary chemical mechanism by attracting metal ions that have developed ionic hydration. Their bioavailability and bioactivity depend on their distribution in the body, which initiates interactions with proteins. Despite this, their huge potential applications, attained by the active structures containing phenolic OH, π-conjugation and C-atoms, not only contribute to initiating interactions with free radicals and other biomolecules but also compensate their mutual effects. Therefore, we conducted very systematic studies by determining the most relevant PCPs as a function of their distribution by affecting their friccohesity in an aqueous medium. We have resolved their solubility by formulating the aqueous-DMSO mixed solvents as the stronger CF of water was a large barrier. The flavonoid distribution patterns in low surface energy mixtures have never been reported yet. In order to develop low-surface energy liquids mixture with naturally higher shear stress that increases the monodispersion of flavonoids, the stronger shear mixtures were chosen for studies. The nD, τ, Z, pH, Walden product and potential, which directly reflect the state of the surface energy/tension of samples, were chosen as PCPs along γ, η, σ and ρ data. In such samples, the flavonoids possess novel therapeutic activities of acute-high potency with low toxicity. However, a more in-depth understanding of the functional sites of bioflavonoids requires the study of their interactions with all possible biological targets, including nucleic acids,1 enzymes3,4 and globular proteins.10 Thus, solubility and stability are two critical factors of the solution for the determination of PCPs for a new drug that affects the performance and formulation developmental process. Pharmacokinetic and pharmacodynamics performances of a formulation dependent on the drug levels in blood plasma, tissues and urine are substantially tuned by philicphobic ratios. After oral administration, the drug levels in plasma depend on the absorption of the drug through the gastrointestinal tract. All these processes are completed in low surface energy mixtures. Moreover, protein–flavonoid interactions require more advanced studies to provide noble and more in-depth information in the areas of structural molecular interaction engineering, biochemistry, solution chemistry, drug formulation and surface chemistry.10–14
BSA, a globular protein, is a highly abundant water-soluble carrier protein in a circulatory system that distributes exogenous and endogenous components in the blood. It has the ability to interact with various biologically active molecules, drugs, fatty acids, steroids, lanthanides, dyes, etc. in the body.5–7 These tune their philicphobic activities and BSA was added into aq-DMSO. Furthermore, BSA also plays an active role in drug delivery and the maintenance of blood pressure in the body because of its transporting nature with adequate friccohesity.6–8 Accordingly, the interacting drug could perform better while the non-interacting drug develops the anticipated pharmacological effect. Various studies have described the drug–BSA interactions where the drug–BSA interactions9,15 are influenced by the surrounding environments, temperature, pH, concentrations, and molecules like biopolymers, surfactants, dendrimers, dyes, ionic liquids and others.16 Moreover, the flavonoid–BSA interaction continuously induces an intervention of drug interaction as the BSA undergoes conformational changes.17 Therefore, the distribution and metabolism of numerous bioinspired compounds, such as flavonoids and drugs, in the body have been associated with their strong interaction affinities towards BSA, which added a biophysical stint to our liquid mixtures. Earlier studies have reported the spectroscopic analysis of the interaction affinity of proteins with therapeutically active flavonoids.2,18–22 Also, research on the nanoformulation of polyphenolic compounds has improved the bioaccessibility of oral drugs. In the past decade, many investigations have been carried out on the study of the spectroscopic interactions of flavonoids with globular proteins and surfactants systems.23–27 No adequate work had been reported in the literature that deals with the study of flavonoids with BSA and surfactants mixtures28–30 in the formation of dispersions at various temperatures.
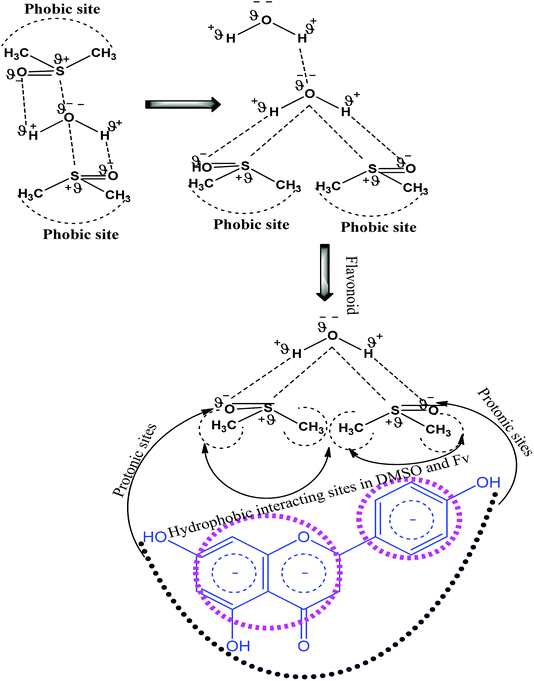
This study aimed to enhance the biological and pharmacological activities of flavonoids with cationic surfactants through the stable nanoemulsion. Stronger hydrophobicity was substantially functionalized to disperse BSA, which could freely interact with free radical by enhancing antioxidant activities. Hydrophobicities that dominate biochemical and biophysical interactions frequently occur in living systems, but neither adequate PCPs nor the thermodynamics studies of PCPs have been yet reported in the presence of BSA. The flavonoid–protein with the increasing hydrophobicity of cationic surfactants interactions has never been reported yet. We chose 10% (w/w) aq-DMSO to disperse the flavonoids, and the pre-processing model for active solvent medium preparation is presented in Fig. 1 and 2. Here, the dipoles of DMSO squeezed out the HB of the water molecule to determine the actual interacting activities of a globular protein with flavonoids as their interactions substantially influence the living system. The experimentation for a real-time process of the dipole–dipole interaction (DDI) model was developed using 10% aq-DMSO solution, which could have in situ dipole orientation to cage out and reach comparatively stronger dipoles like BSA and flavonoids and is noted in step ≠ 01 for H2O–DMSO as a dipolar solvent model.
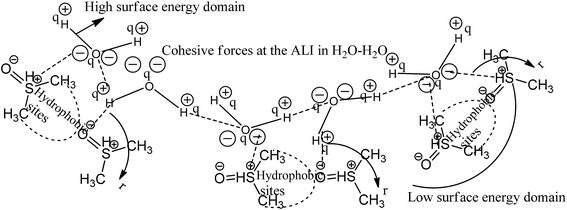 |
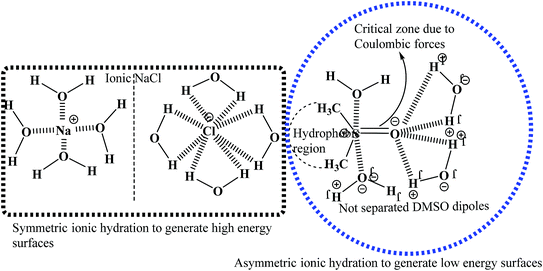
| | Fig. 1 Cohesive and coulombic interactions of H2O–H2O and H2O–DMSO for higher and lower surface energy domains. | |
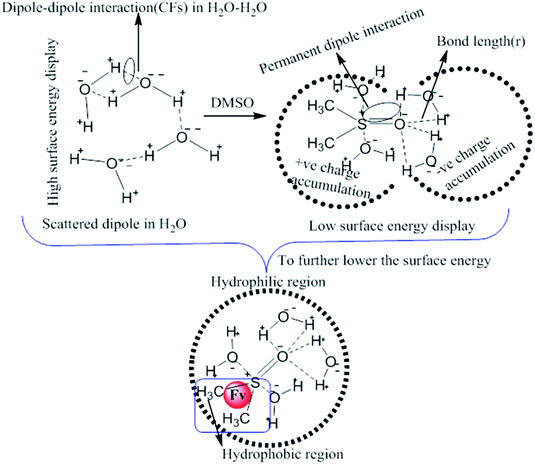 |
| | Fig. 2 Pre-processing and working model for H2O–DMSO with Fv (flavonoids) interactions. | |
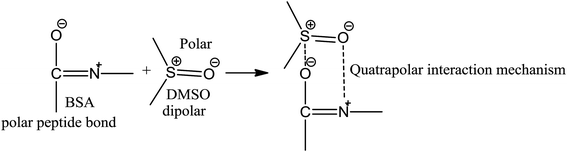
BSA explains the role of the polypeptide bond (PPB) and α, β-sheet, β-turns, random coils, and the role of the dipole moment of H2O and DMSO for the BSA interaction mechanism. aq-DMSO reported a linear increase in ρ, η, and σ data (Table S1, Fig. S2 and 3†) which infers a similar mechanism of HB disruption as a 1st-order physicochemical process. The electrostatic H2O and DMSO structures were established through coulombic forces by the Lennard-Jones potential as:
The coulombic forces weaken as per kinetic energy (KE) rather than undergoing transitional changes. The DMSO dipoles align the water dipoles, after disrupting its HB upon developing an individual zeta potential due to ion-dipole interaction (IDI) and electrostatic interaction. The DDI of H2O–DMSO (Table S1†) is stronger than the dipolar interactions of DMSO and H2O individually. This is supported by an increased η value, as shear stress and strain increased due to the stronger H2O–DMSO interactions which have been the master control for flavonoid and BSA interactions with their chosen stoichiometries. The weakening of the similar dipole run model is supported upon decreasing the γ values. Since coulombic interactions at air–liquid interfaces (ALI) are weakened by DMSO interactions with H2O, a dipolar interaction weakens the tension of a thin film noted as:
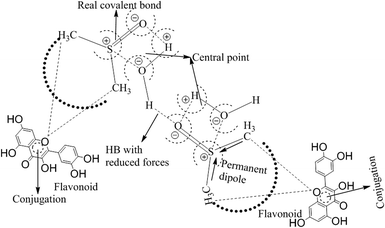
Since the hydrophobic chain of DMSO is shorter, the effect of the hydrophobic interaction of these DMSO dipole interactions with the residual van der Waal forces of H2O dipoles alone due to the interaction of DMSO dipoles with the dipoles of H2O in the bulk phase can be noted. The bulk DDI influence the tension caused by residual forces of H2O–H2O dipoles.
These aligned charges (Fig. 3) could attract H+ ions from phenolic –OH groups, as there is asymmetric charge accumulation around the S+ ion as compared to the O− ion. The dipole moment value (Table S2†) was calculated by using the reported equation.23
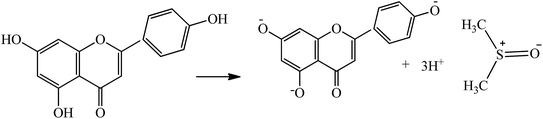 |
| | Fig. 3 Solubilization of flavonoids through electrostatic interaction in the aq-DMSO system. | |
This proton (3H+) could further activate the destabilized H2O as:
These models tune the monodispersion of the flavonoid in WBD medium, where the monodispersed flavonoid can attain a larger surface area with stronger activities to furnish the H+ to scavenge the free radicals. All the calculated PCPs act as sensors, while the ρ, η, γ, surface excess concentration (Γmax), apparent molar volume (Vϕ) and u reported in our previous study30 illustrate the coagulation, anticoagulation, and transitional H2O agglomeration, which affect the free radical scavenging actions of the flavonoid. The earlier reported PCPs show ambiguity, and no clear-cut sensing mechanism was established. Therefore, nD, pH, electrostatic potential, Λm, τ, the Walden product, ΔS, ΔH, ΔG, ε∞, C, Z, DFI, friccohesity shift coefficient and R data illustrate the tentropic sites of the flavonoids, which could focus the H+ releasing activities by synergising their tentropic activities. Thus, these properties resolve the said ambiguities and allow the exploration of advanced working models for H2O with BSA or DMSO, which could reorient the whole chemical process. Thus, a state of doubt emerges as to whether the drug has an affinity towards H2O, which is structurally engaged with flavonoids or BSA. The τ value fundamentally depicts internal binding, which preferentially interacts due to stronger tentropy, as the tentropy causes many dissimilarities in the interfaces of the molecules. Therefore, the tentropic faces cause favorable or non-favorable surfaces for interactions. These promote the fast recovery of molecules to optimize and maintain the symmetric structure despite the energetic surfaces, which induce Z as the structured linkage that could oppose the structural optimization and is predicted by a relation with the viscous flow. Also, the nD fundamentally tracks such reorientational changes as the light penetrates each and every vertical and horizontal cross-sections of the dispersed molecules. These activities could be aligned to bring positive and negative surfaces together, so the ε∞ value was measured. Furthermore, the energy of light as a photon passes through the solution is hν. Thus, the denser and lighter patches or interaction nanoclusters could be symmetric and construct or destruct the interference, so the C data was chosen to track the same. This fundamental science could assist in the development of CF with adequate adhesive forces, which can furnish information about the multicomponent systems. Hence, DFI has found critical relevance along with structural thermodynamics incorporating ΔG, ΔH and ΔS through variable pH, and Λm. These critical evaluations about the flavonoid vis-a-vis BSA and DMSO were not explored in our previous studies.30 These studies offer a fundament overtone of the interactions with flavonoids dispersed with a momentum p, which is related to the Boltzmann distribution factor as:
where
m denotes mass,
kB is the Boltzmann constant,
T is the temperature in Kelvin, and
ρ is the density. We have investigated the role of the ACL of C
nTAB in enhancing the interaction affinities of flavonoids towards BSA at three temperatures that change flavonoid dispersibility
via structurochemical interaction methods, an increase in ACL due to a formation of nanoemulsion with stronger interaction affinity of flavonoid towards BSA. Thus when the CFs are weakened, Δ
S increased and Δ
G decreased. This mechanism was designed through the friccohesity shift model (FSM) to explain the flavonoid–BSA interaction mechanism. It could be used to understand the activities of a protein and the increasing hydrophobicity of C
nTAB (Fig. S4
†) with thermodynamically and kinetically stable nanoemulsion formulation. Such a formulation could be applied to drug delivery, biochemistry, drug formulation, the functionalization of graphene oxide and drug dispersion.
2. Materials and methods
2.1. Materials
All the chemicals were used without further purification and their specifications are given in Table 11. Before use, DTAB, TDTAB and HDTAB were stored in a P2O5 filled vacuum desiccator to avoid contact from the environment.
2.2. Methods
0.999 millimol per kg flavonoid, quercetin, apigenin and naringenin were added separately into 2 g L−1 aqueous BSA with 10% w/w aq-DMSO and was used as a stock solution for 0.01 to 0.10 mol kg−1 CnTAB. All the solutions were maintained under continuous stirring at 1000 rpm for 30 min to obtain a stable homogeneous solution. The WBD (water + BSA + DMSO) solution was prepared by dissolving 2 g L−1 BSA into 10% (w/w) aq-DMSO. All the solutions were prepared separately at T = 298.15 K and p = 0.1 MPa with Milli-Q water (Milli-Q SAS 67/20 Mosheim) of 0.71 μS cm−1 and at pH 7. Mettler Toledo New Classic MS was used for weighing, with <±0.1 × 10−6 kg repeatability. All the solutions filled in an airtight volumetric flask were stored at T = 277.15 K in the dark until use to avoid evaporation and contamination. Their densities and sound velocities were measured by using an Anton Paar DSA 5000M density meter with ±5 × 10−6 g cm−3 and ±0.5 m s−1 uncertainties, respectively. A built-in Peltier device had controlled the temperature with a standard deviation of ±1 × 10−3 K. The repeatability of the instrument showed ±1 × 10−3 kg m−3 accuracy in the density measurement.31 The instrument was calibrated with aq-NaCl (1.0 mol kg−1) and 5, 10, 15 and 20% (w/w) aq-DMSO (Table S3†) at T = 298.15 K.32,33 The reported densities data were an average of at minimum three repeated measurements with a standard deviation of ±4 × 10−6 g cm−3. The sound velocities (u) were determined at 3 MHz frequency. All the experiments were conducted at T = 298.15, 303.15 and 308.15 K with ±0.01 K accuracy. Sound velocity worked based on the oscillation periods of quarts U-tube with air, solvent and solutions.34 After each measurement, the tube was cleaned using acetone and dried by passing air through using an air pump with a U-tube. The drying process was continued until a constant oscillation period for air was attained and noted as an initial calibration. Viscosity (η) and surface tension (γ) were measured by using a Borosil Mansingh Survismeter35 (Cal.no. 06070582/1.01/C-0395, NPL, India) via viscous flow time (VFT) and pendant drop number (PDN) methods. The temperature was controlled using a Lauda Alpha KA 8 thermostat with ±0.05 K accuracy. After attaining a thermal equilibrium, the VFT was recorded using an electronic timer with ±0.01 s accuracy. The instrument was properly washed with Milli-Q water and was then dried using acetone before the measurements. Viscosity and surface tension values were an average of at minimum three replicate measurements with ±2 × 10−6 kg m−1 s−1 and ±0.03 mN m−1 uncertainties, respectively. For calibrating the density, viscosity and refractive index values (Table S4†), 5, 10, 15 and 20% (w/w) aq-DMSO were compared with literature values.33,36
2.2.1. Antioxidant activity measurement. The antioxidant activities of the flavonoid formulations were assessed through the free radical scavenging activity of DPPH˙ measured through previously reported spectrophotometric methods.37,38 For the determination of radical scavenging activities (RSA), 0.006% DPPH˙ solution in ethanol was prepared. For screening RSA, pure DPPH˙ solution was mixed with flavonoid formulation at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Thereafter, after vigorous shaking, these samples were kept in dark for an incubation period of 30 min. The relative radical scavenging activities (RSAs) were evaluated as a measure of comparative % decrease in the absorbance of pure DPPH˙ at λmax = 520 nm, ascertained by measuring the absorbance of the DPPH + flavonoid formulation 1
1 ratio. Thereafter, after vigorous shaking, these samples were kept in dark for an incubation period of 30 min. The relative radical scavenging activities (RSAs) were evaluated as a measure of comparative % decrease in the absorbance of pure DPPH˙ at λmax = 520 nm, ascertained by measuring the absorbance of the DPPH + flavonoid formulation 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture at the same wavelength. The measurements were made with a Spectro2060 plus model UV/Vis spectrophotometer. The respective RSAs were calculated using the following equation:
1 mixture at the same wavelength. The measurements were made with a Spectro2060 plus model UV/Vis spectrophotometer. The respective RSAs were calculated using the following equation:
where A0 and As are the absorbance of pure DPPH˙ and flavonoid formulation, measured at 520 nm.
2.2.2. Refractometer. The refractive index was measured by a Rudolph Research analytical J series Refractometer model 57. The surface of the Refractometer prism was cleaned with HPLC-grade ethanol and a lens wiper in measurements. This process ensured complete cleaning with no stains or air bubbles left on the prism surface. About 15–20 measurements were made for precision. The literature and the experimental refractive index values for 5, 10, 15 and 20% (w/w) aq-DMSO with a standard deviation at T = 298.15 K (Table S4†) show accuracy and calibration of instruments and uncertainty value of refractive index with an uncertainty of ±1 × 10−4.
2.2.3. Conductance measurement. Conductance values were measured at T = 298.15, 303.15 and 308.15 K using a digital conductivity meter (Lab, India Conductivity meter PICO+) and at 50 Hz frequency using a dip-type cell with an 0.89 cm−1 cell constant. The instrument was calibrated using the earlier-reported method.39 A Lauda Alpha KA 8 thermostat was used for temperature control with a standard deviation of ±0.05 K.
2.2.4. Electrostatic potentiostat measurement. An Advance Potentiostat 848 Titrino Plus (Metrohm) was used for potential measurement. The potentiometer had an inbuilt temperature control facility and was calibrated for each surfactant solution with Milli-Q. Once the measurement was done, the surface of the electrode was cleaned with Milli-Q water to avoid contamination and to obtain accurate results.
2.2.5. pH measurement. The pH values were measured with a pH meter (SV4 Digital) with a built-in power source of 50 Hz, 230 Volts, with ±0.01 accuracy. The pH meter was calibrated with standard buffers of pH 4, 7 and 11 solutions.40 The pH value was noted after 2–3 minutes of electrode insertion.
3. Results and discussion
3.1. Stability determination through physicochemical properties (PCPs)
The 10% DMSO composition exhibited a shift from weaker aq-DMSO dipolar interactions via a quadrupolar model of their dipoles, which develop a central electronic shift/domain confined to a central point. This is similar to the conjugation of the benzene ring and the outer electronic environment of a quadrupolar area monitoring the solubilization of flavonoids. It is likely that the hydrophobic part of flavonoid could intensify its spontaneity towards (CH3)2 > S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O through their philicphobic nature. The shift for 10% DMSO could be extended to other single and mixed solvent systems. Such chemical engineering to formulate the workability of solvents has never yet been reported. Thus, our model could open a new area of research in engineering the solvents as these play a critical role in the quality of the products formed, similar to benzene conjugation. The linear γ value decreases upon increasing DMSO concentration, which suggests that more and more DMSO could break the HB of H2O. The HB of H2O led to the development of CFs with a higher γ value. But DMSO decreases the γ value, as the DMSO dipoles attack the H2O dipoles and put pressure on the HB of water. Ultimately the HB of H2O is disrupted by DMSO, which decreases the γ value to form a low surface energy liquid mixture. Hence, our data (Table S1†) support the following model.
O through their philicphobic nature. The shift for 10% DMSO could be extended to other single and mixed solvent systems. Such chemical engineering to formulate the workability of solvents has never yet been reported. Thus, our model could open a new area of research in engineering the solvents as these play a critical role in the quality of the products formed, similar to benzene conjugation. The linear γ value decreases upon increasing DMSO concentration, which suggests that more and more DMSO could break the HB of H2O. The HB of H2O led to the development of CFs with a higher γ value. But DMSO decreases the γ value, as the DMSO dipoles attack the H2O dipoles and put pressure on the HB of water. Ultimately the HB of H2O is disrupted by DMSO, which decreases the γ value to form a low surface energy liquid mixture. Hence, our data (Table S1†) support the following model.
The DMSO attack utilizes the dipolar energy of H∂+ and O∂−−, so the polar atoms tend toward DMSO (Fig. 4). Such attraction of DMSO dipoles developed a weak CF of H2O with a lower γ value. Apigenin increased the γ value with the WBD system, but naringenin has the lowest γ value. A single double bond of apigenin interacted with DMSO and BSA that has freed the bound water and strengthened the H2O structure with high CF and higher surface tension. However, naringenin without any double bond in C-ring makes it support surfactant-like surface activities.
 |
| | Fig. 4 Substantial model illustrates Fv interaction with aq-DMSO systems. | |
Moreover, the addition of apigenin into WBD-form WBDA that decreases the dipole moment contrary to quercetin and naringenin comparatively infers the stronger engagement of water dipoles by apigenin, as apigenin contains only 3-OH groups with a complete delocalized loop (Fig. S1†). The fewer –OH groups with delocalized π-electron nanowires stabilize stronger interactions with H2O dipoles. However, naringenin further increases the dipole moment of the WBDN system, so missing a delocalized π-electron and σ-bond inhibits the formulation of nanowires. Naringenin does not develop stronger hydrophilic interactions but initiates the hydrophobic interaction with BSA, which releases H2O that could be engaged with BSA before the addition of naringenin by pushing the BSA and naringenin, so their activated complex affects the air–water interface (AWI), which decreases the γ value.
DMSO and H2O develop permanent dipoles and form a quadrupolar arrangement (Fig. 5). For 1.5% DMSO, stronger HB disruption of H2O with weaker CFs occurs and lower the γ values. Similarly, likely at 3.2% DMSO, maximum DMSO molecules moved towards the flavonoid (quercetin) cluster, releasing H2O from the DMSO hydration domain, causing hydrophobic–hydrophobic (HbHb) interaction of DMSO with quercetin. This mechanism increased CF with higher γ values. The solubility model of flavonoid in aq-DMSO is most fascinating as <10% DMSO could not solubilize the flavonoid, but >10% DMSO has homogeneously solubilized the flavonoid in aq-DMSO, noted as a mixed low surface energy solvent. DMSO here acted as an interlocutor to stabilize the link between H2O and the flavonoid. <10% DMSO could not sufficiently destabilize the HB of H2O, making H2O free with both larger surface area and kinetic energy (KE), but >10% DMSO destabilized the HB structure of H2O.
| |
 | (1) |
 |
| | Fig. 5 Dispersion mechanism of flavonoids in 10% aq-DMSO system. | |
>10% DMSO generated adequate H2O monomers to interact with the flavonoid through coulombic forces generated out of dipolar interactions.
The flavonoid could not disrupt H2O structure, but DMSO disrupted its structure via the dipolar quadrupolar model due to high- and low-energy surfaces, respectively (Fig. 6). Both quadrupolar models are disrupted DMSO–DMSO interactions. Hence, their individual CFs decreased with a decrease in surface tension. These decreasing γ values with increasing DMSO molecules infer the disruption of water CFs. So, their dipolar arrangement was disrupted, providing a lower dipole moment value.
| |
 | (2) |
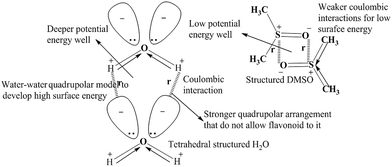 |
| | Fig. 6 Quadrupolar model of H2O–H2O and DMSO–DMSO molecules to weaken the cohesive forces of H2O. | |
The attraction forces (AFs) were stronger before >10% DMSO; AFH2O and AFDMSO both are independently stronger. Since ρ continuously increases with increasing DMSO concentration, the DMSO disrupts H2O HB aggregates but up to <10% DMSO; the flavonoid does not dissolve in <10% DMSO liquid mixtures. Such scientific models of aq-DMSO–BSA–flavonoids have never been reported yet.
η decreases with the flavonoids in a zigzag manner, not spherical or symmetric in geometry. Hence, this asymmetric solvated DMSO (Fig. 7) undergoes irregular orientation or reorientation, rotational, translational, and vibrational oscillatory motions. No regular trends in the η, γ, σ and κ values are noted with the flavonoid. Hence, the hydrophobic head of the (CH3)2– groups induces unbalanced kinetic, dynamic and stretching activities, which become dominant in laminar flow to organize adhesive forces during continuum and non-continuum flows in the capillaries of the Survismeter. The special heads of solvated DMSO substantially affect capillary action. For example, if the hydrophobic face occupies the frontal position, then the flow dynamics differs from the fluid dynamics when the negative charges of the O-atoms surface occupy the frontal position similar to the positive charges of the H+ ion. Thin film is responsible for the surface energy or tension, but the spatial positions of the hydrophobic, negatively charged O-atom and positively charged H-atoms keep rotating at the surfaces, which cause the irregular trend of γ values. However, when more hydrophobic quercetin molecules are added, the irregular surface energy trends become more irregular (Fig. S3C†). Before >10% DMSO, the quercetin is loosely bound with solvated DMSO to create a scene for solvated DMSO, because the adequate hydrophobicity of (CH3)2– was not available. Hence, to provide adequate hydrophobicity, the concentration of DMSO was increased, which show a fluctuation in PCPs values. This has compatibility with the activities of FF and also of CFs. However, when adequate hydrophobicity is made available by increasing the DMSO concentration, the fluctuation in PCPs values is minimized. The adequate hydrophobicity of (CH3)2– develops considerable hydrophobic interactions with quercetin, which make a resultant structure reproducible as a state function. Hence, the η, γ, σ and κ trends after 11% DMSO show no fluctuations. Quercetin demonstrates anti-surfactant activities, as it strongly engages the hydrophobic (CH3)2– domain, which could release some H2O from solvated DMSO. The released H2O develops stronger CFs with comparatively higher γ than solvated DMSO systems (Table S1†). Noticeably, the increasing concentration of DMSO decreases the γ value and the DMSO continuous destabilizes the HB of H2O structure, which reduces the CF with decreasing γ values. A decrease in γ occurs in both cases but decreases more in solvated DMSO due to higher DMSO solubilization, but the solubilization of DMSO with quercetin is lowered. This finds the role of quercetin vis-à-vis the hydrophobicity of (CH3)2– groups. Quercetin, which may furnish H+ from its 5 –OH functional groups, could also approach H2O molecules attached in solvated DMSO domains. These H+ ions develop the H3O+, which could come out of solvated DMSO domain to the H2O phase, increasing the γ value. Thus, quercetin could act as a catalyst to restructure H2O, so the flavonoids have been functionalized in aq-DMSO. The parameters of the flavonoid and water make them mutually insoluble, but 10% DMSO has overcome the solubility factor of flavonoids (Fig. 8).
 |
| | Fig. 7 Asymmetric hydration representation of the DMSO–H2O system. | |
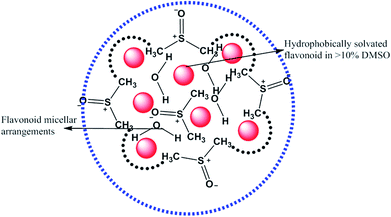 |
| | Fig. 8 Low-energy aq-DMSO nanoemulsion to monodisperse the flavonoids. | |
Had the flavonoids been hydrophilic, then they would have been solubilized in H2O, but they were solubilized in 10% DMSO. 10% DMSO creates an adequate specific hydrophobic void/pocket/localized shape which has the highest spontaneity towards the hydrophobic domain. The 10v × ρ = m of DMSO has a total m × 6.023 × 1023 DMSO molecules. These are huge numbers and, hence, undergo a self-orientation to attract HbHb –CH3 groups towards their own sides as shown in Fig. 3. These hydrophobic pockets accommodate the flavonoids, which are >98 hydrophobic. Generally, HbHbI is entropy driven chemical activities, which are supported by higher ΔS values, but a void formation creates orderedness with lower ΔS values. Thus, aq-DMSO shows a higher dipole moment, while quercetin with aq-DMSO decreases the dipole moment value. Quercetin could decrease the resultant vector forces (RVF), which are present in H2O–H2O (Fig. 9), DMSO–H2O and H2O–DMSO molecules. Similar to the inclusion of BSA into the aq-DMSO solution, the dipole moment decreases to a value lower than WDQ because BSA has the diffused PPB in its unfolded structure. BSA could decrease the RVF with quercetin, apigenin and naringenin in WBD solution. The dipole moment values are as Q > N > A in WBD solution. Quercetin shows a higher dipole moment than apigenin and naringenin, as it has stronger hydrophilicity. So, a stronger interaction affinity towards a solvent system consequently slightly increased the RVF, and the dipole moment values of WBDQ increased. The dipoles infer an attraction affinity (resultant forces) between similar and dissimilar molecules. The value of the dipole moment depends upon electron donating and electron withdrawing groups, which are attached to the ionic species of atom and groups. Quercetin has 5 –OH groups, causing a stronger interaction affinity, so the RVF increases more than WBDA or WBDN while decreases as compared to the aq-DMSO solution. The dipole moment depends upon the nature and population of the resultant charges in adjacent molecules. However, for DMSO in the aqueous system, its electronegative O− atom pulls up the H+ to the O− ion of H2O. The r follows as rDMSO−H2O > rH2O–H2O.
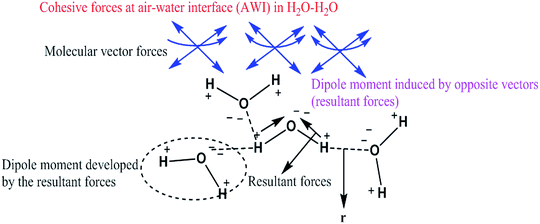 |
| | Fig. 9 H2O–H2O interaction through dipole moments with high surface energy. | |
The r value infers the distance between opposite charges, which is present in similar or dissimilar molecules. The r value is inversely proportional to the dipole moment. Naringenin acts as co-surfactants, but two π-conjugated benzene rings which separately undergo delocalization weaken the H2O dipole interactions. Naringenin initiates quantum mechanics by engaging the electron-rich and electron-deficient poles of H2O with its respective poles. With BSA in aq-DMSO solution, its dipole moment further decreases. The defused PPB of BSA has a stronger interaction affinity, so the resultant forces decrease with the decreased dipole moment. The dipole moment plays a vital role in determining the dispersibility and stability of the solution. We have prepared the nanoemulsions of flavonoids to study the effects of temperature and hydrophobicity, where BSA was used as a stabilizer due to its philicphobic nature. The flavonoids express philicphobic properties like oils, so the study is novel in the fields of drug formulation, food chemistry, solution chemistry, and biochemistry. The chosen formulation is as:
| H2O + DMSO + BSA + flavonoids (Fv) + surfactants (with mutual residual forces) |
Stoichiometric balance to formulate the thermodynamically and kinetically stable nanoemulsions was attained by varying ingredients as per their hydrophilicity and hydrophobicity monitoring activities. The fractionated solvent aligns around the core as a stern layer that counterbalances the residual charges. DMSO was used to disperse the flavonoids and BSA to monitor intrinsically active surfactants as the key dispersant. Therefore, the pentanary systems were developed for an absolute expression of the antioxidant activities of flavonoids. Natural systems like photosynthesis and protein synthesis energetically involve varieties of chemical species, which induce adequate activities for the high yield of formulation. Similarly, we chose five components to formulate nanoemulsions to meet the need and potential of interacting abilities in a friccohesically designed flavonoid nanoemulsions to attain working stoichiometric control over the free radical scavenging activities of flavonoids. The stern layer charges align the nanoparticle core, and its fractionated solvent was placed at the Lennard Jone potential distance with adequate coulombic forces. However, a clustering with larger particle size and lower surface area disbalances the counterbalances of charges. Thereby, the lowest chemical potential induces the stability of nanoemulsions contrary to indirect excess charge, subtle at larger volumes, which induce a coagulating tendency. In such a situation, many molecules are needed to induce favourable chemical activities naturally, which make the multicomponent systems similar to the biological process. For example, in the cell, varieties of components exist to perform numerous functions to attain the chemical activities needed for the survival of the cell.
3.2. Dispersibility and antioxidant activities of nanoemulsions
A weaker CF increases the surface activities of flavonoids in 10% aq-DMSO, which facilitate flavonoids forming small-sized hydrophobic clusters. BSA (2 g L−1) with 10% aqueous BSA–DMSO (WBD) solution acted as a stabiliser for the formulation of stable aqueous CnTAB by varying its compositions with WBD. UV-visible spectra diluted quercetin formulation with 0.04 mol kg−1 CnTAB of variable ACL: C-12 (DTAB), C-14 (TDTAB), and C-16 (HDTAB). Quercetin in aqueous medium did not show any peaks within the 300–450 nm range (Fig. 10) because of an unstable dispersion of quercetin in aqueous solution with no absorption peak. The solutions prepared in the presence and absence of BSA with surfactant in the aq-DMSO system expressed stronger absorption peaks within the 300–450 nm range. The absorbances reported in Table S5† are such that (Q + W) < WDQ-DTAB < WDQ-TDTAB < WDQ-HDTAB (without BSA) and (Q + W) < WBDQ-DTAB ≤ WBDQ-TDTAB < WBDQ-HDTAB (with BSA). Also, (WBDQ-HDTAB) < (WDQ-HDTAB); (WBDQ-TDTAB) > (WDQ-TDTAB); and (WBDQ-DTAB) > (WDQ-DTAB). BSA with surfactant acted as cosurfactants and increased the overall dispersibility of quercetin. With BSA, the absorbance of formulations made with DTAB, TDTAB and HDTAB decreased drastically (Table S5†), as shown in Fig. S5.† BSA induced the homogeneity of the CnTAB dispersion of variable ACL by nullifying an impact of the AC of CnTAB in formulation stability and disparity. Such formulations, due to the high surface area of quercetin and excellent homogeneous dispersibility of quercetin have resulted in a better scavenging activity of free radicals (FRs) as compared to poorly dispersed quercetin. For preparing stable nanoemulsions (NEs) of flavonoids, the PCPs and thermodynamic properties of formulations illustrate the role played by solute–solute interaction (SLSLI) and solute–solvent interaction (SLS0I) in regards to kinetic and thermodynamic stability. CnTAB in water decreased γ, which helped in the formulation of kinetically stable NEs, because the intensity of CF acting between the water molecules drastically reduced with increasing ACL. Since friccohesity (σ) is a multiple of the CF and FF of solvents, a decrease in CF was compensated with the development of FF in terms of SLS0I. This increased SLSLI result increased the dispersibility of solute molecules observed in all the formulations studied (Fig. S6†). In Fig. S7,† BSA acts as hydrophobic oil molecules, whereas α and β sheet platelets act as of the hydrophobic domain similar to an alkyl chain of oil. As such, NEs similar to syrups act as a chemically effective kinetic medium to homogenized drugs which are not dispersed in the ordering medium. NEs contain many physicochemical properties, high surface area, optically transparent appearance, tunable rheology, robust stability, and high distribution capacity; because of such properties, NEs could be used for the recovery of petrochemicals, physiologically toxic wastes from recalcitrant streams and in pharmaceuticals.30 With an increasing concentration and hydrophobicity of CnTAB in WBD systems, the surface energy decreases, while shear stress increases due to the weakening of CFs and stronger IMF with linear order (Fig. S8†). The flavonoid in WBD with CnTAB decreases surface energy and increases shear stress with polynomial order, so the flavonoid, having philicphobic nature, could induce irregularities (Fig. S9†). The magnitude and trends of PCPs are very exciting, so the data were processed to extract an extraordinary science in a most expressive elucidation to illustrate the dispersion of flavonoids. Thus, their mechanistic stoichiometry could be extended to dipolar DMSO, DMF and others vis-à-vis their philicphobic potential compatible with BSA to explore a state-of-the-art aq-DMSO–BSA–Fv-surfactant string as a most constitutional framework. The abovementioned science constitutes a more stable nanoemulsion for more than four months, where no phase separation, clustering or agglomeration occurs. Our formulations have been industrially very important with their higher shelf life and high solubilizing potential as well.
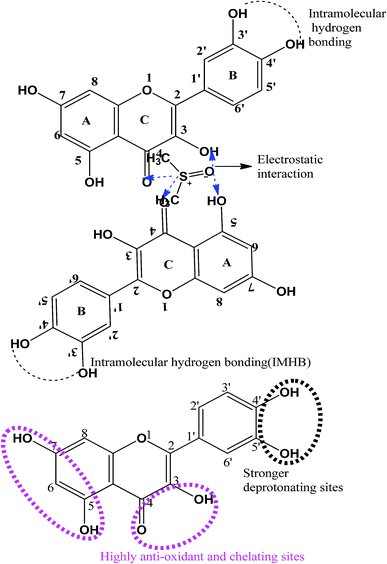 |
| | Fig. 10 Possible interacting sites in the quercetin molecular structure. | |
3.3. Viscometric study (η)
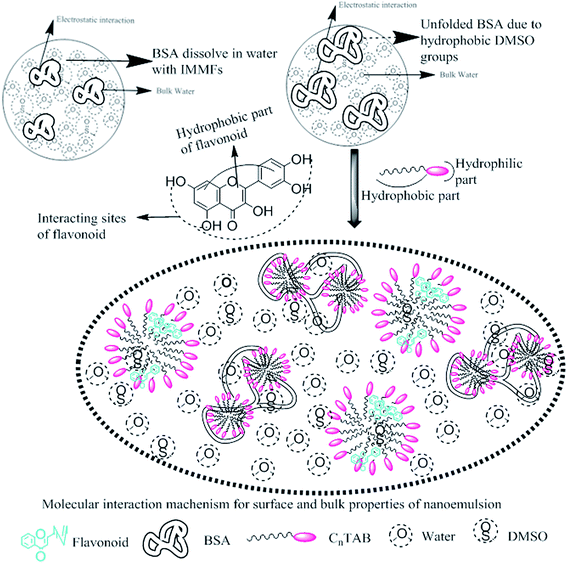
The η data for CnTAB with mixed solvents were measured at T = 298.15, 303.15 and 308.15 K and are reported in Table S6.† Viscosity is the scanning and transporting property of a liquid mixture, which works based on frictional forces (FFs) between the solute–solvent and FFs of capillaries with the solution molecules. The η data can calculate relative viscosity (ηr) as:41| |
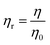 | (3) |
where η0 and η are the viscosities of the solvent and solution, respectively. The ηr values are given in Table 1. The behaviour of ηr vs. the m of CnTAB (Fig. S10–13†) is similar to surfactant solutions.42–44 The ηr value of the solvent systems are such that WBDA > WBDN > WBDQ > WBD. Apigenin shows a higher ηr value, as it belongs to a flavone class having 3 –OH groups, one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and one double bond at the C-ring in its molecular structure, compared to a single bond in naringenin. However, apigenin has 1 –OH group at the B-ring that could induce stronger interaction affinity towards BSA and could not form intramolecular hydrogen bonding (IMHB). Quercetin has 5 –OH groups and one double bond with π-conjugation at the C-ring due to the 2 –OH groups placed at the B-ring and could form IMHB (Fig. 10) with decreasing interacting sites. Apigenin shows a higher ηr value than naringenin or quercetin. Spectroscopic interaction study of flavonoids with proteins by the quenching constant and the binding constant of apigenin with proteins show higher interactions than quercetin or naringenin.45 For example, CnTAB with WBDQ, WBDA and WBDN showed different trends of ηr values at T = 298.15, 303.15 and 308.15 K. The surfactants could form micelles with air gates;46,47 with increasing ACL, air could enter the micelles through the air gates, so increasing the temperature created an asymmetric trend of ηr values. Upon increasing the ACL, the ηr value increased with the weakening of CF in addition to stronger electrostatic interaction and IMF (Fig. 11). With increasing temperature, the ηr value decreased because of the increased KE as the binding forces (BF) and IMMF weakened.
O group and one double bond at the C-ring in its molecular structure, compared to a single bond in naringenin. However, apigenin has 1 –OH group at the B-ring that could induce stronger interaction affinity towards BSA and could not form intramolecular hydrogen bonding (IMHB). Quercetin has 5 –OH groups and one double bond with π-conjugation at the C-ring due to the 2 –OH groups placed at the B-ring and could form IMHB (Fig. 10) with decreasing interacting sites. Apigenin shows a higher ηr value than naringenin or quercetin. Spectroscopic interaction study of flavonoids with proteins by the quenching constant and the binding constant of apigenin with proteins show higher interactions than quercetin or naringenin.45 For example, CnTAB with WBDQ, WBDA and WBDN showed different trends of ηr values at T = 298.15, 303.15 and 308.15 K. The surfactants could form micelles with air gates;46,47 with increasing ACL, air could enter the micelles through the air gates, so increasing the temperature created an asymmetric trend of ηr values. Upon increasing the ACL, the ηr value increased with the weakening of CF in addition to stronger electrostatic interaction and IMF (Fig. 11). With increasing temperature, the ηr value decreased because of the increased KE as the binding forces (BF) and IMMF weakened.
Table 1 Relative viscosity (ηr) of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol kg−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1 respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa, and expanded uncertainties Uc (95% confidence interval) is Uc (ηr) = ±0.0041. |
| 0.00 |
0.9482 |
0.9759 |
0.9660 |
0.9482 |
0.9759 |
0.9660 |
0.9482 |
0.9759 |
0.9660 |
| 0.01 |
1.0025 |
0.9906 |
1.0240 |
1.0794L |
1.0306 |
1.1609 |
1.0933 |
1.1450 |
1.1611 |
| 0.02 |
1.0108 |
1.0430 |
1.0438 |
1.1037 |
1.0883 |
1.1675 |
1.2258 |
1.2553 |
1.2578 |
| 0.04 |
1.0040 |
1.1235 |
1.1021 |
1.1299 |
1.1659 |
1.1909 |
1.4018 |
1.3163 |
1.2962 |
| 0.06 |
1.0844 |
1.1726 |
1.1410 |
1.3035 |
1.2341 |
1.2230 |
1.7073 |
1.3699 |
1.3562 |
| 0.08 |
1.1756 |
1.2174 |
1.2149 |
1.5088 |
1.2964 |
1.2615 |
1.9608 |
1.4239 |
1.3835 |
| 0.10 |
1.3510 |
1.2504 |
1.2585 |
1.8906 |
1.3396 |
1.2956 |
2.3867 |
1.5113 |
1.4270 |
| m/mol kg−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.01 |
1.0063 |
0.9817 |
0.9589 |
1.0307 |
1.0468 |
0.9914 |
1.2737 |
1.0532 |
1.0340 |
| 0.02 |
1.0833 |
1.0849 |
1.1258 |
1.0810 |
1.1064 |
1.0196 |
1.3665 |
1.1250 |
1.1340 |
| 0.04 |
1.0813 |
1.2662 |
1.1901 |
1.1257 |
1.0760 |
1.1301 |
1.1945 |
1.2593 |
1.1635 |
| 0.06 |
1.1352 |
1.0579 |
1.0636 |
1.1785 |
1.1585 |
1.1992 |
1.2706 |
1.2718 |
1.2606 |
| 0.08 |
1.1805 |
1.2162 |
1.1332 |
1.2424 |
1.3308 |
1.2120 |
1.3472 |
1.3221 |
1.3322 |
| 0.10 |
1.1964 |
1.2634 |
1.1718 |
1.2845 |
1.2415 |
1.2848 |
1.4187 |
1.4949 |
1.1049 |
| m/mol kg−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1.0095 |
0.9615 |
1.0477 |
1.0095 |
0.9615 |
1.0477 |
1.0095 |
0.9615 |
1.0477 |
| 0.01 |
0.9935 |
1.1550 |
0.9431 |
1.0270 |
1.0916 |
0.9735 |
1.0511 |
1.0906 |
1.0837 |
| 0.02 |
1.0189 |
1.1932 |
1.1087 |
1.0441 |
1.1390 |
1.0028 |
1.1892 |
1.1800 |
1.0156 |
| 0.04 |
1.0732 |
1.1005 |
1.1736 |
1.1522 |
1.1936 |
1.1140 |
1.2877 |
1.5281 |
1.1159 |
| 0.06 |
1.0874 |
1.2003 |
1.0498 |
1.1704 |
1.2968 |
1.1833 |
1.3238 |
1.5714 |
1.1467 |
| 0.08 |
1.1309 |
1.2276 |
1.1187 |
1.2073 |
1.3143 |
1.1962 |
1.3749 |
1.6665 |
1.2430 |
| 0.10 |
1.1498 |
1.2588 |
1.1572 |
1.2951 |
1.3407 |
1.2682 |
1.4662 |
1.7459 |
1.3143 |
| m/mol kg−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
0.9963 |
1.1063 |
1.0926 |
0.9963 |
1.1063 |
1.0926 |
0.9963 |
1.1063 |
1.0926 |
| 0.01 |
1.0017 |
0.9958 |
1.1016 |
1.0321 |
0.9419 |
0.9899 |
1.2614 |
1.0365 |
1.1516 |
| 0.02 |
1.0304 |
0.9352 |
1.1570 |
1.0704 |
0.9237 |
0.9757 |
1.2846 |
1.0083 |
1.1122 |
| 0.04 |
1.0500 |
0.9740 |
1.0540 |
1.1262 |
1.0913 |
0.9885 |
1.3170 |
1.3120 |
1.0563 |
| 0.06 |
1.0835 |
0.9640 |
1.1221 |
1.1897 |
1.0797 |
1.0934 |
1.2557 |
1.1239 |
1.1670 |
| 0.08 |
1.1425 |
0.9952 |
1.1022 |
1.2122 |
1.1441 |
1.1394 |
1.3161 |
1.2168 |
1.2891 |
| 0.10 |
1.2314 |
1.1444 |
1.0494 |
1.2919 |
1.3736 |
1.2116 |
1.4563 |
1.2113 |
1.2760 |
 |
| | Fig. 11 Stoichiometry interaction mechanism of BSA–flavonoid with CnTAB in 10% (w/w) aq-DMSO for the dispersibility of the flavonoid. | |
PCPs have the most authentic data, which sequentially reflect the chemical activities attained by studying the structural interactions of flavonoids and BSA in aqueous DMSO surfactant mixtures. In CnTAB, n = 12–16 had weakened the cohesive force of aq-DMSO to attain a longer surface area of the interacting species, which favoured monodispersion. The PCPs depict a state of nanoformulation which was achieved by the function of CnTAB, where n = 12–16 surfactants. The PCPs acted as an authentic indicator to determine the nanoemulsion state and dispersibility of flavonoids as the higher surface tension inferred the anti-dispersion and viscosity of the dispersing activities, respectively.30 Thus, the study of the PCPs was initiated to formulate a nanoemulsion to monodisperse the antioxidants or biocatalysts or biocompatible gold, silver, or magnetic nanoparticles to monodisperse without facing any hurdles of chemical activities like the stronger cohesive forces of the medium. Stronger cohesive forces with higher surface tension favour agglomeration rather than monodispersion without applying any external forces like UV light or electric or magnetic forces. For these especially, UV light induces undesired electronic transitions and damage the structures that initiate a secondary chemical process. Therefore, the surface tension directly reflects the state of cohesive forces complemented by the viscosity data along with the refractive index, conductance, and others. The surfactants reduced the cohesive forces that reduce the binding energy, so a lowering of surface tension increases the surface area with a larger monodispersion of flavonoids in the medium. This was supplemented with an increase in the shear stress and shear rate depicted with higher viscosity values with a subsequent decrease in conductance data.
The comparatively low hydrophobicity of DTAB increases ΔS with a decrease in ΔG, which meet at T/K, but their behaviour changes with increasing C-atoms in their ACL. The increasing kinetic energy (KE) noted is affected by their chemical activities:
| |
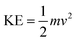 | (4) |
where
m is the mass and
v is the velocity. Fig. S10–13
† shows that the quercetin, apigenin and naringenin in WBD solution increase the
ηr values, because the flavonoids increase the hydrophobicity and weaken the CF with stronger FF, IDI and higher
Pint. Furthermore, the
ηr value is close to unity, which implies that the molecular rearrangements of C
nTAB with BSA–flavonoids solution are minimized with increasing
ηr values. The BSA–flavonoid with C
nTAB could finally act as an electrolyte, and the charged species of surfactants increased the
ηr values (
Table 1). This assumes that the combination of C
nTAB may form micelles with a solvent, causing an expansion in 10% (w/w) aq-DMSO. When the saturation interaction of C
nTAB with the BSA–flavonoid systems is reached, then the 0.10 mol kg
−1 C
nTAB, BSA and flavonoid increase their dispersibility. This induces an increment in ionic strength.
48 The
η values were used to calculate the viscous relaxation time (
τ) by through the following equation:
49| |
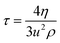 | (5) |
where
ρ is the density (Table S7
†),
η is the viscosity (Table S6
†) and
u is the sound velocity (Table S8
†) used for
τ measurement.
30 The calculated
τ values are given in
Table 2 and are plotted in Fig. S14–17.
† The
τ value depends on C
nTAB concentration and the interaction ability of flavonoids with BSA, where the temperature may be related to the structural relaxation process occurring due to the rearrangement of molecules.
50 With increasing temperature, the
τ value decreased due to the weakening of IMF and electrostatic interaction. The
τ values are such that WBDA > WBDN > WBD > WBDQ; this order is similar to the
ηr and
ρ data. Upon increasing the ACL, the
τ value increased due to the weakening of surface forces in addition to stronger electrostatic interaction and ion-hydrophobic interaction (IH
bI). With the inclusion of DTAB into the solvent systems, the
τ value decreased with WBD, WBDA, and WBDN, while with WBDQ, it slightly increased. Consequently, for TDTAB and HDTAB systems, the
τ values increase for 0.01 to 0.1 mol kg
−1 C
nTAB. The hydrophobicity causes a more stable effect than the temperature effect (Fig. 1S
†) because, at each temperature, the DTAB with C-12 atoms produced a lower
ηr, suggesting a lower shear. However, from C-14 to C-16 atoms in the AC of TDTAB and HDTAB, respectively,
ηr increased, which further strengthen the shear stress with increasing ACL. The continuous increment in
ηr upon increasing C-atoms predicts the stronger hydrophobic interaction of surfactant with DMSO and BSA. A rise in temperature could not change the trend, as the increased hydrophobicity upon increasing the C-atoms in AC did not disrupt their hydrophobic–hydrophobic interactions (H
bH
bI) from 298.15 to 308.15 K. The increasing AC also develops the hydrophobic interactions with BSA and DMSO. Quercetin develops stable interactions with a definite state function with DTAB, but with TDTAB and HDTAB, the interactions wavered with no stable state formation. Quercetin with 5 –OH groups engaged H
2O five times as:
| H2O:: +H+ → H3O+ → H2O–H+ → H3O+ |
Table 2 Viscous relaxation time (τ/ps) of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m.mol kg−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1 respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa, and expanded uncertainties Uc (95% confidence interval) is Uc (τ) = ±0.001 ps. |
| 0.00 |
0.572 |
0.477 |
0.462 |
0.572 |
0.477 |
0.462 |
0.572 |
0.477 |
0.462 |
| 0.01 |
0.570 |
0.469 |
0.470 |
0.614 |
0.489 |
0.534 |
0.623 |
0.544 |
0.535 |
| 0.02 |
0.572 |
0.493 |
0.479 |
0.627 |
0.515 |
0.537 |
0.698 |
0.596 |
0.580 |
| 0.04 |
0.568 |
0.530 |
0.505 |
0.642 |
0.552 |
0.548 |
0.797 |
0.625 |
0.597 |
| 0.06 |
0.614 |
0.554 |
0.523 |
0.741 |
0.585 |
0.563 |
0.971 |
0.650 |
0.625 |
| 0.08 |
0.665 |
0.575 |
0.557 |
0.857 |
0.615 |
0.581 |
1.115 |
0.676 |
0.638 |
| 0.10 |
0.764 |
0.590 |
0.577 |
1.074 |
0.635 |
0.597 |
1.358 |
0.718 |
0.658 |
| m/mol kg−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
0.568 |
0.478 |
0.479 |
0.568 |
0.478 |
0.479 |
0.568 |
0.478 |
0.529 |
| 0.01 |
0.569 |
0.467 |
0.457 |
0.584 |
0.500 |
0.473 |
0.722 |
0.504 |
0.495 |
| 0.02 |
0.611 |
0.515 |
0.535 |
0.610 |
0.525 |
0.485 |
0.770 |
0.534 |
0.539 |
| 0.04 |
0.608 |
0.600 |
0.565 |
0.635 |
0.511 |
0.538 |
0.674 |
0.598 |
0.554 |
| 0.06 |
0.639 |
0.501 |
0.505 |
0.664 |
0.550 |
0.571 |
0.716 |
0.603 |
0.599 |
| 0.08 |
0.664 |
0.576 |
0.538 |
0.700 |
0.632 |
0.577 |
0.759 |
0.627 |
0.634 |
| 0.10 |
0.673 |
0.599 |
0.557 |
0.725 |
0.590 |
0.612 |
0.799 |
0.709 |
0.526 |
| m/mol kg−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
0.576 |
0.457 |
0.483 |
0.576 |
0.457 |
0.483 |
0.576 |
0.457 |
0.483 |
| 0.01 |
0.572 |
0.527 |
0.456 |
0.593 |
0.501 |
0.476 |
0.608 |
0.501 |
0.530 |
| 0.02 |
0.587 |
0.544 |
0.536 |
0.601 |
0.520 |
0.487 |
0.685 |
0.539 |
0.493 |
| 0.04 |
0.613 |
0.500 |
0.565 |
0.663 |
0.545 |
0.539 |
0.740 |
0.698 |
0.541 |
| 0.06 |
0.623 |
0.546 |
0.505 |
0.673 |
0.592 |
0.572 |
0.760 |
0.718 |
0.555 |
| 0.08 |
0.648 |
0.558 |
0.538 |
0.693 |
0.599 |
0.577 |
0.788 |
0.761 |
0.601 |
| 0.10 |
0.658 |
0.572 |
0.556 |
0.744 |
0.611 |
0.612 |
0.837 |
0.798 |
0.636 |
| m/mol kg−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
0.576 |
0.532 |
0.510 |
0.576 |
0.532 |
0.510 |
0.576 |
0.532 |
0.510 |
| 0.01 |
0.568 |
0.523 |
0.556 |
0.590 |
0.500 |
0.503 |
0.719 |
0.549 |
0.584 |
| 0.02 |
0.581 |
0.489 |
0.580 |
0.608 |
0.486 |
0.493 |
0.730 |
0.530 |
0.562 |
| 0.04 |
0.592 |
0.508 |
0.528 |
0.639 |
0.573 |
0.498 |
0.749 |
0.690 |
0.534 |
| 0.06 |
0.611 |
0.503 |
0.562 |
0.673 |
0.567 |
0.549 |
0.712 |
0.591 |
0.588 |
| 0.08 |
0.643 |
0.519 |
0.551 |
0.687 |
0.601 |
0.574 |
0.746 |
0.640 |
0.650 |
| 0.10 |
0.693 |
0.597 |
0.525 |
0.731 |
0.721 |
0.610 |
0.825 |
0.637 |
0.643 |
Such wavering was seen in Fig. S10b and c† because the hydrophobicity developed with increasing C-atoms, which could not disrupt their HbHbI from 298.15 to 308.15 K. The increasing AC aided in the development of hydrophobic interactions with the BSA and DMSO. In apigenin, the 3 –OH groups engaged H2O with H+ thrice to cause the following reaction H2O:: → H3O+ with comparatively less wavering (Fig. S10b and c†) to infer constitutional parameters like viscous relaxation time (τ) the response of apigenin, quercetin and naringenin with the medium as synchromatic or asynchromatic.
3.4. Walden product
The Walden product (Table 3) was calculated with eqn (6):51| |
Walden![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) product = η0κ0 product = η0κ0
| (6) |
where η0 is the limiting viscosity and κ0 is the limiting specific conductance of solution. The Walden product depends on mobility, size, the concentration of ions and the nature of solute–solvent interactions (SLS0I). Walden product is such that WBDA > WBD > WBDQ > WBDN with DTAB, WBDQ > WBDA > WBDN > WBD with TDTAB, and WBDQ > WBDN > WBD > WBDA with HDTAB. Table 3 shows that the increasing ACL (hydrophobic spacer group), decrease the Walden product value. BSA with both the hydrophobic and hydrophilic domains in its structure unfold with stronger IHbI ion hydrophilic interaction (IHI). This decreases the mobility of ions with a decrease in specific conductance and Walden product. Apigenin shows a higher Walden product with DTAB as compared to WBDQ and WBDN with TDTAB and HDTAB. Apigenin with 3 –OH groups and one (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) bond at its C-ring has structural homology to quercetin except for two additional –OH groups at the A- and B-rings. Apigenin shows a higher Walden product with DTAB than quercetin or naringenin. The Walden product value is such that DTAB > TDTAB > HDTAB. This leads to DTAB having a higher charge density and stronger IHI with higher specific conductance.
) bond at its C-ring has structural homology to quercetin except for two additional –OH groups at the A- and B-rings. Apigenin shows a higher Walden product with DTAB than quercetin or naringenin. The Walden product value is such that DTAB > TDTAB > HDTAB. This leads to DTAB having a higher charge density and stronger IHI with higher specific conductance.
Table 3 Walden product (Λ0η0) of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| T/K |
Λ0η0 |
| WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality to a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol−1 kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1 respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa. |
| 298.15 |
0.1846 |
0.1563 |
0.0743 |
| 303.15 |
0.1646 |
0.1340 |
0.0696 |
| 308.15 |
0.1706 |
0.1187 |
0.0701 |
| |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 |
0.1808 |
0.1794 |
0.1787 |
| 303.15 |
0.1731 |
0.1543 |
0.1184 |
| 308.15 |
0.2031 |
0.1919 |
0.1135 |
| |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 |
0.2252 |
0.1756 |
0.0687 |
| 303.15 |
0.2319 |
0.1516 |
0.0717 |
| 308.15 |
0.2129 |
0.1500 |
0.0613 |
| |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 |
0.1552 |
0.1662 |
0.0886 |
| 303.15 |
0.1710 |
0.1491 |
0.0715 |
| 308.15 |
0.1703 |
0.1416 |
0.0658 |
3.5. Thermodynamic parameters
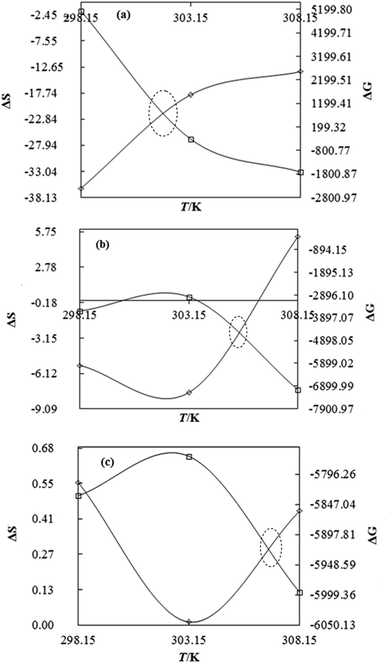
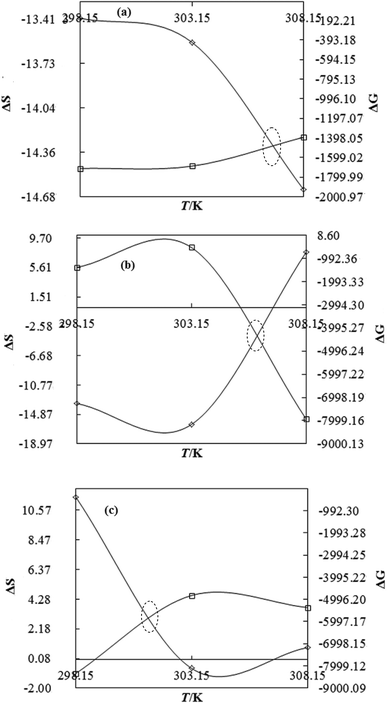
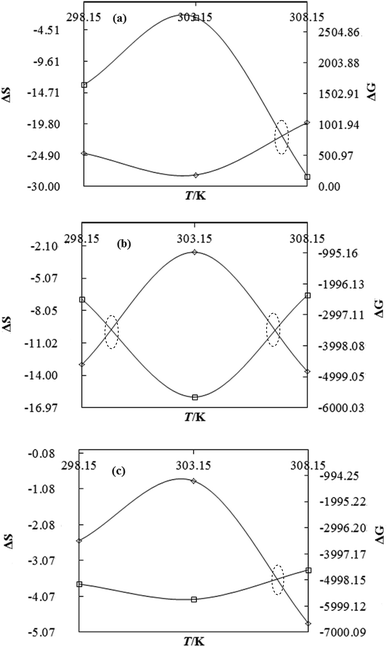
Nanoclusters of CnTAB with solvent systems are reoriented at T = 298.15, 303.15 and 308.15 K which are relevant for understanding the molecular interacting mechanism of BSA and flavonoids with CnTAB in aq-DMSO. The activation energy (E*) plays a vital role in the formation of a stable nanoemulsion. So, we calculated E* to calculate the ΔS, ΔG (Fig. 12–15) and ΔH values (Table S9†). E* is calculated using the Arrhenius equation at T = 298.15, 303.15 and 308.15 K and was fitted as:| |
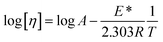 | (7) |
where [η] is the intrinsic viscosity, T is the temperature (Kelvin), R is the gas constant (8.314 J mol−1 K−1), A is the frequency factor, and E* is the activation energy (J mol−1), log[η] versus 1/T. Furthermore, E* data was used to calculate the ΔH as shown below.
 |
| | Fig. 12 The ΔS (◊) and ΔG (□) value of WBD with DTAB (a), TDTAB (b) and HDTAB (c) at T = 298.15, 303.15 and 308.15 K. | |
 |
| | Fig. 13 The ΔS (◊) and ΔG (□) value of WBDQ with DTAB (a), TDTAB (b) and HDTAB (c) at T = 298.15, 303.15 and 308.15 K. | |
 |
| | Fig. 14 The ΔS (◊) and ΔG (□) value of WBDA with DTAB (a), TDTAB (b) and HDTAB (c) at T = 298.15, 303.15 and 308.15 K. | |
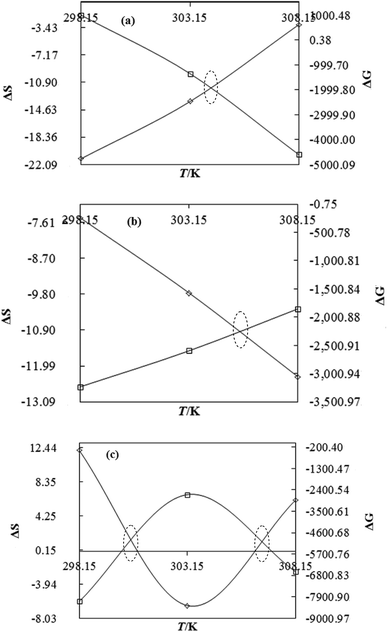 |
| | Fig. 15 The ΔS (◊) and ΔG (□) value of WBDN with DTAB (a), TDTAB (b) and HDTAB (c) at T = 298.15, 303.15 and 308.15 K. | |
ΔG and ΔS for stable nanoemulsions were calculated with the equations given as:
| |
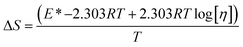 | (9) |
| |
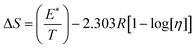 | (10) |
| |
ΔG = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[η] log[η]
| (11) |
DTAB shows a symmetric increase in ΔS with a decrease in ΔG with respect to temperature (Fig. 16). The longer C-atom (TDTAB) is regularly loose, as a weaker alignment keeps developing that convolutes to align and orient towards hydrophobic or hydrophilic monitored activities. With T/K, the regulatory activities are disturbed due to KE with different trends observed in Fig. 15a and b. The surfactants increase the ΔS value (Table S10†) by interfering with the IMMF mediated by non-covalent forces, HB, electrostatic interaction and van der Waals interactions. An increasing surfactant concentration could denature maximum BSA structure upon increasing the ΔS value. With increasing temperature, the ΔS value increases because the molecules gain more energy haphazardly. The oscillation (rotational, vibrational, and translational motions) could be induced in molecules to increases the ΔS value. The WBD system shows a lower ΔS value than WBDQ, WBDA or WBDN. The BSA in the aq-DMSO solution with amphiphilic DMSO and BSA could form a cluster with stronger electrostatic interaction to order with lower the ΔS values. With the inclusion of quercetin into the WBD system, the ΔS value increases as it has two aromatic rings and one heterocyclic C-ring, which develop stronger hydrophobicity. Upon increasing the ACL of CnTAB, the ΔS value increased due to stronger hydrophobicity with a maximum HB disruption of solute and solvent molecules that increased the haphazardness. With apigenin and naringenin in the WBD systems, the changes in the ΔS values were very close to each other because of their similar structures except for the absence of one double bond at the C-ring. Naringenin showed a stronger hydrophobicity than apigenin. CnTAB with WBDA showed a lower ΔS value than WBDQ or WBDN. Apigenin showed higher ρ, ηr, τ and Walden product values with stronger IMF and also formed a more stable nanoemulsion. The surfactants in the WBDA system consumed the maximum energy for the disruption of the apigenin bond. However, the rest of the energy could be involved in the bond association or dissociation processes. Apigenin and naringenin with C-14 and C-16, respectively, show varied ΔS and ΔG trends with T/K. This proves that temperature substantially affects the interactions, repeating similar paths like clock reactions. Temperature plays a vital role vis-a-vis thermodynamic properties, which depend on energy. As the temperature increased, the oscillations could commence, and because of oscillations, the intermolecular bonding of either association or dissociation processes occurred. During the formation of a complex, more energy is consumed in bond formation, which decreases ΔS. The ΔH value infers that for the binding energy for the inclusion of quercetin into WBD, ΔS decreased with increasing temperature. Quercetin has 5 –OH groups, two benzene rings (A and B) and one double bond at the heterocyclic C-ring in its molecular structure, which could develop strong interaction with the WBD systems. So, as the temperature increased, the ΔS value of the WBDQ system decreased due to stronger IHI and IDI. So, with quercetin in the WBD system, BSA could be unfolded with a growing binding site for interaction. aq-DMSO acts as a linker, causing the stronger interaction of BSA with flavonoids that decreases the ΔS value. ΔS decreased for WBDQ with DTAB and TDTAB, while with HDTAB, ΔS increased due to HDTAB having a longer ACL, which could be disrupted the higher number of HB. For CnTAB with WBDA, ΔS increased with increasing temperature. The molecular structure of apigenin is very similar to quercetin except for the two fewer –OH groups. So, the 2 –OH groups present at the B- and C-rings could hinder oscillation as the temperature increased. Due to IMHB formation, the interacting sites decreased and the hydrophobicity increased. Hence, maximum BSA could be unfolded to develop stronger electrostatic interactions. Similar to WBDN with DTAB, the ΔS value increased with increasing temperature, while the HDTAB decreased the ΔS value in relation to TDTAB, naringenin itself was more hydrophobic than quercetin or apigenin due to the absence of a double bond at the C-ring. The stoichiometric properties and temperature played a vital role in understanding the molecular interaction mechanism. WBDA showed a more negative entropy and heat capacity, as apigenin has a higher interaction ability that increases the electron spin KE as well as the rotational, vibrational and translational motions. This demonstrates a higher heat holding capacity as compared to quercetin and naringenin. Apigenin, naringenin and quercetin having hydrophobic constituents could develop stronger dispersion and Brownian motion upon decreasing the dipole interaction of the aq-DMSO system.
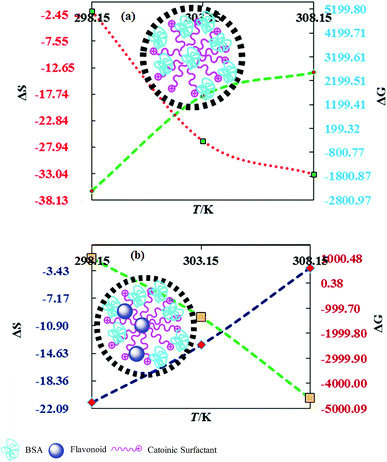 |
| | Fig. 16 Effect of thermodynamic properties on BSA–CnTAB and BSA–flavonoid–CnTAB in 10 % (w/w) aq-DMSO. | |
ΔH is the highest and ΔS is the lowest, hence
3.6. Gibbs free energy (ΔG) and enthalpy (ΔH)
As the ACL with the WBD system increased, the ΔH value increased, disrupting the HB upon increasing the binding energy through strong electrostatic interaction and van der Waal forces. The ΔH values are such that WBDN > WBDA > WBD > WBDQ with CnTAB. ΔS is higher for WBDN with CnTAB, as naringenin showed a higher hydrophobicity than apigenin or quercetin. It could denature the maximum BSA structure with a stronger IHbI upon forming a stable formulation. It also increases the ΔH values with stronger non-covalent bonding. The functional group, molecular configuration, formation of a double bond and atomic size act as a structural sensor to express flavonoids under prescribed physical conditions. Fig. 15 shows the structural effect of the hydrophobicity or entropic distribution of flavonoids at the cost of their structural disruption, which occurs at a ΔG value (Table S11†).
Lowering ΔG with increasing C-atoms in AC infers that stronger HbHbI and flavonoids could induce BSA unfolding activities because lowering ΔG infers a higher utilization of medium energy. This causes unfolding through BSA–Fv interactions, where the DMSO with two hydrophobic CH3– groups and >s+![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) o− hydrophilic ions catalyse the BSA unfolding and HB disruption of H2O. In regards to DMSO and flavonoids, the smaller molecules penetrate α to β BSA sheets increases unfolding from α → β convolutions, where the DMSO and the flavonoid KE destabilize.
o− hydrophilic ions catalyse the BSA unfolding and HB disruption of H2O. In regards to DMSO and flavonoids, the smaller molecules penetrate α to β BSA sheets increases unfolding from α → β convolutions, where the DMSO and the flavonoid KE destabilize.
Flavonoids with DMSO could approach α → β convolutions that could weaken the potential energy (PE) of BSA, which increase ΔS but decrease ΔG (Fig. 17). BSA unfolds and a BSA–Fv interaction induces much disturbance in the molecules.
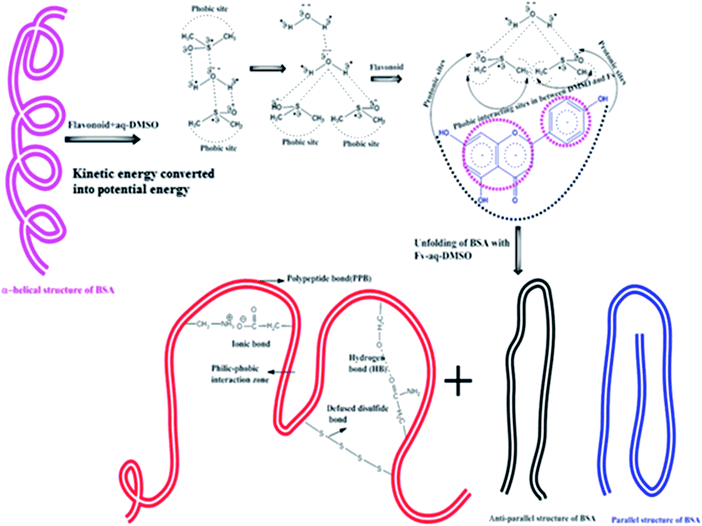 |
| | Fig. 17 Unfolding of BSA with Fv in the aq-DMSO system through the conversion of potential energy (PE) to kinetic energy (KE). | |
ηD and viscous flow time (VFT) both are higher and ΔS is lower for apigenin; it has produced high VFT and ηD both due to stronger interaction of WBD in the development of stronger IMF. The stronger IMF makes the resultant apigenin highly condensed or structured, which was proven by the higher τ as the structured liquid takes longer to set into the original dimension of fluid dynamics. ΔG decreases with increasing ΔS with a weaker binding force (BF). The lowest ΔG value induces robust bond motion or bond moment (BM), causing a maximum dynamism in the mixture.
| |
η = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ae−E/RT Ae−E/RT
| (12) |
| |
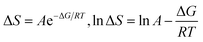 | (13) |
| |
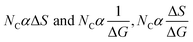 | (14) |
or
| |
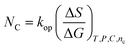 | (15) |
kop is an operating constant,
NC is the number of carbon,
T is the temperature in Kelvin and
C is the concentration, which explain the drug-friccohesity interaction (DFI) model:
| |
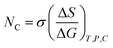 | (16) |
where
σ is the friccohesity, which shifts in the case of hydrophobicity or hydrophilicity; the trend is reversed due to the ionic field. The additive role is fitted in friccohesity shift model (FSM) as per their hydrophobicity and hydrophilicity. It acts as an additive or destructive or constructive interference caused in the nanoemulsion as nanodispersion due to the thermodynamic friccohesity shift.
| |
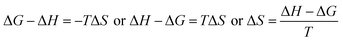 | (17) |
If ΔH = (−) ve is an exothermic process but ΔH = (+) ve is an endothermic process, ΔH depends on the hydration sphere of hydrophobes and the hydrophilic nature of SLS0I and SLSLI. The negative ΔG infers spontaneous interaction. According to the views of Ross and Subramanian,50 when ΔH < 0 or ΔH ≈ 0 and ΔS > 0, the main force is due to electrostatic interactions; when ΔH < 0 and ΔS < 0, the main force is due to van der Waals or hydrogen bonding; and when ΔH > 0 and ΔS > 0, the main force is due to hydrophobic interactions, which are applicable in our studies.
3.7. Binding modes
The binding sites are calculated for CnTAB with solvent systems by using the van't Hoff equation:43| |
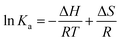 | (18) |
where Ka is the binding constant, T is the temperature in Kelvin and R is the gas constant. The four types of non-covalent interactions existing in drug binding to proteins could occur. These are hydrogen bonds, electrostatic forces, van der Waals forces, and hydrophobic interaction forces.52 In order to elucidate the interaction between flavonoids and BSA with CnTAB, the thermodynamic parameters were calculated from van't Hoff plots. ΔH was calculated from the slope of the van't Hoff relationship. ΔG was then estimated from eqn (16). A negative value of ΔH suggests an exothermic binding reaction while a negative ΔG depicts a thermodynamically favourable process. Positive ΔS and negative ΔH values were invoked to characterize the hydrophobic interactions in the binding phenomenon.44,52 For water structure, a positive ΔS signifies a hydrophobic interaction, since the water molecules are arranged in an orderly fashion to acquire a more random configuration as a result of the hydrophobic interaction.52 For the BSA and surfactants in aq-DMSO solution, both the DMSO and BSA have hydrophobicity that could the break the HB as more and more energy is released from the system, so we found negative values for the heat holding capacity (Δq) (Table 4).| |
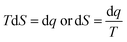 | (19) |
| | |
T1dS1 = dq1, T2dS2 = dq2 and T3dS3 = dq3
| (20) |
| |
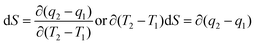 | (21) |
Table 4 The Δq/J K−1 of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| T/K |
Δq/J K−1 |
| WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa. |
| 298.15 |
−10835.52 |
−1625.84 |
165.77 |
| 303.15 |
−5482.38 |
−2340.65 |
3.58 |
| 308.15 |
−4179.31 |
1652.48 |
136.79 |
| |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 |
−3997.42 |
−3983.25 |
3431.59 |
| 303.15 |
−4116.81 |
−4933.43 |
−185.25 |
| 308.15 |
−4509.74 |
2374.97 |
264.48 |
| |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 |
−7329.36 |
−3880.57 |
−752.23 |
| 303.15 |
−8522.85 |
−811.35 |
−261.83 |
| 308.15 |
−6035.42 |
−4203.63 |
−1489.6279 |
| |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 |
−6347.14 |
−2227.60 |
3617.24 |
| 303.15 |
−4096.95 |
−2960.90 |
−1975.32 |
| 308.15 |
−936.13 |
−3799.70 |
1901.75 |
In Table 4, apigenin shows a higher negative heat capacity as compared to quercetin and naringenin. This due to its π-conjugation and higher binding sites.
3.8. Refractive index (nD)
The molecular interactions developed an internal pressure (Pint) to optimize the resultant state of the liquid mixture. Density (ρ) defines the Pint of liquid mixtures. Also, cohesion and cohesion–adhesion become prominent activities in such a liquid mixture, which can be explained with friccohesity (σ) via surface energy or surface tension (γ).Pint structurally affects the CF of the solvent and solution. The chemical activities as a packing factor influence the ρ of the medium. A higher ρ of the medium creates a larger diversion in light, which can be explained by the nD. The ρ, σ and nD data depict Pint, the strength of IMF, and coulombic attraction via DDI. DMSO acts as a precursor to modulate solvent structures so that the solvent could solubilise the flavonoids. The nD value for 0.01 to 0.10 mol kg−1 CnTAB with solvent systems at T = 298.15, 303.15 and 308.15 K are given in Table 5 and plotted in Fig. S18–21.† Increasing the CnTAB concentration increases nD. nD is directly associated with the interactions existing in solutions, as supported by the earlier study.53 The value of nD depends on the molecular polarizability and packing factor and polarizability increases with increasing CnTAB concentration.
Table 5 Refractive index (nD) of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol g−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa, and combined expanded uncertainties Uc (95% confidence interval) is Uc(nD) = ±0.0010. |
| 0.00 |
1.3465 |
1.3460 |
1.3454 |
1.3465 |
1.3460 |
1.3454 |
1.3465 |
1.3460 |
1.3454 |
| 0.01 |
1.3468 |
1.3466 |
1.3457 |
1.3464 |
1.3459 |
1.3451 |
1.3466 |
1.3462 |
1.3454 |
| 0.02 |
1.3473 |
1.3472 |
1.3464 |
1.3475 |
1.3476 |
1.3464 |
1.3478 |
1.3472 |
1.3463 |
| 0.04 |
1.3481 |
1.3479 |
1.3469 |
1.3483 |
1.3481 |
1.3472 |
1.3486 |
1.3486 |
1.3475 |
| 0.06 |
1.3489 |
1.3488 |
1.3477 |
1.3493 |
1.3487 |
1.3482 |
1.3492 |
1.3496 |
1.3483 |
| 0.08 |
1.3497 |
1.3495 |
1.3486 |
1.3512 |
1.3499 |
1.3498 |
1.3504 |
1.3513 |
1.3492 |
| 0.10 |
1.3506 |
1.3501 |
1.3493 |
1.3515 |
1.3510 |
1.3501 |
1.3514 |
1.3509 |
1.3504 |
| m/mol g−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1.3465 |
1.3457 |
1.3451 |
1.3465 |
1.3457 |
1.3451 |
1.3465 |
1.3457 |
1.3451 |
| 0.01 |
1.3468 |
1.3462 |
1.3452 |
1.3472 |
1.3465 |
1.3459 |
1.3466 |
1.3461 |
1.3455 |
| 0.02 |
1.3474 |
1.3470 |
1.3464 |
1.3477 |
1.3471 |
1.3465 |
1.3474 |
1.3471 |
1.3460 |
| 0.04 |
1.3483 |
1.3481 |
1.3472 |
1.3487 |
1.3486 |
1.3474 |
1.3484 |
1.3481 |
1.3471 |
| 0.06 |
1.3491 |
1.3484 |
1.3477 |
1.3501 |
1.3493 |
1.3482 |
1.3494 |
1.3497 |
1.3482 |
| 0.08 |
1.3499 |
1.3496 |
1.3488 |
1.3505 |
1.3504 |
1.3494 |
1.3504 |
1.3500 |
1.3492 |
| 0.10 |
1.3508 |
1.3504 |
1.3499 |
1.3518 |
1.3509 |
1.3500 |
1.3515 |
1.3512 |
1.3491 |
| m/mol g−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1.3469 |
1.3457 |
1.3450 |
1.3469 |
1.3457 |
1.3450 |
1.3469 |
1.3457 |
1.3450 |
| 0.01 |
1.3468 |
1.3461 |
1.3455 |
1.3465 |
1.3460 |
1.3452 |
1.3468 |
1.3461 |
1.3458 |
| 0.02 |
1.3474 |
1.3470 |
1.3464 |
1.3471 |
1.3465 |
1.3460 |
1.3474 |
1.3470 |
1.3463 |
| 0.04 |
1.3483 |
1.3476 |
1.3467 |
1.3483 |
1.3477 |
1.3471 |
1.3485 |
1.3477 |
1.3473 |
| 0.06 |
1.3491 |
1.3487 |
1.3481 |
1.3493 |
1.3486 |
1.3484 |
1.3495 |
1.3487 |
1.3484 |
| 0.08 |
1.3499 |
1.3499 |
1.3490 |
1.3500 |
1.3498 |
1.3484 |
1.3504 |
1.3498 |
1.3494 |
| 0.10 |
1.3505 |
1.3499 |
1.3491 |
1.3515 |
1.3509 |
1.3498 |
1.3513 |
1.3509 |
1.3502 |
| m/mol g−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1.3464 |
1.3455 |
1.3451 |
1.3464 |
1.3455 |
1.3451 |
1.3464 |
1.3455 |
1.3451 |
| 0.01 |
1.3469 |
1.3459 |
1.3455 |
1.3469 |
1.3461 |
1.3453 |
1.3471 |
1.3460 |
1.3456 |
| 0.02 |
1.3474 |
1.3471 |
1.3462 |
1.3477 |
1.3470 |
1.3461 |
1.3481 |
1.3470 |
1.3465 |
| 0.04 |
1.3483 |
1.3477 |
1.3472 |
1.3484 |
1.3478 |
1.3470 |
1.3490 |
1.3489 |
1.3479 |
| 0.06 |
1.3492 |
1.3487 |
1.3479 |
1.3492 |
1.3490 |
1.3478 |
1.3495 |
1.3489 |
1.3483 |
| 0.08 |
1.3498 |
1.3494 |
1.3489 |
1.3502 |
1.3500 |
1.3489 |
1.3505 |
1.3500 |
1.3497 |
| 0.10 |
1.3505 |
1.3499 |
1.3494 |
1.3512 |
1.3508 |
1.3500 |
1.3517 |
1.3508 |
1.3504 |
The nD values infer a high-frequency limiting dielectric constant (ε∞) with the following equation.51 nD can be obtained as per Snell–Descartes law:
| |
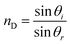 | (22) |
where sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi and sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θr
θr are the angles of incident and refractive light of the medium, respectively.
The ε∞ values given in Table S12† are plotted in Fig. S22–25.† The ε∞ values of the solvents are such that WBDA > WBDN > WBD = WBDQ and are supported with ηr, ΔS, τ and the Walden product. Apigenin shows a stronger interaction affinity with WBD than naringenin or quercetin. The stable, permanent dipole vectors produce an ε∞ value. As the temperature increases, weakening the BF and dipole forces, the nD value decreases. The states of the dipoles scatter and counteract the charges to each other with the decreased ε∞ value. Increasing the AC with stronger Brownian motion and the London dispersive forces (LDF) when the CF is weakened disrupts the permanent dipole that decreases the ε∞ value. The ε∞ value increases with increasing CnTAB concentration, supporting the dependence of CnTAB electronic polarizability on the solvent environment, which is due to the displacement of electrons and ions.51
3.9. Comparative study between light and sound velocities
The ηD value of the medium is inversely proportional to the velocity of light (C). As the ηD of a medium increases, the speed of light going through that medium decreases. The C values (Table 6) for CnTAB with solvent systems are calculated by using eqn (24):| |
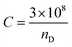 | (24) |
where C = 3 × 108/m s−1 is the velocity of light in a vacuum and nD is the refractive index. Table 6 shows that for increasing CnTAB concentration, the sound velocity (u) increased but C decreased. The ionic hydration and ion-water interaction (IWI) act individually in a different media for u (Table S8†) and the values of C are inversely proportional to compressibility. Such a relationship is similar to energy conservation, where a form of energy is consumed (a decrease in C value), and another form (an increase in u value) occurs. Upon increasing the temperature, C increased due to an average KE, which is proportional to temperature. Hence, the σ and IMF theory may open a new window in modern drug-binding affinity using a friccohesity shift coefficient parameter. The compressibility brings the ion-molecules to a closer packing state with a decrease of ions-molecular interaction (IMI), length or intermolecular free length. The intermolecular free length is a predominant factor in determining the variation of ultrasonic velocity.54 Such an increase in the Z values further elucidates the possibility of IMI due to IDI. The nD, C and molar refraction (R), at T = 298.15, 3.03.15 and 308.15 K, where nD decreases with increasing temperature. This infers that with composition, the compressed medium provides a constricted path for light waves, but with thermal agitation, this pathway becomes looser.
Table 6 The 108 C/m s−1 of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol kg−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) =±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa, and expanded uncertainties Uc (95% confidence interval) is Uc (C) = ±0.02 m s−1. |
| 0.00 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.01 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.02 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.04 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.22 |
2.22 |
2.23 |
| 0.06 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.23 |
| 0.08 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| 0.10 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| m/mol g−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.01 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.02 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.04 |
2.23 |
2.23 |
2.23 |
2.22 |
2.22 |
2.23 |
2.22 |
2.23 |
2.23 |
| 0.06 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.23 |
| 0.08 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| 0.10 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| m/mol g−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.01 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.02 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.04 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.22 |
2.23 |
2.23 |
| 0.06 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| 0.08 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| 0.10 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| m/mol g−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.01 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.02 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
2.23 |
| 0.04 |
2.23 |
2.23 |
2.23 |
2.22 |
2.23 |
2.23 |
2.22 |
2.22 |
2.23 |
| 0.06 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.23 |
2.22 |
2.22 |
2.23 |
| 0.08 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
| 0.10 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
2.22 |
3.10. Acoustic impedance (Z)
The higher Z value of the solution than the solvent shows the interaction between flavonoids with BSA in the presence of CnTAB. The specified sound pressure influence the packing factor on account of varying compositions with increasing Z in a compressible medium of closer packing and a parallel decrease in the ion-molecular interaction length.55,56 Z is a measure of the resistance offered by molecular domains towards an efficient structural expression with concentration-dependent thermodynamic variation. For DTAB in the WBD system, the Z value increased and also increased with increasing CnTAB concentration, but the rate of Z value decreased (Table 7). The sound pressure is generated by vibration due to SLSOI; the Z value is calculated by using eqn (25).
Table 7 TheZ of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol kg−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa, and expanded uncertainties Uc (95% confidence interval) is Uc (Z) = ±0.02 g cm−2 s−1. |
| 0.00 |
1557.10 |
1560.69 |
1564.41 |
1557.10 |
1560.69 |
1564.41 |
1557.10 |
1560.69 |
1564.41 |
| 0.01 |
1561.77 |
1567.94 |
1569.82 |
1559.94 |
1565.75 |
1568.41 |
1558.79 |
1564.21 |
1567.03 |
| 0.02 |
1565.44 |
1569.48 |
1571.26 |
1562.56 |
1567.25 |
1568.54 |
1560.47 |
1565.18 |
1566.84 |
| 0.04 |
1565.91 |
1570.07 |
1572.46 |
1562.64 |
1567.02 |
1569.22 |
1561.69 |
1565.41 |
1567.43 |
| 0.06 |
1566.14 |
1569.86 |
1571.93 |
1562.94 |
1566.68 |
1568.51 |
1561.81 |
1565.16 |
1567.28 |
| 0.08 |
1566.28 |
1570.04 |
1572.16 |
1563.10 |
1566.73 |
1568.32 |
1561.78 |
1564.83 |
1566.94 |
| 0.10 |
1566.41 |
1570.10 |
1571.97 |
1563.05 |
1566.64 |
1568.26 |
1561.90 |
1564.65 |
1566.80 |
| m/mol g−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1556.84 |
1560.85 |
1563.75 |
1556.84 |
1560.85 |
1563.75 |
1556.84 |
1560.85 |
1563.75 |
| 0.01 |
1560.10 |
1564.69 |
1567.38 |
1557.60 |
1561.65 |
1566.17 |
1557.88 |
1560.16 |
1564.31 |
| 0.02 |
1562.14 |
1567.23 |
1569.73 |
1561.96 |
1566.28 |
1568.71 |
1563.18 |
1566.68 |
1569.09 |
| 0.04 |
1564.65 |
1568.96 |
1570.80 |
1562.50 |
1566.74 |
1568.23 |
1561.89 |
1566.18 |
1568.32 |
| 0.06 |
1565.03 |
1569.19 |
1570.94 |
1563.04 |
1567.20 |
1568.82 |
1563.94 |
1567.99 |
1569.90 |
| 0.08 |
1565.47 |
1569.42 |
1571.54 |
1563.21 |
1567.16 |
1568.93 |
1564.03 |
1567.80 |
1569.21 |
| 0.10 |
1564.95 |
1568.82 |
1571.04 |
1562.49 |
1566.43 |
1568.37 |
1563.87 |
1567.75 |
1569.22 |
| m/mol g−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1559.27 |
1564.25 |
1567.32 |
1559.27 |
1564.25 |
1567.32 |
1559.27 |
1564.25 |
1567.32 |
| 0.01 |
1558.29 |
1564.93 |
1562.54 |
1555.70 |
1560.20 |
1553.36 |
1553.58 |
1559.41 |
1551.11 |
| 0.02 |
1558.87 |
1566.00 |
1563.52 |
1558.72 |
1564.15 |
1559.81 |
1557.58 |
1563.56 |
1558.03 |
| 0.04 |
1564.73 |
1569.53 |
1568.91 |
1559.21 |
1564.87 |
1564.32 |
1559.45 |
1564.55 |
1561.63 |
| 0.06 |
1563.74 |
1568.84 |
1570.24 |
1559.94 |
1565.35 |
1566.43 |
1560.90 |
1564.63 |
1564.10 |
| 0.08 |
1563.15 |
1569.25 |
1571.58 |
1561.11 |
1566.00 |
1568.25 |
1562.44 |
1564.70 |
1565.07 |
| 0.10 |
1564.98 |
1569.10 |
1571.48 |
1561.33 |
1566.48 |
1568.33 |
1565.57 |
1564.70 |
1565.34 |
| m/mol g−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1547.19 |
1552.24 |
1555.37 |
1547.19 |
1552.24 |
1555.37 |
1547.19 |
1552.24 |
1555.37 |
| 0.01 |
1560.57 |
1564.22 |
1563.06 |
1553.65 |
1555.95 |
1557.09 |
1555.27 |
1553.22 |
1557.63 |
| 0.02 |
1565.59 |
1569.35 |
1569.33 |
1558.62 |
1562.87 |
1563.64 |
1558.17 |
1561.78 |
1562.91 |
| 0.04 |
1566.42 |
1570.51 |
1572.15 |
1560.66 |
1564.86 |
1567.14 |
1558.57 |
1562.59 |
1563.52 |
| 0.06 |
1566.62 |
1570.71 |
1573.27 |
1563.35 |
1565.05 |
1569.48 |
1560.60 |
1564.13 |
1566.35 |
| 0.08 |
1567.25 |
1571.07 |
1573.90 |
1562.26 |
1565.77 |
1568.21 |
1561.23 |
1564.23 |
1567.15 |
| 0.10 |
1567.49 |
1570.99 |
1573.89 |
1562.63 |
1565.72 |
1568.73 |
1561.81 |
1564.38 |
1566.91 |
The Z value infers an increase in sound pressure at a fixed composition and temperature. Upon increasing the AC, the Z value decreases, while with increasing temperature, the Z value increases. The Z data is directly proportional to the sound velocity (u). At higher temperatures, the molecules oscillate and the sound can travel quickly with increasing Z value. The Z value of solvent systems are such that WBDA > WBD > WBDQ > WBDN. The Z values are supported by ρ, τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and ηD data. The higher Z value of apigenin with WBD, as compared to quercetin and naringenin due to the π-conjugation and 1 –OH group at the B-ring, could not form IMHB with the increasing number of interaction sites. Quercetin has 2 –OH groups at the B-ring that form IMHB and reduce the interacting sites, developing weak electrostatic, ion-dipole and IMI. However, in naringenin an in the absence of π-conjugation in its molecular structure, the electron density as well as the Z value decreases. The solvent system with CnTAB are such that WBD > WBDN > WBDQ > WBDA with DTAB, WBD > WBDQ > WBDA > WBDN with TDTAB, and WBD > WBDQ > WBDN > WBDA with HDTAB at T = 298.15, 303.15 and 308.15 K, respectively. WBD with DTAB, TDTAB and HDTAB, shows a higher Z value. BSA, due to unfolding, exhibits increased surface area, interacting sites and Z value. DTAB has a shorter ACL than TDTAB or HDTAB, and naringenin has higher hydrophobicity than apigenin or quercetin due to the stronger IHbI with increasing Z value. While with naringenin TDTAB and HDTAB, the Z value decreased due to stronger LDF. For TDTAB and HDTAB with quercetin and apigenin, quercetin due to stronger electrostatic interaction, the Z value increases. To understanding total polarizability, the molar refraction (R) was calculated with the Lorentz–Lorenz equation57 shown below.
and ηD data. The higher Z value of apigenin with WBD, as compared to quercetin and naringenin due to the π-conjugation and 1 –OH group at the B-ring, could not form IMHB with the increasing number of interaction sites. Quercetin has 2 –OH groups at the B-ring that form IMHB and reduce the interacting sites, developing weak electrostatic, ion-dipole and IMI. However, in naringenin an in the absence of π-conjugation in its molecular structure, the electron density as well as the Z value decreases. The solvent system with CnTAB are such that WBD > WBDN > WBDQ > WBDA with DTAB, WBD > WBDQ > WBDA > WBDN with TDTAB, and WBD > WBDQ > WBDN > WBDA with HDTAB at T = 298.15, 303.15 and 308.15 K, respectively. WBD with DTAB, TDTAB and HDTAB, shows a higher Z value. BSA, due to unfolding, exhibits increased surface area, interacting sites and Z value. DTAB has a shorter ACL than TDTAB or HDTAB, and naringenin has higher hydrophobicity than apigenin or quercetin due to the stronger IHbI with increasing Z value. While with naringenin TDTAB and HDTAB, the Z value decreased due to stronger LDF. For TDTAB and HDTAB with quercetin and apigenin, quercetin due to stronger electrostatic interaction, the Z value increases. To understanding total polarizability, the molar refraction (R) was calculated with the Lorentz–Lorenz equation57 shown below.
| |
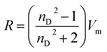 | (26) |
where
Vm is the molar volume and
nD is the refractive index. The calculated
R-values (
Table 8) predicted that the concentration-dependent molar refraction is a physical state of solutions and is slightly affected by temperature.
54 Upon increasing the ACL, the
R value (Fig. S26–29
†) increased due to the stronger IMMI and FFs, which could cause the higher compactness of
Pint and IMI in solution.
Table 8 The R/cm−3 mol−1 of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol kg−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) to a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa, and expanded uncertainties Uc (95% confidence interval) is Uc(R) = ±0.02 cm3 mol−1. |
| 0.00 |
21.13 |
21.14 |
21.15 |
21.13 |
21.14 |
21.15 |
21.13 |
21.14 |
21.15 |
| 0.01 |
21.14 |
21.15 |
21.15 |
21.14 |
21.13 |
21.13 |
21.16 |
21.16 |
21.16 |
| 0.02 |
21.15 |
21.18 |
21.19 |
21.17 |
21.20 |
21.20 |
21.19 |
21.19 |
21.20 |
| 0.04 |
21.19 |
21.21 |
21.20 |
21.21 |
21.23 |
21.23 |
21.23 |
21.26 |
21.25 |
| 0.06 |
21.23 |
21.26 |
21.25 |
21.25 |
21.26 |
21.28 |
21.25 |
21.32 |
21.29 |
| 0.08 |
21.27 |
21.29 |
21.29 |
21.35 |
21.32 |
21.37 |
21.32 |
21.41 |
21.34 |
| 0.10 |
21.32 |
21.33 |
21.33 |
21.37 |
21.38 |
21.38 |
21.37 |
21.39 |
21.40 |
| m/mol g−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
21.13 |
21.13 |
21.14 |
21.13 |
21.13 |
21.14 |
21.13 |
21.13 |
21.14 |
| 0.01 |
21.14 |
21.14 |
21.13 |
21.17 |
21.17 |
21.17 |
21.14 |
21.15 |
21.15 |
| 0.02 |
21.17 |
21.18 |
21.20 |
21.19 |
21.19 |
21.21 |
21.17 |
21.20 |
21.18 |
| 0.04 |
21.20 |
21.23 |
21.24 |
21.23 |
21.26 |
21.25 |
21.21 |
21.24 |
21.24 |
| 0.06 |
21.24 |
21.24 |
21.25 |
21.30 |
21.29 |
21.29 |
21.27 |
21.32 |
21.29 |
| 0.08 |
21.28 |
21.30 |
21.30 |
21.32 |
21.35 |
21.34 |
21.32 |
21.33 |
21.33 |
| 0.10 |
21.33 |
21.35 |
21.36 |
21.39 |
21.38 |
21.37 |
21.38 |
21.39 |
21.32 |
| m/mol g−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
21.15 |
21.12 |
21.12 |
21.15 |
21.12 |
21.12 |
21.15 |
21.12 |
21.12 |
| 0.01 |
21.15 |
21.12 |
21.23 |
21.14 |
21.13 |
21.25 |
21.17 |
21.15 |
21.31 |
| 0.02 |
21.18 |
21.17 |
21.25 |
21.18 |
21.16 |
21.26 |
21.20 |
21.19 |
21.31 |
| 0.04 |
21.22 |
21.20 |
21.24 |
21.23 |
21.22 |
21.27 |
21.25 |
21.23 |
21.32 |
| 0.06 |
21.26 |
21.26 |
21.28 |
21.28 |
21.26 |
21.31 |
21.30 |
21.28 |
21.34 |
| 0.08 |
21.29 |
21.32 |
21.32 |
21.31 |
21.32 |
21.29 |
21.34 |
21.33 |
21.37 |
| 0.10 |
21.32 |
21.32 |
21.32 |
21.38 |
21.38 |
21.37 |
21.38 |
21.39 |
21.40 |
| m/mol g−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
21.17 |
21.15 |
21.18 |
21.17 |
21.15 |
21.18 |
21.17 |
21.15 |
21.18 |
| 0.01 |
21.14 |
21.13 |
21.20 |
21.17 |
21.16 |
21.20 |
21.19 |
21.27 |
21.24 |
| 0.02 |
21.16 |
21.18 |
21.21 |
21.20 |
21.20 |
21.21 |
21.23 |
21.23 |
21.26 |
| 0.04 |
21.20 |
21.20 |
21.23 |
21.22 |
21.23 |
21.23 |
21.26 |
21.32 |
21.29 |
| 0.06 |
21.24 |
21.25 |
21.25 |
21.25 |
21.28 |
21.26 |
21.28 |
21.30 |
21.30 |
| 0.08 |
21.27 |
21.28 |
21.29 |
21.31 |
21.33 |
21.31 |
21.33 |
21.34 |
21.36 |
| 0.10 |
21.31 |
21.31 |
21.31 |
21.36 |
21.38 |
21.37 |
21.39 |
21.38 |
21.39 |
3.11. Molar conductance (Λm)
Conductivity analysis is related to the number of ions, ionic association and the relative solvation ability of solvents for ions. The molar conductivities of CnTAB with solvents were calculated using eqn (27) and, the values are given in Table S13.† For the calculation of Λm, the ρ values for the molality (m) into molarity (M) were used in eqn (27):| |
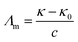 | (27) |
where κ (S cm−1) and κ0 (S cm−1) are the specific conductance of the solution and solvent, respectively. Fig. 18–21 show a decrease in Λm with increasing CnTAB concentration.
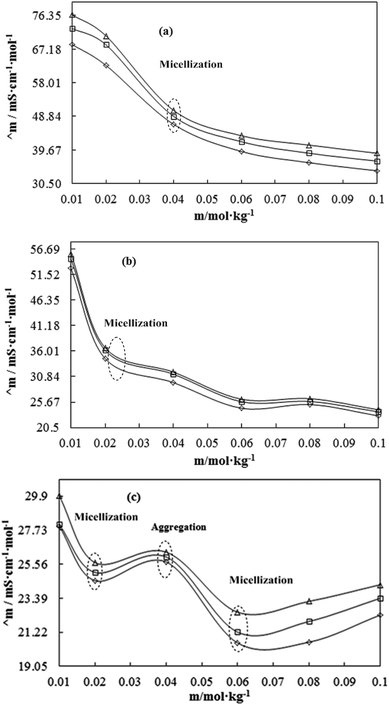 |
| | Fig. 18 The Λm value of DTAB (a), TDTAB (b) and HDTAB (c) with WBD at T = 298.15 (◊), 303.15 (□) and 308.15 K (Δ), respectively. | |
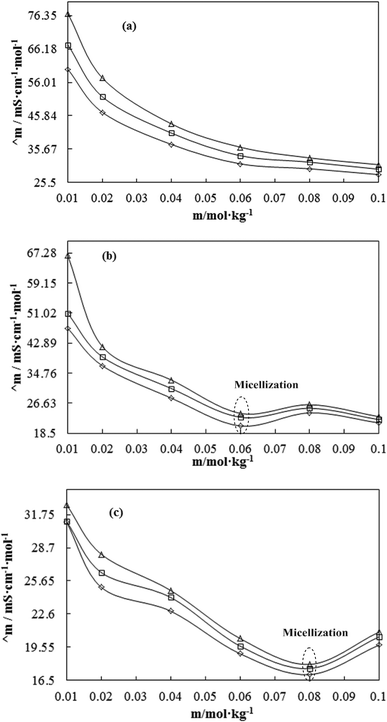 |
| | Fig. 19 The Λm value of DTAB (a), TDTAB (b) and HDTAB (c) with WBDQ at T = 298.15 (◊), 303.15 (□) and 308.15 K (Δ), respectively. | |
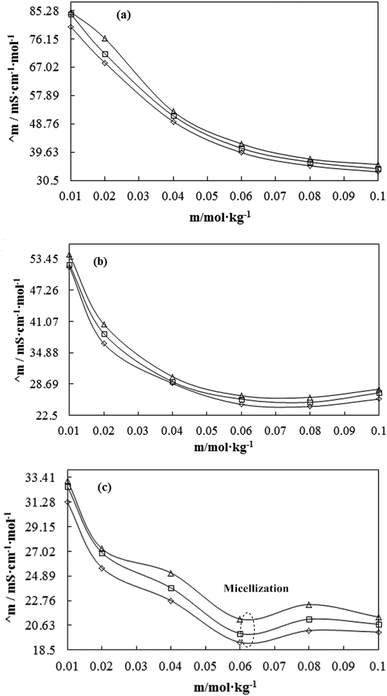 |
| | Fig. 20 The Λm value of DTAB (a), TDTAB (b) and HDTAB (c) with WBDA at T = 298.15 (◊), 303.15 (□) and 308.15 K (Δ), respectively. | |
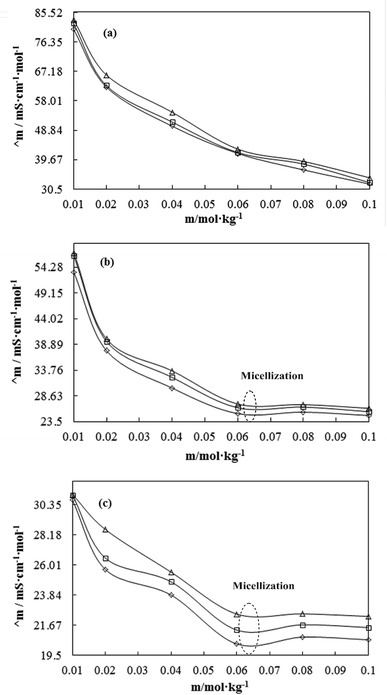 |
| | Fig. 21 The Λm value of DTAB (a), TDTAB (b) and HDTAB (c) with WBDN at T = 298.15 (◊), 303.15 (□) and 308.15 K (Δ), respectively. | |
This could be due to (i) the increased viscosity (η) of the solution, retarding –N+(CH3)3 and Br− ions (the head ions of CnTAB) mobility or (ii) the increased hydrodynamic radii (Rh) of ions due to enhanced electrostatic attraction among CnTAB and –COO−, NH2−, −OH−, –NH3+, H+ and >S+–O− of solvent molecules. This causes the pre-solvation of ions by –COO−, −OH−, –NH3+, H+ and >S+–O− retarding the –N+ (CH3)3 and Br− ion mobility. Increasing temperature weakens the electrostatic forces, resulting higher ion mobility. The Λm of CnTAB with a solvent are such that WBDN > WBDA > WBD > WBDQ. So, the longer the AC is, the greater the hindrance that decreases the ionic mobility.
Fig. 18–21 show the micellisation and aggregation processes (Fig. 22), where the localized maximum H2O disrupted through the hydrophobic part of the counterpart of CnTAB via structural breakage. In the central site of the micelle, the formation process (Fig. 23) occurs with a stronger HbHbI, so for micellization, the two processes of structural breakage and formation occur. However, in the aggregation process, such processes could not occur in aggregation, as the molecules interact via electrostatic and intermolecular interaction. Λm increases with the formation of aggregation (Fig. 18), while for micellization (Fig. 18–21) Λm decreases. Thus, during micelle formation, the hydrophobic part of the head region could act as a disruption of CFs of H2O (HB), the hydrophobic part of CnTAB could form HbHbI, which is present at the core site of micelles.58 Hence, structural breakage and formation are possible but with aggregation, no symmetric orientations occur. The surfactant into the binary or ternary system with interaction ability of the counterpart of the surfactant with the solvent system could be higher. This could allow the repulsion of water molecules from other molecules; these water molecules induce CFs with high Λm value. The Λm values of CnTAB with their counterions and charged micelles with increasing Λm values of the ionic surfactant depend on ionic charge and mobility. With an increasing concentration and ACL, the Λm values decrease. The CnTAB with the shortest AC (DTAB) as compared to TDTAB and HDTAB shows a higher Λm value with solvent systems at all CnTAB concentrations (Table S13†). With increasing temperature, the energy gained could induce oscillations in the ions; the mobility of ions also increased with increasing Λm values. The Λm value decreases with increasing ACL at constant temperature. This was anticipated since longer ACL could reduce mobility because of increased the van der Waals interactions with stronger LDF. The limiting molar conductivity (Λ0) was calculated using the Λm values in eqn (28) given below:
| |
Λm = Λ0 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + Am + Bm2 + Am + Bm2
| (28) |
where
Λ0 (S cm
−1 mol
−1) is the limiting molar conductivity of C
nTAB with solvents systems depicting the nature of S
LS
0I, while
A (S cm
2 mol
−2) and B (S cm
5 mol
−3) are the empirical parameters and interpreted solute–solute (interionic) interactions (S
LS
LI). The variations in
Λ0 values are such that WBDA > WBDN > WBD > WBDQ with DTAB, while WBDN > WBDA > WBD > WBDQ with TDTAB, and WBDQ > WBDA > WBDN > WBD with HDTAB (Table S14
†). The C
nTAB with the solvent systems shows a reverse trend for
η (Table S6
†) and Walden rule.
59 C
nTAB with WBDN and WBDA show the highest
Λ0 values due to stronger IHI dominance over IH
bI, while this was weakest for C
nTAB with WBDQ and WBD due to IH
bI dominance over IHI with the decreased
Λ0 value. An inclusion of flavonoids and C
nTAB into WBD induces the IH
bI. The DTAB with the highest charge density and the shortest ACL induces the highest charge density, whereas HDTAB with a longer ACL developed the weakest charge density with a decreased
Λ0 value.
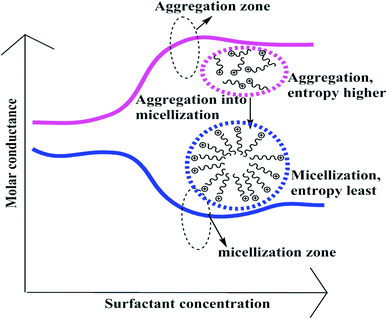 |
| | Fig. 22 Aggregation and micellization processes of CnTAB with WBD–Fv systems. | |
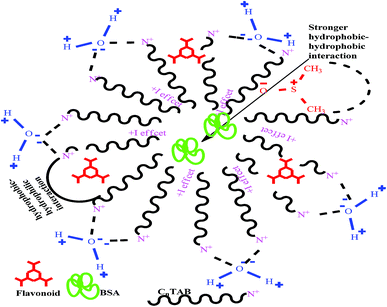 |
| | Fig. 23 Micellisation form of flavonoids in the aq-DMSO system. | |
3.12. Potentiometric study
The electrostatic potential values were produced to determine the ionic species that are useful in academic and industrial fields. The voltammetric systems with electrodes and complete voltammetric cells were referred to analyse various analytes. Potentiostat, pH and κ parameters directly depend on the population and nature of ions. The potential values (Table 9) for 0.01 to 0.10 mol kg−1 CnTAB with solvent systems at T = 298.15, 303.15 and 308.15 K infer flavonoids with WBD to increases potential values. The flavonoids act as a reducing agent by increasing the population of H+ ions with increasing potential value. Apigenin showed the highest potential range (17.7 mV) and also stronger reducing activities, which induced maximum H+ ions. The potentials of the solvents systems are such that WBDA > WBDN > WBDQ > WBD. Apigenin showed a higher potential as compared to naringenin and quercetin; the ρ, ηr, τ, z, ηD, and Walden product supports the potential values. Naringenin has 3 –OH groups as well as no adjacent –OH groups and the absence of π-conjugation at the C-ring that decreased the potential values. Naringenin could act as a weaker reducing agent, as it produces fewer H+ ions with a decrease in potential value. For flavonoids with WBD, the potential values increase, (a) which suggests that flavonoids have hydrophobic rings that weaken the CFs with stronger IMF, electrostatic interaction and DDI with a decrease in γ and an increase in η. The decreasing γ increases surface area and ionic charges at the surfaces. The flavonoids act as cosurfactants. For flavonoids in the WBD solution, the BSA structure could be denatured to a maximum, changing the conformatory structure and forming the α-helices, random coils, β-turns, intra-aggregates and β-sheets. The interaction affinity of BSA increased as the number of interacting sites increased due to the unfolding of BSA structure. The hydrophobic part of the flavonoids could form clusters, which increase the dispersion of flavonoids and enhanced the number of ionic species. So for a flavonoid in BSA, the potential value increased. Upon increasing the CnTAB concentration, the potentiostat value increased as the population of counterions increased. Contrary to increasing AC, the potential decreased as the AC could show a strong interacting affinity towards BSA in aq-DMSO solution. With increasing CnTAB concentration, the potential value increased. This was due to (a) stronger IHI dominance over IHbI with increasing potential value while (b) increasing the CnTAB concentration with increased potential value as the hydrophobicity of CnTAB strengthens the HbHbI. The potential value determines the role of ions in interaction for thermodynamic and kinetically stable nanoemulsions.
Table 9 Electrostatic potential of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol g−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in the molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa. |
| 0.00 |
−11.6 |
−9.43 |
−8.07 |
−8.07 |
−9.43 |
−11.6 |
−8.07 |
−9.43 |
−11.6 |
| 0.01 |
64.6 |
65.50 |
66.90 |
96.50 |
101.57 |
103.3 |
55.17 |
56.17 |
58.0 |
| 0.02 |
81.9 |
81.10 |
78.80 |
126.43 |
129.20 |
131.2 |
98.23 |
101.47 |
102.5 |
| 0.04 |
93.8 |
93.37 |
88.63 |
155.17 |
157.37 |
158.6 |
49.20 |
48.63 |
48.2 |
| 0.06 |
97.0 |
96.20 |
94.33 |
168.77 |
171.60 |
172.1 |
96.53 |
98.53 |
99.4 |
| 0.08 |
105.1 |
105.30 |
103.67 |
186.43 |
186.93 |
187.1 |
113.33 |
112.67 |
112.1 |
| 0.10 |
104.6 |
103.60 |
102.17 |
182.47 |
183.67 |
183.9 |
109.47 |
109.00 |
108.7 |
| m/mol g−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
−9.67 |
−9.03 |
−5.53 |
−9.67 |
−9.03 |
−5.53 |
−9.67 |
−9.03 |
−5.53 |
| 0.01 |
105.07 |
105.90 |
106.10 |
116.37 |
119.33 |
120.17 |
189.90 |
190.20 |
190.47 |
| 0.02 |
115.37 |
114.40 |
114.10 |
126.53 |
129.43 |
131.07 |
141.53 |
140.80 |
141.20 |
| 0.04 |
107.77 |
108.03 |
108.90 |
150.06 |
152.37 |
153.53 |
133.70 |
133.63 |
133.83 |
| 0.06 |
110.43 |
109.63 |
108.37 |
161.06 |
162.10 |
162.40 |
131.20 |
130.77 |
131.03 |
| 0.08 |
119.30 |
119.73 |
120.07 |
180.36 |
181.27 |
181.40 |
134.50 |
134.87 |
135.03 |
| 0.10 |
112.57 |
112.43 |
112.73 |
178.83 |
178.50 |
178.33 |
135.20 |
135.60 |
135.73 |
| m/mol g−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
17.7 |
19.63 |
22.60 |
17.7 |
19.63 |
22.60 |
17.7 |
19.63 |
22.60 |
| 0.01 |
96.0 |
98.93 |
103.03 |
110.57 |
112.93 |
113.5 |
100.53 |
101.63 |
102.1 |
| 0.02 |
107.0 |
106.13 |
104.67 |
124.43 |
126.20 |
126.8 |
107.10 |
106.70 |
106.5 |
| 0.04 |
113.6 |
113.00 |
111.33 |
153.53 |
156.00 |
157.1 |
108.50 |
109.00 |
109.7 |
| 0.06 |
113.9 |
113.50 |
113.07 |
167.63 |
170.20 |
171.0 |
112.37 |
114.07 |
114.8 |
| 0.08 |
119.5 |
122.57 |
126.63 |
175.60 |
177.10 |
177.6 |
118.57 |
119.07 |
119.3 |
| 0.10 |
111.6 |
112.27 |
113.40 |
184.50 |
185.03 |
185.3 |
123.70 |
124.53 |
124.7 |
| m/mol g−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
1.20 |
1.33 |
1.7 |
1.20 |
1.33 |
1.7 |
1.20 |
1.33 |
1.7 |
| 0.01 |
104.4 |
105.93 |
111.50 |
136.13 |
137.13 |
137.5 |
105.13 |
106.80 |
107.1 |
| 0.02 |
122.2 |
121.00 |
118.20 |
141.73 |
145.37 |
146.5 |
113.80 |
114.43 |
114.6 |
| 0.04 |
120.8 |
119.67 |
117.63 |
158.03 |
164.40 |
166.5 |
112.70 |
112.97 |
113.1 |
| 0.06 |
132.1 |
131.07 |
127.07 |
177.63 |
178.00 |
178.2 |
128.63 |
129.17 |
129.6 |
| 0.08 |
138.4 |
137.80 |
137.30 |
189.30 |
190.77 |
191.7 |
126.70 |
127.00 |
126.8 |
| 0.10 |
137.1 |
135.80 |
134.53 |
197.57 |
196.50 |
195.9 |
134.20 |
134.33 |
134.6 |
The flavonoid with WBD system contains –OH groups, which release H+ ions that decrease pH. Upon increasing the temperature, the orientation could be disturbed with a decrease in potential value. Quercetin within the WBD system shows the negative PE due to H3O+, and the resultant negative ion population could be high, so we obtained a negative potential value for the WBDQ system.
3.13. pH study
The interactions depend on pH, temperature, and other physiological conditions for in vivo or in vitro study. The molecular interaction depends on temperature, pH, solvents, cofactors, etc. The pH values (Table 10) of CnTAB with solvent systems at T = 298.15, 303.15 and 308.15 K, respectively, are such that WBD > WBDQ > WBDN > WBDA. The order of pH value is supported by potential data; apigenin shows the lowest pH and highest potential value because it acts as a stronger reducing agent as the population of H+ ions increases. The potential value increases and the pH value decreases due to stronger electrostatic interactions and the decreased pH values of WBDQ, WBDA and WBDN systems as compared to the WBD system. WBD shows higher pH values due to (CH3)2 hydrophobic groups in DMSO that unfold the BSA structure. Unfolded BSA contains α-sheet; β-turn, random coil, intra-aggregates and β-sheets with increased H+ ion population and increase the pH value. For 0.01–0.10 mol kg−1 CnTAB with solvent systems, the pH is such that WBD > WBDA > WBDN > WBDQ with DTAB, WBD > WBDA > WBDQ > WBDN with TDTAB, and WBD > WBDA > WBDN > WBDQ with HDTAB. WBD shows higher pH values with CnTAB, while the pH value with WBDQ, WBDA and WBDN decreased. The flavonoids act as reducing agents, which increase the amount of H+ ions with decreasing pH value.
Table 10 The pH of CnTAB with WBD, WBDQ, WBDA and WBDN at T = (298.15, 303.15 and 308.15) K and p = 0.1 MPaa
| m/mol g−1 |
WBD-DTAB |
WBD-TDTAB |
WBD-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| m (mol kg−1) is the CnTAB molality with WBD, WBDQ, WBDA and WBDN solvents separately. The combined uncertainties in molality at a 95% confidence interval Uc(m) of CnTAB = ±3 × 10−4m/mol kg−1. Standard uncertainties (u) in solvent compositions (WBD) at a 95% confidence interval u(M) = ±0.9 × 10−4M/mol L−1; WBDQ, WBDA and WBDN u(m) = ±1.0 × 10−4m/mol kg−1, respectively. Standard uncertainties are u(T) = ±0.01 K, u(p) = ±0.01 MPa. |
| 0.00 |
10.03 |
9.36 |
9.38 |
10.03 |
9.36 |
9.38 |
10.03 |
9.36 |
9.38 |
| 0.01 |
8.57 |
8.60 |
8.62 |
7.86 |
7.87 |
7.88 |
8.66 |
8.64 |
8.63 |
| 0.02 |
8.25 |
8.27 |
8.30 |
7.42 |
7.45 |
7.48 |
7.89 |
7.91 |
7.93 |
| 0.04 |
8.06 |
8.08 |
8.10 |
6.96 |
6.99 |
7.03 |
8.80 |
8.76 |
8.67 |
| 0.06 |
7.99 |
8.02 |
8.04 |
6.73 |
6.77 |
6.81 |
7.95 |
7.97 |
7.99 |
| 0.08 |
7.88 |
7.92 |
7.96 |
6.48 |
6.53 |
6.59 |
7.75 |
7.79 |
7.82 |
| 0.10 |
7.86 |
7.89 |
7.92 |
6.54 |
6.59 |
6.64 |
7.80 |
7.83 |
7.81 |
| m/mol g−1 |
WBDQ-DTAB |
WBDQ-TDTAB |
WBDQ-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
9.73 |
9.72 |
9.72 |
9.73 |
9.73 |
9.72 |
9.73 |
9.73 |
9.72 |
| 0.01 |
7.87 |
7.91 |
7.94 |
7.60 |
7.62 |
7.65 |
6.43 |
6.49 |
6.54 |
| 0.02 |
7.68 |
7.72 |
7.75 |
7.41 |
7.44 |
7.47 |
7.27 |
7.32 |
7.36 |
| 0.04 |
7.82 |
7.85 |
7.89 |
7.04 |
7.08 |
7.11 |
7.39 |
7.43 |
7.46 |
| 0.06 |
7.77 |
7.80 |
7.82 |
6.90 |
6.94 |
6.99 |
7.42 |
7.46 |
7.49 |
| 0.08 |
7.63 |
7.68 |
7.71 |
6.58 |
6.64 |
6.69 |
7.36 |
7.39 |
7.43 |
| 0.10 |
7.73 |
7.50 |
7.54 |
6.62 |
6.67 |
6.72 |
7.35 |
7.39 |
7.42 |
| m/mol g−1 |
WBDA-DTAB |
WBDA-TDTAB |
WBDA-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
9.44 |
9.46 |
9.48 |
9.44 |
9.46 |
9.48 |
9.44 |
9.46 |
9.48 |
| 0.01 |
8.05 |
8.11 |
8.15 |
7.71 |
7.73 |
7.76 |
7.91 |
7.94 |
7.96 |
| 0.02 |
7.83 |
7.85 |
7.87 |
7.49 |
7.51 |
7.54 |
7.84 |
7.87 |
7.90 |
| 0.04 |
7.71 |
7.74 |
7.76 |
6.97 |
7.01 |
7.05 |
7.78 |
7.80 |
7.82 |
| 0.06 |
7.73 |
7.77 |
7.80 |
6.74 |
6.79 |
6.84 |
7.69 |
7.72 |
7.75 |
| 0.08 |
7.64 |
7.69 |
7.73 |
6.64 |
6.69 |
6.74 |
7.62 |
7.66 |
7.69 |
| 0.10 |
7.76 |
7.80 |
7.83 |
6.51 |
6.56 |
6.61 |
7.53 |
7.57 |
7.60 |
| m/mol g−1 |
WBDN-DTAB |
WBDN-TDTAB |
WBDN-HDTAB |
| 298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
298.15 K |
303.15 K |
308.15 K |
| 0.00 |
9.60 |
9.59 |
9.58 |
9.60 |
9.59 |
9.58 |
9.60 |
9.59 |
9.58 |
| 0.01 |
7.89 |
7.93 |
7.95 |
7.32 |
7.38 |
7.43 |
7.83 |
7.85 |
7.88 |
| 0.02 |
7.56 |
7.58 |
7.61 |
7.15 |
7.19 |
7.22 |
7.70 |
7.74 |
7.77 |
| 0.04 |
7.61 |
7.62 |
7.64 |
6.81 |
6.83 |
6.86 |
7.73 |
7.77 |
7.79 |
| 0.06 |
7.40 |
7.43 |
7.47 |
6.63 |
6.67 |
6.61 |
7.45 |
7.49 |
7.52 |
| 0.08 |
7.30 |
7.34 |
7.38 |
6.41 |
6.46 |
6.51 |
7.50 |
7.53 |
7.57 |
| 0.10 |
7.33 |
7.67 |
7.40 |
6.33 |
6.38 |
6.43 |
7.37 |
7.41 |
7.44 |
Table 11 Provenance and purity of the chemicals studied in this worka
| Chemicals |
Purity |
Mw |
Source |
CAS no. |
| Dodecyltrimethyl ammonium bromide (DTAB), tetradecyltrimethyl ammonium bromide (TDTAB), hexadecyltrimethyl ammonium bromide (HDTAB), dimethyl sulfoxide (DMSO), Bovine Serum Albumin (BSA). |
| DTAB |
∼99% |
308.34 |
Sigma-Aldrich |
1119-94-4 |
| TDTAB |
98% |
336.40 |
Alfa-Aesar |
1119-97-7 |
| HDTAB |
98% |
364.46 |
Alfa-Aesar |
57-09-0 |
| Apigenin |
97% |
270.24 |
Alfa-Aesar |
520-36-5 |
| Naringenin |
>95% |
272.26 |
SRL |
480-41-1 |
| Quercetin dihydrate |
>99% |
338.27 |
SRL |
6151-25-3 |
| DMSO |
99% |
78.13 |
SRL |
67-68-5 |
| BSA |
98% |
66.740 |
SRL |
9048-46-8 |
3.14. Drug friccohesity interaction (DFI) model
Drug friccohesity interactions determine a correlation in between the cohesive forces (CF) and frictional forces (FF) of CnTAB with flavonoid–BSA in 10% (w/w) aq-DMSO solution.40 The molecular interacting mechanism of flavonoids with BSA and CnTAB reflects a comparative study of the η and γ of CnTAB with solvent systems (Fig. 24). Upon increasing the concentration and ACL of CnTAB due to the disruption of molecular bonding, the CFs weaken with a lower γ value. Upon increasing the concentration from 0.01 to 0.10 mol kg−1 in CnTAB with solvent systems, the γ value decreased and the η value increased as the CFs weakened with stronger molecular forces (Fig. 24). The DFI mechanism60 could determine the % of flavonoid molecules that interact with BSA in the presence of CnTAB.
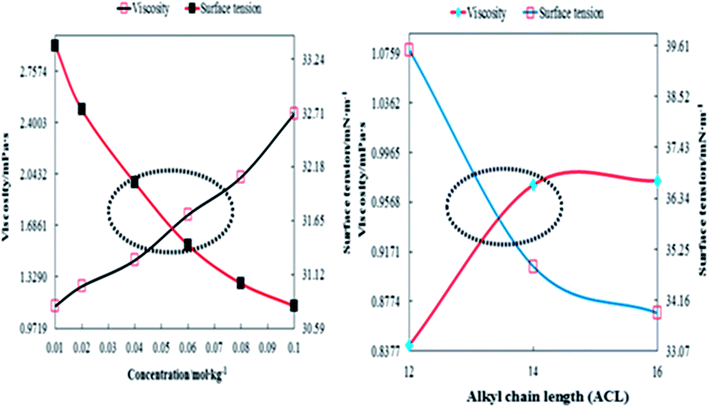 |
| | Fig. 24 Effect of increasing concentration and ACL of CnTAB on the η and γ values of flavonoid–BSA through DFI study. | |
Upon increasing the ACL, the γ value decreased with increasing FFs. Fig. 24 infers the rationalized decrease in the CFs of the medium and the distribution of particles with higher shear stress due to WBD–Fv with CnTAB interaction. An increment in C-12 to 16 atoms increased the η value, which saturates at C-16 with a continuous decrease in the γ value. For flavonoids in the WBD system, the γ value decreased, and a comparative study of η and γ of CnTAB with solvent systems explained the DFI mechanism. The interactive nature of flavonoids with BSA increases with increasing ACL and concentration of CnTAB in 10% (w/w) aq-DMSO at T = 298.15, 303.15 and 308.15 K. Since the flavonoids strongly interact with BSA in the presence of CnTAB, the dispersion or interacting affinity of flavonoids towards BSA increased due to stronger HB and stronger electrostatic interaction. The DFI study inferred that CnTAB to develop a stronger interaction affinity with flavonoids that could enhance the interaction activities of flavonoids. η and γ are not able to track the electronic configuration driven molecular activities due to the functional double bond, atomic size and π-bond to optimize spatial molecular geometry. This generates specific structural sensing vis-à-vis solvent surfactants. The value of η show a linear trend, whereas γ tracks the surrounding surficial energy spontaneously. There is a need to track the kinetic weakening of CF leading to SLS0I. The σ parameter simultaneously follows both changes; hence, it is the best alternative or structural sensor to infer solvent structure disruption. σ data have higher resolution and reproducibility and illustrate the interfaces of CF and FF, where these forces are the core theories for η and γ measurements, respectively.
The studies focus on the development of the monodispersion of various components in aqueous DMSO, and the hydrogen bonding of water; DMSO in aq-DMSO vis-à-vis acquaints with the structures of the flavonoid, BSA and surfactants to homogenize them together. Therefore, the PCPs which deal with the cohesive forces of individual components to monodisperse in aq-DMSO are illustrated. For example, surface tension depicted the coagulation or clustering of similar molecules, and the viscosity data reflect the monodispersion of flavonoid, BSA, and surfactants. Therefore, their effective molecular interactions engineer their mutual solubilization and monodispersion by weakening γ and increasing the η values upon the loading of aq-DMSO with ingredients. Also, the magnitudes and mutual trends of the γ and η data both define a state of inducing the compactness of medium. This is reflected by the refractive index and relaxation time. The molecular interactions depicted the dispersion noted in terms of η, which is also mutually reflected by the conductance monitored by pH upon forming the H3O-based Lewis acid and base conjugate model as shown:
Thus, the parameters which structurally define the overall structural changes, like orientations, reorientations, molecular motions, transport and compactness of the medium, have been measured and interpreted to optimize the overall state of the resultant liquid mixtures. The main outcome of this research is to solve the problem of the solubility of flavonoids in aqueous mixed medium and also to study the effects of temperature on their solubility in the aq-DMSO medium. This work also aimed to explore the potential of flavonoids and protein interfaces to find the possible chemistry of flavonoid vis-à-vis the unfolding of proteins. Therefore, the outcome and fundamental mechanism of our studies explore bright prospects for conducting the studies with other globular proteins, DNA, enzymes, biocatalysts, and buffers in place of aqueous DMSO at variable pH and temperatures. The surfactants could be replaced with ionic liquids and amino acids so that the functional bioactive nanoemulsion medium could be developed not only to study PCPs but also to extend their applications to investigate the free radical scavenging of various species.
4. Conclusions
The nanodispersion stability of flavonoids with surfactants in the aq-DMSO system was examined with τ, ηD, Z, the Walden product, pH, the electrostatic potentiostat, and Λm measurements. Upon increasing the concentration and ACL of CnTAB, the dispersion of flavonoids increased, which is confirmed by the PCPs and thermodynamic determination. Apigenin has shown stronger interacting abilities with solvent systems which were determined with τ, ηD, Z, the Walden product, ΔS and Δq. The η data of CnTAB with solvent systems at T = 298.15, 303.15 and 308.15 K determined the bulk properties ηr and τ, ΔS, ΔH, ΔG, the Walden product, DFI and friccohesity shift coefficient with regards to the structural consequences of IMI present between the components. Upon increasing the temperature and concentration, the C and u parameters both are inversely proportional to each other. As the concentration of CnTAB increased, the ηD values increased with the increasing electronic polarizability in solution. The lowest Λ0 and highest η values for HDTAB weakened the CFs with stronger IMF. Increasing the ACL and temperature increased the ΔS values due to the longer hydrophobic spacer of CnTAB from the higher clusters. Upon increasing the ACL and concentration of CnTAB, the BSA structure denatured with the change in the conformatory structure of BSA and increased dispersion, which increased the surface area and interacting sites. This can work as a suitable model for use in drug delivery, pharmaceutical industries, and cosmetics. The friccohesity and DFI define the interacting and distribution dynamics based on molecular motion, molecular stretching, and inquorate functional moiety as well as the electrostatic interaction of medium and additives.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors are thankful to the Central University of Gujarat for infrastructures and experimental facilities support. RGNF is acknowledged for the SRF awarded (F1-17.1/2015-16/RGNF-2015-17-SC-UTT-13082/(SA-III/Website)) to K. M. Sachin for financial support.
References
- Y. Zhang, S. Shi, X. Chen, W. Zhang, K. Huang and M. Peng, J. Agric. Food Chem., 2011, 59, 8499–8506 CrossRef CAS PubMed.
- L. Peng, X. Hongyu, L. Xi, R. Lifang and Z. Chaocan, Biol. Trace Elem. Res., 2007, 118, 97–103 CrossRef PubMed.
- R. E. Olson and D. D. Christ, Annu. Rep. Med. Chem., 1996, 31, 327–336 CAS.
- U. Kragh-Hansen, Pharmacol. Rev., 1981, 33, 17–53 CAS.
- N. Shahabadi, M. Maghsudi, Z. Kiani and M. Pourfoulad, Food Chem., 2011, 124, 1063–1068 CrossRef CAS.
- X. L. Wei, J. B. Xiao, Y. Wang and Y. Bai, Spectrochim. Acta, Part A, 2010, 75, 299–304 CrossRef PubMed.
- V. Guillaume, D. Hervé, C. Karine, C.-R. Cécile, T. Nellie, A. Anne, G. Anne, C. Louis and M. L. Xavier, J. Hepatol., 2011, 54, 348–356 CrossRef PubMed.
- E. Abuin, C. Calderon and E. Lissi, J. Photochem. Photobiol., A, 2008, 195, 295–300 CrossRef CAS.
- Y. Ni, X. Zhang and S. Kokot, Spectrochim. Acta, Part A, 2009, 71, 1865–1872 CrossRef PubMed.
- P. Athina, J. G. Rebecca and A. F. Richard, J. Agric. Food Chem., 2005, 53, 158–163 CrossRef PubMed.
- M. F. Mahomoodally, A. Gurib-Fakim and A. H. Subratty, Pharm. Biol., 2005, 43, 237–242 CrossRef.
- A. K. Pandey, Natl. Acad. Sci. Lett., 2007, 30, 383–386 Search PubMed.
- J. R. Bacon and M. J. C. Rhodes, J. Agric. Food Chem., 2000, 48, 838–843 CrossRef CAS PubMed.
- V. de Freitas and N. Mateus, J. Agric. Food Chem., 2001, 49, 940–945 CrossRef CAS PubMed.
- R. A. Frazier, A. Papadopoulou, I. Mueller-Harvey, D. Kissoon and R. J. Green, J. Agric. Food Chem., 2003, 51, 5189–5195 CrossRef CAS PubMed.
- Y. Chen and A. E. Hagerman, J. Agric. Food Chem., 2004, 52, 4008–4011 CrossRef CAS PubMed.
- E. Jobstl, J. O'Connell, J. P. A. Fairclough and M. P. Williamson, Biomacromolecules, 2004, 5, 942–949 CrossRef PubMed.
- A. Bolli, M. Marino, G. Rimbach, G. Fanali, M. Fasano and P. Ascenzi, Biochem. Biophys. Res. Commun., 2010, 398, 444–449 CrossRef CAS PubMed.
- X. L. Shi, X. W. Li, M. Y. Gui, H. Y. Zhou, R. J. Yang, H. Q. Zhang and Y. R. Jin, J. Lumin., 2010, 130, 637–644 CrossRef CAS.
- L. Matei and M. Hillebrand, J. Pharm. Biomed. Anal., 2010, 51, 768–773 CrossRef PubMed.
- J. Xiao, M. Suzuki, X. Y. Jiang, X. Q. Chen, K. Yamamoto, F. L. Ren and M. Xu, J. Agric. Food Chem., 2008, 56, 2350–2356 CrossRef CAS PubMed.
- J. B. Xiao, H. Cao, Y. F. Wang, K. Yamamoto and X. L. Wei, Mol. Nutr. Food Res., 2010, 54, 253–260 CrossRef PubMed.
- X. Tang, P. Tang and L. Liu, Molecules, 2017, 22, 1036 CrossRef PubMed.
- Y. Zhang, S. Shi, X. Chen, W. Zhang, K. Huang and M. Peng, J. Agric. Food Chem., 2011, 59, 8499–8506 CrossRef CAS PubMed.
- J. J. M. Medinaa, L. G. Nasob, A. L. Pérezc, A. Rizzic, N. B. Okulika, E. G. Ferrerb and P. A. M. Williamsb, J. Photochem. Photobiol., A, 2017, 344, 84–100 CrossRef.
- B. Pang, S. Bin, Y. Wang, L. Yan and T. Wang, J. Lumin., 2012, 132, 895–900 CrossRef CAS.
- S. Shi, Y. Zhang, X. Chen and M. Peng, J. Agric. Food Chem., 2011, 59, 10761–10769 CrossRef CAS PubMed.
- C. Ban, S. J. Park, S. Lim, S. J. Choi and Y. J. Choi, J. Agric. Food Chem., 2015, 63, 5266–5272 CrossRef CAS PubMed.
- R. Joshi, Y. A. Kulkarni and S. Wairkar, Life Sci., 2018, 215, 43–56 CrossRef CAS PubMed.
- K. M. Sachin, A. Chandra and M. Singh, J. Mol. Liq., 2017, 246, 379–395 CrossRef CAS.
- S. Ryshetti, A. Gupta, S. J. Tangeda and R. L. Gardas, J. Chem. Thermodyn., 2014, 77, 123–130 CrossRef CAS.
- L. A. Romanklw and I. MlngChou, J. Chem. Eng. Data, 1983, 28, 300–305 CrossRef.
- R. G. Lebel and D. A. I. Goring, J. Chem. Eng. Data, 1962, 7, 100–101 CrossRef CAS.
- A. Pal, R. Gaba and S. Sharma, J. Chem. Eng. Data, 2008, 53, 1643–1648 CrossRef CAS.
- M. Singh, J. Biochem. Biophys. Methods, 2006, 67, 151–161 CrossRef CAS PubMed.
- A. Naseem and A. J. Jamal, J. Mol. Liq., 2013, 181, 68–76 CrossRef.
- R. M. Patel and J. N. Patel, J. Adv. Pharm. Educ. Res., 2011, 1, 52–68 Search PubMed.
- V. N. Enujiugha, J. Y. Talabi, S. A. Malomo and A. I. Olagunju, Food Nutr. Sci., 2012, 3, 7–13 Search PubMed.
- J. E. Lind Jr, J. J. Zwolenik and R. M. Fuoss, J. Am. Chem. Soc., 1959, 81, 1557 CrossRef.
- A. K. Jangid, P. Malik and M. Singh, J. Mol. Liq., 2018, 259, 439–452 CrossRef CAS.
- K. Sharma and S. Chauhan, Thermochim. Acta, 2014, 578, 15–27 CrossRef CAS.
- B. Lindmann and H. Wennerstrom, Springer-Verlag, New York, 1980, p. 87.
- J. Greener, B. A. Contestable and M. D. Bale, Macromolecules, 1987, 20, 2490–2498 CrossRef CAS.
- J. George, S. M. Nair and L. Sreejith, J. Surfactants Deterg., 2008, 11, 29–32 CrossRef CAS.
- S. Jian and C. Hui, Rev. Bras. Farmacogn., 2011, 21, 594–600 CrossRef.
- K. M. Sachin, S. Karpe, M. Singh and A. Bhattarai, Macromol. Symp., 2018, 379, 1700034 CrossRef.
- K. M. Sachin, S. A. Karpe, M. Singh and A. Bhattarai, J. Chem., 2018, 2018, 1–17 CrossRef.
- F. Oosawa, Polyelectrolytes, Marcel Dekker, New York, 1st edn, 1971 Search PubMed.
- S. Chauhan, V. Sharma and K. Sharma, Fluid Phase Equilib., 2013, 354, 236–244 CrossRef CAS.
- S. S. Aswale, S. R. Aswale and R. S. Hajare, J. Chem. Pharm. Res., 2012, 4, 2671–2677 CAS.
- A. Alexander, J. Phys. Chem. B, 2008, 112, 7032–7044 CrossRef PubMed.
- L. A. Romanklw and I. MlngChou, J. Chem. Eng. Data, 1983, 28, 300–305 CrossRef.
- R. Singh, S. Chauhan and K. Sharma, J. Chem. Eng. Data, 2017, 62, 1955–1964 CrossRef CAS.
- R. K. Ameta, M. Singh and R. K. Kale, J. Chem. Thermodyn., 2013, 60, 159–168 CrossRef CAS.
- M. S. Raman, M. Kesavan, K. Senthilkumar and V. Ponnuswamy, J. Mol. Liq., 2015, 2, 115–124 CrossRef.
- S. Nithiyanantham and L. Palaniappan, Arabian J. Chem., 2012, 5, 25–30 CrossRef CAS.
- A. Z. Tasic, B. D. Djordjevic, D. K. Grozdanic and N. Radojkovic, J. Chem. Eng. Data, 1992, 37, 310–313 CrossRef CAS.
- K. M. Sachin, S. A. Karpe, M. Singh and A. Bhattarai, R. Soc. Open Sci., 2019, 6, 181979 CrossRef CAS PubMed.
- Z. B. Zhou, H. Matsumoto and K. Tatsumi, ChemPhysChem, 2005, 6, 1324–1332 CrossRef CAS PubMed.
- R. K. Ameta, N. K. Sharma and C. B. Sangani, Int. J. Chem. Sci., 2017, 15, 152 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00851a |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Man Singh
and
Man Singh *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DTAB, Cn = 12; TDTAB, Cn = 14; HDTAB, Cn = 16). The flavonoids with cationic surfactants strongly interacted with BSA, as illustrated by the physicochemical parameters (PCPs), refractive index (nD), Walden product, pH, electrostatic potential and molar conductance (Λm). Viscosity (η), density (ρ), ηD, sound velocity (u) and specific conductance (k) data were used to calculate the relative viscosity (ηr), viscous relaxation time (τ), Walden product, entropy (ΔS), enthalpy (ΔH), Gibbs free energy (ΔG), heat capacity (Δq) limiting dielectric constant (ε∞), speed of light (C), acoustic impedance (Z) and molar refraction (R). These PCPs have quantitatively predicted the hydrophilic and hydrophobic (philicphobic) interactions developed are on increasing the alkyl chain (AC) of CnTAB. These interactions assist a monodispersion of the flavonoids, and a similar mechanism could equally be applicable to monodisperse the antioxidants in the aqueous nanoemulsions. Their philicphobic stoichiometry weakened the cohesive forces (CF) when the shear stress was increased, and enhanced surface activities were achieved that facilitated the flavonoids to interact with BSA due to intermolecular forces (IMF) to develop a stable nanoemulsion; Upon increasing the CnTAB concentrations, the nD value increases since the polarizability increases with stronger shear stress due to van der Waal forces and electrostatic interactions to achieve better flavonoid–BSA linkages.
DTAB, Cn = 12; TDTAB, Cn = 14; HDTAB, Cn = 16). The flavonoids with cationic surfactants strongly interacted with BSA, as illustrated by the physicochemical parameters (PCPs), refractive index (nD), Walden product, pH, electrostatic potential and molar conductance (Λm). Viscosity (η), density (ρ), ηD, sound velocity (u) and specific conductance (k) data were used to calculate the relative viscosity (ηr), viscous relaxation time (τ), Walden product, entropy (ΔS), enthalpy (ΔH), Gibbs free energy (ΔG), heat capacity (Δq) limiting dielectric constant (ε∞), speed of light (C), acoustic impedance (Z) and molar refraction (R). These PCPs have quantitatively predicted the hydrophilic and hydrophobic (philicphobic) interactions developed are on increasing the alkyl chain (AC) of CnTAB. These interactions assist a monodispersion of the flavonoids, and a similar mechanism could equally be applicable to monodisperse the antioxidants in the aqueous nanoemulsions. Their philicphobic stoichiometry weakened the cohesive forces (CF) when the shear stress was increased, and enhanced surface activities were achieved that facilitated the flavonoids to interact with BSA due to intermolecular forces (IMF) to develop a stable nanoemulsion; Upon increasing the CnTAB concentrations, the nD value increases since the polarizability increases with stronger shear stress due to van der Waal forces and electrostatic interactions to achieve better flavonoid–BSA linkages.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Thereafter, after vigorous shaking, these samples were kept in dark for an incubation period of 30 min. The relative radical scavenging activities (RSAs) were evaluated as a measure of comparative % decrease in the absorbance of pure DPPH˙ at λmax = 520 nm, ascertained by measuring the absorbance of the DPPH + flavonoid formulation 1
1 ratio. Thereafter, after vigorous shaking, these samples were kept in dark for an incubation period of 30 min. The relative radical scavenging activities (RSAs) were evaluated as a measure of comparative % decrease in the absorbance of pure DPPH˙ at λmax = 520 nm, ascertained by measuring the absorbance of the DPPH + flavonoid formulation 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture at the same wavelength. The measurements were made with a Spectro2060 plus model UV/Vis spectrophotometer. The respective RSAs were calculated using the following equation:
1 mixture at the same wavelength. The measurements were made with a Spectro2060 plus model UV/Vis spectrophotometer. The respective RSAs were calculated using the following equation:![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O through their philicphobic nature. The shift for 10% DMSO could be extended to other single and mixed solvent systems. Such chemical engineering to formulate the workability of solvents has never yet been reported. Thus, our model could open a new area of research in engineering the solvents as these play a critical role in the quality of the products formed, similar to benzene conjugation. The linear γ value decreases upon increasing DMSO concentration, which suggests that more and more DMSO could break the HB of H2O. The HB of H2O led to the development of CFs with a higher γ value. But DMSO decreases the γ value, as the DMSO dipoles attack the H2O dipoles and put pressure on the HB of water. Ultimately the HB of H2O is disrupted by DMSO, which decreases the γ value to form a low surface energy liquid mixture. Hence, our data (Table S1†) support the following model.
O through their philicphobic nature. The shift for 10% DMSO could be extended to other single and mixed solvent systems. Such chemical engineering to formulate the workability of solvents has never yet been reported. Thus, our model could open a new area of research in engineering the solvents as these play a critical role in the quality of the products formed, similar to benzene conjugation. The linear γ value decreases upon increasing DMSO concentration, which suggests that more and more DMSO could break the HB of H2O. The HB of H2O led to the development of CFs with a higher γ value. But DMSO decreases the γ value, as the DMSO dipoles attack the H2O dipoles and put pressure on the HB of water. Ultimately the HB of H2O is disrupted by DMSO, which decreases the γ value to form a low surface energy liquid mixture. Hence, our data (Table S1†) support the following model.


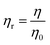
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and one double bond at the C-ring in its molecular structure, compared to a single bond in naringenin. However, apigenin has 1 –OH group at the B-ring that could induce stronger interaction affinity towards BSA and could not form intramolecular hydrogen bonding (IMHB). Quercetin has 5 –OH groups and one double bond with π-conjugation at the C-ring due to the 2 –OH groups placed at the B-ring and could form IMHB (Fig. 10) with decreasing interacting sites. Apigenin shows a higher ηr value than naringenin or quercetin. Spectroscopic interaction study of flavonoids with proteins by the quenching constant and the binding constant of apigenin with proteins show higher interactions than quercetin or naringenin.45 For example, CnTAB with WBDQ, WBDA and WBDN showed different trends of ηr values at T = 298.15, 303.15 and 308.15 K. The surfactants could form micelles with air gates;46,47 with increasing ACL, air could enter the micelles through the air gates, so increasing the temperature created an asymmetric trend of ηr values. Upon increasing the ACL, the ηr value increased with the weakening of CF in addition to stronger electrostatic interaction and IMF (Fig. 11). With increasing temperature, the ηr value decreased because of the increased KE as the binding forces (BF) and IMMF weakened.
O group and one double bond at the C-ring in its molecular structure, compared to a single bond in naringenin. However, apigenin has 1 –OH group at the B-ring that could induce stronger interaction affinity towards BSA and could not form intramolecular hydrogen bonding (IMHB). Quercetin has 5 –OH groups and one double bond with π-conjugation at the C-ring due to the 2 –OH groups placed at the B-ring and could form IMHB (Fig. 10) with decreasing interacting sites. Apigenin shows a higher ηr value than naringenin or quercetin. Spectroscopic interaction study of flavonoids with proteins by the quenching constant and the binding constant of apigenin with proteins show higher interactions than quercetin or naringenin.45 For example, CnTAB with WBDQ, WBDA and WBDN showed different trends of ηr values at T = 298.15, 303.15 and 308.15 K. The surfactants could form micelles with air gates;46,47 with increasing ACL, air could enter the micelles through the air gates, so increasing the temperature created an asymmetric trend of ηr values. Upon increasing the ACL, the ηr value increased with the weakening of CF in addition to stronger electrostatic interaction and IMF (Fig. 11). With increasing temperature, the ηr value decreased because of the increased KE as the binding forces (BF) and IMMF weakened.

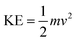
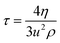
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) product = η0κ0
product = η0κ0
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) bond at its C-ring has structural homology to quercetin except for two additional –OH groups at the A- and B-rings. Apigenin shows a higher Walden product with DTAB than quercetin or naringenin. The Walden product value is such that DTAB > TDTAB > HDTAB. This leads to DTAB having a higher charge density and stronger IHI with higher specific conductance.
) bond at its C-ring has structural homology to quercetin except for two additional –OH groups at the A- and B-rings. Apigenin shows a higher Walden product with DTAB than quercetin or naringenin. The Walden product value is such that DTAB > TDTAB > HDTAB. This leads to DTAB having a higher charge density and stronger IHI with higher specific conductance.
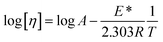




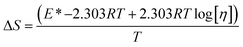
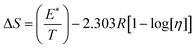
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[η]
log[η]

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) o− hydrophilic ions catalyse the BSA unfolding and HB disruption of H2O. In regards to DMSO and flavonoids, the smaller molecules penetrate α to β BSA sheets increases unfolding from α → β convolutions, where the DMSO and the flavonoid KE destabilize.
o− hydrophilic ions catalyse the BSA unfolding and HB disruption of H2O. In regards to DMSO and flavonoids, the smaller molecules penetrate α to β BSA sheets increases unfolding from α → β convolutions, where the DMSO and the flavonoid KE destabilize.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ae−E/RT
Ae−E/RT
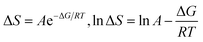
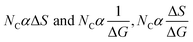
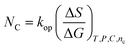
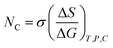
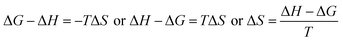
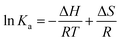
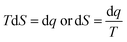
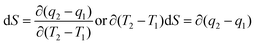
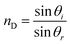
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi and sin
θi and sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θr are the angles of incident and refractive light of the medium, respectively.
θr are the angles of incident and refractive light of the medium, respectively.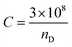
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and ηD data. The higher Z value of apigenin with WBD, as compared to quercetin and naringenin due to the π-conjugation and 1 –OH group at the B-ring, could not form IMHB with the increasing number of interaction sites. Quercetin has 2 –OH groups at the B-ring that form IMHB and reduce the interacting sites, developing weak electrostatic, ion-dipole and IMI. However, in naringenin an in the absence of π-conjugation in its molecular structure, the electron density as well as the Z value decreases. The solvent system with CnTAB are such that WBD > WBDN > WBDQ > WBDA with DTAB, WBD > WBDQ > WBDA > WBDN with TDTAB, and WBD > WBDQ > WBDN > WBDA with HDTAB at T = 298.15, 303.15 and 308.15 K, respectively. WBD with DTAB, TDTAB and HDTAB, shows a higher Z value. BSA, due to unfolding, exhibits increased surface area, interacting sites and Z value. DTAB has a shorter ACL than TDTAB or HDTAB, and naringenin has higher hydrophobicity than apigenin or quercetin due to the stronger IHbI with increasing Z value. While with naringenin TDTAB and HDTAB, the Z value decreased due to stronger LDF. For TDTAB and HDTAB with quercetin and apigenin, quercetin due to stronger electrostatic interaction, the Z value increases. To understanding total polarizability, the molar refraction (R) was calculated with the Lorentz–Lorenz equation57 shown below.
and ηD data. The higher Z value of apigenin with WBD, as compared to quercetin and naringenin due to the π-conjugation and 1 –OH group at the B-ring, could not form IMHB with the increasing number of interaction sites. Quercetin has 2 –OH groups at the B-ring that form IMHB and reduce the interacting sites, developing weak electrostatic, ion-dipole and IMI. However, in naringenin an in the absence of π-conjugation in its molecular structure, the electron density as well as the Z value decreases. The solvent system with CnTAB are such that WBD > WBDN > WBDQ > WBDA with DTAB, WBD > WBDQ > WBDA > WBDN with TDTAB, and WBD > WBDQ > WBDN > WBDA with HDTAB at T = 298.15, 303.15 and 308.15 K, respectively. WBD with DTAB, TDTAB and HDTAB, shows a higher Z value. BSA, due to unfolding, exhibits increased surface area, interacting sites and Z value. DTAB has a shorter ACL than TDTAB or HDTAB, and naringenin has higher hydrophobicity than apigenin or quercetin due to the stronger IHbI with increasing Z value. While with naringenin TDTAB and HDTAB, the Z value decreased due to stronger LDF. For TDTAB and HDTAB with quercetin and apigenin, quercetin due to stronger electrostatic interaction, the Z value increases. To understanding total polarizability, the molar refraction (R) was calculated with the Lorentz–Lorenz equation57 shown below.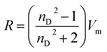
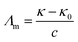




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + Am + Bm2
+ Am + Bm2