Open Access Article
Open Access ArticleDevelopment of a nano-QSPR model to predict band gaps of spherical metal oxide nanoparticles†
Jiaxing Wang‡
a,
Ya Wang‡a,
Yang Huanga,
Willie J. G. M. Peijnenburg bc,
Jingwen Chen
bc,
Jingwen Chen a and
Xuehua Li
a and
Xuehua Li *a
*a
aKey Laboratory of Industrial Ecology and Environmental Engineering (MOE), School of Environmental Science and Technology, Dalian University of Technology, Linggong Road 2, Dalian 116024, China. E-mail: lixuehua@dlut.edu.cn
bInstitute of Environmental Sciences, Leiden University, 2300 RA Leiden, The Netherlands
cNational Institute of Public Health and the Environment, Center for the Safety of Substances and Products, 3720 BA Bilthoven, The Netherlands
First published on 14th March 2019
Abstract
Antibacterial activities and cytotoxicity of metal oxide nanoparticles are determined by their special band structures, which also influence their potential ecological risks. Traditional experimental determination of the band gap is time-consuming, while the accuracy of theoretical computation depends on the selected algorithm, for which higher precision algorithms, being more expensive, can give a more accurate band gap. Therefore, in this study, a quantitative structure–property relationship (QSPR) model, highlighting the influence of crystalline type and material size, was developed to predict the band gap of metal oxide nanoparticles rapidly and accurately. The structural descriptors for metal oxide nanoparticles were generated via quantum chemistry computations, among which heat of formation and beta angle of the unit cell were the most important parameters influencing band gaps. The developed model shows great robustness and predictive ability (R2 = 0.848, RMSE = 0.378 eV, RMSECV = 0.478 eV, QEXT2 = 0.814, RMSEP = 0.408 eV). The current study can assist in screening the ecological risks of existing metal oxide nanoparticles and may act as a reference for newly designed materials.
1. Introduction
Metal oxide nanoparticles (MONs) are used widely in many fields due to their unique properties.1 Some of these properties, such as optical and electronic properties, are determined by their special band structure, which can be characterized by three parameters: EC (energy of conduction band), EV (energy of valence band) and Eg (energy of band gap). For example, as a very important optical property, the ability to generate reactive oxygen species (ROS) is tightly related to the band structure of the material. TiO2 and ZnO nanoparticles could generate three types of ROS (·O2−, H2O2,·OH) under UV irradiation while other metal oxides generate only one or two types or even do not generate any type of ROS at all.2 Different metal oxide nanoparticles also generate different amounts of ROS, and consequently, they have different antibacterial activities or abilities to degrade organic pollutants.3,4Meanwhile, as the wide applications of MONs increase rapidly, their potential ecological risks have drawn more and more attention.2 One of the main mechanisms of oxidative damage caused by MONs is the overlap of conduction band energy (EC) levels with the cellular redox potential. The overlap of EC with the redox potential leads to the transfer of electrons from reductive substances, which then generate reactive oxygen species (ROS) which could eventually damage cells.3–5 Therefore, the EC value is a meaningful parameter for the assessment of the ecological risks of MONs. EC can be calculated by means of eqn (1): EC refers to the conduction band energy; Eg is the band gap energy and χoxide is the absolute electronegativity of the metal oxide.6
| Ec = χoxide + 0.5Eg | (1) |
The absolute electronegativity can be calculated by a set of equations reported by Portier et al.7 Values of the band gaps of MONs can be obtained from experimental determination and from estimation.
The experimental determination of band gaps requires diffuse reflectance UV-vis spectroscopic analysis, which can accurately measure the band gaps of MONs. However, considering the increase of emerging MONs both in amount and types as well as taking into account that band gaps of MONs vary when crystalline types, sizes and shapes are different,8 experimental determinations of band gaps are inefficient and cannot provide any guide at all for the design of novel MONs that are safe with regard to their ecological impacts.
Estimation methods were proposed, including theoretical computation and empirical equation to obtain band gaps efficiently and conveniently. As for theoretical computation, its inaccuracy is the main obstacle which undermines its authorization and application domain. For example, the band gaps of solids could be underestimated with an accuracy of 30–100% in a typical density functional theory calculation.9 Building a cluster of unit cells was tried,10 but computation for a cluster commensurate with real material requires vast investment of computational resources. As for empirical estimation, Portier et al.,11 demonstrated the correlation between band gap and thermodynamic properties, and put forward an empirical equation to estimate band gap of bulk metal oxides by using enthalpies of formation (eqn (2)).
Eg = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e0.34EΔH e0.34EΔH
| (2) |
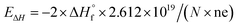 | (3) |
In the eqn (3), 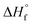 refers to the standard enthalpy of formation of the oxide in cal mol−1 and the coefficient A is determined by cation ion of the oxide, N is Avogadro's number, ne refers to the number of valence electron. For s-block, p-block, d-block and f-block of metal elements, the reported A values are 0.80, 1.35, 1.00 and 0.80 respectively.11 Using this empirical equation, the band gaps of binary oxides can be calculated very quickly. But this equation ignores the effects of size differences. Therefore, it is required to develop a prediction method to obtain the band gap of MONs with different crystalline type and particle size accurately and efficiently.
refers to the standard enthalpy of formation of the oxide in cal mol−1 and the coefficient A is determined by cation ion of the oxide, N is Avogadro's number, ne refers to the number of valence electron. For s-block, p-block, d-block and f-block of metal elements, the reported A values are 0.80, 1.35, 1.00 and 0.80 respectively.11 Using this empirical equation, the band gaps of binary oxides can be calculated very quickly. But this equation ignores the effects of size differences. Therefore, it is required to develop a prediction method to obtain the band gap of MONs with different crystalline type and particle size accurately and efficiently.
Quantitative structure–property relationships (QSPRs) have been used to predict various properties of chemicals.12,13 QSPRs can be applied fast, they are low-cost and efficient compared with other methods. For MONs, several QSPRs models were reported to predict photo-induced toxicity of MONs, including toxicity of MONs to E. coli and to human keratinocyte cells as well as the cell uptake rate of MONs.14–17 Wyrzykowska et al. developed a nano-QSPR model to predict the zeta potential of MONs in KCl aqueous solution of MONs.18
In this study, we developed a nano-QSPR model, considering different crystalline types and sizes, to predict band gaps of MONs. Besides, band gaps were also calculated by two other estimation methods to compare the predictive ability of different methods. From a wider perspective, this study could help screen the potential ecological risk of MONs and provide reference for newly designed MONs.
2. Methods
2.1. Data set for band gaps
Experimental band gaps of MONs were obtained by collection from literature3,19–50 and by experimental determination.To control variables that influence band gaps of MONs as much as possible and to ensure the consistency of collected band gaps, a qualified data point from literature must meet the following demands: size of material is in the nanometer scale; particles must be spherical or approximate a spherical shape; particles have a single chemical makeup without any chemical modification on the surface; characterizations including X-ray diffraction, which verifies the crystalline structure of MONs, and UV-vis spectroscopic analysis are required.
Seven kinds of MONs (5 nm anatase-TiO2, 25 nm anatase-TiO2, 40 nm anatase-TiO2, 100 nm anatase-TiO2, 40 nm rutile-TiO2, 100 nm rutile-TiO2 and 50 nm ZnO) bought from Aladdin (http://www.aladdin-e.com/) were prepared for UV-vis spectroscopic analysis using UV-550 spectrophotometer produced by JASCO Corporation. To minimize possible errors, each determination for each material was repeated three times and the eventual outcome is the arithmetic mean of parallel experiments. The raw data of UV-vis spectroscopic analysis were transformed according to the Kubelka–Munk equation.51
The total data set of band gaps of MONs was split randomly into a training set and a validation set with a ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (30
1 (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10).
10).
2.2. Date pre-processing
Previous studies indicated that the band gap of relatively large particles (size > 10 nm) is not affected by size whereas the quantum confinement effect only occurs when the size of nanoparticle is smaller than approximately 10 nm, consequently leading to a larger value of band gap.52,53 Therefore, the value of the band gaps of materials with size smaller than 10 nm was used directly. In case of material with a size larger than 10 nm, the average size and the average band gap were calculated and included in either the training set or the validation set.2.3. Descriptors
The descriptors used to develop the nano-QSPR were derived from theoretical calculation, as well as from literature and experimental characterization. (1) Theoretical descriptors were calculated by using the Vienna Ab initio Simulation Package (VASP) 5.4.1 (ref. 54) and MOPAC2016 (ref. 55) (2) reported descriptors of MONs in literatures, such as the ratio of metal atoms to oxygen atoms and weight of atoms, were included in this study, remaining to be selected further.4,56 (3) Experimental characterization outcomes such as size, crystalline type information and the number of unit cells contained by the material were included.To consider the influence of crystalline types to band gaps of materials in calculation, input files should specify crystalline type, which must be consistent with corresponding band gap of every material. The XRD outcomes or joint committee powder diffraction standards (JCPDS) number was collected from the same literature from which the value of the band gap of MONs was collected. MDI JADE 5.0 (ref. 57) was utilized to analyze collected XRD patterns and to match the corresponding standard XRD cards, which could specify crystalline type. Based on the crystalline type information derived from standard cards, the corresponding crystalline file in common intermediate format (CIF) was obtained in FindIt58 before being transformed by Open Babel 2.4.1 (ref. 59) into standard input files. Single cell units were optimized by the general gradient approximate (GGA) of VASP before descriptor computation and the error of optimization for structure was verified to be within 5%. Descriptors of VASP computation were obtained from POTCAR and OUTCAR after structure optimization. The PM7 method was used to generate various descriptors in MOPAC computation. In order to validate the acceptability of descriptors derived from the computation being based on single cell units, important descriptors selected in model were compared with their experimental values.
In order to ensure that the correlation between descriptors and band gaps is linear, several parameters were processed before they were suited as descriptor. Heat of formation of the unit cell, computed by MOPAC, was transformed according to a previously reported empirical equation.11 The reciprocal value of the squared diameter was processed as a descriptor according to the Brus equation (eqn (4)).52
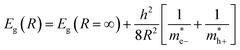 | (4) |
2.4. QSPR modeling
Partial least square (PLS) regression was utilized to develop the QSPR model. The SIMCA 13.0 software package was used to provide PLS as well as the subsequent analysis.60 The PLS approach was established around 1975 by Herman Wold for the modelling of complicated data sets.61 The basic principle of PLS could be interpreted as PLS being the combination of principal components analysis (PCA), correlation analysis (CA) and multiple linear regression (MLR).62 Unlike MLR, PLS can analyze data with strongly collinear, noisy and numerous X variables.63 In our study, the amount of descriptors is relatively large and the correlation between various descriptors is difficult to demonstrate. Therefore, PLS was used to develop this model.A genetic algorithm (GA), developed by means of the R program,64 was used to select descriptors for developing prediction models. The number of descriptors in the model was further decreased by using a method reported in literature:65 Based on the values of the variable influence for the projection (VIP), descriptors with lower VIP values were deleted from the model until the model shows best validation performance.
2.5. Model characterization
In order to ensure the reliability and predictive ability of the developed model, various analyses were done to characterize the performance of the model. The correlation coefficient R2 between predicted and observed Eg and the root mean standard error of estimation (RMSEE) measure the fitting performance. The performance of internal validation could be indicated by the root mean standard error of cross validation (RMSECV), which is based on the leave-one-out (LOO) test. As for external validation, the predictive power of the developed QSPR model was estimated by means of calculating the root mean standard error of prediction (RMSEP) and QEXT2 defined by means of eqn (5), where yi and ŷi are the measured and predicted value of Eg in the validation set, respectively; ȳi is the average value of Eg for the training set. A value of QEXT2 larger than 0.5 indicates a good predictive capability of the model and a value of QEXT2 larger than 0.9 indicates excellent predictive ability.
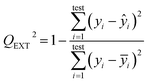 | (5) |
According to the OECD guideline,66 the applicability domain of the developed model was determined by the method reported by K. Roy et al.67 Firstly, descriptors in training set were normalized. If all of the normalized descriptors for a material are larger than 3, that material can be judged as an outlier. On the contrary, a material is treated as non-outlier if all of its normalized descriptors are smaller than 3. For a material who has some descriptors larger than 3 but the others not, it will be further investigated.
3. Results and discussion
3.1. Data set of band gaps
Through data collection, 91 values of band gaps of 22 different MONs were collected.3,19–50 Band gaps ranged from 1.85 eV to 6.07 eV with an average of 3.60 eV and a standard deviation of 0.8 eV. The particles diameters ranged from 2.5 nm to 100 nm with an average of 26.0 nm and a standard deviation of 24.8 nm. All collected data are shown in Table S1† and the data set processed according to particles size for model development is displayed in Table 1.| No. | Metal oxide | a | b | c | α | β | γ | Size (nm) | Eexp. (eV) | Epred. (eV) | Set |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a T: training set; V: validation set; Eexp.: experimental gaps; Epred.: predicted gaps. | |||||||||||
| 1 | Al2O3 | 4.81 | 4.81 | 13.12 | 90 | 90 | 120 | 76.0 | 5.97 | 5.74 | T |
| 2 | CeO2 | 5.46 | 5.46 | 5.46 | 90 | 90 | 90 | 12.0 | 3.39 | 3.74 | T |
| 3 | 3.6 | 3.68 | 3.82 | T | |||||||
| 4 | 2.6 | 3.44 | 3.89 | T | |||||||
| 5 | Cr2O3 | 4.58 | 4.58 | 14.72 | 90 | 90 | 120 | 26.5 | 4.22 | 4.11 | T |
| 6 | 38.2 | 3.70 | 4.11 | V | |||||||
| 7 | Cu2O | 4.31 | 4.31 | 4.31 | 90 | 90 | 90 | 4.0 | 2.90 | 2.35 | T |
| 8 | 9.0 | 2.50 | 2.29 | V | |||||||
| 9 | 6.0 | 2.83 | 2.31 | V | |||||||
| 10 | 20.0 | 2.04 | 2.28 | V | |||||||
| 11 | Fe2O3 | 4.74 | 4.74 | 13.49 | 90 | 90 | 120 | 100.0 | 2.38 | 2.96 | V |
| 12 | Fe3O4 | 8.04 | 8.04 | 8.04 | 90 | 90 | 90 | 12.0 | 1.85 | 2.61 | T |
| 13 | Ga2O3 | 12.50 | 3.10 | 5.92 | 90 | 103.7 | 90 | 65.0 | 4.85 | 4.81 | T |
| 14 | 2.5 | 5.10 | 5.00 | T | |||||||
| 15 | HfO2 | 5.14 | 5.19 | 5.31 | 90 | 99.2 | 90 | 17.0 | 6.07 | 5.66 | T |
| 16 | In2O3 | 10.35 | 10.35 | 10.35 | 90 | 90 | 90 | 17.0 | 3.85 | 4.37 | T |
| 17 | La2O3 | 3.94 | 3.94 | 6.18 | 90 | 90 | 120 | 30.0 | 4.98 | 4.30 | T |
| 18 | MgO | 4.25 | 4.25 | 4.25 | 90 | 90 | 90 | 7.0 | 4.27 | 4.54 | T |
| 19 | Mn2O3 | 9.03 | 9.03 | 9.03 | 90 | 90 | 90 | 30.2 | 3.27 | 3.38 | T |
| 20 | NiO | 4.16 | 4.16 | 4.16 | 90 | 90 | 90 | 3.5 | 3.67 | 3.62 | T |
| 21 | 4.6 | 3.63 | 3.58 | T | |||||||
| 22 | 5.5 | 3.62 | 3.57 | V | |||||||
| 23 | 10.1 | 3.62 | 3.54 | T | |||||||
| 24 | 12.4 | 3.61 | 3.54 | T | |||||||
| 25 | 22.0 | 3.27 | 3.53 | T | |||||||
| 26 | Sb2O3 | 5.18 | 16.61 | 5.51 | 90 | 90 | 90 | 11.8 | 4.49 | 4.77 | T |
| 27 | SnO2 | 4.83 | 4.83 | 3.24 | 90 | 90 | 90 | 4.5 | 4.20 | 3.80 | T |
| 28 | 4.0 | 4.10 | 3.81 | V | |||||||
| 29 | 5.0 | 4.21 | 3.79 | T | |||||||
| 30 | 5.2 | 4.20 | 3.79 | V | |||||||
| 31 | 3.7 | 4.33 | 3.82 | T | |||||||
| 32 | 30.0 | 3.74 | 3.75 | T | |||||||
| 33 | TiO2-a | 3.82 | 3.82 | 9.70 | 90 | 90 | 90 | 17.3 | 3.25 | 3.44 | T |
| 34 | TiO2-b | 9.28 | 5.52 | 5.19 | 90 | 90 | 90 | 7.9 | 3.48 | 3.85 | T |
| 35 | 18.9 | 3.11 | 3.83 | V | |||||||
| 36 | TiO2-r | 4.66 | 4.66 | 2.97 | 90 | 90 | 90 | 70.0 | 3.00 | 3.00 | T |
| 37 | WO3 | 5.39 | 5.36 | 7.84 | 90 | 91.8 | 90 | 42.0 | 2.77 | 2.98 | T |
| 38 | Y2O3 | 10.65 | 10.65 | 10.65 | 90 | 90 | 90 | 14.6 | 5.30 | 5.38 | V |
| 39 | ZnO | 3.29 | 3.29 | 5.31 | 90 | 90 | 120 | 35.0 | 3.24 | 2.62 | T |
| 40 | ZrO2 | 5.19 | 5.24 | 5.38 | 90 | 99.2 | 90 | 40.0 | 5.04 | 5.36 | T |
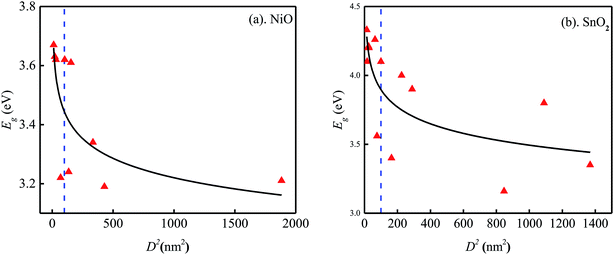
The distribution of band gaps values for MON with multiple sizes was investigated in more detail. First of all, the arithmetic means and standard deviations of the band gaps were calculated: CeO2 (3.50 ± 0.13 eV), Cr2O3 (3.82 ± 0.24 eV), Cu2O (2.57 ± 0.34 eV), Fe2O3 (2.38 ± 0.33 eV), Ga2O3 (4.93 ± 0.12 eV), NiO (3.43 ± 0.19 eV), SnO2 (3.93 ± 0.38 eV), TiO2 (3.25 ± 0.03 eV), ZnO (3.25 ± 0.08 eV). Fig. 1a and b show the distribution of band gaps of NiO and SnO2 respectively as a function of their squared diameter. It can be observed clearly from these plot that band gaps increase as size decreases to values below 10 nm, indicating the occurrence of a quantum confinement effect around 10 nm. However, ambiguity does exist. For example, band gaps increase was not observed for some particles smaller than 10 nm. Besides, large variance of values of band gaps were observed, especially for SnO2 larger than 10 nm. NiO with size of 10.1 nm and 12.4 nm were treated as two single points although their sizes are larger than 10 nm because they display significant difference from other data with size larger than 10 nm. It is the same with Cr2O3. These phenomena might due to these materials are from different literatures, in which materials were synthesized by different methods in different conditions. These differences are hard to characterize because of limited information. Therefore, using the average value of data points with size larger than 10 nm could avoid this unexplainable difference and will minimize the uncertainty of data generated in different laboratories.
3.2. Model development and evaluation
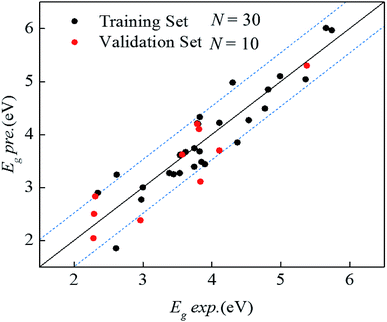
Through PLS regression and descriptor selection, the model was obtained as given in eqn (6) (standard error of regression coefficients are listed in Table S5†). The coefficient of every descriptor in the reported equation is unscaled in order to be convenient for subsequent use. Fig. 2 was plotted to visualize the observed experimental Eg values vs. predicted values of Eg as calculated by eqn (6). The correlation coefficient R2 and the RMSEE of the training set containing 30 values of band gaps of MONs are 0.848 and 0.378 eV, indicating an excellent goodness-of-fit. QEXT2 and RMSEP are 0.814 and 0.408 eV respectively, indicating good predictive ability. The developed model contains three principal components (N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = 10
A = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
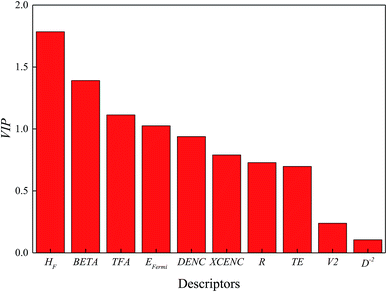
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, N: number of data in training set, A: number of principal components), which accounts for 85 percent explanation of the total variance. The physical meaning and the loading weights of the descriptors in the first two principal components are displayed in Table 2. In the first principal component, heat of formation, beta angle of unit cell and the Thomas Fermi vector outweigh the other descriptors. For the second principle component, Fermi energy, heat of formation and the ratio of metal atoms to oxygen atoms are the most significant descriptors. The VIP values of selected descriptors are plotted in Fig. 3. The VIPs of heat of formation, beta angle of unit cell and Thomas Fermi vector are larger than 1, indicating that these descriptors explain most of the variance of band gaps. Computed heat of formation was compared with the experimental ones in Table S4 and Fig. S1† to validate the acceptability of computed descriptors derived from small molecular model computation, which displayed acceptable fitting performance.
1, N: number of data in training set, A: number of principal components), which accounts for 85 percent explanation of the total variance. The physical meaning and the loading weights of the descriptors in the first two principal components are displayed in Table 2. In the first principal component, heat of formation, beta angle of unit cell and the Thomas Fermi vector outweigh the other descriptors. For the second principle component, Fermi energy, heat of formation and the ratio of metal atoms to oxygen atoms are the most significant descriptors. The VIP values of selected descriptors are plotted in Fig. 3. The VIPs of heat of formation, beta angle of unit cell and Thomas Fermi vector are larger than 1, indicating that these descriptors explain most of the variance of band gaps. Computed heat of formation was compared with the experimental ones in Table S4 and Fig. S1† to validate the acceptability of computed descriptors derived from small molecular model computation, which displayed acceptable fitting performance.| Eg = 0.553HF + 0.0806BETA + 1.09D−2 − 0.0121V2 + 0.18EFermi − 2.23TFW + 0.803R + 0.00469ET − 0.000305DENC − 0.00403XCENC + 0.168 | (6) |
| Descriptor | Physical meaning | Source | w*c [1] | w*c [2] |
|---|---|---|---|---|
| a w*c [1]: loading weight of component [1] w*c [2]: loading weight of component [2]. | ||||
| HF | Heat of formation | MOPAC | 0.65 | 0.57 |
| BETA | Beta angle of unit cell | — | 0.51 | 0.34 |
| D−2 | Reciprocal of square diameter | — | 0.04 | 0.03 |
| V2 | Length of second vector of unit cell | VASP | −0.06 | −0.12 |
| EFermi | Energy of Fermi level | VASP | 0.03 | 0.72 |
| TFW | Thomas Fermi vector | VASP | −0.35 | 0.14 |
| R | Ratio of metal atoms to oxygen atoms | — | −0.08 | 0.45 |
| ET | Total energy | MOPAC | 0.26 | 0.12 |
| DENC | Electron–electron repulsion energy | VASP | 0.28 | −0.04 |
| XCENC | Exchange and correlation energy | VASP | −0.20 | 0.14 |
The applicability domain of the developed model was determined by the reported method mentioned above. Data points from both training set and validation set were investigated. The detailed information of the calculation process is provided in Table S2.† There are 5 and 4 data points with at least one outlier of descriptor in the training set and the validation set respectively. But there is only one material (Y2O3 in validation set) that was judged as an outlier, mainly because its heat of formation deviates far from that of most metal oxides in this model.
3.3. Mechanistic interpretation
Heat of formation and beta angle of unit cell are the most significant descriptors. The correlation between band gap and heat of formation has already been demonstrated by previous studies, that is: bulk metal oxides with larger heat of formation tend to have a larger band gap.68–70 In this study, this correlation for metal oxide nanoparticles was also observed (p < 0.001), which means that this relation remains irrespective of a decrease of material size. It needs to be notified that in this study, heat of formation was calculated by MOPAC PM7. This calculation may not be as accurate as experimental determination but provides a quick method for obtaining heat of formation. Crystalline types could be reflected by not only direct variables characterizing crystalline type such as beta angle and length of vector but also by indirect variables like the E-Fermi and the Thomas Fermi vector because these parameters were calculated based on specific crystalline types. The presence of the beta angle (p < 0.05) and the length of unit cell in the developed model indicates that crystalline type is an important parameter influencing the band gap of MONs. Beta angle and length of vector contribute to the interference of the wave vector of electrons and consequently determine the density of electrons and eventually influence band gaps.The VIP of materials size is not large, which coincides with the Brus equation and the computed standard deviation of materials with multiple sizes. Although the effect of size has been taken into consideration during data pre-processing, it needs to be noted that some variables which may influence the band gap of MONs, were not contained in the developed model. For example, the annealing temperature, time and the ratio of different precursor materials might also affect the value of the band gap. However, these variables are difficult to describe because of the numerous types of MONs and numerous methods to synthesize nanoparticles. Different experimental conditions may lead to unknown differences in the composition of materials, which need to be characterized further.
3.4. Model comparison
The developed QSPR model was compared with empirical equation. Band gaps were calculated with the computed and experimental heat of formation according to the empirical equations.11 The results of comparison are shown in Table 3.| Predictive method | R2 | RMSE (eV) | Reference |
|---|---|---|---|
| QSPR model | 0.848 | 0.378 | This study |
| Empirical equation based on computed heat of formation | 0.490 | 2.24 | Portier et al., 2001 |
| Empirical equation based on experimental heat of formation | 0.571 | 1.58 | Portier et al., 2001 |
The empirical equation using experimental heat of formation to predict band gap, shows better performance than the empirical equation which used computed heat of formation. However, R2 did not change significantly while there was a decrease in RMSE. During characterization the performance of these two empirical methods, it is found that these two methods underestimate or overestimate band gaps. Our QSPR model developed by PLS performs better than previous empirical equations.
4. Conclusions
A nano-QSPR model, covering various crystalline types and material sizes, was developed to predict band gaps for metal oxide nanoparticles. The established QSPR model performs well in terms of goodness-of-fit, robustness and predictive ability. Heat of formation and the beta angle of unit cell are the most important parameters influencing the band gaps of metal oxide nanoparticles. Compared with empirical equation related to the heat of formation, the developed QSPR model had a larger value of R2 and a smaller RMSE. This newly developed QSPR model could thus contribute significantly to the rapid screening of the ecological risk of existing MONs and could assist the design of novel MONs that are environmentally safe.Conflicts of interest
The author declares no competing financial interest.Acknowledgements
This study was supported by The National Key Research and Development Program (2017YFD020030603) of China and the National Natural Science Foundation (21477016, 21777019) of China.References
- Y. Pan, T. Li, J. Cheng, D. Telesca, J. I. Zink and J. Jiang, Nano-QSAR modeling for predicting the cytotoxicity of metal oxide nanoparticles using novel descriptors, RSC Adv., 2016, 6(31), 25766–25775 RSC.
- H. J. Eom and J. Choi, Oxidative stress of CeO2 nanoparticles via p38-Nrf-2 signaling pathway in human bronchial epithelial cell, Beas-2B, Toxicol. Lett., 2009, 187(2), 77–83 CrossRef CAS PubMed.
- H. Zhang, Z. Ji, T. Xia, H. Meng, C. Low-Kam, R. Liu, S. Pokhrel, S. Lin, X. Wang, Y. P. Liao and M. Wang, Use of metal oxide nanoparticle band gap to develop a predictive paradigm for oxidative stress and acute pulmonary inflammation, ACS Nano, 2012, 6(5), 4349–4368 CrossRef CAS PubMed.
- R. Liu, H. Y. Zhang, Z. X. Ji, R. Rallo, T. Xia, C. H. Chang, A. Nel and Y. Cohen, Development of structure–activity relationship for metal oxide nanoparticles, Nanoscale, 2013, 5(12), 5644–5653 RSC.
- C. Kaweeteerawat, A. Ivask, R. Liu, H. Zhang, C. H. Chang, C. Low-Kam, H. Fischer, Z. Ji, S. Pokhrel, Y. Cohen and D. Telesca, Toxicity of metal oxide nanoparticles in Escherichia coli correlates with conduction band and hydration energies, Environ. Sci. Technol., 2015, 49(2), 1105–1112 CrossRef CAS PubMed.
- Y. Xu and M. A. Schoonen, The absolute energy positions of conduction and valence bands of selected semiconducting minerals, Am. Mineral., 2000, 85(3–4), 543–556 CrossRef CAS.
- J. Portier, G. Campet, A. Poquet, C. Marcel and M. A. Subramanian, Degenerate semiconductors in the light of electronegativity and chemical hardness, Int. J. Inorg. Mater., 2001, 3(7), 1039–1043 CrossRef CAS.
- K. T. Selvi, K. A. Mangai, M. Priya, M. Rathnakumari and P. S. Kumar, Effect of solvent and annealed temperature on band gap energies of MgO nanoparticles, in 2014 International Conference on Science Engineering and Management Research (ICSEMR), IEEE, 2014, pp. 1–6 Search PubMed.
- C. S. Wang and W. E. Pickett, Density-functional theory of excitation spectra of semiconductors: application to Si, Phys. Rev. Lett., 1983, 51(7), 597 CrossRef CAS.
- K. Jagiello, B. Chomicz, A. Avramopoulos, A. Gajewicz, A. Mikolajczyk, P. Bonifassi, M. G. Papadopoulos, J. Leszczynski and T. Puzyn, Size-dependent electronic properties of nanomaterials: how this novel class of nanodescriptors supposed to be calculated?, Struct. Chem., 2017, 28(3), 635–643 CrossRef CAS.
- J. Portier, G. Campet, C. W. Kwon, J. Etourneau and M. A. Subramanian, Relationships between optical band gap and thermodynamic properties of binary oxides, Int. J. Inorg. Mater., 2001, 3(7), 1091–1094 CrossRef CAS.
- G. P. Moss, J. C. Dearden, H. Patel and M. T. Cronin, Quantitative structure–permeability relationships (QSPRs) for percutaneous absorption, Toxicol. In Vitro, 2002, 16(3), 299–317 CrossRef CAS PubMed.
- Y. Shao, J. Liu, M. Wang, L. Shi, X. Yao and P. Gramatica, Integrated QSPR models to predict the soil sorption coefficient for a large diverse set of compounds by using different modeling methods, Atmos. Environ., 2014, 88, 212–218 CrossRef CAS.
- T. Puzyn, B. Rasulev, A. Gajewicz, X. Hu, T. P. Dasari, A. Michalkova, H. M. Hwang, A. Toropov, D. Leszczynska and J. Leszczynski, Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles, Nat. Nanotechnol., 2011, 6(3), 175 CrossRef CAS PubMed.
- S. Kar, A. Gajewicz, T. Puzyn and K. Roy, Nano-quantitative structure–activity relationship modeling using easily computable and interpretable descriptors for uptake of magnetofluorescent engineered nanoparticles in pancreatic cancer cells, Toxicol. In Vitro, 2014, 28(4), 600–606 CrossRef CAS PubMed.
- K. Pathakoti, M. J. Huang, J. D. Watts, X. He and H. M. Hwang, Using experimental data of Escherichia coli to develop a QSAR model for predicting the photo-induced cytotoxicity of metal oxide nanoparticles, J. Photochem. Photobiol., B, 2014, 130, 234–240 CrossRef CAS PubMed.
- S. Kar, A. Gajewicz, K. Roy, J. Leszczynski and T. Puzyn, Extrapolating between toxicity endpoints of metal oxide nanoparticles: Predicting toxicity to Escherichia coli and human keratinocyte cell line (HaCaT) with Nano-QTTR, Ecotoxicol. Environ. Saf., 2016, 126, 238–244 CrossRef CAS PubMed.
- E. Wyrzykowska, A. Mikolajczyk, C. Sikorska and T. Puzyn, Development of a novel in silico model of zeta potential for metal oxide nanoparticles: a nano-QSPR approach, Nanotechnology, 2016, 27(44), 445702 CrossRef PubMed.
- R. Bharthasaradhi and L. C. Nehru, Structural and phase transition of α-Al2O3 powders obtained by co-precipitation method, Phase Transitions, 2016, 89(1), 77–83 CrossRef CAS.
- R. Bharthasaradhi and L. C. Nehru, Preparation and characterisation of nanoscale α-Al2O3 by precipitation method, American Institute of Physics Conference Series. AIP Publishing LLC, 2015 Search PubMed.
- A. A. Ansari, J. Labis, M. Alam, S. M. Ramay, N. Ahmad and A. Mahmood, Influence of copper ion doping on structural, optical and redox properties of CeO2 nanoparticles, J. Electroceram., 2016, 36(1–4), 150–157 CrossRef CAS.
- K. Anandan and V. Rajendran, Sheet, spherical and plate-like chromium sesquioxide (Cr2O3) nanostructures synthesized via ionic surfactants assisted facile precipitation method, Mater. Lett., 2015, 146, 99–102 CrossRef CAS.
- K. Anandan and V. Rajendran, Studies on structural, morphological, magnetic and optical properties of chromium sesquioxide (Cr2O3) nanoparticles: synthesized via facile solvothermal process by different solvents, Mater. Sci. Semicond. Process., 2014, 19, 136–144 CrossRef CAS.
- B. Balamurugan, I. Aruna, B. R. Mehta and S. M. Shivaprasad, Size-dependent conductivity-type inversion in Cu2O nanoparticles, Phys. Rev. B, 2004, 69(16), 165419 CrossRef.
- M. Srivastava, J. Singh, R. K. Mishra and A. K. Ojha, Electro-optical and magnetic properties of monodispersed colloidal Cu2O nanoparticles, J. Alloys Compd., 2013, 555, 123–130 CrossRef CAS.
- X. Zhang, Y. Niu, Y. Li, X. Hou, Y. Wang, R. Bai and J. Zhao, Synthesis, optical and magnetic properties of α-Fe2O3 nanoparticles with various shapes, Mater. Lett., 2013, 99, 111–114 CrossRef CAS.
- G. Sinha, D. Ganguli and S. Chaudhuri, Ga2O3 and GaN nanocrystalline film: reverse micelle assisted solvothermal synthesis and characterization, J. Colloid Interface Sci., 2008, 319(1), 123–129 CrossRef CAS.
- D. Shiojiri, D. Fukuda, R. Yamauchi, N. Tsuchimine, K. Koyama, S. Kaneko, A. Matsuda and M. Yoshimoto, Room-temperature laser annealing for solid-phase epitaxial crystallization of β-Ga2O3 thin films, Appl. Phys. Express, 2016, 9(10), 105502 CrossRef.
- B. Zhao, X. Li, L. Yang, F. Wang, J. Li, W. Xia, W. Li, L. Zhou and C. Zhao, β-Ga2O3 Nanorod Synthesis with a One-step Microwave Irradiation Hydrothermal Method and its Efficient Photocatalytic Degradation for Perfluorooctanoic Acid, Photochem. Photobiol., 2015, 91(1), 42–47 CrossRef CAS PubMed.
- S. K. Tripathi, C. Kaur and R. Kaur, Effect of calcination temperature on phase transformation of HfO2 nanoparticles, AIP Publishing, 2015 Search PubMed.
- C. Latha, M. Raghasudha, Y. Aparna, D. Ravinder, P. Veerasomaiah and D. Shridhar, Effect of capping agent on the morphology, size and optical properties of In2O3 nanoparticles, Mater. Res., 2017, 20(1), 256–263 CrossRef.
- M. A. Farrukh, F. Imran, S. Ali, M. Khaleeq-ur-Rahman and I. I. Naqvi, Micelle assisted synthesis of La2O3 nanoparticles and their applications in photodegradation of bromophenol blue, Russ. J. Appl. Chem., 2015, 88(9), 1523–1527 CrossRef CAS.
- G. A. Bagheri, M. Sabbaghan and Z. Mirgani, A comparative study on properties of synthesized MgO with different templates, Spectrochim. Acta, Part A, 2015, 137, 1286–1291 CrossRef PubMed.
- S. Gnanam and V. Rajendran, Synthesis of CeO2 or α–Mn2O3 nanoparticles via sol–gel process and their optical properties, J. Sol-Gel Sci. Technol., 2011, 58(1), 62–69 CrossRef CAS.
- W. J. Duan, S. H. Lu, Z. L. Wu and Y. S. Wang, Size effects on properties of NiO nanoparticles grown in alkali salts, J. Phys. Chem. C, 2012, 116(49), 26043–26051 CrossRef CAS.
- A. Tang, X. Li, Z. Zhou, J. Ouyang and H. Yang, Mechanochemical synthesis of Ni(OH)2 and the decomposition to NiO nanoparticles: thermodynamic and optical spectra, J. Alloys Compd., 2014, 600, 204–209 CrossRef CAS.
- A. Muthuvinayagam, N. Melikechi, P. D. Christy and P. Sagayaraj, Investigation on mild condition preparation and quantum confinement effects in semiconductor nanocrystals of SnO2, Phys. B, 2010, 405(4), 1067–1070 CrossRef CAS.
- S. Begum, T. B. Devi and M. Ahmaruzzaman, L-lysine monohydrate mediated facile and environment friendly synthesis of SnO2 nanoparticles and their prospective applications as a catalyst for the reduction and photodegradation of aromatic compounds, J. Environ. Chem. Eng., 2016, 4(3), 2976–2989 CrossRef CAS.
- A. Bhattacharjee, M. Ahmaruzzaman and T. Sinha, A novel approach for the synthesis of SnO2 nanoparticles and its application as a catalyst in the reduction and photodegradation of organic compounds, Spectrochim. Acta, Part A, 2015, 136, 751–760 CrossRef CAS.
- Y. He, P. Tang, J. Li, J. Zhang, F. Fan and D. Li, Ultrafast response and recovery ethanol sensor based on SnO2 quantum dots, Mater. Lett., 2016, 165, 50–54 CrossRef CAS.
- W. B. Soltan, M. Mbarki, R. Bargougui, S. Ammar, O. Babot and T. Toupance, Effect of hydrolysis ratio on structural, optical and electrical properties of SnO2 nanoparticles synthesized by polyol method, Opt. Mater., 2016, 58, 142–150 CrossRef CAS.
- V. Senthilkumar, P. Vickraman, M. Jayachandran and C. Sanjeeviraja, Synthesis and characterization of SnO2 nanopowder prepared by precipitation method, J. Dispersion Sci. Technol., 2010, 31(9), 1178–1181 CrossRef CAS.
- S. Naghibi, M. A. F. Sani and H. R. M. Hosseini, Application of the statistical Taguchi method to optimize TiO2 nanoparticles synthesis by the hydrothermal assisted sol–gel technique, Ceram. Int., 2014, 40(3), 4193–4201 CrossRef CAS.
- Ü. Ö. A. Arıer and F. Z. Tepehan, Controlling the particle size of nanobrookite TiO2 thin films, J. Alloys Compd., 2011, 509(32), 8262–8267 CrossRef.
- J. G. Li, T. Ishigaki and X. Sun, Anatase, brookite, and rutile nanocrystals via redox reactions under mild hydrothermal conditions: phase-selective synthesis and physicochemical properties, J. Phys. Chem. C, 2007, 111(13), 4969–4976 CrossRef CAS.
- P. Sivakarthik, V. Thangaraj and M. Parthibavarman, A facile and one-pot synthesis of pure and transition metals (M = Co & Ni) doped WO3 nanoparticles for enhanced photocatalytic performance, J. Mater. Sci.: Mater. Electron., 2017, 28(8), 5990–5996 CrossRef CAS.
- G. Bhavani and S. Ganesan, Structural, Morphological and Optical Study of Bismuth and Zinc Co-Doped Yttrium Oxide Prepared by Solvothermal and Wet Chemical Method, Acta Phys. Pol., A, 2016, 130(6), 1373–1379 CrossRef CAS.
- L. Jing, X. Sun, D. Zheng, Y. Xu, W. Li and W. Cai, Quantum size effect and photocatalytic properties of ZnO ultrafine particles, J. Harbin Inst. Technol., 2001, 33, 345–348 Search PubMed.
- R. Nasser, W. B. H. Othmen, H. Elhouichet and M. Férid, Preparation, characterization of Sb-doped ZnO nanocrystals and their excellent solar light driven photocatalytic activity, Appl. Surf. Sci., 2017, 393, 486–495 CrossRef CAS.
- S. Klubnuan, P. Amornpitoksuk and S. Suwanboon, Structural, optical and photocatalytic properties of MgO/ZnO nanocomposites prepared by a hydrothermal method, Mater. Sci. Semicond. Process., 2015, 39, 515–520 CrossRef CAS.
- P. Kubelka and F. Munk, An article on optics of paint layers, Z. Tech. Phys., 1931, 12, 593–601 Search PubMed.
- L. E. Brus, A simple model for the ionization potential, electron affinity, and aqueous redox potentials of small semiconductor crystallites, J. Chem. Phys., 1983, 79(11), 5566–5571 CrossRef CAS.
- V. I. Klimov, A. A. Mikhailovsky, S. Xu, A. Malko, J. A. Hollingsworth, A. C. Leatherdale, H. J. Eisler and M. G. Bawendi, Optical gain and stimulated emission in nanocrystal quantum dots, Science, 2000, 290(5490), 314–317 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Software vasp, Vienna, 1999 Search PubMed.
- J. J. Stewart, Stewart computational chemistry—MOPAC home page, 2016 Search PubMed.
- K. Tämm, L. Sikk, J. Burk, R. Rallo, S. Pokhrel, L. Mädler, J. J. Scott-Fordsmand, P. Burk and T. Tamm, Parametrization of nanoparticles: development of full-particle nanodescriptors, Nanoscale, 2016, 8(36), 16243–16250 RSC.
- Jade, M. D. I. 2010. 9.5; Materials Data. Inc., Livermore, CA, USA.
- FindIt, I. C. S. C. Inorganic Crystal Structure Database, 2009.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, Open Babel: an open chemical toolbox, J. Cheminf., 2011, 3(1), 33 Search PubMed.
- M. Bylesjö, M. Rantalainen, O. Cloarec, J. K. Nicholson, E. Holmes and J. Trygg, OPLS discriminant analysis: combining the strengths of PLS-DA and SIMCA classification, J. Chemom., 2006, 20(8–10), 341–351 CrossRef.
- H. Wold, Soft modeling: the basic design and some extensions, in Systems under Indirect Observation, 1982, vol. 2, p. 343 Search PubMed.
- S. Wold, A. Ruhe, H. Wold and W. J. Dunn III, The collinearity problem in linear regression. The partial least squares (PLS) approach to generalized inverses, SIAM Journal on Scientific and Statistical Computing, 1984, 5(3), 735–743 CrossRef.
- S. Wold, M. Sjöström and L. Eriksson, PLS-regression: a basic tool of chemometrics, Chemom. Intell. Lab. Syst., 2001, 58(2), 109–130 CrossRef CAS.
- R. C. Team, R language definition, R Foundation for Statistical Computing, Vienna, Austria, 2000 Search PubMed.
- P. P. Roy and K. Roy, On some aspects of variable selection for partial least squares regression models, QSAR Comb. Sci., 2008, 27(3), 302–313 CrossRef CAS.
- OECD, Guidance document on the validation of (Quantitative) Structure-Activity Relationship [(Q)SAR] models, 2007 Search PubMed.
- K. Roy, S. Kar and P. Ambure, On a simple approach for determining applicability domain of QSAR models, Chemom. Intell. Lab. Syst., 2015, 145, 22–29 CrossRef CAS.
- R. G. Pearson, Recent advances in the concept of hard and soft acids and bases, J. Chem. Educ., 1987, 64(7), 561 CrossRef CAS.
- R. G. Pearson, Maximum chemical and physical hardness, J. Chem. Educ., 1999, 76(2), 267 CrossRef CAS.
- R. G. Parr and P. K. Chattaraj, Principle of maximum hardness, J. Am. Chem. Soc., 1991, 113(5), 1854–1855 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10226k |
| ‡ These authors contributed equally to the paper. |
| This journal is © The Royal Society of Chemistry 2019 |