Influence of magnetic field on electrical and thermal transport in the hole doped ferromagnetic manganite: La_0.9Na_0.1MnO₃

Abstract

We report the magnetization (M), magnetostriction, electrical resistivity (ρ), thermal conductivity (κ) and thermopower (S) of polycrystalline La_0.9Na_0.1MnO₃ over a wide temperature range of 5 to 360 K. This sample undergoes a paramagnetic to ferromagnetic transition around T_C = 274 K and electrical resistivity ρ shows an insulator–metal transition around T_IM = 292 K. The sign of thermopower S is positive in the entire temperature range which indicates that majority charge carriers are holes. Thermopower exhibits a peak and thermal conductivity shows a dip at T_C in the absence of magnetic field. Large difference between the experimentally determined activation energies of ρ and S in the insulating state indicates small polaron hopping dominant conduction above T_IM. Polaron formation above T_C, was further confirmed from the anomaly observed in thermal expansion (ΔL/L₀) which shows a change in slope at T_IM. In the vicinity of T_C at 3 T applied field, magneto-thermopower (∼61.5%) is larger than magnetothermal conductivity (∼12.7%) and magnetoresistance (∼49%).

---

1. Introduction

Perovskites containing Mn ions (i.e. La_1−xA_xMnO₃, A = Ca²⁺, Ba²⁺, Sr²⁺ etc.) have been one of the hot areas of research in physics and materials chemistry because of their colossal magnetoresistance (CMR) property and its prospective applications.^1–3 Researchers are intrigued by the rich distinctive physical properties of every member of the manganite-family. From a fundamental point of view, manganites show diverse phenomena such as ferromagnetism, antiferromagnetism, multiferroism, magnetically coupled or independent structural transitions, nano- meso- and micro-scale phase separation, insulator–metal (IM) transition, spin-, charge- and orbital ordering etc.^1,4

LaMnO₃ (LMO) containing Mn³⁺ (t³_2ge¹_g) cations is a layered A-type antiferromagnetic (AFM) insulator with a Neel temperature (T_N) of 140 K. Substitution with divalent alkaline earth cations (A = Ca²⁺, Sr²⁺ etc.) at the La³⁺ site transforms Mn³⁺ into an equal amount of Mn⁴⁺ (t³_2ge⁰_g) and introduces ferromagnetic (FM) spin ordering for x = ∼0.18–0.45 in La_1−xA_xMnO₃.⁵ Ferromagnetism and metallic conduction in the divalent ion doped manganites are understood in terms of Zener's double exchange (DE) model.⁶ Ferromagnetic metallic state can also be induced by substitution of monovalent cations such as Na¹⁺, K¹⁺ or Ag¹⁺ for La³⁺ which theoretically should introduce twice the number of holes (or Mn⁴⁺) in the structure compared to the same concentration of divalent cation substitution and hence ferromagnetism can be obtained for a smaller amount of Na¹⁺ or K¹⁺ compared to any divalent ions.

Although thermal transport of hole doped LMO has been investigated in the past few years, the role of magnetic field on the thermal transport of Na¹⁺ doped LMO system has been scarcely studied so far. Thermopower (S) is sensitive to band structure and also can probe majority charge carriers. Also S is less affected by the grain boundaries and hence probe intrinsic electrical conduction within grains unlike dc resistivity whose magnitude and temperature dependence is severely modified by grain boundaries. Therefore, S is an effective way to study the transport properties in polycrystalline samples.^7–9 Both Shimura et al.¹⁰ and Ahmed et al.¹¹ obtained a negative S in La_1−xA_xMnO₃ (x ≥ 0.10) above ferromagnetic transition temperature, but they did not shed light on the trend of thermopower or thermal conductivity under the influence of magnetic field. Studies show that the sign of S(T) can be negative or positive both reflecting holelike or electronlike transport, depending on the temperature and the degree of elemental substitution. 10% Na doping is a critical composition form the point of view that in Ca²⁺ or Sr²⁺ doped compositions S alters the sign with lowering temperature as Mn⁴⁺ content becomes as high as ∼26% (ref. 12) or ∼25%,¹³ respectively. La_0.9Na_0.1MnO₃ belongs to space group R3̄c like the parent compound with a small decrease in Mn–O bond length and increase in 〈Mn–O–Mn〉 angle compared to undoped LMO.^14–16 A doping level exceeding 20% changes the structure from rhombohedral to orthorhombic one.¹⁶ Considering tight-binding approximation for ABO₃ structures, doping Na¹⁺ at La³⁺ site affects charge-carrier (e_g electron) bandwidth, W (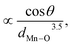 where θ = 180 − 〈Mn–O–Mn〉 and d_Mn–O is the Mn–O bond length) advancing DE interaction in the structure.¹⁷ W rises rapidly with a small increase in 〈Mn–O–Mn〉 angle or decrease in Mn–O length favoring the evolution of the insulator–metal transition¹⁶ which explains the enhancement of T_C by ∼150 K in only 10% Na doped LMO.¹⁸

Recently, nearly 100% suppression of thermopower (negative magneto-thermopower) was reported in antiferromagnetic Nd_0.75Na_0.25MnO₃.¹⁹ An interesting correlation between magneto-thermopower and magnetoresistance was also reported in the same. There has been no report on combined study of thermopower, thermal conductivity and resistivity in Na-doped LaMnO₃. In this work, we report simultaneous measurements of the dc electrical resistivity (ρ), thermal conductivity (κ) and thermopower (S) of polycrystalline La_0.9Na_0.1MnO₃ as a function of temperature without and with an external magnetic field. In addition, magnetization, linear thermal expansion and field dependence of magnetostriction are also reported. Our investigation on temperature dependence of magnetization indicates paramagnetic (PM) to ferromagnetic transition at T_C = 274 K upon cooling. Magnetic ordering is accompanied by an insulator–metal transition identified by the peak in resistivity curve at T_IM = 292 K. Thermopower S reveals a hole doping characteristics above and below T_IM. The theoretical fitting of S(T) curve indicates that at the FM metallic region, diffusion; phonon drag; magnon drag all coexist whereas at low temperatures (below 80 K), magnon drag dominates the thermopower value. Temperature and field dependent measurements show dominant lattice contribution to the heat conductivity κ.

2. Experimental details

Polycrystalline La_0.9Na_0.1MnO₃ sample was synthesized by solid-state method using high purity La₂O₃, MnO₂ and NaCO₃ powders. Stoichiometric amount of the well mixed powders was calcined at 1000 °C for 24 h followed by sintering at 1150 °C for 48 h in few steps of intermediate grinding. The Rietveld refinement of the XRD data reveals the sample belongs to space group R3̄c of the rhombohedral crystal structure. Refined lattice constants of the unit cell are a = b = 5.5226 Å; c = 13.3481 Å. Magnetization measurements were performed using a Physical Property Measuring System (PPMS), equipped with a vibrating sample magnetometer. The temperature dependence of linear thermal expansion and field dependence of thermal expansion (Joule magnetostriction) were measured using a miniaturized capacitance dilatometer probe designed for PPMS.²⁰ Four probe dc resistivity, thermopower and thermal conductivity were measured simultaneously at each stabilized temperature using the standard thermal transport option (TTO) for PPMS. In TTO, thermal conductivity (κ) is measured directly from the applied heater power used to create temperature gradient (ΔT) between two ends of the sample. Any heat loss during the measurement is also estimated by the software and the errors due to heat loss is excluded during calculation. However, for thermopower (S) the voltage drop (ΔV) across the hot and cold thermometer probes is also monitored by the TTO system and measured once a stable temperature gradient is created across these two thermometer probes due to the application of heat. PPMS served as a platform to vary temperature and magnetic field. The error for S is almost negligible, whereas, for κ it is <±0.1% at T = 10–100 K and <±5% at higher temperatures. Density of the pellet used for TTO measurement was estimated using Archimedes' principle which was close to 95% of its theoretical value. Magnetoresistance (MR), magnetothermal conduction (MTC) and magneto-thermopower (MTEP) at 3 T magnetic field of the sample is calculated using the standard relations: 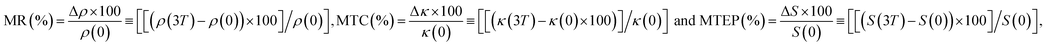respectively.

3. Results and discussion

3.1 Magnetic properties

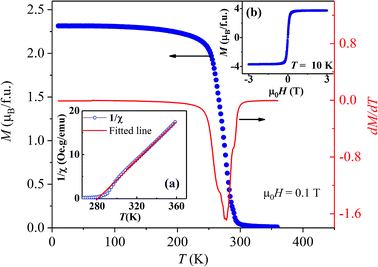
Fig. 1 shows the temperature dependent magnetization (M) of polycrystalline La_0.9Na_0.1MnO₃ (LNMO) sample measured in an applied field of μ₀H = 0.1 T. The rapid increase of magnetization at T = T_C indicates the onset of ferromagnetism. The ferromagnetic Curie temperature T_C = 274 K is determined from the minimum of dM/dT curve as shown in the same figure. The temperature variation of inverse susceptibility (1/χ) and high temperature Curie–Weiss fit, 1/χ = C/(T − θ_W) of the data points are shown in the inset (a) of Fig. 1. C is the Curie constant given by C= Nμ₀μ_B²μ_eff²/3k_B, where N is the total number of PM entities per cubic meter. Best fitting above T_C in the linear region of 1/χ, gives effective moment μ_eff = 5.98μ_B and Weiss temperature θ_W of 279.3 K which is few kelvin higher than the T_C obtained from M–T curve. The theoretical effective magnetic moment is calculated using the equation,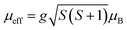 where, g is the Lande factor and S is the total spin quantum number. In La_1−xNa_xMnO₃, as we have both Mn³⁺ and Mn⁴⁺ spin, the modified S will be, S_avg = 2x × S^Mn4+ + (1 − 2x) × S^Mn3+. As both Mn ions are in the high spin state, i.e. S^Mn4+ = 3/2 and S^Mn3+ = 2, the experimentally estimated μ_eff is higher than the theoretically expected value of 4.68μ_B, considering effective moment of non-interacting Mn³⁺ and Mn⁴⁺ ions are 4.89μ_B and 3.87μ_B, respectively. Enhanced μ_eff indicates that spins are not completely independent in the PM state. It is reported that dynamical ferromagnetic nanoclusters do exists in many manganites such as in (Sm_0.65Sr_0.35)MnO₃ and Pr_0.65Ca_0.25Ba_0.1MnO₃ above T_C.^21,22 Therefore, the above mentioned findings (high values of μ_eff and θ_W > T_C) indicate existence of small fraction of ferromagnetic cluster above T_C in LNMO. Inset (b) of Fig. 1 shows field dependence of M at 10 K. It shows soft FM behavior (coercive field = 58.05 Oe) with a maximum moment of 3.7μ_B/f.u at 3 T field, which could reach the saturation value of 3.8μ_B/f.u expected for 20% Mn⁴⁺ doped LMO at higher magnetic field. Hence, 10% Na¹⁺ substitution dopes nearly 20% of Mn⁴⁺ in the system.

Fig. 1 Temperature dependence of magnetization (M) and dM/dT at an applied field μ₀H = 0.1 T, inset (a) shows inverse susceptibility vs. temperature plot, here solid line represents the Curie–Weiss fitting and (b) shows field dependent magnetization of La_0.9Na_0.1MnO₃ at 10 K.

3.2 Thermal expansion properties

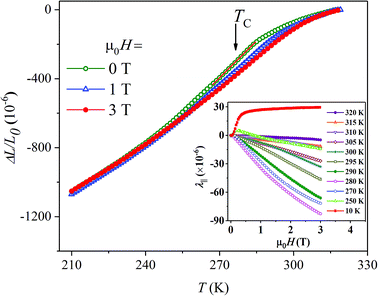
Fig. 2 shows the linear thermal expansion (ΔL/L₀) of LNMO upon cooling from 320 K to 200 K at an external magnetic field of μ₀H = 0, 1 and 3 T. L₀ is the value of L at 320 K (normalizing temperature), the maximum operating temperature of the capacitance dilatometer. At zero field, ΔL/L₀ decreases with lowering temperature, which indicates a contraction in length of the sample. However, ΔL/L₀ changes slope at the onset of paramagnetic–ferromagnetic transition similar to La_0.6Y_0.07Ca_0.33MnO₃.²³ As the external field is applied, the value of ΔL/L₀ decreases around T_C and the change of slope also shifts towards higher temperature because T_C itself increases with increasing strength of the magnetic field. The anomaly in ΔL/L₀ around T_C can be attributed to the localization–delocalization transition of magnetic polarons as in La_0.6Y_0.07Ca_0.33MnO₃ (ref. 23) as well as in La_0.67Ca_0.33MnO₃.²⁴ Magnetic polaron is an entity in which Mn³⁺ (d⁴) spins are ferromagnetically aligned locally around a Mn⁴⁺ (d³) ions: e_g carrier hops freely within these superparamagnetic clusters. Due to Jahn–Teller nature of Mn³⁺, lattice distortion also accompanies local spin polarization. Localization of magnetic polarons above T_C causes extra contribution to thermal expansion, which is released when magnetic polarons collapses below T_C leading to decrease in volume. Upon application of magnetic field above T_C, size of magnetic polaron expands and they start percolating which results in enhancement of T_C and shift of the thermal expansion anomaly towards higher temperature. As the magnetic field strength exceeds a critical value, the anomaly is suppressed as the crossover between the low-volume FM and high-volume PM state disappears.

Fig. 2 Temperature dependence of thermal expansion, ΔL/L₀ (normalizing temperature 320 K) at 0, 1 and 3 T applied fields of La_0.9Na_0.1MnO₃ sample. Inset shows magnetostriction, λ_∥ (= [L(H) − L(H = 0)]/L₀) at various temperatures. The measurement uncertainty is about <±3%. The error bar is not shown for purposes of clarity.

The inset of Fig. 2 shows the field dependence of longitudinal magnetostriction i.e., λ_∥ (= [L(H) − L(H = 0)]/L₀) at selected temperatures covering both paramagnetic and ferromagnetic regions. At 10 K, λ_∥ increases rapidly in the low magnetic fields and saturates above 0.5 T. However, in the proximity of T_C (250–310 K), λ_∥ decreases with increasing strength of the magnetic field and does not show saturation. λ_∥ decreases continuously, reaches a minima of −83 × 10⁻⁶ near T_C with a subsequent increase for higher temperatures indicating strong spin–lattice and charge–lattice coupling at T_C. The positive magnetostriction at 10 K is caused by increase in length (anisotropic in nature) due to spin–orbit interaction below T_C. However, negative magnetostriction at and above T_C is due to the collapse of magnetic polarons.

The maximum volume magnetostriction is given by ω = λ_∥ + 2λ_⊥, where λ_∥ and λ_⊥ are the longitudinal and transverse components of magnetostriction. They are usually measured using strain gauge technique. It was not possible to measure λ_⊥ in our dilatometer probe as it can only measure magnetostriction along field direction, i.e. λ_∥. In manganites,²³ magnetostriction in the PM state and close to T_C is isotropic, i.e., λ_∥ ∼ λ_⊥. Therefore, ω near T_C in LNMO can also be expressed as ω = 3λ_∥ which decreases at T_C in zero field.

3.3 Electrical and thermal transport properties

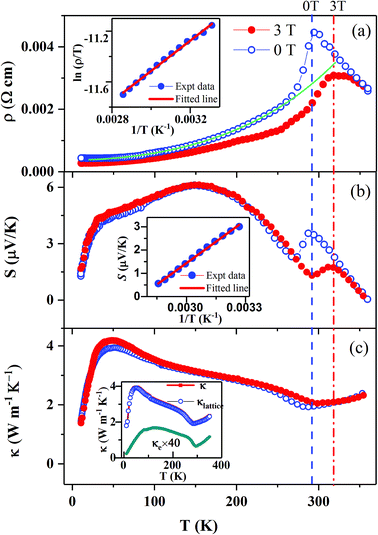
Temperature dependence of the direct-current (DC) resistivity (ρ) at μ₀H = 0 and 3 T magnetic fields are shown in Fig. 3(a). Upon lowering the temperature, ρ(T, H = 0 T) initially increases as like a semiconductor and exhibits a sharp peak at T_IM = 292 K followed by metallic-like behaviour with lowering the temperature further. The insulator–metal (IM) transition temperature T_IM i.e. the position of resistivity peak is higher than T_C (= 274 K), determined from magnetization measurements, is similar to the report by Ye et al.²⁵ The IM transition temperature is also higher than θ_W (= 279.31 K) estimated from the Curie–Weiss fitting with inverse magnetic susceptibility. Previous reports on similar compounds showed a broad maximum below the resistivity peak due to grain boundaries, those act as regions of enhanced scattering for the conduction electrons and such maximum is absent in our sample.^15,16,18 The peak value of resistivity is reduced and T_IM is shifted up under the application of magnetic field.

Fig. 3 Variation of (a) resistivity ρ (b) thermoelectric power S and (c) thermal conductivity κ with temperature of La_0.9Na_0.1MnO₃ at zero field (open symbol) and 3 T (closed symbol). The solid curve in (a) is the function ρ(T) = ρ₀ + AT² + BT^4.5. Inset (a) shows ln(ρ/T) vs. 1/T plot, and the solid line is obtained by fitting the data according to the small polaron hopping model. Inset (b) includes S vs. 1/T plot and the solid line is a fitting based on the data. Inset (c) shows plot of κ, κ_e and κ_lattice vs. temperature.

Fig. 3(b) and (c) show the temperature dependence of thermopower S and thermal conductivity κ, respectively, measured together with dc resistivity. In zero field, sign of S is positive throughout the whole temperature region, which reflects e_g hole of Mn⁴⁺: t³_2ge⁰_g is the majority charge carrier. Shimura et al.¹⁰ obtained a negative S above T_C for La_0.88Na_0.09Mn_0.96O₃ and La_0.84Na_0.12Mn_0.97O₃ which was attributed to doping induced alteration of conduction from charge transfer type to the Mott-type. In the PM state, S(T) increases with lowering temperature and exhibits a peak at the IM transition and below which it decreases rapidly. However, in the FM state S increases again and shows a broad maximum around 154 K. S(T) shows a striking resemblance with ρ in the presence of an external magnetic field. Applied magnetic field lowers S value prominently in the vicinity of T_IM and shifts the peak position to high temperature but it neither influences the value nor the position of the broad maximum at low temperature.

Thermal conductivity (κ) in the paramagnetic state decreases with decreasing temperature (i.e. dκ/dT > 0) which is unusual for a crystalline compound showing insulating like behavior (Fig. 3(c)) but similar to other hole-doped manganites.^26,27 κ(T) shows a dip in the vicinity of the magnetic ordering and a few kelvins below the peak in ρ(T) and S(T). Within the FM state below T_C, κ(T) increases down to ∼43 K, where it reaches a peak and below that κ decreases rapidly. The magnitude of κ in the metallic region varies in the range of 2–4.13 W m⁻¹ K⁻¹ which is higher than the parent compound (<1 W m⁻¹ K⁻¹ below room temperature)²⁸ but comparable with the divalent ion doped systems with similar Mn⁴⁺ concentration (κ ∼ 2.3 W m⁻¹ K⁻¹ in La_0.8Ca_0.2MnO₃).⁸ The behavior of κ in the paramagnetic region is amorphous like i.e., κ decreases with decreasing T. Such characteristic of κ is attributed to the local anharmonic lattice distortions associated with small polarons or dynamical JT distortion in A-site doped manganites.²⁶ In general, κ has lattice component κ_lattice due to phonon vibrations, electronic component κ_e and the spin wave component κ_m, κ = κ_lattice + κ_e + κ_m. Above T_C, κ_m is negligible and the thermal conductivity is primarily due to the other two components. Measured value of ρ is used to calculate κ_e using the Wiedemann–Franz law, expressed by κ_e = L₀T/ρ, where L₀ = π²k_B²/3e² is the Lorentz constant for metals where charge carriers behave like free-electrons (degenerate limit).²⁹ The estimated κ_e is two orders of magnitude smaller than the total κ in the LNMO sample, which indicates phonon contribution to κ (inset of Fig. 3(c)) is dominant than heat carried by electrical charges. Enhancement of κ on entering the metallic state was argued due to the weakening of JT distortion and delocalization of the charge carriers.²⁶ The pair distribution function based on the neutron scattering data shows that MnO₆ octahedra in La_1−xCa_xMnO₃ (x = 0.2 and 0.25) has uniform Mn–O and O–O bond lengths at low-temperature and when the temperature rises towards IM transition the disorder of Mn–O bond lengths increases followed by the formation of small polarons.³⁰ Reduction of ρ under magnetic field should have increased κ_e contribution, but in the whole temperature range κ_e value is negligible. A dip in κ(T) at T_C or T_N is also seen in other magnetic oxides such as MnO,³¹ and it is likely to be caused by decrease in scattering of thermal phonon by spin-fluctuations, which decreases with lowering temperature. The peak at the temperature ∼ 43 K is due to transition from umklapp scattering to defect dominated scattering at lower temperatures.

Fig. 4 gives a clear picture of the influence of magnetic field on the physical properties of the system. MR increases with lowering temperature in the paramagnetic state and it reaches a peak value (∼49%) at T_C. MR remains significant below T_C and reaches ∼40% at 10 K. In the ordered state, ρ rises sharply due to narrowing band width which leads to localization of charges and the formation of small polarons. Application of external magnetic field reduces the relative angle between spins which increases the electron bandwidth and enhances mobility of electrons. In addition to this, destruction of magnetic polarons under applied magnetic field gives rise to a large negative MR. For T ≪ T_C, the magnetoresistance is due to grain boundary effect: tunnelling of spin-polarized electrons between ferromagnetic grains via thin grain boundaries.³² MTEP curve (Fig. 4(b)) reveals very interesting fact that S is affected by the external field mostly around IM transition temperature, whereas S in the FMM region (T < 260 K) remains unaffected unlike ρ(T). MTEP is much larger than MR in the temperature interval between T_C (=274 K) and T_IM (=292 K) where the spin ordering is destroyed. Unlike MR which is proportional to the density of states (DOS) at the Fermi level, MTEP depends on the asymmetry of DOS around the Fermi level due to the spin-up and spin-down states.³³ Hence, in the FMM state MR is higher than MTEP but as the magnetic ordering collapses MTEP value enhances more than MR. However, MTEP observed here at comparatively low magnetic field (61.5% at 3 T) is comparable with the value (∼80–100%) reported for antiferromagnetic Nd_0.75Na_0.25MnO₃ system obtained at 5 T.¹⁹ The magnitude of MTEP of LNMO is also close to the similar amount of hole doped La_0.8Ca_0.2MnO₃ which shows 80% change in thermopower but at 5.7 T magnetic field⁸ and single crystal La_0.92Sr_0.18MnO₃ showing MTEP of almost 90% at 7 T.¹³ Suppression of S with magnetic field as in LNMO, is observed in few other oxides too.^34,35 Yamamoto et al.³⁴ have shown that in the weakly ferromagnetic CaRu_0.8Sc_0.2O₃ external magnetic field suppresses S, with little influence on ρ. They have also showed a correlation between the spin entropy and magnetothermopower. A similar explanation was also put forward by Repaka et al.³⁶ for the room temperature ferromagnet. In antiferromagnetic Nd_0.75Na_0.25MnO₃, a significant magnetothermopower was found above the Neel temperature even though magnetoresistance was negligible.¹⁹ However in the present study, ρ and S both are significantly affected by the magnetic field around T_IM (much above T_C). It appears that S is affected by the change in magnetization to a larger extend than the resistivity. A possible explanation is the decrease in the magnitude of thermopower is partly from the suppression of spin entropy. Another possibility is that the magnetic field affects the spin-dependent band structure around the Fermi level and it is reflected in magnetothermopower as mentioned before. Theoretical modelling is certainly needed to have deeper understanding.

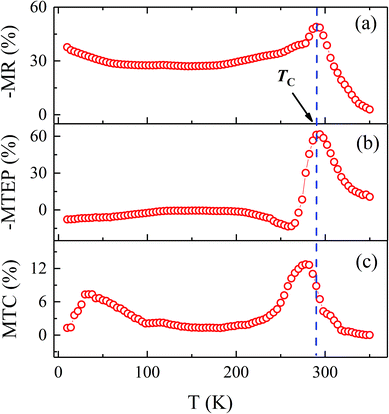Fig. 4 (a) Plot of magnetoresistance (MR), (b) magneto-thermal conduction (MTC) and (c) magneto-thermopower (MTEP) of La_0.9Na_0.1MnO₃.

At first sight, thermal conductivity seemed to have very small dependency on external magnetic field (Fig. 3(c)). However, measurement of κ(T) in magnetic field makes it easier to understand the influence of spins on the heat transport property of LNMO. Temperature dependence of κ in the hole doped manganites is attributed to two different processes; first one is considered due to the scattering of phonons by Jahn–Teller (JT) distorted Mn³⁺O₆ octahedra²⁶ and second is to the scattering of phonons by spin fluctuations.⁸ At 3 T field, reduction of spin fluctuation facilitates heat flow in the material produces a positive MTC value of about 12.7% near T_C, suggesting spin–phonon scattering as a decisive factor in κ (Fig. 4(c)). Under magnetic field, suppression of the dip in κ around T_C and marginal enhancement in conductivity can be attributed to the scattering of phonons by spin-wave. MR and MTC results unquestionably establish a strong electron–phonon–spin coupling in the Na doped LMO compound.

In manganites, high temperature transport mechanism is often analyzed using fitting of variable-range hopping or small-polaron hopping model with the ρ(T) data. However, in some cases, it is difficult to reach to a satisfactory conclusion based on the fitting results of ρ(T) alone, such as in electron doped La_0.9Te_0.1MnO₃ system³⁷ which makes it necessary to fit the S(T) data as well. In our sample, high temperature (T_IM ≤ T ≤ 370 K) ρ(T) and S(T) data fitted well with the small-polaron hopping (SPH) model, given by

ρ(T) = ρ₀T exp(E_ρ/k_BT) (1)

and

S(T) = k_B/e(E_S/k_BT + α), (2)

respectively, where ρ₀ and α are constants, k_B is the Boltzmann constant, e is the electron's charge and E_ρ and E_S are the activation energy values obtained from resistivity and thermopower data fitting, respectively (inset of Fig. 3(a) and (b)). We found that E_ρ (103.14 meV) is an order of magnitude higher than E_S (6.13 meV). E_ρ ≫ E_S is a hall mark of electrical conduction by small polaron hopping between the neighboring sites.^38,39 E_S corresponds to the hopping energy of carriers between energetically equivalent sites with Fermi level as a reference point for the entropy, while E_ρ contains energy to create the carriers too. Obtained value of E_ρ agrees well with the proper stoichiometric La_0.87Na_0.13MnO₃ compound studied by Malavasi et al.⁴⁰ Thus, the electrical conduction in LNMO is governed by hopping of small polarons with the energy given by 2(E_ρ − E_S) = 194.02 meV.⁸

The thermal variation of resistivity below the upturn near T_C (T < 260 K) is dominated by electron–electron scattering (T² dependency)⁴¹ and electron–magnon or, spin wave scattering in the ferromagnetic phase (T^4.5 dependency).^41,42 We have fitted the present experimental data in the FMM phase using an expression of the form, ρ(T) = ρ₀ + AT² + BT^4.5 nearly perfectly as shown by the solid line in Fig. 3(a), where ρ₀ is the residual resistivity due to the temperature independent scattering processes. The fitting parameter A (∼2.17 × 10⁻⁸ Ω cm K⁻²) obtained for our samples is similar to that reported by Urushibara et al.⁴¹ for La–Sr–Mn–O system and suggests an important role of the electron–electron scattering process below 260 K in the resistivity. Value of B (∼4.73 × 10⁻¹⁵ Ω cm K^−4.5), related to the T^4.5 behavior suggests that electron–magnon scattering too strongly contributes to the electrical conduction in the FMM region and causes the observed trend in ρ at this temperature range.

The thermopower data in the low temperature metallic region is analyzed using an equation,³⁷

S = S₀ + S₁T + S_3/2T^3/2 + S₃T³ + S₄T⁴ (3)

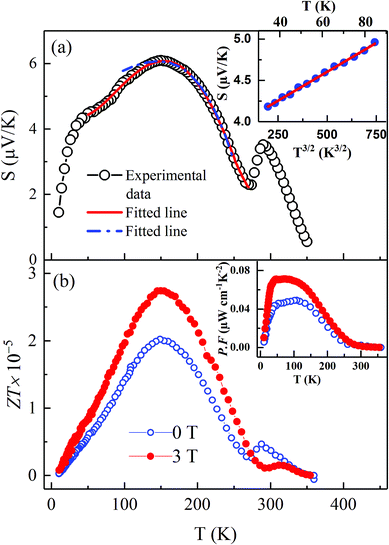
Here, the first term S₀ is estimated from the high temperature data extrapolation at T = 0 K. Second term represents contribution from diffusion, the third term of the equation denotes magnon drag or the single-magnon scattering processes, while the fourth term with T³ dependency is related to the phonon drag contribution and the last term represents the spin-wave fluctuation in the FM phase below T_C. In general, S(T) of manganites in FM region is analysed without considering the diffusion and phonon drag terms which was quite logical considering the position of low temperature broad peak. Phonon drag peak in thermopower is usually observed near temperature θ_D/5, where Debye temperature θ_D is about 320 K for LMO.⁴³ Thus, the phonon drag contribution is supposed to show maximum around 60 K much below the observed thermopower peak here at 150 K. To ratify further, LNMO data below T ≪ T_C was fitted with equations considering (i) all the terms in eqn (3) and (ii) excluding the diffusion and phonon drag contribution terms in eqn (3). Fig. 5(a) shows a better fitting for the first case throughout a wide temperature range (49–260 K) whereas, the latter one fits the experimental data points only between 150–260 K. Best fitting results (S₀ = 5.7 μV K⁻¹, S₁ = −0.116 μV K⁻², S_3/2 = 0.013 μV K^−5/2, S₃ = −2.77 × 10⁻⁶ μV K⁻⁴ and S₄ = 4.06 × 10⁻⁹ μV K⁻⁵) show S_3/2 ≫ S₃, suggesting that the electron–magnon scattering strongly affects the broad peak in the S vs. T curve but phonon drag is not negligible either. However, in the temperature range below the broad peak (80–30 K) thermopower decreases rapidly showing a T^3/2 dependence (inset of 4(a)) like in other hole doped manganites.^9,44

Fig. 5 (a) Temperature dependence of the thermopower for the La_0.9Na_0.1MnO₃ sample. The solid line (red) corresponds to the expression (i) S = S₀ + S₁T + S_3/2T^3/2 + S₃T³ + S₄T⁴ and dashed line (blue) represent the fitting with (ii) S = S₀ + S_3/2T^3/2 + S₄T⁴ as discussed in the text, (b) temperature dependence of figure of merit, ZT for the same sample. Inset of (a) shows T^3/2 dependency of S at low temperature and (b) power factor (S²/ρ) at 0 and 3 T fields.

Fig. 5(b) shows the figure of merit ZT, expressed by 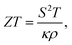a characteristic parameter for the thermoelectric materials. As ZT has a square term of thermopower, it shows a peak around the maxima of S(T). 10% Na doped LMO exhibits better value of ZT compared to La_0.9Te_0.1MnO₃ at room temperature³⁷ but it is still quite low to be useful for the practical purpose of a thermoelectric material for which ZT ≥ 1. In the inset of Fig. 5(b), the temperature variation of power factor 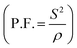is shown. At zero and 3 T applied field, P.F. shows a similar trend with decreasing temperature. It starts increasing rapidly below T_C, goes through a maximum value and then decreases to zero. P.F. has highest value of 0.07 μW cm⁻¹ K⁻² around 47 K at 3 T field.

4. Conclusions

To conclude, effects of magnetic field on the thermal expansion, charge transport and thermal conduction mechanism for aliovalent Na¹⁺ doped LaMnO₃ were investigated. We have found anomaly in thermal expansion behavior around T_C. Electrical resistivity and thermopower data analysis in the insulating region reveal that conductivity at high temperature is governed by small-polaron hopping mechanism in La_0.9Na_0.1MnO₃. Anomaly of κ around paramagnetic–ferromagnetic transition suggests coupling between thermal conductivity and magnetism. Application of magnetic field enhances thermal conductivity while suppresses the magnitude of thermopower and resistivity. The magnitude of magneto-thermopower (∼61.5%) is larger than the magnetoresistance (∼49%) and magnetothermal conductivity (∼12.7%).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. M. thanks the Ministry of Education for supporting this work (Grant no. MOE2014-T2-48/R144-000-349-112 and MOE2016-T2-2-098/R144-000-381-112).

References

1. C. N. R. Rao and B. Raveau, Colossal Magnetoresistance, Charge Ordering, and Related Properties of Manganese Oxides, World Scientific, Singapore, 1998.
2. J. Hu, L. Shi, Q. Liu, H. Huang and T. Jiao, Improved oxygen reduction activity on silver modified LaMnO₃–graphene via shortens the conduction path of adsorbed oxygen, RSC Adv., 2015, 5, 92096.
3. H. Xu, Y. Ma, S. Zhao, W. Huang, Z. Qua and N. Yan, Enhancement of Ce_1−xSn_xO₂ support in LaMnO₃ for the catalytic oxidation and adsorption of elemental mercury, RSC Adv., 2016, 6, 63559.
4. Y. Tokura, Critical features of colossal magnetoresistive manganites, Rep. Prog. Phys., 2006, 69, 797.
5. G. H. Jonker and J. H. Van Santen, Ferromagnetic Compounds of Manganese with Perovskite Structure, Physica, 1950, 16, 337–349.
6. C. Zener, Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure, Phys. Rev., 1951, 82, 403.
7. A. Bhaskar, M.-S. Huang and C. –J. Liu, Effects of Fe doping on the thermal hysteresis of the La_0.5Ca_0.5MnO₃ system, RSC Adv., 2017, 7, 11543.
8. B. Chen, A. G. Rojo, C. Uher, H. L. Ju and R. L. Greene, Magnetothermal conductivity of La_0.8Ca_0.2MnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15471.
9. P. Mandal, Temperature and doping dependence of the thermopower in LaMnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14675.
10. T. Shimura, T. Hayashi, Y. Inaguma and M. Itoh, Magnetic and Electrical Properties of La_yA_xMn_wO₃ (A = Na, K, Rb, and Sr) with Perovskite-Type Structure, J. Solid State Chem., 1996, 124, 250–263.
11. A. M. Ahmed, S. A. Saleh, E. M. M. Ibrahim and H. F. Mohamed, Crystal structure and some transport properties of Na-doped LaMnO_y, J. Magn. Magn. Mater., 2006, 301, 452–457.
12. R. Mahendiran, S. K. Tiwary, A. K. Raychaudhuri, R. Mahesh and C. N. R. Rao, Thermopower and nature of the hole-doped states in LaMnO₃ and related systems showing giant magnetoresistance, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, R9604.
13. A. Asamitsu, Y. Moritomo and Y. Tokura, Thermoelectric effect in La_1−xSr_xMnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R2952.
14. M. P. Sharma, et al., Electric transport behaviour of sodium-substituted perovskites La_1−xNa_xMnO₃ (for x = 0.1 and 0.2) and the effect of magnetic fields, J. Phys.: Condens. Matter, 2008, 20, 425220.
15. S. Das and T. K. Dey, Structural and magnetocaloric properties of La_1−yNa_yMnO₃ compounds prepared by microwave processing, J. Phys. D: Appl. Phys., 2007, 40, 1855.
16. S. Roy, Y. Q. Guo, S. Venkatesh and N. Ali, Interplay of structure and transport properties of sodium-doped lanthanum manganite, J. Phys.: Condens. Matter, 2001, 13, 9547.
17. P. G. Radaelli, G. Iannone, M. Marezio, H. Y. Hwang, S.-W. Cheong, J. D. Jorgensen and D. N. Argyrion, Structural effects on the magnetic and transport properties of perovskite A_1−xA_x′MnO₃ (x = 0.25, 0.30), Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8265.
18. G. H. Rao, J. R. Sun, K. Bärner and N. Hamad, Crystal structure and magnetoresistance of Na doped LaMnO₃, J. Phys.: Condens. Matter, 1999, 11, 1523.
19. D. V. Maheswar Repaka and R. Mahendiran, Giant magnetothermopower in charge ordered Nd_0.75Na_0.25MnO₃, Appl. Phys. Lett., 2013, 103, 162408.
20. R. Küchler, T. Bauer, M. Brando and F. Steglich, A compact and miniaturized high resolution capacitance dilatometer for measuring thermal expansion and magnetostriction, Rev. Sci. Instrum., 2012, 83, 095102.
21. R. P. Borges, F. Ott, R. M. Thomas, V. Skumryev, J. M. D. Coey, J. I. Arnaudas and L. Ranno, Field-induced transition in the paramagnetic state of (Sm_0.65Sr_0.35)MnO₃ associated with magnetic clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 12847.
22. A. Mleiki, R. Hanen, H. Rahmouni, N. Guermazi, K. Khirouni, E. K. Hlile and A. Cheikhrouhou, Study of magnetic and electrical properties of Pr_0.65Ca_0.25Ba_0.1MnO₃ manganite, RSC Adv., 2018, 8, 31755.
23. M. R. Ibarra, P. A. Algarabel, C. Marquina, J. Blasco and J. García, Large Magnetovolume Effect in Yttrium Doped La-Ca-Mn-O perovskite, Phys. Rev. Lett., 1995, 75, 3541.
24. C. Zhu, R. Zheng, J. Su and J. He, Ultrasonic anomalies in La_0.67Ca_0.33MnO₃ near the Curie temperature, Appl. Phys. Lett., 1999, 74, 3504.
25. S. L. Ye, W. H. Song, J. M. Dai, K. Y. Wang, S. G. Wang, J. J. Du, Y. P. Sun, J. Fang, J. L. Chen and B. J. Gao, Large room-temperature magnetoresistance and phase separation in La_1−xNa_xMnO₃ with 0.1 ≤ x ≤ 0.3, J. Appl. Phys., 2001, 90, 2943.
26. D. W. Visser, A. P. Ramirez and M. A. Subramanian, Thermal Conductivity of Manganite Perovskites: Colossal Magnetoresistance as a Lattice-Dynamics Transition, Phys. Rev. Lett., 1997, 78, 3947.
27. A. Ray and T. K. Dey, Thermal conductivity of La_0.67(Ca_xSr_1−x)_0.33MnO₃ (x = 0, 0.5, 1) and La_0.6Y_0.07Ca_0.33MnO₃ pellets between 10 and 300 K, Solid State Commun., 2003, 126, 147.
28. J. L. Cohn, J. J. Neumeier, C. P. Popoviciu, K. J. McClellan and Th. Leventouri, Local lattice distortions and thermal transport in perovskite manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R8495.
29. H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, Characterization of Lorenz number with Seebeck coefficient measurement, APL Mater., 2015, 3, 041506.
30. S. J. L. Billinge, R. G. DiFrancesco, G. H. Kwei, J. J. Neumeier and J. D. Thompson, Direct Observation of Lattice Polaron Formation in the Local Structure of La_1−xCa_xMnO₃, Phys. Rev. Lett., 1996, 77, 715.
31. G. A. Slack and R. Newman, Thermal Conductivity of MnO and NiO, Phys. Rev. Lett., 1958, 1, 359.
32. R. Mahesh, R. Mahendiran, A. K. Raychaudhuri and C. N. R. Rao, Effect of particle size on the giant magnetoresistance of La_0.7Ca_0.3MnO₃, Appl. Phys. Lett., 1996, 68, 2291.
33. M. Czerner, M. Bachmann and C. Heiliger, Spin caloritronics in magnetic tunnel junctions: ab initio studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 132405.
34. T. D. Yamamoto, H. Taniguchi, Y. Yasui, S. Iguchi, T. Sasaki and I. Terasaki, Magneto-thermopower in the Weak Ferromagnetic Oxide CaRu_0.8Sc_0.2O₃: An Experimental Test for the Kelvin Formula in a Magnetic Material, J. Phys. Soc. Jpn., 2017, 86, 104707.
35. A. Kumar, C. V. Tomy and A. D. Thakur, Magnetothermopower, magnetoresistance and magnetothermal conductivity in La_0.95Sr_0.05Co_1−xMn_xO₃ (0.00 ≤ x ≤ 1.00), Mater. Res. Express, 2018, 5, 086110.
36. D. V. Maheswar Repaka, T. S. Tripathi, M. Aparnadevi and R. Mahendiran, Magnetocaloric effect and magnetothermopower in the room temperature ferromagnet Pr_0.6Sr_0.4MnO₃, J. Appl. Phys., 2012, 112, 123915.
37. J. Yang, Y. P. Sun, W. H. Song and Y. P. Lee, Thermopower and thermal conductivity of the electron-doped manganite La_0.9Te_0.1MnO₃, J. Appl. Phys., 2006, 100, 123701.
38. A. J. Millis, P. B. Littlewood and B. I. Shraiman, Double Exchange Alone Does Not Explain the Resistivity of La_1−xSr_xMnO₃, Phys. Rev. Lett., 1995, 74, 5144.
39. M. Jaime, M. B. Salamon, K. Pettit, M. Rubinstein, R. E. Treece, J. S. Horwitz and D. B. Chrisey, Magnetothermopower in La_0.67Ca_0.33MnO₃ thin films, Appl. Phys. Lett., 1996, 68, 1576.
40. L. Malavasi, M. Cristina Mozzati, P. Ghigna, C. B. Azzoni and G. Flor, Lattice Disorder, Electric Properties, and Magnetic Behavior of La_1−xNa_xMnO_3+δ Manganites, J. Phys. Chem. B, 2003, 107, 2500–2505.
41. A. Urushibara, Y. Moritomo, T. Arima, A. Asamitsu, G. Kido and Y. Tokura, Insulator-metal transition and giant magnetoresistance in La_1−xSr_xMnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 14103.
42. K. Kubo and N. Ohata, A Quantum Theory of Double Exchange. I, J. Phys. Soc. Jpn., 1972, 33, 21.
43. B. F. Woodfield, M. L. Wilson and J. M. Byers, Low-Temperature Specific Heat of La_1−xSr_xMnO_3+δ, Phys. Rev. Lett., 1997, 78, 3201.
44. M. Jaime, P. Lin, M. B. Salamon and P. D. Han, Low-temperature electrical transport and double exchange in La_0.67(Pb, Ca)_0.33MnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R5901.

---