Open Access Article
Open Access ArticleTheoretical prediction of HfB2 monolayer, a two-dimensional Dirac cone material with remarkable Fermi velocity†
Zhongfei Liua,
Peihong Wanga,
Qiaoyu Cuia,
Guang Yangb,
Shaowei Jin *ac and
Kuangwei Xiong*d
*ac and
Kuangwei Xiong*d
aSchool of Physics and Materials Science, Anhui University, Hefei 230601, P. R. China. E-mail: jinsw@mail.ustc.edu.cn
bCollege of Energy and Environmental Engineering, Hebei University of Engineering, Handan 056038, Hebei Province, P. R. China
cAnhui Key Laboratory of Information Materials and Devices, Hefei 230601, Anhui Province, P. R. China
dDepartment of Physics, East China Jiaotong University, Nanchang 330013, Jiangxi Province, P. R. China
First published on 21st January 2019
Abstract
Searching for new two-dimensional (2D) Dirac cone materials has been popular since the discovery of graphene with a Dirac cone structure. Based on density functional theory (DFT) calculations, we theoretically designed a HfB2 monolayer as a new 2D Dirac material by introducing the transition metal Hf into a graphene-like boron framework. This newly predicted HfB2 monolayer has pronounced thermal and kinetic stabilities along with a Dirac cone with a massless Dirac fermion and Fermi velocities (3.59 × 105 and 6.15 × 105 m s−1) comparable to that of graphene (8.2 × 105 m s−1). This study enriches the diversity and promotes the application of 2D Dirac cone materials.
Introduction
Since the discovery of graphene by Novoselov et al.,1 two-dimensional (2D) materials with Dirac cones, which are characterized by linear dispersion bands in the vicinity of the Fermi level, have garnered tremendous interest due to their unconventional properties, such as half-integer,2,3 fractional4–6 and fractal7 quantum Hall effects along with ultra-high carrier mobility.8,9 These fascinating characteristics have promoted the exploration of other 2D Dirac cone materials. Given the rigorous requirements for the existence of Dirac cones in 2D materials, to date, only graphene,2 silicone and germanene,10 carbon allotropes,11–13 boron allotropes14–16 and a handful of other systems17–21 have been verified to be Dirac cone materials.Boron atom exhibits flexible bonding characteristics because its three valence electrons can occupy four available orbitals. Attempting to compensate for the electron deficiency boron is an effective strategy to form an isoelectronic structure like carbon. Based on this strategy, some 2D boron-based Dirac materials including monolayer TiB2,22 single-layer FeB2,23 and hydrogenated boron sheets have been predicted.24 In these boron-based Dirac materials, freestanding monolayer TiB2 sheets tend to bend into tubular shapes and exhibit bending instability; thus, planar TiB2 needs to be stabilized on a substrate. In addition, other 2D boron-based materials in the P6/mmm space group, such as MgB6 (ref. 25) and MnB6 (ref. 26), are not Dirac materials, although they have stable structures. Therefore, exploring boron-based compounds for new 2D Dirac cone materials is a priority in both experimental and theoretical efforts.
In this paper, we theoretically predict a new 2D Dirac material, HfB2 monolayer, with Fermi velocities of 3.59 × 105 and 6.15 × 105 m s−1. We embedded the electron-rich transition metal Hf (5d26s2) into a graphene-like boron network to stabilize the unstable boron sheets. The band structures of HfB2 display a Dirac cone at the high-symmetric K point in the absence of spin–orbit coupling (SOC). Meanwhile, the predicted HfB2 monolayer presents ultra-high maximum Fermi velocities of 3.59 × 105 and 6.15 × 105 m s−1 along with excellent thermodynamic stability. Our analysis of monolayer HfB2 provides theoretical guidance for predicting and developing 2D Dirac materials.
Computational method
For first-principles calculations, the Vienna Ab initio Simulation Package (VASP)27 was employed within the framework of the Perdew–Burke–Ernzerhof (PBE)28 generalized gradient approximation. Ion–electron interactions were treated by the projector augmented wave method.29 The energy cutoff was set to 600 eV, and the energy precision was set to 10−5 eV. Geometries were fully relaxed until the residual force on each atom was less than 10−4 eV Å−1. In the geometry optimization and self-consistent computations, the first Brillouin zone was sampled with a 9 × 9 × 1 Γ-centered Monkhorst–Pack k-point grid. The Heyd–Scuseria–Ernzerhof (HSE06)30 hybrid functional was used to calculate more reliable band structures.A vacuum layer larger than 15 Å was used to avoid interactions between neighboring layers. The dynamic stabilities of HfB2 were checked based on the phonon dispersion spectra, as implemented in the phonopy code,31 interfaced with density functional perturbation theory implemented in VASP. Thermal stability was evaluated via ab initio molecular dynamics (AIMD) simulations in the NVT ensemble at temperatures of 300, 500, 800 and 1200 K. The temperature was controlled using the Nosé–Hoover method.32 The computational benchmarks are detailed in the ESI (Fig. S1).†
Results and discussion
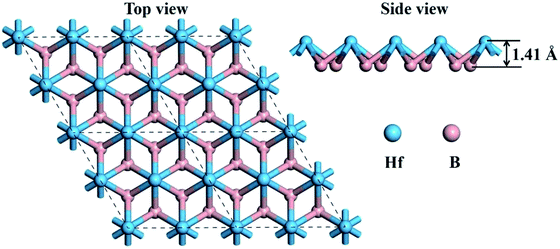
Graphene-like boron sheets are unstable since there are only six electrons for each boron atom. Thus, additional atoms are needed to complete the outer electron shell. Embedding the electron-rich metal Hf into graphene-like boron layers can stabilize the boron sheets. The top view and side view of the optimized structure of monolayer HfB2 is shown in Fig. 1. As seen in Fig. 1, the 2D HfB2 monolayer belongs to the space group P6/mmm, in which B atoms are arranged in a honeycomb structure, and each Hf atom coordinates with six members of boron rings to form a quasi-planar hexacoordination. The quasi-planar structure of the HfB2 monolayer is as a result of spontaneous symmetry lowering due to Pseudo Jahn–Teller instability in its planar form.33–37The B–B and B–Hf bond lengths are 1.85 and 2.32 Å, respectively. The vertical distance between the Hf atom and B layer is 1.41 Å. The B–B bond length (1.85 Å) is almost equivalent to that in the FeB2 monolayer (1.83 Å)23 and slightly longer than those in the TiB2 monolayer (1.79 Å),22 hydrogenated boron sheet (1.72 Å)24 and boron sheet (1.67 Å).38 The B–Hf bond length (2.32 Å) is smaller than that in bulk HfB2 (2.53 Å),39 indicating a much stronger interaction between the Hf atoms and boron layer.
To assess the stability of the HfB2 monolayer, we calculated its cohesive energy Ecoh, which was defined as
| Ecoh = (nEHf + 2nEB − nEHfB2)/N, | (1) |
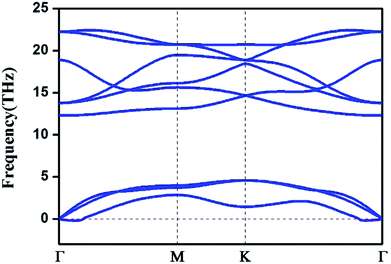
We also computed the phonon spectrum to check the kinetic stabilities of the HfB2 monolayer (Fig. 2). A tiny imaginary frequency was found near the Γ point. This phenomenon was also found in the phonon spectra of germanene,10 borophene,41 arsenene42 and other two-dimensional systems.43 It is not a sign of structural instability and may be the result of numerical instability when accurately calculating rapidly decreasing interatomic forces.43 Our analysis of the phonon dispersion curves suggests that the HfB2 sheet can be dynamically stable.
We then carried out AIMD simulations to examine the thermal stability of HfB2 monolayer at the temperatures of 300, 400, 500, and 800 K. A 5 × 5 × 1 supercell was adopted to reduce the constraints of the periodic boundary conditions. As shown in Fig. 3, the HfB2 monolayer does not undergo obvious structural distortion at 400 K. However, drastic structure collapse is observed at 500 K. In particular, the hexacoordination of Hf atom transfers to an even higher coordination at the temperatures of 500 and 800 K. The above results suggest that the HfB2 monolayer is stable at room temperature.
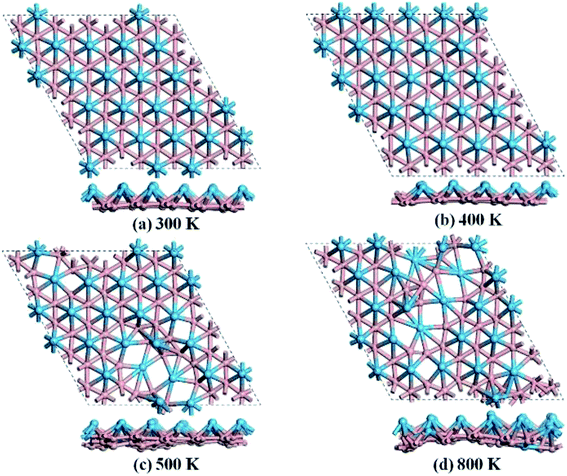 | ||
| Fig. 3 Snapshots of the equilibrium structures of the HfB2 monolayer after the ab initio molecular dynamics simulations at (a) 300 K, (b) 400 K, (c) 500 K, and (d) 800 K. | ||
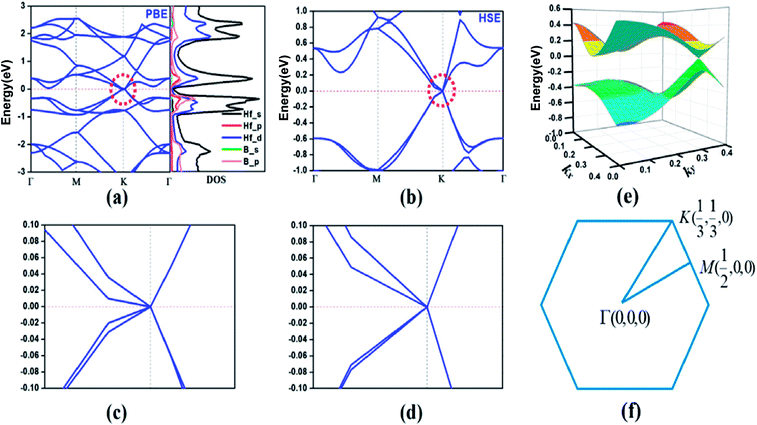
According to the calculated cohesive energies, phonon spectra and AIMD simulations, the predicted HfB2 monolayer have pronounced thermodynamic stability. Therefore, we next investigated its band structure and corresponding projected density of states (PDOS). As shown in Fig. 4a, two bands cross each other linearly around the Fermi level, which creates an intrinsic Dirac cone. The meeting point of the conduction band (CB) and valence band (VB) is located at the high-symmetry K (1/3, 1/3, 0) point. The PDOS shows that the VB and CB near the Fermi level mainly originate from hybridized Hf-s, Hf-d and B-p orbitals.
To confirm the existence of the Dirac cone, we recalculated the band structure using the HSE06 hybrid functional, which has been shown to be more reliable in the calculation of electronic structures.44–48 Fig. 4b shows that the Dirac cone still exists (Fig. 4c and d show the enlarged band structure approach to the Dirac cone). The three-dimensional (3D) plot (Fig. 4e) exhibits a notable conical feature near the Fermi level. It is believed that the Dirac cone is a lower energy configuration compared to the Fermi level in the HfB2 monolayer, which is a property intrinsic to this system.
Considering the strong SOC effect of Hf atoms, which might open up the band gap, we further investigated the effect of SOC on the electronic structure using the HSE06 hybrid functional method. The SOC effect introduces a gap of 146 meV (Fig. S2, ESI†), which is mainly due to the orbital contribution close to the nucleus. Additionally, the band lines crossing the Fermi level suggest the metallic property of the HfB2 monolayer in consideration of the SOC effect.
The linear dispersion of the energy bands means that the carriers in CB and VB behave as Dirac fermions with zero mass, which results in excellent carrier transport characteristics near the Fermi level. We calculated the Fermi velocity νf of the HfB2 monolayer with the expression νf = ∂E/(ℏ∂k). The calculated maximum velocities were determined to be 3.59 × 105 m s−1 along the M → K direction and 6.15 × 105 m s−1 along the K → Γ direction using the HSE06 method. The velocities are comparable to those of graphene (8.2 × 105 m s−1)49 and 2D boron-based Dirac cone materials such as FeB2 monolayer (6.54 × 105 m s−1)23 and B2S monolayer (6.7 × 105 m s−1 along the kx direction and 4.8 × 105 m s−1 along the ky direction).17
Additionally, the Fermi velocity is largely arbitrary and strongly dependent on the stoichiometry along with the long-range geometry. To verify the reproducibility of these notable Fermi velocities, we also simulated the HfB2 monolayer with one Hf atom replaced by a Zr atom (Zr@HfB2). The dopant is expected to induce distortions. Considering the high cost of HSE06 computations, the Fermi velocities of pure HfB2 and Zr@HfB2 monolayers were obtained by analyzing the band structure computed by PBE functionals (Fig. S3†). The PBE computations suggest that the Fermi velocities of Zr@HfB2 are 4.40 × 103 m s−1 along the M → K direction and 9.10 × 103 m s−1 in the K → Γ direction, which are comparable to those of HfB2 monolayer (5.46 × 103 and 7.74 × 103 m s−1, respectively). The above-mentioned Fermi velocities based on the PBE functionals are smaller than those obtained by the HSE06 method, which is due to the underestimation of the slopes of the band lines by the PBE method. Notably, the well-maintained Fermi velocities in Zr@HfB2 with lattice distortion suggest that the remarkable Fermi velocities of HfB2 monolayer are reproducible.
The strong connection between the Hf and B atoms suggest the experimental feasibility and thermodynamic stability of HfB2 (Table S1†), which were confirmed by the phonon dispersion and AIMD results. We also computed the band structures of HgB2, RuB2, AuB2 and IB2 and found no Dirac cones within the band structures of these materials, with the exception of RuB2 (Fig. S4†). The follow-up computations will be performed to further investigated the electronic properties of RuB2. In addition, the HfB2 monolayers with Hf atoms substituted by Ti and Zr atoms in the same main group were simulated, and no Dirac cones were found (Fig. S5†), indicating the unique characteristics of the HfB2 sheet.
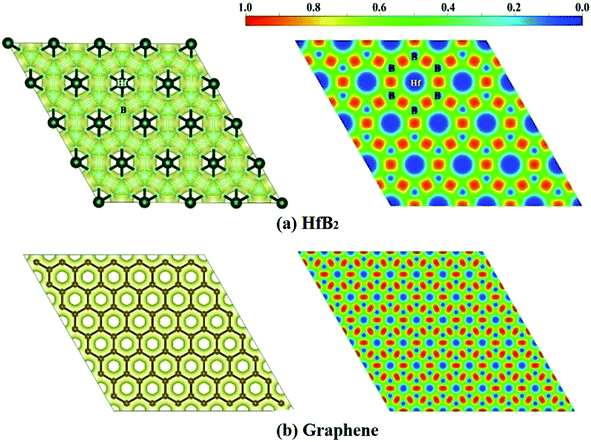
Finally, we computed the electron localization function (ELF)50 of the HfB2 monolayer to analyze its electron distribution. As shown in the ELF map in Fig. 5a, the electrons are mainly distributed around the B atoms, and remarkable electron transfer from Hf to B atoms is observed. The ELF map of HfB2 monolayer is similar to that of graphene (Fig. 5b), which may be the root cause of the existence of the Dirac point.
From the perspective of the practical application of the predicted 2D HfB2 monolayer, the HfB2 film must be deposited on a suitable substrate.51–53 We chose MoS2 (lattice constant of 2 × 2 supercell: 6.30 Å) as a substrate to support the HfB2 film (lattice constant of unit cell: 6.41 Å) to form the HfB2@MoS2 heterostructure, in which the lattice mismatch is only 1.7% (Fig. S6†). After full structural relaxation, the interlayer distance is 2.92 Å, and the binding energy is 45 meV per atom, which is comparable to that of the FeB2/MoS2 heterostructure and suggests the presence of van der Waals interactions between HfB2 and the MoS2 substrate.23 From the above discussion, MoS2 is an ideal substrate for the predicted HfB2 monolayer to achieve potential device applications.
Based on the analysis of cohesive energies, phonon spectra, AIMD simulations and growth substrate, the HfB2 monolayer is a 2D Dirac cone material with pronounced thermodynamic stability and experimental feasibility. In addition, the high carrier mobility and excellent electronic transport properties will likely make it a useful material in many fields, such as nanoelectronics, sensing and energy devices.
Conclusions
In summary, we successfully predicted a HfB2 monolayer, a novel 2D boron-based Dirac cone material that can be constructed by embedding the electron-rich transition metal Hf into a graphene-like boron network. The HfB2 monolayer is thermally and kinetically stable and possesses a promising Fermi velocity on the same order of magnitude as that of graphene. Orbital analysis shows that the Dirac cone near the Fermi level predominantly originates from hybridized Hf-s, Hf-d and B-p orbitals. Our work is expected to promote experimental efforts to synthesize predicted 2D boron-based Dirac materials and extend their applications in electronics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China (61671017) and the Key Natural Science Research Program of Anhui Educational Committee (KJ2018ZD001, KJ2013A030).Notes and references
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- Y. B. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Stormer and P. Kim, Nature, 2009, 462, 196–199 CrossRef CAS PubMed.
- X. Du, I. Skachko, F. Duerr, A. Luican and E. Y. Andrei, Nature, 2009, 462, 192–195 CrossRef CAS PubMed.
- B. Hunt, J. D. Sanchez-Yamagishi, A. F. Young, M. Yankowitz, B. J. LeRoy, K. Watanabe, T. Taniguchi, P. Moon, M. Koshino, P. Jarillo-Herrero and R. C. Ashoori, Science, 2013, 340, 1427–1430 CrossRef CAS PubMed.
- C. R. Dean, L. Wang, P. Maher, C. Forsythe, F. Ghahari, Y. Gao, J. Katoch, M. Ishigami, P. Moon, M. Koshino, T. Taniguchi, K. Watanabe, K. L. Shepard, J. Hone and P. Kim, Nature, 2013, 497, 598–602 CrossRef CAS PubMed.
- K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355 CrossRef CAS.
- E. H. Hwang and S. Das Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115449 CrossRef.
- S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804 CrossRef CAS PubMed.
- Z. Wang, X. F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186 CrossRef CAS PubMed.
- L. C. Xu, R. Z. Wang, M. S. Miao, X. L. Wei, Y. P. Chen, H. Yan, W. M. Lau, L. M. Liu and Y. M. Ma, Nanoscale, 2014, 6, 1113–1118 RSC.
- M. Zhao, W. Dong and A. Wang, Sci. Rep., 2013, 3, 3532 CrossRef PubMed.
- H. Zhang, Y. Xie, Z. Zhang, C. Zhong, Y. Li, Z. Chen and Y. Chen, J. Phys. Chem. Lett., 2017, 8, 1707–1713 CrossRef CAS PubMed.
- X. F. Zhou, X. Dong, A. R. Oganov, Q. Zhu, Y. Tian and H. T. Wang, Phys. Rev. Lett., 2014, 112, 085502 CrossRef.
- F. Ma, Y. Jiao, G. Gao, Y. Gu, A. Bilic, Z. Chen and A. Du, Nano Lett., 2016, 16, 3022–3028 CrossRef CAS PubMed.
- Y. Zhao, X. Li, J. Liu, C. Zhang and Q. Wang, J. Phys. Chem. Lett., 2018, 1815–1820 CrossRef CAS PubMed.
- H. Pan, H. Zhang, Y. Sun, J. Li, Y. Du and N. Tang, Phys. Rev. B, 2017, 96, 155448 CrossRef.
- P. F. Liu, L. Zhou, S. Tretiak and L. M. Wu, J. Mater. Chem. C, 2017, 5, 9181–9187 RSC.
- Y. Ma, Y. Jing and T. Heine, 2D Mater., 2017, 4, 025111 CrossRef.
- B. Wang, S. Yuan, Y. Li, L. Shi and J. Wang, Nanoscale, 2017, 9, 5577–5582 RSC.
- L. Z. Zhang, Z. F. Wang, S. X. Du, H. J. Gao and F. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 161402(R) CrossRef.
- H. Zhang, Y. Li, J. Hou, A. Du and Z. Chen, Nano Lett., 2016, 16, 6124–6129 CrossRef CAS PubMed.
- Y. Jiao, F. Ma, J. Bell, A. Bilic and A. Du, Angew. Chem., Int. Ed., 2016, 55, 10292–10295 CrossRef CAS PubMed.
- S. Y. Xie, X. B. Li, W. Q. Tian, N. K. Chen, Y. Wang, S. Zhang and H. B. Sun, Phys. Chem. Chem. Phys., 2015, 17, 1093–1098 RSC.
- J. Li, X. Fan, Y. Wei, J. Liu, J. Guo, X. Li, V. Wang, Y. Liang and G. Chen, J. Mater. Chem. C, 2016, 4, 10866–10875 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 169–186 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- G. J. K. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- D. Jose and A. Datta, Acc. Chem. Res., 2014, 47, 593–602 CrossRef CAS PubMed.
- T. K. Mandel, D. Jose, A. Nijamudheen and A. Datta, J. Phys. Chem. C, 2014, 118, 12115–12120 CrossRef.
- A. Nijamudheen, R. Bhattacharjee, S. Choudhury and A. Datta, J. Phys. Chem. C, 2015, 119, 3802–3809 CrossRef CAS.
- C. Chowdhury, S. Jahiruddin and A. Datta, J. Phys. Chem. Lett., 2016, 7, 1288–1297 CrossRef CAS PubMed.
- C. Chowdhury and A. Datta, J. Phys. Chem. Lett., 2017, 8, 2909–2916 CrossRef CAS PubMed.
- H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501 CrossRef PubMed.
- J. D. Zhang, X. L. Cheng and D. H. Li, J. Alloys Compd., 2011, 509, 9577–9582 CrossRef CAS.
- H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651 CrossRef CAS PubMed.
- M. Gao, Q. Z. Li, X. W. Yan and J. Wang, Phys. Rev. B, 2017, 95, 024505 CrossRef.
- C. Kamal and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085423 CrossRef.
- H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- H. Zhang, D. Wu, Q. Tang, L. Liu and Z. Zhou, J. Mater. Chem. A, 2013, 1, 2231–2237 RSC.
- H. Zhang, X. Zuo, H. Tang, G. Li and Z. Zhou, Phys. Chem. Chem. Phys., 2015, 17, 6280–6288 RSC.
- H. Zhang, Y. Liao, G. Yang and X. Zhou, ACS Omega, 2018, 3, 10517–10525 CrossRef CAS.
- H. Zhang, X. Zhang, G. Yang and X. Zhou, J. Phys. Chem. C, 2018, 122, 5291–5302 CrossRef CAS.
- H. Zhang, Y. Li, Q. Tang, L. Liu and Z. Zhou, Nanoscale, 2012, 4, 1078–1084 RSC; H. Zhang, X. Li, X. Meng, S. Zhou, G. Yang and X. Zhou, J. Phys.: Condens. Matter, 2019 DOI:10.1088/1361-648X/aafea4.
- D. Malko, C. Neiss, F. Vines and A. Goerling, Phys. Rev. Lett., 2012, 108, 086804 CrossRef PubMed.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- T. Teshome and A. Datta, J. Phys. Chem. C, 2018, 122, 15047–15054 CrossRef CAS.
- T. Teshome and A. Datta, ACS Appl. Mater. Interfaces, 2017, 9, 34213–34220 CrossRef CAS PubMed.
- C. Chowdhury, S. Karmakar and A. Datta, ACS Energy Lett., 2016, 1, 253–259 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra08291j |
| This journal is © The Royal Society of Chemistry 2019 |