DOI:
10.1039/C8RA09492F
(Paper)
RSC Adv., 2019,
9, 2731-2739
Structural growth pattern of neutral and negatively charged yttrium-doped silicon clusters YSin0/− (n=6–20): from linked to encapsulated structures†
Received
19th November 2018
, Accepted 3rd January 2019
First published on 21st January 2019
Abstract
A global search for the low energy of neutral and anionic doped Si clusters YSin0/− (n = 6–20) was performed using the ABCluster global search technique coupled with a hybrid density functional method (mPW2PLYP). In light of the calculated energies and the measured photoelectron spectroscopy values, the true minima of the most stable structures were confirmed. It is shown that the structural growth pattern of YSin− (n = 6–20) is from Y-linked two subcluster structure to a Y-encapsulated structure in Si cages, while that of YSin (n = 6–20) is from substitutional to linked structures, and as the number of Si atoms increases, it evolves toward the encapsulated structure. Superatom YSi20− with a high-symmetry endohedral Ih structure has an ideal thermodynamic stability and chemical reactivity, making it the most suitable building block for novel optical, optoelectronic photosensitive or catalytic nanomaterials.
Introduction
Rare-earth metal silicides as novel functional materials have been extensively used in various fields such as microelectronics and optical instruments due to their remarkable magnetic, electrical, and optical properties and their chemical stabilities.1–3 For instance, silicon is a poor photonic material owing to its very short non-radiative lifetime and indirect band gap, but introducing erbium to a silicon microcrystal can be used as a silicon based optical source.4 Yttrium silicides are ideal in devices such as large scale integrated circuits, infrared detectors, ohmic contacts and rectifying contacts because the interfaces of yttrium and silicon have very small lattice mismatches, sharp interfaces, high conductivity, low Schottky barrier heights and very good thermal stability.5,6 In the past few decades, a great deal of research on yttrium silicide has been performed. These studies focus mainly on the formation of amorphous yttrium silicide and have proposed that nanoclusters play a role in such physical and chemical processes. Nanoclusters have been one of the central issues of nanomaterial sciences because of their unique structures and properties.7–10 Consequently, it is very important to probe the evolution of yttrium silicide aggregates in the transition from the molecular to the condensed phase.
Several efforts have been made in the past decade to study the structural and electronic properties of yttrium doped silicon clusters.11–17 The structures, stabilities and electronic properties of small-sized YSin (n = 1–6) were evaluated by using single-hybrid B3LYP density functional.11,12 Ren and co-workers13 probed the geometries and electron properties of YSin with n up to 16 by means of a relativistic density functional investigation and concluded that (i) the spin–orbit correction is small and negligible; (ii) the most stable structures keep analogous frameworks to the Sin+1 cluster for n = 1–14, but encapsulated geometries starting from n = 15. For anions, silicon clusters doped with yttrium atoms, YSin− (n = 6–20) were generated by a double-laser vaporization technique and their electronic and geometric stabilities were characterized with adsorption reactivity and photoelectron spectroscopy (PES).2,3 In addition, the structure of the YSin− clusters was deduced by a chemical probe method,2,3 and it was found that the YSin− clusters evolved from incomplete cage-type structures to cage-type structures from n = 16 to n = 20.2,3 After these experiments, a simulated annealing approach combined with a B3PW91 theoretical simulation for YSin− (n = 4–20) was achieved by Jaiswal et al.17 They found that YSi16−, YSi17− and YSi20− adopt the cage structures and YSi18− and YSi19− adopt the linked structures. Obviously, this growth behavior is different from that of the experimental results.2,3
Although these theoretical studies concentrated on the structural stability and evolution of yttrium-doped neutral and anionic Sin (n ≤ 20) clusters and provided important information for further theoretical and experimental research, some questions still remain open in yttrium-doped silicon clusters: (i) the functional dependence on the predicted lowest-energy structure may occur for small- or medium-clusters, especially for species including rare earth- or transition-metal atoms. Therefore, the choice of calculation method is very important.18 Based on our previous studies about REM-doped Si clusters (REM = Sm, Eu Gd, Ho, Pr),19–24 compared to the pure or single-hybrid density functional (such as PBE, B3LYP, PBE0, TPSSh, wB97X, and wB97XD), the adiabatic electron affinities (AEAs) calculated at the B2PLYP and mPW2PLYP level show a better comparison with the experimental information. In addition, the theoretical and experimental photoelectron spectroscopy (PES) spectra are in good agreement at the mPW2PLYP and the B2PLYP level.19,22,23 (ii) It is possible to leave out the most stable structure during the initial configuration selection without a global search technique.25,26,27 For small-sized clusters, the global optimization approach is a very effective method and can completely solve the problem of ground state structure loss. Without doubt it is impossible to make an “ergodic” sampling on the potential energy surface of large clusters by a global search technique. Consequently, it is reasonable and necessary to take into account a substitutional structure (this can be regarded as replacing a Si atom of Sin+1 with a metal atom), an attaching structure (this can be viewed as adding a metal atom to the Sin geometry) and so on as a complement to the global search method. (iii) A detailed comparison of the theoretical and experimental results, such as PES, infrared or Raman spectra, is the most effective strategy because there is no experimental method for directly measuring the most stable structure of clusters so far. (iv) As the diversity of the properties of Y-doped Si clusters can hardly be explained without understanding the structural evolution patterns, in this paper the ABCluster global search technique combined with a double-hybrid density functional scheme was adopted for the geometry optimization of neutral and anionic Y-doped Sin (n = 6–20) clusters with the aim of elucidating the structural evolution pattern of their ground states, studying their electronic properties, understanding their bonding characteristics, and providing significant information for further theoretical and experimental explorations of semiconductor clusters doped with other transition or rare-earth metals. Good agreement between the theoretical and experimental data, including PES, vertical detachment energy (VDE) and adiabatic electron affinity (AEA), strongly supports the validity of our global minimum geometries.
Computational details
To search for the most stable structure for YSin (n = 6–20) and their anions, three techniques were adopted to search their initial configurations. First, we use the free program “ABCluster” to perform the global search.28 The ABCluster program uses the artificial bee colony (ABC) algorithm to conduct the global search for clusters. Initially, we used the ABCluster program generating 300 cluster structures for YSin0/− (n = 6–20) at the PBE/BSI level (BSI: Si: 6-31G; Y: LANL2DZ).29,30 Then, the isomers with an energy difference within 0.8 eV of the lowest energy clusters were selected and re-optimized at the PBE/BSII level (BSII: Si: cc-pVTZ; Y: SDD).31–33 Second, the substitutional structures were collected, in which a Si atom in the most stable structure of Sin+1 was replaced with a Y atom. Third, isomers already presented in the preceding literature13,17 were adopted. Vibrational frequency calculations were carried out at the same level to assure the nature of the stationary points. After completion of the initial geometry optimization by PBE, we selected, again, the low-lying isomers and reoptimized them by means of a double hybrid mPW2PLYP functional34 at the same level. Vibrational frequency was not carried out at the mPW2PLYP level. In order to further refine the energies, single-point energy calculations were carried out at the mPW2PLYP level with the aug-cc-pVTZ basis set33 for Si atoms (basis set for Y atoms unchanged). According to Koopmans' theorem,35,36 we simulated the PES spectra of anionic species at the mPW2PLYP level with the Multiwfn program37 and compared them with the experimental PES spectra. In light of the adaptive natural density partitioning (AdNDP),38 chemical bonding analyses were performed to gain chemical insight. To further understand the interaction between the Y atom and silicon clusters, natural population analyses (NPA) were also performed. We also performed the calculations with an all-electron basis set for Y atoms (in optimization an all-electron TZP basis set39 was substituted for the effective core potentials SDD basis set,31,32 and in single-point energy calculation the aug-TZP basis set39 was substituted for the SDD basis set) and compared these with SDD basis set calculations. The results revealed that the SDD Y–Si bond distances are averagely longer than those of the all-electron TZP basis set by 0.021 Å (see Fig. S1 in ESI†), and the mean absolute deviations of AEA and VDE between SDD and the all-electron TZP basis set are only 0.02 eV. Consequently, the results calculated with the SDD basis set for Y should be reliable and the discussions below are based on the SDD results. All of the calculations were implemented using the GAUSSIAN 09 package.40
Results and discussion
The most stable structures
The most stable structures of YSin0/− (n = 6–20) clusters are displayed in Fig. 1 and 2. The corresponding low-lying isomers, relative energies and point groups are displayed in Fig. S2 and S3 (in ESI†). The electronic state, HOMO–LUMO energy gap, average binding energies, and NPA charges on the Y atom for the most stable structure are summarized in Table 1. For anionic clusters, the calculated spin states of YSin− (n ≤ 20) are single with the exception of YSi− and YSi2− which are triplet. For neutral clusters, the predicted spin states are single excluding YSi, which is quartet.
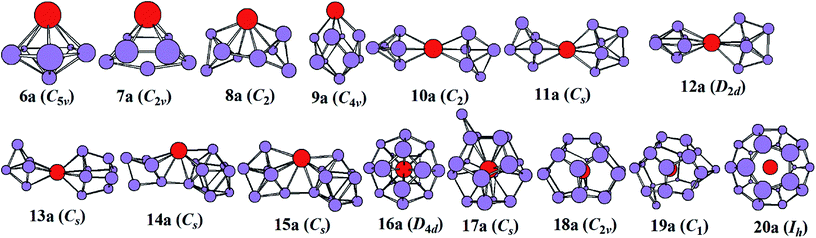 |
| | Fig. 1 The most stable structures of YSin− (n = 6–20) and their point groups. | |
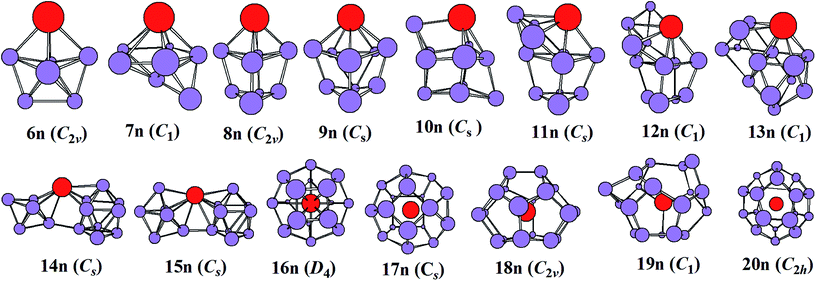 |
| | Fig. 2 The most stable structures of YSin (n = 6–20) and their point groups. | |
Table 1 Electronic state, average bonding energy Eb (eV), HOMO–LUMO energy gap Egap (eV), and the charge on the Y atom Q(Y) (a.u.) of the most stable structures of YSin0/− (n = 6–20) clusters
| n |
YSin− |
YSin |
| State |
Eb |
Egap |
Q(Y) |
State |
Eb |
Egap |
Q(Y) |
| 6 |
1A1 |
4.36 |
3.51 |
0.52 |
2A1 |
4.25 |
3.73 |
0.71 |
| 7 |
1A1 |
4.42 |
3.30 |
0.34 |
2A |
4.28 |
3.76 |
0.70 |
| 8 |
1A |
4.52 |
3.32 |
0.43 |
2A1 |
4.38 |
2.86 |
0.72 |
| 9 |
1A1 |
4.62 |
3.07 |
0.55 |
2A′ |
4.46 |
3.63 |
0.69 |
| 10 |
1A |
4.63 |
4.59 |
0.44 |
2A′ |
4.48 |
3.31 |
0.71 |
| 11 |
1A′ |
4.66 |
4.50 |
0.19 |
2A′ |
4.52 |
3.35 |
0.46 |
| 12 |
1A1 |
4.68 |
4.48 |
−0.13 |
2A |
4.54 |
3.43 |
0.28 |
| 13 |
1A′ |
4.69 |
4.44 |
0.03 |
2A |
4.57 |
3.31 |
0.62 |
| 14 |
1A′ |
4.73 |
3.73 |
0.21 |
2A′ |
4.60 |
4.19 |
0.42 |
| 15 |
1A′ |
4.73 |
3.47 |
−0.07 |
2A′ |
4.61 |
4.00 |
0.10 |
| 16 |
1A1 |
4.78 |
3.58 |
−3.38 |
2B2 |
4.63 |
3.50 |
−3.36 |
| 17 |
1A′ |
4.74 |
3.19 |
−3.33 |
2A′ |
4.61 |
2.84 |
−3.19 |
| 18 |
1A1 |
4.79 |
2.30 |
−2.82 |
2A1 |
4.68 |
2.61 |
−2.93 |
| 19 |
1A |
4.78 |
2.50 |
−2.93 |
2A |
4.67 |
2.73 |
−3.00 |
| 20 |
1Ag |
4.89 |
2.48 |
−2.57 |
2Au |
4.76 |
2.39 |
−2.88 |
The structural evolution of the anionic yttrium doped silicon clusters is from the linked to encapsulated configurations based on our results of ABCluster global search technique combined with the double-hybrid density functional scheme. The most stable structure is a pentagonal bipyramid for n = 6 and a bi-face-capped tetragonal bipyramid for n = 7. For n = 8–15, the most stable structure is linked configurations excluding YSi9− which is a bi-face-capped (one of them is a Y atom) tetragonal antiprism. The Y atom in YSi8− links two subclusters of Si4 tetrahedrons, that in YSi10− links two orthogonal subclusters of a Si5 trigonal bipyramid, that in YSi11− links a Si5 trigonal bipyramid and a Si6 capped trigonal bipyramid, that in YSi12− links two orthogonal subclusters of a Si6 capped trigonal bipyramid, that in YSi13− links a Si5 trigonal bipyramid and a Si8 distorted bicapped octahedron, that in YSi14− links a Si5 trigonal bipyramid and a tricapped trigonal prism (TTP) Si9 motif, and that in YSi15− links a Si6 capped trigonal bipyramid and a Si9 TTP subcluster. For n = 16–20, the most stable structure is the encapsulated configuration with the Y atom centering in the Si cage. The most stable structures of YSi16− and YSi20− are high-symmetry fullerene-like D4d and Ih, respectively, endohedrons. The most stable structure of YSi17− can be viewed as capping a Si atom to the ground state structure of YSi16−. The most stable structures of YSi18− and YSi19− can be regarded as removing one and two Si atoms from the ground state structure of YSi20−, respectively. These results are different from the previously reported linked structures.17 For anionic yttrium doped Si clusters, the most stable YSin− (n = 7, 10–14) structures reported in ref. 15 correspond to 7a3, 10a3, 11a5, 12a5, 13a2, and 14a3 in Fig. S2.† As shown in Fig. S2,† their energies are about 0.04–1.09 eV higher than those of the corresponding most stable structures in our work.
The structural evolution of the neutral YSin (n = 6–20) from substitutional structures to linked configurations and finally to an encapsulated fullerene-like motif occurs at n = 14 and 16, respectively. For n = 6–13, the most stable structures differ from those of the corresponding anions, and they belong to substitutional structures with the exception of YSi7, which is a face-capped pentagonal bipyramid and is only more stable in energy than the substitutional structure 7n2 (in Fig. S3 of ESI†) by 0.02 eV. The most stable structures of YSi6, YSi8, YSi9, YSi10, YSi11, YSi12, and YSi13 can be viewed as the most stable structures of the Si7 pentagonal bipyramid,41 Si9 distorted bicapped pentagonal bipyramid,40 Si10 tetracapped trigonal prism,41–43 Si11 pentacapped trigonal prism,43 Si12 hexacapped trigonal prism,44 Si13 (a distorted TTP with an additional rhombus capped on one edge of the prism) and Si14 (two stacked rhombi with distortion and one fivefold ring capped with an atom),44 respectively, with a Si atom replaced by a Y atom. For n = 14 and 15, the most stable configurations are analogous to those of their anions, in other words, linked structures. As for n = 16–20, their most stable structures are an encapsulated configuration with the Y atom located at the center of the Si cage. The ground state structures of YSi16 and YSi20 are slightly distorted and of reduced symmetries compared with those of the corresponding anions. The most stable configurations of YSi18 and YSi19 are similar to those of their anions, while the most stable structure of YSi17 is different from that of its anion. It is noted that the most stable structures of YSi13, YSi14 and YSi15 presented in this work differ from those reported previously.13 The most stable YSin (n = 13–15) structures reported in ref. 11 correspond to 13n5, 14n3 and 15n2 in Fig. S3† of our work. As shown in Fig. S3,† their energies are about 0.32–0.89 eV higher than those of the corresponding most stable structures in our work.
Photoelectron spectroscopy (PES) of anionic clusters
It is necessary to verify the validity of the predicted most stable structures. It is known that PES is a significant technology to extract conformational fingerprints from the ground state structures, which can provide more information about the underlying electronic structures. Therefore, the validity of the predicted most stable structures can be tested by means of comparing their theoretical and experimental PES spectra. We used two criteria in comparing the theoretical results with the experimental data: (i) AEA and first VDE and (ii) the number of different peaks and their relative position in the low-binding-energy portion of the PES spectra. The simulated PES spectra of the lowest-energy structures coupled with the experimental PES spectra are pictured in Fig. 3. The calculated first VDE are summarized in Table 2 along with experimental data. It can be seen from the simulated PES of YSi6− that there are three major peaks (X, A, and B) located at 3.18, 4.44, and 5.41 eV, which are in excellent agreement with the three peaks of 3.25, 4.50, and 5.40 eV observed in the experimental research.2 The simulated PES of YSi7− also has three peaks (X, A, and B) located at 2.86, 4.52, and 5.66 eV, which match the experimental data of 3.10, 4.40 and 5.70 eV.2 For YSi8−, four discrete peaks (X, A–C) centered at 2.98, 3.56, 4.41, and 5.31 eV are obtained and they agree with the experimental values of 3.25, 3.70, 4.40, and 5.30 eV,2 especially for the latter three peaks. For YSi9−, two peaks (X and A) of 3.23 and 4.38 eV are in concord with experimental data of 3.40 and 4.40 eV.2 For YSi10−, there are three distinct peaks (X, A, and B) centered at 4.10, 5.05 and 5.30 eV, which reproduce well the experimental values of 4.20, 4.90 and 5.20 eV.2 Unfortunately, the simulated and experimental PES spectra2 of YSi11− have large differences. There are three peaks (X, A, and B) located at the simulated PES, while only two peaks are observed in the experimental PES. The first peak (X) located at 3.81 eV does not match the experimental value of 4.20 eV. For YSi12−, the first three distinct peaks (X, A, and B) centered at 3.57, 4.42 and 5.14 eV are close to the experimental data of 3.70, 4.60 and 5.40 eV.2 The simulated PES of YSi13− yields two major peaks (X and A) at 4.33 and 5.23 eV, in excellent agreement with the experimental data of 4.30 and 5.10 eV.2 The first two peaks (X and A) located at 3.65 and 4.17 eV for YSi14− are very close to the experimental data of 3.75 and 4.20 eV.2 For n = 15–18 and 20, their first three peaks (X, A, and B) located, respectively, at 3.46, 4.08 and 4.88 eV, 4.00, 5.01 and 5.45 eV, 4.04, 5.10 and 5.83 eV, 3.92, 4.75 and 5.24 eV, and 4.28, 5.29 and 5.98 eV reproduce well those of experiments.2 The three peaks (X, A and B located at 4.40, 5.00 and 5.40 eV) of the experimental spectra of YSi19− are almost simulated by the calculations with a shift of the first three peaks (X, A and B centered at 3.60, 4.26 and 4.72 eV) to a higher binding energy. In addition to YSi11− and YSi19−, quantitative analyses revealed that the mean absolute error of the calculated first VDEs of YSin− (n = 6–10, 12–18, 20) from the experimental data are 0.15 eV. Good agreement between the theoretical and experimental PES spectra sheds further light on the validity of the predicted global minimum structures. Based on our reliable theoretical predictions, we suggest that the experimental PES of the YSi11− cluster should be checked further.
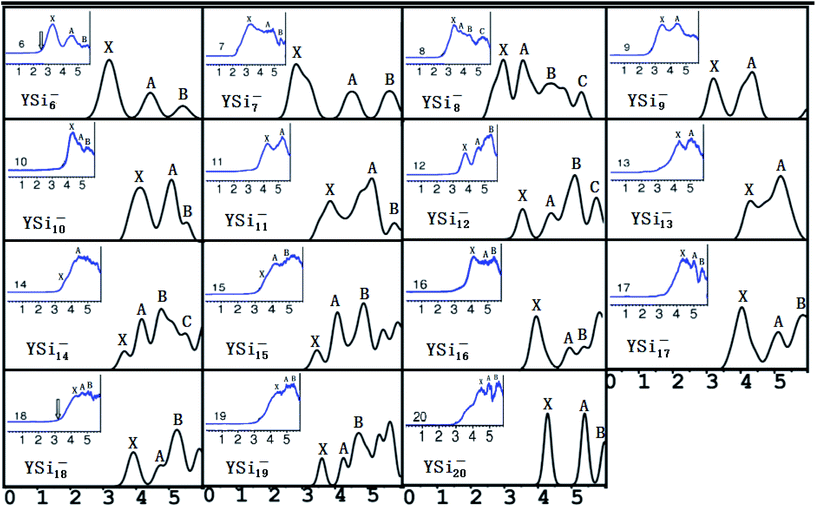 |
| | Fig. 3 Simulated PES spectra of the ground state YSin− (n = 6–20) species. The insets show experimental PES spectra.2 | |
Table 2 The theoretical and experimental adiabatic electron affinity (AEA) and first vertical detachment energy (VDE) for YSin− (n = 6–20)
| n |
VDE |
AEA |
| Theor. |
Exp. |
ΔVDEb |
Theor. |
Exp. |
ΔAEAb |
| Ref. 2. Δ = theor. − exp. |
| 6 |
3.18 |
3.25 ± 0.1a |
0.07 |
2.16 |
2.50 ± 0.004a |
0.34 |
| 7 |
2.86 |
3.10 ± 0.1a |
0.24 |
2.41 |
2.20 ± 0.004a |
−0.21 |
| 8 |
2.98 |
3.25 ± 0.1a |
0.27 |
2.63 |
2.60 ± 0.004a |
−0.03 |
| 9 |
3.23 |
3.40 ± 0.1a |
0.17 |
2.95 |
2.70 ± 0.004a |
−0.25 |
| 10 |
4.10 |
4.20 ± 0.1a |
0.10 |
3.00 |
3.60 ± 0.004a |
0.60 |
| 11 |
3.81 |
4.20 ± 0.1a |
0.39 |
3.09 |
3.30 ± 0.004a |
0.21 |
| 12 |
3.57 |
3.70 ± 0.1a |
0.13 |
3.27 |
3.20 ± 0.004a |
−0.07 |
| 13 |
4.33 |
4.30 ± 0.1a |
−0.03 |
3.06 |
3.00 ± 0.004a |
−0.06 |
| 14 |
3.65 |
3.75 ± 0.1a |
0.10 |
3.31 |
3.10 ± 0.004a |
−0.21 |
| 15 |
3.46 |
3.60 ± 0.1a |
0.14 |
3.30 |
3.10 ± 0.004a |
−0.20 |
| 16 |
4.00 |
4.10 ± 0.1a |
0.10 |
3.50 |
3.20 ± 0.004a |
−0.30 |
| 17 |
4.04 |
4.20 ± 0.1a |
0.16 |
3.27 |
3.20 ± 0.10a |
−0.07 |
| 18 |
3.92 |
4.20 ± 0.1a |
0.28 |
3.08 |
3.10 ± 0.004a |
0.02 |
| 19 |
3.60 |
4.40 ± 0.1a |
0.80 |
3.05 |
3.20 ± 0.004a |
0.15 |
| 20 |
4.28 |
4.40 ± 0.1a |
0.12 |
3.83 |
3.00 ± 0.004a |
−0.83 |
AEA is defined as the energy difference in the manner:19
| | |
AEA = Eneutral − Eanion + ΔEsc
| (1) |
where
Eneutral and
Eanion are the most stable energy of the neutral and anionic species, respectively, and Δ
Esc is the structural correction factor related to the charge of rare-earth atom in the anion clusters. As an empirical correction, the values of Δ
Esc are assigned to be 0.00, −0.20 and −0.40 eV for no-cage, half-cage, and cage structures, respectively. As seen in
Table 1, the NPA charges on the Y atom are positive or slightly negative when
n = 6–15, while they are negatively charged when
n = 16–20. Therefore, the YSi
n−/0 clusters (
n = 6–15) are no-cage structures, while the YSi
n−/0 clusters (
n = 16–20) are cage structures. This empirical correction, Δ
Esc, has been successfully used in the ScSi
n−/0 clusters in
ref. 19. Since the radius of the Y atom is larger than that of the Sc atom,
19 the Y-doped silicon clusters do not appear as the half-cage like the Sc-doped silicon clusters. Therefore, the Δ
Esc for YSi
n− with
n = 6–15 is 0.00 eV, and −0.40 eV for
n = 16–20. The theoretical and experimental AEA are listed in
Table 2. It can be seen from
Table 2 that the theoretical AEAs of YSi
n (
n = 7–9, 11–15, 17–19) are in good concord with the experimental data. The mean absolute errors are by 0.15 eV. The deviation of the theoretical and experimental AEA for
n = 6, 10, 16 and 20 may be attributed to their PES with a long round tail without obvious features, which makes it difficult to determine the precise experimental AEA. Taking YSi
16− as an example, the spectral diagram of the redistributed AEA is given in Fig. S4 (ESI
†), where the black arrow corresponds to the original assigned AEA,
2 and the red dashed line corresponds to the newly allocated AEA. It is obvious that the dot corresponding to the red dashed line as the threshold is more reasonable than the dot corresponding to the black arrow as the threshold. That is, the experimental AEA value may be 3.50 ± 0.10 eV, but not 2.97 ± 0.15 eV (
ref. 3) or 3.20 ± 0.004 eV.
2 The good agreement between the calculated and experimental AEAs supports the validity of the predicted most stable structure for neutral YSi
n. Among all of these AEAs, the theoretical AEA of YSi
20− is the maximum (3.83 eV), which indicates that the YSi
20− cluster has a high stability.
Relative stability
Two important parameters related to thermodynamic and relative stability, atomization energy (AE) and second energy difference (Δ2E), were examined for the determined global minimum structures of YSin0/− (n = 6–20) clusters. The AE is the energy required for the following reactions:| | |
YSin− → (n − 1)Si + Si− + Y
| (3) |
Δ2E refers to the following reactions:
| | |
2YSin → YSin+1 + YSin−1
| (4) |
| | |
2YSin− → YSin+1− + YSin−1−
| (5) |
The predicted AE and Δ2E are sketched in parts (a) and (b) of Fig. 4, respectively. From Fig. 4a we can conclude that (i) the AE data of the anionic clusters are all larger than those of corresponding neutral clusters in respect that the YSin species are open-shell electronic configurations, while the YSin− clusters are closed-shell electronic configurations which minimize the electronic repulsions in light of the Pauli exclusion principle. The larger the values of AE, the higher the relative stabilities; (ii) Starting from n = 12 for anionic clusters and n = 14 for neutral clusters, the cluster size distributions exhibit even–odd alternations. An even number of Si atoms is are more stable than those with an odd number. And the even–odd alternations are more and more obvious from the linked motif to the encapsulated configuration. This conclusion is clearly reproduced in Fig. 4b because the Δ2E is a susceptive survey for relative stability. The HOMO–LUMO energy gap is a significant physical parameter can be regarded as an indicator of chemical reactivity. The larger the HOMO–LUMO energy gap, the weaker the chemical reactivity. Fig. 4c pictures the HOMO–LUMO energy gaps of YSin0/− (n = 6–20) clusters. From Fig. 4c the odd–even oscillation behavior is not observed for the clusters. For YSin−, the HOMO–LUMO energy gaps of n = 10–13 are relatively large and range from 4.44 to 4.59 eV, which broaden the HOMO–LUMO energy gaps of the corresponding anionic Sin− clusters (for the values for Sin− see ref. 17). The rest of the Y-doped anionic Sin− clusters narrow the HOMO–LUMO energy gap. For n = 18–20, their HOMO–LUMO energy gaps are relatively small and range from 2.30 to 2.50 eV, which indicates that they have good chemical activity and are beneficial to the preparation of novel functional materials, such as optical and optoelectronic photosensitive materials or catalytic materials, especially so for YSi20−, which possesses a good thermodynamic stability, as discussed above. For neutral YSin, Y-doped Sin clusters narrow the HOMO–LUMO energy gap. The HOMO–LUMO energy gaps for n = 14 and 15 are relatively large, and relatively small for n = 8, 17–20. The HOMO–LUMO energy gap of neutral YSi20 is very close to that of the corresponding anion, showing that an extra electron does not change the chemical reactivity, but improves the thermodynamic stability.
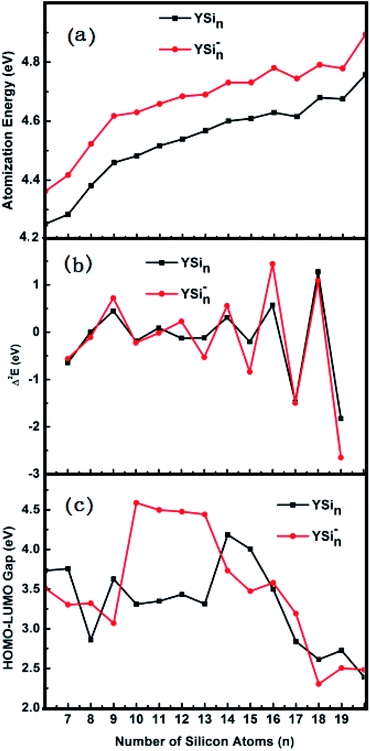 |
| | Fig. 4 Size dependences of (a) atomization energy (AE), (b) second energy difference (Δ2E), and (c) HOMO–LUMO energy gap for the most stable YSin− (n = 6–20) clusters. | |
Chemical bonding analysis
To gain an in-depth understanding of the ideal thermodynamic stability and chemical reactivity of anionic YSi20−, the molecular orbitals (MOs), as plotted in Fig. 5, are firstly analyzed. Based on the spherical jellium model and the MO energies, the electronic shells for superatom YSi20− with the magic number of 84 valence electrons are best described as 1S21P61D101F141G82S21G102P62D103S22F14, in which the 1S jellium model shell features σ bonds between the s-orbitals of the peripheral Si atoms and the centric Y atom. The 2S and 3S features π and π + δ bonds between the p-orbitals of the peripheral Si atoms and the d-orbital of the nuclear Y atom, respectively. Both 1P and 2P jellium model shells are threefold degenerate, and are characterized with π orbitals primarily originating from Si 3p and Y 4d. Both 1D and 2D jellium model shells are fivefold degenerate, and are σ + π bonds formed mainly by s- and p-orbitals of the peripheral Si atoms. The 1F, 1G, and 2F, excluding HOMO−3, HOMO−4, HOMO−5 and HOMO−6, are also σ + π bonds formed primarily by s- and p-orbitals of the Si atoms. The occupied MOs HOMO−3, HOMO−4, HOMO−5 and HOMO−6 are fourfold degenerate, and characterized with π + δ bonds mainly derived from 3p orbitals of the peripheral Si atoms and 4d orbitals of the centric Y atom. Through the above analyses, we can find that (i) the high occupied orbitals degeneracy may be attributed to the high symmetry Ih of the YSi20− clusters; and (ii) the 4d orbitals of the Y atom have significant contributions to the occupied MOs and reinforce the interactions between the outer fullerene Si20 cage and the nuclear Y atom. Secondly, the AdNDP method36 is was employed to perform a quantitative insight into the nature of the bonding between the Y atom and Si20 shell. As can be seen from Fig. 6, the chemical bonding of 84 valence electrons can be classified into two classes: 2c–2e and 6c–2e. The Si20 cages are characterized by thirty 2c–2e localized σ Si–Si bonds with 1.86–1.93 |e| in each bond. The twelve delocalized 6c–2e bonds with 1.95–1.96 |e| in each bond are responsible for the conjugation between the central Y atom and the outer fullerene-shell of Si20 and stabilize the encapsulated YSi20− species.
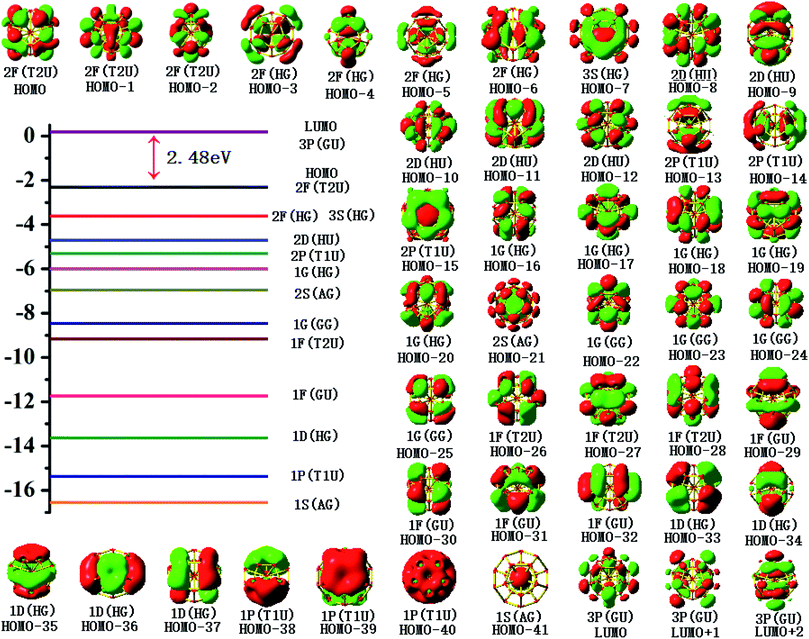 |
| | Fig. 5 Molecular orbital maps of the HOMOs and LUMOs of the YSi20− cluster. | |
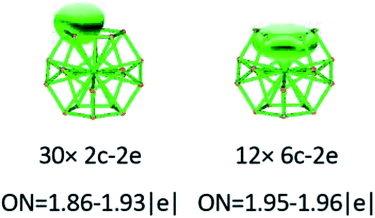 |
| | Fig. 6 AdNDP analysis of the YSi20− cluster. ON stands for the occupation number. | |
Conclusions
We have achieved a global search for the low energy of neutral and anionic Y-doped Si clusters YSin0/− (n = 6–20) by means of the ABCluster structure searching method combined with the mPW2PLYP double-hybrid density functional. Based on the calculated energies and the measured photoelectron spectroscopy data, the true minima of the most stable structures are confirmed. The results showed that the structural growth patterns of YSin− (n = 6–20) are from a Y-linked two subcluster to a Y encapsulated in Si cages, while for the neutral clusters, from a substitutional structure to a linked one, and in the end to the encapsulated structure with the number of Si atoms increasing from 6 to 20. The theoretical adiabatic electron affinity and vertical detachment energy is in good agreement with the experimental values. Analyses of chemical bonding, chemical reactivity, and relative stability indicate that the YSi20− has an ideal thermodynamic stability and chemical reactivity in a high-symmetry endohedral Ih structure, which may make it the most suitable building block for novel optical, optoelectronic photosensitive or catalytic nanomaterials.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 21863007, 21263010), by the Program for Innovative Research Team in Universities of Inner Mongolia Autonomous Region (Grant No. NMGIRT-A1603), and by the Natural Science Foundation of Inner Mongolia (Grant No. 2016MS0307).
References
- A. Grubisic, Y. J. Ko, H. P. Wang and K. H. Bowen, J. Am. Chem. Soc., 2009, 131, 10783–10790 CrossRef CAS PubMed.
- K. Koyasu, J. Atobe, S. Furuse and A. Nakajima, J. Chem. Phys., 2008, 129, 214301 CrossRef PubMed.
- K. Koyasu, J. Atobe, M. Akutsu, M. Mitsui and A. Nakajima, J. Phys. Chem. A, 2007, 111, 42–49 CrossRef CAS PubMed.
- A. J. Kenyon, Semicond. Sci. Technol., 2005, 20, R65–R84 CrossRef CAS.
- G. H. Cocoletzi, M. T. R. D. L. Cruz and N. Takeuchi, Surf. Sci., 2008, 602, 644–649 CrossRef CAS.
- S. Sanna, C. Dues, W. G. Schmidt, F. Timmer, J. Wollschlager, M. Franz, S. Applfeller and M. Dahne, Phys. Rev. B, 2016, 93, 195407 CrossRef.
- X. X. Xia, A. Hermann, X. Y. Kuang, Y. Y. Jin, C. Lu and X. D. Xing, J. Phys. Chem. C, 2016, 120, 677–684 CrossRef CAS.
- W. G. Sun, J. J. Wang, C. Lu, X. X. Xia, X. Y. Kuang and A. Hermann, Inorg. Chem., 2017, 56, 1241–1248 CrossRef CAS PubMed.
- W. G. Sun, X. X. Xia, C. Lu, X. Y. Kuang and A. Hermann, Phys. Chem. Chem. Phys., 2018, 20, 23740–23746 RSC.
- H. Tsunoyama, M. Shibuta, M. Nakaya, T. Eguchi and A. Nakajima, Acc. Chem. Res., 2018, 51, 1735–1745 CrossRef CAS PubMed.
- C. Y. Xiao, J. Blundell, F. Hagelberg and W. A. Lester, Int. J. Quantum Chem., 2004, 96, 416–425 CrossRef CAS.
- Z. J. Wu and Z. M. Su, J. Chem. Phys., 2006, 124, 184306 CrossRef CAS PubMed.
- A. P. Yang, Z. Y. Ren, P. Guo and G. H. Wang, J. Mol. Struct., 2008, 856, 88–95 CrossRef CAS.
- J. Li, L. Zhang, Z. H. Gao, S. Zhang, C. Lu and G. Q. Li, Struct. Chem., 2016, 27, 983–992 CrossRef CAS.
- L. J. Guo, X. H. Zheng, Z. Zeng and C. Zhang, Chem. Phys. Lett., 2012, 550, 134–137 CrossRef CAS.
- V. Kumar, A. K. Singh and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 125411 CrossRef.
- S. Jaiswal, V. P. Babar and V. Kumar, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085412 CrossRef.
- G. Maroulis, Int. J. Quantum Chem., 2012, 112, 2231–2241 CrossRef CAS.
- Y. M. Liu, J. C. Yang and L. Cheng, Inorg. Chem., 2018, 57, 12934–12940 CrossRef CAS PubMed.
- J. C. Yang, Y. T. Feng, X. H. Xie, H. W. Wu and Y. M. Liu, Theor. Chem. Acc., 2016, 135, 204 Search PubMed.
- S. He and J. C. Yang, Theor. Chem. Acc., 2017, 136, 93 Search PubMed.
- L. Y. Hou, J. C. Yang and Y. M. Liu, J. Mol. Model., 2017, 23, 117 CrossRef PubMed.
- Y. T. Feng, J. C. Yang and Y. M. Liu, Theor. Chem. Acc., 2016, 135, 258 Search PubMed.
- H. M. Ning, Y. S. Gu, L. Cheng and J. C. Yang, Chin. J. Struct. Chem., 2018, 37, 854–870 Search PubMed.
- W. Y. Jiang, M. L. Laury, M. Powell and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 4102–4111 CrossRef CAS PubMed.
- B. L. Chen, W. G. Sun, X. Y. Kuang, C. Lu, X. X. Xia, H. X. Shi and G. Maroulis, Inorg. Chem., 2018, 57, 343–350 CrossRef PubMed.
- Y. Y. Jin, G. Maroulis, X. Y. Kuang, L. P. Ding, C. Lu, J. J. Wang, J. Lv, C. Z. Zhang and M. Ju, Phys. Chem. Chem. Phys., 2015, 17, 13590–13597 RSC.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1991, 78, 247–266 CrossRef CAS.
- D. E. Woon and T. H. D. Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 4398–4401 RSC.
- J. Akola, M. Manninen, H. Häkkinen, U. Landman, X. Li and L. S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R11297 CrossRef CAS.
- D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 10180–10189 CrossRef CAS.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- L. S. C. Martins, F. A. L. D. Souza, G. A. Ceolin, F. E. Jorge, R. C. D. Berrêdo and C. T. Campos, Comput. Theor. Chem., 2013, 1013, 62–69 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc, Wallingford CT, 2010 Search PubMed.
- J. C. Yang, W. G. Xu and W. S. Xiao, J. Mol. Struct., 2005, 719, 89–102 CrossRef CAS.
- I. Vasiliev, S. öğüt and J. R. Chelikowsky, Phys. Rev. Lett., 1997, 78, 4805 CrossRef CAS.
- S. Nigam, C. Majumder and S. K. Kulshreshtha, J. Chem. Phys., 2006, 125, 074303 CrossRef PubMed.
- X. L. Zhu, X. C. Zeng and Y. A. Lei, J. Chem. Phys., 2004, 120, 8985–8995 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09492f |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a






