Elevated effective dimension in tree-like nanomagnetic Cayley structures†
Michael
Saccone
 *ab,
Kevin
Hofhuis
*ab,
Kevin
Hofhuis
 cd,
David
Bracher
e,
Armin
Kleibert
cd,
David
Bracher
e,
Armin
Kleibert
 e,
Sebastiaan
van Dijken
e,
Sebastiaan
van Dijken
 b and
Alan
Farhan
b and
Alan
Farhan
 *bd
*bd
aPhysics Department, University of California, 1156 High Street, Santa Cruz, CA 95064, USA. E-mail: msaccone@ucsc.edu
bNanoSpin, Department of Applied Physics, Aalto University School of Science, P.O. Box 15100, FI-00076 Aalto, Finland. E-mail: alan.farhan@gmx.net
cLaboratory for Mesoscopic Systems, Department of Materials, ETH Zurich, 8093 Zurich, Switzerland
dLaboratory for Multiscale Materials Experiments, Paul Scherrer Institute, 5232 Villigen PSI, Switzerland
eSwiss Light Source, Paul Scherrer Institute, 5232 Villigen PSI, Switzerland
First published on 26th November 2019
Abstract
Using state-of-the-art electron-beam lithography, Ising-type nanomagnets may be defined onto nearly any two-dimensional pattern imaginable. The ability to directly observe magnetic configurations achieved in such artificial spin systems makes them a perfect playground for the realization of artificial spin glasses. However, no experimental realization of a finite-temperature artificial spin glass has been achieved so far. Here, we aim to get a significant step closer in achieving that goal by introducing an artificial spin system with random interactions and increased effective dimension: dipolar Cayley tree. Through synchrotron-based photoemission electron microscopy, we show that an improved balance of ferro- and antiferromagnetic ordering can be achieved in this type of system. This combined with an effective dimension as high as d = 2.72 suggests that future systems generated out of these building blocks can host finite temperature spin glass phases, allowing for real-time observation of glassy dynamics.
1 Introduction
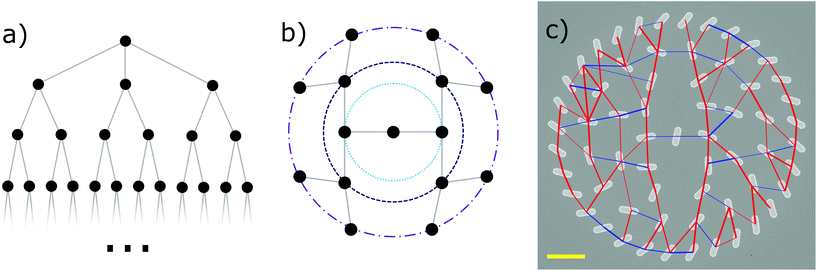
In magnetism, when interactions between magnetic moments are in conflict with each other, frustration arises. Systems incorporating such frustrated interactions are characterized by extensive degeneracies, exotic emergent phenomena, and non-trivial ground states.1–4 Spin glasses have been one of the most prominent examples of frustrated magnetism. They usually consist of a jumble of competing ferro- and antiferromagnetic order, leading interactions to compete with one another.5,6 Unlike other frustrated systems, the interaction between their spins are highly disordered. When competing interactions are sufficiently random, the system does not easily transition by single spin flips. Often a transition to a lower energy state requires a reconfiguration of a large portion of the system. This makes many states become metastable and the true ground state elusive. These complex energy landscapes and the associated behaviors, magnetic susceptibility cusps, difference in field cooled (FC) and zero field cooled (ZFC) magnetic moment, and non-uniform relaxation times, are all characteristic of spin glasses. The extensive degeneracy and nature of the ground state in spin glasses have been an area of extensive research over multiple decades, resulting in theoretical spin glass models that became, among other examples, the basis of error-correcting codes,7 problems of optimization,8 and brain science paradigms.9,10 Inspired by recent research on artificial frustrated systems,11–28 a first step towards the realization of artificial Ising spin glasses was made recently.29 There, Ising-type single-domain nanomagnets are lithographically arranged onto Gaussian random sites and orientations with a controlled degree of disorder, the feature commonly believed to be the main ingredient in spin glasses. However, these Gaussian patterns of Ising-type nanomagnets, while exhibiting partial short-range order, fell short in accessing a typical spin glass phase, in part because of unbalanced competing ferro- and anti-ferromagnetic ordering. This raises several open questions, regarding the prospect of realizing an artificial spin glass system. For example, can a different system design be implemented that would better optimize the balance of competing interactions in such disordered systems, so that spin glass degeneracy might arise? Also, can this goal be achieved by designing structures that would exhibit a higher effective dimension?30Here, we aim to address these questions by defining dipolar-coupled Ising-type nanomagnets onto Cayley trees, finite portions of Bethe lattices (see Fig. 1). These structures bear three main advantages: first, their tree-like pattern increases the effective dimension,30 which is linked to accessing spin glass behavior.31 Second, the balance of competing ferro- and antiferromagnetic interactions between the magnetic moments can be better tuned compared to structures with a simple Gaussian-type disorder.29 Third, considering the complexity of the quest to achieve an artificial spin glass, these finite-size structures offer a comfortable building block approach in addressing this purpose. Such a bottom-up approach has already been successfully applied to gain an understanding of ordering phenomena in the highly-frustrated artificial kagome spin ice.11,32 We begin with a methods section that describes our theoretical approach and how dipolar Cayley structures are designed, fabricated, and characterized using X-ray photoemission electron microscopy (X-PEEM). This is followed by a section where we describe the obtained results, starting from discussing moment configurations achieved after thermal annealing and the characterization of these ordering patterns in terms of spin correlations, effective dimension, and potential links to glassy behavior. We then conclude with a summary and outlook section where we assess the advantages of our Cayley tree structures as promising building blocks for the generation of the first artificial spin glass systems.
2 Methods
2.1 Theoretical concept and design of dipolar Cayley trees
Cayley trees are a finite subset of infinite Bethe lattices. A Bethe lattice (see Fig. 1a) is a tree-like graph with the helpful property that many models in statistical physics are exactly solvable on it.33 To construct a Bethe lattice with a coordination number k, the number of connections per node, is chosen. k nodes are connected to a central lattice site. From each of these nodes k − 1 new nodes are attached, then k − 1 additional nodes are attached from each of those. This continues ad infinitum in the case of a Bethe lattice and to a finite number of layers for a Cayley tree. Fig. 1a shows an example where k = 3. Multiple studies suggest a non-zero spin glass transition temperature could be obtained if spins would be mapped onto a Bethe lattice,34–36 which is easily implemented by the patterning of Ising-type nanomagnets. To observe glassy dynamics, the spin glass transition temperature needs to be higher than the so-called blocking temperature TB of the patterned nanomagnets, as spin freezing occurs below TB.11,16,19,29,32Our nanomagnet samples mimic the essence of the Cayley tree's structure to create higher dimensional interaction networks. However, they differ from Cayley trees in three major ways. First, the spins interact via dipolar coupling. This increases the significance of next nearest neighbor effects, enabling the interaction network to leap from one branch to another. The finite-size nature of the fabricated Cayley trees serves as an advantage, as the increasing network density would cause nanomagnets to overlap and interactions between next nearest neighbors to grow. Finally, the central spin is only given two neighbors to reduce the eventual crowding at the sample boundary. Implementing these compromises, we design modified Cayley trees for embedding in two dimensions (see Fig. 1b). The positions of the islands are uniformly spaced on concentric circles. The size of the circles is chosen to keep the distance of connected nodes constant (see grey lines in Fig. 1b). Here this sets the nearest neighbor distance to a = 500 nm. The orientation of the magnets is chosen to create random interactions while simultaneously supporting the Cayley structure. To do so, one nanomagnet per circle has its orientation selected randomly from a uniform distribution. The members of the same circle should not interact with one another, to maintain the tree-like structure. Thus, their orientations are chosen to place them perpendicular to the dipolar magnetic field of their direct neighbors within each circle. Circles are added until next-nearest neighbor interactions begin to break down the tree-like structure, allowing for five circles in our systems. In Fig. 1c we show a typical structure and the network of interactions created by its geometry.
The illustrated network was formed by first considering the dipolar coupling strength between islands i and j,
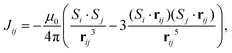 | (1) |
2.2 Sample fabrication and XMCD imaging
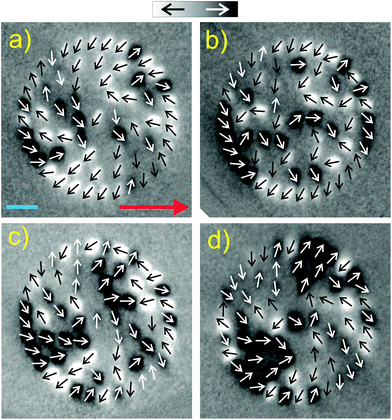
We used lift-off assisted electron-beam lithography to fabricate our samples (see Fig. 1). First, a 70 nm-thick layer of polymethylmethacrylate (PMMA) resist was spin-coated on top of a 1 × 1 cm2 silicon (100) substrate. Designed Cayley tree patterns are then exposed on the substrate using a VISTEC EBPG 5000PlusES system. A 2.6 nm permalloy (Ni80Fe20) thin film was then evaporated at a base pressure of 3.6 × 10−6 mbar, together with a 1.5 nm thick aluminum capping layer, to avoid fast oxidation of the structures. This is followed by a lift-off process in acetone, where all unwanted material is removed from top of the substrate. This results in Cayley structures consisting of nanomagnets with lengths L = 300 nm and widths W = 100 nm. The size of the nanomagnets is chosen to ensure a mono-domain state and their elongated shape is set, so that the magnetization within each nanomagnet can only point in one of two possible directions along the long axis of the nanomagnet. Therefore, each nanomagnet represents a macroscopic Ising spin. Similar to our previous work,4,16,19,29 the individual volume of the nanomagnets is chosen so that the blocking temperature TB = 140–180 K. With regard to XMCD imaging (see below), we define the blocking temperature as the temperature where magnetic moment re-orientations within the patterned nanomagnets start to occur at timescales equivalent to the time needed to record an XMCD image, which is about 7 seconds.Following sample fabrication, and after a waiting period of three days in high vacuum at room temperature (T = 298 K), the sample was transferred into a photoemission electron microscope (PEEM).37 There, the sample was cooled down to temperatures around 120 K, ensuring that magnetic moments stay frozen within the timescale of hours, and magnetic imaging was performed employing X-ray magnetic circular dichroism (XMCD) at the Fe L3 edge.38 The dark and bright contrast in a so-called XMCD image is a direct measure of the orientation of the magnetic moment of a nanomagnet relative to the X-ray polarization vector (see Fig. 2).
3 Results
3.1 Spin–spin correlations and ordering preferences
The relatively small size of these systems does not provide enough statistical relevance for a reliable extraction of typical or spin glass correlation lengths. However, since our concern is equalizing antiferro- and ferromagnetic ordering, we focus on local correlations. Using a similar approach as in our most recent work,29 we introduce a neighbor correlation function: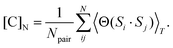 | (2) |
Θ(x) = −1 if x is less than zero and Θ(x) = 1 otherwise, the sum was either taken over nearest neighbor (NN, rij ≤ a), next-nearest neighbor (NNN, rij ≤ 2a), or next-next-nearest neighbor (NNNN, rij ≤ 3a) pairs, and Npair is the number of those pairs in a particular sum. This provides a consistent basis for measuring local correlations in these systems without translational invariance. A value below zero indicates predominantly antiferromagnetic coupling while one above zero indicates ferromagnetic coupling. These correlations are plotted for all systems of interest in Fig. 3a.
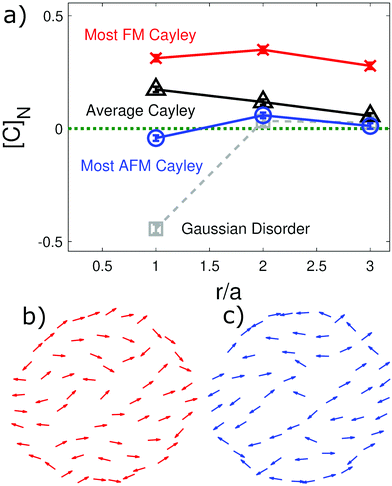 | ||
| Fig. 3 Neighbor correlations in randomized magnetic systems. In (a), the nearest-neighbor (r/a = 1), next-nearest-neighbor (r/a = 2), and next-next-nearest neighbor (r/a = 3) correlations are plotted for the most ferromagnetically ordered Cayley tree system (red crosses), the average of all 21 Cayley tree systems (black triangles), the most anti-ferromagnetically ordered Cayley tree system (blue circles) and the most disordered system from a previously investigated artificial spin system with Gaussian disorder29 (grey squares). The green dotted line at [C]N = 0 represents balanced antiferro- and ferromagnetic correlations. (b) Moment configurations of the Cayley structure with the highest degree of ferromagnetic-type ordering [red crosses and lines in (a)]. (c) Moment configurations of the Cayley structure with the strongest anti-ferromagnetic spin ordering [blue circles and lines in (a)]. | ||
A glance at these correlation measures reveals that nearest-neighbor correlations in the Cayley tree structures have a weaker antiferromagnetic tendency when compared to structures with Gaussian disorder29 (compare blue, black and red lines with the dotted grey line in Fig. 3a). There seems a tendency towards more ferromagnetic-type ordering in the Cayley tree structures, which can even be visually seen when looking at magnetic configurations shown in Fig. 2 through clusters of five to nine adjacent moments pointing in the same direction. Overall, the balance of ferro- and antiferromagnetic correlations is significantly improved in comparison to structures with Gaussian disorder,29 as indicated by nearest-neighbor correlations that are closer to zero (see Fig. 3a). As seen in Fig. 3b and c, this is manifested by a reduction of the ferromagnetic cluster size and regions of antiferromagnetic ordering. These results provide a first strong indication that such tree-like structures are better candidates in achieving artificial spin glasses. However, a finite non-zero spin glass transition temperature is still an obstacle that needs to be overcome.29,31 One strategy moving towards that goal relies on elevating the effective dimensions of such disordered structures, which is discussed in the following subsection.
3.2 Effective dimension
The dipolar Cayley trees discussed here, as any other artificial frustrated system, can be viewed as a network that consists of nodes (nanomagnets) and their connections (dipolar coupling between nanomagnets). While this network is embedded in two-dimensional space, inter-nanomagnet connections via dipolar coupling go beyond neighboring nanomagnets. As we will explain here, this can be used to elevate the effective dimension.30 The notion of an effective network dimension may be understood in terms of how “scale” and “mass” relate to one another in different dimensions. One could consider a hypothetical shape existing in an arbitrary dimension, d′. Its size may be changed by altering a length scale r′ (the side length of a cube or a golden rectangle, for example). How does mass, or some other quantity present in the space, encompassed by this shape relate to this scale? If the density is constant and the dimension is an integer, the answer is simple. m′(r′) = m′0r′d′ where m′(r′) is the mass, m′0 is the mass of the shape when r′ = 1, r′ is the scale of that shape, and d′ is the dimension. Because d′ is the exponent, we can tell that larger dimensions allow access to more “stuff” (mass, charge, magnetic moments etc.) with less scale. If the density is not constant or there are different ways of leaping from place to place, more or less stuff may be accessed than what is considered typical for dimension d′. In these more complex systems, d′ is replaced with d and is allowed to vary as a real number, taking on the name “effective dimension”.30 This definition allows the comparison of theoretical models on non-integer dimensions to real models with non-integer effective dimensions.30 In spin glass models, the spin glass transition temperature depends on the effective dimension and for a critical dimension of dc = 2.520 the spin glass transition temperature has been predicted to be finite.39 We will compare the effective dimension of our systems to this critical value to assess their viability as spin glasses.To calculate the effective dimension of our experimental spin systems, a spin i corresponding to a point rl=0 was chosen. l labels the degree of separation from this spin. All spins connected to spin i, those with coupling strength Jij exceeding 20% of the maximum strength, were accessed. The average distance between connected spins and the initial spin, rl=1, was calculated. This can be considered the “scale” of the network's “shape”. The total number of spins with this proximity, m(rl=1) (in analogy to the mass of a shape), were counted. This was repeated for further steps away from the center (l = 2 through 5, see the colored dots in Fig. 4a). The process was reiterated for all spins i less than 1.3 μm from the center of the lattice to avoid edge effects. The resulting data were fit to m(r) = m0rdvia linear regression to determine d, the effective dimension (see curves of best fit and text in Fig. 4a). Notably, a true Cayley tree's density of nodes would exponentially grow from the origin, thus making the effective dimension infinite. In our case, the effective dimensions of the finite-sized Cayley trees exceed that of previously studied systems with Gaussian disorder,29d = 2.17 (see Fig. 4a) and the critical dimension dc = 2.520. They exhibit an average effective dimension of 2.61 and a maximum d = 2.72 (see Fig. 4a). Fig. 4b and c shows that the Cayley tree interaction structures expand this effective dimension with their tree-like arrangement.
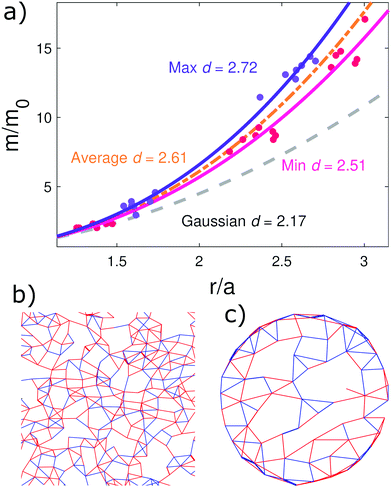 | ||
| Fig. 4 Effective dimension of randomized magnetic systems. (a) m(r) and its fits are plotted to demonstrate effective dimension d. To better compare between systems, each data point is divided by the m0 determined by its fit. The purple and pink circles represent data from the Cayley trees with the largest (d = 2.72) and smallest (d = 2.51) effective dimensions, respectively, while the curves of corresponding color are their fits. The dashed curve represents the average effective dimension of all 21 investigated Cayley tree structures (d = 2.61). The dashed grey line corresponds to the effective dimension (d = 2.17) of a system with mere Gaussian disorder.29 (b) and (c) Representative graphs of interactions for systems with Gaussian disorder and a typical Cayley tree, respectively. | ||
Although the elevated spin glass transition temperature is not observable directly, we simulated the fabricated systems with the Monte Carlo method to probe their low-temperature behavior. A comparison of their field cooled and zero field cooled magnetic moments indicated that these systems could transition to a spin glass phase below 12.8 K (see Fig. S1†). This is far below the freezing temperature of these nanomagnets but non-zero as anticipated. We conclude that a prospective extended structure built on an interaction concept similar to Fig. 4c could have the appropriate effective dimension and balance of competing interactions that would allow the realization of the first artificial Ising spin glass.
4 Conclusions
Despite the inherent difficulties in building tree-like interaction networks in two dimensions, our dipolar Cayley tree structures overcome previous limitations that hindered the achievement of artificial spin glass systems.29 However, not all randomly generated samples possess the same physics because of variations in the balancing of ferro- and antiferromagnetic interactions. The finite size of our samples produces fluctuations from average ordering (black triangles in Fig. 3a), allowing individual samples to exhibit more ideally balanced ordering ([C]N ≈ 0, see blue circles in Fig. 3a). This tunability is a substantial improvement over ordering in systems with Gaussian disorder29 (grey squares in Fig. 3a). Though less markedly variable, the effective dimension of the Cayley trees is also tunable, ranging from just below dc at d = 2.51 all the way to d = 2.72. Even though long range interactions break the perfect Cayley tree structure (see Fig. 4c), its dimension almost always remains high enough to allow a finite spin glass transition temperature. By contrast, the purely Gaussian-disordered system29 did not alter its interactions into a network with high enough effective dimension (Fig. 4b), so that a finite-temperature spin glass phase could be accessed.This work has taken two outstanding problems, unbalanced ordering and low effective dimension, and condensed them into one: making a larger Cayley tree system. This clear next step would allow for a raised spin glass transition temperature and novel, direct observation of spin glass dynamics via XMCD imaging. By simulating combinations of Cayley trees before they are fabricated, they may be vetted for balanced ordering and high effective dimension. Individual trees could then be combined as building blocks of a larger system, similar to how information is passed between logic gates in nanomagnetic computing.40 To further raise the transition temperature, interaction strength of the system could be augmented in comparison to the blocking temperature of the nanomagnets through stronger dipolar coupling. This future work would use model systems to bridge the gap between spin glass theory and experiment by exploring non-equilibrium thermodynamics of the spin glass phase.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank A. P. Young for fruitful discussions. This work was supported by the Swiss National Science Foundation (projects 174306 and 172774), the Swiss Nanoscience Institute (Grant No. P1502) and the Academy of Finland (project 316857). Part of the work was performed at the SIM beamline at the Swiss Light Source (SLS), Paul Scherrer Institute, 5232 Villigen, Switzerland.References
- M. J. Harris, S. T. Bramwell, D. F. McMorrow, T. Zeiske and K. W. Godfrey, Phys. Rev Lett., 1997, 79, 2554 CrossRef CAS.
- M. Fu, T. Imai, T.-H. Han and Y. S. Lee, Science, 2015, 350, 655 CrossRef CAS PubMed.
- C. Castelnovo, R. Moessner and S. L. Sondhi, Nature, 2008, 451, 42 CrossRef CAS PubMed.
- A. Farhan, M. Saccone, C. F. Petersen, S. Dhuey, R. V. Chopdekar, Y.-L. Huang, N. Kent, Z. Chen, M. J. Alava, T. Lippert, A. Scholl and S. van Dijken, Sci. Adv., 2019, 5, eaav6380 CrossRef CAS PubMed.
- K. Binder and A. P. Young, Rev. Mod. Phys., 1986, 58, 801 CrossRef CAS.
- J. A. Mydosh, Rep. Prog. Phys., 2015, 78, 052501 CrossRef CAS PubMed.
- N. Sourlas, Nature, 1989, 339, 693 CrossRef.
- S. Kirkpatrick, C. D. Gelatt Jr. and M. P. Vecchi, Science, 1983, 220, 671 CrossRef CAS PubMed.
- I. Recio and J. J. Torres, Neural Networks, 2016, 84, 91 CrossRef CAS PubMed.
- A. G. Hudetz, C. J. Humphries and J. R. Binder, Front. Syst. Neurosci., 2014, 8, 234 Search PubMed.
- A. Farhan, P. M. Derlet, A. Kleibert, A. Balan, R. V. Chopdekar, M. Wyss, L. Anghinolfi, F. Nolting and L. J. Heyderman, Nat. Phys., 2013, 9, 375 Search PubMed.
- J. M. Porro, A. Bedoya-Pinto, A. Berger and P. Vavassori, New J. Phys., 2013, 15, 055012 CrossRef.
- A. Farhan, P. M. Derlet, L. Anghinolfi, A. Kleibert and L. J. Heyderman, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 064409 CrossRef.
- I. Gilbert, G.-W. Chern, S. Zhang, L. O'Brien, B. Fore, C. Nisoli and P. Schiffer, Nat. Phys., 2014, 10, 670 Search PubMed.
- Y. Perrin, B. Canals and N. Rougemaille, Nature, 2016, 540, 410 CrossRef CAS PubMed.
- A. Farhan, A. Scholl, C. F. Petersen, L. Anghinolfi, C. Wuth, S. Dhuey, R. V. Chopdekar, P. Mellado, M. J. Alava and S. van Dijken, Nat. Commun., 2016, 7, 12635 CrossRef CAS PubMed.
- B. Canals, I.-A. Chioar, V.-D. Nguyen, M. Hehn, D. Lacour, F. Montaigne, A. Locatelli, T. O. Menteş, B. S. Burgos and N. Rougemaille, Nat. Commun., 2016, 7, 11446 CrossRef CAS PubMed.
- J. Drisko, T. Marsh and J. Cumings, Nat. Commun., 2017, 8, 14009 CrossRef CAS PubMed.
- A. Farhan, C. F. Petersen, S. Dhuey, L. Anghinolfi, Q.-H. Qin, M. Saccone, S. Velten, C. Wuth, S. Gliga, P. Mellado, M. J. Alava, A. Scholl and S. van Dijken, Nat. Commun., 2017, 8, 995 CrossRef PubMed.
- P. Andriushchenko, J. Magn. Magn. Mater., 2018, 476, 284 CrossRef.
- M. Saccone, K. Hofhuis, Y.-L. Huang, S. Dhuey, Z. Chen, A. Scholl, R. V. Chopdekar, S. van Dijken and A. Farhan, Phys. Rev. Mater., 2019, 3, 104402 CrossRef CAS.
- D. Shi, Z. Budrikis, A. Stein, S. A. Morley, P. D. Olmsted, G. Burnell and C. H. Marrows, Nat. Phys., 2018, 14, 309 Search PubMed.
- V. Brajuskovic, A. Addi, C. Phatak and A. K. Petford-Long, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 094424 CrossRef CAS.
- J. Sklenar, Y. Lao, A. Albrecht, J. D. Watts, C. Nisoli, G.-W. Chern and P. Schiffer, Nat. Phys., 2019, 15, 191 Search PubMed.
- R. Macêdo, G. M. Macauley, F. S. Nascimento and R. L. Stamps, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 014437 CrossRef.
- D. Y. Lee and P. Tierno, Phys. Rev. Mater., 2018, 2, 112601(R) CrossRef.
- R. A. Stancioli and L. A. S. Mól, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 024432 CrossRef CAS.
- C. F. Petersen, A. Farhan, S. Dhuey, Z. Chen, M. J. Alava, A. Scholl and S. van Dijken, Appl. Phys. Lett., 2018, 112, 092403 CrossRef.
- M. Saccone, A. Scholl, S. Velten, S. Dhuey, K. Hofhuis, C. Wuth, Y.-L. Huang, Z. Chen, R. V. Chopdekar and A. Farhan, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 224403 CrossRef CAS.
- L. Daqing, K. Kosmidis, A. Bunde and S. Havlin, Nat. Phys., 2011, 7, 481 Search PubMed.
- A. K. Hartmann and A. P. Young, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 180404(R) CrossRef.
- A. Farhan, A. Kleibert, P. M. Derlet, L. Anghinolfi, A. Balan, R. V. Chopdekar, M. Wyss, S. Gliga, F. Nolting and L. J. Heyderman, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214405 CrossRef.
- M. Ostilli, Phys. Rev. A, 2012, 391, 3417 Search PubMed.
- D. J. Thouless, Phys. Rev. Lett., 1986, 56, 1082 CrossRef PubMed.
- J. M. Carlson, J. T. Chayes, L. Chaves, J. P. Senthna and D. J. Thouless, Europhys. Lett., 1988, 5, 355 CrossRef.
- M. Mézard and G. Parisi, Eur. Phys. J. B, 2001, 20, 217 CrossRef.
- L. Le Guyader, A. Kleibert, A. Fraile Rodríguez, S. El Moussaoui, A. Balan, M. Buzzi, J. Raabe and F. Nolting, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 371 CrossRef CAS.
- J. Stöhr, Y. Wu, B. D. Hermsmeier, M. G. Samant, G. R. Harp, S. Koranda, D. Dunham and B. P. Tonner, Science, 1993, 259, 658 CrossRef.
- M. Demirtaş, A. Tuncer and A. N. Berker, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022136 CrossRef PubMed.
- H. Arava, N. Leo, D. Schildknecht, J. Cui, J. Vijayakumar, P. M. Derlet, A. Kleibert and L. J. Heyderman, Phys. Rev. Appl., 2019, 11, 054086 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR07510K |
| This journal is © The Royal Society of Chemistry 2020 |