Germagraphene as a promising anode material for lithium-ion batteries predicted from first-principles calculations†
Junping
Hu
 ab,
Chuying
Ouyang
ab,
Chuying
Ouyang
 c,
Shengyuan A.
Yang
c,
Shengyuan A.
Yang
 *ad and
Hui Ying
Yang
*ad and
Hui Ying
Yang
 *a
*a
aResearch Laboratory for Quantum Materials, Singapore University of Technology and Design, Singapore 487372, Singapore. E-mail: shengyuan_yang@sutd.edu.sg; yanghuiying@sutd.edu.sg
bSchool of Science, Nanchang Institute of Technology, Nanchang 330099, China
cDepartment of Physics, Laboratory of Computational Materials Physics, Jiangxi Normal University, Nanchang 330022, China
dCenter for Quantum Transport and Thermal Energy Science, School of Physics and Technology, Nanjing Normal University, Nanjing 210023, China
First published on 28th November 2018
Abstract
Finding electrode materials with high capacity is a key challenge for developing lithium-ion batteries (LIBs). Graphene was once expected to be a promising candidate, but it turns out to be too inert to interact with Li. Here, by using first-principles calculations, we predict that germanium doped graphene, termed as Germagraphene, which has been achieved in a recent experiment, is a promising LIB anode material. We find that at the optimal Ge concentration, which corresponds to the chemical formula C17Ge, the specific capacity for Germagraphene can be as high as 1734 mA h g−1, over four times larger than that of graphite. We show that the material has good electrical conduction before and after Li adsorption. We also investigate the diffusion process of Li on Germagraphene, and find that the diffusion barrier is low (∼0.151 eV), implying fast Li diffusion. The calculated average intercalation potential is very low (∼0.03 V), which is beneficial for increasing the working voltage for full-cells. In addition, during the process of Li intercalation, the lattice change for the material is quite small (∼0.48%), implying a good cycling performance. These results suggest that Germagraphene could be a promising high-capacity anode material for LIBs.
Conceptual insightsGraphene is the most prominent 2D material, but unfortunately it cannot be used as an electrode material for lithium-ion batteries (LIBs), because its interaction with Li is too weak. In this work, we discover that implantation of Ge into graphene, which has been realized in a recent experiment [ACS Nano, 2018, 12, 4641, ref. 17] via a low-energy ion implantation technique, can make an almost ideal LIB electrode material. The resulting material, termed as Germagraphene, can reach an extremely high capacity of ∼1734 mA h g−1, larger than most 2D materials studied so far. It also enjoys the advantages of a low diffusion barrier (∼0.151 eV), a very low intercalation potential (∼0.03 V), and a very small lattice change (∼0.48%) during Li intercalation. This idea has not been proposed before. Our work not only reveals a promising new material for enhancing the LIB performance, but also offers an insight that same-group substitutional doping (achievable using a low-energy ion implantation technique) could be a general strategy for engineering 2D materials for energy storage applications. |
1. Introduction
From smart phones to laptops and to electric vehicles, lithium-ion batteries (LIBs) are powering a wide range of electronics. However, as consumer technology becomes more powerful, LIB technology has always been struggling to keep pace. Researchers have made a significant effort to achieve cost-effective, long-cycle-life, and especially high-capacity energy storage systems. For example, a new strategy is to use a sulfur positive electrode and a lithium-metal negative electrode to increase the capacity.1,2 At the same time, with the rapid development of two-dimensional (2D) materials, there is increasing interest in exploring 2D materials as possible electrode materials,3–10 owing to their unique 2D structures, possibly high electrical conductivity, and most importantly, large specific surface area. It has been demonstrated that 2D materials typically can store large amounts of Li or other metal ions, to achieve very high storage capacities. In addition, 2D materials may also enjoy the advantages of rapid ion migration and a relatively small volume change during ion intercalation and de-intercalation processes. These two factors are critical for the rate performance and for maintaining the structural integrity.Among the many 2D materials studied to date, graphene is undoubtedly the most prominent one. It has high mobility, excellent flexibility, and good structural and electrochemical stability, which is comparable to or better than the commercial anode materials, but a severe disadvantage of graphene is that it is too inert to interact with Li, so the storage capacity is low. In order to enhance the interaction between graphene and Li, researchers have applied various modification methods on graphene, such as introducing defects or functional groups,11–15 which has indeed improved the Li storage capacity to some extent; however, the conductivity, the ion diffusion rate, the first cycle Coulomb efficiency, and the structural stability during cycling are often degraded in the meantime. These shortcomings severely limit the wide application of graphene-based nanomaterials for LIBs. Another approach is via same-group doping, i.e., to replace a percentage of carbon atoms in graphene by elements from the same group. In a recent work, Wang et al. proposed a new 2D material called Siligraphene which can be viewed as graphene with Si doping. They found that the interaction between Li ions and the host is greatly enhanced, resulting in a very high Li storage capacity (a theoretical value of up to ∼1520 mA h g−1).16 The proposed material not only avoids the volume expansion problem for bulk silicon, but is also free from the stability issue with silicene under ambient conditions.
Most Recently, Tripathi et al. reported that they succeeded in doping Ge into graphene by using the low-energy ion implantation technique,17 and the doping concentration can be controlled in experiments. We note that similar to bulk silicon, germanium in the bulk form has also been tested as an electrode material, and high storage capacity has been demonstrated; however, the large volume expansion and the issue of oxidation in air limit its applications.18 Inspired by Siligraphene, one naturally wonders: will the Ge implanted graphene, which may be termed as Germagraphene, be a promising 2D electrode material?
Motivated by the experimental breakthrough mentioned above, in this communication, we investigate the performance of Germagraphene as an electrode material for LIBs via first-principles calculations. We find that Germagraphene can achieve a high Li storage capacity, with a maximum value of about 1734 mA h g−1 for the optimal doping concentration (corresponding to a chemical formula of C17Ge). The material remains conductive before and after Li adsorption, and it has a low Li diffusion barrier of ∼0.151 eV, which is desired for a good electrode material. The calculated average intercalation potential is very low (∼0.03 V), which would be beneficial for expanding the working voltage window for full-cells. In addition, during the process of Li intercalation, the lattice change of C17Ge is quite small (∼0.48%), indicating that the material should have good cycling performance. Thus, our work reveals the great potential of Germagraphene as an electrode material, and it also offers a new insight in engineering 2D materials for energy storage applications.
2. Computational details
Our first-principles calculations are based on density functional theory (DFT) using the plane-wave pseudopotentials19,20 as implemented in the Vienna ab initio Simulation Package (VASP).21,22 The exchange–correlation effect is modelled in the local density approximation (LDA) with the Ceperly–Alder functional23 parameterized by Perdew and Zunger.24 Carbon 2s22p2 and Germanium 4s24p2 electrons are treated as valence electrons in all the calculations. A cutoff energy of 500 eV is employed for the plane wave expansion. The Brillouin zone is sampled with a 5 × 5 × 1 Monkhorst–Pack k-point mesh25 for the structural optimization, and with a 7 × 7 × 1 mesh for the electronic structure calculations. The convergence criteria for the total energy and ionic forces are set to be 10−5 eV and 10−3 eV Å−1, respectively. Phonon spectra calculations are performed using the phonopy package.26 In our calculations, periodic images of the monolayer along the plane's normal direction are separated by a vacuum layer greater than 18.0 Å, so that the interaction between the images is negligible.It should be mentioned that we adopt the LDA functional instead of the GGA functional, because LDA usually gives a better description for 2D carbon materials due to an internal double error elimination.27,28 It has been reported that the LDA Ceperly–Alder functional gave more reasonable results for the interaction between Li and 2D carbon materials than GGA functionals.16,29
The adsorption energy (Ead) for Li atoms on the Germagraphene monolayer is defined as:
| Ead = (ECxGeyLiz − ECxGey − zELi)/z | (1) |
The difference in total energies before and after Li intercalation is used to determine the average intercalation potential. The volume and entropy effects are usually negligible during the reaction, hence they are omitted. Then the average intercalation potential for a reaction involving zLi+ ions can be approximately calculated from the energy difference:
| Vave = −(ECxGeyLiz − ECxGey − zELi)/ze | (2) |
3. Results and discussion
3.1 Ge concentration and Li storage capacity
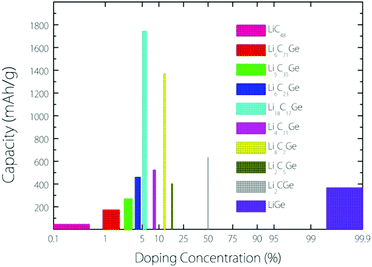
From the experimental observation, it has been found that an implanted Ge atom could directly substitute a C atom in graphene, bonding to three carbon neighbours and forming a buckled out-of-plane structure, which is also predicted by DFT calculations.17 Based on this kind of buckled out-of-plane configuration, we estimate the Li storage capacity under different Ge doping concentrations for a Germagraphene monolayer. Our results are shown in Fig. 1. Here, we have investigated a total of 10 concentrations, namely, 0%, 1.39% (1/72), 2.78% 2.78% (1/36), 4.18% (1/24), 5.56% (1/18), 8.33% (1/12), 12.50% (1/8), 16.67% (1/6), 50% (1/2), and 100% (1/1). For modelling the different concentrations, two different supercells that contain 6 and 8 carbon atoms in graphene are adopted (see Fig. S1 in the ESI†). Each model is fully relaxed before and after Li intercalation.For each model, the adsorption energy for each adsorption site (see Fig. 3) is calculated by eqn (1). If the adsorption is energetically favourable, then the amount of adsorbed Li is further increased. When the average Li insertion voltage becomes close to 0 V, the number of Li intercalations is taken as the basis for calculating the Li storage capacity. For the concentration of 0%, it actually corresponds to pristine graphene. For this case, the calculated Li-adsorption ratio 1/48 is even smaller than the Li/C ratio for a completely exhausted graphite anode (LiC6, corresponding to a capacity of 372 mA h g−1). This is consistent with the previous finding that the Li-graphene interaction is very weak.16
The capacity as a function of Ge concentration in Fig. 1 exhibits a quasi-normal distribution. The highest capacity value (>1700 mA h g−1) is reached at a doping concentration of 1/18, and the corresponding chemical formula is C17Ge. In the following discussion, we shall focus on this optimal case.
3.2 Structure of Germagraphene C17Ge
Before investigating the energy storage properties of Germagraphene C17Ge, we first perform a detailed examination of its crystal structure. In the structure, there are in total five different bond lengths, as labelled in Fig. 2(a). The lengths of bond 1 to bond 5 are 1.845 Å, 1.401 Å, 1.448 Å, 1.412 Å, and 1.433 Å, respectively. The average bond length here is longer than the carbon–carbon bond length of 1.420 Å in graphite.30 As we mentioned before, Ge is located slightly above the C plane. The height of the Ge atom relative to the C plane is about 0.72 Å. The buckling breaks the mirror symmetry of the structure. In Fig. 2(b), we label the two sides of the monolayer plane as side A and side B.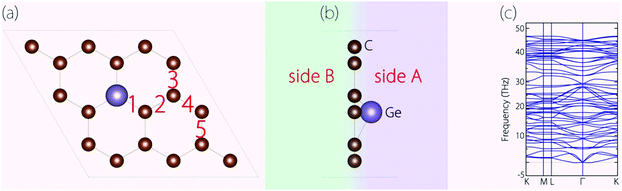 | ||
| Fig. 2 (a) Top view and (b) side view of the optimized C17Ge. (c) Calculated phonon spectrum for C17Ge. | ||
We have also investigated the dynamical stability of the structure, which can be inferred from its phonon spectrum. Fig. 2(c) shows the phonon spectrum for C17Ge. Clearly, there is no imaginary frequency mode, which demonstrates that the structure is dynamically stable.
3.3 Li adsorption
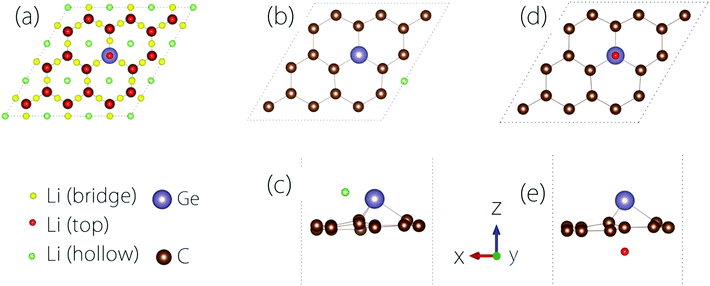
The conductivity of the electrode material is important to the rate performance of LIBs. It is desirable that the material has a good electrical conductivity before and after Li adsorption. In practice, metals or semiconductors with gaps <1 eV are typically considered as good candidates.To study the Li adsorption on Germagraphene, we first need to determine the most favourable adsorption site for the Li atom. The possible adsorption sites that we have tested are shown in Fig. 3(a). These sites can be classified into three types [see Fig. 3(a)]: the bridge site between two atoms, the top site on an atom, and the hollow site above a hexagonal ring. Moreover, since the two sides of Germagraphene are asymmetric, for each type of site, we also need to consider the two sides A and B separately.
The preference for Li adsorption at these sites is characterized by the adsorption energy: the lower the adsorption energy, the more stable the adsorption configuration. For adsorption on side A, the most stable adsorption site is near a hollow site above a C6 ring [see Fig. 3(b and c)]. The corresponding adsorption energy is 0.57 eV. For adsorption on side B, the most stable adsorption site is the top site above Ge [see Fig. 3(d and e)], and the corresponding adsorption energy is about 0.94 eV. During the adsorption, there is a charge transfer between Li and the Germagraphene layer. For example, for the case in Fig. 3(d and e), we find from the Bader charge analysis that both Li and Ge lose ∼0.85e charge and become positively charged while each C atom obtains ∼0.09e and becomes negatively charged.
To check whether the material can remain conductive before and after Li adsorption, we calculate the density of states (DOS) before and after Li adsorption and the results are plotted in Fig. 4. One can observe that Germagraphene C17Ge has a small gap of about 0.2 eV before Li adsorption, and the DOS near the fermi level is dominated by the contribution from C orbitals. The result is in agreement with a previous theoretical work.31 Upon Li adsorption, the system is metallic for the two configurations discussed above. Furthermore, the DOS at the Fermi level is greatly enhanced by Li adsorption, suggesting that more carriers are generated in the system. As a result, the electronic conduction should become better, which is beneficial for LIBs.
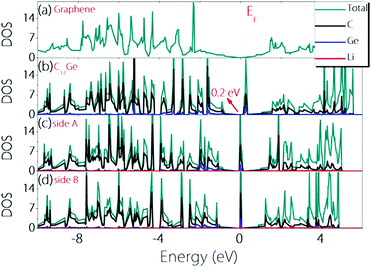 | ||
| Fig. 4 Density of states for (a) graphene, (b) pristine C17Ge, (c) LiC17Ge (adsorption on side A), and (d) LiC17Ge (adsorption on side B). | ||
3.4 Li diffusion barrier
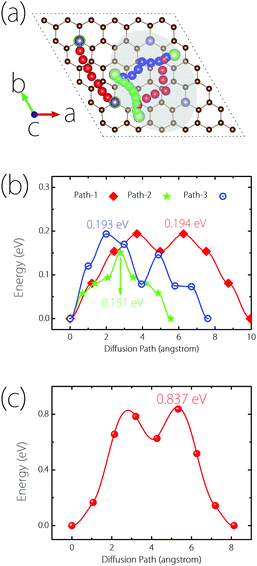
Next, we turn to study the Li diffusion process on Germagraphene, which is critical for the rate performance of LIBs. In order to reduce the artificial interaction effect between neighbouring images, a 2 × 2 supercell containing 68 C atoms and 4 Ge atoms is employed for the calculation. The climbing-image nudged elastic band (NEB) method32 is used to determine the diffusion energy barrier height, and to seek the optimal diffusion pathways as well as the saddle points. Again, due to the asymmetry between side A and side B, the diffusion processes on the two sides are considered separately.For side A, we consider three possible migration pathways, according to the movement of Li atoms between two neighbouring most stable adsorption sites. The three pathways are marked in the shadowed region in Fig. 5(a). The images for the Li atom along the paths are indicated by red (path-1), green (path-2), and blue (path-3) colours, respectively. It can be clearly seen that the three paths all become curved after NEB calculations, and are no longer straight as they are set initially. The calculated energy barriers are plotted in Fig. 5(b), which are 0.194, 0.193, and 0.151 eV, respectively. These three values are all smaller than the Li diffusion barriers for pristine graphene (∼0.277 eV), graphene with a point defect (∼0.366 eV to 0.538 eV),33 and graphite (∼0.47 eV),34 promising a fast Li diffusion. For side B, since the most stable adsorption site is the top site of Ge, only one migration pathway needs to be considered [see Fig. 5(a)]. The corresponding barrier height is found to be 0.837 eV, as shown in Fig. 5(c). Although this value is higher than side A and graphene, it is still acceptable for a practical electrode material.
3.5 Li storage capacity
The Li storage capacity and the average intercalation potential are the key characteristics for the LIB electrode materials. To study these properties, based on our discussion in the previous Section 3.3, we increase the concentration of adsorbed Li atoms on Germagraphene. In estimating the maximum possible capacity for Li adsorption, we still use the 18-atom unit cell in Fig. 3(a), and increase the number of Li atoms adsorbed on both sides of the monolayer. The average intercalation potential can be approximately calculated from the energy difference as in eqn (2) for the intercalation reaction involving z Li ions:| C17Ge + zLi+ + ze− ↔ LizC17Ge | (3) |
Starting from occupying the most stable adsorption site, the number of adsorbed Li atoms is increased one by one. At each step, we scan all possible sites again to locate the most stable one for the next adsorbed Li atom. We calculate the average Li insertion voltage according to eqn (2), and at the same time, we calculate the sequential adsorption energy, as defined below:
| Esae = EC17GeLim+1 − EC17GeLim − ELi | (4) |
The capacity for Germagraphene is very high. We can compare this value with several other 2D anode materials proposed so far (see Fig. 6). This value for Germagraphene is 5–7 times that for MoS2/graphene35 (∼335 mA h g−1) and GeS nanosheets36 (∼256 mA h g−1); 3–4 times that for most MXenes, including Nb2C (∼542 mA h g−1), Mo2C37 (∼526 mA h g−1) and Ti3C238,39 (∼319 mA h g−1); and almost 2 times that of the recently reported silicone40 (∼954 mA h g−1) and V2C41 (∼941 mA h g−1). This capacity is only slightly lower than that for the β12-borophene (∼1984 mA h g−1)8 but is even larger than the capacity for χ3-borophene (∼1240 mA h g−1)8 and siligraphene (∼1520 mA h g−1 (g-SiC5)).16
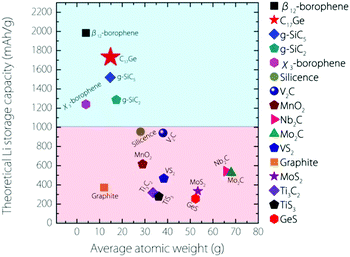 | ||
| Fig. 6 Comparison of the theoretical Li storage capacity values between Germagraphene C17Ge and other 2D anode materials (plus graphite). | ||
The discussion above shows that Germagraphene can be a high capacity anode material for LIBs. The enhanced interaction between Li and Germagraphene increases the charge and discharge voltages, and also allows a large amount of Li to be absorbed. Obviously, the presence of Ge is the reason for the enhanced interaction with Li. To further see this, we perform the Bader charge analysis for the system before and after Li adsorption. The results are listed in Table 1. As can be seen, the Ge atom in C17Ge loses ∼0.96e and becomes positively charged, because the electronegativity of C (2.55) is larger than that of Ge (2.01). As the Li intercalation process progresses, the total number of gained electrons for C atoms is always greater than the number of electrons lost for the Ge atom, and the Li atoms are always in the state of electron loss, indicating that the presence of Ge is beneficial for the Li adsorption.
| Average charge state | |||
|---|---|---|---|
| Li | C | Ge | |
| C17Ge | — | 4.05(−0.05) | 3.04(+0.96) |
| LiC17Ge | 0.15(+0.85) | 4.09(−0.09) | 3.15(+0.85) |
| Li6C17Ge | 0.27(+0.73) | 4.27(−0.27) | 3.78(+0.22) |
| Li12C17Ge | 0.29(+0.71) | 4.51(−0.51) | 3.93(+0.07) |
| Li18C17Ge | 0.35(+0.65) | 4.68(−0.68) | 4.18(−0.18) |
4. Discussion and conclusion
We have two remarks before closing. First, if the Ge dopant is changed to other elements from the same group such as Sn, the chemical properties of the doped material should be similar. We expect that doping with Sn can also enhance the Li adsorption. However, an obvious drawback is that the specific capacity will be smaller compared to Ge doping, because Sn is heavier than Ge.Second, the chemical stability of the electrode material in contact with an electrolyte is an important issue for batteries. It can approximately be inferred from the comparison between the material's Fermi level and the HOMO and LUMO of the electrolyte molecule.42 Generally, if the Fermi level is in the gap between the HOMO and the LUMO, the chemical stability is likely to be maintained. In addition, for an anode material, even if the Fermi level is slightly higher than the HOMO, the possible redox reaction can often be suppressed by the formation of the solid electrolyte interface (SEI) film. It has been shown experimentally that graphene is stable with currently used electrolytes,43 and the graphene Fermi level is close to the HOMO of the electrolytes. Our DFT calculation finds that Ge doping only slightly changes the Fermi level (from −4.483 eV for graphene to −4.494 eV for C17Ge, with a reference to the vacuum level). Thus, the Fermi level for Germagraphene should also be in the stable range, which implies its chemical stability when made in contact with electrolytes.
In conclusion, by using first-principles calculations, we demonstrate that Germagraphene is a promising high-capacity LIB anode material. We find that the capacity at the optimal Ge concentration (C17Ge) can reach ∼1734 mA h g−1, larger than most other 2D materials studied so far. We show that the material has good electrical conduction before and after Li adsorption. The Li diffusion barrier can be as low as 0.151 eV, indicating a fast rate-performance. The calculated average intercalation potential is very low (∼0.03 V), which is beneficial for expanding the working voltage window for the full-cells. Finally, in the process of Li intercalation, we find that the lattice change of C17Ge is quite small (only about 0.48%), indicating that the material should have a good cycling performance as well. Experimentally, Germagraphene with a controlled Ge concentration has been demonstrated by using low-energy ion implantation, which is expected to be a scalable and precise technique for controllably doping 2D materials.17 Our work not only reveals a promising candidate material with an ultrahigh capacity for LIBs, but also offers a new insight in engineering 2D materials for energy storage applications.
Conflicts of interest
There is no conflict of interest to declare.Acknowledgements
The authors thank D. L. Deng for valuable discussions. This work is supported by the National Research Foundation Prime Minister's Office Singapore under the NRF-ANR Joint Grant Call (Award No. NRF2015-NRF-ANR000-CEENEMA), the Natural Science Foundation of China (Grant No. 11564016), and the Singapore Ministry of Education Academic Research Fund Tier 2 (MOE2015-T2-2-144). We acknowledge the computational support from the Texas Advanced Computing Center and the National Supercomputing Centre Singapore.Notes and references
- W. Xu, J. L. Wang, F. Ding, X. L. Chen, E. Nasybutin, Y. H. Zhang and J. G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 RSC.
- A. Manthiram, Y. Z. Fu, S. H. Chung, C. X. Zu and Y. S. Su, Chem. Rev., 2014, 114, 11751–11787 CrossRef CAS PubMed.
- Q. Tang, Z. Zhou and P. W. Shen, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS PubMed.
- Y. Jing, Z. Zhou, C. R. Cabrera and Z. Chen, J. Phys. Chem. C, 2013, 117, 25409–25413 CrossRef CAS.
- D. Er, J. Li, M. Naguib, Y. Gogotsi and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 11173–11179 CrossRef CAS PubMed.
- J. P. Hu, B. Xu, S. A. Yang, S. Guan, C. Y. Ouyang and Y. G. Yao, ACS Appl. Mater. Interfaces, 2015, 7, 24016–24022 CrossRef CAS.
- H. R. Jiang, Z. Lu, M. C. Wu, F. Ciucci and T. S. Zhao, Nano Energy, 2016, 23, 97–104 CrossRef CAS.
- X. Zhang, J. Hu, Y. Cheng, H. Y. Yang, Y. Yao and S. A. Yang, Nanoscale, 2016, 8, 15340–15347 RSC.
- L. Shi, T. S. Zhao, A. Xu and J. B. Xu, J. Mater. Chem. A, 2016, 4, 16377–16382 RSC.
- D. Wang, Y. Gao, Y. Liu, D. Jin, Y. Gogotsi, X. Meng, F. Du, G. Chen and Y. Wei, J. Phys. Chem. C, 2017, 121, 13025–13034 CrossRef CAS.
- M. E. Stournara and V. B. Shenoy, J. Power Sources, 2011, 196, 5697–5703 CrossRef CAS.
- D. Datta, J. Li and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 1788–1795 CrossRef CAS.
- H. Yildirim, A. Kinaci, Z. J. Zhao, M. K. Y. Chan and J. P. Greeley, ACS Appl. Mater. Interfaces, 2014, 6, 21141–21150 CrossRef CAS.
- T. Bhardwaj, A. Antic, B. Pavan, V. Barone and B. D. Fahlman, J. Am. Chem. Soc., 2010, 132, 12556–12558 CrossRef CAS.
- D. Datta, J. W. Li, N. Koratkar and V. B. Shenoy, Carbon, 2014, 80, 305–310 CrossRef CAS.
- H. Wang, M. Wu, X. Lei, Z. Tian, B. Xu, K. Huang and C. Ouyang, Nano Energy, 2018, 49, 67–76 CrossRef CAS.
- M. Tripathi, A. Markevich, R. Böttger, S. Facsko, E. Besley, J. Kotakoski and T. Susi, ACS Nano, 2018, 12, 4641–4647 CrossRef CAS PubMed.
- C. K. Chan, X. F. Zhang and Y. Cui, Nano Lett., 2008, 8, 307 CrossRef CAS.
- G. Kresse and J. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- K. Toyoura, Y. Koyama, A. Kuwabara and I. Tanaka, J. Phys. Chem. C, 2010, 114, 2375–2379 CrossRef CAS.
- K. R. Kganyago and P. E. Ngoepe, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 205111 CrossRef.
- B. Xu, M. S. Wu, G. Liu and C. Y. Ouyang, J. Appl. Phys., 2012, 111, 124325 CrossRef.
- S. Stankovich, R. D. Piner, X. Chen, N. Wu, S. T. Nguyen and R. S. Ruoff, J. Mater. Chem., 2006, 16, 155–158 RSC.
- M. L. Ould Ne, A. Abbassi, A. G. El hachimi, A. Benyoussef, H. Ez-Zahraouy and A. El Kenz, Opt. Quantum Electron., 2017, 49, 218 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- L. J. Zhou, Z. F. Hou and L. M. Wu, J. Phys. Chem. C, 2012, 116, 21780–21787 CrossRef CAS.
- K. Toyoura, Y. Koyama, A. Kuwabara, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 214303 CrossRef.
- L. David, R. Bhandavat and G. Singh, ACS Nano, 2014, 8, 1759–1770 CrossRef CAS PubMed.
- F. Li, Y. Qu and M. Zhao, J. Mater. Chem. A, 2016, 4, 8905–8912 RSC.
- Q. Sun, Y. Dai, Y. Ma, T. Jing, W. Wei and B. Huang, J. Phys. Chem. Lett., 2016, 7, 937–943 CrossRef CAS PubMed.
- D. Er, J. Li, M. Naguib, Y. Gogotsi and V. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 11173–11179 CrossRef CAS.
- Y. Xie, Y. DallAgnese, M. Naguib, Y. Gogotsi, M. W. Barsoum, H. L. Zhuang and P. R. Kent, ACS Nano, 2014, 8, 9606–9615 CrossRef CAS PubMed.
- G. Tritsaris, E. Kaxiras, S. Meng and E. Wang, Nano Lett., 2013, 13, 2258–2263 CrossRef CAS PubMed.
- J. Hu, B. Xu, C. Ouyang, S. A. Yang and Y. Yao, J. Phys. Chem. C, 2014, 118, 24274–24281 CrossRef CAS.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- H. Yoshitake, K. Abe, T. Kitakura, J. B. Gong, Y. S. Lee., H. Nakamura and M. Yoshio, Chem. Lett., 2003, 32, 134–135 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nh00333e |
| This journal is © The Royal Society of Chemistry 2019 |