Open Access Article
Open Access ArticleMechanical anisotropy of two-dimensional metamaterials: a computational study†
Ning
Liu
a,
Mathew
Becton
a,
Liuyang
Zhang
b,
Keke
Tang
c and
Xianqiao
Wang
 *a
*a
aCollege of Engineering, University of Georgia, Athens, GA 30602, USA. E-mail: xqwang@uga.edu
bState Key Laboratory for Manufacturing Systems Engineering, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, China
cSchool of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China
First published on 31st May 2019
Abstract
Metamaterials, rationally designed multiscale composite systems, have attracted extensive interest because of their potential for a broad range of applications due to their unique properties such as negative Poisson's ratio, exceptional mechanical performance, tunable photonic and phononic properties, structural reconfiguration, etc. Though they are dominated by an auxetic structure, the constituents of metamaterials also play an indispensable role in determining their unprecedented properties. In this vein, 2D materials such as graphene, silicene, and phosphorene with superior structural tunability are ideal candidates for constituents of metamaterials. However, the nanostructure–property relationship and composition–property relationship of these 2D material-based metamaterials remain largely unexplored. Mechanical anisotropy inherited from the 2D material constituents, for example, may substantially impact the physical stability and robustness of the corresponding metamaterial systems. Herein, classical molecular dynamics simulations are performed using a generic coarse-grained model to explore the deformation mechanism of these 2D material-based metamaterials with sinusoidally curved ligaments and the effect of mechanical anisotropy on mechanical properties, especially the negative Poisson's ratio. The results indicate that deformation under axial tensile load can be divided into two stages: bending-dominated and stretching-dominated, in which the rotation of junctions in the former stage results in auxetic behavior of the proposed metamaterials. In addition, the auxetic behavior depends heavily on both the amplitude/wavelength ratio of the sinusoidal ligament and the stiffness ratio between axial and transverse directions. The magnitude of negative Poisson's ratio increases from 0 to 0.625, with an associated increase of the amplitude/wavelength ratio from 0 to 0.225, and fluctuates at around 0.625, in good agreement with the literature, with amplitude/wavelength ratios greater than 0.225. More interestingly, the magnitude of negative Poisson's ratio increases from 0.47 to 0.87 with the increase of the stiffness ratio from 0.125 to 8, in good agreement with additional all-atom molecular dynamics simulations for phosphorene and molybdenum disulfide. Overall, these research findings shed light on the deformation mechanism of auxetic metamaterials, providing useful guidelines for designing auxetic 2D lattice structures made of 2D materials that can display a tunable negative Poisson's ratio.
1. Introduction
Recent years have witnessed the explosive growth of research into metamaterials, rationally designed multiscale composite systems which exhibit material properties not found in most conventional materials, due to their potential for a broad range of applications.1–6 The unique properties of these materials, e.g. negative Poisson's ratio,5,7,8 superior mechanical performance9–11 and structural reconfiguration,12–14 are usually dominated by their structure, although the influence of their composition cannot be neglected either. Among candidates for constituents of metamaterials, two-dimensional materials with one-atom thickness have attracted significant interest due to their unique physical and chemical properties.1,2,7,15–26 Lattice metamaterials made of two-dimensional materials such as graphene have attracted extensive research interest, indicating great potential in applications such as flexible electronic devices,5,27–30 photonic and phononic devices,31–34 and mechanically controllable thermal devices.5,35–37 However, the microstructure–property relationship and composition–property relationship of metamaterials made of two-dimensional materials remain an open question. Previous research studies set up a solid foundation for future studies investigating the structure–property relationship for 2D lattice structures.5,25,38,39 For 2D lattice structures with multiple cut patterns, several theoretical models have been proposed to predict the microstructure–property relationship, which could not be well explained through classical theory in composite materials.5,25 Other studies focus on edge termination problems for 2D lattice structures made of 2D materials, which is a critical issue for mechanical performance and structural stability.38,39 Despite these remarkable advances, the composition–property relationship has long been overlooked. For example, two-dimensional materials with a highly symmetric crystalline structure, such as graphene,40 silicene,41 and molybdenum disulfide,42 exhibit isotropic mechanical properties while other materials with less symmetric structures, such as phosphorene,43 are highly anisotropic along in-plane directions. The intrinsic mechanical anisotropy has potential to promote the tunability of mechanical properties of the associated metamaterials. Another important factor is the Föppl–von Kármán number,44,45 an indication of the ratio between in-plane stiffness and out-of-plane bending stiffness, with high numbers corresponding to membranes that more easily bend and crumple than they stretch and shear. Graphene exhibits exceptional in-plane stretching stiffness, around 1 TPa in both armchair and zigzag directions,46 due to the strong covalent bonding between adjacent carbon atoms, while the bending stiffness is significantly low due to its ultra-low thickness, ranging from 0.83 to 1.61 eV as measured experimentally7 and calculated theoretically.47,48 In contrast, the in-plane stiffness of molybdenum disulfide is moderate, around 330 GPa, compared to graphene, while the bending stiffness (8.7–13.4 eV)49 is much higher than that of graphene due to its three-atom thickness. Consequently, with a low Föppl–von Kármán number, metamaterials made of materials like graphene could exhibit low stability compared to those made of materials like molybdenum, in which the out-of-plane buckling appears early under external mechanical loading. Overall, the mechanical anisotropy of 2D materials would significantly influence the stability and property tunability of the associated metamaterials. In this paper, we strive to address the above issue through coarse-grained molecular dynamics simulations, a widely accepted computational technique for two-dimensional materials,50,51 with a focus on the relationship between mechanical anisotropy and negative Poisson's ratio.In recent years, extensive efforts have also been put into designing microstructures and understanding deformation mechanisms for metamaterials with auxeticity, also known as negative Poisson's ratio.1,2,52,53 For most conventional engineering materials, transverse contraction (expansion) would happen in association with tension (compression) along the loading direction. Auxetic materials, however, will expand (shrink) transversely when they are axially stretched (compressed), which enhances the energy absorption capability and fracture toughness, and thus the stability and robustness of the associated nano-devices.28–30 Various architectures, e.g. kirigami-based structures,7,19,23 fractal hierarchical structures,54,55 and dimpled elastic sheets,52 have been implemented in designing multifunctional materials. However, microstructures with a corrugated configuration, which may improve mechanical performance such as the stretchability of the associated metamaterials, have been overlooked.56–58 Moreover, the J-shape mechanical responses59 under external tension are intrinsically similar to those of many natural soft bio-materials,60–62 potentially improving the physiological compatibility of the corresponding nano-devices.30,63 Therefore, architectures with sinusoidally curved beams are implemented to design auxetic 2D lattice metamaterials. In this work, Section 2 will briefly summarize the structural design of the proposed metamaterial and the computational techniques implemented here. In Section 3, simulation results are presented and discussed, and the specific focus is the effect of amplitude/wavelength ratio and stiffness ratio on the magnitude of negative Poisson's ratio. Finally, we conclude in Section 4 the deformation mechanism and effects of both geometrical factors and mechanical anisotropy on the auxetic behavior of the proposed 2D material system.
2. Computational methods and models
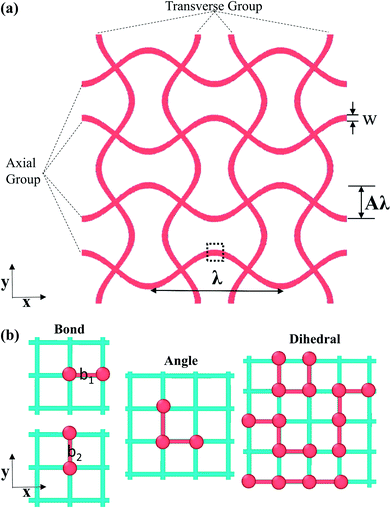
As discussed before, nanostructure designs with a curved configuration would dramatically improve the mechanical performance, such as stretchability, of 2D material systems.56–58 In addition, the associated J-shape mechanical responses, similar to natural soft bio-matter, could enable good biocompatibility for nano-devices for biomedical applications.30,63 Moreover, buckled structures are also promising in tuning phononic bandgaps, enabling many potential applications.32 Therefore, as shown in Fig. 1(a), two-dimensional networks with curved sinusoidal beams were created as the initial configuration. Three series of parameters, namely wavelength λ, amplitude/wavelength ratio A and band width w, can be tuned here to investigate their effects on the mechanical properties of two-dimensional kirigami, especially Poisson's ratio. Note that A is calculated by dividing the amplitude of sinusoidal curves by wavelength λ as shown in Fig. 1(a). For further quantitative analysis, the beams involved are classified into two groups: an axial group parallel to the loading direction and a transverse group perpendicular to the loading direction.As mentioned in the introduction, there are huge differences in mechanical properties among 2D materials,40–43,53,64–67 which could bring interesting changes in the auxetic behaviors of 2D-material-based nanostructures. However, there are few general molecular models which could be tuned to accurately reproduce the mechanical properties of different 2D material systems. In order to model interactions among particles, a generic coarse-grained molecular dynamics (CG-MD) model of 2D materials is used as shown in Fig. 1(b), in which a squared lattice structure is connected by covalent bonds between adjacent particles. Each of those particles represents a cluster of atoms in a given 2D material system. The corresponding interactions can be divided into three categories, namely bond interactions which control the in-plane Young's modulus, angle interactions which define the in-plane shear modulus, and dihedral interactions which affect the out-of-plane bending stiffness. One of the advantages of this generic CG-MD model is that the mechanical properties can be tuned through varying the interaction parameters in a decoupled manner.51 For example, the Young's modulus along the x and y directions can be tuned through varying the stiffness of the b1 and b2 bonds respectively, as shown in Fig. 1(b), which provides a robust way to represent different kinds of 2D materials with widely varied and anisotropic mechanical properties. Accordingly, the total potential energy is calculated based on the following expressions
| U = Ubond + Uangle + Udihedral | (1) |
| Ubond = kbond(d − d0)2 | (2) |
| Uangle = kangle(θ − θ0)2 | (3) |
| Udihedral = kdihedral(1 − cos(2φ)) | (4) |
| Connection type | Analytical expression | Parameters |
|---|---|---|
| Bond 1 | U bond(d1) = kbond1(d1 − d01)2 | d 01 = 2.8 Å |
| k bond 1 = 20.46 eV Å−2 | ||
| Bond 2 | U bond(d2) = kbond 2(d2 − d02)2 | d 02 = 2.8 Å |
| k bond 2 = 2.56–20.46 eV Å−2 | ||
| Angle | U angle(θ) = kangle(θ − θ0)2 | k angle = 17.75 eV |
| θ 0 = 90° | ||
| Dihedral | U dihedral(r) = kdihedral(1 − cos(2φ)) | k dihedral = 100 × 0.180 eV |
The simulation setup is briefly summarized as follows. The simulation box was fixed at 60 nm × 60 nm × 4 nm, in which periodic boundary conditions were applied along the x and y directions while shrink-boundary conditions were applied along the z direction. To perform a uniaxial tensile test, a strain-controlled loading method was adopted, in which a strain increment was added along the x direction every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps via elongation of the box while the lateral y direction was free to change through a pressure control set at 1 atm. The loading rate is around 1 × 107 s−1, falling into the conventional strain rate regime (107 to 109 s−1) as commonly used in molecular dynamics studies.71–73 To eliminate the effect of thermal fluctuations, temperature was controlled at around 1 K. Unless otherwise stated, time integration was performed on Nose–Hoover style non-Hamiltonian equations of motion from the isothermal–isobaric (NPT) ensemble,74 in which the time step was set to 1 fs for both stability and accuracy. All the simulations were performed by implementing a parallel solver for molecular dynamics LAMMPS,75 and the results were visualized through the OVITO76 package.
000 time steps via elongation of the box while the lateral y direction was free to change through a pressure control set at 1 atm. The loading rate is around 1 × 107 s−1, falling into the conventional strain rate regime (107 to 109 s−1) as commonly used in molecular dynamics studies.71–73 To eliminate the effect of thermal fluctuations, temperature was controlled at around 1 K. Unless otherwise stated, time integration was performed on Nose–Hoover style non-Hamiltonian equations of motion from the isothermal–isobaric (NPT) ensemble,74 in which the time step was set to 1 fs for both stability and accuracy. All the simulations were performed by implementing a parallel solver for molecular dynamics LAMMPS,75 and the results were visualized through the OVITO76 package.
3. Results and discussions
3.1 Deformation mechanism and geometry effect on Poisson's ratio
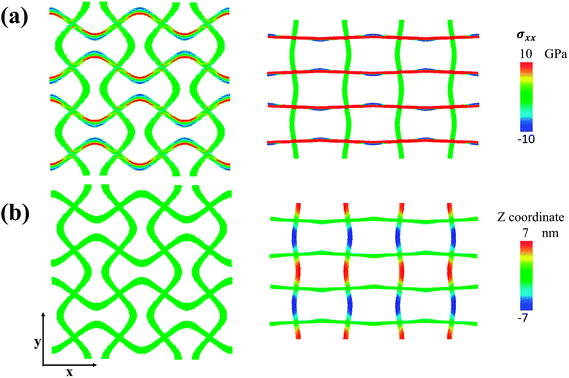
To obtain a comprehensive understanding of the auxeticity of our structure, the stress–strain and strain–strain behaviors of a typical sample were investigated first, in which the amplitude/wavelength ratio A is equal to 0.3, wavelength λ = 30 nm, and band width w = 2.4 nm. As shown in Fig. 2(a), the deformation history could be roughly divided into two stages, namely bending-dominated stage and stretching-dominated stage. The mechanical responses in the two stages are intrinsically different. In the bending-dominated stage, the axial group (marked in Fig. 1(a)) experiences both tension and bending due to its initial curved shape while the transverse group undergoes pure bending induced by bending of the axial group, resulting in unconventional transverse expansion under axial tension as shown in Fig. 2(a), which reveals a negative Poisson's ratio. In the bending-dominated stage, the local strain is much lower compared with the nominal strain of the whole sample, in which the deformation is mainly attributed to “rigid body rotation”. Consequently, the global nominal stress increases slowly. Simultaneously, the lateral expansion along the y direction is almost linearly related to the axial strain along the x direction as shown in Fig. 2(a), and the resultant Poisson's ratio is 0.625, which is in good agreement with the literature.32 Note that in this stage the out-of-plane buckling can be neglected as shown in Fig. 2(b). However, as the axial group is further “straightened” beyond a strain of 0.2, the transverse group tends to buckle to release its accumulated bending energy as we can see from Fig. 2(b). Profiles of the out-of-plane displacement can be found in Fig. S1 and S2 in the ESI material.† It can be seen that when the strain is below 0.2, the out-of-plane displacement for the entire structure is marginal, which is consistent with Fig. 2(b). Accordingly, the transverse group shrinks, and the whole sample experiences a sharp transition from negative Poisson's ratio to positive Poisson's ratio as shown in Fig. 2(a). In Fig. S1 and S2,† it can be seen that the out-of-plane displacement for the entire structure quickly increases when the strain is larger than 0.2, in which the shape of the entire structure is sinusoidal from the loading direction. Moreover, as the axial group is gradually straightened, instead of bending, stretching starts to dominate. Consequently, the nominal stress increases dramatically as shown in Fig. 2(a). The deformation patterns seen in the two different stages are further confirmed through the stress profile in the left-subfigure of Fig. 3(a). When the strain is equal to 0.1, it can be seen that the stress component σxx in the transverse group is around zero while σxx shows large variations in the axial group in which the stress is negative on one edge (compression) and positive (tension) on the other edge. Due to the unique structure, the transverse group cannot sustain loads along the x direction, while the axial group carries the most load along the x direction. Moreover, forces along the x direction not only induce tension inside the axial group but also produce bending, which cause rotation of the junctions, which also helps straighten out the transverse group. Consistent with Fig. 2(b), the out-of-plane coordinates of the whole sample are around zero as shown in the left sub-figure of Fig. 3(b) when strain is 0.1, indicating that there is no buckling in the bending-dominated stage. As the axial strain proceeds beyond 0.2, the load increment along the x direction can only generate minor bending moments due to the straightened shape of the axial group. Simultaneously, the axial group tends to be stretched rather than straightened under loads along the x direction. As shown in the right (0.4 strain) sub-figure of Fig. 3(a), the stress component σxx is positive in most areas of the axial group, despite several minor regions with negative stress when strain is equal to 0.4, indicating that the deformation is stretching-dominated. Meanwhile, the transverse group shows significant buckling as shown in the right (0.4 strain) sub-figure of Fig. 3(b), in which positive and negative z coordinates are expressed alternatively in adjacent regions within a single strand.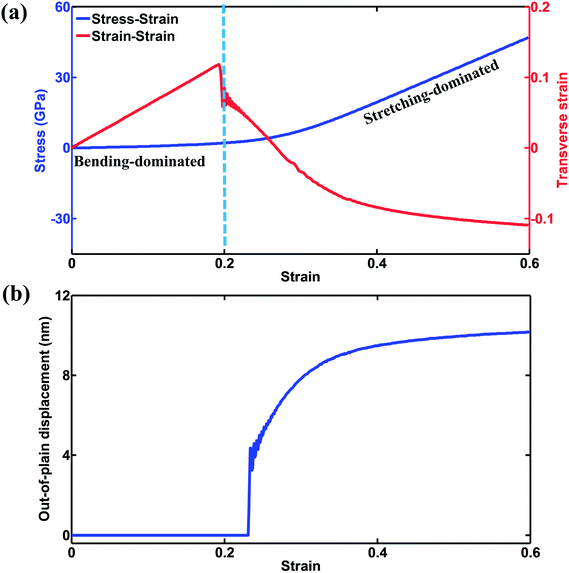 | ||
| Fig. 2 (a) Stress–strain and strain–strain curves under uniaxial tension along the x direction. (b) Evolution of the out-of-plane displacement during uniaxial tensile tests along the x direction. | ||
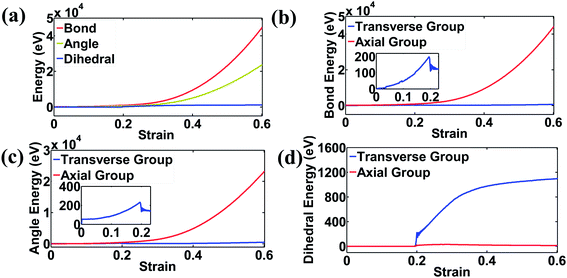
The energetic analysis results in Fig. 4 show the overall energy change classified as bond, angle and dihedral energy. As can be seen from Fig. 4(a), bond and angle energy changes are the main contributors to the global potential energy variation, while the dihedral energy change is at least one order of magnitude smaller than the former two terms, indicating the relative domination of in-plane deformation. Note that the angle energy change is significantly smaller than the bond energy change, indicating the larger role of bond energy towards in-plane deformation, which is consistent with the literature.50 In accordance with Fig. 2(a), when the strain is below 0.2 (bending-dominated stage), the potential energy undergoes a slow increase, as the deformation at this stage is mainly attributed to “rigid body motion”. In contrast, in the stretching-dominated stage (>0.2 strain), the potential energy increases dramatically for all three terms, and most of the energy change comes from the axial group, as can be seen from Fig. 4(b) and (c). The transition between these two stages is reflected in the sharp potential energy drop in the graphs for bond and angle energies, as well as the sharp increase in the dihedral energy of the transverse group, as shown in the insets of Fig. 4(b–d).
As discussed in the literature,32 the amplitude/wavelength ratio is typically set as a relatively large value, such as 1/3, to ensure significant auxetic behaviors. However, a systematic understanding of the effect of amplitude/wavelength ratio is still lacking for topology optimization for proposed nanostructures. Next, a systematic parameter study is performed to understand the effect of amplitude/wavelength ratio (A) on the low-strain Poisson's ratio of the structure. As can be seen from Fig. 5(a), the curves can be divided into two stages, consistent with the results seen in Fig. 2(a). Interestingly, as A decreases, the critical strain for the transition from a negative Poisson's ratio to a positive Poisson's ratio will decrease, and is associated with an early out-of-plane buckling. Moreover, when A is 0.1, it can be seen that the strain–strain relation shows strong nonlinearity. Fig. 5(b) shows the relationship between the low-strain Poisson's ratio and A, in which the given Poisson's ratio has been calculated via a linear fitting of data points below a strain of 0.05. It can be observed that the magnitude of Poisson's ratio increases gradually and approaches 0.63, in good agreement with a value of 0.65 in the literature,32 as A increases. Due to this saturation effect, an amplitude of 0.3, falling into the saturation regime, is chosen for the amplitude in simulations hereafter. Note that wavelength λ and band width w also play an important role in the mechanical properties of the proposed 2D lattice structures, but these two geometrical parameters have a limited influence on the magnitude of Poisson's ratio,32 and are not investigated in this paper. Relevant results and discussions about the effect of wavelength λ and bandwidth w could be found in Fig. S3 in the ESI material.†
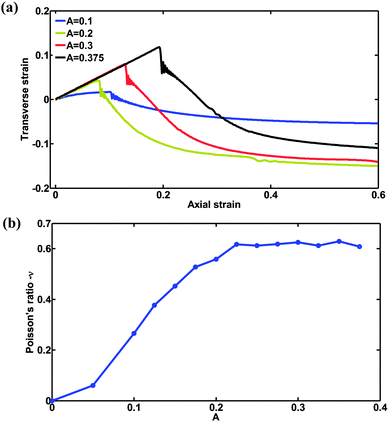 | ||
| Fig. 5 (a) Strain–strain responses for samples with different amplitude/wavelength ratios A as shown in Fig. 1(a). (b) Poisson's ratio versus amplitude/wavelength ratio A. | ||
3.2 Effect of mechanical anisotropy
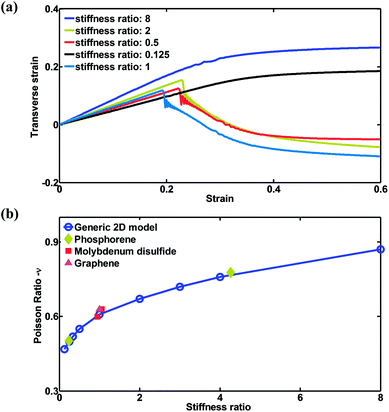
As is extensively investigated in the literature, 2D materials can exhibit exceptional mechanical performance, and among 2D materials some are isotropic while others are anisotropic.40–43,64–67 Moreover, due to the anisotropy of the underlying material, the Poisson's ratio of this proposed 2D lattice structure strongly depends on the stiffness ratio between the axial group and the transverse group, in which mechanical anisotropy plays a very important role. Therefore, it would be interesting to study the effect of stiffness ratio between the x and y directions on the magnitude of the Poisson's ratio, in order to expand our results to a plethora of potential 2D materials. In this section, the stiffness ratio, defined as the ratio between the Young's moduli in the x and y directions, can be tuned by varying the bond stiffness in the y direction, while the bond stiffness (and Young's modulus) in the x direction remains constant. Note that for stiffness ratios 8 and 0.125, tensile tests are performed for the same sample along the x and y directions, respectively, which is also true for stiffness ratios 2 and 0.5. Fig. 6(a) shows the strain–strain responses for samples with different stiffness ratios ranging from 0.125 to 8. The general trend of the curves is consistent with those in Fig. 2(a) and 5(a). However, significant differences are seen for the Poisson's ratio between samples with different stiffness ratios as shown in Fig. 6(b), in which the Poisson's ratio increases as the stiffness ratio increases. Additional all-atom molecular dynamics simulations are performed for isotropic molybdenum disulfide and anisotropic phosphorene as shown in Fig. S4 in the ESI material.† It can be seen that the resultant Poisson's ratios can be well fitted into the curve shown in Fig. 6(b), indicating that the stiffness ratio, or the ratio between Young's moduli of the x and y directions, is the dominating factor in determining the Poisson's ratio of the proposed 2D lattice structure among the given intrinsic mechanical properties of the material used.It is interesting to note that, for some cases, there would be a sharp transition of Poisson's ratio from negative to positive, indicating the out-of-plane buckling in Fig. 6 as well as Fig. 2, 5, and S3.† However, in other cases, there would be a smooth transition of Poisson's ratio from negative to zero as shown in Fig. 6 and S3.† Potential causes for these differences are detailed as follows: firstly, the out-of-plane buckling results from competition between out-of-plane bending and in-plane bending of transverse groups as shown in Fig. 1(a). Near the critical point, the huge bending energy stored in the transverse group would induce out-of-plane buckling. As shown in Fig. 4(b–d), the bond and angle energies, indicators of in-plane bending, experience a sharp drop while the dihedral energy, an indicator of out-of-plane buckling, experiences a sharp increase. Overall, the critical strain depends heavily on the ratio between out-of-plane bending stiffness and in-plane bending stiffness. Secondly, without out-of-plane buckling, Poisson's ratio of the lattice structures would experience a smooth transition from negative Poisson's ratio to zero Poisson's ratio as shown in Fig. 6(a) (stiffness ratio 8 and 0.125) and Fig. S3(c)† (width w = 1.2 nm). The negative Poisson's ratio at the initial stage results from the “straightening” and thus “elongation” of the transverse group induced by rotation of junctions due to the bending deformation of the axial group. In contrast, as the axial group is fully straightened out, the deformation of the axial group would not induce rotation of junctions, leading to zero Poisson's ratio. Given that the out-of-plane bending stiffness is sufficiently large, 2D lattice structures here would experience smooth transition from negative Poisson's ratio to zero Poisson's ratio.
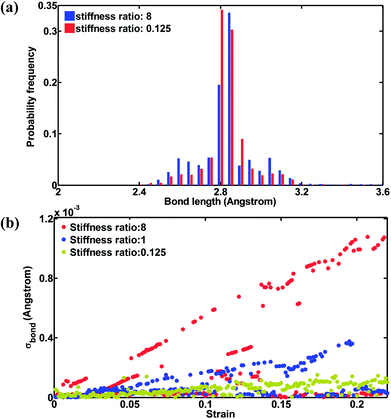
To understand the mechanical anisotropy effect from the perspective of the atomic structure, bond length changes are analyzed as shown in Fig. 7. Fig. 7(a) shows the bond length distribution of the transverse group when the axial strain is 0.2, in which the bond distribution for stiffness ratio 8 is skewed when compared with that for stiffness ratio 1. As discussed in Section 3.1, the transverse group experiences pure bending during uniaxial tension along the axial direction, and as such the bonds in the transverse group experience elongation or compression depending on the local bending moment generated. When the stiffness ratio is larger than 1, indicating that the initial bending stiffness of the transverse group is smaller than that of the axial group, the transverse group can be straightened more easily, comparatively. Consequently, the bonds in the transverse group experience larger changes in length than their counterparts when the stiffness ratio is no larger than 1, due to the difference in bond stiffness and geometry. This mechanism can be further confirmed in Fig. 7(b), which shows the standard deviation of bond lengths in the transverse group, σbond. As shown in Fig. 7(b), the values of σbond are larger at lower strain as the stiffness ratio increases from 0.125 to 1 to 8. The fluctuation of σbond could be attributed to the boundary conditions in the y direction, where pressure is controlled through controlling the box size in the transverse direction during axial elongation. Fig. 8 shows the stress profile at a strain of 0.2 for stiffness ratios of 8 and 0.125. It can be seen that the stress intensity of the transverse group for a stiffness ratio of 8 is lower and occurs over a smaller area. Based on the theory of elasticity, stress on a certain point of the cross section is proportional to both the curvature change and Young's modulus. For both cases with different stiffness ratios, the geometrical shapes of the transverse groups are identical. On the one hand, from Fig. 6(a), it can be seen that the transverse strain for a stiffness ratio of 8 is roughly 2 times that for a stiffness ratio of 0.125, indicating that the curvature change for a stiffness ratio of 8 is roughly 2 times that for a stiffness ratio of 0.125. On the other hand, the Young's modulus of the transverse group for a stiffness ratio of 8 is 0.125 times that of the transverse group for a stiffness ratio of 0.125. Therefore, at a given location, the stress of the transverse group for a stiffness ratio of 8 is roughly 0.25 times that for a stiffness ratio of 0.125. Consequently, the stress intensity for a stiffness ratio of 8 is much lower than that for a stiffness ratio of 0.125, as shown in Fig. 8. Overall, from these results, we can clearly see the major impact of stiffness anisotropy on the mechanical properties and behaviors of lattice-like metamaterials.
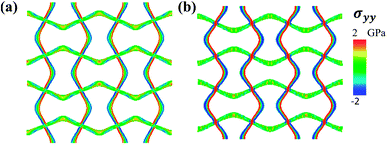 | ||
| Fig. 8 Global stress profile when strain is 0.2. (a) Stiffness ratio of 8. (b) Stiffness ratio of 0.125. | ||
4. Conclusions
In this paper, we investigate the auxeticity of the proposed 2D lattice structure made of 2D materials through a systematic study of the effects of both geometrical factors and tuned mechanical anisotropy through implementing CG-MD simulations. First, the results indicate that the deformation of the proposed 2D lattice structure can be divided into two stages, namely bending-dominated, in which the Poisson's ratio is constant and negative, and stretching-dominated, where the Poisson's ratio becomes positive. The auxeticity could be attributed to the cooperative deformation of the axial group and the transverse group, where the bending moment generated by tension on the axial group causes rotation of the axial/transverse junctions, thus straightening out the transverse group. The transition between bending-dominated and stretching-dominated stages is associated with out-of-plane buckling, leading to the transition from a negative to a positive Poisson's ratio. Second, a systematic study of the effect of geometrical factors on Poisson's ratio reveals that it increases with the increase of amplitude/wavelength ratio A, representing the curvature of the beams, and that the Poisson's ratio reaches saturation at A = 0.225. Finally, the effect of mechanical anisotropy of the underlying 2D material forming the lattice on the structure's auxeticity is investigated. The results indicate that the magnitude of Poisson's ratio increases with the increase of the stiffness ratio between Young's moduli in the loading direction and the transverse direction. Additional all-atom MD simulations for phosphorene, graphene, and molybdenum disulfide were also performed to validate the relationship observed between the stiffness ratio and Poisson's ratio, indicating the general applicability of the obtained rule to 2D materials. The above relationship between the stiffness ratio and Poisson's ratio could be attributed to the cooperative deformation of the transverse and axial groups, in which the transverse group is more easily straightened at lower stiffness. Overall, these research findings can provide useful guidelines for the design of auxetic 2D lattice structures composed of anisotropic 2D materials, allowing for a tunable negative Poisson's ratio.Conflicts of interest
There are no conflicts to declare.Acknowledgements
N. L. and X. W. acknowledge the support from the National Science Foundation (Grant No. CMMI-1610812).References
- L. Wang and M. C. Boyce, Bioinspired Structural Material Exhibiting Post-Yield Lateral Expansion and Volumetric Energy Dissipation During Tension, Adv. Funct. Mater., 2010, 20, 3025–3030 CrossRef CAS.
- Q. Zhang, X. Xu, D. Lin, W. Chen, G. Xiong and Y. Yu, et al. Hyperbolically Patterned 3D Graphene Metamaterial with Negative Poisson's Ratio and Superelasticity, Adv. Mater., 2016, 28, 2229–2237 CrossRef CAS PubMed.
- J.-H. Lee, J. P. Singer and E. L. Thomas, Micro-/Nanostructured Mechanical Metamaterials, Adv. Mater., 2012, 24, 4782–4810 CrossRef CAS PubMed.
- T. Frenzel, C. Findeisen, M. Kadic, P. Gumbsch and M. Wegener, Tailored Buckling Microlattices as Reusable Light-Weight Shock Absorbers, Adv. Mater., 2016, 28, 5865–5870 CrossRef CAS PubMed.
- W. Yang, Q. Liu, Z. Gao, Z. Yue and B. Xu, Theoretical search for heterogeneously architected 2D structures, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, E7245–E7254 CrossRef PubMed.
- J. Christensen, M. Kadic, O. Kraft and M. Wegener, Vibrant times for mechanical metamaterials, MRS Commun., 2015, 5, 453–462 CrossRef CAS.
- M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill and P. Y. Huang, et al. Graphene kirigami, Nature, 2015, 524, 204 CrossRef CAS PubMed.
- J. N. Grima, S. Winczewski, L. Mizzi, M. C. Grech, R. Cauchi and R. Gatt, et al. Tailoring Graphene to Achieve Negative Poisson's Ratio Properties, Adv. Mater., 2015, 27, 1455–1459 CrossRef CAS PubMed.
- X. Zheng, W. Smith, J. Jackson, B. Moran, H. Cui and D. Chen, et al. Multiscale metallic metamaterials, Nat. Mater., 2016, 15, 1100 CrossRef CAS PubMed.
- J. Bauer, A. Schroer, R. Schwaiger and O. Kraft, Approaching theoretical strength in glassy carbon nanolattices, Nat. Mater., 2016, 15, 438 CrossRef CAS PubMed.
- J. B. Berger, H. N. G. Wadley and R. M. McMeeking, Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness, Nature, 2017, 543, 533 CrossRef CAS PubMed.
- E. T. Filipov, T. Tachi and G. H. Paulino, Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials, Proc. Natl. Acad. Sci. U.S.A., 2015, 112, 12321–12326 CrossRef CAS PubMed.
- H. Yasuda, T. Tachi, M. Lee and J. Yang, Origami-based tunable truss structures for non-volatile mechanical memory operation, Nat. Commun., 2017, 8, 962 CrossRef PubMed.
- B. Haghpanah, L. Salari-Sharif, P. Pourrajab, J. Hopkins and L. Valdevit, Multistable Shape-Reconfigurable Architected Materials, Adv. Mater., 2016, 28, 7915–7920 CrossRef CAS PubMed.
- S. Jianfeng, H. Yizhe, L. Chen, Q. Chen and Y. Mingxin, Synthesis of Amphiphilic Graphene Nanoplatelets, Small, 2009, 5, 82–85 CrossRef PubMed.
- N. Levy, S. A. Burke, K. L. Meaker, M. Panlasigui, A. Zettl and F. Guinea, et al. Strain-Induced Pseudo–Magnetic Fields Greater Than 300 Tesla in Graphene Nanobubbles, Science, 2010, 329, 544–547 CrossRef CAS PubMed.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Penta-graphene: A new carbon allotrope, Proc. Natl. Acad. Sci. U.S.A., 2015, 112, 2372–2377 CrossRef CAS PubMed.
- B. F. Grosso and E. J. Mele, Bending Rules in Graphene Kirigami, Phys. Rev. Lett., 2015, 115, 195501 CrossRef PubMed.
- Z. Qi, D. K. Campbell and H. S. Park, Atomistic simulations of tension-induced large deformation and stretchability in graphene kirigami, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245437 CrossRef CAS.
- Y. Zhao, C. Wang, J. Wu, C. Sui, S. Zhao and Z. Zhang, et al. Carbon nanotubes kirigami mechanical metamaterials, Phys. Chem. Chem. Phys., 2017, 19, 11032–11042 RSC.
- L. Tapasztó, G. Dobrik, P. Lambin and L. P. Biró, Tailoring the atomic structure of graphene nanoribbons by scanning tunnelling microscope lithography, Nat. Nanotechnol., 2008, 3, 397 CrossRef PubMed.
- J. Annett and G. L. W. Cross, Self-assembly of graphene ribbons by spontaneous self-tearing and peeling from a substrate, Nature, 2016, 535, 271 CrossRef CAS PubMed.
- P. Z. Hanakata, Z. Qi, D. K. Campbell and H. S. Park, Highly stretchable MoS2 kirigami, Nanoscale, 2016, 8, 458–463 RSC.
- Y. Wang, A. Vallabhaneni, J. Hu, B. Qiu, Y. P. Chen and X. Ruan, Phonon Lateral Confinement Enables Thermal Rectification in Asymmetric Single-Material Nanostructures, Nano Lett., 2014, 14, 592–596 CrossRef CAS PubMed.
- Y. Gao, W. Yang and B. Xu, Tailoring Auxetic and Contractile Graphene to Achieve Interface Structures with Fully Mechanically Controllable Thermal Transports, Adv. Mater. Interfaces, 2017, 4, 1700278 CrossRef.
- O. Akhavan, Graphene Nanomesh by ZnO Nanorod Photocatalysts, ACS Nano, 2010, 4, 4174–4180 CrossRef CAS PubMed.
- A. Miyamoto, S. Lee, N. F. Cooray, S. Lee, M. Mori and N. Matsuhisa, et al. Inflammation-free, gas-permeable, lightweight, stretchable on-skin electronics with nanomeshes, Nat. Nanotechnol., 2017, 12, 907 CrossRef CAS PubMed.
- S. Xu, Y. Zhang, J. Cho, J. Lee, X. Huang and L. Jia, et al. Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems, Nat. Commun., 2013, 4, 1543 CrossRef PubMed.
- J. A. Fan, W.-H. Yeo, Y. Su, Y. Hattori, W. Lee and S.-Y. Jung, et al. Fractal design concepts for stretchable electronics, Nat. Commun., 2014, 5, 3266 CrossRef PubMed.
- J. Liu and Y. Zhang, A Mechanics Model of Soft Network Materials With Periodic Lattices of Arbitrarily Shaped Filamentary Microstructures for Tunable Poisson's Ratios, J. Appl. Mech., 2018, 85, 051003 CrossRef.
- D. Mousanezhad, S. Babaee, R. Ghosh, E. Mahdi, K. Bertoldi and A. Vaziri, Honeycomb phononic crystals with self-similar hierarchy, Phys. Rev. B, 2015, 92, 104304 CrossRef.
- Y. Chen, T. Li, F. Scarpa and L. Wang, Lattice Metamaterials with Mechanically Tunable Poisson's Ratio for Vibration Control, Phys. Rev. Appl., 2017, 7, 024012 CrossRef.
- N. I. Zheludev and E. Plum, Reconfigurable nanomechanical photonic metamaterials, Nat. Nanotechnol., 2016, 11, 16 CrossRef CAS PubMed.
- Y. Tang, G. Lin, S. Yang, Y. K. Yi, R. D. Kamien and J. Yin, Programmable Kiri-Kirigami Metamaterials, Adv. Mater., 2017, 29, 1604262 CrossRef PubMed.
- A. A. Balandin, Thermal properties of graphene and nanostructured carbon materials, Nat. Mater., 2011, 10, 569 CrossRef CAS PubMed.
- N. Wei, Y. Chen, K. Cai, J. Zhao, H.-Q. Wang and J.-C. Zheng, Thermal conductivity of graphene kirigami: Ultralow and strain robustness, Carbon, 2016, 104, 203–213 CrossRef CAS.
- Y. Gao and B. Xu, Controllable Interface Junction, In-Plane Heterostructures Capable of Mechanically Mediating On-Demand Asymmetry of Thermal Transports, ACS Appl. Mater. Interfaces, 2017, 9, 34506–34517 CrossRef CAS PubMed.
- Z. Gao, D. Liu and D. Tománek, Two-Dimensional Mechanical Metamaterials with Unusual Poisson Ratio Behavior, Phys. Rev. Appl., 2018, 10, 064039 CrossRef CAS.
- N. Karathanasopoulos, H. Reda and J.-f Ganghoffer, Designing two-dimensional metamaterials of controlled static and dynamic properties, Comput. Mater. Sci., 2017, 138, 323–332 CrossRef.
- C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- R. E. Roman and S. W. Cranford, Mechanical properties of silicene, Comput. Mater. Sci., 2014, 82, 50–55 CrossRef CAS.
- A. A. Tedstone, D. J. Lewis, R. Hao, S.-M. Mao, P. Bellon and R. S. Averback, et al. Mechanical Properties of Molybdenum Disulfide and the Effect of Doping: An in Situ TEM Study, ACS Appl. Mater. Interfaces, 2015, 7, 20829–20834 CrossRef CAS PubMed.
- Q. Wei and X. H. Peng, Superior mechanical flexibility of phosphorene and few-layer black phosphorus, Appl. Phys. Lett., 2014, 104, 5 Search PubMed.
- T. von Kármán Festigkeitsprobleme im maschinenbau, Teubner, 1910 Search PubMed.
- D. A. Foppl Vorlesungen uber technische mechannik, 1909 Search PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- P. Koskinen and O. O. Kit, Approximate modeling of spherical membranes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235420 CrossRef.
- M. Arroyo and T. Belytschko, Finite crystal elasticity of carbon nanotubes based on the exponential Cauchy-Born rule, Phys. Rev. B, 2004, 69, 115415 CrossRef.
- X. Si and C. Guoxin, Bending response of single layer MoS 2, Nanotechnology, 2016, 27, 105701 CrossRef PubMed.
- L. Ruiz, W. Xia, Z. Meng and S. Keten, A coarse-grained model for the mechanical behavior of multi-layer graphene, Carbon, 2015, 82, 103–115 CrossRef CAS.
- S. Cranford, D. Sen and M. J. Buehler, Meso-origami: Folding multilayer graphene sheets, Appl. Phys. Lett., 2009, 95, 123121 CrossRef.
- F. Javid, E. Smith-Roberge, M. C. Innes, A. Shanian, J. C. Weaver and K. Bertoldi, Dimpled elastic sheets: a new class of non-porous negative Poisson's ratio materials, Sci. Rep., 2015, 5, 18373 CrossRef CAS PubMed.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Poisson's ratio and modern materials, Nat. Mater., 2011, 10, 823 CrossRef CAS PubMed.
- Y. Cho, J.-H. Shin, A. Costa, T. A. Kim, V. Kunin and J. Li, et al. Engineering the shape and structure of materials by fractal cut, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 17390–17395 CrossRef CAS PubMed.
- D. Lu, Y. F. Li, H. Seifi, S. Zhou, Z.-L. Zhao and Y. M. Xie, Designing novel structures with hierarchically synchronized deformations, Extreme Mech. Lett., 2018, 19, 1–6 CrossRef.
- K.-I. Jang, S. Y. Han, S. Xu, K. E. Mathewson, Y. Zhang and J.-W. Jeong, et al. Rugged and breathable forms of stretchable electronics with adherent composite substrates for transcutaneous monitoring, Nat. Commun., 2014, 5, 4779 CrossRef CAS PubMed.
- K.-I. Jang, H. U. Chung, S. Xu, C. H. Lee, H. Luan and J. Jeong, et al. Soft network composite materials with deterministic and bio-inspired designs, Nat. Commun., 2015, 6, 6566 CrossRef CAS PubMed.
- Q. Ma, H. Cheng, K.-I. Jang, H. Luan, K.-C. Hwang and J. A. Rogers, et al. A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures, J. Mech. Phys. Solids, 2016, 90, 179–202 CrossRef PubMed.
- C. Thurnherr, L. Ruppen, G. Kress and P. Ermanni, Non-linear stiffness response of corrugated laminates in tensile loading, Compos. Struct., 2016, 157, 244–255 CrossRef.
- W. Yang, V. R. Sherman, B. Gludovatz, E. Schaible, P. Stewart and R. O. Ritchie, et al. On the tear resistance of skin, Nat. Commun., 2015, 6, 6649 CrossRef CAS PubMed.
- S. Ling, Q. Zhang, D. L. Kaplan, F. Omenetto, M. J. Buehler and Z. Qin, Printing of stretchable silk membranes for strain measurements, Lab Chip, 2016, 16, 2459–2466 RSC.
- P. Chamiot-Clerc, X. Copie, J.-F. Renaud, M. Safar and X. Girerd, Comparative reactivity and mechanical properties of human isolated internal mammary and radial arteries, Cardiovasc. Res., 1998, 37, 811–819 CrossRef CAS.
- K. Bertoldi, V. Vitelli, J. Christensen and M. van Hecke, Flexible mechanical metamaterials, Nat. Rev. Mater., 2017, 2, 17066 CrossRef CAS.
- N. Liu, R. Pidaparti and X. Wang, Abnormal linear elasticity in polycrystalline phosphorene, Phys. Chem. Chem. Phys., 2018, 20, 8668–8675 RSC.
- N. Liu, J. Hong, X. Zeng, R. Pidaparti and X. Wang, Fracture mechanisms in multilayer phosphorene assemblies: from brittle to ductile, Phys. Chem. Chem. Phys., 2017, 19, 13083–13092 RSC.
- N. Liu, J. Hong, R. Pidaparti and X. Wang, Fracture patterns and the energy release rate of phosphorene, Nanoscale, 2016, 8, 5728–5736 RSC.
- L. Ning, H. Jiawang, P. Ramana and W. Xianqiao, Abnormality in fracture strength of polycrystalline silicene, 2D Materials, 2016, 3, 035008 CrossRef.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- J. Jin-Wu, Parametrization of Stillinger–Weber potential based on valence force field model: application to single-layer MoS 2 and black phosphorus, Nanotechnology, 2015, 26, 315706 CrossRef PubMed.
- Q. Peng, X. Wen and S. De, Mechanical stabilities of silicene, RSC Adv., 2013, 3, 13772–13781 RSC.
- G. Jung, Z. Qin and M. J. Buehler, Molecular mechanics of polycrystalline graphene with enhanced fracture toughness, Extreme Mech. Lett., 2015, 2, 52–59 CrossRef.
- W. J. Xia and S. Keten, Size-dependent mechanical behavior of free-standing glassy polymer thin films, J. Mater. Res., 2015, 30, 36–45 CrossRef CAS.
- T. Zhang, X. Li, S. Kadkhodaei and H. Gao, Flaw Insensitive Fracture in Nanocrystalline Graphene, Nano Lett., 2012, 12, 4605–4610 CrossRef CAS PubMed.
- E. T. Mark, A. José, L.-R. Roberto, L. J. Andrea and J. M. Glenn, A Liouville-operator derived measure-preserving integrator for molecular dynamics simulations in the isothermal–isobaric ensemble, J. Phys. A: Math. Gen., 2006, 39, 5629 CrossRef.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Alexander, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00312f |
| This journal is © The Royal Society of Chemistry 2019 |