Open Access Article
Open Access ArticleHost dependence of the electron affinity of molecular dopants†
Jing
Li
 a,
Ivan
Duchemin
a,
Ivan
Duchemin
 b,
Otello Maria
Roscioni
b,
Otello Maria
Roscioni
 c,
Pascal
Friederich‡
c,
Pascal
Friederich‡
 d,
Marie
Anderson
e,
Enrico
Da Como
d,
Marie
Anderson
e,
Enrico
Da Como
 e,
Gabriele
Kociok-Köhn
e,
Gabriele
Kociok-Köhn
 f,
Wolfgang
Wenzel
d,
Claudio
Zannoni
f,
Wolfgang
Wenzel
d,
Claudio
Zannoni
 c,
David
Beljonne
c,
David
Beljonne
 g,
Xavier
Blase
g,
Xavier
Blase
 a and
Gabriele
D'Avino
a and
Gabriele
D'Avino
 *a
*a
aInstitut Néel, CNRS and Grenoble Alpes University, F-38042 Grenoble, France. E-mail: gabriele.davino@neel.cnrs.fr
bGrenobles Alpes University, CEA, INAC MEM, L_Sim, F-38000 Grenoble, France
cDipartimento di Chimica Industriale “Toso Montanari”, Università di Bologna, viale Risorgimento 4, 40136 Bologna, Italy
dKarlsruhe Institute of Technology, Institute of Nanotechnology Hermann-von- Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
eDepartment of Physics and Centre for Photonics and Photonic Materials, University of Bath, Bath, BA2 7AY, UK
fChemical Characterization and Analysis Facility, University of Bath, Bath, BA2 7AY, UK
gLaboratory for the Chemistry of Novel Materials, University of Mons, Place du Parc 20, Mons, BE-7000, Belgium
First published on 2nd October 2018
Abstract
Charge carriers energetics is key in electron transfer processes such as those that enable the electrical doping of organic semiconductors. In this study, we take advantage of the quantitative accuracy of embedded GW calculations to perform a series of virtual experiments that allow measuring the electron affinity of p-type dopants in different host solids. Our calculations show that the energy levels of a molecular impurity strongly depend on the host environment as a result of electrostatic intermolecular interactions. In particular, the electron affinity of a dopant impurity in a given semiconductor is found to be up to 1 eV lower than that of the pure dopant crystal. This result questions the pertinence of the electron affinity measured for pure dopants in order to predict doping efficiency in a specific host. The role of the Coulomb electron–hole interaction for the dopant-to-semiconductor charge transfer and for the release of doping-induced charges is discussed.
Conceptual insightsThe electron affinity of molecular p-type dopants is considered to be the crucial quantity for determining the efficiency of the electrical doping of organic semiconductors. In this communication we demonstrate that the electron affinity of a dopant does strongly depend on the molecular host as a result of intermolecular electrostatic interactions. The latter can reduce the electron affinity by up to 1 eV when going from the dopant crystal to a dopant impurity in an organic semiconductor. Our accurate electronic structure calculations hence disprove the common belief that the electron affinity is an intrinsic molecular properties that can be measured on films of pure dopants and then applied to discuss doping in semiconductors. Furthermore, we draw the attention on the excitonic electron–hole interaction, which on one hand is necessary to have a dopant to semiconductor charge transfer, but on the other hand leads to Coulombically pinned carriers. Our modeling suggests that performance optimization would require a trade off between these two factors. |
Introduction
Molecular doping, i.e. the introduction of controlled amounts of strong electron withdrawing or donating molecules, is an established technique that allows the tuning of the electrical properties of organic semiconductors (OSCs). Doping of organic semiconducting layers is key for the success of organic opto-electronic devices such as light emitting diodes or solar cells, as it allows the enhancement of the electrical conductivity or the engineering of charge injection barrier at interfaces to other materials.1–3 Despite the fact that molecular doping is at the heart of efficient and stable devices, the fundamentals of its mechanism are largely unclear, sparkling an outstanding research effort.4–10The first step in the doping process is generally regarded as an electron transfer between the dopant impurity and the host semiconductor. In the case of p-type doping, a strong electron acceptor molecule oxidizes the host, a process that is usually discussed in the literature by comparing the electron affinity of the dopant (EAD) and the ionization potential of the host semiconductor (IPS), with doping becoming effective when the difference EAD − IPS is negative or vanishingly small.1,11–14
The simple argument that the effectiveness of doping would only depend on the energetics of the donating and accepting energy levels finds plausible confirmations in experimental literature. Common molecular hole-transporting materials, such as pentacene (PEN, IP = 4.9 eV for films of standing molecules15) or N,N′-di(1-naphthyl)-N,N′-diphenyl-(1,1′-biphenyl)-4,4′-diamine (NPB or NPD, IP = 5.2 eV12), are successfully doped by strong oxidants such as 2,3,5,6-tetrafluoro-tetracyanoquinodimethane (F4TCNQ, EA = 5.08–5.24 eV16,17) or 2,2′-(perfluoronaphthalene-2,6-diylidene)dimalononitrile (F6TCNNQ, EA = 5.37–5.60 eV13,18). On the polymer side, F4TCNQ proved able to dope poly(3-hexylthiophene) (P3HT, IP = 4.6 eV6), while the oxidation of a diketopyrrolopyrrole-based polymer with IP = 5.49 eV14 could be attained only by the very strong acceptor hexacyano-trimethylene-cyclopropane19,20 (CN6-CP, EA = 5.87 eV14).
Special attention should be, however, payed while comparing experimental data from different sources. Indeed, while IP and EA are intrinsic properties of a given individual (isolated or gas-phase) molecule, environmental interactions in condensed phase make such quantities strongly dependent on the measurement technique (e.g. photoelectron spectroscopy vs. cyclic voltammetry) and on the molecular organization in the solid state. Even in the simpler case of pristine compounds, differences in the IP up to 0.6 eV have been reported between films of standing vs. laying molecules,15,21 pointing to the crucial role of intermolecular electrostatic interactions.22–24
The implications of environmental phenomena on the EA of dopants have been largely overlooked so far. While the comparison between IP and EA of the pure phases of host and dopant is the most common practice in the literature,1,11–14 the current understanding of intermolecular interactions23–25 suggests that the EA of a dopant could be influenced to some extent by the host environment. Probing the EA of a dopant impurity can be experimentally challenging, owing to the weak signal expected at low concentration, but also because the EA of (neutral) dopants cannot be determined by inverse photoemission spectroscopy (IPES) in a sample where dopants are ionized.
Theoretical calculations do not suffer from the above-mentioned limitations and have the potential to elucidate the role of the host environment on the EA of molecular dopants, provided that an accurate description of the molecular electronic structure is combined with a proper account of environmental effects. Embedded many-body perturbation theory techniques of very recent development,26–28 combining in a hybrid quantum/classical (QM/MM) framework state-of-the art Green's function GW29–34 and Bethe–Salpeter equation formalisms35–40 with a careful atomistic description of the molecular environment,24,41 do exactly respond to the above mentioned requirements. Gas-phase GW calculations are receiving increasing attention in the context of molecular systems thanks to a very favorable balance between accuracy, demonstrated by extensive benchmark studies,42–47 and computational cost of atomic-orbital implementations,48–51 which allow describing systems up to a few hundreds of atoms.28,50,52,53 The embedded GW formalism has recently demonstrated quantitative accuracy in the determination of the IP and EA of the prototypical organic semiconductors PEN and perfluoro-PEN, thanks to a proper account of polarization and electrostatics (crystal field) effects at crystal surfaces.25 While GW periodic boundary conditions calculations have proven their ability in describing pristine OSCs,54–56 our embedded formalism further allows the study of systems where periodicity is broken by a dopant impurity or disorder.
In a recent work, we have shown that in the paradigmatic case of F4TCNQ-doped PEN4,11,57 the acceptor level lies deep in the PEN gap (∼0.7 eV) and that ionization can occur as a result of the strong electron–hole (e–h) Coulomb binding that stabilizes charge-transfer states, reconciling conflicting results in optical4 and scanning tunneling spectroscopy11 experiments.28 While acknowledging the importance of IPS and EAD in the energetics of the charge transfer process, our theoretical findings challenged the simplistic picture solely based on photoemission levels, calling instead for an excitonic58 explanation of the doping mechanism.28 The crucial role of the e–h interaction has been emphasized in a very recent joint experimental and theoretical study on n-doped semiconductors, where the Coulomb binding has been assessed from photoelectron spectroscopy data and successfully correlated to conductivity.10
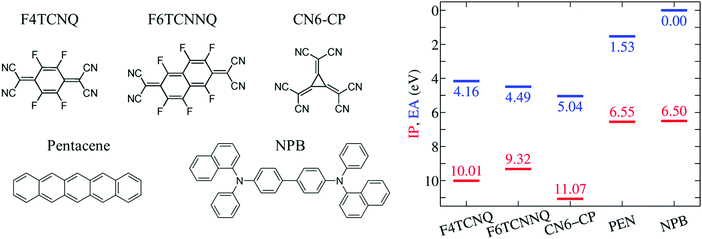
In the present Communication, we take advantage of our recent methodological advancements and design a set of computational experiments addressing the influence of the host environment on the EA of the prototypical p-dopants F4TCNQ, F6TCNNQ and CN6-CP (see Fig. 1). Our accurate calculations show that the EA of a dopant impurity does strongly depend on its solid state environment, mostly because of electrostatic potential exerted by the neighboring molecules in both crystalline and amorphous phases. This result questions the applicability of the energy levels measured or calculated for the pristine OSC and dopant solids, which results in a systematic and large (up to 1 eV) underestimation of the EAD − IPS difference. Our results rationalize the deep acceptor levels of dopant impurities in host OSCs, clarifying the crucial role of the Coulomb e–h (excitonic) interaction for the dopant ionization and its implications on the possible generation of free charges.
Results
We start our discussion from the IP and EA of the selected p-type dopants and host molecules in the gas phase as obtained from GW calculations (see Fig. 1). This is an important step as it allows the quantification of the intrinsic electron attracting or donating character of an individual molecule, i.e. before introducing the effect of the environment. To our knowledge, gas-phase experimental ion energetics data are available only for PEN among the selected molecules.59 The excellent agreement obtained for PEN, within 0.1 eV for both IP and EA in the present study (complete basis set limit) gives us full confidence in the predictive value of our methodology.Results in Fig. 1 show that the EA of isolated dopants progressively increases along the F4TCNQ, F6TCNNQ, CN6-CP series, with the EA of CN6-CP being 0.9 eV larger than in F4TCNQ. PEN and NPB present very similar IP, hence a similar electron-donating character is expected for the two semiconducting molecules. The difference between the EA of the dopant and the IP of the host, ranges between 2.3 eV for F4TCNQ–NPB and 1.5 eV for PEN–CN6-CP in the gas phase. Such a large IPS − EAD gap makes the OSC to dopant electron transfer energetically prohibitive in the gas phase.
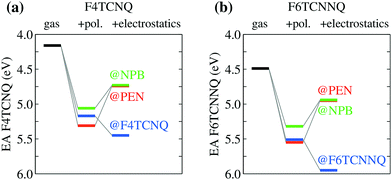
We turn our attention to the energy levels obtained for molecules in the solid state. To such an aim, we consider first the dopant molecules F4TCNQ and F6TCNNQ as substitutional impurities in the lattice of the host OSCs PEN and NPB, along with the pure crystals of dopants and hosts. While it can be somehow expected that the energy levels of a given molecule depend on the host crystal, our embedded GW calculations (see Table 1) reveal that environmental effects on the energetics are surprisingly large. As shown in Fig. 2a, the EA of F4TCNQ is 5.45 eV in its pure crystal phase, while it attains the values of 4.73 and 4.72 eV when the molecule is inserted into the PEN and NPB crystal lattice, respectively. Very similar EA values have been previously calculated for F4TCNQ in amorphous MTDATA, another common OSC host.60 The EA of the F4TCNQ crystal and that of the same molecule as dopant in common host semiconductors hence differ by 0.7 eV and such a host-dependent spread of EA values reaches 1 eV of magnitude in the case of F6TCNNQ, shown in Fig. 2b. We notice that the relative doping strength of isolated dopants is preserved in the solid state, with, for instance, F6TCNNQ remaining a stronger dopant than F4TCNQ also in hole transporting hosts. This results from the fact that the environmental contribution to the energy levels mostly depends on the host and similar shifts are expected for different molecules in the same host (see below).
| Guest@host | IP | EA |
|---|---|---|
| F4TCNQ@F4TCNQ | 9.38 (9.28) | 5.45 (5.55) |
| F4TCNQ@PEN | 8.38 | 4.73 |
| F4TCNQ@NPB | 8.80 | 4.72 |
| F6TCNNQ@F6TCNNQ | 8.82 (8.66) | 5.95 (6.01) |
| F6TCNNQ@PEN | 7.75 | 4.95 |
| F6TCNNQ@NPB | 8.15 | 4.94 |
| PEN@PEN | 5.38 (5.16) | 2.50 (2.77) |
| NPB@NPB | 5.58 (5.54) | 0.79 (0.90) |
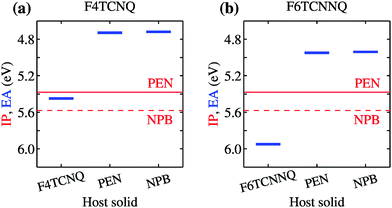 | ||
| Fig. 2 Dependence of the EA of (a) F4TCNQ and (b) F6TCNNQ on the solid-state host environment. Horizontal lines show the bulk IP of the PEN and NPB for comparison. Results obtained considering the ionization of individual molecules embedded in a crystalline host (localized charge picture). Bandwidth effects does not qualitatively alter the result (see Table 1 and ESI†). | ||
Fig. 2 also reports the IP of PEN and NPB, allowing a straightforward comparison with the acceptor levels of the dopants. Present results are consistent with our earlier embedded GW calculations for a 7-molecule PEN–F4TCNQ complex,28 featuring a HOMO–LUMO gap of 0.67 eV, and with the experimental evidence that the EA of pure dopant films are comparable to or larger than the IP of the pristine host semiconductor.1,11–14 Most importantly, these results question the relevance of photoelectron spectroscopy measurements in pristine systems as a mean to predict ionization of dopants in a given semiconductor. We note that electronic band dispersion does also contribute to the IP and EA of pristine crystals, yet this smaller effect does not alter qualitatively the picture arising from the localized-charge picture presented in Fig. 2 (see values in parenthesis in Table 1).
In order to understand the physical origin of the stunningly large impact of the host on dopants energy levels, we have partitioned the environmental shifts into their different contributions, namely polarization, reflecting the dynamical reaction of the dielectric medium to ionization, and electrostatics, accounting for the interaction of the ionized molecule with the electrical multipoles of the surrounding neutral molecules in the solid.24,25 Results in Fig. 3 show that polarization always increases the EA of the dopants by 1 ± 0.2 eV in all the hosts. Such a rather universal levels shift follows from the similar dielectric constant of organic solids (εr ∼ 3–4) and might be approximately captured also with simpler approaches such as the continuum polarizable model. At the same time, polarization effects reduce the IP of the host (see Table 1), leading eventually to a reduction of the IPS − EAD difference by ∼2 eV with respect to gas-phase data in Fig. 1.
The pronounced host dependence of the dopants EAs arises instead from electrostatics, affecting the EAD by up to 0.6 eV in magnitude, but with opposite trends when dopants are embedded in their pure crystals or in the two hole-transporting hosts PEN and NPB (see Fig. 3). In particular, the electrostatic contribution increases the EA of F4TCNQ or F6TCNNQ in their pure crystal phases, while it reduces EA for dopants as impurities in semiconducting hosts. The opposite electrostatic shifts in the different types of host suggests that the EA of a p-type dopant inserted as an impurity in a given OSC host would be largely overestimated by the values measured for the pure phase of a dopant.
Considering the relevance of the energy levels of impurities for the mechanistic understanding of doping, it is important to understand if the above conclusion does apply to other systems, including amorphous morphologies which are usually found in real devices. As far as dopants act as substitutional defects in the OSC crystal lattice, electrostatics shifts do mostly depend on the host, and specifically on the charge density (electrostatic layout) of host molecules and their packing in the crystal. In this case, the knowledge gathered for pristine OSCs can be directly applied to dopant impurities. Extensive data accumulated by different groups in the last decade25,41,61–66 (see ESI† for a compilation of literature data) show that molecules with an electrostatic layout characterized by electron-attracting groups (e.g. cyano or halogens) functionalizing the molecular periphery, such as p-type dopants like F4TCNQ, F6TCNNQ or electron-transporting OSCs (e.g. perfluoropentacene) usually present electrostatic shifts increasing the EA (and the IP). Conversely, electrostatic shifts reducing the EA were observed in hole-transporting OSCs featuring electron-rich π-conjugated cores, thus suggesting that the EA measured (or calculated) in the pure dopant phase would systematically underestimate the energy of the acceptor level of an impurity in an OSC matrix.
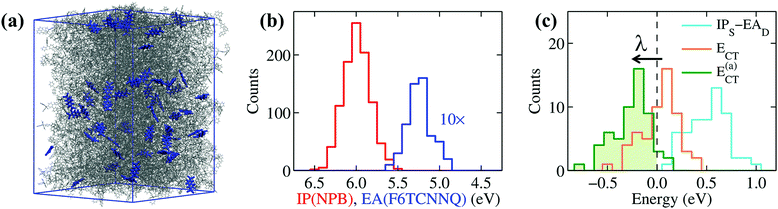
To extend the reach of our study towards realistic morphologies, we have considered amorphous NPB samples doped with F6TCNNQ obtained with atomistic force-field simulations mimicking the formation of doped films by vapor co-deposition (see Methods and ESI† for details). These simulations allowed us to obtain a good statistics over the electronic properties of realistic amorphous structures. Results for a system of 5% doping, shown in Fig. 4, are comparable to what obtained for molar concentrations between 2 and 10%. Fig. 4b shows the distributions of the IP of NPB and the EA of F6TCNNQ. The difference IPS − EAD, measured between the mean values of the two distributions, is of 0.8 eV, a value that closely compares to that previously obtained for ideal crystalline structures (see Table 1). The average EA of F6TCNNQ (5.13 eV) in the amorphous host, mostly composed of NPB molecules, closely compares to the value obtained for the idealized structure (4.96 eV). The small discrepancy can be attributed to the weaker dielectric screening in the amorphous system characterized by a non-optimal molecular packing, while, most importantly, in both cases electrostatic interactions reduce the EA of F6TCNNQ by 0.4 eV. This result confirms that EAD is largely reduced in a host OSC by electrostatic interactions with the environment, irrespective on the crystalline or amorphous nature of the host.
The distributions in Fig. 4b are remarkably broad, reflecting the differences in the local environment and conformation experienced by each molecule. The little overlap between the distributions of IPS and EAD might suggest some possibility for OSC-to-dopant electron transfer, yet overlapping tails do not actually correspond to neighboring F6TCNNQ–NPB pairs. This is revealed by the distribution of the IPS − EAD differences calculated for nearest-neighbor dopant-OSC dimers, shown as a light-blue line Fig. 4c, which peaks at energy values above 0.5 eV and whose tail does not extend down to negative energies.
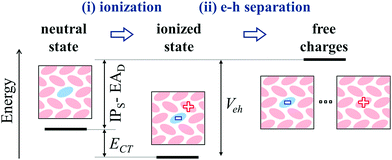
The key quantity determining the possibility for the spontaneous dopant ionization is, however, the energy ECT = IPS − EAD + Veh of the charge-transfer state presenting an electron sitting on the dopant and the hole on one of the neighboring NPB.67 This quantity includes the Coulomb electron–hole (e–h) excitonic interaction Veh, which has been recently shown to be crucial for the ionization of dopants, even in the presence of very deep impurity acceptor levels.28 The e–h interaction can exceed 0.5 eV of magnitude for neighboring F6TCNNQ–NPB molecules, consistently with previous estimates for a F4TCNQ dopant in pentacene.28 The large values of Veh are decisive for the ionization, as can be seen from the distribution of ECT in Fig. 4c that presents a sizable fraction of its area (43%) at negative energies, which corresponds to the fraction of spontaneously ionized dopants.
The large IPS − EAD difference in F6TCNNQ-doped NPB is approximately compensated by the Coulomb e–h binding, similarly to what previously concluded for F4TCNQ–pentacene.28 In the presence of such a subtle balance of competing interactions, smaller effects can play an important role, the most important of which is structural relaxation upon charging. Such a polaronic effect can be effectively introduced in the present analysis by replacing the vertical (i.e. at frozen geometry) values of IP and EA discussed hitherto with the adiabatic (relaxed) ones. The distribution of the adiabatic charge-transfer states energies (Fig. 4c), E(a)CT = ECT − λ, being λ = λ+(NPB) + λ−(F6TCNNQ) = 0.28 eV (gas-phase PBE0/def2-SVP level) the relaxation energy, leads us to conclude that the vast majority (95%) of F6TCNNQ dopants ionize upon accounting for the Coulomb e–h interaction and intramolecular structural relaxation.
Discussion and conclusion
The mechanism for molecular doping in organic semiconductors has been depicted as a two-step process involving (i) a spontaneous electron transfer and (ii) the subsequent dissociation of Coulombically bound e–h pairs9 (see Fig. 5). The present work focused on the first step, clearing common misconceptions in the literature by means of state-of-the-art electronic structure calculations. In the case of p-type doping, the initial electron transfer is usually discussed by comparing the IP of the OSC and the dopant's EA, based on the energy levels measured in the pure phases of the two materials. Upon considering several host-OSC combinations in both crystalline and amorphous morphologies, we have shown that the dopant EA does strongly depend (up to 1 eV) on the host medium and that energy levels of pure materials are not relevant for doping, as they tend to systematically underestimate the IPS − EAD difference. The host dependence of charge transport levels of guest molecules in molecular blends has possible implications also for n-type doping, as well as for charge transfer to emitters in OLED devices.Dopant ionization results from the competition between the neutral and ionized state and it can spontaneously occur (ECT < 0), in spite of very deep acceptor levels, because of the Coulomb interaction between electron and hole, with a smaller but often determinant contribution from structural relaxation (polaronic effects). As shown in Fig. 5, the very same e–h binding (Veh) that is crucial for ionization, corresponds to the energy that is necessary to free the hole from the dopant and hence make it contributing to transport. Such an energy barrier is independent on the dopant's EA. Our findings hence suggest that future efforts for performances optimization should focus on the morphology and in particular on the relative positions of dopants and π-conjugated cores, which in turn controls Veh. Having a small barrier for charge release should be, however, compensated by a dopant's EA large enough to ensure the ionization of the semiconductor. The present work clarifies the early steps of the doping mechanism, providing solid grounds to pursue investigations on the many-body problem corresponding to heavily doped organic semiconductors.
Methods
Electron addition and removal energies have been evaluated with GW calculations performed on individual molecules in the gas phase, as well as embedded in a given solid state environment described at the atomistic level. In order to fully capture the effect of the medium on the electronic structure of the embedded molecule (i.e. the QM molecule of our QM/MM framework), both the ground-state DFT calculation and the subsequent GW one should properly take into account the embedding environment. The energy of the nth level of the embedded molecule can be conveniently partitioned as| En(GWe|DFTe) = En(GWg|DFTg) + ΔnP + ΔnE, | (1) |
| ΔnP = En(GWe|DFTg) − En(GWg|DFTg) | (2) |
| ΔnE = En(GWe|DFTe) − En(GWe|DFTg). | (3) |
For calculations on crystalline materials, atomic coordinates were taken from published X-ray crystal structures of PEN,68 NPB69 and F4TCNQ.70 The crystal structure of F6TCNNQ has been determined with single-crystal X-ray diffraction in the present study. F6TCNNQ was provided by Novaled GmbH and used as received. It crystallizes in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group (cell parameters: a = b = 17.533 Å, c = 11.484 Å) with 9 molecules per unit cell (Z = 9). Detailed crystallographic information is given in the ESI† and in the deposited CIF file (CCDC no. 1859755).† A substitutional impurity of F4TCNQ or F6TCNNQ was introduced in the OSC (PEN or NPB) crystal lattice assuming that the dopant molecule retains the same position orientation of the backbone of the replaced molecule. The molecular geometries in the crystal structure were also used in gas-phase calculations, except for CN6-CP that was fully optimized in the vacuum at the PBE0/6-311++G** level.
space group (cell parameters: a = b = 17.533 Å, c = 11.484 Å) with 9 molecules per unit cell (Z = 9). Detailed crystallographic information is given in the ESI† and in the deposited CIF file (CCDC no. 1859755).† A substitutional impurity of F4TCNQ or F6TCNNQ was introduced in the OSC (PEN or NPB) crystal lattice assuming that the dopant molecule retains the same position orientation of the backbone of the replaced molecule. The molecular geometries in the crystal structure were also used in gas-phase calculations, except for CN6-CP that was fully optimized in the vacuum at the PBE0/6-311++G** level.
GW calculations have been performed with the FIESTA package,48 starting from ground-state density functional theory (DFT) calculations (PBE0 functional), the latter obtained with the NWCHEM suite.71 Calculations were performed with a partial self-consistent scheme on the eigenvalues (evGW), employing Gaussian basis functions of the correlation-consistent family (cc-pVXZ).72 Quasiparticle energy levels have been extrapolated to the complete basis set limit. The universal Weigend Coulomb fitting set of functions73 has been adopted as auxiliary basis in the resolution of the identity (RI-V) scheme.74 The charge response model,61 as implemented in the MESCAL code,41 has been adopted for the atomistic description of the classical (MM) sub-system, in virtue of the excellent description of the anisotropic dielectric response of molecular crystals.41,75 The potential of MM molecules has been described with point atomic charges from electrostatic fitting (ESP scheme).76
Realistic amorphous morphologies of F6TCNNQ-doped NPB have been obtained with atomistic force-field simulations. The simulation protocol adopted here consists of two steps: (i) vapor-phase deposition of doped films of different doping concentrations and 1050 molecules in total with the linear-scaling Monte Carlo-based DEPOSIT scheme;77 (ii) subsequent thermalization at ambient temperature and pressure with molecular dynamics simulations (NPT ensemble) as to obtain well-equilibrated bulk samples. The sampling of electronic properties over amorphous samples is performed with a computationally viable approach (including GW, DFT and charge response model41,61 calculations) that ensures comparability of results with embedded GW calculations for crystalline morphologies.
Full detail on the computational approach can be found in the ESI.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully thank Antoine Kahn and Yoann Olivier for stimulating discussions, and Novaled GmbH for providing F6TCNNQ. This project has received funding from the European Union Horizon 2020 research and innovation programme under grant agreement no. 646176 (EXTMOS). Work in Karlsruhe was also supported by the MSMEE project. This research used computational resources from the French GENCI-CINES/IDRIS, the Belgian CECI/CENAERO and the German ForHLR I (funded by the Ministry of Science, Research and the Arts Baden-Württemberg and Deutsche Forschungsgemeinschaft).Notes and references
- K. Walzer, B. Maennig, M. Pfeiffer and K. Leo, Chem. Rev., 2007, 107, 1233–1271 CrossRef CAS PubMed.
- I. Salzmann, G. Heimel, M. Oehzelt, S. Winkler and N. Koch, Acc. Chem. Res., 2016, 49, 370–378 CrossRef CAS PubMed.
- I. E. Jacobs and A. J. Moulé, Adv. Mater., 2017, 29, 1703063 CrossRef PubMed.
- I. Salzmann, G. Heimel, S. Duhm, M. Oehzelt, P. Pingel, B. M. George, A. Schnegg, K. Lips, R.-P. Blum, A. Vollmer and N. Koch, Phys. Rev. Lett., 2012, 108, 035502 CrossRef PubMed.
- A. Mityashin, Y. Olivier, T. Van Regemorter, C. Rolin, S. Verlaak, N. G. Martinelli, D. Beljonne, J. Cornil, J. Genoe and P. Heremans, Adv. Mater., 2012, 24, 1535–1539 CrossRef CAS PubMed.
- H. Méndez, G. Heimel, S. Winkler, J. Frisch, A. Opitz, K. Sauer, B. Wegner, M. Oehzelt, C. Röthel, S. Duhm, D. Többens, N. Koch and I. Salzmann, Nat. Commun., 2015, 6, 8560 CrossRef PubMed.
- R.-Q. Png, M. C. Y. Ang, M.-H. Teo, K.-K. Choo, C. G. Tang, D. Belaineh, L.-L. Chua and P. K. H. Ho, Nat. Commun., 2016, 7, 11948 CrossRef CAS PubMed.
- K. Kang, S. Watanabe, K. Broch, A. Sepe, A. Brown, I. Nasrallah, M. Nikolka, Z. Fei, M. Heeney, D. Matsumoto, K. Marumoto, H. Tanaka, S.-I. Kuroda and H. Sirringhaus, Nat. Mater., 2016, 15, 896 CrossRef CAS PubMed.
- M. L. Tietze, J. Benduhn, P. Pahner, B. Nell, M. Schwarze, H. Kleemann, M. Krammer, K. Zojer, K. Vandewal and K. Leo, Nat. Commun., 2018, 9, 1182 CrossRef PubMed.
- C. Gaul, S. Hutsch, M. Schwarze, K. S. Schellhammer, F. Bussolotti, S. Kera, G. Cuniberti, K. Leo and F. Ortmann, Nat. Mater., 2018, 17, 439–444 CrossRef CAS PubMed.
- S. D. Ha and A. Kahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195410 CrossRef.
- W. Gao and A. Kahn, J. Appl. Phys., 2003, 94, 359–366 CrossRef CAS.
- F. Zhang and A. Kahn, Adv. Funct. Mater., 2018, 28, 1703780 CrossRef.
- Y. Karpov, T. Erdmann, I. Raguzin, M. Al-Hussein, M. Binner, U. Lappan, M. Stamm, K. L. Gerasimov, T. Beryozkina, V. Bakulev, D. V. Anokhin, D. A. Ivanov, F. Günther, S. Gemming, G. Seifert, B. Voit, R. Di Pietro and A. Kiriy, Adv. Mater., 2016, 28, 6003–6010 CrossRef CAS PubMed.
- I. Salzmann, S. Duhm, G. Heimel, M. Oehzelt, R. Kniprath, R. L. Johnson, J. P. Rabe and N. Koch, J. Am. Chem. Soc., 2008, 130, 12870–12871 CrossRef CAS PubMed.
- K. Kanai, K. Akaike, K. Koyasu, K. Sakai, T. Nishi, Y. Kamizuru, T. Nishi, Y. Ouchi and K. Seki, Appl. Phys. A: Mater. Sci. Process., 2009, 95, 309–313 CrossRef CAS.
- W. Gao and A. Kahn, Appl. Phys. Lett., 2001, 79, 4040–4042 CrossRef CAS.
- P. K. Koech, A. B. Padmaperuma, L. Wang, J. S. Swensen, E. Polikarpov, J. T. Darsell, J. E. Rainbolt and D. J. Gaspar, Chem. Mater., 2010, 22, 3926–3932 CrossRef CAS.
- T. Fukunaga, J. Am. Chem. Soc., 1976, 98, 610–611 CrossRef CAS.
- T. Fukunaga, M. D. Gordon and P. J. Krusic, J. Am. Chem. Soc., 1976, 98, 611–613 CrossRef CAS.
- S. Duhm, G. Heimel, I. Salzmann, H. Glowatzki, R. L. Johnson, A. Vollmer, J. P. Rabe and N. Koch, Nat. Mater., 2008, 7, 326 CrossRef CAS PubMed.
- B. J. Topham and Z. G. Soos, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165405 CrossRef.
- G. Heimel, I. Salzmann, S. Duhm and N. Koch, Chem. Mater., 2011, 23, 359–377 CrossRef CAS.
- G. D'Avino, L. Muccioli, F. Castet, C. Poelking, D. Andrienko, Z. G. Soos, J. Cornil and D. Beljonne, J. Phys.: Condens. Matter, 2016, 28, 433002 CrossRef PubMed.
- J. Li, G. D'Avino, I. Duchemin, D. Beljonne and X. Blase, Phys. Rev. B, 2018, 97, 035108 CrossRef.
- I. Duchemin, D. Jacquemin and X. Blase, J. Chem. Phys., 2016, 144, 164106 CrossRef PubMed.
- J. Li, G. D'Avino, I. Duchemin, D. Beljonne and X. Blase, J. Phys. Chem. Lett., 2016, 7, 2814–2820 CrossRef CAS PubMed.
- J. Li, G. D'Avino, A. Pershin, D. Jacquemin, I. Duchemin, D. Beljonne and X. Blase, Phys. Rev. Mater., 2017, 1, 025602 CrossRef.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- G. Strinati, H. Mattausch and W. Hanke, Phys. Rev. Lett., 1980, 45, 290–294 CrossRef CAS.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413 CrossRef CAS.
- R. W. Godby, M. Schlüter and L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10159–10175 CrossRef.
- F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys., 1998, 61, 237 CrossRef CAS.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- E. E. Salpeter and H. A. Bethe, Phys. Rev., 1951, 84, 1232–1242 CrossRef.
- W. Hanke and L. J. Sham, Phys. Rev. Lett., 1979, 43, 387–390 CrossRef CAS.
- G. Onida, L. Reining, R. W. Godby, R. Del Sole and W. Andreoni, Phys. Rev. Lett., 1995, 75, 818–821 CrossRef CAS PubMed.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 80, 3320–3323 CrossRef CAS.
- L. X. Benedict, E. L. Shirley and R. B. Bohn, Phys. Rev. Lett., 1998, 80, 4514–4517 CrossRef CAS.
- X. Blase, I. Duchemin and D. Jacquemin, Chem. Soc. Rev., 2018, 47, 1022–1043 RSC.
- G. D'Avino, L. Muccioli, C. Zannoni, D. Beljonne and Z. G. Soos, J. Chem. Theory Comput., 2014, 10, 4959–4971 CrossRef PubMed.
- M. J. van Setten, F. Caruso, S. Sharifzadeh, X. Ren, M. Scheffler, F. Liu, J. Lischner, L. Lin, J. R. Deslippe, S. G. Louie, C. Yang, F. Weigend, J. B. Neaton, F. Evers and P. Rinke, J. Chem. Theory Comput., 2015, 11, 5665–5687 CrossRef CAS PubMed.
- T. Rangel, S. M. Hamed, F. Bruneval and J. B. Neaton, J. Chem. Theory Comput., 2017, 12, 2834–2842 CrossRef PubMed.
- C. Faber, C. Attaccalite, V. Olevano, E. Runge and X. Blase, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115123 CrossRef.
- K. Krause, M. E. Harding and W. Klopper, Mol. Phys., 2015, 113, 1952–1960 CrossRef CAS.
- F. Kaplan, M. E. Harding, C. Seiler, F. Weigend, F. Evers and M. J. van Setten, J. Chem. Theory Comput., 2016, 12, 2528–2541 CrossRef CAS PubMed.
- J. W. Knight, X. Wang, L. Gallandi, O. Dolgounitcheva, X. Ren, J. V. Ortiz, P. Rinke, T. Körzdörfer and N. Marom, J. Chem. Theory Comput., 2016, 12, 615–626 CrossRef CAS PubMed.
- X. Blase, C. Attaccalite and V. Olevano, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115103 CrossRef.
- F. Bruneval, J. Chem. Phys., 2012, 136, 194107 CrossRef PubMed.
- B. Baumeier, D. Andrienko and M. Rohlfing, J. Chem. Theory Comput., 2012, 8, 2790–2795 CrossRef CAS PubMed.
- M. J. van Setten, F. Weigend and F. Evers, J. Chem. Theory Comput., 2013, 9, 232–246 CrossRef CAS PubMed.
- I. Duchemin, T. Deutsch and X. Blase, Phys. Rev. Lett., 2012, 109, 167801 CrossRef CAS PubMed.
- D. Niedzialek, I. Duchemin, T. B. de Queiroz, S. Osella, A. Rao, R. Friend, X. Blase, S. Kümmel and D. Beljonne, Adv. Funct. Mater., 2015, 25, 1972–1984 CrossRef CAS.
- M. L. Tiago, J. E. Northrup and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 115212 CrossRef.
- S. Sharifzadeh, A. Biller, L. Kronik and J. B. Neaton, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125307 CrossRef.
- Y. Kang, S. H. Jeon, Y. Cho and S. Han, Phys. Rev. B, 2016, 93, 035131 CrossRef.
- H. Kleemann, C. Schuenemann, A. A. Zakhidov, M. Riede, B. Lüssem and K. Leo, Org. Electron., 2012, 13, 58–65 CrossRef CAS.
- The term excitonic is used to identify a Coulombically bound state with an electron on the dopant and the hole on the host semiconductor. Since the electron is localized on the dopant, such an exciton in expected to be much less mobile than in pristine semiconductors.
- V. Coropceanu, M. Malagoli, D. A. da Silva Filho, N. E. Gruhn, T. G. Bill and J. L. Brédas, Phys. Rev. Lett., 2002, 89, 275503 CrossRef CAS PubMed.
- T. Schneider, F. Limberg, K. Yao, A. Armin, N. Jurgensen, J. Czolk, B. Ebenhoch, P. Friederich, W. Wenzel, J. Behrends, H. Kruger and A. Colsmann, J. Mater. Chem. C, 2017, 5, 770–776 RSC.
- E. V. Tsiper and Z. G. Soos, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195124 CrossRef.
- J. M. Sin, E. V. Tsiper and Z. G. Soos, Europhys. Lett., 2002, 60, 743 CrossRef CAS.
- S. M. Ryno, S. R. Lee, J. S. Sears, C. Risko and J.-L. Brédas, J. Phys. Chem. C, 2013, 117, 13853–13860 CrossRef CAS.
- H. Yoshida, K. Yamada, J. Tsutsumi and N. Sato, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075145 CrossRef.
- M. Schwarze, W. Tress, B. Beyer, F. Gao, R. Scholz, C. Poelking, K. Ortstein, A. A. Gunther, D. Kasemann, D. Andrienko and K. Leo, Science, 2016, 352, 1446–1449 CrossRef CAS PubMed.
- C. Poelking and D. Andrienko, J. Chem. Theory Comput., 2016, 12, 4516–4523 CrossRef CAS PubMed.
- The localization of the hole on one NPB molecule is here assumed given the disordered nature of the medium. Intramolecular nuclear degrees of freedom further drive hole localization also in ordered systems.
- T. Siegrist, C. Kloc, J. H. Schön, B. Batlogg, R. C. Haddon, S. Berg and G. A. Thomas, Angew. Chem., Int. Ed., 2001, 40, 1732–1736 CrossRef CAS PubMed.
- J.-A. Cheng and P.-J. Cheng, J. Chem. Crystallogr., 2010, 40, 557–560 CrossRef CAS.
- T. J. Emge, M. Maxfield, D. O. Cowan and T. J. Kistenmacher, Mol. Cryst. Liq. Cryst., 1981, 65, 161–178 CrossRef CAS.
- M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. V. Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- I. Duchemin, J. Li and X. Blase, J. Chem. Theory Comput., 2017, 13, 1199–1208 CrossRef CAS PubMed.
- G. D'Avino, D. Vanzo and Z. G. Soos, J. Chem. Phys., 2016, 144, 034702 CrossRef PubMed.
- B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- T. Neumann, D. Danilov, C. Lennartz and W. Wenzel, J. Comput. Chem., 2013, 34, 2716–2725 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1859755. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8mh00921j |
| ‡ Present address: Harvard University, Department of Chemistry CV 23, 12 Oxford Street, Cambridge, MA 02138, USA. |
| This journal is © The Royal Society of Chemistry 2019 |