 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Residence times of nanoconfined CO2 in layered aluminosilicates†
Merve
Yeşilbaş
 *,
Michael
Holmboe
and
Jean-François
Boily
*,
Michael
Holmboe
and
Jean-François
Boily
 *
*
Department of Chemistry, Umeå University, SE-901 87, Umeå, Sweden. E-mail: merve.yesilbas@umu.se; jean-francois.boily@umu.se; Tel: +46 722 19 5760
First published on 5th November 2018
Abstract
Nanoconfinement of CO2 in layered aluminosilicates contributes to the capture and release of this greenhouse gas in soils. In this work, we show that the residence times of CO2 in montmorillonite are lowered by 15 min for each 1 °C increment in temperature during venting. Molecular simulations showed that activation energies of release are no more than half of the experimentally derived value of 34 kJ mol−1. This raised the possibility of additional processes limiting CO2 mobility in real materials, including (chemi)sorption at reactive sites or frayed edges or defects. The residence times (∼1616 min at −50 °C to ∼6 min at 60 °C) for some of the driest (∼1.4 mmol H2O per g) montmorillonites that can be produced at ambient temperatures are readily lowered by inclusion of additional water. They are, in turn, prolonged again as the water content and interlayer spacing become smaller through venting. These efforts showed that soil-building clay minerals will lose their propensity to dynamically exchange CO2 as temperatures continue to rise, yet they may retain CO2 more efficiently in cold seasons as soils will become depleted in moisture content.
Environmental significanceDynamic exchange of atmospheric CO2 with terrestrial environments includes important contributions from nanometer-thick interlayer regions of clay nanominerals. With the aim of understanding how global warming will impact soil CO2 exchanges in the forthcoming decades, we resolved the lifetimes of this greenhouse gas under nanoconfinement in montmorillonite, a representative soil-building clay nanomineral. Our study shows that montmorillonite will lose its propensity to dynamically exchange CO2 as soil temperatures continue to rise, yet it may retain CO2 more efficiently in cold seasons if soils become depleted in moisture content. This study thus shines new light on the important roles that nanoparticles play in the progressively shifting biogeochemical and hydrogeological cycles of soils under a warming climate. |
Introduction
Layered aluminosilicate minerals play important roles in technology and nature due to their tremendous solute and solvent exchange capacities. Those of the expandable type can readily confine gases between nanometer-thick interlamellar layers. Exchanges between these materials and CO2 are under increasing scrutiny to follow the fate of this greenhouse gas in soils and for its deep geological storage. In particular, thawing of soils of the cryosphere is of great concern as mineral-bound and newly bio-respired CO2 are expected to be released into the atmosphere over the next few decades.1–3 Along these lines, a 2018 report4 by the Intergovernmental Panel on Climate Change highlights the devastating impact that a 1.5 °C hike in global warming could have by the end of the century.The positive feedback to a CO2-driven warming climate is of particular concern given that frozen soils contain about one-third of Earth's soil carbon, and that all soils contain about three times more carbon than the atmosphere.5 Understanding how global warming will alter land–air exchanges requires knowledge of the ability of soil-building minerals to dynamically exchange CO2 with the atmosphere as soils begin to thaw. This is central to our ability to evaluate possibilities for geological storage of CO2.
A primary focus on common soil-building swelling clay minerals is central because this important class of phyllosilicates entraps CO2 between nanometre-thick layers of negatively charged aluminosilicate layers (Fig. 1).6–11 CO2 molecules are intercalated with their main axis parallel to the basal face (Fig. 1), either as dimers or as part of the hydration shell of interlayer cations (e.g. sodium).12–14 Studies9,15–20 under supercritical CO2 conditions show that humidity facilitates uptake, and that the greatest loadings are achieved with interlayers populated with ∼1 monolayer (1W) of water. Less CO2 can be stored at greater humidity as thicker water interlayers (>1W) suppress cation–CO2 and CO2–CO2 interactions.12 Additionally, other studies21,22 under environmentally relevant conditions show that very high CO2 pressures and prolonged exposure times are required to intercalate CO2 in dehydrated clays. Seasonal and climatic variations in moisture levels – from wet to dry and from warm to cold – should therefore exert important changes in the dynamic exchanges of CO2 with soil-building clay minerals. This can have especially important implications on the loadings and isotopic signatures of soil inorganic carbon.23,24
To address this issue, we measured the rates of CO2 release from the interlayer of montmorillonite (MMT), a representative soil-building swellable clay mineral. The rates were calculated from time-resolved vibration spectra of CO2 released by venting dry and hydrated MMT over a range of temperatures well covering those of the cryosphere up to the warmest regions of the planet. Molecular simulations provided the insight needed to explain molecular interactions controlling CO2 mobility in the interlayer region. In this study we suggest that the dynamic breathing25 of CO2 by clays will be attenuated by warming soils.
Results and discussion
CO2 was intercalated in the interlayer of MMT upon exposure to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm CO2, a representative amount in high CO2 soils.26,27 To uncover the intrinsic abilities of MMT to dynamically exchange CO2, intercalation was first carried out on MMT with the lowest levels of water that can be achieved after a 30 min period of outgassing in vacuo. We note that all final water loadings were no more than 26 mg H2O per g MMT (∼1.4 mmol H2O per g), which is equivalent to (i) ∼23% of a 1W (∼112 mg H2O per g MMT)28 or (ii) ∼1.6 H2O per interlayer Na+ if water is homogeneously distributed throughout the particles (cf. ESI† for details and Fig. S1–S5). This hydration level can therefore be regarded as one of the lowest that could be achieved by MMT in dry air at ambient temperatures. Additionally, it is responsible for maintaining a partially opened interlayer region needed to intercalate CO2. The expanded interlayer of our samples was confirmed via mixed layer modelling of X-ray diffraction data, as discussed in the ESI† (Fig. S5).
000 ppm CO2, a representative amount in high CO2 soils.26,27 To uncover the intrinsic abilities of MMT to dynamically exchange CO2, intercalation was first carried out on MMT with the lowest levels of water that can be achieved after a 30 min period of outgassing in vacuo. We note that all final water loadings were no more than 26 mg H2O per g MMT (∼1.4 mmol H2O per g), which is equivalent to (i) ∼23% of a 1W (∼112 mg H2O per g MMT)28 or (ii) ∼1.6 H2O per interlayer Na+ if water is homogeneously distributed throughout the particles (cf. ESI† for details and Fig. S1–S5). This hydration level can therefore be regarded as one of the lowest that could be achieved by MMT in dry air at ambient temperatures. Additionally, it is responsible for maintaining a partially opened interlayer region needed to intercalate CO2. The expanded interlayer of our samples was confirmed via mixed layer modelling of X-ray diffraction data, as discussed in the ESI† (Fig. S5).
CO2 intercalated in Na-exchanged MMT was readily identified through a single asymmetric band of the stretching mode (ν3) at 2343 cm−1 (Fig. 2a). The 2343 cm−1 band of CO2 in this MMT was most clearly seen once free gaseous and sorbed CO2 were evacuated from the clay (Fig. 2a and S6†). It was strongly comparable to that for supercritical CO2 in clays15,16 and in liquid29 or solid30,31 water, as well as in organic-based frameworks.32 The confining effects of the MMT interlayer on CO2 are also confirmed by the absence of rotational sidebands, which are typical of gaseous CO2 (Fig. 2a).33 The spectra provided no other evidence of changes in water content, (bi)carbonate formation or the formation of solid CO2 ice34 (Fig. S2†).
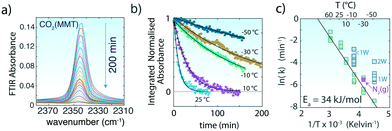 | ||
Fig. 2 (a) Asymmetric (ν3) stretching region of CO2 of MMT (∼0W) originally exposed to CO2(g) at −30 °C during the 200 min evacuation (<0.3 Pa). (b) Examples of loss of the normalized band area of the 2343 cm−1 band during evacuation of MMT originally exposed to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm CO2. Lines are generated from a first-order kinetic model. (c) Arrhenius plot of the first-order rate constants for the release of CO2 from the interlayer region of MMT with ∼0W. The release rate of CO2 resulting from evacuation with 101 kPa N2(g) is shown through the pink data point at −30 °C (see Fig. S4† for data and analysis). Enhanced release rates with ∼1W and 2W at −10 °C and −50 °C, respectively, are shown in turquoise. 000 ppm CO2. Lines are generated from a first-order kinetic model. (c) Arrhenius plot of the first-order rate constants for the release of CO2 from the interlayer region of MMT with ∼0W. The release rate of CO2 resulting from evacuation with 101 kPa N2(g) is shown through the pink data point at −30 °C (see Fig. S4† for data and analysis). Enhanced release rates with ∼1W and 2W at −10 °C and −50 °C, respectively, are shown in turquoise. | ||
Intercalated CO2 was systematically removed by prolonged exposure to vacuum, a means to simulate the action of venting on soils by displacing pore gases outside clay mineral particles. No or little changes in ∼1.4 mmol H2O per g interlayer water took place during CO2 release (Fig. S2†). While complete removal took place well within ∼10 min at 60 °C, it took a substantially longer time than the ∼20 min originally needed to intercalate CO2 at lower temperatures. Consequently, this provided a first level of indication pointing to molecular forces responsible for holding CO2 in the interlayer region.
The loss in area (a) of the 2343 cm−1 band with evacuation follows first-order reaction kinetics (ln(a/a0) = −kt, where a0 is the band area prior to venting and k is the reaction rate), confirming that the loss of CO2 from the interlayer region is predominantly a simple molecular desorption process (Fig. 2b). These rates revealed CO2 residence times (τ = 1/k) ranging from τ = ∼6 min at 60 °C to ∼1616 min at −50 °C. Additionally, these rates were unchanged when CO2 was vented by a flow of 101 kPa N2(g) instead of vacuum (Fig. 3).
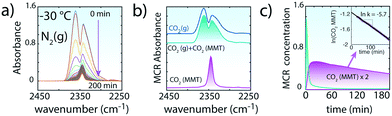 | ||
| Fig. 3 Evacuation of CO2 upon flushing of 200 sccm N2(g) to CO2-loaded MMT (∼0.1W) at −30 °C. (a) ν3 region of CO2 during the ∼200 min evacuation period. In contrast to in vacuo removal, gaseous CO2 lingers over ∼60 min in the reaction cell as MMT-bound CO2 begins to be released to the atmosphere. The strong overlap between the spectra of free CO2(g) and intercalated CO2 required a multivariate curve resolution alternating least squares (MCR, version 2004)35 analyses. (b) MCR spectral components for CO2(g) + CO2(MMT) and CO2(MMT). (c) Concentration profiles of MCR-ALS components of (b). The values of CO2(MMT) were used to estimate the first-order rate constant for the evacuation of CO2 from MMT by N2(g). | ||
The temperature dependence of these rate constants obeys the Arrhenius relationship (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = ln
k = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A + Ea/RT), with an activation energy of Ea = 34 kJ mol−1 (Fig. 2c). This value is ∼2.3 times larger than the one estimated for site-hopping of CO2 within the interlayer13 but is most comparable to experimental desorption activation energies from bridged-bonded oxygens on TiO2 (ref. 36) and on Mg2SiO4 (∼30–40 kJ mol−1).37 We note that the pre-exponential factor (A = 3.8 × 104 min−1) is seven to nine orders of magnitude lower than typical values for in vacuo desorption of CO2 from open mineral surfaces.36,37 We ascribe this difference to the effects of interlayer confinement, which is expected to decrease the frequency of desorption events.
A + Ea/RT), with an activation energy of Ea = 34 kJ mol−1 (Fig. 2c). This value is ∼2.3 times larger than the one estimated for site-hopping of CO2 within the interlayer13 but is most comparable to experimental desorption activation energies from bridged-bonded oxygens on TiO2 (ref. 36) and on Mg2SiO4 (∼30–40 kJ mol−1).37 We note that the pre-exponential factor (A = 3.8 × 104 min−1) is seven to nine orders of magnitude lower than typical values for in vacuo desorption of CO2 from open mineral surfaces.36,37 We ascribe this difference to the effects of interlayer confinement, which is expected to decrease the frequency of desorption events.
In another set of experiments, CO2 removal rates were tracked in MMT containing interlayer water at −10 °C and −50 °C (Fig. 4). The rates were generally 2–4 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k larger than in ∼1.4 mmol H2O per g but were also strongly coupled to the stability of interlayer water (Fig. 4b and c), which we estimate here from the O–H stretching region of water, as explained in Fig. 4 and S8.† The loss of water in 1W-bearing MMT at −10 °C was rapid within the first ∼10 min (τ = 14 min) but then slowed considerably after ∼40 min of evacuation (τ = 1213 min) (Fig. S9†). CO2 evacuation rates followed accordingly, as highlighted by the instantaneous rates shown in Fig. 4a. In contrast, higher loadings of interlayer water were retained over longer time periods at −50 °C (Fig. 4c). High CO2 removal rates were therefore maintained under extended periods of venting.
k larger than in ∼1.4 mmol H2O per g but were also strongly coupled to the stability of interlayer water (Fig. 4b and c), which we estimate here from the O–H stretching region of water, as explained in Fig. 4 and S8.† The loss of water in 1W-bearing MMT at −10 °C was rapid within the first ∼10 min (τ = 14 min) but then slowed considerably after ∼40 min of evacuation (τ = 1213 min) (Fig. S9†). CO2 evacuation rates followed accordingly, as highlighted by the instantaneous rates shown in Fig. 4a. In contrast, higher loadings of interlayer water were retained over longer time periods at −50 °C (Fig. 4c). High CO2 removal rates were therefore maintained under extended periods of venting.
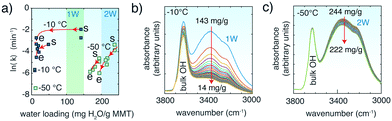 | ||
Fig. 4 CO2 release in MMT with 10–15 mg H2O per g MMT and 1W at −10 °C and 2W at −50 °C over ∼60 min reaction time. MMT was previously loaded at the same water loadings with 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm at −50 °C for ∼20 min. (a) Rate constants for CO2 release. Instantaneous rates (red lines) were obtained by the first derivative of a 2nd-order polynomial function of ln(area) versus t of data (see Fig. S7† for examples). Arrows show the direction of the change in rate as water is removed from the interlayer region, from the start (‘s’) to the end (‘e’) of the evacuation period. Interlayer water loadings are estimated from the time dependence of the O–H stretching band intensities during evacuation of CO2-loaded MMT at (b) −10 °C and (c) −50 °C. See section 1 of the ESI† and Fig. S8 and S9 for details. 000 ppm at −50 °C for ∼20 min. (a) Rate constants for CO2 release. Instantaneous rates (red lines) were obtained by the first derivative of a 2nd-order polynomial function of ln(area) versus t of data (see Fig. S7† for examples). Arrows show the direction of the change in rate as water is removed from the interlayer region, from the start (‘s’) to the end (‘e’) of the evacuation period. Interlayer water loadings are estimated from the time dependence of the O–H stretching band intensities during evacuation of CO2-loaded MMT at (b) −10 °C and (c) −50 °C. See section 1 of the ESI† and Fig. S8 and S9 for details. | ||
Theoretical calculations of CO2 diffusion in the interlayer region of Na-exchanged MMT added further insight into the mechanisms affecting the removal of CO2 during venting (Fig. 5) (for basal spacing data, see Fig. S9–S11†). First, we note that simulations confirmed previous findings19,20 showing that oxygen atoms of CO2 at low hydration levels predominantly lie in the middle of the interlayer, with one oxygen atom above Si tetrahedra and the other over ditrigonal cavities (Fig. 1). The carbon atom interacts predominantly with the basal oxygens sharing a Si-tetrahedral edge, or occasionally with a corner sharing tetrahedral oxygen when CO2 oxygen atoms are positioned over two corner-sharing Si tetrahedra. Under completely dehydrated conditions (0W), CO2 molecules remain in the middle of the interlayer nanopore, but with oxygen atoms coordinating to Na+, which is often in ditrigonal cavities of the basal plane adjacent to sites of isomorphic substitution. Simulations also suggest that large CO2 loadings favour dimers and clusters with a slipped plane parallel coordination.13 However, no such configurations could be unambiguously ascertained in the vibrational spectra (Fig. 2a) because of the strong overlap of the main 2343 cm−1 band with those of dimers.38,39
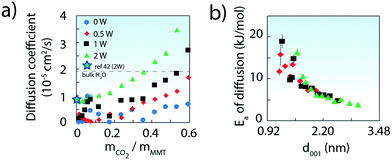 | ||
| Fig. 5 a) Computed diffusion coefficients of CO2 in the interlayer region of MMT (25 °C). Values from bulk water (ref. 40) and from a comparable MD simulation of MMT at low CO2 loadings (ref. 42) are also shown. (b) Activation energies (Ea) with d-spacing. Values were obtained from the Arrhenius relationship of diffusion coefficients obtained by molecular dynamics simulations from −10 to 50 °C. | ||
Simulated CO2 diffusion coefficients (Fig. 5a and S10†) were as small as 10% of bulk H2O values40,41 at both low CO2 and H2O loadings. Values were however greatly enhanced at larger CO2 loadings, or by intercalation of greater populations of water (see full results in Tables S1–S5†). We note that our 2W value at low CO2 loadings falls in line with another simulated value42 in 2W MMT.
Activation energies for diffusion (Ea), obtained by the Arrhenius relationship to computed diffusion coefficients, were also strongly loading dependent. Values were as large as ∼15–20 kJ mol−1 at the lowest CO2 loadings, and down to ∼5 kJ mol−1 above 0.4 g CO2 per g MMT (Fig. S12†). Expressed on a d-spacing basis, the trend of Fig. 5 denotes a decrease in Ea of ∼4–6 kJ mol−1 per nanometer of interlayer expansion, irrespective of water loading. Expansion of the interlayer region, which can result from gains in both CO2 and water, therefore shortens the energetic threshold of CO2 removal during venting.
Finally, we note that the calculated Ea values are in line with previously estimated energies with site-hopping values on clays,13 and yet are no more than 50–60% of our experimentally derived value of 34 kJ mol−1. This latter difference could point to more convoluted processes limiting the interlayer mobility of CO2 in real materials. For instance, contributions from clay particle packing motifs, frayed particle edges,43 internal defects or chemisorption could have contributed to these differences. Resolution of these and related phenomena should add further insight needed in predicting gaseous exchange involving natural soil-building materials.
Conclusions
Atmospheric exchanges of CO2 with MMT are strongly affected by water content and temperature. MMT with low levels of resilient interlayer water (up to ∼1.4 mmol H2O per g) stored CO2 with residence times as long as ∼1616 min at −50 °C to ∼6 min at 60 °C. The activation energy for the release of CO2 is 34 kJ mol−1, and thus at least twice that expected from theoretical simulations on idealised MMT.Our results suggest that as even the driest soils thaw under a warming climate, we should expect a decrease in the residence times of CO2 of ∼15 min for each 1 °C rise in temperature. These residence times are even shorter under conditions of stable interlayer water, and especially below −10 °C, where smaller release rates of water promote CO2 release by maintaining a large interlayer spacing in MMT. Residence times will nonetheless continue to be longer than in the warmest regions of the planet. However, considering the vast quantities of carbon stored in cold terrestrial environments, these accelerated rates are likely to result in important shifts in land–air fluxes of CO2.
Consequently, this work suggests that exposure of CO2-bearing soil clay minerals to increasingly longer periods of thawing will accelerate fluxes of CO2 to the atmosphere. Conversely, exposure to cold and dry periods will increase the residence time of CO2 in soils. Given that soil warming of the planet's cold regions is expected to be faster in the winter than in the summer months,44 wintertime venting of soil CO2 will likely be an increasing contributor to terrestrial emissions of CO2 to the atmosphere in the years to come.
Experimental section
Materials
The MMT was Wyoming clay powder (SWy-2) obtained from the Clay Mineral Repository. A portion of this clay was Na-exchanged, as detailed by Schaef et al.45 The Brunauer–Emmett–Teller specific surface area (25.3 m2 g−1) was calculated from 90-point adsorption/desorption N2 gas isotherms (Micromeritics). X-ray photoelectron spectroscopy (Kratos Axis Ultra DLD electron spectrometer) was used to detect the surface compositions of Na-exchanged MMT (Na/Fe/Mg/Al/Si/O = 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.3
2.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.8) and to confirm that the particles were free of impurities, other than adventitious forms of atmospheric carbon at the 285.0 eV line.
7.8) and to confirm that the particles were free of impurities, other than adventitious forms of atmospheric carbon at the 285.0 eV line.
Fourier transform infrared spectroscopy (FTIR)
Aqueous suspensions of MMT of 25 g L−1 in deionized water (18.2 MΩ cm) were equilibrated for 30 min and then centrifuged at ∼2000g for 10 min. The top-to-middle portion of the centrifuged wet paste was sampled to avoid accessory minerals and then applied as a thin layer on a fine tungsten mesh (Unique wire weaving, 0.002′′ mesh diameter). Then, it was dried under N2(g) overnight, and the mass (7–8 mg) of the resulting dry MMT film was determined. Next, the dried sample–tungsten support assembly was inserted into an electrically heated or N2(l)-cooled copper shaft connected to a K-type thermocouple used to monitor temperature. The shaft was thereafter inserted into a transmission optical gas reaction chamber (AABSPEC #2000-A) equipped with CaF2 windows.The sample was dried further in vacuo (<0.3 Pa, the detection limit of the capacitance manometer; MKS, Baratron) in the reaction chamber for 30 min at 25 °C to remove atmospheric gases bound to the materials (Fig. S1†). Next, the sample was either heated or cooled to reach the desired temperature in this study (−50 °C, −30 °C, −10 °C, 10 °C, 25 °C, and 60 °C; experiments at 95 °C and 135 °C were abandoned due to excessively high rates of CO2 release). Then, the sample was equilibrated for another 30 min. During this time, residual water contents were monitored through the O–H stretching (∼3250 cm−1) and water bending (∼1630 cm−1) bands. The water content in the clay was quantified using the ratio of the intensities of the 1630 cm−1 (ν3 from interlayer water) and the 1850 cm−1 combination band (Si–O stretch of MMT + OH deformation),46,47 using the water vapor binding data from Yeşilbaş et al.28 A Matlab (The MathWorks, Inc.) code using this strategy is given in Table S6.†
CO2 was intercalated in the samples upon exposure to a flow of 200 square cubic centimetres per minute (sccm) of ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm CO2. This gas mixture was prepared by mixing a 7 sccm flow of pure CO2(g) with 193 sccm dry N2(g) and controlled by mass-flow controllers (MKS, Baratron). A non-dispersible infrared device (Li-7000, Licor, Inc.) was used to continuously monitor the partial pressures of CO2(g) and to ensure that the gases were free of H2O(g). Removal of intercalated CO2 was then observed as a function of time through the asymmetric C–O stretching band (ν3) at 2343 cm−1 upon evacuation of the reaction cell (<0.3 Pa). Repeated sessions of intercalation and evacuation showed that an exposure time of ∼20 min was sufficient to maximize the 2343 cm−1 band. One experiment at −30 °C involved CO2 removal by flushing with 200 sccm N2(g).
000 ppm CO2. This gas mixture was prepared by mixing a 7 sccm flow of pure CO2(g) with 193 sccm dry N2(g) and controlled by mass-flow controllers (MKS, Baratron). A non-dispersible infrared device (Li-7000, Licor, Inc.) was used to continuously monitor the partial pressures of CO2(g) and to ensure that the gases were free of H2O(g). Removal of intercalated CO2 was then observed as a function of time through the asymmetric C–O stretching band (ν3) at 2343 cm−1 upon evacuation of the reaction cell (<0.3 Pa). Repeated sessions of intercalation and evacuation showed that an exposure time of ∼20 min was sufficient to maximize the 2343 cm−1 band. One experiment at −30 °C involved CO2 removal by flushing with 200 sccm N2(g).
All FTIR spectra of the samples were collected in transmission mode using a Bruker Vertex 70/v FTIR spectrometer equipped with a DLaTGS detector. The FTIR spectra were collected in the spectral range of 600–4000 cm−1 at 4 cm−1 resolution with a 10 Hz forward/reverse scanning rate. We used the Blackman–Harris three-term apodisation function with 16 cm−1 phase resolution and the Mertz phase correction algorithm. Each spectrum was obtained from 100 co-added spectra and collected over an 89 s period.
Chemometrics
Multivariate curve resolution alternating least squares (MCR, version 2004)35 was used to separate strongly overlapping bands of free and MMT-bound CO2. MCR applies the Beer–Lambert law (A = εC) to extract the spectral components (ε ≥ 0) and their correlated concentrations (C ≥ 0) from a sequence of experimental absorbance (A). Calculations were performed in the computational environment of Matlab (The MathWorks, Inc.)Molecular dynamics
Molecular dynamics simulations of CO2-intercalated and hydrated Na+–MMT systems were modelled with the MD package Gromacs 2016.3.48 Simulation cells consisted of 4 × 6 × 3 MMT unit cells with the average structural formula Na0.66(Al3.33Mg0.66)(Si8O20)OH4, corresponding to a structural charge of −0.11 C m−2, a value typical for Wyoming montmorillonites.The CLAYFF19,49 force field, modified with a Morse potential for O–H vibrations,50 was used to model clay minerals, and a flexible EPM2 model19 was used to treat CO2 molecules. Na+ was modelled with the pair potentials originally optimized for the SPC/E water model.51 In this study, however, water was modelled with a flexible SPC water model.52 The harmonic and anharmonic terms of this model have better dielectric, vibrational and diffusive properties compared to the SPC water model used in the original parameterization of CLAYFF. CO2 or H2O removal from the interlayer region was mimicked through a custom-made simulation protocol allowing simulation systems to automatically generate sequentially reduced loadings. This was achieved by removing either CO2 or H2O molecules between production runs. Systems of fixed water populations (0–2W) were simulated with varying CO2 content (0–10 molecules per unit cell; 0.5 gCO2 gclay−1). Systems denoting 1.5 CO2 and 3.0 CO2 contained a fixed amount of 1.5 and 3.0 CO2 molecules per MMT unit cell, and were simulated as a function of water loading by varying between 0 and 20 water molecules per MMT unit cell (0.6 gwater gclay−1).
The initial configurations with maximum loadings were equilibrated by energy minimization, a 50 ps solute restrained simulation under NVT conditions, followed by 5 ns of volume optimization under fixed NPT conditions. The production runs were performed under fixed NPT conditions for 5 ns with a 0.5 fs time step and preceded by a short equilibration step of 100 ps between the evaporative steps. Selected configurations were also simulated for an additional 10 ns using a 1 fs time step under fixed NVT conditions and individual thermostating, in order to obtain diffusion coefficients at −10 °C, 10 °C, 25 °C and 50 °C. The simulation results were analysed by computing density maps, radial distribution functions, and diffusion coefficients from the mean square displacement.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the insightful comments of three anonymous reviewers on an earlier version of this manuscript. This work was supported by the Swedish Research Council (2016-03808). The authors thank Eugene Ilton and Odeta Qafoku (Pacific Northwest National Laboratory) for providing the MMT samples used in this study, and the Swedish National Infrastructure for Computing (SNIC) for access to the computational facilities at the High Performance Computer Center North (HPC2N) of Umeå University and the PDC Center for High Performance Computing at KTH.Notes and references
- D. G. Kim, R. Vargas, B. Bond-Lamberty and M. R. Turetsky, Biogeosciences, 2012, 9, 2459–2483 CrossRef CAS.
- B. Elberling, A. Michelsen, C. Schadel, E. A. G. Schuur, H. H. Christiansen, L. Berg, M. P. Tamstorf and C. Sigsgaard, Nat. Clim. Change, 2013, 3, 890–894 CrossRef CAS.
- E. A. G. Schuur, A. D. McGuire, C. Schädel, G. Grosse, J. W. Harden, D. J. Hayes, G. Hugelius, C. D. Koven, P. Kuhry, D. M. Lawrence, S. M. Natali, D. Olefeldt, V. E. Romanovsky, K. Schaefer, M. R. Turetsky, C. C. Treat and J. E. Vonk, Nature, 2015, 520, 171 CrossRef CAS PubMed.
- IPCC, Global Warming of 1.5 °C, 2018 Search PubMed.
- S. A. Zimov, E. A. G. Schuur and F. S. Chapin, Science, 2006, 312, 1612–1613 CrossRef CAS PubMed.
- E. Sendula, M. Páles, B. P. Szabó, B. Udvardi, I. Kovács, P. Kónya, Á. Freiler, A. Besnyi, C. Király, E. Székely, C. Szabó and G. Falus, Energy Procedia, 2017, 114, 4934–4947 CrossRef CAS.
- J. J. Fripiat, M. I. Cruz, B. F. Bohor and J. Thomas Jr., Clays Clay Miner., 1974, 22, 22–30 CrossRef.
- L. Michels, J. O. Fossum, Z. Rozynek, H. Hemmen, K. Rustenberg, P. A. Sobas, G. N. Kalantzopoulos, K. D. Knudsen, M. Janek, T. S. Plivelic and G. J. da Silva, Sci. Rep., 2015, 5, 8775 CrossRef CAS PubMed.
- Q. Rao and Y. Leng, J. Phys. Chem. C, 2016, 120, 2642–2654 CrossRef CAS.
- G. Rother, E. S. Ilton, D. Wallacher, T. Hauβ, H. T. Schaef, O. Qafoku, K. M. Rosso, A. R. Felmy, E. G. Krukowski, A. G. Stack, N. Grimm and R. J. Bodnar, Environ. Sci. Technol., 2013, 47, 205–211 CrossRef CAS PubMed.
- P. R. Jeon, J. Choi, T. S. Yun and C. H. Lee, Chem. Eng. J., 2014, 255, 705–715 CrossRef CAS.
- G. M. Bowers, H. T. Schaef, J. S. Loring, D. W. Hoyt, S. D. Burton, E. D. Walter and R. J. Kirkpatrick, J. Phys. Chem. C, 2017, 121, 577–592 CrossRef CAS.
- M. M. Sena, C. P. Morrow, R. J. Kirkpatrick and M. Krishnan, Chem. Mater., 2015, 27, 6946–6959 CrossRef CAS.
- J. J. Fripiat, in Clays and Clay Minerals: Proceedings of the Twelfth National Conference on Clays and Clay Minerals, Atlanta, Georgia, September 30, October 2, 1963, ed. W. F. Bradley, N. A. o. S. C. o. C. Minerals and N. R. Council, Symposium Publications Division. Pergamon Press, 1964 Search PubMed.
- J. S. Loring, E. S. Ilton, J. Chen, C. J. Thompson, P. F. Martin, P. Bénézeth, K. M. Rosso, A. R. Felmy and H. T. Schaef, Langmuir, 2014, 30, 6120–6128 CrossRef CAS PubMed.
- J. S. Loring, H. T. Schaef, R. V. F. Turcu, C. J. Thompson, Q. R. S. Miller, P. F. Martin, J. Hu, D. W. Hoyt, O. Qafoku, E. S. Ilton, A. R. Felmy and K. M. Rosso, Langmuir, 2012, 28, 7125–7128 CrossRef CAS PubMed.
- H. T. Schaef, J. S. Loring, V.-A. Glezakou, Q. R. S. Miller, J. Chen, A. T. Owen, M.-S. Lee, E. S. Ilton, A. R. Felmy, B. P. McGrail and C. J. Thompson, Geochim. Cosmochim. Acta, 2015, 161, 248–257 CrossRef CAS.
- H. T. Schaef, N. Loganathan, G. M. Bowers, R. J. Kirkpatrick, A. O. Yazaydin, S. D. Burton, D. W. Hoyt, K. S. Thanthiriwatte, D. A. Dixon, B. P. McGrail, K. M. Rosso, E. S. Ilton and J. S. Loring, ACS Appl. Mater. Interfaces, 2017, 9, 36783–36791 CrossRef CAS PubMed.
- R. T. Cygan, V. N. Romanov and E. M. Myshakin, J. Phys. Chem. C, 2012, 116, 13079–13091 CrossRef CAS.
- V. N. Romanov, Int. J. Greenhouse Gas Control, 2013, 14, 220–226 CrossRef CAS.
- L. Michels, J. O. Fossum, Z. Rozynek, H. Hemmen, K. Rustenberg, P. A. Sobas, G. N. Kalantzopoulos, K. D. Knudsen, M. Janek, T. S. Plivelic and G. J. da Silva, Sci. Rep., 2015, 5, 9 Search PubMed.
- H. Hemmen, L. R. Alme, J. O. Fossum and Y. Meheust, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 11 CrossRef PubMed.
- E. Webb Elizabeth, A. G. Schuur Edward, M. Natali Susan, L. Oken Kiva, R. Bracho, P. Krapek John, D. Risk and R. Nickerson Nick, J. Geophys. Res.: Biogeosci., 2016, 121, 249–265 CrossRef.
- S. A. Sistla, J. C. Moore, R. T. Simpson, L. Gough, G. R. Shaver and J. P. Schimel, Nature, 2013, 497, 615–618 CrossRef CAS PubMed.
- S. Ishihara, P. Sahoo, K. Deguchi, S. Ohki, M. Tansho, T. Shimizu, J. Labuta, J. P. Hill, K. Ariga, K. Watanabe, Y. Yamauchi, S. Suehara and N. Iyi, J. Am. Chem. Soc., 2013, 135, 18040–18043 CrossRef CAS PubMed.
- D. Sotomayor and C. W. Rice, J. Environ. Qual., 1999, 28, 784–793 CrossRef CAS.
- C. Kammann, L. Grunhage and H. J. Jager, Eur. J. Soil Sci., 2001, 52, 297–303 CrossRef CAS.
- M. Yeşilbaş, M. Holmboe and J.-F. Boily, ACS Earth Space Chem., 2018, 2, 38–47 CrossRef.
- T. Schadle, B. Pejcic and B. Mizaikoff, Anal. Methods, 2016, 8, 756–762 RSC.
- O. Galvez, B. Mate, V. J. Herrero and R. Escribano, Icarus, 2008, 197, 599–605 CrossRef CAS.
- M. G. Trainer, M. A. Tolbert, C. P. McKay and O. B. Toon, Icarus, 2010, 206, 707–715 CrossRef CAS.
- K. L. Kauffman, J. T. Culp, A. Goodman and C. Matranga, J. Phys. Chem. C, 2011, 115, 1857–1866 CrossRef CAS.
- P. E. Martin and E. J. Barker, Phys. Rev., 1932, 41, 209–303 Search PubMed.
- K. Isokoski, C. A. Poteet and H. Linnartz, Astron. Astrophys., 2013, 555, 6 CrossRef.
- J. Jaumot, R. Gargallo, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2005, 76, 101–110 CrossRef CAS.
- R. S. Smith, Z. J. Li, L. Chen, Z. Dohnalek and B. D. Kay, J. Phys. Chem. B, 2014, 118, 8054–8061 CrossRef CAS PubMed.
- R. S. Smith, Z. J. Li, Z. Dohnalek and B. D. Kay, J. Phys. Chem. C, 2014, 118, 29091–29100 CrossRef CAS.
- J. Norooz Oliaee, M. Dehghany, M. Rezaei, A. R. W. McKellar and N. Moazzen-Ahmadi, J. Chem. Phys., 2016, 145, 174302 CrossRef CAS PubMed.
- M. A. Walsh, T. H. England, T. R. Dyke and B. J. Howard, Chem. Phys. Lett., 1987, 142, 265–270 CrossRef CAS.
- B. Jahne, G. Heinz and W. Dietrich, J. Geophys. Res.: Oceans, 1987, 92, 10767–10776 CrossRef.
- D. L. Wise and G. Houghton, Chem. Eng. Sci., 1966, 21, 999–1010 CrossRef CAS.
- G. Gadikota, B. Dazas, G. Rother, M. C. Cheshire and I. C. Bourg, J. Phys. Chem. C, 2017, 121, 26539–26550 CrossRef.
- J. Wan, T. K. Tokunaga, P. D. Ashby, Y. Kim, M. Voltolini, B. Gilbert and D. J. DePaolo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 873–878 CrossRef CAS PubMed.
- J. H. E. A. Chrisensen, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group 1 to the Fifth Assessment Report of the Intergovernmental Panel on Climate Changed, Press Cambridge, U.K., and New York, 2013 Search PubMed.
- H. T. Schaef, E. S. Ilton, O. Qafoku, P. F. Martin, A. R. Felmy and K. M. Rosso, Int. J. Greenhouse Gas Control, 2012, 6, 220–229 CrossRef CAS.
- M. Szczerba, A. Kuligiewicz, A. Derkowski, V. Gionis, G. D. Chryssikos and A. G. Kalinichev, Clays Clay Miner., 2016, 64, 452–471 CrossRef CAS.
- A. Kuligiewicz, A. Derkowski, M. Szczerba, V. Gionis and G. D. Chryssikos, Clays Clay Miner., 2015, 63, 15–29 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- R. T. Cygan, J. J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS.
- J. A. Greathouse, J. S. Durkin, J. P. Larentzos and R. T. Cygan, J. Chem. Phys., 2009, 130, 7 CrossRef PubMed.
- I. S. Joung and T. E. Cheatham, III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- D. M. Ferguson, J. Comput. Chem., 1995, 16, 501–511 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S11 and Tables S1–S6. See DOI: 10.1039/c8en01156g |
| This journal is © The Royal Society of Chemistry 2019 |

